第三章二自由度系统振动的理论及工程应用
合集下载
0727第三章 两自由度系统振动(讲)共20页文档
第三章 两自由度系统振动§3-1 概述单自由度系统的振动理论是振动理论的基础。
在实际工程问题中，还经常会遇到一些不能简化为单自由度系统的振动问题，因此有必要进一步研究多自由度系统的振动理论。
两自由度系统是最简单的多自由度系统。
从单自由度系统到两自由度系统，振动的性质和研究的方法有质的不同。
研究两自由度系统是分析和掌握多自由度系统振动特性的基础。
所谓两自由度系统是指要用两个独立坐标才能确定系统在振动过程中任何瞬时的几何位置的振动系统。
很多生产实际中的问题都可以简化为两自由度的振动系统。
例如，车床刀架系统（a ）、车床两顶尖间的工件系统（b ）、磨床主轴及砂轮架系统（c ）。
只要将这些系统中的主要结合面（或芯轴）视为弹簧（即只计弹性，忽略质量），将系统中的小刀架、工件、砂轮及砂轮架等视为集中质量，再忽略存在于系统中的阻尼，就可以把这些系统近似简化成图（d ）所示的两自由度振动系统的动力学模型。
以图3.1（c ）所示的磨床磨头系统为例分析，因为砂轮主轴安装在砂轮架内轴承上，可以近似地认为是刚性很好的，具有集中质量的砂轮主轴系统支承在弹性很好的轴承上，因此可以把它看成是支承在砂轮架内的一个弹簧——质量系统。
此外，砂轮架安装在砂轮进刀拖板上，如果把进刀拖板看成是静止不动的，而把砂轮架与进刀拖板的结合面看成是弹簧，把砂轮架看成是集中的质量，则砂轮架系统又近似地可以看成是支承在进刀拖板上的另一个弹簧——质量系统。
这样，磨头系统就可以近似地简化为图示的支承在进刀拖板上的两自由度系统。
在这一系统的动力学模型中，m 1是砂轮架的质量，k 1是砂轮架支承在进刀拖板上的静刚度，m 2是砂轮及其主轴系统的质量，k 2是砂轮主轴支承在砂轮架轴承上的静刚度。
取每个质量的静平衡位置作为坐标原点，取其铅垂位移x 1及x 2分别作为各质量的独立坐标。
这样x 1和x 2就是用以确定磨头系统运动的广义坐标。
(工程实际中两自由度振动系统) [工程实例演示]§3-2 两自由度系统的自由振动一、系统的运动微分方程（①汽车动力学模型）②以图3.2的双弹簧质量系统为例。
两自由度系统的振动
5.2
图5-5（a）表示两个摆长，质量相同的单摆，中间以弹簧相连，形成两自由度系统。
图5-5双摆拍振
取 、 表示摆的角位移，逆钟向转动为正，每个摆的受力如图5-5（b）。根据刚体绕定轴转动方程，当 、 角位移很小时，得到摆做微小振动的微分方程
,
用与前面类似的分析方法，得到系统的第一阶和第二阶固有频率为
(5-5)
保证式(5-5)具有非零解的充分必要条件是式(5-5)的系数行列式等于零，即
展开后为
(5-6)
式(5-6)唯一确定了频率 满足的条件，通常称为频率分程或特征方程。它是 的二次代数方程，它的两个特征根为
(5-7)
由于式(5-7)确定的 的两个正实根仅取决于系统本身的物理性质，与运动的初始条件无关，因此 称为系统的固有频率。较小的一个称为第一阶固有频率，较大的一个称为第二阶固有频率。
图5-9动力减振器系统中主系统的幅频特性曲线
5.6阻尼对强迫振动的影响
为了把问题简化，以上的分析都没有考虑系统的阻尼。本节以图5-10所示系统为例，讨论阻尼对两自由度系统受迫振动的影响。这个系统是在上节的动力减振器的两个质量块之间增加一个阻尼器而成。其运动微分方程为
(5-20)
仍只考虑稳态运动。若利用复指数形式，则激振力为 ，而稳态运动的形式为
解：（1）建立运动微分方程式
分别以两物体的平衡位置为坐标原点，取两物体离开其平衡位置的距离x1、x2为广义坐标，两物体沿x方向的受力图如图5-3(b)所示，它们的运动微分方程分别为
若写成(5-2)的标准形式，则
所以
解出， 。因此，系统的第一阶和第二阶固有频率为
（3）求主振型
将 、 分别代入式(5-26)，得
第
应用单自由度系统的振动理论，可以解决机械振动中的一些问题。但是，工程中有很多实际问题必须简化成两个或两个以上自由度，即多自由度的系统，才能描述其机械振动的主要特征。多自由度系统的振动特性与单自由度系统的振动特性有较大的差别，例如，有多个固有频率、主振型、主振动和多个共振频率等。本章主要介绍研究两自由度系统机械振动的基本方法。
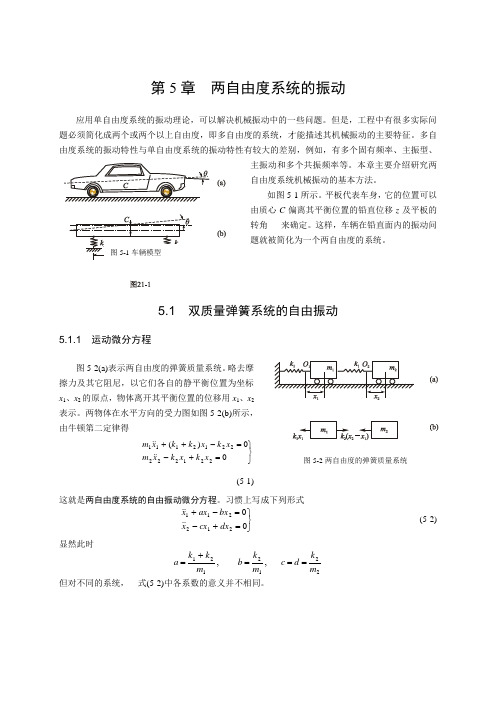
图5-5（a）表示两个摆长，质量相同的单摆，中间以弹簧相连，形成两自由度系统。
图5-5双摆拍振
取 、 表示摆的角位移，逆钟向转动为正，每个摆的受力如图5-5（b）。根据刚体绕定轴转动方程，当 、 角位移很小时，得到摆做微小振动的微分方程
,
用与前面类似的分析方法，得到系统的第一阶和第二阶固有频率为
(5-5)
保证式(5-5)具有非零解的充分必要条件是式(5-5)的系数行列式等于零，即
展开后为
(5-6)
式(5-6)唯一确定了频率 满足的条件，通常称为频率分程或特征方程。它是 的二次代数方程，它的两个特征根为
(5-7)
由于式(5-7)确定的 的两个正实根仅取决于系统本身的物理性质，与运动的初始条件无关，因此 称为系统的固有频率。较小的一个称为第一阶固有频率，较大的一个称为第二阶固有频率。
图5-9动力减振器系统中主系统的幅频特性曲线
5.6阻尼对强迫振动的影响
为了把问题简化，以上的分析都没有考虑系统的阻尼。本节以图5-10所示系统为例，讨论阻尼对两自由度系统受迫振动的影响。这个系统是在上节的动力减振器的两个质量块之间增加一个阻尼器而成。其运动微分方程为
(5-20)
仍只考虑稳态运动。若利用复指数形式，则激振力为 ，而稳态运动的形式为
解：（1）建立运动微分方程式
分别以两物体的平衡位置为坐标原点，取两物体离开其平衡位置的距离x1、x2为广义坐标，两物体沿x方向的受力图如图5-3(b)所示，它们的运动微分方程分别为
若写成(5-2)的标准形式，则
所以
解出， 。因此，系统的第一阶和第二阶固有频率为
（3）求主振型
将 、 分别代入式(5-26)，得
第
应用单自由度系统的振动理论，可以解决机械振动中的一些问题。但是，工程中有很多实际问题必须简化成两个或两个以上自由度，即多自由度的系统，才能描述其机械振动的主要特征。多自由度系统的振动特性与单自由度系统的振动特性有较大的差别，例如，有多个固有频率、主振型、主振动和多个共振频率等。本章主要介绍研究两自由度系统机械振动的基本方法。
机械振动学(第三章)-多自由度振动系统
装备制造学院
College of Equipment Manufacture
利用直接法，对下图所示的三自由度振动系统建立微分方程。。
装备制造学院
College of Equipment Manufacture
解：1）受力分析 选取 m1， m2和m3离开平衡位置的坐标x1， x2和 x3 为3 个独立 坐标。受力分析如图所示 2）建立振动微分方程 (c c ) x c x ( k k ) x k x p (t ) x m1： m 2 2 2 2 2 ( c 2 c 3 ) x 2 c2 x 1 c 3 x 3 ( k 2 k 3 ) x 2 k 2 x1 k 3 x 3 p 2 ( t ) x m2: m 2 2 2 2 3 c 3 x 3 c3 x 2 k 3 x3 k 3 x 2 p 3 (t ) x m3: m 3
装备制造学院
College of Equipment Manufacture
本章结束
装备制造学院 College of Equipment Manufacture
3 ）如果将应为能量耗散函数 D 引起的阻尼力也从其他的非势 力的广义力中分离出来，并使Qi仅代表外部作用的广义激振力， 则可将非保守系统的拉格朗日方程改为：
d dt ( T i q ) T i q U qi D i q Q i ( i 1, 2 , 3 ,...., n )
车 身 车 轮 二 自 由 度 振 动 问 题
装备制造学院
College of Equipment Manufacture
装备制造学院
College of Equipment Manufacture
振动力学(两自由度系统和多自由度系统)
两自由度是多自由度系统最简单的情况。
2
振动理论及应用
第3章 多自由度系统的振动
3.1 两自由度系统的振动方程 ——刚度矩阵和质量矩阵
建立运动微分方程的方法和单自由度系统基本一样, 但难 度更大。
3.1.1 运动微分方程
标准的m-k-c系统，对每一质量利用牛顿定律得：
3
振动理论及应用
坐标原点仍取在静平衡位置
具体求解时，只假设j坐标处的位移为1，其它各坐标的位 移均为0。
7
振动理论及应用
5.2.3 惯性影响系数与质量矩阵
第3章 多自由度系统的振动
质量矩阵[M]中的元素称为惯性（质量）影响系数，其 mij的力学意义是：仅在j坐标处产生单位广义加速度，需在i坐 标处施加的广义力。
具体求解时，只假设j坐标处的加速度为1，其它各坐标的 加速度均为0。
2
x1 5 kx1 5 kx2
V x2
2 5
kx1
1 5
kx2
26
振动理论及应用
第3章 多自由度系统的振动
计算广义力，设只有x1处产生虚位移x1，则
Q1
cx1 x1 x1
cx1
同样设x2处产生虚位移x2，则
Q2
c 0
x2
0
代入拉格朗日方程即可。
27
振动理论及应用
第3章 多自由度系统的振动
5l 3
48EI
k12
l3 3EI
k22
1
求出各个刚度系数即组 成刚度矩阵[K]。
17
振动理论及应用
第3章 多自由度系统的振动
用拉格朗日方程 建立振动系统的运动微分方程
对于非标准的m-k-c多自由度振动系统，用传统的动力学 方法建立运动微分方程比较困难，更适合使用拉格郎日方程和 能量的方法。拉格郎日方程为：
2
振动理论及应用
第3章 多自由度系统的振动
3.1 两自由度系统的振动方程 ——刚度矩阵和质量矩阵
建立运动微分方程的方法和单自由度系统基本一样, 但难 度更大。
3.1.1 运动微分方程
标准的m-k-c系统，对每一质量利用牛顿定律得：
3
振动理论及应用
坐标原点仍取在静平衡位置
具体求解时，只假设j坐标处的位移为1，其它各坐标的位 移均为0。
7
振动理论及应用
5.2.3 惯性影响系数与质量矩阵
第3章 多自由度系统的振动
质量矩阵[M]中的元素称为惯性（质量）影响系数，其 mij的力学意义是：仅在j坐标处产生单位广义加速度，需在i坐 标处施加的广义力。
具体求解时，只假设j坐标处的加速度为1，其它各坐标的 加速度均为0。
2
x1 5 kx1 5 kx2
V x2
2 5
kx1
1 5
kx2
26
振动理论及应用
第3章 多自由度系统的振动
计算广义力，设只有x1处产生虚位移x1，则
Q1
cx1 x1 x1
cx1
同样设x2处产生虚位移x2，则
Q2
c 0
x2
0
代入拉格朗日方程即可。
27
振动理论及应用
第3章 多自由度系统的振动
5l 3
48EI
k12
l3 3EI
k22
1
求出各个刚度系数即组 成刚度矩阵[K]。
17
振动理论及应用
第3章 多自由度系统的振动
用拉格朗日方程 建立振动系统的运动微分方程
对于非标准的m-k-c多自由度振动系统，用传统的动力学 方法建立运动微分方程比较困难，更适合使用拉格郎日方程和 能量的方法。拉格郎日方程为：
汽车振动学基础及应用课件：二自由度振动系统 -
x1 x2
2 i 1
r1i
xm
2,i
s
in(
ni
t
i
)
2 i 1
r1i
xm2,i
sin i
c os ni t
r1i
xm2,i
c os i
sin
ni t
2 i 1
C1,i
r1i
c
os
ni
t
C
2,i
r1i
s
in
ni
t
3.2無阻尼二自由度系統的振動
式中：C1,i xm2,i sin i , C2,i xm2,i cosi 是任意常數，由初始條件決定。
3.3 有阻尼二自由度振動系統
3.3.1對初始激勵的回應
當沒有激勵作用於二自由度阻尼系統時，式(3-3)變為以下形式：
M x Cx Kx 0
方程的通解為：x Aest 代入上式得：
(M s2 Cs K )A 0
A 有非零解的條件是： (M s2 Cs K) 0
展開得：M11M 22 s 4 (M11C22 M 22C11 )s3 (M11K 22 M 22 K11 C11C22 C122 )s 2 (C11K22 C22 K11 2C12 K12 )s K11K22 K122 0
振幅為 組，並將
和z10 ，z2則0 解為
z 1 z10 e j；t z 2 z20 e jt； 代入微分方程
k m2；02 k kt m1代t入2 上式，可得
(
0
2
(k /
2 m1 )z
)z
20
20
0 (t 2
2 z10
0 2 )z10
0
第3章二自由度振动
二自由度线性系统的强迫振动
我们只研究稳态振动，设微分方程组有简谐 振动的特解：
x1 x2
B1 sin t B2 sin tx1 x2源自B1 cost B2 cost
x1 x2
B1 2 sin t B2 2 sin t
将上式带入运动方程：
二自由度线性系统的强迫振动
得：
(a 2 cB1
m m e
m Jc
e
1
x
q
k
k1 2l4
k2 k1
l
3
k2l4
k
2
l
2 4
k1l3
k
1
l
2 3
x
q
0 0
动力耦合或惯性耦合
静力耦合或弹性耦合
第3章 多自由度线性系统的振动 3. 3 解耦与主坐标
坐标的耦合
动力耦合和静力耦合
广义坐标：x1，q 1
力和力矩平衡方程为
m x1 k1 ( x1l1 q 1 ) k2 ( x1 l2 q 1 ) 0
由于，这不是真实的振幅，而只是振幅的一个相对的
， 比频值率，作许振多动教时材的中两用个振幅1 相1211对 比值代；表两2 自1222由 ，度代系表统两以自n1
由度系统以n2频率作振动时的两个振幅相对比值。
二自由度自由振动
称{}1和{}2为特征向量、振型向量或模态向量。 固有频率和振型向量构成系统振动的固有模态的基本参 数，简称为模态参数。
二自由度线性系统的强迫振动
1、系统运动微分方程
m1x1 k1x1 m2x2 k2 (
x2
k2
( x2 x1 )
x1 0
)
P0
sin
t
振动理论及工程应用3 第三章 两自由度系统的振动
例3-1 试求图示两个自由度系统振动的固有频率和主
振型。已知m1= m2=m , k1= k3=k, k2= 4k，再求该系统对以下 两组初始条件的响应：（1）t＝0，x10＝1cm， x20＝0,
x&10 x&20 0（2） t＝0，x10＝1cm， x20＝-1cm, x10 x20 0
表示振动位移的两个以上坐标出现在同一个运动方程式 中时，就称这些坐标之间存在静力耦联或弹性耦联。
当一个微分方程式中出现两个以上的加速度项时，称为 在坐标之间有动力耦联或质量耦联.
静力与动力耦联
m ml1
ml1 J1
x1
k1 k
k2l
2
k2l k2l 2
(4)将初始条件（1）代入式，解得
x10 A1(1) sin 1 A1(2) sin 2 1 x20 1 A1(1) sin 1 2 A1(2) sin 2 0 x10 A1(1) p1 cos1 A1(2) p2 cos 2 0 x20 A1(1)1 p1 cos1 A1(2) 2 p2 cos 2 0
设
a k11 , m11
特征方程可写为
b k12 , m11
c k 21 , m22
d k 22 m22
p 4 (a d ) p 2 ad bc 0
特征方程的两组特征根
p12,2
a
d 2
a
2
d
2
(ad
bc)
a
d 2
a d 2 bc 2
系统的稳态响应。设特解为
二自由度系统
第3章 二自由度系统
3.3 不同坐标系下的运动微分方程 例：研究汽车上
下振动和俯仰振动 的力学模型 表示车体的刚性杆 AB的质量为m， 杆绕质心C的转动 惯量为Ic
A k
1
l
l2
l1 D C
B k
e
a
1
a
2
2
悬挂弹簧和前后轮胎的弹性用刚度为 k1 和 k2 的两个弹簧来表示
选取D点的垂直位移 xD和绕D点的角位移 D为坐标 写出车体微振动的微分方程
2
当θ 很小，有 对方程线性化
sin
cos 1
0 mgl x F (t ) 0
c 0 x k x M m ml ml 2 m l 0 0 0
26
第3章 二自由度系统
MD
A
PD
D C
B
D
xD
xC
k2 ( xD a2 D )
k1 ( xD a1 D )
d L L D ( ) 0 i qi q i dt q
或 Qi
Q1 PD
Q2 M D
第3章 二自由度系统
1 1 2 2 T m( xD e D ) I c D 2 2
其他非保守力
W F (t )* x
第3章 二自由度系统
•对广义坐标分别运用lagrange方程得
cos m l ( sin ) k xc x m ml F (t ) M x x
m l cos m g l sin 0 ml x
第3章 二自由度系统
振动微分方程的建立 （方法三：能量法） 先写出系统中动能ET，势能U及损耗能D的表达式， 便有：
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
� �
x1 x2
�0� � 0��
�a�
令
b
�
�12m2 �11m1
�
c
�
�21m1 �22m2
�
d
�
1�
�11m1
e
�
1
�22m2
�b�
则方程�a�可改写为
�x�1 � b�x�2 � dx1 � 0� c�x�1 � �x�2 � ex2 � 0
�c�
设上述方程解的形式为
x1 � Asin(� t � � )� x2 � B sin(� t � � )
整理后得
(b � � 2 )A � cB � 0� � dA � (d � � 2 )B � 0
系统发生振动时�方程具有非零解
b��2
�d d
�c
��2
�0
� 4 � (b � d )� 2 � d(b � c) � 0
�2 1,2
�
b
�d 2
�
(b � d )2 � d(b � c) 2
整理得
A2 B2
�
c
b � �22
�
d � �22
d
�
1
�2
A1 B1
�
c
b � �12
�
d � �12
d
�
1
�1
�1
�
B1 A1
�
b � �12
c
�
1[b � d c2
�
( b � d )2 � cd ] � 0 2
�2
�
B2 A2
�
b � �22
c
�
1[b � d c2
�
( b � d )2 � cd 来自 � 0 2�12,2 � (d � e) �
(d � e)2 � 4(1 � cb)de 2(1 � cb)
m�x�1 � (k1 � k2 )x1 � m2 �x�2 � k2 x1 � k2 x2
k2 x2 �0
�
0� � �
上式是一个二阶线性齐次微分方程组
令
b � k1 � k2 � c � k2 � d � k2
m1
m1
m2
�x�1 � bx1 � cx2 � 0� �x�2 � dx1 � dx2 � 0
图b表示在第一主振动中振动形状
称为第一主振型
图c表示在第二主振动中振动形状
称为第二主振型
图c中的点C是始终不振动的节点
主振型和固有频率一样都只与系统本身的参数有关
自由振动微分方程的全解为
即
x1 � A1 sin(�1t � �1 ) � A2 sin(�2t � �2 ) x2 � � 1 A1 sin(�1t � �1 ) � � 2 A2 sin(�2t � �2 )
它的运动规律为
x(1) 1
�
A1 sin(�1t
� �1 ) �
x(1) 2
�
� 1 A1 sin(�1t
� �1 )
对应于第二固有频率 �2的振动称为第二主振动
它的运动规律为
x(2) 1
�
A2
sin(�2t
��2)�
x(2) 2
�
� 2 A2
sin(�2t
��2)
�2 1,2
�
b�d 2
�
( b � d )2 � cd 2
�d�
将式�d�代入方程�c�得
(d � � 2 )A � b� 2 B � 0� � c� 2 A � (e � � 2 )B � 0
�e�
频率方程为
d ��2 � c� 2
� b� 2 e ��2
�0
将行列式展开�得
(1 � bc)� 4 � (d � e)� 2 � ed � 0
解此代数方程� 得到关于频率 �的2 两个根
上列方程组的解为
x1 � Asin(� t � � )� x2 � B sin(� t � � )
其中�A、B是振幅� ω为角频率
将上式代入
�x�1 � bx1 � cx2 � 0� �x�2 � dx1 � dx2 � 0
� A� 2 sin(� t � � ) � bAsin(� t � � ) � cB sin(� t � � ) � 0 � B� 2 sin(� t � � ) � dAsin(� t � � ) � dBsin(� t � � ) � 0
其中包含4个待定常数 A1�A2��1��2
它们应由运动的4个初始条件 x10�x20�x�10�x�20确定
例
已知�如图表示一具有两个集中质量 m1�m2 的简支梁 在质量 m1�m2 处梁的影响系数分别为 �11��22
和 �12��21 梁的质�量忽略不计。
求�系统的固有频率和主振型。
解� 这是两个自由度的振动系统 惯性力分别为 m1�x�1 m2�x�2 � 根据达朗贝尔原理和材料力学中的变形叠加原理
系统作主振动时�任何瞬时各点位移之间具有一定 的相对比值�即整个系统具有确定的振动形态�称为主 振型�主振型和固有频率一样�只决定于系统本身的物 理性质�而与初始条件无关�
§�-1 无阻尼二自由度系统的自由振动
�-�.1 固有频率和主振型
例子�汽车的振动
两个物块的振动微分方程
m1 �x�1 � �k1 x1 � k2( x2 � x1 ) m2 �x�2 � �k2( x2 � x1 )
�2 1,2
�
b
�d 2
�
( b � d )2 � cd 2
其中第一根 �1较小�称为第一阶固有频率或称基频。
其中第二根�2 较大�称为第二阶固有频率。
结论
两个自由度系统具有两个固有频率�这两个固有 频率只与系统的质量和刚度等参数有关�而与振动的 初始条件无关。
�2 1,2
�
b�d 2
�
( b � d )2 � cd 2
(b � � 2 )A � cB � 0� � dA � (d � � 2 )B � 0
对应于频率�1的振幅为 A1�B1
对应于频率�2的振幅为 A2�B2
A1 B1
�
c
b � �12
�
d
� �12
d
�
1
�1
A2 B2
�
c
b � �22
�
d
�
�
2 2
d
�
1
�2
其中� 1 和 � 2 为比例常数
对应于第一固有频率�1 的振动称为第一主振动
由两个惯性力在m1和 m2 处产生的挠度分别为
x1 � �11(�m1 �x�1 ) � �12(�m2 �x�2 ) x2 � �21(�m1 �x�1 ) � �22(�m2 �x�2 )
整理得系统的运动微分方程
�11m1�x�1 �21m1�x�1
� �
�12m2 �x�2 �22m2 �x�2
工程中的大量振动问题不能简化为单自由度系统进 行分析�而往往需要简化成多个自由度系统才能合理地 解决�二自由度系统是最简单的多自由度系统�因此� 研究二自由度系统是分析和了解多自由度系统振动特性 的基础�
二自由度系统具有两个不同数值的固有频率�在一 些特殊情况下其数值相等或其中有一个等于零��
当系统按其中某一固有频率做自由振动时�称为主 振动�主振动是一种简谐振动�