2019年中考数学总复习第六章圆第一节圆的基本性质好题随堂演练
2019年中考数学总复习第六章圆第一节圆的基本性质课件

【自主解答】分两种情况进行讨论:①弦AB和CD在圆心同 侧;②弦AB和CD在圆心异侧.作出半径和弦心距,利用勾
股定理和垂径定理可知弦心距分别为6 cm,8 cm,①当弦 AB和CD在圆心同侧时,距离为8-6=2(cm);②当弦AB和CD 在圆心异侧时, 距离为8+6=14(cm).∴弦AB与CD之间的 距离为14 cm或2 cm.
第六章 ห้องสมุดไป่ตู้ 第一节 圆的基本性质
考点一 圆周角定理及其推论 例1(2017·安徽)如图,在四边形ABCD中,AD=BC,∠B= ∠D,AD不平行于BC,过点C作CE∥AD交△ABC的外接圆⊙O于 点E,连接AE. (1)求证:四边形AECD为平行四边形; (2)连接CO,求证:CO平分∠BCE.
【分析】 (1)根据圆周角定理的推论得到∠B=∠E,从而得 到∠E=∠D,根据平行线的性质和判定定理得到AE∥CD,证 得结论; (2)作OM⊥BE于M,ON⊥CB于N,根据垂径定理、角 平分线的判定定理证明.
1.(2018·盐城)如图,AB为⊙O的直径,CD是⊙O的弦, ∠ADC=35°,则∠CAB的度数为( C )
A.35° B.45° C.55° D.65°
2.如图,在⊙O中,A,B是圆上的两点,已知∠AOB=40°, 直径CD∥AB,连接AC,则∠BAC=__3_5__度.
考点二 垂径定理及其推论
【自主解答】 (1)证明:∵∠B=∠D,∠B=∠E, ∴∠D=∠E. ∵CE∥AD,∴∠E+∠DAE=180°, ∴∠D+∠DAE=180°,∴AE∥DC. 又∵CE∥AD,∴四边形AECD为平行四边形;
安徽省2019年中考数学总复习第六章圆第一节圆的基本性质好题随堂演练
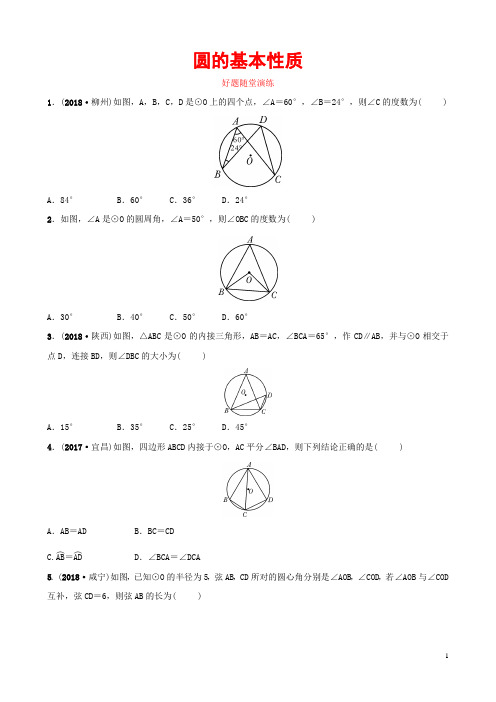
圆的基本性质好题随堂演练1.(2018·柳州)如图,A ,B ,C ,D 是⊙O 上的四个点,∠A=60°,∠B=24°,则∠C 的度数为( )A .84°B .60°C .36°D .24°2.如图,∠A 是⊙O 的圆周角,∠A=50°,则∠OBC 的度数为( )A .30°B .40°C .50°D .60°3.(2018·陕西)如图,△ABC 是⊙O 的内接三角形,AB =AC ,∠BCA=65°,作CD∥AB,并与⊙O 相交于点D ,连接BD ,则∠DBC 的大小为( )A .15°B .35°C .25°D .45°4.(2017·宜昌)如图,四边形ABCD 内接于⊙O,AC 平分∠BAD,则下列结论正确的是( )A .AB =ADB .BC =CD C.AB ︵=AD ︵ D .∠BCA=∠DCA5.(2018·咸宁)如图,已知⊙O 的半径为5,弦AB ,CD 所对的圆心角分别是∠AOB,∠COD,若∠AOB 与∠COD 互补,弦CD =6,则弦AB 的长为( )A.6 B.8 C.5 2 D.5 36.如图,四边形ABCD为⊙O的内接四边形,已知∠C=∠D,则AB与CD的位置关系是______________.7.(2018·宜昌)如图,在△ABC中,AB=AC,以AB为直径的圆交AC于点D,交BC于点E,延长AE至点F,使EF=AE,连接FB,FC.(1)求证:四边形ABFC是菱形;(2)若AD=7,BE=2,求半圆和菱形ABFC的面积.参考答案1.D 2.B 3.A 4.B 5.B 6.AB∥CD7.(1)证明:∵AB是直径,∴∠AEB=90°,即AE⊥BC,∵AB=AC,∴BE=CE,∵AE=EF,∴四边形ABFC是平行四边形,∵AC=AB ,∴四边形ABFC 是菱形.(2)解:设CD =x.如解图,连接BD.∵AB 是直径,∴∠ADB=∠BDC=90°, ∴AB 2-AD 2=CB 2-CD 2,∴(7+x)2-72=42-x 2,解得x =1或-8(舍去), ∴AC=8,BD =82-72=15,∴S 菱形ABFC =AC·BD=815.S 半圆=12·π·42=8π.。
2019年中考数学知识点《圆的基本性质》精选考题练习 (含答案解析)

第 12 题答图
所 以 BC = CE = 3 = 3 AC AD 3 BC
在 Rt△ACB 中, sin BAC = = 3 , AC
所以BAC = 60 , 又因为OA = OC , 所以△AOC 是等边三角形, 所以ACO = 60 , 因为直线 DE 与 O 相切于点 C, 所以OC ⊥ DE , 因为 AD ⊥ DE , OC ⊥ DE , 所以 AD//OC, 所以DAC = ACO = 60 , 所以ACD = 90 − DAC = 30 ,
9.(2019·陇南)如图,点 A,B,S 在圆上,若弦 AB 的长度等于圆半径的 ()
倍,则∠ASB 的度数是
A.22.5° 【答案】C
B.30°
C.45°
D.60°
【解析】作 AB 的垂直平分线,交圆与点 C,D,设圆心为 O,CD 与 AB 交于点 E,∵AB= 2 OA,∴
2 OA
AE= 2 OA ,∴ sin AOE = OE = 2
第 12 题答图
所以BCE + ACD = 90 ,
所以BCE = DAC , 在△ADC 与△CED, 因为ADC = CEB = 90 , BCE = DAC 所以△ADC∽△CED,
所 以 BC = CE = 3 = 3 AC AD 3 BC
在 Rt△ACB 中, sin BAC = = 3 , AC
A. 13 + 3 B. 2 2 + 3 C. 4 2 D. 2 2 + 2
【答案】D
【解题过程】连接 PA、PB、PC,过点 P 分别作 PF⊥ AB, PE⊥ OC, 垂足为 F,E.
中考数学总复习第六章圆第一节圆的基本性质好题随堂演练

——教学资料参考参考范本——中考数学总复习第六章圆第一节圆的基本性质好题随堂演练______年______月______日____________________部门好题随堂演练1.(20xx·广东省卷)同圆中,已知弧AB所对的圆心角是100°,则弧AB所对的圆周角是________°.2.如图,⊙O的半径为13,弦AB的长度是24,ON⊥AB,垂足为点N,则ON=________.3.如图,已知∠C=∠D,则AB与CD的位置关系是_____________________________________________________________________________.4.如图,正六边形ABCDEF内接于半径为4的圆,则B、E两点间的距离为________.5.如图,在⊙O中,=,点D在⊙O上,∠CDB=25°,则∠AOB=( )A.45° B.50° C.55° D.60°6.(20xx·菏泽)如图,在⊙O中,OC⊥AB,∠ADC=32°,则∠OBA的度数是( )A.64° B.58° C.32° D.26°7.(20xx·黄石)如图,已知⊙O为四边形ABCD的外接圆,O为圆心,若∠BCD=120°,AB=AD=2,则⊙O的半径为( )A. B. C. D.2338.(20xx·牡丹江)如图,四边形ABCD内接于⊙O,AB经过圆心,∠B =3∠BAC,则∠ADC等于( )A.100° B.112.5°C.120° D.135°9.(20xx·南充)如图,BC是⊙O的直径,A是⊙O上一点,∠OAC=32°,则∠B的度数是( )A.58° B.60° C.64° D.68°10.(20xx·宜昌)如图,四边形ABCD内接于⊙O,AC平分∠BAD,则下列结论正确的是( )A.AB=AD B.BC=CDC.=D.∠BCA=∠DCA11.(20xx·邵阳)如图所示,四边形ABCD为⊙O的内接四边形,∠BCD=120°,则∠BOD的大小是( )A.80° B.120° C.100° D.90°12.(20xx·牡丹江)如图,在⊙O中,=,CD⊥OA于点D,CE⊥OB于点E,求证:AD=BE.13.如图,正方形ABCD内接于⊙O,M为的中点,连接BM,CM.(1)求证:BM=CM;(2)当⊙O的半径为2时,求∠BOM的度数.参考答案1.502.5 【解析】∵ON⊥AB,AB=24,∴AN=12,∴ON===5. 3.AB∥CD 4.85.B 6.D 7.D 8.B9.A 【解析】∵OA=OC,∴∠C=∠OAC=32°,∴∠B=90°-∠C =58°.10.B 11.B12.证明:如解图,连接OC.∵=,∴∠AOC=∠BOC.∵CD⊥OA于点D,CE⊥OB于点E,∴∠CDO=∠CEO=90°. 在△COD 和△COE 中,⎩⎪⎨⎪⎧∠DOC=∠EOC,∠CDO=∠CEO=90°,CO =CO ,∴△COD≌△COE(AAS), ∴OD=OE. 又∵AO=BO , ∴AD=BE.13.(1)证明:∵四边形ABCD 是正方形, ∴AB=CD , ∴=,∵M 为的中点, ∴=,∴+=+,即=, ∴BM=CM ;(2)解:连接OM ,OB ,OC ,如解图, ∵=,∴∠BOM=∠COM,∵正方形ABCD 内接于⊙O,∴∠BOC==90°,∴∠BOM=×(360°-90°)=135°.。
安徽省中考数学总复习 第六章 圆 第一节 圆的基本性质好题随堂演练-人教版初中九年级全册数学试题

圆的基本性质好题随堂演练1.(2018·某某)如图,A ,B ,C ,D 是⊙O 上的四个点,∠A=60°,∠B=24°,则∠C 的度数为( )A .84° B.60° C.36° D.24°2.如图,∠A 是⊙O 的圆周角,∠A=50°,则∠OBC 的度数为( )A .30° B.40° C.50° D.60°3.(2018·某某)如图,△ABC 是⊙O 的内接三角形,AB =AC ,∠BCA=65°,作CD∥AB,并与⊙O 相交于点D ,连接BD ,则∠DBC 的大小为( )A .15° B.35° C.25° D.45°4.(2017·某某)如图,四边形ABCD 内接于⊙O,AC 平分∠BAD,则下列结论正确的是( )A .AB =AD B .BC =CDC.AB ︵=AD ︵D .∠BCA=∠DCA5.(2018·某某)如图,已知⊙O 的半径为5,弦AB ,CD 所对的圆心角分别是∠AOB ,∠COD ,若∠AOB 与∠COD 互补,弦CD =6,则弦AB 的长为( )A .6B .8C .5 2D .5 36.如图,四边形ABCD为⊙O的内接四边形,已知∠C=∠D,则AB与CD的位置关系是______________.7.(2018·某某)如图,在△ABC中,AB=AC,以AB为直径的圆交AC于点D,交BC于点E,延长AE至点F,使EF=AE,连接FB,FC.(1)求证:四边形ABFC是菱形;(2)若AD=7,BE=2,求半圆和菱形ABFC的面积.参考答案1.D 2.B 3.A 4.B 5.B 6.AB∥CD7.(1)证明:∵AB是直径,∴∠AEB=90°,即AE⊥BC,∵AB=AC,∴BE=CE,∵AE=EF,∴四边形ABFC是平行四边形,∵AC=AB,∴四边形ABFC是菱形.(2)解:设CD=x.如解图,连接BD.∵AB是直径,∴∠ADB=∠BDC=90°,∴AB 2-AD 2=CB 2-CD 2,∴(7+x)2-72=42-x 2,解得x =1或-8(舍去), ∴AC=8,BD =82-72=15,∴S 菱形ABFC =AC·BD=815.S 半圆=12·π·42=8π.。
2019届中考数学复习随堂演练 第六章圆第一节 圆的有关概念及性质
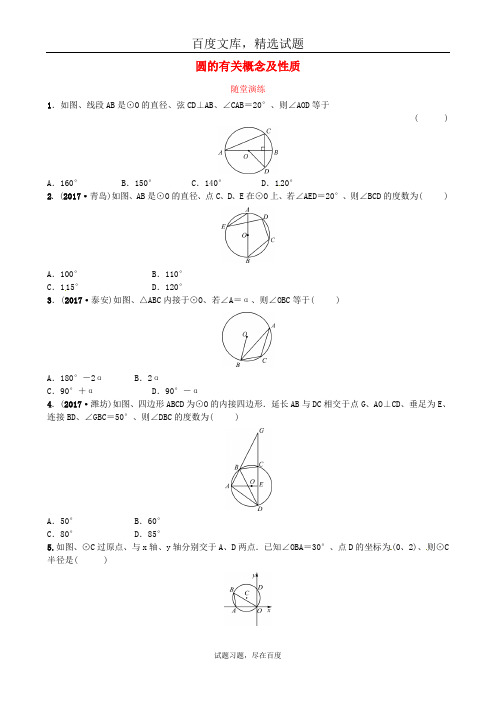
圆的有关概念及性质随堂演练1.如图、线段AB是⊙O的直径、弦CD⊥AB、∠CAB=20°、则∠AOD等于( )A.160° B.150° C.140° D.120°2.(2017·青岛)如图、AB是⊙O的直径、点C、D、E在⊙O上、若∠AED=20°、则∠BCD的度数为( )A.100° B.110°C.115° D.120°3.(2017·泰安)如图、△ABC内接于⊙O、若∠A=α、则∠OBC等于( )A.180°-2αB.2αC.90°+αD.90°-α4.(2017·潍坊)如图、四边形ABCD为⊙O的内接四边形.延长AB与DC相交于点G、AO⊥CD、垂足为E、连接BD、∠GB C=50°、则∠DBC的度数为( )A.50° B.60°C.80° D.85°5.如图、⊙C过原点、与x轴、y轴分别交于A、D两点.已知∠OBA=30°、点D的坐标为(0、2)、则⊙C 半径是( )6.如图、圆内接四边形ABCD中两组对边的延长线分别相交于点E、F、且∠A=55°、∠E=30°、则∠F =______.7.如图、水平放置的圆柱形排水管道的截面直径是1m、其中水面的宽AB为0.8 m、则排水管内水的深度为_____m.8.(2017·临沂)如图、∠BAC的平分线交△ABC的外接圆于点D、∠ABC的平分线交AD于点E.(1)求证:DE=DB;(2)若∠BAC=90°、BD=4.求△ABC外接圆的半径.参考答案1.C 2.B 3.D 4.C 5.B6.40°7.0.88.(1)证明:∵AD平分∠BAC、BE平分∠ABC、∴∠BAD=∠CAD、∠ABE=∠CBE、又∠BED=∠ABE+∠BAD、∠DBE=∠D BC+∠CBE、∠DBC=∠DAC、∴∠BED=∠DBE、∴DE=DB.(2)解:如图、连接CD.∵∠BAC=90°、∴BC 是圆的直径、 ∴∠BDC=90°.∵∠BAD=∠CAD、∴BD ︵=CD ︵、 ∴BD=CD 、∴△BCD 是等腰直角三角形. ∵BD=4、∴BC =42、∴△ABC 的外接圆的半径为2 2.。
安徽省2019年中考数学总复习-第一部分-系统复习-成绩基石-第六章-圆-第22讲-圆的基本性质课件
1
A.
B.5
C. 5 3
D.5 3
2
2
8.[2018·白银]如图,⊙A过点O(0,0),
C( 3 ,0),D(0,1),点B是 x 轴下方⊙A
上的一点,连接BO,BD,则∠OBD的度 数是( B ) A.15° B.30° C.45° D.60°
类型4 圆的确定 9. [2018·烟台]如图,方格纸上每个小正方形 的边长均为1个单位长度,点O,A,B,C在 格点(两条网格线的交点叫格点)上,以点O为 原点建立直角坐标系,则过A,B,C三点的 圆的圆心坐标为 (-1,-2) .
考点2 圆周角定理及推论
1.圆周角定理 (1)一条弧所对的圆周角等于它所对的圆心角的 一半 . (2)圆周角定理和推论:①在同圆或等圆中,同弧或等弧所对的圆周 角相等;相等的圆周角所对的弧也相等.②半圆(或直径)所对的圆 周角是直角;90°的圆周角所对的弦是直径、所对的弧是半圆.
2.圆内接四边形的性质:圆内接四边形的对角 互补 ;圆内接四边 形的任意一个外角等于它的内对角(相邻的内角的对角).
解题要领►三角形三条边的垂直平分线交于一点,该点叫做三角 形的外心,即三角形外接圆的圆心;三角形外接圆的圆心到三角 形三个顶点的距离相等;确定三角形的外心,只需作三ห้องสมุดไป่ตู้形两条 边的垂直平分线,两条垂直平分线的交点即为三角形的外心.
10.[2018·内江]已知△ABC的三边a,b,c,满足a+b2+|c-6|+
5.[2018·双清模拟] 如 A等D图分分,点别矩(与A︵G形该>A圆BG︵C相FD)交,的于B顶G点点交EAA,,F于FB,在点G圆H是,上A︵若,F的AB︵BC三的, 度数为30°,则∠GHF等于( A )
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
圆的基本性质
好题随堂演练
1.(2018·柳州)如图,A ,B ,C ,D 是⊙O 上的四个点,∠A=60°,∠B=24°,则∠C 的度数为( )
A .84° B.60° C.36° D.24°
2.如图,∠A 是⊙O 的圆周角,∠A=50°,则∠OBC 的度数为( )
A .30° B.40° C.50° D.60°
3.(2018·陕西)如图,△ABC 是⊙O 的内接三角形,AB =AC ,∠BCA=65°,作CD∥AB,并与⊙O 相交于点D ,连接BD ,则∠DBC 的大小为( )
A .15° B.35° C.25° D.45°
4.(2017·宜昌)如图,四边形ABCD 内接于⊙O,AC 平分∠BAD,则下列结论正确的是( )
A .A
B =AD B .B
C =CD
C.AB ︵=AD ︵D .∠BCA=∠DCA
5.(2018·咸宁)如图,已知⊙O 的半径为5,弦AB ,CD 所对的圆心角分别是∠AOB,∠COD,若∠AOB 与∠COD 互补,弦CD =6,则弦AB 的长为( )
A.6 B.8C.52D.5 3
6.如图,四边形ABCD为⊙O的内接四边形,已知∠C=∠D,则AB与CD的位置关系是______________.
7.(2018·宜昌)如图,在△ABC中,AB=AC,以AB为直径的圆交AC于点D,交BC于点E,延长AE至点F,使EF=AE,连接FB,FC.
(1)求证:四边形ABFC是菱形;
(2)若AD=7,BE=2,求半圆和菱形ABFC的面积.
参考答案
1.D2.B3.A4.B5.B6.AB∥CD
7.(1)证明:∵AB是直径,
∴∠AEB=90°,即AE⊥BC,
∵AB=AC,∴BE=CE,
∵AE=EF,∴四边形ABFC是平行四边形,。
