一阶系统的时域分析解析
一阶系统时域分析
能达到稳态值的0.632, 经过3T或4T的时间系统输出响应分加别
达到稳态值的0.95或0.98。
线性系统的时域分析法>>一阶系统的时域分析
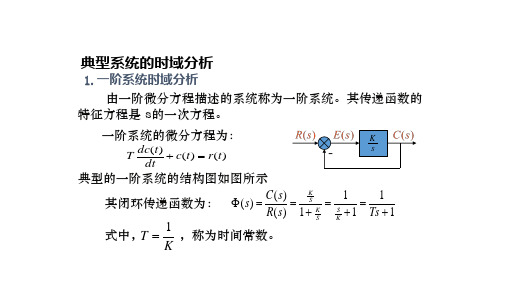
一阶系统响应的特点: (1) t=T时,输出达到稳态值的0.632
h(0) 1 e0 0 ——— t= 0时, 输出为0 h(T ) 1 e1 0.632 —— t=∞时,输出达到稳态值1 h(3T ) 1 e3 0.95 —— t=T时,输出达到稳态值的0.632 h(4T ) 1 e4 0.98 —— t=3T时,输出达到稳态值的0.95
典型系统的时域分析
1.一阶系统时域分析
由一阶微分方程描述的系统称为一阶系统。其传递函数的 特征方程是 s的一次方程。
一阶系统的微分方程为:
T dc(t) c(t) r(t) dt
典型的一阶系统的结构图如图所示
K
-
s
其闭环传递函数为:
(s) C(s)
K S
1
1
R(s)
1
K S
S K
1
Ts 1
式中,T 1 ,称为时间常数。
K
线性系统的时域分析法>>一阶系统的时域分析
1.一阶系统的单位阶跃响应
r(t) 1(t), R(s) 1 s
11
C(s)
,
Ts 1 s
h(t) L1[ 1 1]
Ts 1 s
L1[1
1
t
] 1 e T
s s 1
T
这是一条指数曲线, t 0
处斜率最大,其值为1/T,若系统保
持此变化速度,在 t=T 时,输出将达到稳态值。而实际系统只
t
c(td ) 1 e T 0.5
3-2一阶系统的时域分析ppt2010

1 T= 3
3 Φ (s ) = 1 + s+2
1 T= 2
∴ t s = 3T = 1s
∴ t s = 3T = 1.5s
r(t)= 1(t) h(t)=1-e-t/T r(t)= t c(t)=t-T+Te-t/T
小结 (补 充)
1 、3个图各如何求 ? 个图各如何求T? 个图各如何求 3 、r(t)=vt时,ess=? 时 ?
2 、调节时间 s=? 调节时间t ? 5 、k≠1时 时
4、求导关系 、
关于响应的导数等于导数的响应 关于响应的导数等于导数的响应(P76) 等于
s 2 + 4s + 2 Φ(s ) = (s + 1)(s + 2)
1 s就是求导, 就是积分 s
h( t ) = 1 − e −2 t + e − t
h( t )中的 1求导 = δ ( t ) h( t )中的 1求导 = 0
Φ (s ) =
4s + 2 (s + 1)(s + 2)
h(t ) = 1 + 2e − t − 3e −2t
封面
3-2目录
1.一阶系统的数学模型 2.一阶系统的单位阶跃响应 3.一阶系统的单位脉冲响应 4.一阶系统的单位斜坡响应 5.一阶系统的单位加速度响应
一阶系统时域分析
1 T
单位脉冲响应(P75)
,T
k 无零点的一阶系统 Φ(s) = Ts + 1
k(t)= 单 位 脉 冲 响 应
0.5 2
- t e
补充) 分子分母同阶的一阶系统(补充 补充
s+2 h(0) = 1, h(∞) = 0.67 Φ(s) = s + 5 h(0) = 1, h(∞) = 2.5 Φ (s ) = s+3 s+2 2 1 −3t h(t) = + e n=[1 5];d=[1 2];step(n,d) 3 3
自动控制原理--一阶系统的时域分析相关知识
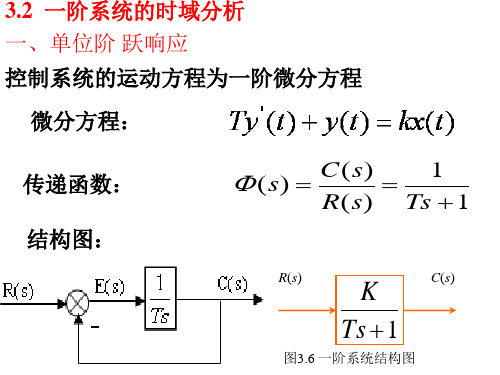
三、 一阶系统的单位脉冲响应
输入信号 r(t) (t) R(s)=1
c(t)
输出信号 C(s) (s)R(s) 1
1/T
Ts 1
斜率-1/T2
0.368/T 0.135/T
c(t) 1 et /T T
拉氏反变换,得 t k(t) L1[C(s)] L1[ (s)]
0 T 2T 3T 图3.10 一阶系统的单位脉冲响应
• 例3-1:
一阶系统如图所示,试求系统单位阶跃响应的调 节时间ts,如果要求ts=0.1秒,试问系统的反馈 系数应如何调整?
• 例3-2:
G(s) 10
已知某元部件的传递函数为:
0.2s 1
采用图示方法引入负反馈,将调节时间减至原来 的0.1倍,但总放大系数保持不变,试选择KH、 K0的值。
1 et /T (t 0) T
三、 一阶系统的单位脉冲响应特点
• 1)可以用时间常数去度量系统的输出量数字。 • 2)初始斜率为-1/T2 。 • 3) 无超调,稳态误差为零 。
h(t)
超调量
1.0 0.9
延迟时
0.5 间
0.1 0
峰值时间
上升时间 调节时间
误差带 0.02或0.05
稳态误差 (t→∞)
s
输出 C (s) (s) R(s)
1 1 Ts 1 s
1 1 取拉氏反变换,得 s Ts 1
h(t) 1 et /T (t 0)
一阶系统单位阶跃响应是终值为1的单调上升过程。
c(t) c(t) 1 et /T dh(t) 1
1
dt t0 T
0.865
0.632
td 0.69T
一阶反馈系统
假设将一阶系统作为反馈控制系统的对象, 放大器增益可调,系统结构图如图所示。
32一阶系统的时域分析

k(0)=
1 T
h’(0)=1/T
K’(0)=
1
Th2(TT)=0.632h(∞)
h(2T)=0.865h(∞)
响应应
h(3T)=0.95h(∞)
问应
1 、3个图各如何求T? h(42T、)=调0.节98时2h间(∞ts=)?
3 、r(t)=vt时,?ess=?
4、求导关系
小结: t d 1(t) d 2 t 1t
什么是二阶系统?凡以二阶微分方程作为运动方 程的控制系统,即为二阶系统。 研究二阶系统的意义:
1. 二阶系统的典型应用极为普遍 2. 不少高阶系统的特性在一定条件下可用二阶系 统特性来表征。
本节主要内容: 一、继续讲二阶系统的时域分析中的几种工作状态。 二、二阶系统的性能改善,关键是改变了阻尼比和
ch(t()t=)1=-1e-e-t/T
63.2% 86.5% 95% 98.2% 99.3%
t
0
T
2T 3T 4T 5T
稳态性能指标:
图 3-4指 数 响 应 曲 线
一阶惯性系统的单位阶跃响没有静态误差
ess
lim r (t )
t
h(t)
1
h()
11
0
讨论:动态指标与时间常数T有关,T越小,其响应过
dt
T dc(t) c(t) r(t)
(3-2)
dt
其中,T=RC为时间常数;取拉氏变换
TsC(s) C(s) R(s)
TsC(s) C(s) R(s)
则一阶系统的传递函数为:
i(t) R
(s) C(s) 1 R(s) Ts 1
(3-3)
r(t)
C c(t)
一阶系统时域分析
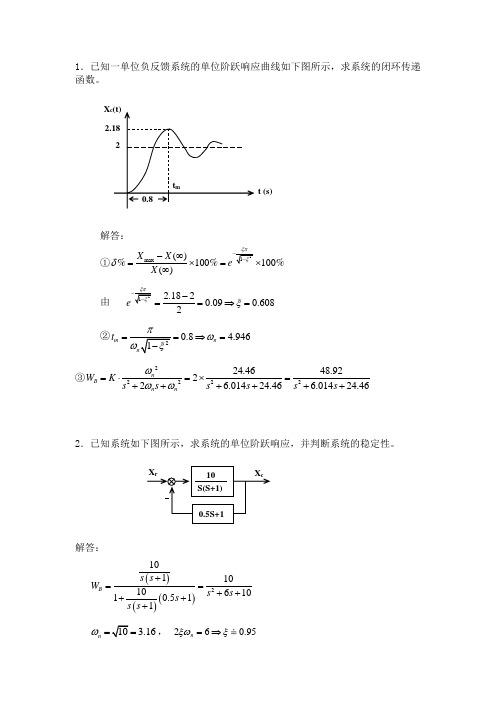
1.已知一单位负反馈系统的单位阶跃响应曲线如下图所示,求系统的闭环传递函数。
解答:①max ()100100()X X %%e %X δ-∞=⨯=⨯∞由2.1820.090.6082eξ-==⇒=②0.8 4.946m n t ω==⇒= ③2222224.4648.9222 6.01424.46 6.01424.46n B n n W K s s s s s s ωωω=⋅=⨯=++++++2.已知系统如下图所示,求系统的单位阶跃响应,并判断系统的稳定性。
解答:()()()2101101061010.511B s s W s s s s s +==+++++3.16n ω==, 260.95n ξωξ=⇒()()1sin n t c X t ξωωθ-=,arctg θ=()31 3.2sin 0.98718.19t e t -=-+︒ (5分)系统根为1,2632P j -±==-±,在左半平面,所以系统稳定。
3.一阶系统的结构如下图所示。
试求该系统单位阶跃响应的调节时间t s ;如果要求t s (5%)≤ 0.1(秒),试问系统的反馈系数应取何值?(1)首先由系统结构图写出闭环传递函数得 T =0.1(s )因此得调节时间 t s =3T =0.3(s),(取5%误差带)(2)求满足t s (5%) ≤0.1(s )的反馈系数值。
假设反馈系数K t (K t >0),那么同样可由结构图写出闭环传递函数由闭环传递函数可得 T = 0.01/K t100()10()100()0.1110.1c B r X s s W s X s s s ===++⨯1001/()1000.0111t B t tK s W s K s s K ==+⨯+根据题意要求 t s (5%) ≤ 0.1(s )则 t s = 3T = 0.03/K t ≤ 0.1(s)所以 K t ≥ 0.34.已知某装置的电路如题图所示。
自动控制原理一阶系统时域分析

R(s)
1 s3
C
(s)
(
s)
R(s)
(1 Ts
) 1
1 s3
A s3
B s2
C s
D s 1
1 s3
T s2
T2 s
T2 s 1
T
T
c(t)
1
t
2
Tt
T
2 (1
1t
eT
)
2
(t 0)
e(t
)r(t)c(t)TtT2
(1
1
eT
t
)
上式表明,跟踪误差随时间推移而增大,直至无限大。因此,一阶系统不 能实现对加速度输入函数的跟踪。
第26页/共27页
感谢您的观看!
第27页/共27页
R(s) + E(s) 1 C(s)
-
Ts
R(s)
1
C(s)
Ts 1
(a)
微分方程: 闭环传递函数:
T dc(t) c(t) r(t) dt
(s) C(s) 1 R(s) Ts 1
(b) 标准形式
第18页/共27页
二、一阶系统单位阶跃响应
r(t) 1(t), R(s) 1 s
1
C(s)
1 Kh 100 / s 1 s / 100Kh
• 要求ts=0.1s,即3T=0.1s, 即
,得 1 0.1 100Kh 3
K h 0.3
• 解题关键:化闭环传递函数为标准形式。
第22页/共27页
二、一阶系统单位脉冲响应
r(t) (t) R(s) 1
C(s) (s)R(s) 1 1/T Ts 1 s 1/T
第15页/共27页
例题:加入给定值阶跃量为2.4,响应 曲线如图所示,求超调量。
一阶系统的时域响应实验报告

一阶系统的时域响应实验报告实验目的:通过实验观察一阶系统的时域响应情况,掌握一阶系统的传递函数及其参数对响应的影响。
实验器材:示波器、信号发生器、直流电源、一阶滤波器。
实验原理:一阶系统的传递函数为H(s)=K/(Ts+1),其中K为系统的增益,T为系统的时间常数。
系统的单位阶跃响应为h(t)=K(1-e^(-t/T))。
实验步骤:1、按照实验电路连接图连接电路。
2、将示波器接在电路输出端,用信号发生器产生一个频率为1kHz的正弦波作为输入信号,调节直流电源,使得输入信号幅值为1V。
3、测量电路输出波形,记录幅值、峰值、频率等数据。
4、将输入信号改为单位阶跃信号,在示波器上观察并记录输出信号的响应过程,测量电路的时间常数T。
实验结果及分析:1、在实验中,我们按照传统的RC低通滤波器的电路连接方式,将滤波器动态系统搭建起来。
2、对于一个RC电路,可以证明其传递函数为H(s)=1/(RCs+1)。
因此在实验中,我们可以通过改变RC电路的$RC$值来改变系统的时间常数,并观察其对系统响应的影响。
3、实验中我们观察到,当输入信号为正弦波时,系统能够对信号进行较好的滤波,输出信号幅值与频率的比例关系为a1=f^-1。
4、当输入信号为单位阶跃信号时,我们能够观察到系统的单位阶跃响应。
在实验中,我们通过观察输出信号的时间常数,可以得到系统的时间常数T。
5、实验中,我们还观察到了系统的过渡过程。
在输入信号发生变化后,系统的输出信号不会立即改变,而是经过一段时间才能够达到稳态。
在实验中,我们通过调节系统的时间常数来观察过渡过程的变化,从而获得了对一阶系统的更深刻的认识。
实验结论:通过本实验,我们详细地了解了一阶系统的时间常数、单位阶跃响应等数学概念,同时还深入掌握了一阶系统的响应机理。
此外,我们还利用实验数据验证了一阶系统的传递函数的正确性,并进一步掌握了如何通过调节时间常数来改变系统响应的技巧。
3-2 一阶系统的时域分析
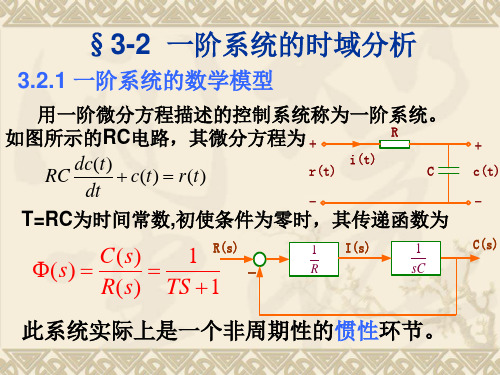
一阶系统结构如图所示, 例: 一阶系统结构如图所示,试求该系统的单位 阶跃响应及调节时间。若要求t 阶跃响应及调节时间。若要求 s<0.1s,试问系 , 统的反馈系数K 应如何选取? 统的反馈系数 t应如何选取?
R(s)
-
100
C(s)
s
Κt
解:系统闭环传递函 数为: 数为:
C ( s) 100 Φ(s) = = R( s) s + 100 K t = 1 Kt 1 100 K t 1 Kt = Ts + 1 s +1
瞬态分量 稳态分量
瞬态分量变化规律由传递函数的极点s=-1/T决定 瞬态分量变化规律由传递函数的极点s=-1/T决定 极点s=
c(t ) = 1 − e
t − T
t≥0
c(t ) = 1 − e
−
t T
t≥0
由于c(t)的终值为1,系统稳态误差为0。 由于c(t)的终值为1,系统稳态误差为0 c(t)的终值为1,系统稳态误差为 动态性能指标: 动态性能指标:
输入信号 输入信号 时域) 复频域) (时域) (复频域) 输出响应 传递函数
δ (t )
1 ⋅ (t )
1
1 s 1 2 s 1 s3
1 e T
−
t T
t≥0
t T
1− e
ห้องสมุดไป่ตู้
−
t≥0
− t T
t
1 2 t 2
t − T + Te
t≥0
− t T
1 Ts + 1
1 2 t − Tt + T 2 (1 − e 2
R(s)
-
100
C(s)
s
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
证明:
a0d dnntc(t)a1d dnn t 11c(t)an1d dct(t)anc(t) b0d dm m tr(t)b1d dm m t 11r(t)bm1d drt(t)bmr(t)
r(t)和c(t)满足方程,两边求导后知:r ( t ) 和 c ( t ) 也满足方程。
对上式求拉氏反变换,得:
1t
1t
c(t)tT(1eT)tTTT e
1t
因为 e(t)r(t)c(t)T(1eT)
所以一阶系统跟踪单位斜坡信号的稳态误差为 esslt i m e(t)T
从图中可以看出:
①一阶系统能跟踪斜坡输入信号。稳态时,输入和输 出信号的变化率完全相同。
②稳态时C(t)滞后于R(t)一个常量T。 ③减小惯性时间常数T可以加快瞬态响应的速度,可 减少系统跟踪斜坡信号的稳态误差。
第三章 时域分析法
第二节 一阶系统时域分析
第二节 一阶系统的时域分析
项目
内容
教学目的
掌握一阶系统在四种典型信号输入下的输出响 应特征。理解时域分析方法。初步了解MATLAB的
使用。
教学重点
一阶系统在四种典型信号输入下的输出响应 特征。掌握系统的时域分析方法。
教学难点
分析一阶系统的四种输出响应,最后总结。
t
c(t) 1e T
由解析式绘制曲线图:
c (t)
1
t
c(t) 1e T
63.2% 86.5% 95% 98.2% 99.3%
0.632
0
T
2T 3T 4T 5T t
确定T的值、 系统是否是 一阶系统
由解析式和曲线图可以得出以下结论:
❖ 可以用时间常数去度量系统的输出量的数值;
❖ 初始斜率为1/T;
及 其 处 理 使用MATLAB工具辅助教学。
一、一阶系统的数学模型
RCdudot(t)uo(t)ui(t)
C(s) 1 R(s) Ts 1
将微分方程为
T
dc(t)+c(t)=r(t),传递函数为
dt
C(s) R(s)
1 Ts 1
的系统叫做一阶系统。
❖ 动态结构图 R:U i(s)U o(s)I(s)R
Ui(s) 1/R I(s) 1/sC Uo(s) Uo(s)
C:U o (s)
I (s) Cs
Ui(s) 1/sRC Uo(s) -
二、一阶系统的单位阶跃响应
将 R ( s ) 1 代入传递函数中,可得:
S
C (s)(s)R (s)T S 1 1S 1S 1T S T 1S 1S 11
T
两边进行拉氏反变换,可得C(t)的时域表达式:
确定T 的值
c (t)
1
0.632
63.2% 86.5% 95% 98.2% 99.3%
0
T
2T 3T 4T 5T t
❖动态性能指标
上升时间 tr 2.20T
t p和%不存在
4T,当2%时 调节时间 ts 3T,当5%时
❖稳态性能指标 ess=1-c(∞)=1-1=0
三、一阶系统的单位脉冲响应
当输入信号为理想单位脉冲函数时,由于
五、一阶系统的单位加速度响应
将 R(s)
1 S3
代入传函表达式,得:
C ( s )( s ) R ( s ) ( T 1 1 S )S 1 3 S A 3 S B 2 C S S D 1 S 1 3 S T 2 T S 2 S T 2 1
T
T
对上式求拉氏反变换,得:
c(t)1t2T tT2(1e T 1t) (t0) e (t) r( 2 t) c (t) T T t2 (1 e T 1 t)
R(s)=1,因此输出量的拉氏变换与系统的传递
函数相同,即
C(s) 1 TS1
c(t)1eTt T
t 0
由图可见,一阶系统的脉冲响应为一单调下降的指数 曲线。系统的惯性时间常数越小,响应的快速性越好。
四、一阶系统的单位斜坡响应
将 得:
C (s)(s)R (s)111TT 2 T S 1S 2 S 2 S 1 TS
上式表明,跟踪误差随时间推移而增大,直至无限大。
因此,一阶系统不能实现对加速度输入函数的跟踪。
小结:一阶系统对典型输入信号的响应
输入信号
(t)
微
1(t)
分
t
输出响应
1eTt T
(t 0)
t
1e T t 0
微
t
分
tTTeT t 0
1 t2
1t2T tT2(1eTt ) t0
2
2
系统对输入信号导数(积分)的响应,就等于系统对该 输入信号响应的导数(积分)。所以只取一种典型形式进 行研究就可以了。
两种输入作用下的输出信号比较
c (t)
1
0.632
63.2% 86.5% 95% 98.2% 99.3%
0
T
2T 3T 4T 5T t
单位阶跃响应曲线
单位斜坡响应曲线
阶跃信号输入
斜坡信号输入
输入输出 初始状态时大,随t 初始状态为0,随t增 位置误差 减小,最后趋于0。 大,最后趋于T。
输出曲 初始状态最大且等 初始状态最小且为0, 线斜率 于1/T,随t趋于0。 随t趋于1。
