体心立方晶格与面心立方晶格
体心立方晶格
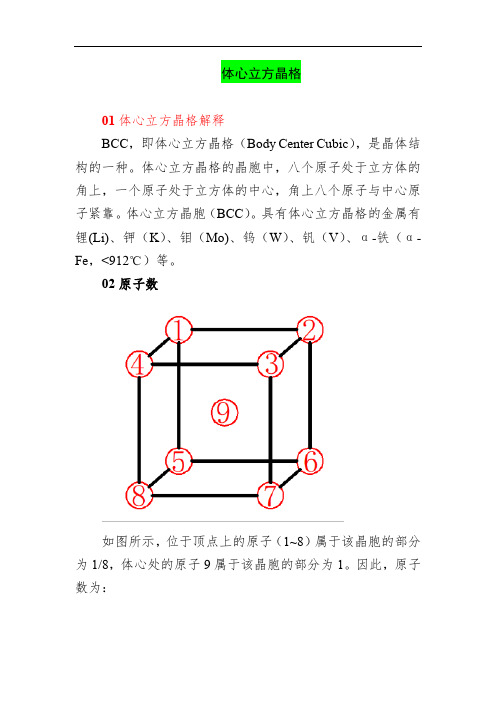
体心立方晶格01体心立方晶格解释BCC,即体心立方晶格(Body Center Cubic),是晶体结构的一种。
体心立方晶格的晶胞中,八个原子处于立方体的角上,一个原子处于立方体的中心,角上八个原子与中心原子紧靠。
体心立方晶胞(BCC)。
具有体心立方晶格的金属有锂(Li)、钾(K)、钼(Mo)、钨(W)、钒(V)、α-铁(α-Fe,<912℃)等。
02原子数如图所示,位于顶点上的原子(1~8)属于该晶胞的部分为1/8,体心处的原子9属于该晶胞的部分为1。
因此,原子数为:03原子半径如图所示,体心处的原子与顶点处的原子均相切(即图2中1,9,7),因此原子半径即为体心处原子与顶点处原子之间距离的一半。
04配位数与任一原子相距最近且距离相等的原子数。
因与体心处原子距离最近且相等的原子位于8个顶点。
故配位数为8。
05致密度原子所占有的体积与该晶胞体积之比。
【注】配位数与致密度数值越大,表明原子堆积越密,紧密程度越大。
06堆垛方式如图所示,位于体心处的原子与顶角的8个原子相接触,顶角的8个原子互不接触,两条斜对角线所组成的面原子排列较为紧密,为了获得较为紧密的排列,第二层次密排面(B 层3,7)的每个原子(3、7号原子)落在第一层(A层2,6,8,4,9)的空隙中心,第三层位于第二层空隙中心上,与第一层重复,因此堆垛方式为AB AB AB..07密排面如图所示,由于9号原子与其他原子均相切,因此由2、4、6、8、9号原子所组成的平面最紧密称为密排面,用{110}表示。
同理,由1、3、5、7、9号原子组成的平面也属于密排面。
08密排方向如图所示,由于位于体对角线的3个原子相切,因此在此方向上是最紧密的方向,称为密排方向,图中5、9、3号原子的方向即为密排方向,用<111>表示。
同理,1、9、7号原子的方向也属于密排方向。
09四面体间隙确定间隙中心:由对称性,间隙中心位于1,2,3,4组成的平面上,x轴1/2处,y轴1/4处,如图6所示,全部间隙中心的位置分布如图7所示。
体心立方晶格与面心立方晶格
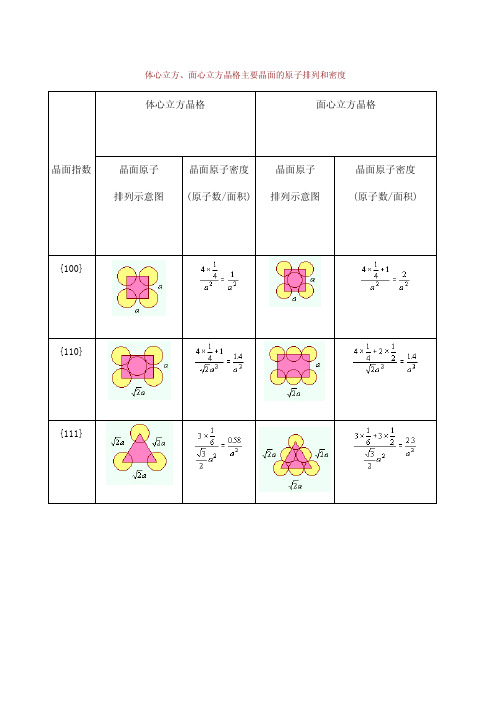
体心立方、面心立方晶格主要晶面的原子排列和密度体心立方、面心立方晶格主要晶向的原子排列和密度第1章 小结1.三种常见金属的晶体结构体心立方晶格(胞):晶格常数a 、90°,晶胞原子数为2个, 原子半径: ,致密度为68%,最大空隙半径 r 四=0.29r 原子,配位数为8面心立方晶格(胞):晶格常数a、90°,晶胞原子数为4个,原子半径:,致密度为74%,最大空隙半径r八=0.414r原子,配位数为12。
密排六方晶格(胞):晶格常数a、c、90°、120°,晶胞原子数为6个,原子半径:,致密度为74%,最大空隙半径r八=0.414r原子,配位数为12。
2.晶面与晶向可用晶面指数与晶向指数来表达。
不同晶面、不同晶向上的原子排列情况不同。
体心立方晶格的最密面为{110},最密方向为<111>。
面心立方晶格的最密面为{111},最密方向为<110>。
密排六方晶格的最密面为{0001},最密方向为。
3.实际金属中含有点缺陷(空位、间隙原子、异类原子)、线缺陷(位错)、面缺陷(晶界、亚晶界)三类晶体缺陷,位错密度增加,材料强度增加。
晶界越多,晶粒越细,金属的强度越高,同时塑性越好(即细晶强化)。
4.合金中有两类基本相:固溶体和金属化合物。
固溶强化是金属强化的一种重要形式。
细小弥散分布的金属化合物可产生弥散强化或第二相强化。
材料的微观组成和微观形貌称组织,材料的组织取决于化学成分和工艺过程。
5.金属材料的性能特点是:强度高,韧性好,塑性变形能力强,综合机械性能好,通过热处理可以大幅度改变机械性能。
金属材料导电、导热性好。
不同的金属材料耐蚀性相差很大,钛、不锈钢耐蚀性好,碳钢、铸铁耐蚀性差。
《金属学与热处理》崔忠圻(第二版)课后答案完整版
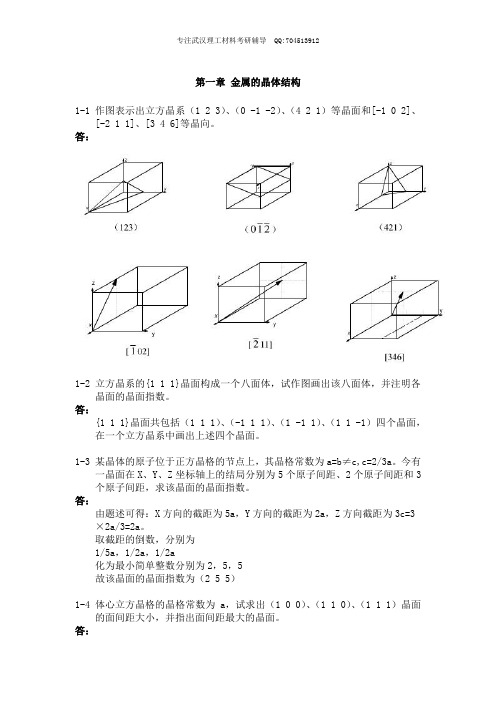
第一章金属的晶体结构1-1 作图表示出立方晶系(1 2 3)、(0 -1 -2)、(4 2 1)等晶面和[-1 0 2]、[-2 1 1]、[3 4 6]等晶向。
答:1-2 立方晶系的{1 1 1}晶面构成一个八面体,试作图画出该八面体,并注明各晶面的晶面指数。
答:{1 1 1}晶面共包括(1 1 1)、(-1 1 1)、(1 -1 1)、(1 1 -1)四个晶面,在一个立方晶系中画出上述四个晶面。
1-3 某晶体的原子位于正方晶格的节点上,其晶格常数为a=b≠c,c=2/3a。
今有一晶面在X、Y、Z坐标轴上的结局分别为5个原子间距、2个原子间距和3个原子间距,求该晶面的晶面指数。
答:由题述可得:X方向的截距为5a,Y方向的截距为2a,Z方向截距为3c=3×2a/3=2a。
取截距的倒数,分别为1/5a,1/2a,1/2a化为最小简单整数分别为2,5,5故该晶面的晶面指数为(2 5 5)1-4 体心立方晶格的晶格常数为a,试求出(1 0 0)、(1 1 0)、(1 1 1)晶面的面间距大小,并指出面间距最大的晶面。
答:H==a/2(1 0 0)==√2a/2H(1 1 0)==√3a/6H(1 1 1)面间距最大的晶面为(1 1 0)1-5 面心立方晶格的晶格常数为a,试求出(1 0 0)、(1 1 0)、(1 1 1)晶面的面间距大小,并指出面间距最大的晶面。
答:==a/2H(1 0 0)H==√2a/4(1 1 0)==√3a/3H(1 1 1)面间距最大的晶面为(1 1 1)注意:体心立方晶格和面心立方晶格晶面间距的计算方法是:1、体心立方晶格晶面间距:当指数和为奇数是H=,当指数和为偶数时H=2、面心立方晶格晶面间距:当指数不全为奇数是H=,当指数全为奇数是H=。
1-6 试从面心立方晶格中绘出体心正方晶胞,并求出它的晶格常数。
答:1-7 证明理想密排六方晶胞中的轴比c/a=1.633。
求晶格常数为a的面心立方和体心立方晶体晶面族hhh的面间距

1、求晶格常数为a 的面心立方和体心立方晶体晶面族(h 1h 2h 3)的面间距。
2、用波长为1.5405A
的X 光对钽金属粉末作为衍射分析,测得布拉格角大小为序的五条眼射线见下表
已知钽金属为体心结构,求:(1)衍射晶面族的晶面指数;(2) 晶格常数a 。
3、有一晶体,平衡时体积为V 0,原子间相互作用势为U 0。
如果相距为r 的两原子相互作用势为n r βα
+=m r -u(r),证明:(1)体积弹性模量为0
09V mn U K =;(2)求出体心立方结构惰性分子晶体的体积模量。
4、雷纳德-琼斯势为])()[(4)(612r
r r u σσε-=,证明:r=1.12σ时,势能最小,且ε-=)r u (;当r=σ时,0(=)
r u ;说明ε和σ的物理意义。
5、如果离子晶体中离子总得相互作用势能为]4[N )(/02
ρλπεμr e Z r q r u ---=,求晶体的压缩系数,其中λ,ρ为常数,Z 为配位数。
6、设两原子间的互作用能可由n m r r r U βα
+-=)(表述。
若m=2,n=10,而且两原子构
成稳定的分子,其核间距离为m 10103-⨯,离解能为eV 4,试计算:① βα和;② 使该分子分裂所必须的力和当分裂发生时原子核的临界间距;③ 使原子间距比平衡距离减少10%时所需的压力?。
立方晶系晶面间距公式

立方晶系晶面间距公式立方晶系是一种晶体结构,它的晶格常数a、b、c相等,轴角α、β、γ都等于90°。
立方晶系有三种类型:简单立方(SC)、面心立方(FCC)和体心立方(BCC)。
不同类型的立方晶系的晶面间距公式也不同。
简单立方晶面间距公式简单立方是最简单的晶体结构,它的每个顶点上都有一个原子。
简单立方的晶面间距公式是:d=a√h2+k2+l2其中,a是晶格常数,h、k、l是晶面指数。
这个公式可以用几何方法推导出来,如下图所示:简单立方晶面间距推导在简单立方中,相邻两个原子的距离就是a,所以我们可以用a作为单位长度。
假设我们要求的晶面为(hkl),它与三个坐标轴的交点分别为A、B、C。
那么,A点的坐标就是(a/h,0,0),B点的坐标就是(0,a/k,0),C点的坐标就是(0,0,a/l)。
由于A、B、C三点共线,所以它们满足以下关系:x a/h =ya/k=za/l这个方程就是(hkl)晶面的方程。
我们可以用它来求出任意一点P(x,y,z)到这个晶面的距离d。
为了方便计算,我们取P点为原点(0,0,0),那么d就等于原点到晶面的垂直距离。
根据点到平面距离的公式,我们有:d=|Ax+By+Cz+D|√A2+B2+C2其中,A、B、C、D是平面方程Ax+By+Cz+D=0的系数。
将(hkl)晶面的方程代入,得到:d=|a/hx+a/ky+a/lz|√(a/h)2+(a/k)2+(a/l)2将P点的坐标(0,0,0)代入,得到:d=a√(h/a)2+(k/a)2+(l/a)2化简后,得到:d=a√h2+k2+l2这就是简单立方晶面间距公式。
面心立方晶面间距公式面心立方是一种常见的金属结构,它在每个顶点和每个面心都有一个原子。
面心立方的晶面间距公式是:d=a√4(h2+k2+l2)其中,a是晶格常数,h、k、l是晶面指数。
这个公式也可以用几何方法推导出来,如下图所示:面心立方晶面间距推导在面心立方中,相邻两个顶点原子的距离是√2a,相邻两个面心原子的距离是a,所以我们可以用a作为单位长度。
固体物理课后习题答案

(
)
⎞ 2π k⎟= −i + j + k 同理 ⎠ a
(
)
(
)
(
)
2π ⎧ ⎪b1 = a −i + j + k ⎪ 2π ⎪ i− j+k ⎨b 2 = a ⎪ 2π ⎪ ⎪b3 = a i + j − k ⎩
(
)
(
)
(
)
由此可得出面心立方格子的倒格子为一体心立方格子; 所以体心立方格子和面心立方格子互为正倒格子。 2.2 在六角晶系中,晶面常用四个指数(hkil)来表示,如图 所示,前三个指数表示晶面族中最靠近原点的晶面在互成 1200的 共面轴 a1 , a2 , a3 上的截距为
设两法线之间的夹角满足
K 1 i K 2 = K1 i K 2 cos γ
K 1iK 2 cos γ = = K1 i K 2 2π 2π (h1 i + k1 j + l1 k )i (h2 i + k2 j + l2 k ) a a 2π 2π 2π 2π (h1 i + k1 j + l1 k )i (h1 i + k1 j + l1 k ) i (h2 i + k2 j + l2 k )i (h2 i + k2 j + l2 k ) a a a a
a1 a2 a3 , , ,第四个指数表示该晶面 h k i
在六重轴c上的截距为
c 。证明: l
i = −(h + k )
并将下列用(hkl)表示的晶面改用(hkil)表示:
2
第一章 晶体的结构
( 001) , (133) , (110 ) , ( 323) , (100 ) , ( 010 ) , ( 213) .
工程材料密排面和密排方向

面心立方晶格
晶向指 数
<100>
晶向原 子
排列示 意图
晶向原 子密度 (原子数/ 长度)
晶向原 子
排列示 意图
晶向原 子密度 (原子数/ 长度)
<110> <111>
晶体的各向异性 多晶型性
金属的实际构造与晶体缺陷
⑴ 单晶体与多晶体
单晶体:其内部晶格方位完 全一致的晶体。
多晶体:
晶粒:实际使用的金属材料 纯铁组织
体心晶体构造中的间隙 四面体间隙 八面体间隙
密排立方晶体构造中的间隙 四面体间隙 八面体间隙
• 1) fcc和hcp都是密排构造,而bcc那么是比较“开放〞的构造, 因为它的间隙较多。
• 2) fcc和hcp金属中的八面体间隙大于四面体间隙,故这些金属 中的间隙原子往往位于八面体间隙中。
• 3〕在bcc晶体中,四面体间隙大于八面体间隙,因而间隙原子 应占据四面体间隙位置。但有些情况下,间隙原子占据八面体间 隙位置〔如碳在α-铁中〕。
位错:晶格中一局部晶体 相对于另一局部晶体发生 局部滑移,滑移面上滑移 区与未
滑移区的交界限称作位错。分为刃型位错和螺型位错。
刃型位错
螺型位错
刃型位错和螺型位错
刃位错的形成
刃型位错:当一个完整晶体某晶面以上的某处多出 半个原子面,该晶面象刀刃一样切入晶体,这个多 余原子面的边缘就是刃型位错。
半原子面在滑移面以上的称正位错,用“ ┴ 〞表示。 半原子面在滑移面以下的称负位错,用“ ┬ 〞表示。
位错密度:单位体积内所包 含的位错线总长度。
= S/V(cm/cm3或1/cm2)
金属的位错密度为104~1012/cm2
位错对性能的影响:金属的 塑性变形主要由位错运动引 起,因此阻碍位错运动是强 化金属的主要途径。
固体物理 讲习题参考答案

解:(1)由平衡条件
∂U ∂r
r0
=
mα r m+1
−
nβ r n+1
=
0 ,得
1
平衡间距
r0
=
nβ mα
n−m
(2)将 U(r)理解为晶体中所有其他原子对某一个原子的相互作用
则系统总的内能为对所有原子求和
U
total
2
r0 ∝ q1−n
,
U0
∝
q2 r0
当 q → 2q ,
r0′
=
4−
1 n−1
r0
因为晶格常数 a ∝ r0 ,故晶格常数满足相同的变化规律
n
结合能 W ′ = −U0′ = 4n−1W0
2.3.若一晶体的相互作用能可以表示为
U (r) = − α + β rm rn
试求(1)平衡间距 r0 (2)结合能 W(单个原子的) (3)体弹性模量 (4)若 m=2,n=10,r0=3A,W=4eV,求α,β值。
1.11
证明六角晶体的介电常数张量为
0
ε2
0
0 0 ε2
证
1:六角晶体,设介电常数为
ε ε
xx yx
ε xy ε yy
ε ε
xz yz
,取坐标架如图示
ε zx ε zy ε zz
选电场方向在 x 轴方向,有
Dx ε xx
Dy
0
− sin 60
,可得
ε yy
= ε zz
cos 60
第六讲
2.2.讨论使离子电荷加倍所引起的对 NaCl 晶格常数及结合能得影响。(排斥势看作不变) 解:NaCl 为离子晶体,系统内能可写为
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
体心立方、面心立方晶格主要晶面的原子排列和密度
体心立方晶格面心立方晶格
晶面指数晶面原子
排列示意图
晶面原子密度
(原子数/面积)
晶面原子
排列示意图
晶面原子密度
(原子数/面积)
{100} {110} {111}
体心立方、面心立方晶格主要晶向的原子排列和密度
体心立方晶格面心立方晶格
晶向指数晶向原子
排列示意图
晶向原子密度
(原子数/长度)
晶向原子
排列示意图
晶向原子密度
(原子数/长度)
<100>
<110>
<111>
第1章小结
1.三种常见金属的晶体结构
体心立方晶格(胞):晶格常数a、90°,晶胞原子数为2个,原子半径:,
致密度为68%,最大空隙半径r四=0.29r原子,配位数为8面心立方晶格(胞):晶格常数a、90°,晶胞原子数为4个,
原子半径:
,
致密度为74%,最大空隙半径r八=0.414r原子,配位数为12。
密排六方晶格(胞):晶格常数a、c、90°、120°,晶胞原子数为6个,
原子半径:,
致密度为74%,最大空隙半径r八=0.414r原子,配位数为12。
2.晶面与晶向可用晶面指数与晶向指数来表达。
不同晶面、不同晶向上的原子排列情况不同。
体心立方晶格的最密面为{110},最密方向为<111>。
面心立方晶格的最密面为{111},最密方向为<110>。
密排六方晶格的最密面为{0001},最密方向为。
3.实际金属中含有点缺陷(空位、间隙原子、异类原子)、线缺陷(位错)、面缺陷(晶界、亚晶界)三类晶体缺陷,位错密度增加,材料强度增加。
晶界越多,晶粒越细,金属的强度越高,同时塑性越好(即细晶强化)。
4.合金中有两类基本相:固溶体和金属化合物。
固溶强化是金属强化的一种重要形式。
细小弥散分布的金属化合物可产生弥散强化或第二相强化。
材料的微观组成和微观形貌称组织,材料的组织取决于化学成分和工艺过程。
5.金属材料的性能特点是:强度高,韧性好,塑性变形能力强,综合机械性能好,通过热处理可以大幅度改变机械性能。
金属材料导电、导热性好。
不同的金属材料耐蚀性相差很大,钛、不锈钢耐蚀性好,碳钢、铸铁耐蚀性差。
6.高分子材料结构由大分子链组成,大分子链之间的相互作用力为分子键,分子链的原子之间、链节之间的相互作用力为共价键。
高分子材料的大分子链结构与聚集态及其性能密切相关。
高分子的聚集态结构分无定形和晶态两种。
线型非晶态高聚物在不同温度下表现三种物理状态:玻璃态、高弹态、粘流态。
高分子材料的性能特点:高聚物轻,其特有的机械性能是高弹性和粘弹性。
由于可以处于不同的力学状态,高分子材料可以是硬脆、强硬、强韧、柔韧或软弱的,机械性能不高,刚度小,强度不高,韧性较低。
高分子材料耐磨、减摩性能好,绝缘、绝热、绝声,耐蚀性能好,但耐热性不高,存在老化问题。
7. 陶瓷材料的生产过程包括原料的制备、坯料的成形和制品的烧结三大步骤。
典型陶瓷的组织由晶体相、玻璃相和气相组成。
晶体相是陶瓷的主要组成,决定材料的基本性能。
普通陶瓷的晶体相主要是硅酸盐,特种陶瓷的晶体相为氧化物、碳化物、氮化物、硼化物和硅化物,金属陶瓷则还有金属。
玻璃相为非均质的酸性和碱性氧化物的非晶态固体,起粘结剂作用。
气相是陶瓷组织中残留的孔洞,极大地破坏材料的机械性能。
陶瓷的性能特点是:具有不可燃烧性、高耐热性、高化学稳定性、不老化性、高的硬度和良好的抗压能力,但脆性很高,温度急变抗力很低,抗拉、抗弯性能差,不易加工。
