四川省成都树德中学(九中)2017年自主招生数学答案
成都树德中学(九中)2016年自主招生考试数学试题
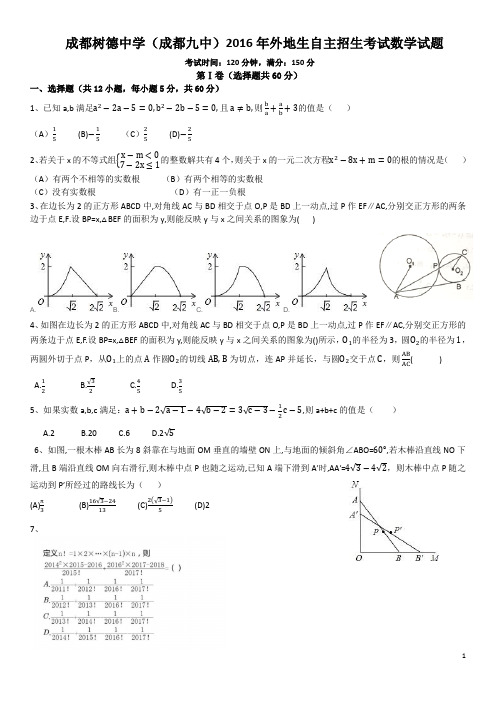
成都树德中学(成都九中)2016年外地生自主招生考试数学试题考试时间:120分钟,满分:150分第Ⅰ卷(选择题共60分)一、选择题(共12小题,每小题5分,共60分)1、已知a,b满足a2−2a−5=0,b2−2b−5=0,且a≠b,则ba +ab+3的值是()(A)15(B)−15(C)25(D)−252、若关于x的不等式组{x−m<07−2x≤1的整数解共有4个,则关于x的一元二次方程x2−8x+m=0的根的情况是()(A)有两个不相等的实数根(B)有两个相等的实数根(C)没有实数根(D)有一正一负根3、在边长为2的正方形ABCD中,对角线AC与BD相交于点O,P是BD上一动点,过P作EF∥AC,分别交正方形的两条边于点E,F.设BP=x,△BEF的面积为y,则能反映y与x之间关系的图象为( )A. B. C. D.4、如图在边长为2的正方形ABCD中,对角线AC与BD相交于点O,P是BD上一动点,过P作EF∥AC,分别交正方形的两条边于点E,F.设BP=x,△BEF的面积为y,则能反映y与x之间关系的图象为()所示,O1的半径为3,圆O2的半径为1,两圆外切于点P,从O1上的点A作圆O2的切线AB,B为切点,连AP并延长,与圆O2交于点C,则ABAC( )A.1 2B.√32C.45D.355、如果实数a,b,c满足:a+b−2√a−1−4√b−2=3√c−3−12c−5,则a+b+c的值是()A.2B.20C.6D.2√56、如图,一根木棒AB长为8斜靠在与地面OM垂直的墙壁ON上,与地面的倾斜角∠ABO=60°,若木棒沿直线NO下滑,且B端沿直线OM向右滑行,则木棒中点P也随之运动,已知A端下滑到A′时,AA′=4√3−4√2,则木棒中点P随之运动到P′所经过的路线长为()(A)π3(B)16√3−2413(C)2(√3−1)5(D)27、8、已知相互垂直的直线、已知相互垂直的直线L 1:y =k 1x +2−k 1与L 2:y =k 2x +2−3k 2交于点P ,O 为坐标原点,则op 的最大值是( )A.√13B.√3+2C.4√2+9D.2√2+19、若图所示,O,I 分别表示△ABC 的外心与内心,已知∠OIB=30°,则∠BAC=A.30°B.45°C.60°D.75°10、若实数x 、y 满足关系式2xy−x−y=2,则x 2+y 2的最小值为( )A. 3−√5B. 3+√5C. 8+4√3D. 8-4√311、已知函数y=cosx,a,b,c 分别为△ABC 的内角A,B,C 所对的边,且a 2+b 2≤c 2,则下列不等式一定成立的是( )(A )cos(sinA)≤cos(cosB) (B)cos(sinA)≤cos(sinB)(C)cos (cosA )≤cos (sinB ) (D)cos(cosA)≤cos(cosB)12、如图,在平面直角坐标系中,矩形OABC 的顶点O 在坐标原点,顶点A. C 分别在x 轴、y 轴的正半轴上,且OA=2,OC=1,矩形对角线AC 、OB 相交于E,过点E 的直线与边OA 、BC 分别相交于点G 、H,以O 为圆心,OC 为半径的圆弧交OA 于D,若直线GH 与弧CD 所在的圆相切于矩形内一点F,则下列结论:①AG=CH;②GH=103;③直线GH 的函数关系式y=−34x+54;④梯形ABHG 的内部有一点P,当☉P 与HG 、GA 、AB 都相切时,☉P 的半径为12.其中正确的有( )(A ) 1个 (B) 2个 (C) 3个 (D)4个第Ⅱ卷 (非选择题 共90分)二、填空题:(共4小题,每小题5分,共20分,把答案填在答题卡的相应位置)13、已知抛物线22)2(212++-+=x x b x y 向右平移2个单位后得到抛物线τ,τ经过点)0,4(A .设点)3,1(-C ,请在抛物线τ的对称轴上确定一点D ,使得CD AD -的值最大,则D 点的坐标为___________________.14、端午节是我国的传统节日,人们有吃粽子的习惯。
四川省成都市树德中学2017届高三(上)10月段考数学试卷(文科)(解析版)

2016-2017学年四川省成都市树德中学高三(上)10月段考数学试卷(文科)一.选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知全集U=Z,集合A={1,6},A∪B={2,0,1,6},那么(∁U A)∩B=()A.∅B.{3,4,5}C.{2,0}D.{1,6}2.复数Z=(i为虚数单位)所对应复平面内的点在()A.第一象限 B.第二象限 C.第三象限 D.第四象限3.已知a,b是平面α内的两条不同直线,直线l在平面α外,则l⊥a,l⊥b是l⊥α的()A.充分不必要条件B.必要不充分条件C.充要条件 D.既不充分也不必要条件4.若[x]表示不超过x的最大整数,如[2,6]=2,[﹣2,6]=﹣3,执行如图所示的程序框图,记输出的值为S0,则=()A.﹣1 B.0 C.1 D.25.函数f(x)=sin(2x+φ)|φ|<)的图象向左平移个单位后关于原点对称,则φ等于()A.B.﹣C.D.6.若等差数列{a n}的公差d≠0,前n项和为S n,若∀n∈N*,都有S n≤S10,则()B.a9•a10>0A.∀n∈N*,都有a n<a n﹣1C.S2>S17D.S19≥07.函数y=e﹣|x﹣1|的图象大致形状是()A.B.C.D.8.已知点P在直线x+3y﹣2=0上,点Q在直线x+3y+6=0上,线段PQ的中点为M(x0,y0),且y0<x0+2,则的取值范围是()A.[﹣,0)B.(﹣,0)C.(﹣,+∞)D.(﹣∞,﹣)∪(0,+∞)9.已知某几何体的三视图如图所示,三视图是边长为1的等腰直角三角形和边长为1的正方形,则该几何体的体积为()A.B.C.D.10.已知函数f(x)=,则使得f(x)>f(2x﹣1)成立的x的取值范围是()A. B.C.D.11.设e1、e2分别为具有公共焦点F1、F2的椭圆和双曲线的离心率,P是两曲线的一个公共点,且满足||=||,则的值为()A.B.2 C.D.112.在锐角△ABC中,A,B,C所对边分别为a,b,c,且b2﹣a2=ac,则﹣的取值范围为()A.(1,+∞)B.(1,)C.(1,)D.(,)二.填空题(每小题5分,共20分)13.若sinx=﹣,则cos2x=.14.已知正数x,y满足x+y﹣xy=0,则3x+2y的最小值为.15.过直线y=x上的一点作圆(x﹣5)2+(y﹣1)2=2的两条切线l1、l2,当直线l1、l2关于y=x对称时,l1、l2所成的角为.16.已知函数f(x)=x2﹣2tx﹣4t﹣4,g(x)=﹣(t+2)2,两个函数图象的公切线恰为3条,则实数t的取值范围为.三.解答题(共70分)17.已知数列{a n}的前n项和S n满足2S n=3a n﹣1,其中n∈N*.(Ⅰ)求数列{a n}的通项公式;(Ⅱ)设a n b n=,求数列{b n}的前n项和为T n.18.如图为某校语言类专业N名毕业生的综合测评成绩(百分制)分布直方图,已知80~90分数段的学员数为21人.(Ⅰ)求该专业毕业总人数N和90~95分数段内的人数n;(Ⅱ)现欲将90~95分数段内的n名人分配到几所学校,从中安排2人到甲学校去,若n 人中仅有两名男生,求安排结果至少有一名男生的概率.19.如图所示,已知正方形ABCD的边长为2,AC∩BD=O.将正方形ABCD沿对角BD折起,得到三棱锥A﹣BCD.(1)求证:平面AOC⊥平面BCD;(2)若三棱锥A﹣BCD的体积为,求AC的长.20.已知椭圆C的中心在原点O,焦点在x轴上,离心率为,椭圆C上的点到右焦点的最大距离为3.(1)求椭圆C的标准方程.(2)斜率存在的直线l与椭圆C交于A,B两点,并且满足以AB为直径的圆过原点,求直线在y轴上截距的取值范围.21.设函数f(x)=(1﹣ax)ln(x+1)﹣bx,其中a和b是实数,曲线y=f(x)恒与x轴相切于坐标原点.(1)求常数b的值;(2)当a=1时,讨论函数f(x)的单调性;(3)当0≤x≤1时关于x的不等式f(x)≥0恒成立,求实数a的取值范围.[选修4-1:几何证明选讲]22.如图,△OAB是等腰三角形,∠AOB=120°.以O为圆心,OA为半径作圆.(Ⅰ)证明:直线AB与⊙O相切;(Ⅱ)点C,D在⊙O上,且A,B,C,D四点共圆,证明:AB∥CD.[选修4-4:坐标系与参数方程]23.在直角坐标系xOy中,以O为原点,Ox轴为极轴,单位长度不变,建立极坐标系,直线l的极坐标方程为:ρsin(θ+)=,曲线C的参数方程为:(1)写出直线l和曲线C的普通方程;(2)若直线l和曲线C相交于A,B两点,定点P(﹣1,2),求线段|AB|和|PA|•|PB|的值.[选修4-5:不等式选讲]24.已知不等式|x﹣2|>3的解集与关于x的不等式x2﹣ax﹣b>0的解集相同.(1)求实数a,b的值;(2)求函数f(x)=a+b的最大值.2016-2017学年四川省成都市树德中学高三(上)10月段考数学试卷(文科)参考答案与试题解析一.选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知全集U=Z,集合A={1,6},A∪B={2,0,1,6},那么(∁U A)∩B=()A.∅B.{3,4,5}C.{2,0}D.{1,6}【考点】交、并、补集的混合运算.【分析】直接利用补集和交集的运算进行求解即可得到答案【解答】解:全集U=Z,集合A={1,6},A∪B={2,0,1,6},∴集合B⊆A∪B,并且一定有0,2,∴∁U A也一定有0,2,∴(∁U A)∩B={0,2}.故选:C.2.复数Z=(i为虚数单位)所对应复平面内的点在()A.第一象限 B.第二象限 C.第三象限 D.第四象限【考点】复数代数形式的乘除运算.【分析】利用复数代数形式的乘除运算化简求得Z所对应点的坐标得答案.【解答】解:由Z==,得复数Z=所对应复平面内的点的坐标为(),在第三象限.故选:C.3.已知a,b是平面α内的两条不同直线,直线l在平面α外,则l⊥a,l⊥b是l⊥α的()A.充分不必要条件B.必要不充分条件C.充要条件 D.既不充分也不必要条件【考点】空间中直线与直线之间的位置关系;必要条件、充分条件与充要条件的判断;空间中直线与平面之间的位置关系.【分析】根据空间线面垂直的判定定理和定义,结合充要条件的定义,可得结论.【解答】解:若l⊥α,则l⊥a,l⊥b,故l⊥a,l⊥b是l⊥α的必要条件;但l⊥a,l⊥b时,l⊥a不一定成立,故l⊥a,l⊥b是l⊥α的不充分条件;综上可得:l⊥a,l⊥b是l⊥α的必要不充分条件,故选:B4.若[x]表示不超过x的最大整数,如[2,6]=2,[﹣2,6]=﹣3,执行如图所示的程序框图,记输出的值为S0,则=()A.﹣1 B.0 C.1 D.2【考点】程序框图.【分析】根据框图的流程依次计算程序运行的结果,直到满足条件n>4,计算输出S的值,即可得出结论.【解答】解:由程序框图知:第一次运行S=1+[]=1,n=1+1=2;第二次运行S=1+[]=1,n=2+1=3;第三次运行S=1+[]=2,n=3+1=4;第四次运行S=2+[]=3,n=4+1=5.满足条件n>4,退出循环,输出S=3.∴=﹣1.故选:A.5.函数f(x)=sin(2x+φ)|φ|<)的图象向左平移个单位后关于原点对称,则φ等于()A.B.﹣C.D.【考点】函数y=Asin(ωx+φ)的图象变换.【分析】由条件根据函数y=Asin(ωx+φ)的图象变换规律,正弦函数的图象的对称性可得+φ=kπ,k∈z,由此根据|φ|<求得φ的值.【解答】解:函数f(x)=sin(2x+φ)φ|<)的图象向左平移个单位后,得到函数y=sin[2(x+)+φ]=sin(2x++φ)的图象,再根据所得图象关于原点对称,可得+φ=kπ,k∈z,∴φ=﹣,故选:D.6.若等差数列{a n}的公差d≠0,前n项和为S n,若∀n∈N*,都有S n≤S10,则()B.a9•a10>0A.∀n∈N*,都有a n<a n﹣1C.S2>S17D.S19≥0【考点】等差数列的前n项和;数列的函数特性.【分析】由∀n∈N*,都有S n≤S10,a10≥0,a11≤0,再根据等差数列的性质即可判断.【解答】解:∵∀n∈N*,都有S n≤S10,∴a10≥0,a11≤0,∴a9+a11≥0,∴S2≥S17,S19≥0,故选:D.7.函数y=e﹣|x﹣1|的图象大致形状是()A.B.C.D.【考点】指数函数的图象变换.【分析】由已知写出分段函数解析式,作出分段函数的图象得答案.【解答】解:∵y=e﹣|x﹣1|=,∴函数函数y=e﹣|x﹣1|的图象大致形状是:故选:B.8.已知点P在直线x+3y﹣2=0上,点Q在直线x+3y+6=0上,线段PQ的中点为M(x0,y0),且y0<x0+2,则的取值范围是()A.[﹣,0)B.(﹣,0)C.(﹣,+∞)D.(﹣∞,﹣)∪(0,+∞)【考点】直线的斜率.【分析】由题意可得,线段PQ的中点为M(x0,y0)到两直线的距离相等,利用,可得x0+3y0+2=0.又y0<x0+2,设=k OM,分类讨论:当点位于线段AB(不包括端点)时,当点位于射线BM(不包括端点B)时,即可得出.【解答】解:∵点P在直线x+3y﹣2=0上,点Q在直线x+3y+6=0上,线段PQ的中点为M (x0,y0),∴,化为x0+3y0+2=0.又y0<x0+2,设=k OM,当点位于线段AB(不包括端点)时,则k OM>0,当点位于射线BM(不包括端点B)时,k OM<﹣.∴的取值范围是(﹣∞,﹣)∪(0,+∞).故选:D.9.已知某几何体的三视图如图所示,三视图是边长为1的等腰直角三角形和边长为1的正方形,则该几何体的体积为()A.B.C.D.【考点】由三视图求面积、体积.【分析】根据几何体的三视图,得出该几何体是棱长为1的正方体中的三棱锥,画出该三棱锥的直观图,求出它的体积.【解答】解:根据几何体的三视图,得;该几何体是棱长为1的正方体中一三棱锥P﹣ABC,如图所示;∴该三棱锥的体积为××12×1=.故选:A.10.已知函数f(x)=,则使得f(x)>f(2x﹣1)成立的x 的取值范围是()A. B.C.D.【考点】其他不等式的解法.【分析】根据函数的表达式求出f(x)的单调性和奇偶性,通过讨论x的符号,从而求出x 的范围即可.【解答】解:∵函数f(x)=,∴x>0时,f(x)=﹣,和随着x的增大而减小,故x>0时,f(x)是减函数,而f(x)在R是偶函数,故x<0时,f(x)是增函数,若f(x)>f(2x﹣1)成立,则|x|<|2x﹣1|,解得:x>1或x<,又1+≠0,解得x≠﹣1,故选:D.11.设e1、e2分别为具有公共焦点F1、F2的椭圆和双曲线的离心率,P是两曲线的一个公共点,且满足||=||,则的值为()A.B.2 C.D.1【考点】圆锥曲线的共同特征.【分析】利用||=||,可知∠F1PF2=90°,设|PF1|=m,|PF2|=n,|F1F2|=2c,不妨设m>n,可得m2+n2=4c2,求出,,再求出平方倒数的和,即可得到结论.【解答】解:设|PF1|=m,|PF2|=n,|F1F2|=2c,不妨设m>n,由||=||,可知∠F1PF2=90°∴m2+n2=4c2,∵,∴∴=故选A.12.在锐角△ABC中,A,B,C所对边分别为a,b,c,且b2﹣a2=ac,则﹣的取值范围为()A.(1,+∞)B.(1,)C.(1,)D.(,)【考点】余弦定理.【分析】根据正弦定理化简已知式子,由二倍角的余弦公式变形、和差化积公式和诱导公式化简后,由内角的范围和正弦函数的性质求出A与B关系,由锐角三角形的条件求出B的范围,利用商得关系、两角差的正弦公式化简所求的式子,由正弦函数的性质求出所求式子的取值范围.【解答】解:∵b2﹣a2=ac,∴由正弦定理得,sin2B﹣sin2A=sinAsinC,=sinAsinC,可得:=sinAsinC,由和差化积公式得cos2A﹣cos2B=﹣2sin(A+B)sin(A﹣B),代入上式得,﹣sin(A+B)sin(A﹣B)=sinAsinC,∵sin(A+B)=sinC≠0,∴﹣sin(A﹣B)=sinA,即sin(B﹣A)=sinA,在△ABC中,B﹣A=A,得B=2A,则C=π﹣3A,∵△ABC为锐角三角形,∴,解得,则<B<,∴﹣===,由<B<,得,sinB∈(,1),则∈(1,),∴﹣取值范围是(1,),故选:B.二.填空题(每小题5分,共20分)13.若sinx=﹣,则cos2x=0.【考点】同角三角函数基本关系的运用.【分析】利用二倍角的余弦公式求得cos2x的值.【解答】解:sinx=﹣,则cos2x=1﹣2sin2x=1﹣2×=0,故答案为:0.14.已知正数x,y满足x+y﹣xy=0,则3x+2y的最小值为5+2.【考点】基本不等式.【分析】得到+﹣=1,根据基本不等式的性质求出3x+2y的最小值即可.【解答】解:∵x+y﹣xy=0,∴+﹣=1,故3x+2y=(3x+2y)(+)=++5≥2+5=5+2,当且仅当=时“=”成立,故答案为:5+2.15.过直线y=x上的一点作圆(x﹣5)2+(y﹣1)2=2的两条切线l1、l2,当直线l1、l2关于y=x对称时,l1、l2所成的角为60°.【考点】圆的切线方程.【分析】过圆心M作直线l:y=x的垂线交于N点,过N点作圆的切线能够满足条件,不难求出夹角.【解答】解:圆(x﹣5)2+(y﹣1)2=2的圆心(5,1),过(5,1)与y=x垂直的直线方程:x+y﹣6=0,它与y=x的交点N(3,3),N到(5,1)距离是2,两条切线l1,l2,它们之间的夹角为60°.故答案为:60°.16.已知函数f(x)=x2﹣2tx﹣4t﹣4,g(x)=﹣(t+2)2,两个函数图象的公切线恰为3条,则实数t的取值范围为(,+∞).【考点】利用导数研究曲线上某点切线方程.【分析】设切点为(x1,f(x1)),(x2,g(x2)),分别求出f(x),g(x)导数,可得切线的方程,由同一直线可得即可化为﹣+=0,即8x23﹣4tx22+1=0有3个非零实根,令h(x)=8x3﹣4tx2+1,有3个非零零点,h(0)=1,求出h(x)导数,对t讨论,分t=0,t>0,t<0,求出单调区间和极值,即可得到所求范围.【解答】解:设切点为(x1,f(x1)),(x2,g(x2)),则f′(x1)=2x1﹣2t,g′(x2)=﹣,切线方程为y﹣f(x1)=f′(x1)(x﹣x1),即y=(2x1﹣2t)x﹣x12﹣4t﹣4;y﹣g(x2)=g′(x2)(x﹣x2),即y=﹣x+﹣t2﹣4t﹣4.即2x1﹣2t=﹣,且﹣x12﹣4t﹣4=﹣t2﹣4t﹣4.即有x1=t﹣,x12=t2﹣,即可化为﹣+=0,即8x23﹣4tx22+1=0有3个非零实根,令h(x)=8x3﹣4tx2+1,有3个非零零点,h(0)=1,h′(x)=24x2﹣8tx=24x(x﹣),当t=0时,h′(x)=24x2>0,h(x)递增,不符合条件;当t>0,当x<0或x>时,h′(x)>0,h(x)递增,0<x<时,h′(x)<0,h(x)递减,h(x)极大值为为h(0)=1>0,h(x)极小值为h()=1﹣t3,由1﹣t3<0,解得t>,若t<0,则当x>0或x<时,h′(x)>0,h(x)递增,<x<0时,h′(x)<0,h(x)递减,h(x)极大值为为h(0)=1>0,h(x)极小值为h()=1﹣t3>0,不符要求.故t>,故答案为:(,+∞).三.解答题(共70分)17.已知数列{a n }的前n 项和S n 满足2S n =3a n ﹣1,其中n ∈N *. (Ⅰ)求数列{a n }的通项公式;(Ⅱ)设a n b n =,求数列{b n }的前n 项和为T n .【考点】数列的求和;数列递推式. 【分析】( I )分n=1与n ≥2讨论,从而判断出{a n }是等比数列,从而求通项公式;( II )化简可得=3(﹣),利用裂项求和法求解.【解答】解:( I )∵,①当n=1时,a 1=a 1﹣,∴a 1=1,当n ≥2时,∵S n ﹣1=a n ﹣1﹣,② ①﹣②得:a n =a n ﹣a n ﹣1, 即:a n =3a n ﹣1(n ≥2), 又∵a 1=1,a 2=3,∴对n ∈N *都成立,故{a n }是等比数列,∴.( II )∵,∴=3(﹣),∴,∴,即T n =.18.如图为某校语言类专业N 名毕业生的综合测评成绩(百分制)分布直方图,已知80~90分数段的学员数为21人.(Ⅰ)求该专业毕业总人数N 和90~95分数段内的人数n ;(Ⅱ)现欲将90~95分数段内的n名人分配到几所学校,从中安排2人到甲学校去,若n 人中仅有两名男生,求安排结果至少有一名男生的概率.【考点】列举法计算基本事件数及事件发生的概率;频率分布直方图.【分析】(Ⅰ)根据频率分布直方图,先求出80~90分数段频率,即可求出N,再用1减去成绩落在其它区间上的频率,即得成绩落在90~95上的频率,继而期初该段的人数(Ⅱ)一一列举出所有的基本事件,再找到满足条件的基本事件,根据概率公式计算即可【解答】解:(Ⅰ)80~90分数段频率为P1=(0.04+0.03)×5=0.35,此分数段的学员总数为21人所以毕业生,的总人数N为N==60,90~95分数段内的人数频率为P1=1﹣(0.01+0.04+0.05+0.04+0.03+0.01)×5=0.1所以90~95分数段内的人数n=60×0.1=6,(Ⅱ)90~95分数段内的6人中有两名男生,4名女生设男生为1,2;女生为3,4,5,6,设安排结果中至少有一名男生为事件A从中取两名毕业生的所有情况(基本事件空间)为12,13,14,15,16,23,24,25,26,34,35,36,45,46,56共15种组合方式,每种组合发生的可能性是相同的,其中,至少有一名男生的种数为12,13,14,15,16,23,24,25,26共9种所以,P(A)==19.如图所示,已知正方形ABCD的边长为2,AC∩BD=O.将正方形ABCD沿对角BD折起,得到三棱锥A﹣BCD.(1)求证:平面AOC⊥平面BCD;(2)若三棱锥A﹣BCD的体积为,求AC的长.【考点】平面与平面垂直的判定;棱柱、棱锥、棱台的体积.【分析】(1)直接根据可得由正方形的性质可得AO⊥BD以及BD⊥CO,根据线面垂直的判定定理,可得AO⊥平面BCD,进而得到结论.(2)先根据三棱锥的体积求出棱锥的高,再分二面角为钝角和锐角两种情况分别求出AC 的长即可.【解答】(本小题满分14分)解:(1)证明:因为ABCD是正方形,所以BD⊥AO,BD⊥CO.…在折叠后的△ABD和△BCD中,仍有BD⊥AO,BD⊥CO.…因为AO∩CO=O,所以BD⊥平面AOC.…因为BD⊂平面BCD,所以平面AOC⊥平面BCD.…(2)解:设三棱锥A﹣BCD的高为h,由于三棱锥A﹣BCD的体积为,所以.…因为,所以.…以下分两种情形求AC的长:①当∠AOC为钝角时,如图,过点A作CO的垂线交CO的延长线于点H,由(1)知BD⊥平面AOC,所以BD⊥AH.又CO⊥AH,且CO∩BD=O,所以AH⊥平面BCD.所以AH为三棱锥A﹣BCD的高,即.…在Rt△AOH中,因为,所以=.…在Rt△ACH中,因为,则.…所以.…②当∠AOC为锐角时,如图,过点A作CO的垂线交CO于点H,由(1)知BD⊥平面AOC,所以BD⊥AH.又CO⊥AH,且CO∩BD=O,所以AH⊥平面BCD.所以AH为三棱锥A﹣BCD的高,即.…在Rt△AOH中,因为,所以=.…在Rt△ACH中,因为,则.…所以.综上可知,AC的长为或.…20.已知椭圆C的中心在原点O,焦点在x轴上,离心率为,椭圆C上的点到右焦点的最大距离为3.(1)求椭圆C的标准方程.(2)斜率存在的直线l与椭圆C交于A,B两点,并且满足以AB为直径的圆过原点,求直线在y轴上截距的取值范围.【考点】椭圆的简单性质.【分析】(1)由题意可知:设椭圆C的方程为(a>b>0),半焦距为c,由题意可知:e==,即a=2c,a+c=3,b2=a2﹣c2,即可求得a和b的值,即可求得椭圆的标准方程;(2)设直线l的方程为y=kx+m,代入椭圆方程,由△>0 求得3+4k2>m2,由韦达定理求得x1+x2=﹣,x1•x2=,由以AB为直径的圆过原点,•=0,由向量数量积的坐标表示x1•x2+y1•y2=0,求得7m2=12+12k2,代入即可求得m2>,7m2=12+12k2≥12,即可求得截距y轴上截距的取值范围.【解答】解:(1)由椭圆的焦点在x轴上,则设椭圆C的方程为(a>b>0),半焦距为c.由椭圆的离心率e==,即a=2c,由椭圆C上的点到右焦点的最大距离3,∴a+c=3,解得:a=2,c=1,由b2=a2﹣c2=3,∴椭圆C的标准方程:;(2)设直线l的方程为y=kx+m,由,整理得:(3+4k2)x2+8kmx+4m2﹣12=0,△=(8km)2﹣4(3+4k2)(4m2﹣12)>0,整理得:3+4k2>m2,设A(x1,y1),B(x2,y2),则x1+x2=﹣,x1•x2=,y1•y2=(kx1+m)(kx2+m)=k2x1•x2+km(x1+x2)+m2,以AB为直径的圆过原点,∴OA⊥OB,则•=0,∴x1•x2+y1•y2=0,即x1•x2+k2x1•x2+km(x1+x2)+m2=0,则(1+k2)x1•x2+km(x1+x2)+m2=0,(1+k2)•﹣km•+m2=0,化简得:7m2=12+12k2,将k2=m2﹣1,代入3+4k2>m2,3+4(m2﹣1)>m2,解得:m2>,又由7m2=12+12k2≥12,从而m2≥,m≥或m≤﹣.∴实m的取值范围(﹣∞,﹣]∪[,+∞).21.设函数f(x)=(1﹣ax)ln(x+1)﹣bx,其中a和b是实数,曲线y=f(x)恒与x轴相切于坐标原点.(1)求常数b的值;(2)当a=1时,讨论函数f(x)的单调性;(3)当0≤x≤1时关于x的不等式f(x)≥0恒成立,求实数a的取值范围.【考点】利用导数研究函数的单调性.【分析】(1)对f(x)求导,根据条件知f'(0)=0,所以1﹣b=0;(2)当a=1时,f(x)=(1﹣x)ln(x+1)﹣x,f(x)的定义域为(﹣1,+∞);令f'(x)=0,则导函数零点x+1=1,故x=0;当x∈(﹣1,0),f'(x)>0,f(x)在(﹣1,0)上单调递增;当x∈(0,+∞)上,f'(x)<0,f(x)在(0,+∞)上单调递减;(3)因为f(x)=(1﹣ax)ln(x+1)﹣x,0≤x≤1,对a进行分类讨论根据函数的单调性求得参数a使得不等式f(x)≥0;【解答】解:(1)对f(x)求导得:f'(x)=﹣aln(x+1)+根据条件知f'(0)=0,所以1﹣b=0,故b=1.(2)当a=1时,f(x)=(1﹣x)ln(x+1)﹣x,f(x)的定义域为(﹣1,+∞)f'(x)=﹣ln(x+1)+﹣1=﹣ln(x+1)+﹣2令f'(x)=0,则导函数零点x+1=1,故x=0;当x∈(﹣1,0),f'(x)>0,f(x)在(﹣1,0)上单调递增;当x∈(0,+∞)上,f'(x)<0,f(x)在(0,+∞)上单调递减;(3)由(1)知,f(x)=(1﹣ax)ln(x+1)﹣x,0≤x≤1f'(x)=﹣aln(x+1)+﹣1f''(x)=﹣①当a时,因为0≤x≤1,有f''(x)≥0,于是f'(x)在[0,1]上单调递增,从而f'(x)≥f'(0)=0,因此f(x)在[0,1]上单调递增,即f(x)≥f(0)而且仅有f(0)=0;②当a≥0时,因为0≤x≤1,有f''(x)<0,于是f'(x)在[0,1]上单调递减,从而f'(x)≤f'(0)=0,因此f(x)在[0,1]上单调递减,即f(x)≤f(0)=0而且仅有f(0)=0;③当﹣<a<0时,令m=min{1,﹣},当0≤x≤m时,f''(x)<0,于是f'(x)在[0,m]上单调递减,从而f'(x)≤f'(0)=0因此f(x)在[0,m]上单调递减,即f(x)≤f(0)而且仅有f(0)=0;综上:所求实数a的取值范围是(﹣∞,﹣].[选修4-1:几何证明选讲]22.如图,△OAB是等腰三角形,∠AOB=120°.以O为圆心,OA为半径作圆.(Ⅰ)证明:直线AB与⊙O相切;(Ⅱ)点C,D在⊙O上,且A,B,C,D四点共圆,证明:AB∥CD.【考点】圆的切线的判定定理的证明.【分析】(Ⅰ)设K为AB中点,连结OK.根据等腰三角形AOB的性质知OK⊥AB,∠A=30°,OK=OAsin30°=OA,则AB是圆O的切线.(Ⅱ)设圆心为T,证明OT为AB的中垂线,OT为CD的中垂线,即可证明结论.【解答】证明:(Ⅰ)设K为AB中点,连结OK,∵OA=OB,∠AOB=120°,∴OK⊥AB,∠A=30°,OK=OAsin30°=OA,∴直线AB与⊙O相切;(Ⅱ)因为OA=2OD,所以O不是A,B,C,D四点所在圆的圆心.设T是A,B,C,D 四点所在圆的圆心.∵OA=OB,TA=TB,∴OT为AB的中垂线,同理,OC=OD,TC=TD,∴OT为CD的中垂线,∴AB∥CD.[选修4-4:坐标系与参数方程]23.在直角坐标系xOy中,以O为原点,Ox轴为极轴,单位长度不变,建立极坐标系,直线l的极坐标方程为:ρsin(θ+)=,曲线C的参数方程为:(1)写出直线l和曲线C的普通方程;(2)若直线l和曲线C相交于A,B两点,定点P(﹣1,2),求线段|AB|和|PA|•|PB|的值.【考点】参数方程化成普通方程.【分析】(1)直线l 的极坐标方程为:ρsin (θ+)=,展开可得:ρ(sin θ+cos θ)=,利用互化公式可得直角坐标方程.曲线C 的参数方程为:,可得x 2=4(1+sin2t )=y ,x ∈.(2)直线l 的参数方程为:,代入曲线C 的方程可得: t ﹣2=0,可得|AB |=|t 1﹣t 2|=,|PA |•|PB |=|t 1t 2|.【解答】解:(1)直线l 的极坐标方程为:ρsin (θ+)=,展开可得:ρ(sin θ+cos θ)=,可得直角坐标方程:x +y ﹣1=0.曲线C 的参数方程为:,x 2=4(1+sin2t )=y ,x ∈.(2)直线l 的参数方程为:,代入曲线C 的方程可得: t ﹣2=0, ∴t 1+t 2=﹣,t 1•t 2=﹣2.∴|AB |=|t 1﹣t 2|===, |PA |•|PB |=|t 1t 2|=2.[选修4-5:不等式选讲]24.已知不等式|x ﹣2|>3的解集与关于x 的不等式x 2﹣ax ﹣b >0的解集相同. (1)求实数a ,b 的值;(2)求函数f (x )=a +b 的最大值.【考点】一般形式的柯西不等式;一元二次不等式的解法.【分析】(1)求出不等式|x ﹣2|>3的解集,即得不等式x 2﹣ax +b >0的解集,利用一元二次方程根与系数的关系求出 a 和b 的值,(2)根据柯西不等式即可求出最大值.【解答】解:(1)不等式|x ﹣2|>3的解集为{x |x <﹣1或x >5},所以不等式x 2﹣ax ﹣b >0的解集为{x |x <﹣1或x >5},所以﹣1,5是方程x 2﹣ax ﹣b=0的两根,所以,解得a=4,b=5.(2)函数f (x )=a +b 的定义域为[3,44],由柯西不等式得:[f(x)]2=(4+5)2≤[(16+25)(x﹣3+44﹣x)]2,.又因为f(x)≥0,所以f(x)≤4,当且仅当5=4时等号成立,即x=时,f(x)=41.所以函数f(x)的最大值为41.2017年1月11日。
(完整)自主招生数学试题及答案,推荐文档

2017年自主招生数学试题(分值: 100分 时间:90分钟)一、选择题(本大题共6小题,每小题5分,共30分,在每小题给出的四个选项中,只有一个选项是正确的)1、若对于任意实数,关于的方程都有实数根,则实数的a x 0222=+--b a ax x b 取值范围是( )A ≤0B ≤C ≤D ≤-1b b 21-b 81-b 2、如图,D 、E 分别是△ABC 的边AB 、BC 上的点,且DE∥AC,已知S △BDE ∶S △CDE =1∶3,则S △DOE ∶S △AOC 的值为( )A .1∶3B .1∶4C .1∶9D .1∶163、某校吴老师组织九(1)班同学开展数学活动,带领同学们测量学校附近一电线杆的高(如图所示)。
已知电线杆直立于地面上,某天在太阳光的照射下,电线杆的影子(折线BCD)恰好落在水平地面和斜坡上,在D 处测得电线杆顶端A 的仰角为300,在C 处测得电线杆顶端A 得仰角为450,斜坡与地面成600角,CD=4m ,则电线杆的高(AB)是( )A .mB .mC .mD .12m )344(+)434(-)326(+4、如图,矩形ABCD 中,AB=8,AD=3.点E 从D 向C 以每秒1个单位的速度运动,以AE 为一边在AE 的右下方作正方形AEFG .同时垂直于CD 的直线MN 也从C 向D 以每秒2个单位的速度运动,当经过( )秒时,直线MN 和正方形AEFG 开始有公共点。
A .53 B .12 C .43 D .23(第2题图) (第3题图) (第4题图)5、如图,在反比例函数的图象上有一动点A ,连接AO 并延长交图象的另一支于xy 2-=点B ,在第一象限内有一点C ,满足AC=BC ,当点A 运动时,点C 始终在函数的图xky =象上运动,若tan∠CAB=2,则k 的值为( )A. 2B. 4C. 6D. 86、如图,O 是等边三角形ABC 内一点,且OA=3,OB=4,OC=5.将线段OB 绕点B 逆时针旋转600得到线段O′B,则下列结论:①△AO′B 可以由△COB 绕点B 逆时针旋转600得到;②∠AOB=1500;③6AOBO'S =+四边形6AOB AOCS S +=△△是( )A.②③④B.①②④C.①④D.①②③O'OCB A(第5题图) (第6题图)二、填空题(本大题共6小题,每小题5分,共30分)7、已知方程组,且,则的取值范围是 。
2017年四川省成都市中考数学试题中考数学试题学含答案

2017年四川省成都市中考数学试卷一、选择题(本大题共10小题,每小题3分,共30分)1.《九章算术》中注有“今两算得失相反,要令正负以名之”,意思是:今有两数若其意义相反,则分别叫做正数与负数,若气温为零上10℃记作+10℃,则﹣3℃表示气温为()A.零上3℃B.零下3℃C.零上7℃D.零下7℃2.如图所示的几何体是由4个大小相同的小立方体组成,其俯视图是()A.B.C.D.3.总投资647亿元的西域高铁预计2017年11月竣工,届时成都到西安只需3小时,上午游武侯区,晚上看大雁塔将成为现实,用科学记数法表示647亿元为()A.647×108B.6.47×109C.6.47×1010D.6.47×10114.二次根式中,x的取值范围是()A.x≥1B.x>1C.x≤1D.x<15.下列图标中,既是轴对称图形,又是中心对称图形的是()A.B.C.D.6.下列计算正确的是()A.a5+a5=a10B.a7÷a=a6C.a3•a2=a6D.(﹣a3)2=﹣a67.学习全等三角形时,数学兴趣小组设计并组织了“生活中的全等”的比赛,全班同学的比赛结果统计如下表:得分(分)60708090100人数(人)7121083则得分的众数和中位数分别为()A.70分,70分B.80分,80分C.70分,80分D.80分,70分8.如图,四边形ABCD和A′B′C′D′是以点O为位似中心的位似图形,若OA:OA′=2:3,则四边形ABCD与四边形A′B′C′D′的面积比为()A.4:9B.2:5C.2:3D.:9.已知x=3是分式方程﹣=2的解,那么实数k的值为()A.﹣1B.0C.1D.210.在平面直角坐标系xOy中,二次函数y=ax2+bx+c的图象如图所示,下列说法正确的是()A.abc<0,b2﹣4ac>0B.abc>0,b2﹣4ac>0C.abc<0,b2﹣4ac<0D.abc>0,b2﹣4ac<0二、填空题(本大题共4小题,每小题4分,共16分)11.(﹣1)0=.12.在△ABC中,∠A:∠B:∠C=2:3:4,则∠A的度数为.13.如图,正比例函数y1=k1x和一次函数y2=k2x+b的图象相交于点A(2,1),当x<2时,y1 y2.(填“>”或“<”).14.如图,在平行四边形ABCD中,按以下步骤作图:①以A为圆心,任意长为半径作弧,分别交AB,AD于点M,N;②分别以M,N为圆心,以大于MN的长为半径作弧,两弧相交于点P;③作AP射线,交边CD于点Q,若DQ=2QC,BC=3,则平行四边形ABCD周长为.三、解答题(本大题共6小题,共54分)15.(1)计算:|﹣1|﹣+2sin45°+()﹣2;(2)解不等式组:.16.化简求值:÷(1﹣),其中x=﹣1.17.随着经济的快速发展,环境问题越来越受到人们的关注,某校学生会为了解节能减排、垃圾分类知识的普及情况,随机调查了部分学生,调查结果分为“非常了解”“了解”“了解较少”“不了解”四类,并将检查结果绘制成下面两个统计图.(1)本次调查的学生共有人,估计该校1200名学生中“不了解”的人数是人;(2)“非常了解”的4人有A1,A2两名男生,B1,B2两名女生,若从中随机抽取两人向全校做环保交流,请利用画树状图或列表的方法,求恰好抽到一男一女的概率.18.科技改变生活,手机导航极大方便了人们的出行,如图,小明一家自驾到古镇C游玩,到达A地后,导航显示车辆应沿北偏西60°方向行驶4千米至B地,再沿北偏东45°方向行驶一段距离到达古镇C,小明发现古镇C恰好在A地的正北方向,求B,C两地的距离.19.如图,在平面直角坐标系xOy中,已知正比例函数y=x的图象与反比例函数y=的图象交于A(a,﹣2),B两点.(1)求反比例函数的表达式和点B的坐标;(2)P是第一象限内反比例函数图象上一点,过点P作y轴的平行线,交直线AB于点C,连接PO,若△POC的面积为3,求点P的坐标.20.如图,在△ABC中,AB=AC,以AB为直径作圆O,分别交BC于点D,交CA的延长线于点E,过点D作DH⊥AC于点H,连接DE交线段OA于点F.(1)求证:DH是圆O的切线;(2)若A为EH的中点,求的值;(3)若EA=EF=1,求圆O的半径.四、填空题(本大题共5小题,每小题4分,共20分)21.如图,数轴上点A表示的实数是.22.已知x1,x2是关于x的一元二次方程x2﹣5x+a=0的两个实数根,且x12﹣x22=10,则a=.23.已知⊙O的两条直径AC,BD互相垂直,分别以AB,BC,CD,DA为直径向外作半圆得到如图所示的图形,现随机地向该图形内掷一枚小针,记针尖落在阴影区域内的概率为P1,针尖落在⊙O内的概率为P2,则=.24.在平面直角坐标系xOy中,对于不在坐标轴上的任意一点P(x,y),我们把点P′(,)称为点P的“倒影点”,直线y=﹣x+1上有两点A,B,它们的倒影点A′,B′均在反比例函数y=的图象上.若AB=2,则k=.25.如图1,把一张正方形纸片对折得到长方形ABCD,再沿∠ADC的平分线DE折叠,如图2,点C落在点C′处,最后按图3所示方式折叠,使点A落在DE的中点A′处,折痕是FG,若原正方形纸片的边长为6cm,则FG=cm.五、解答题(本大题共3小题,共30分)26.随着地铁和共享单车的发展,“地铁+单车”已成为很多市民出行的选择,李华从文化宫站出发,先乘坐地铁,准备在离家较近的A,B,C,D,E中的某一站出地铁,再骑共享单车回家,设他出地铁的站点与文化宫距离为x(单位:千米),乘坐地铁的时间y1(单位:分钟)是关于x的一次函数,其关系如下表:地铁站A B C D Ex(千米)891011.513y1(分钟)1820222528(1)求y1关于x的函数表达式;(2)李华骑单车的时间(单位:分钟)也受x的影响,其关系可以用y2=x2﹣11x+78来描述,请问:李华应选择在那一站出地铁,才能使他从文化宫回到家所需的时间最短?并求出最短时间.27.问题背景:如图1,等腰△ABC中,AB=AC,∠BAC=120°,作AD⊥BC于点D,则D为BC 的中点,∠BAD=∠BAC=60°,于是==;迁移应用:如图2,△ABC和△ADE都是等腰三角形,∠BAC=∠ADE=120°,D,E,C三点在同一条直线上,连接BD.①求证:△ADB≌△AEC;②请直接写出线段AD,BD,CD之间的等量关系式;拓展延伸:如图3,在菱形ABCD中,∠ABC=120°,在∠ABC内作射线BM,作点C关于BM的对称点E,连接AE并延长交BM于点F,连接CE,CF.①证明△CEF是等边三角形;②若AE=5,CE=2,求BF的长.28.如图1,在平面直角坐标系xOy中,抛物线C:y=ax2+bx+c与x轴相交于A,B两点,顶点为D(0,4),AB=4,设点F(m,0)是x轴的正半轴上一点,将抛物线C绕点F旋转180°,得到新的抛物线C′.(1)求抛物线C的函数表达式;(2)若抛物线C′与抛物线C在y轴的右侧有两个不同的公共点,求m的取值范围.(3)如图2,P是第一象限内抛物线C上一点,它到两坐标轴的距离相等,点P在抛物线C′上的对应点P′,设M是C上的动点,N是C′上的动点,试探究四边形PMP′N能否成为正方形?若能,求出m的值;若不能,请说明理由.2017年四川省成都市中考数学试卷参考答案与试题解析一、选择题(本大题共10小题,每小题3分,共30分)1.《九章算术》中注有“今两算得失相反,要令正负以名之”,意思是:今有两数若其意义相反,则分别叫做正数与负数,若气温为零上10℃记作+10℃,则﹣3℃表示气温为()A.零上3℃B.零下3℃C.零上7℃D.零下7℃【考点】11:正数和负数.【分析】此题主要用正负数来表示具有意义相反的两种量:若零上记为正,则零下就记为正,直接得出结论即可.【解答】解:若气温为零上10℃记作+10℃,则﹣3℃表示气温为零下3℃.故选:B.2.如图所示的几何体是由4个大小相同的小立方体组成,其俯视图是()A.B.C.D.【考点】U2:简单组合体的三视图.【分析】根据从上边看得到的图形是俯视图,可得答案.【解答】解:从上边看一层三个小正方形,故选:C.3.总投资647亿元的西域高铁预计2017年11月竣工,届时成都到西安只需3小时,上午游武侯区,晚上看大雁塔将成为现实,用科学记数法表示647亿元为()A.647×108B.6.47×109C.6.47×1010D.6.47×1011【考点】1I:科学记数法—表示较大的数.【分析】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值>1时,n是正数;当原数的绝对值<1时,n是负数.【解答】解:647亿=64700000000=6.47×1010,故选:C.4.二次根式中,x的取值范围是()A.x≥1B.x>1C.x≤1D.x<1【考点】72:二次根式有意义的条件.【分析】根据二次根式有意义的条件即可求出答案.【解答】解:由题意可知:x﹣1≥0,∴x≥1,故选(A)5.下列图标中,既是轴对称图形,又是中心对称图形的是()A.B.C.D.【考点】R5:中心对称图形;P3:轴对称图形.【分析】根据轴对称图形和中心对称图形的概念对各选项分析判断即可得解.【解答】解:A、不是轴对称图形,也不是中心对称图形,故本选项错误;B、不是轴对称图形,是中心对称图形,故本选项错误;C、是轴对称图形,不是中心对称图形,故本选项错误;D、既是轴对称图形,又是中心对称图形,故本选项正确.故选D.6.下列计算正确的是()A.a5+a5=a10B.a7÷a=a6C.a3•a2=a6D.(﹣a3)2=﹣a6【考点】48:同底数幂的除法;35:合并同类项;46:同底数幂的乘法;47:幂的乘方与积的乘方.【分析】利用同底数幂的乘法和除法法则以及合并同类项的法则运算即可.【解答】解:A.a5+a5=2a5,所以此选项错误;B.a7÷a=a6,所以此选项正确;C.a3•a2=a5,所以此选项错误;D.(﹣a3)2=a6,所以此选项错误;故选B.7.学习全等三角形时,数学兴趣小组设计并组织了“生活中的全等”的比赛,全班同学的比赛结果统计如下表:得分(分)60708090100人数(人)7121083则得分的众数和中位数分别为()A.70分,70分B.80分,80分C.70分,80分D.80分,70分【考点】W5:众数;W4:中位数.【分析】根据众数的定义,找到该组数据中出现次数最多的数即为众数;根据中位数定义,将该组数据按从小到大依次排列,处于中间位置的两个数的平均数即为中位数.【解答】解:70分的有12人,人数最多,故众数为70分;处于中间位置的数为第20、21两个数,都为80分,中位数为80分.故选:C.8.如图,四边形ABCD和A′B′C′D′是以点O为位似中心的位似图形,若OA:OA′=2:3,则四边形ABCD与四边形A′B′C′D′的面积比为()A.4:9B.2:5C.2:3D.:【考点】SC:位似变换.【分析】根据题意求出两个相似多边形的相似比,根据相似多边形的性质解答.【解答】解:∵四边形ABCD和A′B′C′D′是以点O为位似中心的位似图形,OA:OA′=2:3,∴DA:D′A′=OA:OA′=2:3,∴四边形ABCD与四边形A′B′C′D′的面积比为:()2=,故选:A.9.已知x=3是分式方程﹣=2的解,那么实数k的值为()A.﹣1B.0C.1D.2【考点】B2:分式方程的解.【分析】将x=3代入原方程即可求出k的值.【解答】解:将x=3代入﹣=2,∴解得:k=2,故选(D)10.在平面直角坐标系xOy中,二次函数y=ax2+bx+c的图象如图所示,下列说法正确的是()A.abc<0,b2﹣4ac>0B.abc>0,b2﹣4ac>0C.abc<0,b2﹣4ac<0D.abc>0,b2﹣4ac<0【考点】H4:二次函数图象与系数的关系.【分析】首先根据图象中抛物线的开口方向、对称轴的位置、与y轴交点的位置来判断出a、b、c的位置,进而判断各结论是否正确.【解答】解:根据二次函数的图象知:抛物线开口向上,则a>0;抛物线的对称轴在y轴右侧,则x=﹣>0,即b<0;抛物线交y轴于负半轴,则c<0;∴abc>0,∵抛物线与x轴有两个不同的交点,∴△=b2﹣4ac>0,故选B.二、填空题(本大题共4小题,每小题4分,共16分)11.(﹣1)0=1.【考点】6E:零指数幂.【分析】直接利用零指数幂的性质求出答案.【解答】解:(﹣1)0=1.故答案为:1.12.在△ABC中,∠A:∠B:∠C=2:3:4,则∠A的度数为40°.【考点】K7:三角形内角和定理.【分析】直接用一个未知数表示出∠A,∠B,∠C的度数,再利用三角形内角和定理得出答案.【解答】解:∵∠A:∠B:∠C=2:3:4,∴设∠A=2x,∠B=3x,∠C=4x,∵∠A+∠B+∠C=180°,∴2x+3x+4x=180°,解得:x=20°,∴∠A的度数为:40°.故答案为:40°.13.如图,正比例函数y1=k1x和一次函数y2=k2x+b的图象相交于点A(2,1),当x<2时,y1<y2.(填“>”或“<”).【考点】FF:两条直线相交或平行问题.【分析】由图象可以知道,当x=2时,两个函数的函数值是相等的,再根据函数的增减性即可得到结论.【解答】解:由腾讯知,当x<2时,y2的图象在y1上右,∴y1>y2.故答案为:<.14.如图,在平行四边形ABCD中,按以下步骤作图:①以A为圆心,任意长为半径作弧,分别交AB,AD于点M,N;②分别以M,N为圆心,以大于MN的长为半径作弧,两弧相交于点P;③作AP射线,交边CD于点Q,若DQ=2QC,BC=3,则平行四边形ABCD周长为15.【考点】N2:作图—基本作图;L5:平行四边形的性质.【分析】根据角平分线的性质可知∠DAQ=∠BAQ,再由平行四边形的性质得出CD∥AB,BC=AD=3,∠BAQ=∠DQA,故可得出△AQD是等腰三角形,据此可得出DQ=AD,进而可得出结论.【解答】解:∵由题意可知,AQ是∠DAB的平分线,∴∠DAQ=∠BAQ.∵四边形ABCD是平行四边形,∴CD∥AB,BC=AD=3,∠BAQ=∠DQA,∴∠DAQ=∠DAQ,∴△AQD是等腰三角形,∴DQ=AD=3.∵DQ=2QC,∴QC=DQ=,∴CD=DQ+CQ=3+=,∴平行四边形ABCD周长=2(DC+AD)=2×(+3)=15.故答案为:15.三、解答题(本大题共6小题,共54分)15.(1)计算:|﹣1|﹣+2sin45°+()﹣2;(2)解不等式组:.【考点】CB:解一元一次不等式组;2C:实数的运算;6F:负整数指数幂;T5:特殊角的三角函数值.【分析】(1)原式利用二次根式性质,特殊角的三角函数值,以及负整数指数幂法则计算即可得到结果.(2)分别求得两个不等式的解集,然后取其公共部分即可.【解答】解:(1)原式=﹣1﹣2+2×+4=﹣1﹣2++4=3;(2),①可化简为2x﹣7<3x﹣3,﹣x<4,x>﹣4,②可化简为2x≤1﹣3,则x≤﹣1.不等式的解集是﹣4<x≤﹣1.16.化简求值:÷(1﹣),其中x=﹣1.【考点】6D:分式的化简求值.【分析】原式括号中两项通分并利用同分母分式的减法法则计算,同时利用除法法则变形,约分得到最简结果,把已知代入计算即可求出值.【解答】解:÷(1﹣)=•=,∵x=﹣1,∴原式==.17.随着经济的快速发展,环境问题越来越受到人们的关注,某校学生会为了解节能减排、垃圾分类知识的普及情况,随机调查了部分学生,调查结果分为“非常了解”“了解”“了解较少”“不了解”四类,并将检查结果绘制成下面两个统计图.(1)本次调查的学生共有50人,估计该校1200名学生中“不了解”的人数是360人;(2)“非常了解”的4人有A1,A2两名男生,B1,B2两名女生,若从中随机抽取两人向全校做环保交流,请利用画树状图或列表的方法,求恰好抽到一男一女的概率.【考点】X6:列表法与树状图法;V5:用样本估计总体;VB:扇形统计图;VC:条形统计图.【分析】(1)用“非常了解”人数除以它所占的百分比即可得到调查的总人数;(2)用总人数乘以“不了解”人数所占的百分比即可得出答案;(3)先画树状图展示所有12个等可能的结果数,再找出恰好是一位男同学和一位女同学的结果数,然后根据概率公式求解.【解答】解:(1)4÷8%=50(人),1200×(1﹣40%﹣22%﹣8%)=360(人);故答案为:50,360;(2)画树状图,共有12根可能的结果,恰好抽到一男一女的结果有8个,∴P(恰好抽到一男一女的)==.18.科技改变生活,手机导航极大方便了人们的出行,如图,小明一家自驾到古镇C游玩,到达A地后,导航显示车辆应沿北偏西60°方向行驶4千米至B地,再沿北偏东45°方向行驶一段距离到达古镇C,小明发现古镇C恰好在A地的正北方向,求B,C两地的距离.【考点】TB:解直角三角形的应用﹣方向角问题;KU:勾股定理的应用.【分析】过B作BD⊥AC于点D,在直角△ABD中利用三角函数求得BD的长,然后在直角△BCD中利用三角函数求得BC的长.【解答】解:过B作BD⊥AC于点D.在Rt△ABD中,AD=AB•cos∠BAD=4cos60°=4×=2(千米),BD=AB•sin∠BAD=4×=2(千米),∵△BCD中,∠CBD=45°,∴△BCD是等腰直角三角形,∴CD=BD=2(千米),∴BC=BD=2(千米).答:B,C两地的距离是2千米.19.如图,在平面直角坐标系xOy中,已知正比例函数y=x的图象与反比例函数y=的图象交于A(a,﹣2),B两点.(1)求反比例函数的表达式和点B的坐标;(2)P是第一象限内反比例函数图象上一点,过点P作y轴的平行线,交直线AB于点C,连接PO,若△POC的面积为3,求点P的坐标.【考点】G8:反比例函数与一次函数的交点问题.【分析】(1)把A(a,﹣2)代入y=x,可得A(﹣4,﹣2),把A(﹣4,﹣2)代入y=,可得反比例函数的表达式为y=,再根据点B与点A关于原点对称,即可得到B的坐标;(2)过P作PE⊥x轴于E,交AB于C,先设P(m,),则C(m,m),根据△POC的面积为3,可得方程m×|m﹣|=3,求得m的值,即可得到点P的坐标.【解答】解:(1)把A(a,﹣2)代入y=x,可得a=﹣4,∴A(﹣4,﹣2),把A(﹣4,﹣2)代入y=,可得k=8,∴反比例函数的表达式为y=,∵点B与点A关于原点对称,∴B(4,2);(2)如图所示,过P作PE⊥x轴于E,交AB于C,设P(m,),则C(m,m),∵△POC的面积为3,∴m×|m﹣|=3,解得m=2或2,∴P(2,)或(2,4).20.如图,在△ABC中,AB=AC,以AB为直径作圆O,分别交BC于点D,交CA的延长线于点E,过点D作DH⊥AC于点H,连接DE交线段OA于点F.(1)求证:DH是圆O的切线;(2)若A为EH的中点,求的值;(3)若EA=EF=1,求圆O的半径.【考点】MR:圆的综合题.【分析】(1)根据同圆的半径相等和等边对等角证明:∠ODB=∠OBD=∠ACB,则DH⊥OD,DH是圆O的切线;(2)如图2,先证明∠E=∠B=∠C,则H是EC的中点,设AE=x,EC=4x,则AC=3x,由OD是△ABC的中位线,得:OD=AC=,证明△AEF∽△ODF,列比例式可得结论;(3)如图2,设⊙O的半径为r,即OD=OB=r,证明DF=OD=r,则DE=DF+EF=r+1,BD=CD=DE=r+1,证明△BFD∽△EFA,列比例式为:,则=,求出r的值即可.【解答】证明:(1)连接OD,如图1,∵OB=OD,∴△ODB是等腰三角形,∠OBD=∠ODB①,在△ABC中,∵AB=AC,∴∠ABC=∠ACB②,由①②得:∠ODB=∠OBD=∠ACB,∴OD∥AC,∵DH⊥AC,∴DH⊥OD,∴DH是圆O的切线;(2)如图2,在⊙O中,∵∠E=∠B,∴由(1)可知:∠E=∠B=∠C,∴△EDC是等腰三角形,∵DH⊥AC,且点A是EH中点,设AE=x,EC=4x,则AC=3x,连接AD,则在⊙O中,∠ADB=90°,AD⊥BD,∵AB=AC,∴D是BC的中点,∴OD是△ABC的中位线,∴OD∥AC,OD=AC=×3x=,∵OD∥AC,∴∠E=∠ODF,在△AEF和△ODF中,∵∠E=∠ODF,∠OFD=∠AFE,∴△AEF∽△ODF,∴,∴==,∴=;(3)如图2,设⊙O的半径为r,即OD=OB=r,∵EF=EA,∴∠EFA=∠EAF,∵OD∥EC,∴∠FOD=∠EAF,则∠FOD=∠EAF=∠EFA=∠OFD,∴DF=OD=r,∴DE=DF+EF=r+1,∴BD=CD=DE=r+1,在⊙O中,∵∠BDE=∠EAB,∴∠BFD=∠EFA=∠EAB=∠BDE,∴BF=BD,△BDF是等腰三角形,∴BF=BD=r+1,∴AF=AB﹣BF=2OB﹣BF=2r﹣(1+r)=r﹣1,在△BFD和△EFA中,∵,∴△BFD∽△EFA,∴,∴=,解得:r1=,r2=(舍),综上所述,⊙O的半径为.四、填空题(本大题共5小题,每小题4分,共20分)21.如图,数轴上点A表示的实数是.【考点】29:实数与数轴.【分析】直接利用勾股定理得出三角形斜边长即可得出A点对应的实数.【解答】解:由图形可得:AO==,则数轴上点A表示的实数是:.故答案为:.22.已知x1,x2是关于x的一元二次方程x2﹣5x+a=0的两个实数根,且x12﹣x22=10,则a=.【考点】AB:根与系数的关系.【分析】由x12﹣x22=0得x1+x2=0或x1﹣x2=0;当x1+x2=0时,运用两根关系可以得到﹣2m﹣1=0或方程有两个相等的实根,据此即可求得m的值.【解答】解:由两根关系,得根x1+x2=5,x1•x2=a,由x12﹣x22=10得(x1+x2)(x1﹣x2)=10,若x1+x2=5,即x1﹣x2=10,∴(x1﹣x2)2=(x1+x2)2﹣2x1•x2=25﹣2a=100,∴a=,故答案为:.23.已知⊙O的两条直径AC,BD互相垂直,分别以AB,BC,CD,DA为直径向外作半圆得到如图所示的图形,现随机地向该图形内掷一枚小针,记针尖落在阴影区域内的概率为P1,针尖落在⊙O内的概率为P2,则=.【考点】X5:几何概率.【分析】直接利用圆的面积求法结合正方形的性质得出P1,P2的值即可得出答案.【解答】解:设⊙O的半径为1,则AD=,=π,故S圆O阴影部分面积为:π×2+×﹣π=2,则P1=,P2=,故=.故答案为:.24.在平面直角坐标系xOy中,对于不在坐标轴上的任意一点P(x,y),我们把点P′(,)称为点P的“倒影点”,直线y=﹣x+1上有两点A,B,它们的倒影点A′,B′均在反比例函数y=的图象上.若AB=2,则k=﹣.【考点】G6:反比例函数图象上点的坐标特征;F8:一次函数图象上点的坐标特征.【分析】设点A(a,﹣a+1),B(b,﹣b+1)(a<b),则A′(,),B′(,),由AB=2可得出b=a+2,再根据反比例函数图象上点的坐标特征即可得出关于k、a、b的方程组,解之即可得出k值.【解答】解:设点A(a,﹣a+1),B(b,﹣b+1)(a<b),则A′(,),B′(,),∵AB=2,∴b﹣a=2,即b=a+2.∵点A′,B′均在反比例函数y=的图象上,∴,解得:k=﹣.故答案为:﹣.25.如图1,把一张正方形纸片对折得到长方形ABCD,再沿∠ADC的平分线DE折叠,如图2,点C落在点C′处,最后按图3所示方式折叠,使点A落在DE的中点A′处,折痕是FG,若原正方形纸片的边长为6cm,则FG=cm.【考点】PB:翻折变换(折叠问题);LB:矩形的性质;LE:正方形的性质.【分析】作GM⊥AC′于M,A′N⊥AD于N,AA′交EC′于K.易知MG=AB=AC′,首先证明△AKC′≌△GFM,可得GF=AK,由AN=4.5cm,A′N=1.5cm,C′K∥A′N,推出=,可得=,推出C′K=1.5cm,在Rt△AC′K中,根据AK=,求出AK即可解决问题.【解答】解:作GM⊥AC′于M,A′N⊥AD于N,AA′交EC′于K.易知MG=AB=AC′,∵GF⊥AA′,∴∠AFG+∠FAK=90°,∠MGF+∠MFG=90°,∴∠MGF=∠KAC′,∴△AKC′≌△GFM,∴GF=AK,∵AN=4.5cm,A′N=1.5cm,C′K∥A′N,∴=,∴=,∴C′K=1.5cm,在Rt△AC′K中,AK==cm,∴FG=AK=cm,故答案为.五、解答题(本大题共3小题,共30分)26.随着地铁和共享单车的发展,“地铁+单车”已成为很多市民出行的选择,李华从文化宫站出发,先乘坐地铁,准备在离家较近的A,B,C,D,E中的某一站出地铁,再骑共享单车回家,设他出地铁的站点与文化宫距离为x(单位:千米),乘坐地铁的时间y1(单位:分钟)是关于x的一次函数,其关系如下表:地铁站A B C D Ex(千米)891011.513y1(分钟)1820222528(1)求y1(2)李华骑单车的时间(单位:分钟)也受x的影响,其关系可以用y2=x2﹣11x+78来描述,请问:李华应选择在那一站出地铁,才能使他从文化宫回到家所需的时间最短?并求出最短时间.【考点】HE:二次函数的应用.【分析】(1)根据表格中的数据,运用待定系数法,即可求得y1关于x的函数表达式;(2)设李华从文化宫回到家所需的时间为y,则y=y1+y2=x2﹣9x+80,根据二次函数的性质,即可得出最短时间.【解答】解:(1)设y1=kx+b,将(8,18),(9,20),代入得:,解得:,故y1关于x的函数表达式为:y1=2x+2;(2)设李华从文化宫回到家所需的时间为y,则y=y1+y2=2x+2+x2﹣11x+78=x2﹣9x+80,∴当x=9时,y有最小值,y min==39.5,答:李华应选择在B站出地铁,才能使他从文化宫回到家所需的时间最短,最短时间为39.5分钟.27.问题背景:如图1,等腰△ABC中,AB=AC,∠BAC=120°,作AD⊥BC于点D,则D为BC 的中点,∠BAD=∠BAC=60°,于是==;迁移应用:如图2,△ABC和△ADE都是等腰三角形,∠BAC=∠ADE=120°,D,E,C三点在同一条直线上,连接BD.①求证:△ADB≌△AEC;②请直接写出线段AD,BD,CD之间的等量关系式;拓展延伸:如图3,在菱形ABCD中,∠ABC=120°,在∠ABC内作射线BM,作点C关于BM的对称点E,连接AE并延长交BM于点F,连接CE,CF.①证明△CEF是等边三角形;②若AE=5,CE=2,求BF的长.【考点】KY:三角形综合题;KD:全等三角形的判定与性质.【分析】迁移应用:①如图②中,只要证明∠DAB=∠CAE,即可根据SAS解决问题;②结论:CD=AD+BD.由△DAB≌△EAC,可知BD=CE,在Rt△ADH中,DH=AD•cos30°=AD,由AD=AE,AH⊥DE,推出DH=HE,由CD=DE+EC=2DH+BD=AD+BD,即可解决问题;拓展延伸:①如图3中,作BH⊥AE于H,连接BE.由BC=BE=BD=BA,FE=FC,推出A、D、E、C四点共圆,推出∠ADC=∠AEC=120°,推出∠FEC=60°,推出△EFC是等边三角形;②由AE=5,EC=EF=2,推出AH=HE=2.5,FH=4.5,在Rt△BHF中,由∠BHF=30°,可得=cos30°,由此即可解决问题.【解答】迁移应用:①证明:如图②∵∠BAC=∠ADE=120°,∴∠DAB=∠CAE,在△DAE和△EAC中,,∴△DAB≌△EAC,②解:结论:CD=AD+BD.理由:如图2﹣1中,作AH⊥CD于H.∵△DAB≌△EAC,∴BD=CE,在Rt△ADH中,DH=AD•cos30°=AD,∵AD=AE,AH⊥DE,∴DH=HE,∵CD=DE+EC=2DH+BD=AD+BD.拓展延伸:①证明:如图3中,作BH⊥AE于H,连接BE.∵四边形ABCD是菱形,∠ABC=120°,∴△ABD,△BDC是等边三角形,∴BA=BD=BC,∵E、C关于BM对称,∴BC=BE=BD=BA,FE=FC,∴A、D、E、C四点共圆,∴∠ADC=∠AEC=120°,∴∠FEC=60°,∴△EFC是等边三角形,②解:∵AE=5,EC=EF=2,∴AH=HE=2.5,FH=4.5,在Rt△BHF中,∵∠BHF=30°,∴=cos30°,∴BF==3.28.如图1,在平面直角坐标系xOy中,抛物线C:y=ax2+bx+c与x轴相交于A,B两点,顶点为D(0,4),AB=4,设点F(m,0)是x轴的正半轴上一点,将抛物线C绕点F旋转180°,得到新的抛物线C′.(1)求抛物线C的函数表达式;(2)若抛物线C′与抛物线C在y轴的右侧有两个不同的公共点,求m的取值范围.(3)如图2,P是第一象限内抛物线C上一点,它到两坐标轴的距离相等,点P在抛物线C′上的对应点P′,设M是C上的动点,N是C′上的动点,试探究四边形PMP′N能否成为正方形?若能,求出m的值;若不能,请说明理由.【考点】HF:二次函数综合题.【分析】(1)由题意抛物线的顶点C(0,4),A(2,0),设抛物线的解析式为y=ax2+4,把A(2,0)代入可得a=﹣,由此即可解决问题;(2)由题意抛物线C′的顶点坐标为(2m,﹣4),设抛物线C′的解析式为y=(x﹣m)2﹣4,由,消去y得到x2﹣2mx+2m2﹣8=0,由题意,抛物线C′与抛物线C在y轴的右侧有两个不同的公共点,则有,解不等式组即可解决问题;(3)情形1,四边形PMP′N能成为正方形.作PE⊥x轴于E,MH⊥x轴于H.由题意易知P (2,2),当△PFM是等腰直角三角形时,四边形PMP′N是正方形,推出PF=FM,∠PFM=90°,易证△PFE≌△FMH,可得PE=FH=2,EF=HM=2﹣m,可得M(m+2,m﹣2),理由待定系数法即可解决问题;情形2,如图,四边形PMP′N是正方形,同法可得M(m﹣2,2﹣m),利用待定系数法即可解决问题.【解答】解:(1)由题意抛物线的顶点C(0,4),A(2,0),设抛物线的解析式为y=ax2+4,把A(2,0)代入可得a=﹣,∴抛物线C的函数表达式为y=﹣x2+4.(2)由题意抛物线C′的顶点坐标为(2m,﹣4),设抛物线C′的解析式为y=(x﹣m)2﹣4,由,消去y得到x2﹣2mx+2m2﹣8=0,由题意,抛物线C′与抛物线C在y轴的右侧有两个不同的公共点,则有,解得2<m<2,∴满足条件的m的取值范围为2<m<2.(3)结论:四边形PMP′N能成为正方形.理由:1情形1,如图,作PE⊥x轴于E,MH⊥x轴于H.由题意易知P(2,2),当△PFM是等腰直角三角形时,四边形PMP′N是正方形,∴PF=FM,∠PFM=90°,易证△PFE≌△FMH,可得PE=FH=2,EF=HM=2﹣m,∴M(m+2,m﹣2),∵点M在y=﹣x2+4上,∴m﹣2=﹣(m+2)2+4,解得m=﹣3或﹣﹣3(舍弃),∴m=﹣3时,四边形PMP′N是正方形.情形2,如图,四边形PMP′N是正方形,同法可得M(m﹣2,2﹣m),把M(m﹣2,2﹣m)代入y=﹣x2+4中,2﹣m=﹣(m﹣2)2+4,解得m=6或0(舍弃),∴m=6时,四边形PMP′N是正方形.。
成都市树德中学2017年自主招生考试数学试卷

成都市树德中学2017年自主招生考试试题数学注意事项:1、本试卷分第I 卷(选择题)和第II 卷(非选择题)两部分,满分150分,考试时间120分钟。
2、请考生用规定用笔将所有试题的答案涂、写在答题卷上,在试题卷上作答无效。
第I 卷(选择题,共60分)一、选择题:共12小题,每小题5分,共60分。
每个小题所给的四个选项中,只有一相符合题目要求。
1.下列各数中,能被4整除的数是( )(A )60847 (B )3514 (C )31196 (D )712352.顺次连接平面凸四边形ABCD 各边的中点得到一个菱形,则四边形ABCD 一定是( )(A )矩形 (B )菱形 (C )正方形 (D )对角线相等的四边形3.将4个数:-2,-1,4,8排列为a ,b ,c ,d ,使得22)()(d c b a +++的值最小为( )(A )41 (B ) 45 (C )53 (D )1534.过⊙O 外一点P 作⊙O 的切线PA ,连OP 交⊙O 于C ,过点C作CE ⊥AP ,垂足为E ,若PA=10cm ,PC=5cm ,则CE=( )(A )2cm (B )3cm (C )4cm (D )7.5cm5.若a ,b ,c 均为实数,且b ac c a b c b a +=+=+x =,则x 值为( )(A )1 (B )21 (C )21或1 (D )21或-1 6.在△ABC 中,︒=∠︒=∠+=30,45,13C B BC ,则ABC ∆的面积为( )(A )213- (B )123+ (C )213+ (D )13+ 7.甲、乙、丙三人用擂台赛的形式进行训练,每局2人进行单打比赛,另一个人当裁判,每一局的输方当下一局的裁判,由原来的裁判向胜者挑战(每局必有胜者),半天训练结束后,发现甲共打了12局,乙打了21局,而丙当了8局裁判,那么整个比赛的第10局输方是( )(A )必为甲 (B )必为乙 (C )必为丙 (D )不能确定8.关于x 的方程01223=+--x x x 的根的情况是( )(A )只有一个正根 (B )有三个正根(C )有两个正根,一个负根 (D )有一个正根,两个负根9.已知锐角ABC ∆的三个内角C B A ,,所对的边分别为c b a ,,,H 为ABC ∆的垂心,H 到三边AB AC BC ,,的距离分别为,,,z y x 则=z y x ::( )(A )ab ca bc :: (B )C B A cos :cos :cos(C )B A A C C B cos cos :cos cos :cos cos (D )B A A C C B cos sin :cos sin :cos sin10.若,1||21=-t t 则t t+1的值为( )(A )25 (B )-1 (C )21 (D )25或0 11.计算22222210030012202112011200119914131211-++-+--++-+- 的值为( ) (A )200 (B )300 (C )400 (D )50012.在ABC ∆中E D ,分别为AB BC ,上的点,且,321∠=∠=∠若ABC ∆,ADCEBD ∆∆,的周长依次为21,,c c c ,则cc c 21+的最大值为( ) (A )23 (B )45 (C )56 (D )1第II 卷(非选择题,共90分)二、填空题:共4个小题,每小题5分,共20分。
2017年四川省成都市中考数学试题(含答案)

成都市二O 一四年高中阶段教育学校统一招生考试(含成都市初三毕业会考)数 学注意事项:1. 全套试卷分为A 卷和B 卷,A 卷满分100分,B 卷满分50分;考试时间120分钟。
2. 在作答前,考生务必将自己的姓名,准考证号涂写在试卷和答题卡规定的地方。
考试结束,监考人员将试卷和答题卡一并收回。
3. 选择题部分必须使用2B 铅笔填涂;非选择题部分也必须使用0.5毫米黑色签字笔书写,字体工整,笔迹清楚。
4. 请按照题号在答题卡上各题目对应的答题区域内作答,超出答题区域书写的答案无效;在草稿纸,试卷上答题均无效。
5. 保持答题卡清洁,不得折叠、污染、破损等。
A 卷(共100分) 第I 卷(选择题,共30分)一、选择题(本大题共10个小题,每小题3分,共30分,每小题均有四个选项,其中只有一项符合题目要求,答案涂在答题卡上) 1.在-2,-1、0、2这四个数中,最大的数是( )(A)-2 (B)-1 (C)0 (D)2 2.下列几何体的主视图是三角形的是( )(A) (B) (C) (D)3.正在建设的成都第二绕城高速全长超过220公里,串起我市二、三圈层以及周边的广汉、简阳等地,总投资达290亿元,用科学计数法表示290亿元应为( ) (A )290×810 (B )290×910 (C )2.90×1010 (D )2.90×11104.下列计算正确的是( )(A )32x x x =+ (B )x x x 532=+ (C )532)(x x = (D )236x x x =÷ 5.下列图形中,不是..轴对称图形的是( )(A) (B) (C) (D) 6.函数5-=x y 中自变量x 的取值范围是( )(A )5-≥x (B )5-≤x (C )5≥x (D )5≤x 7.如图,把三角板的直角顶点放在直尺的一边上,若∠1=30°,则∠2的度数为( )(A )60° (B )50° (C )40° (D )30°8.近年来,我国持续大面积的雾霾天气让环保和健康问题成为焦点.为进一步普及环保和健康知识,我市某校举行了“建设宜居成都,关注环境保护”的知识竞赛,某班的学生成绩统计如下:则该办学生成绩的众数和中位数分别是( )(A )70分,80分 (B )80分,80分 (C )90分,80分 (D )80分,90分9.将二次函数322+-=x x y 化为k h x y +-=2)(的形式,结果为( ) (A )4)1(2++=x y (B )2)1(2++=x y (C )4)1(2+-=x y (D )2)1(2+-=x y10.在圆心角为120°的扇形AOB 中,半径OA =6cm ,则扇形AOB 的面积是( ) (A )π62cm (B )π82cm (C )π122cm (D )π242cm第Ⅱ卷(非选择题,共70分)二.填空题(本大题共4个小题,每小题4分,共16分,答案写在答题卡上)11.计算:=-2_______________.12.如图,为估计池塘两岸边A ,B 两点间的距离,在池塘的一侧选取点O ,分别去OA 、OB 的中点M ,N ,测的MN=32 m ,则A ,B 两点间的距离是_____________m.13.在平面直角坐标系中,已知一次函数12+=x y 的图像经过),(11y x P x ,),(222y x P两点,若21x x <,则1y ________2y .(填”>”,”<”或”=”)14.如图,AB 是⊙O 的直径,点C 在AB 的延长线上,CD 切⊙O 于点D ,连接AD ,若∠A =25°,则∠C =__________度.三.解答题(本大题共6个小题,共54分,解答过程写在答题卡上) 15.(本小题满分12分,每题6分)(1)计算202)2014(30sin 49--+-π .(2)解不等式组⎩⎨⎧+<+>-②① .,7)2(2513x x x16.(本小题满分6分)如图,在一次数学课外实践活动中,小文在点C 处测得树的顶端A 的仰角为37°,BC =20m ,求树的高度AB .(参考数据:60.037sin ≈,80.037cos ≈,75.037tan ≈)17.(本小题满分8分) 先化简,再求值:221ba b b a a -÷⎪⎭⎫⎝⎛--,其中13+=a ,13-=b .18.(本小题满分8分)第十五届中国“西博会”将于2017年10月底在成都召开,现有20名志愿者准备参加某分会场的工作,其中男生8人,女生12人.(1)若从这20人中随机选取一人作为联络员,求选到女生的概率;(2)若该分会场的某项工作只在甲、乙两人中选一人,他们准备以游戏的方式决定由谁参加,游戏规则如下:将四张牌面数字分别为2、3、4、5的扑克牌洗匀后,数字朝下放于桌面,从中任取2张,若牌面数字之和为偶数,则甲参加,否则乙参加.试问这个游戏公平吗?请用树状图或列表法说明理由.19.(本小题满分10分)如图,一次函数5+=kx y (k 为常数,且0≠k )的图像与反比例函数xy 8-=的图像交于()b A ,2-,B 两点.(1)求一次函数的表达式;(2)若将直线AB 向下平移)0(>m m 个单位长度后与反比例函数的图像有且只有一个公共点,求m 的值.20.(本小题满分10分)如图,矩形ABCD 中,AB AD 2=,E 是AD 边上一点,AD nDE 1=(n 为大于2的整数),连接BE ,作BE 的垂直平分线分别交AD 、BC 于点F ,G ,FG 与BE 的交点为O ,连接BF 和EG .(1)试判断四边形BFEG 的形状,并说明理由; (2)当a AB =(a 为常数),3=n 时,求FG 的长; (3)记四边形BFEG 的面积为1S ,矩形ABCD 的面积为2S , 当301721=S S 时,求n 的值.(直接写出结果,不必写出解答过程)CDGB 卷(共50分)一、填空题(本大题共5个小题,每小题4分,共20分,答案写在答题卡上) 21. 在开展“国学诵读”活动中,某校为了解全校1300名学生课外阅读的情况,随机调查了50名学生一周的课外阅读时间,并绘制成如图所示的条形统计图.根据图中数据。
2019年四川省成都九中自主招生数学试卷含答案
2019年四川省成都九中自主招生数学试卷一、选择题(本大题共10小题,每小题5分,共50分)1.(5分)当a<1时,化简的结果是()A.a B.﹣a C.a D.﹣a2.(5分)满足的所有实数x的和为()A.3B.4C.5D.63.(5分)五张如图所示的长为a,宽为b(a>b)的小长方形纸片,按如图的方式不重叠地放在矩形ABCD 中,未被覆盖的部分(两个矩形)用阴影表示.设左上角与右下角的阴影部分的面积的差为S,当BC的长度变化时,按照同样的放置方式,S始终保持不变,则a,b满足的关系式为()A.a=2b B.a=3b C.3a=2b D.2a=3b+14.(5分)如图△ABC为圆O的内接三角形,D为BC中点,E为OA中点,∠ABC=40°,∠BCA=80°,则∠OED的大小为()A.15°B.18°C.20°D.22°5.(5分)如图所示,将形状、大小完全相同的“●”和线段按照一定规律摆成下列图形,第1幅图形中“●”的个数为a1,第2幅图形中“●”的个数为a2,第3幅图形中“●”的个数为a3,…,以此类推,则+++…+的值为()A.B.C.D.6.(5分)如图,菱形ABCD中,AB=2,∠B=60°,M为AB的中点.动点P在菱形的边上从点B出发,沿B→C→D的方向运动,到达点D时停止.连接MP,设点P运动的路程为x,MP2=y,则表示y与x 的函数关系的图象大致为()A.B.C.D.7.(5分)某校初三年级有四个班,每班挑选乒乓球男女运动员各一人,组成年级混合双打代表队.那么,四对混合双打中,没有一对选手是同班同学的概率是()A.B.C.D.8.(5分)如图,以G(0,1)为圆心,半径为2的圆与x轴交于A、B两点,与y轴交于C、D两点,点E为⊙G上一动点,CF⊥AE于F.当点E从点B出发顺时针运动到点D时,点F所经过的路径长为()A.B.C.D.9.(5分)设a、b、c为实数,且a≠0,抛物线y=ax2+bx+c,顶点在y=﹣2上,与x轴交于点A,B,与y轴交于点C,当△ABC为直角三角形时,S△ABC的最大值是()A.1B.C.3D.410.(5分)设,则的整数部分是()A.61B.62C.63D.64二、填空题(本大题共6小题,每小题5分,共30分)11.(5分)已知x,y都是非负数,且满足x2+2xy+y2+x+y﹣12=0,则x(1﹣y)的最大值为.12.(5分)已知实数a满足a2﹣a﹣1=0.则a8+7a﹣4的值为.13.(5分)如图,O是正方形ABCD边上一点,以O为圆心,OB为半径画圆与AD交于点E,过点E作⊙O的切线交CD于F,将△DEF沿EF对折,点D的对称点D'恰好落在⊙O上.若AB=6,则OB的长为.14.(5分)已知a、b是实数,且a2+ab+b2=5.若a2﹣ab+b2的最大值是m,最小值是n,则m+n的值是.15.(5分)如图,菱形ABCD中,AB=2,∠C=60°,菱形ABCD在直线l上向右作无滑动的翻滚,每绕着一个顶点旋转60°叫一次操作,则经过45次这样的操作菱形中心O所经过的路径总长为.(结果保留π)16.(5分)如图,平行四边形ABCD中,AB:BC=4:3,∠ABC=120°,E是AB的中点,F在BC上,且BF:FC=2:1,过D分别作DG⊥AF于G,作DH⊥CE于H,则DG:DH=.三、解答题(本大题共6小题,共70分)17.(10分)(1)已知a2+4a+1=0,且,求m的值.(2)解方程:.18.(10分)一条笔直的公路L穿过草原,公路边有一卫生站A距公路30km的地方有一居民点B,A、B 之间的距离为90km.一天某司机驾车从卫生站送一批急救药品到居民点.已知汽车在公路上行驶的最快速度是60km/h,在草地上行驶的最快速度是30km/h.问司机应在公路上行驶多少千米?全部所用的行车时间最短?最短时间为多少?19.(12分)已知m,n,p为正整数,m<n.设A(﹣m,0),B(n,0),C(0,p),O为坐标原点.若∠ACB=90°,且OA2+OB2+OC2=3(OA+OB+OC).(1)求图象经过A,B,C三段的二次函数的解析式;(2)点D是抛物线上的一动点,直线AD交线段BC于点Q,若△ACQ,△ABQ的面积S△ACQ,S△ABQ 满足S△ACQ:S△ABQ=1:3,求此时点D的坐标.20.(12分)如图,在扇形OAB中,∠AOB=90°,OA=12,点C在OA上,AC=4,点D为OB的中点,点E为弧AB上的动点,OE与CD的交点为F.(1)当四边形ODEC的面积S最大时,求EF;(2)求CE+2DE的最小值.21.(12分)阅读下列两则材料,回答问题材料一:我们将(+)与(﹣)称为一对“对偶式”因为(+)(﹣)=()2﹣()2=a﹣b,所以构造“对偶式”相乘可以有效地将(+)和(﹣)中的“”去掉例如:已知﹣=2,求+的值.解:(﹣)×(+)=(25﹣x)﹣(15﹣x)=10∵﹣=2,∴+=5材料二:如图,点A(x1,y1),点B(x2,y2),以AB为斜边作Rt△ABC,则C(x2,y1),于是AC=|x1﹣x2|,BC=|y1﹣y2|,所以AB=.反之,可将代数式的值看作点(x1,y1)到点(x2,y2)的距离.例如===.所以可将代数式的值看作点(x,y)到点(1,﹣1)的距离.(1)利用材料一,解关于x的方程:﹣=2,其中x≤4;(2)①利用材料二,求代数式的最小值,并求出此时y与x的函数关系式,写出x的取值范围;②将①所得的y与x的函数关系式和x的取值范围代入y=+中解出x,直接写出x的值.22.(14分)我们定义:有一组对角相等而另一组对角不相等的凸四边形叫做“等对角四边形”,例如:如图1,四边形ABCD是“等对角四边形”,∠A≠∠C,∠A=75°,∠D=85°,则∠C=115°.(1)已知:在“等对角四边形”ABCD中,∠DAB=60°,∠ABC=90°,AB=4,AD=3,求对角线AC的长;(2)已知:如图2,在平面直角坐标系xOy中,四边形ABCD是“等对角四边形”,其中A(﹣2,0)、C(2,0)、B(﹣1,﹣),点D在y轴上,抛物线过点A、C,点P在抛物线上,满足∠APC=∠ADC的点至少有3个时,总有不等式2n﹣成立,求n的取值范围.2019年四川省成都九中自主招生数学试卷参考答案与试题解析一、选择题(本大题共10小题,每小题5分,共50分)1.(5分)当a<1时,化简的结果是()A.a B.﹣a C.a D.﹣a【解答】解:∵a<1,∴1﹣a>0,∵﹣a3(1﹣a)≥0,∴a≤0,∴=|a|=﹣a,故选:B.2.(5分)满足的所有实数x的和为()A.3B.4C.5D.6【解答】解:当2﹣x=1,即x=1时,满足题意.当2﹣x=﹣l,即x=3时,由于,所以满足题意.当2﹣x≠±1且2﹣x≠0,即x≠1 且x≠3 且x≠2时,令x2﹣x﹣2=0,得x=﹣1.因此,所求和为1+3+(﹣l)=3.故选:A.3.(5分)五张如图所示的长为a,宽为b(a>b)的小长方形纸片,按如图的方式不重叠地放在矩形ABCD 中,未被覆盖的部分(两个矩形)用阴影表示.设左上角与右下角的阴影部分的面积的差为S,当BC的长度变化时,按照同样的放置方式,S始终保持不变,则a,b满足的关系式为()A.a=2b B.a=3b C.3a=2b D.2a=3b+1【解答】解:左上角阴影部分的长为AE,宽为AF=2b,右下角阴影部分的长为PC,宽为a,∵AD=BC,即AE+ED=AE+a,BC=BP+PC=3b+PC,∴AE+a=3b+PC,即AE﹣PC=3b﹣a,∴阴影部分面积之差S=AE•AF﹣PC•CG=2b×AE﹣a×PC=2b(PC+3b﹣a)﹣aPC=(2b﹣a)PC+6b2﹣2ab,则2b﹣a=0,即a=2b,故选:A.4.(5分)如图△ABC为圆O的内接三角形,D为BC中点,E为OA中点,∠ABC=40°,∠BCA=80°,则∠OED的大小为()A.15°B.18°C.20°D.22°【解答】解:如图,连接OC,取OC中点F,连接EF、DF,∴∠AOC=2∠ABC=80°,OE=OF,∴∠OEF=∠OFE=(180°﹣80°)=50°,连接OB,∵D为BC中点,∴BD=CD,OD⊥BC,∴∠DOC=,∵∠BAC=BOC,∴∠DOC=∠BAC,∴∠DOC=∠BAC=180°﹣40°﹣80°=60°,∵F为OC中点,∴OF=FD,∴△OFD为等边三角形,∴OD=OF=OE,∴点O是△EFD外接圆的圆心,∴,∴∠OED=50°﹣30°=20°.故选:C.5.(5分)如图所示,将形状、大小完全相同的“●”和线段按照一定规律摆成下列图形,第1幅图形中“●”的个数为a1,第2幅图形中“●”的个数为a2,第3幅图形中“●”的个数为a3,…,以此类推,则+++…+的值为()A.B.C.D.【解答】解:a1=3=1×3,a2=8=2×4,a3=15=3×5,a4=24=4×6,…,a n=n(n+2);∴+++…+=+++…+=×(1﹣+﹣+﹣+…+﹣)=×(1+﹣﹣)=×=,故选:D.6.(5分)如图,菱形ABCD中,AB=2,∠B=60°,M为AB的中点.动点P在菱形的边上从点B出发,沿B→C→D的方向运动,到达点D时停止.连接MP,设点P运动的路程为x,MP2=y,则表示y与x 的函数关系的图象大致为()A.B.C.D.【解答】解:(1)当0≤x≤时,如图1,过M作ME⊥BC与E,∵M为AB的中点,AB=2,∴BM=1,∵∠B=60°,∴BE=,ME=,PE=﹣x,在Rt△BME中,由勾股定理得:MP2=ME2+PE2,∴y==x2﹣x+1;(2)当<x≤2时如图2,过M作ME⊥BC与E,由(1)知BM=1,∠B=60°,∴BE=,ME=,PE=x﹣,∴MP2=ME2+PE2,∴y==x2﹣x+1;(3)当2<x≤4时,如图3,连接MC,∵BM=1,BC=AB=2,∠B=60°,∴∠BMC=90°,MC==,∵AB∥DC,∴∠MCD=∠BMC=90°,∴MP2=MC2+PC2,∴y==x2﹣4x+7;综合(1)(2)(3),只有B选项符合题意.故选:B.7.(5分)某校初三年级有四个班,每班挑选乒乓球男女运动员各一人,组成年级混合双打代表队.那么,四对混合双打中,没有一对选手是同班同学的概率是()A.B.C.D.【解答】解:∵先把四个女运动员任意排列,设为ABCD,和A配合的男运动员有4个选择;和B配合的男运动员剩下3种选择;和C配合的男运动员剩下2种选择;最后一个和D配合.所以总共有24种.∴4男4女组成四队混合双打的情况共有:4×3×2=24种,设一、二、三、四班的男、女选手分别为A1、B1、A2、B2、A3、B3、A4、B4,则四队混合双打中,没有一对选手是同班同学的情景如下:由上得共有9种情形.故四对混合双打中,没有一对选手是同班同学的概率是:=.故选:C.8.(5分)如图,以G(0,1)为圆心,半径为2的圆与x轴交于A、B两点,与y轴交于C、D两点,点E为⊙G上一动点,CF⊥AE于F.当点E从点B出发顺时针运动到点D时,点F所经过的路径长为()A.B.C.D.【解答】解:连接AC,AG,∵GO⊥AB,∴O为AB的中点,即AO=BO=AB,∵G(0,1),即OG=1,∴在Rt△AOG中,根据勾股定理得:AO==,∴AB=2AO=2,又CO=CG+GO=2+1=3,∴在Rt△AOC中,根据勾股定理得:AC==2,∵CF⊥AE,∴△ACF始终是直角三角形,点F的运动轨迹为以AC为直径的半圆,当E位于点B时,CO⊥AE,此时F与O重合;当E位于D时,CA⊥AE,此时F与A重合,∴当点E从点B出发顺时针运动到点D时,点F所经过的路径长,在Rt△ACO中,tan∠ACO==,∴∠ACO=30°,∴度数为60°,∵直径AC=2,∴的长为=π,则当点E从点B出发顺时针运动到点D时,点F所经过的路径长π.故选:B.9.(5分)设a、b、c为实数,且a≠0,抛物线y=ax2+bx+c,顶点在y=﹣2上,与x轴交于点A,B,与y轴交于点C,当△ABC为直角三角形时,S△ABC的最大值是()A.1B.C.3D.4【解答】解:设y=ax2+bx+c交y轴于点C(0,c),c≠0,交x轴于点A(x1,0)、B(x2,0),且x1<0<x2,由△ABC是直角三角形知,点C必为直角顶点,且c2=(﹣x1)x2=﹣x1x2(射影定理的逆定理),由根与系数的关系得,,,∴,,又=﹣2,即8a=4+b2≥4,∴,∴,=,==,当且仅当,b=0,c=﹣2时等号成立,因此,Rt△ABC的最大面积是4.故选:D.10.(5分)设,则的整数部分是()A.61B.62C.63D.64【解答】解:∵,2050﹣2018+1=33,∴M>且M<,∴<M<,∴<<,即61<<62,∵>>>…>,∴M>,∴<=61,∴61<<61,∴的整数部分为61,故选:A.二、填空题(本大题共6小题,每小题5分,共30分)11.(5分)已知x,y都是非负数,且满足x2+2xy+y2+x+y﹣12=0,则x(1﹣y)的最大值为3.【解答】解:x2+2xy+y2+x+y﹣12=0(x+y)2+(x+y)﹣12=0,(x+y+4)(x+y﹣3)=0∵x、y为非负数,∴x+y+4>0,∴x+y=3,即x=3﹣y,∴0≤x≤3,0≤y≤3,∴x(1﹣y)=(3﹣y)(1﹣y)=(y﹣2)2﹣1≤3,故答案为:3.12.(5分)已知实数a满足a2﹣a﹣1=0.则a8+7a﹣4的值为48.【解答】解:∵a2﹣a﹣1=0,∴两边都除以a得,a﹣a﹣1=1,∴a2+a﹣2=3,a4+a﹣4=7,∴a8+7a﹣4,=a4•a4+a4•a﹣4﹣1+7a﹣4,=a4(a4+a﹣4)+7a﹣4﹣1,=7a4+7a﹣4﹣1,=7×7﹣1,=48.故答案为:48.13.(5分)如图,O是正方形ABCD边上一点,以O为圆心,OB为半径画圆与AD交于点E,过点E作⊙O的切线交CD于F,将△DEF沿EF对折,点D的对称点D'恰好落在⊙O上.若AB=6,则OB的长为.【解答】解:∵正方形ABCD,∴∠ABC=90°,∵OB为半径,∴BC是⊙O的切线,连接OE、OD′,作OH⊥ED′于H,∴EH=D′H=ED′∵ED′=ED,∴EH=ED,∵正方形ABCD,∴∠A=90°,AB=AD=6,∵EF是⊙O的切线,∴OE⊥EF,∴∠OEH+∠D′EF=90°,∠AEO+∠DEF=90°,∵∠DEF=∠D′EF,∴∠AEO=∠HEO,在△AEO和△HEO中∴△AEO≌△HEO(AAS),∴AE=EH=ED,∴AE=AD=2,设OB=OE=x.则AO=6﹣x,在Rt△AOE中,x2=22+(6﹣x)2,解得:x=,∴OB=,故答案为.14.(5分)已知a、b是实数,且a2+ab+b2=5.若a2﹣ab+b2的最大值是m,最小值是n,则m+n的值是.【解答】解:设a2﹣ab+b2=k,∵a2+ab+b2=5,∴a2+b2=,ab=,∵a2+b2≥2|ab|,∴≥2||,即≥|5﹣k|,∴﹣≤5﹣k≤,解得,≤k≤15,∴m=15,n=,∴m+n=,故答案为:.15.(5分)如图,菱形ABCD中,AB=2,∠C=60°,菱形ABCD在直线l上向右作无滑动的翻滚,每绕着一个顶点旋转60°叫一次操作,则经过45次这样的操作菱形中心O所经过的路径总长为10π+5π.(结果保留π)【解答】解:菱形ABCD中,AB=2,∠C=60°,所以第一、二次旋转形成弧的半径是,圆心角是60°,所以第一、二次旋转的弧长和=,因为第三次旋转形成弧的半径是1,圆心角是60°,所以第三次旋转的弧长=,因为一个周期为3,所以45÷3=15,所以菱形中心O所经过的路径总长为:.故答案为:10π+5π.16.(5分)如图,平行四边形ABCD中,AB:BC=4:3,∠ABC=120°,E是AB的中点,F在BC上,且BF:FC=2:1,过D分别作DG⊥AF于G,作DH⊥CE于H,则DG:DH=:14.【解答】解:设BC=21a,则BF=14a,FC=7a,AB=28a,∴AE=EB=14a,∵∠ABC=120°,∴,∴CE=7a,∵S△ADF=S△DEC,∴,∴.三、解答题(本大题共6小题,共70分)17.(10分)(1)已知a2+4a+1=0,且,求m的值.(2)解方程:.【解答】解:(1)由已知可得a2+1=﹣4a,∴a4+1=(a2+1)2﹣2a2=14a2,∴由原式可得,∴m+14=5(m﹣12)=5m﹣60,∴4m=74,∴.(2)令∴x2﹣3x=t2﹣3,∴原方程化为:x2+(x2﹣3x)+2xt=1,∴x2+t2﹣3+2xt=1,∴(x+t)2=4,∴x+t=±2,∴若x+t=﹣2,则t2=x2+4x+4=x2﹣3x+3,解得:,经检验,x=﹣是增根,若x+t=2,则t2=x2+4﹣4x=x2﹣3x+3,解得x=1,经检验,x=1是方程的解,∴综上所述,x=1是原方程的解.答:(1)m的值为;(2)方程的解为x=1.18.(10分)一条笔直的公路L穿过草原,公路边有一卫生站A距公路30km的地方有一居民点B,A、B 之间的距离为90km.一天某司机驾车从卫生站送一批急救药品到居民点.已知汽车在公路上行驶的最快速度是60km/h,在草地上行驶的最快速度是30km/h.问司机应在公路上行驶多少千米?全部所用的行车时间最短?最短时间为多少?【解答】解:如图,作射线AM交BC的延长线于M,使得∠MAC=30°,作DH⊥AM.∵时间t==(AD+BD),DH=AD,∴时间t=(DH+BD),∴当D,H,B共线,且BH⊥AM时,时间t最小,作BH′⊥AM于H′交AC于D′,此时时间最小值=•BH′,∵AB=90km,BC=30km,∴AC=60(km),∴CM=AC•tan30°=20(km),在Rt△BMH′中,BH′=BM•cos30°=(20+30)×=(30+15)(km),∴t的最小值=+.此时AD′=.19.(12分)已知m,n,p为正整数,m<n.设A(﹣m,0),B(n,0),C(0,p),O为坐标原点.若∠ACB=90°,且OA2+OB2+OC2=3(OA+OB+OC).(1)求图象经过A,B,C三段的二次函数的解析式;(2)点D是抛物线上的一动点,直线AD交线段BC于点Q,若△ACQ,△ABQ的面积S△ACQ,S△ABQ 满足S△ACQ:S△ABQ=1:3,求此时点D的坐标.【解答】解:(1)∵∠ACB=90°,OC⊥AB,∴OA•OB=OC2,即mn=p2.∵OA2+OB2+OC2=3(OA+OB+OC),∴m2+n2+p2=3(m+n+p).又∵m2+n2+p2=(m+n+p)2﹣2(mn+np+mp)=(m+n+p)2﹣2(p2+np+mp)=(m+n+p)2﹣2p(m+n+p)=(m+n+p)(m+n﹣p),∴m+n﹣p=3,即m+n=p+3.∵mn=p2,m+n=p+3,∴m,n是关于x的一元二次方程x2﹣(p+3)x+p2=0①的两个不相等的正整数根,∴△=[﹣(p+3)]2﹣4p2>0,解得﹣1<p<3.又∵p为正整数,故p=1或p=2.当p=1时,方程①为x2﹣4x+1=0,没有整数解.当p=2时,方程①为x2﹣5x+4=0,两根为m=1,n=4.综合知:m=1,n=4,p=2.设图象经过A,B,C三点的二次函数的解析式为y=k(x+1)(x﹣4),将点C(0,2)的坐标代入得2=k×1×(﹣4),解得.∴图象经过A,B,C三点的二次函数的解析式为.∴图象经过A,B,C三段的二次函数的解析式为y=﹣x2+x+2.(2)如图,直线AD交线段BC于点Q,由S△ACQ:S△ABQ=1:3,得CQ:QB=1:3,∴,,∴,∵A(﹣1,0),∴,联立,消去y整理可得,2x2﹣3x﹣5=0,由韦达定理:,而x A=﹣1,∴,∴,∴D点坐标为:.20.(12分)如图,在扇形OAB中,∠AOB=90°,OA=12,点C在OA上,AC=4,点D为OB的中点,点E为弧AB上的动点,OE与CD的交点为F.(1)当四边形ODEC的面积S最大时,求EF;(2)求CE+2DE的最小值.【解答】解:(1)分别过O、E作ON⊥CD于N,EM⊥CD于M,∵CD=10,∴四边形ODEC=S△OCD+S△CDE=≤CD•OE==60,此时OM、EN、OE重合,∵ON•CD=OC•OD,∴10×ON=6×8,∴ON=,∴;(2)延长OB至点G,使BG=OB,连接GE、GC、DE,则,∵点D为OB的中点,OB=OE,∴,∴,又∠DOE=∠EOG,∴△DOE∽△EOG,,∴EG=2DE,∴CE+2DE=CE+EG,当C、E、G三点在同一直线上上时,CE+EG最小,CO=OA﹣AC=12﹣4=8,OG=OB+BG=12+12=24,此时,故CE+2DE有最小值为.21.(12分)阅读下列两则材料,回答问题材料一:我们将(+)与(﹣)称为一对“对偶式”因为(+)(﹣)=()2﹣()2=a﹣b,所以构造“对偶式”相乘可以有效地将(+)和(﹣)中的“”去掉例如:已知﹣=2,求+的值.解:(﹣)×(+)=(25﹣x)﹣(15﹣x)=10∵﹣=2,∴+=5材料二:如图,点A(x1,y1),点B(x2,y2),以AB为斜边作Rt△ABC,则C(x2,y1),于是AC=|x1﹣x2|,BC=|y1﹣y2|,所以AB=.反之,可将代数式的值看作点(x1,y1)到点(x2,y2)的距离.例如===.所以可将代数式的值看作点(x,y)到点(1,﹣1)的距离.(1)利用材料一,解关于x的方程:﹣=2,其中x≤4;(2)①利用材料二,求代数式的最小值,并求出此时y与x的函数关系式,写出x的取值范围;②将①所得的y与x的函数关系式和x的取值范围代入y=+中解出x,直接写出x的值.【解答】解:(1)根据材料一;∵(﹣)×(+)=(20﹣x)﹣(4﹣x)=16∵﹣=2,∴+=8,∴=5=3∴解得:x=﹣5∴y=2x+6(﹣2≤x≤1)(2)①解:由材料二知:=====.∴可将的值看作点(x,y)到点(1,8)的距离的值看作点(x,y)到点(﹣2,2)的距离∴=+.∴当代数式取最小值即点(x,y)与点(1,8),(﹣2,2)在同一条直线上,并且点(x,y)位点(1,8)(﹣2,2)的中间∴的最小值===3且﹣2≤x≤1设过(x,y),(1,8),(﹣2,2)的直线解析式为:y=kx+b∴解得:∴y=2x+6(﹣2≤x≤1)②:∵y=+中∵y=2x+6∴+=2x+6 ①又∵(+)(﹣)=2x2+5x+12﹣(2x2+3x+6)=2x+6∴﹣=1 ②由①+②式得:=x+解得:x1=>1(舍)x2=∴x的值为1﹣22.(14分)我们定义:有一组对角相等而另一组对角不相等的凸四边形叫做“等对角四边形”,例如:如图1,四边形ABCD是“等对角四边形”,∠A≠∠C,∠A=75°,∠D=85°,则∠C=115°.(1)已知:在“等对角四边形”ABCD中,∠DAB=60°,∠ABC=90°,AB=4,AD=3,求对角线AC的长;(2)已知:如图2,在平面直角坐标系xOy中,四边形ABCD是“等对角四边形”,其中A(﹣2,0)、C(2,0)、B(﹣1,﹣),点D在y轴上,抛物线过点A、C,点P在抛物线上,满足∠APC=∠ADC的点至少有3个时,总有不等式2n﹣成立,求n的取值范围.【解答】(1)①如图1,∠B=∠D=90°时延长AD,BC交于点E,∵∠DAB=60°,∴∠E=30°,又∵AB=4,AD=3∴BE=4,AE=8,DE=5,∴CE==,BC=4﹣=,∴AC==;②如图,∠A=∠C=60°时,过D分别作DE⊥AB于E,DF⊥BC于点F,∵∠DAB=∠BCD=60°,又∵AB=4,AD=3,∴AE=,DE=BF=,∴BE=DF=,∴CF=,BC=+=,∴AC==;综上,AC=或;(2)∵A(﹣2,0)、C(2,0)、B(﹣1,﹣),∴AB=2,BC=2,AC=4,∴AB2+BC2=AC2,∴∠ABC=90°,∵AD=CD,AB≠BC,∴∠BAD≠∠BCD,∵四边形ABCD是“等对角四边形”,∴∠ADC=∠ABC=90°,∴D(0,2),∵抛物线y=ax2+bx+c过点A、C,∴y=a(x+2)(x﹣2)=ax2﹣4a,即:a=﹣c,令t=2c2+16a﹣8,则t=2c2﹣4c﹣8,以D(0,2)为圆心,AD长为半径作⊙D,以D'(0,﹣2)为圆心,AD长为半径作⊙D',如图所示,⊙D交y轴正半轴于点E,⊙D'交y轴负半轴于点F.当点P在优弧AEC和优弧AFC上时,∠APC=∠ADC,当抛物线过E点时满足题意的P点有3个,此时,c=OE=OD+ED=2+2,当满足∠APC=∠ADC的P点至少有3个时,c≥2+2,当c≥2+2时,t=2c2﹣4c﹣8≥16,∵总有不等式2n﹣≤2c2+16a﹣8成立,∴2n﹣≤16,∴n≤.。
2013年成都树德中学(九中)自主招生考试数学试题及答案
第Ⅰ卷一、选择题:本题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的.1、一列火车花了H 小时行程D 公里从A 城抵达B 城,晚点两小时,那么应该以什么样的速度才能准点到达( ) A .2H + B .2D H + C .2D H - D .2DH + 2、若30,350x y z x y z x y z ++=⎧⎨+-=⎩、、均为非负整数,则542M x y z =++的取值范围是:( ) A .100110M ≤≤ B .110120M ≤≤ C .120130M ≤≤ D .130140M ≤≤3、某天,学校研究性学习小组的同学从8时起骑自行车外出调查,17时回到学校,小组离开学校的距离和时间的关系可用图中的曲线表示,根据这个曲线图,下列说法错误的是( )A .在离校最远的地方调查的时间是14~15时B .第一次调查从9时开始,历时2hC .中午12~13时休息的地方离校15kmD .返校的速度最慢 4、已知函数282y x x =--和(y kx k k =+为常数)则不论k 为何值,这两个函数的图像( ) A .只有一个交点 B .只有二个交点 C .只有三个交点 D .只有四个交点5、如果x y 、是非零实数,使得330x y x y x ⎧+=⎪⎨+=⎪⎩,那么x y +等于( ) A .3 B .13 C .113- D .413- 6、一列数:23420087,7,7,7,,7•••.其中末位数字是3的有( )A .502个B .500个C .1004个D .256个7、在ABC ∆中,,,,90,BC a AC b AB c C CD ===∠=和BE 是ABC ∆的两条中线,且CD BE ⊥,那么::a b c =( )A .1:2:3B .3:2:1C .3:2:1D .1:2:38、已知三角形的三个内角的度数都是质数,则这三个内角中必定有一个内角等于:( )A .2度B .3度C .5度D .7度 9、已知:221m n mn m n +++-=-,则11m n+的值等于( ) A .1- B .0 C .1 D .2 10、积11111111111324359810099101⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫+++•••++ ⎪⎪⎪ ⎪⎪⨯⨯⨯⨯⨯⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭值的整数部分是:( ) A .1 B .2 C .3 D .4第Ⅱ卷二、填空题:本大题共6个小题,每小题5分,共30分。
2017年四川省成都市中考数学真题及答案 精品
成都市二O一四年高中阶段教育学校统一招生考试(含成都市初三毕业会考)数学注意事项:1. 全套试卷分为A卷和B卷,A卷满分100分,B卷满分50分;考试时间120分钟。
2. 在作答前,考生务必将自己的姓名,准考证号涂写在试卷和答题卡规定的地方。
考试结束,监考人员将试卷和答题卡一并收回。
3. 选择题部分必须使用2B铅笔填涂;非选择题部分也必须使用0.5毫米黑色签字笔书写,字体工整,笔迹清楚。
4. 请按照题号在答题卡上各题目对应的答题区域内作答,超出答题区域书写的答案无效;在草稿纸,试卷上答题均无效。
5. 保持答题卡清洁,不得折叠、污染、破损等。
A卷(共100分)第I卷(选择题,共30分)一、选择题(本大题共10个小题,每小题3分,共30分,每小题均有四个选项,其中只有一项符合题目要求,答案涂在答题卡上)1.在-2,-1、0、2这四个数中,最大的数是()(A)-2 (B)-1 (C)0 (D)22.下列几何体的主视图是三角形的是( )(A) (B) (C)(D)3.正在建设的成都第二绕城高速全长超过220公里,串起我市二、三圈层以及周边的广汉、简阳等地,总投资达290亿元,用科学计数法表示290亿元应为( )(A )290×810 (B )290×910 (C )2.90×1010 (D )2.90×1110 4.下列计算正确的是( )(A )32x x x =+ (B )x x x 532=+ (C )532)(x x = (D )236x x x =÷ 5.下列图形中,不是..轴对称图形的是( )(A) (B) (C) (D)6.函数5-=x y 中自变量x 的取值范围是( )(A )5-≥x (B )5-≤x (C )5≥x (D )5≤x 7.如图,把三角板的直角顶点放在直尺的一边上,若∠1=30°,则∠2的度数为( )(A )60° (B )50° (C )40° (D )30°8.近年来,我国持续大面积的雾霾天气让环保和健康问题成为焦点.为进一步普及环保和健康知识,我市某校举行了“建设宜居成都,关注环境保护”的知识竞赛,某班的学生成绩统计如下:成绩(分)60708090100人 数4812115则该办学生成绩的众数和中位数分别是( )(A )70分,80分 (B )80分,80分 (C )90分,80分 (D )80分,90分9.将二次函数322+-=x x y 化为k h x y +-=2)(的形式,结果为( ) (A )4)1(2++=x y (B )2)1(2++=x y (C )4)1(2+-=x y (D )2)1(2+-=x y10.在圆心角为120°的扇形AOB 中,半径OA =6cm ,则扇形AOB 的面积是( )(A )π62cm (B )π82cm (C )π122cm (D )π242cm第Ⅱ卷(非选择题,共70分)二.填空题(本大题共4个小题,每小题4分,共16分,答案写在答题卡上)11.计算:=-2_______________.12.如图,为估计池塘两岸边A ,B 两点间的距离,在池塘的一侧选取点O ,分别去OA 、OB 的中点M ,N ,测的MN=32 m ,则A ,B 两点间的距离是_____________m.13.在平面直角坐标系中,已知一次函数12+=x y 的图像经过),(11y x P x ,),(222y x P 两点,若21x x <,则1y ________2y .(填”>”,”<”或”=”)14.如图,AB 是⊙O 的直径,点C 在AB 的延长线上,CD 切⊙O 于点D ,连接AD ,若∠A =25°,则∠C=__________度.三.解答题(本大题共6个小题,共54分,解答过程写在答题卡上) 15.(本小题满分12分,每题6分) (1)计算202)2014(30sin 49--+-π .(2)解不等式组⎩⎨⎧+<+>-②① . ,7)2(2513x x x16.(本小题满分6分)如图,在一次数学课外实践活动中,小文在点C 处测得树的顶端A 的仰角为37°,BC =20m ,求树的高度AB .(参考数据:60.037sin ≈ ,80.037cos ≈ ,75.037tan ≈ )17.(本小题满分8分) 先化简,再求值:221ba b b a a -÷⎪⎭⎫⎝⎛--,其中13+=a ,13-=b .18.(本小题满分8分)第十五届中国“西博会”将于2017年10月底在成都召开,现有20名志愿者准备参加某分会场的工作,其中男生8人,女生12人.(1)若从这20人中随机选取一人作为联络员,求选到女生的概率; (2)若该分会场的某项工作只在甲、乙两人中选一人,他们准备以游戏的方式决定由谁参加,游戏规则如下:将四张牌面数字分别为2、3、4、5的扑克牌洗匀后,数字朝下放于桌面,从中任取2张,若牌面数字之和为偶数,则甲参加,否则乙参加.试问这个游戏公平吗?请用树状图或列表法说明理由.19.(本小题满分10分)如图,一次函数5+=kx y (k 为常数,且0≠k )的图像与反比例函数xy 8-=的图像交于()b A ,2-,B 两点. (1)求一次函数的表达式;(2)若将直线AB 向下平移)0(>m m 个单位长度后与反比例函数的图像有且只有一个公共点,求m 的值.20.(本小题满分10分)如图,矩形ABCD 中,AB AD 2=,E 是AD 边上一点,AD nDE 1= (n 为大于2的整数),连接BE ,作BE 的垂直平分线分别交AD 、BC 于点F ,G ,FG 与BE 的交点为O ,连接BF 和EG .(1)试判断四边形BFEG 的形状,并说明理由; (2)当a AB =(a 为常数),3=n 时,求FG 的长; (3)记四边形BFEG 的面积为1S ,矩形ABCD 的面积为2S ,当301721 S S 时,求n 的值.(直接写出结果,不必写出解答过程)B 卷(共50分)CDG一、填空题(本大题共5个小题,每小题4分,共20分,答案写在答题卡上)21. 在开展“国学诵读”活动中,某校为了解全校1300名学生课外阅读的情况,随机调查了50名学生一周的课外阅读时间,并绘制成如图所示的条形统计图.根据图中数据。
2017年四川省成都市中考数学试卷(含解析版)(2021年整理精品文档)
(完整版)2017年四川省成都市中考数学试卷(含解析版)编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望((完整版)2017年四川省成都市中考数学试卷(含解析版))的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为(完整版)2017年四川省成都市中考数学试卷(含解析版)的全部内容。
2017年四川省成都市中考数学试卷A卷(共100分)一、选择题(本大题共10小题,每小题3分,共30分)1.(3分)《九章算术》中注有“今两算得失相反,要令正负以名之”,意思是:今有两数若其意义相反,则分别叫做正数与负数,若气温为零上10℃记作+10℃,则﹣3℃表示气温为()A.零上3℃B.零下3℃C.零上7℃D.零下7℃2.(3分)如图所示的几何体是由4个大小相同的小立方体组成,其俯视图是()A.B.C.D.3.(3分)总投资647亿元的西成高铁预计2017年11月竣工,届时成都到西安只需3小时,上午游武侯区,晚上看大雁塔将成为现实,用科学记数法表示647亿元为( )A.647×108B.6.47×109C.6。
47×1010D.6。
47×10114.(3分)二次根式中,x的取值范围是()A.x≥1 B.x>1 C.x≤1 D.x<15.(3分)下列图标中,既是轴对称图形,又是中心对称图形的是( )A.B.C.D.6.(3分)下列计算正确的是( )A.a5+a5=a10B.a7÷a=a6 C.a3•a2=a6 D.(﹣a3)2=﹣a67.(3分)学习全等三角形时,数学兴趣小组设计并组织了“生活中的全等”的比赛,全班同学的比赛结果统计如下表:得分(分) 60 70 80 90 100人数(人) 7 12 10 8 3则得分的众数和中位数分别为()A.70分,70分B.80分,80分C.70分,80分D.80分,70分8.(3分)如图,四边形ABCD和A′B′C′D′是以点O为位似中心的位似图形,若OA:OA′=2:3,则四边形ABCD与四边形A′B′C′D′的面积比为()A.4:9 B.2:5 C.2:3 D.:9.(3分)已知x=3是分式方程﹣=2的解,那么实数k的值为()A.﹣1 B.0 C.1 D.210.(3分)在平面直角坐标系xOy中,二次函数y=ax2+bx+c的图象如图所示,下列说法正确的是( )A.abc<0,b2﹣4ac>0 B.abc>0,b2﹣4ac>0C.abc<0,b2﹣4ac<0 D.abc>0,b2﹣4ac<0二、填空题(本大题共4小题,每小题4分,共16分)11.(4分)(﹣1)0= .12.(4分)在△ABC中,∠A:∠B:∠C=2:3:4,则∠A的度数为.13.(4分)如图,正比例函数y1=k1x和一次函数y2=k2x+b的图象相交于点A(2,1),当x<2时,y1y2.(填“>”或“<").14.(4分)如图,在平行四边形ABCD中,按以下步骤作图:①以A为圆心,任意长为半径作弧,分别交AB,AD于点M,N;②分别以M,N为圆心,以大于MN的长为半径作弧,两弧相交于点P;③作AP射线,交边CD于点Q,若DQ=2QC,BC=3,则平行四边形ABCD周长为.三、解答题(本大题共14小题,共104分)15.(12分)(1)计算:|﹣1|﹣+2sin45°+()﹣2;(2)解不等式组:.16.(6分)化简求值:÷(1﹣),其中x=﹣1.17.(8分)随着经济的快速发展,环境问题越来越受到人们的关注,某校学生会为了解节能减排、垃圾分类知识的普及情况,随机调查了部分学生,调查结果分为“非常了解"“了解”“了解较少”“不了解”四类,并将调查结果绘制成下面两个统计图.(1)本次调查的学生共有人,估计该校1200名学生中“不了解"的人数是人;(2)“非常了解"的4人有A1,A2两名男生,B1,B2两名女生,若从中随机抽取两人向全校做环保交流,请利用画树状图或列表的方法,求恰好抽到一男一女的概率.18.(8分)科技改变生活,手机导航极大方便了人们的出行,如图,小明一家自驾到古镇C游玩,到达A地后,导航显示车辆应沿北偏西60°方向行驶4千米至B地,再沿北偏东45°方向行驶一段距离到达古镇C,小明发现古镇C恰好在A地的正北方向,求B,C两地的距离.19.(10分)如图,在平面直角坐标系xOy中,已知正比例函数y=x的图象与反比例函数y=的图象交于A(a,﹣2),B两点.(1)求反比例函数的表达式和点B的坐标;(2)P是第一象限内反比例函数图象上一点,过点P作y轴的平行线,交直线AB于点C,连接PO,若△POC的面积为3,求点P的坐标.20.(12分)如图,在△ABC中,AB=AC,以AB为直径作圆O,分别交BC于点D,交CA的延长线于点E,过点D作DH⊥AC于点H,连接DE交线段OA于点F.(1)求证:DH是圆O的切线;(2)若A为EH的中点,求的值;(3)若EA=EF=1,求圆O的半径.B卷(共50分)一、填空题(本大题共5个小题,每小题4分,共20分)21.(4分)如图,数轴上点A表示的实数是.22.(4分)已知x1,x2是关于x的一元二次方程x2﹣5x+a=0的两个实数根,且x12﹣x22=10,则a= .23.(4分)已知⊙O的两条直径AC,BD互相垂直,分别以AB,BC,CD,DA为直径向外作半圆得到如图所示的图形,现随机地向该图形内掷一枚小针,记针尖落在阴影区域内的概率为P1,针尖落在⊙O内的概率为P2,则= .24.(4分)在平面直角坐标系xOy中,对于不在坐标轴上的任意一点P(x,y),我们把点P′(,)称为点P的“倒影点”,直线y=﹣x+1上有两点A,B,它们的倒影点A′,B′均在反比例函数y=的图象上.若AB=2,则k= .25.(4分)如图1,把一张正方形纸片对折得到长方形ABCD,再沿∠ADC的平分线DE折叠,如图2,点C落在点C′处,最后按图3所示方式折叠,使点A落在DE的中点A′处,折痕是FG,若原正方形纸片的边长为6cm,则FG=cm.二、解答题(本大题共3个小题,共30分)26.(8分)随着地铁和共享单车的发展,“地铁+单车"已成为很多市民出行的选择,李华从文化宫站出发,先乘坐地铁,准备在离家较近的A,B,C,D,E中的某一站出地铁,再骑共享单车回家,设他出地铁的站点与文化宫距离为x(单位:千米),乘坐地铁的时间y1(单位:分钟)是关于x的一次函数,其关系如下表:地铁站A B C D Ex(千米)891011.513y1(分钟)1820222528(1)求y1关于x的函数表达式;(2)李华骑单车的时间(单位:分钟)也受x的影响,其关系可以用y2=x2﹣11x+78来描述,请问:李华应选择在那一站出地铁,才能使他从文化宫回到家所需的时间最短?并求出最短时间.27.(10分)问题背景:如图1,等腰△ABC中,AB=AC,∠BAC=120°,作AD⊥BC于点D,则D 为BC的中点,∠BAD=∠BAC=60°,于是==;迁移应用:如图2,△ABC和△ADE都是等腰三角形,∠BAC=∠DAE=120°,D,E,C三点在同一条直线上,连接BD.①求证:△ADB≌△AEC;②请直接写出线段AD,BD,CD之间的等量关系式;拓展延伸:如图3,在菱形ABCD中,∠ABC=120°,在∠ABC内作射线BM,作点C关于BM的对称点E,连接AE并延长交BM于点F,连接CE,CF.①证明△CEF是等边三角形;②若AE=5,CE=2,求BF的长.28.(10分)如图1,在平面直角坐标系xOy中,抛物线C:y=ax2+bx+c与x轴相交于A,B两点,顶点为D(0,4),AB=4,设点F(m,0)是x轴的正半轴上一点,将抛物线C绕点F 旋转180°,得到新的抛物线C′.(1)求抛物线C的函数表达式;(2)若抛物线C′与抛物线C在y轴的右侧有两个不同的公共点,求m的取值范围.(3)如图2,P是第一象限内抛物线C上一点,它到两坐标轴的距离相等,点P在抛物线C′上的对应点P′,设M是C上的动点,N是C′上的动点,试探究四边形PMP′N能否成为正方形?若能,求出m的值;若不能,请说明理由.2017年四川省成都市中考数学试卷参考答案与试题解析一、选择题(本大题共10小题,每小题3分,共30分)1.(3分)《九章算术》中注有“今两算得失相反,要令正负以名之”,意思是:今有两数若其意义相反,则分别叫做正数与负数,若气温为零上10℃记作+10℃,则﹣3℃表示气温为( )A.零上3℃B.零下3℃C.零上7℃D.零下7℃【解答】解:若气温为零上10℃记作+10℃,则﹣3℃表示气温为零下3℃.故选:B.2.(3分)如图所示的几何体是由4个大小相同的小立方体组成,其俯视图是()A.B.C.D.【解答】解:从上边看一层三个小正方形,故选:C.3.(3分)总投资647亿元的西成高铁预计2017年11月竣工,届时成都到西安只需3小时,上午游武侯区,晚上看大雁塔将成为现实,用科学记数法表示647亿元为()A.647×108B.6。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2017成都树德中学自主招生考试数学答案
一、 选择题
1—5:CDBBD 6—10:CACCA 11—12:CB
二、填空题
13. 14. 45 15. 113
11- 16. 4
三、解答题
17.(1)xy a =,x
b y =⇒x y == (2)1ab
c += ①
1b c a += ②
1a c b += ③
① — ②:0ab c bc a +--=
()()10b a c --=
⇒1b =或a c =
当a c = 无解
当1b = 代入 1,0
0,1a c a c ==⎧⎨==⎩或
又∵0a > ∴舍掉
∴1a =,1b =,0c =
18.(1) 34512ABC C =++= , 当t=1,即BF=6-1-3=2
∴9
8,55F ⎛⎫
⎪⎝⎭ ∴1
13y x =+
(2)∵AF+AE=6,∴AF=t+2⇒3
12
4
(2),555F t t ⎛⎫+- ⎪⎝⎭,直线y=kx+t 过3124(2),555F t t ⎛⎫
+- ⎪⎝⎭
∴k=4310
322t
t t -=-+++ ∵0<t<4, ∴4
3-<k<2
19.(1)(5,0)B r ,(,0)A r -
顶点(2,4)D r r -
∴()224y a x r r =-- ⇒49a r =
由4b r a -= ⇒169
b =- 由25
c r a =- ⇒ 209
c r =- (2)241620999y x x r r =--,20(0,)9
C r - 6A B r = ∴12ABC S AB OC =⨯ 120206293
r r =⨯⨯=,1r = ∴241620999y x x =-- 20.(1)证明:∵AD 为∠GAC 的角平分线 ∴BG S BDG DB DG CH S CDH DC DH ⨯==⨯
∴BG DC DH CH DB DG ⨯⨯=⨯⨯ …①
又∵,CE BD BF CD ∴,GB GD HC HD BE DC CF DB == ∴BF BG DC DH CF CH DB DG = …②
∴由①②得 1
BE CF = ∴BE CF =
(2)取BC 中点为k , ∴作∠MKN 角平分线KP KP ⊥MN
BE ∥MK,CF ∥NK ,∴同理AD ⊥MN
21.(1)当a=1,2y x bx c =++ 2233x c x b x c +=++ 24(3)03b c =--= …①
227233x x x c -+-=+ 80803c ==-= 15b =⎧⎨⎩或(舍)c=3
(2)a>0.开口向上,b>0.
①若0
2b a -<,即b ≥4a 时
(2)1(1)7f f -=-⎧⎨=⎩ ⇒ 4217a b c a b c -+=-⎧⎨++=⎩⇒83b a x =+ 显然 a b 不能同为整数 ∴无解
②若1222b a -<-
<- 即4a b a <<
2
4147ac b a a b c ⎧-=-⎪⎨⎪++=⎩
将c=7-(a+b)代入 得: ()2
474a a b b a -+-=-⎡⎤⎣⎦⇒()2232a b a +=
由a<b,则()2229a b a
+>
∴2329a a >∴329
a <∴a 只可取1,2,3 当a=1,
b 不为整数,舍去
当a=2,b=4,c-1,可取
当a=3,b 不为整数,舍
② 若1022b a -<-<,即0<b<a 此时2
414427ac b a a b c ⎧-=-⎪⎨⎪-+=⎩
将c=7-(4-2b)代入得:2(4)32a b a
-= 又222(4)(4)9a b a a a
->-=
∴2932a a < 329a < 即a 可取1,2,3
∴当a=1,b 无整数解 舍去
当a=2,
当a=3 ∴无解
综上:只有a=2,b=4,c=1可取
22.(1)c=29 (2)存在5个 (a,b,c )=(6,25,29),(7,15,20),(9,10,17),(5,12,13),(6,8,10)。
