精选题11压杆稳定
压杆稳定习题

第九章压杆稳固姓名班级学号一、填空和选择1.理想平均直杆与轴向力 F=F cr 时处于直线均衡状态, 当其遇到一细小横向扰乱力后发生微 小曲折变形,若此时排除扰乱力,则压杆( ) A 曲折变形消逝,恢复直线形状; B 曲折变形减小,不可以恢复直线形状;C 微弯变形状态不变;D 曲折变形持续增大 2. 压杆的柔度集中地反应了压杆的( )对临界应力的影响A 长度、拘束条件、截面形状和尺寸;B 资料、长度和拘束条件;C 资料、拘束条件、截面形状和尺寸;D 资料、长度、截面形状和尺寸3.两头铰支圆截面修长压杆,在某一截面上开一个小孔,对于小孔对杆承载能力的影响, 以下阐述正确的选项是( )A 对强度和稳固承载能力都有较大消弱;B 对强度有较大消弱,对稳固承载能力消弱极微C 对强度无消弱,对稳固承载能力有较大消弱;D 对强度和稳固承载能力都不会消弱 4.修长杆在图示拘束状况下,其长度要素μ的大小在( )范围内。
(A) μ>2;(B) 2>μ >;(C) >μ >;(D) μ <。
题4图题5图5. 上端自由、下端固定的压杆,横截面为 80*80*5 号等边角钢,失稳时截面会绕轴弯曲。
(A) z 或 y 轴;(B)zc 或 yc 轴;(C) y0 轴; (D) z0 轴。
6. 图示为支撑状况不一样的圆截面修长杆,各杆的直径和资料同样, 的柔度最大, 数值为 ; 的柔度最小, 数值为 ; 的临界力最大,数值为 ; 的临界力最小,数值为 ;7. 两根修长压杆的长度、横截面面积、拘束状态以及资料均同样,若横截面形状分为正方 形和圆形, 则截面形状为 的柔度大, 截面形状为 的临界力大。
8. 以下对于压杆临界应力cr 的结论中,( )是正确的。
A 修长杆的cr 与杆的资料没关;B 中长杆的crC 中长杆的cr 与杆的资料没关; D 短粗杆的cr与杆的柔度没关与杆的柔度没关二、图示两头铰支压杆,用两根8 号槽钢( Q235 钢)按图示方式组合而成,试确立两根槽钢间距为多少时组合杆的临界力最大,并计算此临界力。
压杆稳定的考题
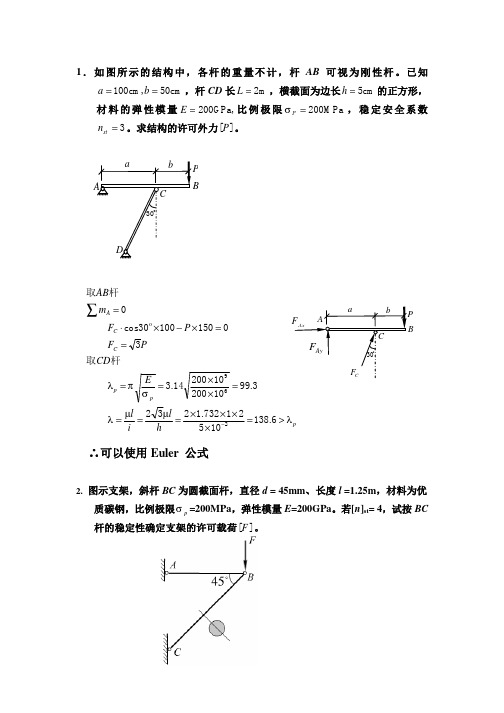
1.如图所示的结构中,各杆的重量不计,杆AB 可视为刚性杆。
已知cm 50,cm 100==b a ,杆CD 长m 2=L ,横截面为边长cm 5=h 的正方形,材料的弹性模量,GPa 200=E 比例极限MPa 200=P σ,稳定安全系数3=st n 。
求结构的许可外力][P 。
pp p C C Ah l i l E CD P F P F mAB λµµλσπλ>=××××====××====×−×⋅=−∑6.13810521732.12323.99102001020014.33015010030cos 0269杆取杆取o∴可以使用Euler 公式2. 图示支架,斜杆BC 为圆截面杆,直径d = 45mm 、长度l =1.25m ,材料为优质碳钢,比例极限p σ=200MPa ,弹性模量E =200GPa 。
若[n ]st = 4,试按BC 杆的稳定性确定支架的许可载荷][F 。
,045sin 00=−⋅=∑F F FBBC y取节点 F F BC =⋅22杆取CD399106200109200143..E πP P =×××==σλλp d l i μl λ>=×===1.111045.0425.14∴ 可以使用Euler 公式 (1分))kN (9.25364)25.11(2045.01020014.3)(49322=×××××==−l EI F CrBC µπ )kN (9.4449.2532222][===∴−n F F stCr BC3、一长为mm 600的钢板尺两端铰接放入实验架中受轴向压力,其横截面积为mm 132×。
已知压应力容许值为MPa 215][=σ,弹性模量GPa 210=E 。
工程力学 第二版 (范钦珊 唐静静 著) 高等教育出版社 课后答案 第11章 压杆的稳定性问题

角钢(连结成一整体)。试确定梁与柱的工作安全因 数。
解:1.查型钢表得
习题 11-12 图
No.16aI:Iz = 1130cm4,Wz = 141cm3 2No. 63×63×5: A = 2 × 6.143 = 12.286 cm2
i y = 1.94cm I y = 2 × 23.17 = 46.34 cm
采用,欧拉公式计算临界力
FPcr = σ cr A =
轴的工作安全因数
2 π E
λ2
=
所以,轴不安全。
11-11 图示正方形桁架结构,由五根圆截面钢杆组成,
连接处均为铰链,各杆直径均为 d=40 mm,a=1 m。材料 均为 Q235 钢,E=200 GPa,[n]st=1.8。试;
网
ww w
.k hd 案
μ =1
co
界力。
m
11-5
图示 a、b、c、d 四桁架的几何尺寸、圆杆的横截面直径、材料、加力点及加力
方向均相同。关于四桁架所能承受的最大外力 FPmax 有如下四种结论,试判断哪一种是正确 的。 (A)FPmax(a)=FPmax(c)<FPmax(b)=FPmax(d); (B)FPmax(a)=FPmax(c)=FPmax(b)=FPmax(d); (C)FPmax(a)=FPmax(d)<FPmax(b)=FPmax(c);
案
对于 A3 钢, λ P = 102,
λs = 61.6 。因此,第一杆为大柔度杆,第二杆为中柔度杆,
网
i μl λ2 = 2 i μl λ3 = 3 i
λ1 =
=
ww w
FPcr = ( a − bλ ) A = (304 − 1.12 × 62.5) × 10 3 ×
静力学11、压杆稳定

Fcr
2 EI l2
μ= 1
2 EI Fcr (0.7l)2
μ= 0.7
2 EI Fcr (0.5 l ) 2
μ= 0.5
2EI Fcr (2l )2
μ= 2
2 EI Fcr l 2
μ= 1
§11.4 欧拉公式的适用范围.经验公式
一、欧拉临界应力公式及使用范围
1.细长压杆的临界应力:临界力除以压杆横截面面积
0
Pcr d EI
k
2d
将边界条件代入统一微分方程的通解得:
式 0
如 图
k 0
1 0 k2
0 1 0
1 0 0
0 0 k
2
C1
C C
2 3
0
sinkL
coskL L 1
k 2 sinkL k 2 coskL 0 0
1 0
Cd4
有非零解的充要条件为:系数行列式值为零;
解得压杆失稳特征方程为:coskL 0
解: (1) 2 E I
Pcr ( l)2
2E d4
64
( l)2
1 16
2E I正
(2)
Pcr 正 Pcr 圆
( l)2 2E I圆
d2 2
a4 4
I正 I圆
12
d4
12
d4
3
( l)2
64
64
例5:五根直径都为 d的细长圆杆铰接构
成平面正方形杆系ABCD,如各杆材料相 同,弹性模量为E。求图 (a)、(b)所示两种 载荷作用下杆系所能承受的最大荷载。
60
2. cr=S时: 强度破坏,采用强度公式。
≤ S—粗短杆(小柔度杆);
表 1 直线公式的系数 a 和 b
压杆稳定习题

压杆稳定一、判断题1.临界力Fij只与压杆的长度及两端的支撑情况有关。
()2.对于细长压杆,临界应力σij的值不应大于比例极限σp。
()3.压杆的柔度与压杆的长度,横截面的形状和尺寸以及两端的支撑情况有关。
()4.压杆的杆端约束作用愈强,那么长度系数越小,临界压力越大。
()5.压杆的临界应力应该由欧拉公式计算。
()6.欧拉公式的适用条件是。
()7.细长压杆,若长度系数μ增大一倍,则临界力Fij增加一倍。
()图 18.两端铰支细长压杆,若在其中加一铰支座如图1所示,则欧拉临界力是原来的4倍。
()9.如果细长压杆有局部削弱,削弱部分对压杆的稳定性没有影响。
()10.在材料,长度,横截面形状和尺寸保持不变的情况下,杆端约束越强,则压杆的临界力越小。
11.压杆的临界荷载是压杆保持不稳定平衡所承受的最大轴向压力。
()二、选择题1.在压杆的材料、长度、横截面形状和尺寸保持不变的情况下,杆端约束越强,则压杆的临界力()。
A. 越大B.保持不变C.越小D.以上三种可能都有2.已知细长压杆两端球形铰支,若截面面积相等时,采用下列那种截面最稳定?()A B CD三、分析题1.在压杆稳定计算中,是一个与_______,________和______有关的参数,称为压杆的。
2.欧拉公式的适用范围是什么?3.图2两根杆件的截面形状、尺寸及材料均相同,试比较哪一根杆件稳定性好?为什么?图 24.两根细长压杆,材料相同,一根截面形状为正方形,一根截面为圆形。
假设两根杆截面面积相同,支承相同,试问:①横截面惯性矩各为多少?②哪根杆容易受压失稳?为什么?5.一压杆两端约束一定,在截面面积不变情况下,为了更有效地提高其临界力应采用()措施。
6.若两根细长压杆的回转半径()相等。
当相等时,它们的柔度()相等,若两杆的柔度相等,当_______相等时,它们的临界应力相等。
7.写出压杆稳定条件的计算公式。
8.图3所示两根直径均为d的圆截面压杆,材料相同,已知,d=20mm,试判断哪根压杆容易失稳图 3四、计算题1.二圆形截面受压杆的材料相同,尺寸如图4所示,已知二杆均为大柔度杆,试比较二杆的临界力和临界应力2.圆形截面受压杆,长L=1.5m,直径d=3cm,钢材的弹性模量,比例极限σp=200Mpa,试求压杆的临界力。
压杆稳定习题及答案

压杆稳定习题及答案【篇一:材料力学习题册答案-第9章压杆稳定】xt>一、选择题1、一理想均匀直杆受轴向压力p=pq时处于直线平衡状态。
在其受到一微小横向干扰力后发生微小弯曲变形,若此时解除干扰力,则压杆( a )。
a、弯曲变形消失,恢复直线形状;b、弯曲变形减少,不能恢复直线形状; c、微弯状态不变; d、弯曲变形继续增大。
2、一细长压杆当轴向力p=pq时发生失稳而处于微弯平衡状态,此时若解除压力p,则压杆的微弯变形( c )a、完全消失b、有所缓和c、保持不变d、继续增大 3、压杆属于细长杆,中长杆还是短粗杆,是根据压杆的( d)来判断的。
a、长度b、横截面尺寸c、临界应力d、柔度 4、压杆的柔度集中地反映了压杆的( a)对临界应力的影响。
a、长度,约束条件,截面尺寸和形状;b、材料,长度和约束条件;c、材料,约束条件,截面尺寸和形状;d、材料,长度,截面尺寸和形状; 5、图示四根压杆的材料与横截面均相同,试判断哪一根最容易失稳。
答案:( a )6、两端铰支的圆截面压杆,长1m,直径50mm。
其柔度为 ( c )a.60;b.66.7;c.80;d.50 7、在横截面积等其它条件均相同的条件下,压杆采用图( d )所示截面形状,其稳定性最好。
≤?≥?- 1 -10、在材料相同的条件下,随着柔度的增大( c)a、细长杆的临界应力是减小的,中长杆不是;b、中长杆的临界应力是减小的,细长杆不是; c、细长杆和中长杆的临界应力均是减小的; d、细长杆和中长杆的临界应力均不是减小的; 11、两根材料和柔度都相同的压杆( a )a. 临界应力一定相等,临界压力不一定相等;b. 临界应力不一定相等,临界压力一定相等;c. 临界应力和临界压力一定相等;d. 临界应力和临界压力不一定相等;a、杆的材质b、杆的长度c、杆承受压力的大小d、杆的横截面形状和尺寸二、计算题1、有一长l=300 mm,截面宽b=6 mm、高h=10 mm的压杆。
材料力学习题压杆稳定

压 杆 稳 定基 本 概 念 题一、选择题1. 如果细长压杆有局部削弱,削弱部分对压杆的影响有四种答案,正确的是( )。
A .对稳定性和强度都有影响 B .对稳定性和强度都没有影响C .对稳定性有影响,对强度没有影响D .对稳定性没有影响,对强度有影响 2. 图示长方形截面压杆,h /b = 1/2;如果将b 改为h 后仍为细长杆,临界力cr P 是原来的( )倍。
A .2倍B .4倍C .8倍D .16倍 3. 细长压杆,若长度系数μ增加一倍,则临界压力cr P 的变化是( )。
题2图A .增加一倍B .为原来的四倍C .为原来的四分之一D .为原来的二分之一4. 图示四根压杆的材料、截面均相同,它们在纸面内失稳的先后次序是( )。
题4图A .(a )、(b )、(c )、(d )B .(d )、(a )、(b )、(c )C .(c )、(d )、(a )、(b )D .(b )、(c )、(d )、(a )5. 正方形截面杆,横截面边长a 和杆长l 成比例增加,它的长细比( )。
A .成比例增加B .保持不变C .按2⎪⎭⎫ ⎝⎛a l 变化D .按2⎪⎭⎫⎝⎛l a 变化6. 如图所示直杆,其材料相同,截面和长度相同,支承方式不同,在轴向压力下,他们的柔度是( )。
A .a λ大,c λ小B .b λ大,d λ小C .b λ大,c λ小D .a λ大,b λ小 -46-7. 若压杆在两个方向上的约束情况不同,且y μ>z μ。
那么该压杆的合理截面应满足的条件是( )。
A .z y I I =B .y I <z IC .y I >z ID .y z λλ=题6图8. 两压杆为管状薄壁容器式的细长杆,管两端封闭,且为铰支承。
(a )杆无内压,(b ) 杆有内压,其它条件相同。
则两杆临界应力的关系是( )。
A .()()b cr a cr σσ=B .()a cr σ>()b cr σC .()a cr σ<()b cr σD .无法比较9. 两根细长杆,直径、约束均相同,但材料不同,且212E E =,则两杆临界应力的关系是( )。
材料力学作业(压杆稳定)答案

两端为固定端,l 2m, l0 1.8m, b 25mm, h 76mm 。试求压杆的临界力。
2EI
钢制成,均布荷载集度 q=48kN/m。梁和支柱的材料均为 Q235 钢,
=170MPa,E=210GPa,
Pcr Pcr(Pcrl)(22lE()22IlE)2I
稳定安全系数 nst=2.5。试检查梁和支柱是否安全。
q
A
B
2m
C 2m
2m 10
解:(1)xy 平面内失稳,z 为中性轴:=1
D
解:这是一次超静定和压杆稳定综合题, (1) 由一次超静定得:F=5ql/8=120KN
(2)xz 平面内失稳,y 为中性轴:=0.5
(2) 校核梁的强度,Mc=-24KN.m:
材料力学作业(压杆稳定)
Pcr
2EI (l)2
班级:
学号:
姓名:
1.图示各杆均为细长压杆,各杆的材料、截面形状和截面面积均相同,试问杆能承 受的压力(d)图中压杆最大,(b)图中压杆最小
3. 图示的结构中,圆杆 CD 由 Q235 钢制成,C、D 两处均为球铰。已知 d=20mm,E=210GPa,
满足梁的强度安全
(3) 校核支柱的稳定,为小柔度杆按强度计算
不满足支柱的强度,不安全.
p 200 MPa
可荷载。 y
d ,稳定安全因数 nst
3
。试根据
CD
压杆的稳定性确定该ຫໍສະໝຸດ 构的许PAyz
ld
P
A
z
l
BP
x
BP
x
答案:[F]=1.88KN
2.图示压杆,E=210GPa,在主视图(a)平面内,两端为铰支,在俯视图(b)平面内, 4.如图所示结构中的梁 AB 及立柱 CD 分别为 16 号工字钢和连成一体的两根 63×63×5 角
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
压杆稳定1. 图示结构,AB 为刚性杆,其它杆均为直径10 mm d =的细长圆杆,弹性模量200 GPa E =, 屈服极限s 360 MPa σ=,试求此结构的破坏载荷F 值。
解:12.37 m, sin 26H α⎛⎫== ⎪⎝⎭,0.169()Cy Dy F F F =-=↓,由杆1,4,N11s 0.507F F A σ==,s 10.507AF σ==由杆2,3,2N2cr 2π0.673 kN EIF F l ===, cr 2 1.33 kN 0.507F ==结构破坏载荷 1.33 kN F =2. 图示桁架由5根圆截面杆组成。
已知各杆直径均为30 mm d =, 1 m l =。
各杆的弹性模量均为200 GPa E =,p 100λ=,061λ=,直线经验公式系数304 MPa a =, 1.12 MPa b =,许用应力[]160 MPa σ=,并规定稳定安全因数st []3n =,试求此结构的许可载荷[]F 。
解:由平衡条件可知杆1,2,3,4受压,其轴力为杆5受拉,其轴力为N5F F = 按杆5的强度条件:N5[], []113 kN F F A Aσσ≤≤= 按杆1,2,3,4的稳定条件 p 133λλ=> 由欧拉公式 cr 78.48 kN F =37.1 kN F ≤ , []37.1 kN F =3. 钢杆和铜杆截面、长度均相同,都是细长杆。
将两杆的两端分别用铰链并联,如图,此时两杆都不受力。
试计算当温度升高多少度时,将会导致结构失稳?已知杆长 2 m l =,横截面积220 cm A =,惯性矩440 cm z I =;钢的弹性模量s 200 GPa E =,铜的弹性模量c 100 GPa E =,钢的线膨胀系数6s 12.510α-=⨯℃-1,铜的线膨系数6c 16.510α-=⨯℃-1。
解:铜杆受压,轴力为Nc F ,钢杆受拉,轴力为Ns F ,Nc Ns N F F F ==由协调条件 s c l l ∆=∆ 即 N N s c s c F l F ltl tl E A E Aαα∆+=∆- 铜杆为细长杆 2c cr 2π98.7 kN E IF l==m当 Nc cr F F =时失稳, 此时 185 C t ∆=o4. 图示矩形截面杆AC 与圆形截面杆CD 均用低碳钢制成,C ,D 两处均为球铰,材料的弹性模量200 GPa E =,强度极限b 400 MPa σ=,屈服极限s 240 MPa σ=,比例极限p 200 MPa σ=,直线公式系数304 MPa a =, 1.118 MPa b =。
p 100λ=,061λ=,强度安全因数[] 2.0n =,稳定安全因数st [] 3.0n =,试确定结构的最大许可载荷F 。
解:(1) 由梁AC 的强度 (2) 由杆CD 的稳定性5. 图示两端固定的工字钢梁,横截面积226.1 cm A =,惯性矩4,长度 6 m l =,材料的弹性模量200 GPa E =,比例极限s 240 MPa σ=,直线公式的系数304 MPa a =, 1.12 MPa b =,线膨胀系数712510/l α-=⨯℃,当工字钢的温度升高10t ∆=℃时,试求其工作安全因数。
解:p 158.799.3λλ=>=由欧拉公式,可得临界应力cr 78.2 MPa σ=温度应力 25 MPa l tE σα=∆= 工作安全因数 crst 3.13n σσ==6. 图示正方形平面桁架,杆AB ,BC ,CD ,DA 均为刚性杆。
杆AC ,BD 为弹性圆杆,其直径20 mm d =,杆长550 mm l =;两杆材料也相同,比例极限p 200 MPa σ=, 屈服极限s 240 MPa σ=,弹性模量200 GPa E =,直线公式系数304 MPa a =, 1.12 MPa b =,线膨胀系数612.510/l α-=⨯℃,当只有杆AC 温度升高,其他杆温度均不变时,试求极限的温度改变量cr t ∆。
解:由平衡方程可得:N N N AC BD F F F == (压) 由变形协调方程,并注意到小变形, 有AC BD ΔΔB即 N N AC BD l F l F ltl EA EAα∆-=又由 p 11099λλ=>=, 知2cr 2πEIF l=令 N cr F F =, 得 22cr 2π130.58d t l α∆==℃7. 图示结构,已知三根细长杆的弹性模量E ,杆长l ,横截面积A 及线膨胀系数α均相同。
问:当升温t ∆为多大时,该结构将失稳。
解:由 N l F ltl EA α∆=, 可得 N l F tEA α=∆细长杆: 2cr 2π EIF l =当 N cr F F =时失稳 22πl EItEA lα∆= 得 22πl I t Al α∆=8. 图示结构ABC 为矩形截面杆,60 mm, 100 mm, 4 m b h l ===,BD 为圆截面杆,直径60 mm d =,两杆材料均为低碳钢,弹性模量200 GPa E =, 比例极限p 200 MPa σ=,屈服极限s 240 MPa σ=,直线经验公式为cr (304 1.12) MPa σλ=-,均布载荷 1 kN/m q =,稳定安全因数st []3n =。
试校核杆BD 的稳定性。
解:(1) 由协调方程,Δcos45BDB l f =o得34N cos45(2)5(2)38448BD F l q l EI EI -o 解得 N 7.06 kN BD F = (2) 杆BD :p 377100λλ=>= 由欧拉公式:cr 39 kN F = cr st st N 5.56[]BDFn n F ==>,安全。
BDAC9. 正方形截面杆,横截面边长a和杆长l成比例增加,它的长细比有4种答案:(A)成比例增加;(B)保持不变;(C)按2(/)l a变化;(D)按2(/)a l变化。
答:B10. 非细长杆如果误用了欧拉公式计算临界力,其结果比该杆的实际临界力。
答:大。
11. 两根细长压杆,横截面面积相等,其中一个形状为正方形,另一个为圆形,其它条件均相同,则横截面为的柔度大,横截面为的临界力大。
答:圆形;正方形。
12. 在水平面ABC上用同材料的三根杆支持F。
A、B、C、D均为铰链节点。
铅直力F的作用线恰好通过等边三角形ABC的形心G。
已知DG AB h==。
三杆截面均为圆形,直径为d,材料的弹性模量为E。
适用欧拉公式的临界柔度是90。
已知20h d=,试确定最大力F。
解:2sin603BEBE h BG BD=︒=====13. 图示结构,由圆杆AB、AC通过铰链联结而成,若二杆的长度、直径及弹性模量均分别相等,BC间的距离保持不变,F为给定的集中力。
试按稳定条件确定用材最省的高度h 和相应的杆直径D。
(设给定条件已满足大柔度压杆的要求。
)解:杆达到临界状态时,cr22πEIFh l2=+,此时之F值为:4222πEIFh l23==+可求得:4D=(a)二杆之总体积为:V==(b)222d0, 5,d2V lh l h hh==+=得所以(c)将(c)式代入(a)式得, 1.303D=14. 长方形截面细长压杆,/1/2b h =;如果将b 改为h 后仍为细长杆,临界力cr F 是原来的多少倍?有4种答案:(A) 2倍; (B) 4倍; (C) 8倍; (D) 16倍。
答:C15. 压杆下端固定,上端与水平弹簧相连,如图所示,则压杆长度因数μ的范围有4种答案:(A)μ<0.5; (B)0.5μ<<0.7; (C)0.5μ<<2; (D)μ<2。
答:C16. 圆截面的细长压杆,材料、杆长和杆端约束保持不变,若将压杆的直径缩小一半,则其临界力为原压杆的 ;若将压杆的横截面改变为面积相同的正方形截面,则其临界力为原压杆的 。
答:1π;163。
17. 试导出具有初始挠度0sin(π/)y a x l =的图示压杆的挠度曲线方程()y x 。
证:2220() , , sin(π/)FEIy F y y k y k y k a x l EI''''=-+=+=-令 由0, 0; 0, , 0; 0x y B x l y A ======得 22sin(π/)πal F x l y EI l F2=-18. 某结构失稳时,挠曲线如图(a)所示,即上端可水平移动但不能转动,下端固定,试推导临界力欧拉公式及挠曲线方程。
证:2e cr cr , [], M F y F y k y EI EI -''''==+由 0,0, 0, 0, x y y A B '=====[1cos(/)], 2x l x l y y δπδ-==,=19. 的临界载荷。
解:给以微干扰,由其平衡状态求F 20. 1k 、2k ,试导出它的临界载荷。
解:由微干扰后的平衡状态21. 导出图示结构在图形平面内失稳的临界载荷。
已知:杆AB 、BC 均为刚性杆,杆CD 的弯曲刚度为EI 。
注:悬臂梁端部受有横向集中力F 时,端点的挠度公式为3/(3)y Fl EI =。
解:cr N 0: A M F F l δ∑==已知 3N cr 23, 3F l EI F EI lδ==得F22. 图示刚架,AB 为刚性杆,BC垂载荷F EI 为常值。
证:由微干扰后的平衡状态知梁BC 在 B 端的外力偶 e cr B M F a δδθ=,=23. 两根直径为d 细长杆考虑确定临界力cr F 。
解:压杆将首先在与两杆组成的平面相垂直的面内失稳。
此时,44cr 222πππ =, 64()128d EI Ed I F l l μμ23=2,==24. 图示压杆,AC 、CB 两杆均为细长压杆,问x 为多大时,承载能力最大?并求此时承载能力与C 处不加支撑时承载能力的比值。
解:(1) 由cr 2π, ()EIF l μ2=当0.7()x l x =-时承载能力最高, (2) 22cr 22cr 1()π/(0.412) 2.89()π/(0.7)F EI l F EI l 2==25. 图示结构,AB 和BC 是两端铰支的细长杆,弯曲刚度均为EI连结在B 、C 两铰点处,在点D 悬挂一重量为P 的重块。
试求: (1) 当3m h =时,能悬挂的P 最大值是多少? (2) h 为何值时悬挂的重量最大?解:(1) 2tan 3α=钢丝绳受力 N 2cos PF α=杆受力 N N N N tan cos , sin 223AB BC P P P F F F F ααα=====由杆AB 求P :2112π2π, 29AB P EI EI P l 2==由杆BC 求P :22max 2π3π3π, , 31616BC P EI EI EIP P l 222===(2) 由杆AB π92EI P2=3NBCN AB由杆BC πtan 9, tan 16216EI P αα2==又由图知 32tan , 3.56 m 9h h α2===26.铰接桁架,由竖杆AB 和斜杆BC 组成,两杆均为弯曲刚度为EI 的细长杆,在节点B 处承受水平力F 作用。
