解析倒格子空间和波矢空间
解析倒格子空间和波矢空间

王晴晴等 解析倒格子空间和波矢空间
73
X 射线是一种波长约为 0������ 001 - 10 nm 的电磁 波ꎬ与晶体中原子间距在同一个数量级ꎬ所以当用 X 射线照射到晶体时可观察到 X 射线的干涉[3]3 -6 、衍 射现象[4] ꎮ 如图 2 所示ꎬ晶面族对 X 射线来说构成 一系列反射面ꎮ 已知波长 λ 的单色 X 射线照射到 晶体后ꎬ同一晶面族不同晶面反射的波会产生位相 差ꎬ干涉的结果使得只有在某特定角度 θ 发生相干 相长( 满足布拉格条件[3]54 - 552dsinθ = nλꎬn 为衍射 级数ꎬd 为面间距)ꎮ 通过对待测晶体进行 X 射线衍 射获得图谱ꎬ可测出衍射峰的相对强度和对应的晶 面间距ꎬ进而求出对应的衍射指数( hkl) ꎮ
图 2 X 射线入射晶体图示
通过 X 射线衍射实验获得的衍射图样直接反 映了晶格结构的特征ꎬ每一个衍射峰对应一组衍射 指数( hkl) ꎮ 具体的衍射峰对应的衍射指数可通过 查阅粉末衍射 - JCPDS 卡片( 简称 PDF 卡片) 查阅ꎬ X 射线衍射图谱就像是晶体的指纹一样ꎬ每种晶体 具有其特定的 X 射线衍射图谱ꎬ可用来确定晶体材 料的物相[5] ꎮ 如图 3 所示为 Si 的标准 X 射线衍射 图谱( JCPDS No. 27 - 1402) ꎬ根据图谱可求出衍射 峰对应的晶面间距 d(hkl) 和晶格常数ꎮ
图 3 Si 的标准 X 射线衍射图谱
2 倒格子空间
为了更好地理解 X 射线衍射图谱并应用于晶
体学研究ꎬ引入了倒格子的概念ꎮ 将晶格中的一族
晶面转化为倒格子空间中的一点ꎬ而倒格矢与衍射
指数具有一一对应关系ꎮ 正格子空间ꎬ即坐标空间ꎬ
其量纲为长度单位ꎬ用显微镜如 SEM 可看到真实晶
固体物理习题及解答

完美导体不具备完全抗磁性,而超导体具有完全抗磁性,此为两者间最
E= B
根本的区别。根据法拉第电磁感应定律:
t ,若将超导体仅仅视
为电阻率为零的完美导体,内部电场强度 E 必为零,其旋度 E 必为零,
B
则磁场强度的时间变化率 t 亦必为零。因此完美导体内部的磁场强度保持 不变,根据外加磁场可为零或一定值;而对于超导体,无论外加磁场有无, 在超导态其内部磁场强度始终保持为零,具有完全抗磁性,其磁化率为-1。
表征。高于
68. 铁磁性物质高于居里温度时转变为顺磁性,并遵从 居里外斯 定律,
居里温度与 交换相互作用强度 成正比。
69. 第二类超导体的相干长度 小于 磁场侵入长度,因此超导态和正常态 的界面自由能为 负 值,可形成涡旋混合态。
70. 晶体衍射的必要条件是满足 Brag 方程,但由于系统消光,其中
-16. 布里渊(Brillouin)区 定义为倒格子空间中的维格纳-赛茨原胞;按
照衍射的劳埃条件,布里渊区边界包括了所有能发生 布拉格(Brag)反射 。
17. 根据布拉格方程,能满足衍射条件的入射 x 射线的波长不得大于 2d ;
入射 x 射线波长变大将导致衍射角
变大
。
18. 晶体结构中由原子或原子集团组成的最小重复单元称为
因此在外磁场为零时,具有 自发磁化 。
65. 根据费米分布函数
,在一定温度下,电子在费米能
级处的占据概率为
1/2
。
66. 原子磁矩在外磁场作用下的转向表现为 郎之万 顺磁性;导电电子
的自旋磁矩在外磁场作用下的转向表现为 泡利 顺磁性;
67. 一定温度下,铁磁性物质的特征物理性质由 磁滞回线 居里温度时转变为顺磁性,并遵从 居里外斯 定律。
1.5 倒格子空间
矢量的方向与矢量 a a 的方向一样 1 2
13:38
倒格基矢定义为:
2π b1 a2 a3 Ω 2π b2 a 3 a1 Ω 2π b3 a1 a 2 Ω
其中 a 1 , a 2 , a 3 是正格基矢,
Ω a1 a 2 a 3
是固体物理学原胞体积
假设
a3 k
2π a
2π b1 a 2 a3 Ω
2π b1 i a 2π b2 j a
2 a j k a
2
2π a
2 i
a
K h h1 b1 h2 b2
2π 倒格是边长为 a 的正方形格子。
13:38
例2:证明体心立方的倒格是面心立方。
解: 体心立方的原胞基矢:
(2)证明 K h h1 b1 h2 b 2 h3 b 3 的长度等于 由平面方程: X n d 得:
2π d h1h2 h3
13:38
。
d h1h2 h3 oA
Kh Kh
dh h h
1 2
3
2π a1 K h a 1 h1 b1 h2 b 2 h3 b 3 h1 K h h1 Kh Kh
b3 2 d3
2 b1 d1 2 b2 d2
3
b3
P P
a3
13:38
b2
a1
a2
取三个矢量 b1 , b2 , b3 为倒格子的基矢 正格子原胞的体积: d
b1
(a1a2 sin ) d3 a1 a2
所以:
2 2 a1 a2 b3 d3
固体物理第二章第四节 倒格子

1 ig r ig Rn 1 ig r ig Rn A( g ) F (r )e e dr F (r )e dr e
A( g ) 0 or
g
A( g )
定义对布拉维格子中所有格矢满足或或m为整数的全部端点的集合构成该布拉维格子称为正格子的倒格子reciprocallattice与倒格子的定义对应由格矢的端点所描述的布拉维格子称为正格子directlattice由端点的集合所描述的布拉维格子称为倒格子reciprocallattice称为倒格矢利用倒格矢满足的傅里叶展开为
ig Rn ig Rn A( g ) A( g )e A( g )[1 e ] 0 ig Rn
ig r F (r ) A( g )e 0
e
1
不合要求,应舍去
所以
e
ig Rn
1
ig Rn 也就是说,一定存在某些 g 使得当 e 1 成立时
同理可得 b2 , b3
所以倒格子基矢与正格子基矢的关系为:
2π b1 a2 a3 Ω 2π b2 a3 a1 Ω 2π b3 a1 a2 Ω
其中 a1 , a2 , a3 是正格基矢 Ω a1 a2 a3
则下式自然成立: n1Gh a1 n2Gh a2 n3Gh a3 2 m 或: Gh a1 2 h1; Gh a2 2 h2 ; Gh a3 2 h3 由于 a1 , a2 , a3为基矢,互不共面,则由 bi a j 2 ij 可知 b1 , b2 , b3 亦应该不共面,从 而可以用 Gh h1b1 h2b2 h3b3 描述倒格子。
固体物理03-倒格子空间

4
dr
nj
(r )r 2
sin Gr Gr
实验发现固体中的原子形状因子与自由原子的差别不大
其它实验手段
1. 电子衍射 (动量空间)
与X射线相比,电子波长更短,所以更加精确;更容易被物体吸收适 合于研究微薄膜、小晶体。
2. 中子散射 (动量空间)
可以测量晶体磁结构
3. 扫描隧道显微镜(实空间,表面)
S v1v2v3 f {1 exp i v2 v3 exp i v1 v3 exp i v1 v2 }
S 4 f 所有指数均为奇数,或均为偶数 S 0 其它情况
面心立方 的x-ray 散射图像
原子形状因子 f j dV n j (ρ)eiGρ
对自由原子:
f j 2 dr r 2 d cos n j exp(iGr cos )
j
ρ r rj
定义原子的形状因子 f j dV n j (ρ)eiGρ
结构因子
化简后可以得到晶体的结构因子
SG
f eiGr j j
j
对于第 j 个原子
G rj v1b1 v2b2 v2b2 x ja1 y ja2 z ja3 2 v1x j v2 y j v3z j
散射幅度
SG
dV n(r)eiGr
cell
结构因子
结构因子
假设晶胞中有 s 个原子,可以把原胞中的电荷密度分配到每一 个原子上(分配方法不唯一),即:
s
n(r) n j (r rj )
j 1
SG
cell dV n j (r r j )eiGr
j
eiGrj cell dV n j (ρ)eiGρ
晶体点阵的Fourier变换,晶体点阵则是倒易点阵的Fourier逆 变换。正格子的量纲是长度 L, 称作坐标空间,倒格子的量钢是 长度的倒数 L-1,称作波矢空间(或称动量空间)。
倒易空间和波矢空间

倒易空间和波矢空间倒易空间和波矢空间在固体物理学研究中扮演着重要的角色。
本文将分别介绍这两种空间的概念、性质及其在固体物理学中的应用。
一、倒易空间倒易空间是晶体学中的重要概念,也叫倒格子空间,是由晶体空间分别沿着三个互相垂直的方向所取得的倒格子面组成的三维空间。
倒易空间与实空间是对偶的,其定义如下:假设有一个空间中的周期晶体,晶格矢量为a1、a2和a3,我们将一个点P通过向该点连接三个不同的坐标轴上的原点,形成一个平行六面体。
在每个棱角上,我们垂直地连接倒晶格点,连接的线称为倒格子矢量,用向量b1、b2和b3表示。
这样就形成了一个由倒格子面组成的空间,这个空间就是倒易空间(或倒格子空间)。
倒易空间与其它物理学中的向量空间不同,因为其中的向量没有固定的起点或终点。
在倒易空间中,每个点表示一个倒格子面,而一个倒格子面的位置就由其倒格子矢量来决定。
倒易空间中的晶体结构即为倒格子结构。
倒易空间具有以下性质:1. 倒易空间的晶格矢量为倒格子的倒数。
2. 在倒易空间中,原点为所有倒格子的交点,称之为倒空间原点。
3. 倒易空间是无限大的,且存在与实空间一样的点群和空间群对称性。
4. 不同晶体的倒易空间不同,同样的晶体在不同条件下有不同的倒易空间表现形式。
倒易空间在固体物理学中有广泛应用。
例如,通过研究倒易空间中的电子能带结构,可以了解晶体材料的导体性、半导体性等性质;倒易空间中的布拉格平面可以对X射线衍射、中子衍射等进行定量描述,在这些领域具有重要的应用价值。
二、波矢空间波矢空间是描述在动量空间内的物理现象的空间。
波矢空间和倒易空间十分相似,只是在它们的定义和性质上存在微小差异。
假设有一个动量空间,其中的波矢k可以用三个互相垂直的分量(kx, ky, kz)表示。
图中所示为二维情况下的波矢空间。
波矢空间的物理意义为动量的取值范围。
在波矢空间中,物理量的取值可能会形成一些稀疏的分布,这些分布就被称为分支,对应实空间中的布里渊区。
《固体物理》能带理论 - 练习题
能带理论 - 练习题袁建勇:1.布洛赫函数满足)()(r e R r n R ik n ϕϕ•=+,何以见得上式中k 具有波矢的意义?[解答] 人们总可以把布洛赫函数)(r ϕ展成傅里叶级数∑•++=hrK Ki h h e K K a r )(//)()(ϕ ,其中/K 是电子的波矢。
将)(r ϕ代入 )()(r e R r nR ik n ϕϕ•=+得到 n nR ik R ik e e••=/其中利用了p p R K n h (2π=•是整数),由上式可知,/k k =, 即 k 具有波矢的意义。
2.波矢空间与倒格空间有何关系?为什么说波矢空间内的状态点是准连续的?[解答] 波矢空间与倒格空间处于统一空间,倒格空间的基矢分别为1b ,2b ,3b ,而波矢空间的基矢分别为 11/N b ,22/N b ,33/N b ;1N ,2N ,3N 分别是沿正格基矢1a ,2a ,3a 方向晶体的原胞数目。
倒格空间中一个倒格点对应的体积为 *321)(Ω=⨯•b b b ,波矢空间中一个波矢点对应的体积为 NN b N b N b *332211)(Ω=⨯• 即波矢空间中一个波矢点对应的体积,是倒格空间中一个倒格点对应的体积的N /1 。
由于N 是晶体的原胞数目,数目巨大,所以一个波矢点对应的体积与一个倒格点对应的体积相比是极其微小的。
也就是说, 波矢点在倒格空间看是极其稠密的。
因此,在波矢空间内作求和处理时,可把波矢空间内的状态点看成是准连续的。
3.一维周期势函数的傅里叶级数 ∑=nnx ain eV x V π2)(中,指数函数的形式是由什么条件决定的?[解答] 周期势函数)(x V 傅里叶级数的通式为 ∑=nxi n n e V x V λ)(。
上式必须满足势场的周期性,即()()()n n n n i x a i x i a i x n n n nnnV x a V e V e e V x V e λλλλ++==⨯==∑∑∑显然 1=ai n eλ 。
固体物理03-倒格子空间
实空间点阵
简立方
a1 a i, a2 a j, a3 a k
倒空间点阵
简立方
2
2
2
b1 a i, b2 a j, b3 a k
2 a 2
a
2 a
四方晶格
简单点阵的倒易点阵也是简单点阵。 正格子的基矢越长,倒格子的基矢越短,反之亦然。
六角点阵
正格子空间六方结构,在倒格子空间亦为六方结构。 不过其基矢尺寸关系发生变化,基矢方向也转了30度。
k 2 2k G G 2 k 2
2k G G 2 (G 和 –G 都是倒格矢)
G
衍射方程(也是布里渊区的边界方程)
k
k ·(G/2)=(G/2)2
Ewald 图解法
1. 选择原点以入射 k 矢长度 为半径作圆,保证另一端 点在倒格矢上。
2. 连接从原点到与圆相交的 所有倒格矢的波矢k’都能 发生衍射。
4
dr
nj
(r )r 2
sin Gr Gr
实验发现固体中的原子形状因子与自由原子的差别不大
其它实验手段
1. 电子衍射 (动量空间)
与X射线相比,电子波长更短,所以更加精确;更容易被物体吸收适 合于研究微薄膜、小晶体。
2. 中子散射 (动量空间)
可以测量晶体磁结构
3. 扫描隧道显微镜(实空间,表面)
4. 原子力显微镜(实空间,表面)
中国散裂中子源
扫描隧道显微镜(STM)
Si (100) 表面
原子力显微镜(AFM)
Si (111) 表面
作业 2
1. 证明正格子与倒格子互易 2. 证明面心立方格子的倒格子是体心立方,体心立方的倒格子是
面心立方!
3. 证明只有 k G' 时,衍射幅度F才不为0。
晶体结构对称性倒空间
a b c,
所属点群(P) 1, 1
School of Physics and Information Technology, SNNU
单斜(Monoclinic)
2) 简单单斜(P) 3) 底心单斜(C)
a b c, 90
2, m, 2 / m
对称轴图示
8二次轴 单斜
9三次轴 10四次轴 11六次轴
对称轴所构成的对称配置投影符号:
C1 (1)
C2 (2)
C3 (3)
C4 (4)
C6 (6)
School of Physics and Information Technology, SNNU
对称面(II类 )
反映(symmetry plane):一假想的平面,称为反映面或镜面。 反映操作是从空间某一点向反映面引垂线,并延长该垂线到反映 面的另一侧,在延长线上取一点,使得到反映面等距 国际符号:m
正四面体的对称操作
2) 绕4个立方体对角线轴转动
—— 8个对称操作 3) 恒等变换 —— 1个对称操作
4) 绕三个立方轴转动 /2,3/2 加中心反演 —— 6个对称操作
School of Physics and Information Technology, SNNU
230 种空间群 space groups
空间群:由点群对称操作和平移对称操作组合而成;由 32 晶体 学点群与 14个Bravais 点阵组合而成; 空间群是一个单胞(包含单胞带心)的平移对称操作;反射、旋 转和旋转反演等点群对称性操作、以及螺旋轴和滑移面对称性操作 的组合。 晶体学中的空间群是三维周期性物体(晶体)变换成它自身的对称 操作(平移,点操作以及这两者的组合)的集合。一共有230种空间 群。 每种空间群唯一的对应一种晶体结构。自然界的晶体结构只能有 230种。 230 空间群符号 = Bravais点阵类型符号 + 点群对称元素
固体物理(第4课)倒易空间
(4) 倒格矢和正点阵晶面族之间的关系: 正点阵中一族晶面,晶面指数为:(h1h2 h3) 倒易点阵中倒格矢: Gh h1b1 h2 b2 h3b3 Gh // ( h1h2 h3 ) 法线方向 2 则有: 证明如下: Gh = d h1h2h3
二维长方晶格的布里渊区
二维六方晶格的十个布里渊区
(3) 三维晶格
a. 简立方晶格
b1 a1 ai b2 a 2 aj a 3 ak b 3
倒易空间示意图
2 a 2 a 2 a i j 倒易点阵仍为简立方晶 格 k
体心立方晶格的倒易晶格是面心立方,其晶胞 常数为 4a 。
c. 面心立方晶格
2 a a1 2 ( j k ) b1 a ( i j k ) 4 a 2 (i j k ) b a2 (i k ) b2 2 a a 2 a a3 (i j ) b3 (i j k ) 2 a
5面心立方晶格的第一布里渊区第一布里渊区为十四面体布里渊区中某些对称点和若干对称轴上的点能量较为容易计算这些点的标记符号布里渊区原点六方面的中心四方面的中心计为轴方向计为轴方向将零级近似下的波矢k移入简约布里渊区能量变化的图像图中定性画出了沿轴的结果3
1.9 1 倒格子(倒易点阵)*的定义:
1 正格矢与倒矢
离原点最近的倒 格点有4个: b1,-b1,b2,-b2.
-b1
b2
b1 -b2
离原点次近的倒 格点有4个: -b1+b2 b1+b2 ,b1-b2 , b2,-b2.
b1+b2
-b1-b2
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
解析倒格子空间和波矢空间
王晴晴;宫昊;程荣龙;葛立新
【摘要】在固体物理学课程中,理解倒格子空间和波矢空间一直是学习的难点之一.从X射线衍射实验出发,并结合正格子空间,对倒格子空间和波矢空间进行了详细的解读,并且采用图形实例给出了凸显物理内涵的解释.
【期刊名称】《蚌埠学院学报》
【年(卷),期】2018(007)005
【总页数】4页(P72-75)
【关键词】倒格子;波矢;X射线衍射;布里渊区
【作者】王晴晴;宫昊;程荣龙;葛立新
【作者单位】蚌埠学院理学院,安徽蚌埠 233030;蚌埠学院理学院,安徽蚌埠233030;蚌埠学院理学院,安徽蚌埠 233030;蚌埠学院理学院,安徽蚌埠 233030【正文语种】中文
【中图分类】G642;O48-4
由大量原子或离子组成的晶体以一定的晶格结构周期性排列,原子或离子排列的具体形式称为晶格,构成了正格子空间。
由于晶体的长程有序,对晶体进行X射线衍射会得到清晰的衍射图像,这也是区别晶体和非晶的重要实验手段,而衍射图样与衍射指数具有一一对应的关系,进而引入了倒格子空间的概念[1-2]。
在探讨晶格振动的周期性边界条件和能带理论的过程中,在倒格子空间的基础上又引入了波
矢空间(或k空间、动量空间)。
至此在学习固体物理及相关课程中有了正格子空间、倒格子空间和波矢空间三个空间体系。
正格子空间相当于拿显微镜将晶体表面放大,看到的是原子或离子,相对好理解;倒格子空间和波矢空间的概念却非常抽象,很难建立清晰的物理图像。
倒格子和波矢是理解X射线衍射、晶格振动、能带理论
和晶体中电子运动行为等相关知识的基础,其物理内涵及其实质非常重要。
教材中通常是从数学上对其定义,很难对其中的物理内涵进行深刻的理解,本文采用图文并茂、通俗易懂的语言从X射线衍射实验开始,带领读者进入倒格子空间和波矢
空间。
1 晶体的X射线衍射实验
晶体是原子的周期排列。
从不同角度看,布拉伐格子将会出现不同的晶面族,如图1所示为晶格的2个不同晶面族,不同晶面族的面间距d不同。
图1 晶格的不同晶面族
X射线是一种波长约为0.001-10 nm的电磁波,与晶体中原子间距在同一个数量级,所以当用X射线照射到晶体时可观察到X射线的干涉[3]3-6、衍射现象[4]。
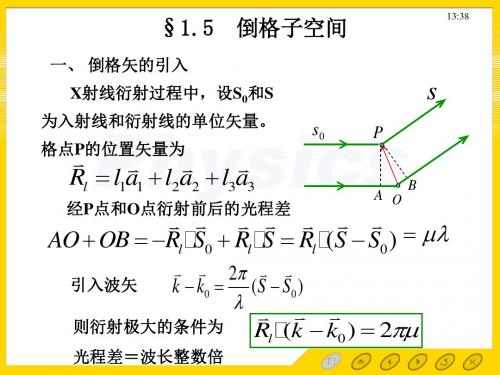
如图2所示,晶面族对X射线来说构成一系列反射面。
已知波长λ的单色X射线
照射到晶体后,同一晶面族不同晶面反射的波会产生位相差,干涉的结果使得只有在某特定角度θ发生相干相长(满足布拉格条件[3]54-552dsinθ = nλ,n为衍射
级数,d为面间距)。
通过对待测晶体进行X射线衍射获得图谱,可测出衍射峰的
相对强度和对应的晶面间距,进而求出对应的衍射指数(hkl)。
图2 X射线入射晶体图示
通过X射线衍射实验获得的衍射图样直接反映了晶格结构的特征,每一个衍射峰
对应一组衍射指数(hkl)。
具体的衍射峰对应的衍射指数可通过查阅粉末衍射-JCPDS卡片(简称PDF卡片)查阅,X射线衍射图谱就像是晶体的指纹一样,每种
晶体具有其特定的X射线衍射图谱,可用来确定晶体材料的物相[5]。
如图3所示
为Si的标准X射线衍射图谱(JCPDS No.27-1402),根据图谱可求出衍射峰对应的晶面间距d(hkl)和晶格常数。
图3 Si的标准X射线衍射图谱
2 倒格子空间
为了更好地理解X射线衍射图谱并应用于晶体学研究,引入了倒格子的概念。
将晶格中的一族晶面转化为倒格子空间中的一点,而倒格矢与衍射指数具有一一对应关系。
正格子空间,即坐标空间,其量纲为长度单位,用显微镜如SEM可看到真实晶格结构映象,对应原子或分子。
倒格子空间,用X射线衍射可看到倒格子的映象,对应晶体中的一族晶面。
同一物理量在正格子空间中的表述和在倒格子空间中的表述之间遵守傅里叶变换[6-8]。
若正格子空间的基矢用表示,正格矢为其中一组(l1、l2、l3)的取值表示正格子空间中的一个格点。
数学上可定义倒格子基矢为[1-2]:
倒格矢为其中一组(h1、h2、h3)的取值表示倒格子空间中的一个格点。
正格子与倒格子之间有如下关系[1]。
(1)
为整数
(2)
(3)
沿晶面族(h1、h2、h3)的法线方向
(4)
(5)晶面族(h1、h2、h3)的面间距为
(5)
其中公式(5)中的晶面指数(h1h2h3)必须为互质整数,与衍射指数(hkl)有所不同。
原因在于发生X射线衍射时若布拉格条件(2dsinθ=nλ)中的衍射级数n不为1即发生二级衍射或者三级衍射时,求出的面间距d将不再是晶面族的最近邻两晶面间距,而是面间距的2倍或者3倍,所以衍射指数不一定是互质整数,而晶面指数对应晶面族最近邻晶面间距必须为互质整数。
每个晶体都可用两套空间格子(正格子和倒格子)描述,且二者互易,如简单立方晶格的倒格子依然是简单立方晶格,体心立方晶格和面心立方晶格互为倒格子。
某一正格子的倒格子之倒格子依然是其本身[9]。
通过引入倒格子,正格子空间的一个二维晶面对应倒格子空间中一个零维的点,在讨论晶体学性质时可简化计算过程。
3 波矢空间
若为N1、N2、N3晶体沿三个基矢方向的原胞数,总原胞数为为倒格子基矢。
则波矢的公式为[1-2]:
为一组整数)
对于一维单原子链,波矢可简化为其中a为原胞间距,L为一维单原子链的长度。
从波矢的公式可看出,波矢代表了波矢空间的均匀分布的点,一组(h1、h2、h3)的取值表示波矢空间中的一个格点,波矢密度为:一维三维波矢方向与倒格子基矢的方向一致,即波矢空间与倒格子空间实际是统一空间,其基矢的方向相同但大小不同。
下面以求二维正方格子的倒格子基矢和波矢空间基矢为例说明倒格子空间和波矢空间的区别与联系。
假设一个二维正方格子的晶格常数为a,其原胞基矢和正
格矢分别为:
根据倒格子的定义,其倒格子基矢和倒格矢分别为:
根据波矢的定义,其波矢空间基矢和波矢分别为:
如图4(a)所示为一个二维正方正格子空间,黑色的圆O代表参考原点,灰色的圆代表格点,为原胞基矢,为正格子空间的正格矢,代表一个格点位置。
如图4(b)所示为两套空间格点:其中灰色的圆构成的格子为图4(a)正格子对应的倒格子空间,黑色的圆O代表倒格子参考原点,为倒格子原胞基矢,为倒格子空间的倒格矢,代表倒格子空间的一个格点位置;黑色的点构成的格子为4(a)正格子对应的波矢空间,黑色的圆O’代表波矢空间参考原点,为波矢空间原胞基矢,为波矢空间的波矢,代表波矢空间中的一个格点位置。
图4 二维正方格子空间(a)、倒格子空间和波矢空间(b)
由于晶体包含大量的原子(约1023个/cm3),即原胞个数N=N1·N2是非常大的数目,所以波矢代表了波矢空间中异常密集的均匀分布的点,可看做是准连续的。
如图4(b)所示波矢与倒格矢可在同一空间描述,两者原胞基矢的大小正好差了整数倍但是方向相同,因此可将波矢空间和倒格子空间看做统一的空间。
4 波矢的物理含义及其应用
一个倒格子原胞包含了N=N1·N2个波矢(k点),即晶体的正格子空间有多少个原胞,一个倒格子原胞就包含了多少个k点,不同的k点对应不同的量子态,代表
原胞不同的相位。
根据布洛赫定理,由于晶格的周期性排列,晶体中电子的运动具有布洛赫函数的形式,即若不同波矢之间正好差了一个倒格矢,根据公式(2),则
即位相差为2π的整数倍,不影响能量本征值因此在描述电子的运动行为时,可用简约波矢即第一布里渊区范围内的波矢来取代整个波矢空间,而第一布里渊区范围是如原胞间距为a的一维单原子链,其第一布里渊区范围是通常在倒格子空间选
取从原点出发的最近邻格点的垂直平分面所包围的区域(即倒格子空间的维格纳赛
兹原胞)为第一布里渊区,第一布里渊区正好包含了N个k点。
如图5所示,其中黑色区域即第一布里渊区,是倒格子空间中最小的周期性单元,其格点在中心,包含一个倒格子格点,反映了倒格子空间的对称性;第一布里渊区包含了N=N1·N2个k点,可用第一布里渊内的波矢代表整个波矢空间的波矢。
在解决实际固体中电子的运动行为问题时,能量动量运动速度有效质量等物理量均可用简约波矢表
示。
因此波矢的概念在讨论固体物理相关课程中非常重要。
图5 二维正方格子的第一布里渊区图像
参考文献:
【相关文献】
[1]黄昆.固体物理学[M].韩汝琦,改编.北京:高等教育出版社,1988:16-18.
[2]胡安,章维益.固体物理学[M].2版.北京:高等教育出版社,2011:14-19.
[3]刘粤惠.X射线衍射分析原理与应用[M].北京:化学工业出版社,2003.
[4]李树棠.晶体X射线衍射学基础[M].北京:冶金工业出版社,1990:7-9.
[5]胡恒亮,穆祥祺.X射线衍射技术[M].北京:纺织工业出版社,1988:55-57.
[6]许富宗,施思齐.固体物理教学中联接正格子和倒格子空间的傅里叶变换过程浅议[J].大学物
理,2017,36(7):77-81.
[7]罗明海,韩亚萍,侯纪伟,等.倒格子不同角度的引入[J].物理通报,2012(3):28-30.
[8]高慧芬,逯美红.三种方式的倒格子定义[J].长治学院学报,2008,25(5):56-58.
[9]李进,李光惠.布里渊区与倒格子原胞[J].大学物理,1997,16(1):29-31.。
