平面应力状态开孔应力场的研究
平面应力问题
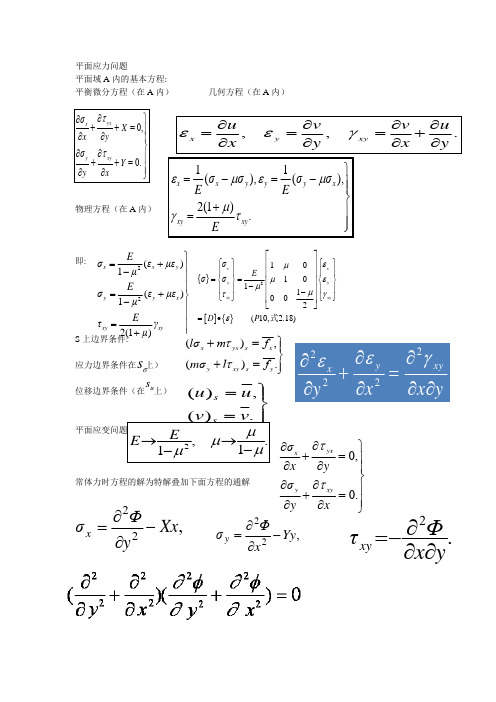
平面应力问题平面域A 内的基本方程:平衡微分方程(在A 内) 几何方程(在A 内)物理方程(在A 内)即: S 上边界条件:应力边界条件在 上)位移边界条件(在 上) 平面应变问题常体力时方程的解为特解叠加下面方程的通解0,0.yx x y xyσX x y σY y x ∂⎫∂++=⎪∂∂⎪⎬∂∂⎪++=⎪∂∂⎭ττ, , .x y xy u v v ux y x yεεγ∂∂∂∂===+∂∂∂∂11(),(),2(1).x x y y y x xy xy σσσσE E Eεμεμμγτ⎫=-=-⎪⎪⎬+⎪=⎪⎭22()1()(a)12(1)x x y y y x xy xyE σεμεμE σεμεμE τγμ⎫=+⎪-⎪⎪=+⎬-⎪⎪=⎪+⎭{}[]{}2101011002(10, 2.18)x x y y xy xy σE σσD P ⎡⎤⎧⎫⎧⎫⎢⎥⎪⎪⎪⎪⎢⎥==⎨⎬⎨⎬⎢⎥-⎪⎪⎪⎪⎢⎥-⎩⎭⎩⎭⎢⎥⎣⎦=•εμμεμμτγε式(),().x yx s x y xy s y l σm f m σl f ττ⎫+=⎪⎬+=⎪⎭σs(),().s s u u v v ⎫=⎪⎬=⎪⎭us 2222y xy x y x x yεγε∂∂∂+=∂∂∂∂.1 ,12μμμμ-→-→E E 0,0.yx x y xyσx y σy x ∂⎫∂+=⎪∂∂⎪⎬∂∂⎪+=⎪∂∂⎭ττ22,y ΦσYy x∂=-∂.2yx Φτxy ∂∂∂-=22,x ΦσXx y∂=-∂二、基本假设 1、连续性假定假定物体是连续的。
因此,各物理量可用连续函数表示。
2、完全弹性假定a.完全弹性—外力取消,变形恢复,无残余变形。
b.线性弹性—应力与应变成正比。
即应力与应变关系可用胡克定律表示(物理线性)。
3、均匀性假定假定物体由同种材料组成,因此, E 、 μ等与位置 无关。
4、各向同性假定假定物体各向同性。
E 、μ与方向无关。
平板开孔应力集中系数

平板开孔应力集中系数引言平板开孔应力集中系数是研究平板开孔结构中应力分布特性的重要参数。
在工程实践中,平板开孔结构广泛应用于各种领域,如航空、航天、汽车、船舶等。
因此,了解平板开孔应力集中系数的计算方法和影响因素对于设计和优化这些结构具有重要意义。
本文将详细介绍平板开孔应力集中系数的概念、计算方法和影响因素,以及其在工程实践中的应用。
一、概念平板开孔应力集中系数是指开孔结构中应力集中程度的一个参数。
在平板开孔结构中,开孔处会引起应力场的改变,导致应力集中。
平板开孔应力集中系数是用来描述这种应力集中程度的一个量化指标。
通常用Kt表示,计算公式为Kt=σmax/σnom,其中σmax为开孔处的最大应力,σnom为无孔平板的应力。
二、计算方法平板开孔应力集中系数的计算方法主要有理论计算方法和实验测量方法两种。
1. 理论计算方法理论计算方法是通过应力场分析和力学原理推导,得到平板开孔应力集中系数的数值。
常用的理论计算方法有应力集中系数图表法、应力函数法和有限元法。
应力集中系数图表法是一种经验方法,通过查表得到平板不同尺寸和不同孔径的应力集中系数。
这种方法适用于简单几何形状的开孔结构。
应力函数法是一种基于弹性力学理论的解析方法,通过求解弹性力学方程得到平板开孔应力场的解析解,进而计算应力集中系数。
这种方法适用于较为复杂的开孔结构。
有限元法是一种数值计算方法,通过将开孔结构离散化为有限个单元,利用数值计算方法求解应力场,进而计算应力集中系数。
这种方法适用于各种复杂的开孔结构,计算结果较为准确。
2. 实验测量方法实验测量方法是通过物理实验手段测量开孔结构中的应力分布,进而计算应力集中系数。
常用的实验测量方法有应变测量法和光弹性法。
应变测量法是通过在开孔结构表面粘贴应变片,利用应变片的变形来测量应力分布,进而计算应力集中系数。
这种方法需要在实验室中进行,操作较为复杂。
光弹性法是通过在开孔结构表面涂覆光弹性涂层,利用光弹性涂层的颜色变化来测量应力分布,进而计算应力集中系数。
平面问题的应力函数法含例题应力场分布图

应力公式及应力分量
所对的应力边界
一次式
=++ 满足双调和方程,其应力 = 。
5/ 11
Email:onexf@
使用教材:《材料固体力学》上册 周益春编著 科学出版社
⎧ ⎪⎪
=
6
ℎ3
(ℎ2
−
2)
+
ℎ
23 4 ℎ2 − 5
22
⎨
=−2 1+ℎ 1− ℎ
⎪⎪ ⎩
6 = − ℎ3
ℎ2
4−
2
根据上式的应力场,可分别得到三个应力分量的分布图。
的大小分布,及 x = l 端面处大小线性分布。
3
4
5
9/ 11
使用教材:《材料固体力学》上册 周益春编著 科学出版社
以下分别为正应力 和 (相互垂直),和剪应力 和 (相互垂直,并与正应力成 450 角)分布。
6
4
2
0 2 4
6
1
6
4
2
0
2
4
6
2
Email:onexf@
10/ 11
使用教材:《材料固体力学》上册 周益春编著 科学出版社
+)
(1) 由对称性定 E、F、G。由于 y 轴是结构和载荷的对称轴,所以应力分量也对称于 y 轴,因此 和 应该是 x 的偶函数,而 应 为 x 的奇函数。则有:E = F = G = 0;
2平面问题的基本理论(平面应力与应变,受力状态,圣维兰原理)

当面积 AB 无限减小而趋于 P 点时,平面 AB 上的 应力就是上述斜面上的应力。 现设斜面上的全应力p可以分解为沿坐标向的分 量( px , py ),或沿法向和切向的分量( σn , τn),如图 2-4b所示。
用n代表斜面AB的外法线方向,其方向余弦为:
cosn, x l, cosn, y m
c
0
,则有
F 0, F Mc 0
x
y
0
yx dy dy dx dx xy dy 1 ( yx dy)dx 1 yx dx 1 0 2 2 y 2 2
力矩方程化简后得到:
xy
1 xy 1 yx dx yx dy 2 x 2 y
x yx fx 0 y x xy y f 0 y x y
4.平衡微分方程适用的条件是,只要求符合连 续性和小变形假定。 5.对于平面应力问题和平面应变问题,平衡微 分方程相同。 6.由于τxy =τyx,以后只作为一个独立未知函数 处理。因此,2个独立的平衡微分方程(2-2) 中含有 3个应力未知函数。
由式(2-4)及(2-5)就可以求得经过P点的任意 斜面上的正应力 n 及切应力 n 。
3.然后,再求出主应力和应力主向
设经过P点的某一斜面上的切应力等于零,则该斜 面上的正应力称为在P点的一个主应力,而该斜面 称为在P点的一个应力主平面,该斜面的法线方向 称为在P点的一个应力主向。
(2)只在侧边上受有平行于板面且不沿厚度变化 的面力和体力,且不沿厚度变化,体力 f x , f y , o 和面 力 f x , f y , o ,只是x,y的函数,并构成平衡力系;
弹性力学-平面应力-平面应变问题

平面应力问题的求解方法
解析法
实验法
通过数学分析的方法,将问题转化为 数学方程进行求解。适用于简单几何 形状和边界条件的问题。
通过实验测试来测量物体的应力分布, 通常需要制作模型并进行加载测试。 适用于无法通过理论分析求解的问题。
有限元法
将物体离散化为有限个小的单元,通 过求解每个单元的平衡方程来得到整 个物体的应力分布。适用于复杂几何 形状和边界条件的问题。
弹性力学的基本方程
描述物体在受力后的应力 与应变之间的关系。
描述物体在受力后发生的 位移和应变关系。
描述物体内部力的平衡关 系03
平面应力问题
平面应力问题的定义
平面应力问题是指在弹性力学中,物 体受到的应力作用在某一平面内,且 在该平面上没有作用力的问题。
平面应力问题通常适用于薄板、薄壳 等二维结构,其中应力分量在某一平 面内变化,而垂直于该平面的方向上 ,应力和应变均为零。
THANKS
感谢观看
04
平面应变问题
平面应变问题的定义
平面应变问题是指在弹性力学中,应变和应力都仅发生在某一平面内的现象。在 此情况下,应变和应力分量都与离开平面的距离无关。
平面应变问题通常出现在薄壁结构、板壳结构等二维结构中,其中主要的变形和 应力分布都在一个平面内。
平面应变问题的求解方法
1 2 3
有限元法
通过将问题离散化为有限个小的单元,利用弹性 力学的平衡方程和变形协调方程,求解每个单元 的应力、应变和位移。
跨学科的研究
与其他学科的交叉研究 可能会带来新的思想和 理论。例如,与物理学 、化学、生物学等学科 的交叉可能会为弹性力 学的研究提供新的视角 和思路。
实验与理论的结 合
实验技术的发展将有助 于更好地验证理论的正 确性和实用性。同时, 理论的发展也将为实验 提供更好的指导。因此 ,实验与理论的结合将 是未来研究的一个重要 方向。
孔边导角对开孔方形平板的应力集中理论解析

孔边导角对开孔方形平板的应力集中理论解析1. 理论背景开孔方形平板是一种常见的工程结构,在实际应用中常会遇到开孔边缘导角的情况。
研究开孔边缘导角对平板应力分布的影响,对于设计和优化结构具有重要意义。
2. 应力集中的原因开孔边缘导角会导致应力集中的现象。
在开孔边缘的导角处,弯曲变形和剪切变形将引起较大的应力集中。
3. 应力分析3.1 面内应力分析根据平面应力理论,考虑平板表面上的应力分量σx、σy和剪应力τxy,可以通过应力函数法等方法求解。
3.2 应力集中系数应力集中系数是描述应力集中程度的一个参数。
对于开孔边缘导角的方形平板,可以采用斯特拉斯解析法或有限元分析来计算应力集中系数Kt。
3.3 裂纹尖端应力分析对于已有裂纹的开孔边缘导角方形平板,可以采用线弹性力学理论进行裂纹尖端应力分析,计算应力强度因子K。
4. 影响因素4.1 开孔尺寸开孔尺寸对应力集中影响较大。
较小的开孔尺寸往往会引起更大的应力集中,进而降低结构的强度。
4.2 导角角度导角角度越小,应力集中越小。
大角度的导角将导致应力集中系数增加,进而削弱结构的强度。
5. 应力集中缓解方法为减小应力集中效应,可以采取以下方法:5.1 圆角缓和法在开孔边缘导角处增加合适的圆角,能够减小应力集中。
合理的圆角尺寸能够降低应力集中系数,从而提高结构的强度。
5.2 加固加强通过在开孔边缘导角处添加加固结构,如加强筋或加固片,可以显著减小应力集中。
5.3 材料选择在设计中选择具有良好韧性和抗拉强度的材料,能够有效减轻应力集中效应,提高结构的抗拉强度。
6. 实际案例以飞机结构为例,飞机机翼翼缘开孔处由于需满足动力特性和减重要求,常会出现开孔边缘导角,对于该种结构,深入分析应力集中情况,有效解决应力集中问题,对于保障飞行安全至关重要。
总结:开孔边缘导角对于开孔方形平板的应力集中有较大影响。
通过采用理论解析方法和有限元分析工具,可以对开孔边缘导角的平板进行应力集中分析,从而有效解决应力集中问题。
§2.3 平面应力状态的图解法

应力 方向截面的代表点在 平面上构成一条曲线,由分析可
应变 分析
知这条曲线是一个封闭的圆,称为该点的应力圆,也称莫尔
及应 圆。
力应
变关
系
讲
义
1
莫尔圆(应力圆)的画法
BRY
(1) 斜截面上应力 , 的符号规定
材 料
该点任意平行于 z 轴方向截面上的
力
正应力 ,以拉为“+”;
学 B
切应力 ,以使单元体有顺时针转动趋势为“+”。
料 为单位 1 的直角楔体微元。
力 学
Fnp 0:
r r
B
B 第
p dAcos r dAsin
2
( q dA) cos ( q dA)sin 0
q
p
A
p
np
章
p cos r sin q cos q sin r p
应力 应变 分析
p cos p sin q cos q sin
BRY
§2.3 平面应力状态的图解法
—— 应力圆(莫尔圆)
材
料
力 应力圆(莫尔圆)
学
B
建立直角坐标系 O ,水平轴为正应力 轴,铅垂轴为
第 切应力 轴。某点若为 xy 平面内的平面应力状态,以该点某
2 章
一平行于 z 轴方向斜截面上的正应力 和切应力 的数值为 坐标,可在 平面上得到一个代表点。所有平行于 z 轴
C(
x
y
,
0)
2
B E
P2
系
讲
D A P1 x
义
4
莫尔圆(应力圆)的作用
BRY
莫尔圆(应力圆)图直观地给出了平面应力状态下单元
孔边导角对开孔方形平板应力集中问题的解析探究

孔边导角对开孔方形平板应力集中问题的解析探究引言:开孔方形平板在工程应用中非常常见,而孔边导角是一种常用的解决孔洞周边应力集中问题的方法。
本文旨在探究孔边导角对开孔方形平板应力集中问题的解析,并分析其优势和适用范围。
一、孔边导角的定义和作用孔边导角是指在开孔结构中,通过对孔洞边缘进行设计和处理,以减小或消除由孔洞引起的应力集中现象。
其主要作用在于改善结构的强度和耐久性,并提高结构的疲劳寿命。
二、孔边导角的原理与机制孔边导角通过改变孔边缘的几何形状和拉伸区域,使应力分布更加均匀,降低应力集中。
具体来说,孔边导角可以分为两个方面的效应:1. 几何效应:通过添加导角,增加孔洞周围的拱形区域,使应力场更加平缓,减少应力集中。
2. 拉伸效应:导角的形状可以改变孔洞周围材料的受力状态,使得应力场分布更加均匀,减小应力集中。
三、导角形状对应力集中的影响导角形状对应力集中的影响是一个重要的研究方向,常见的导角形状包括圆角、梯形、V型等。
以下是几种常见导角形状的特点和适用范围的分析:1. 圆角导角:圆角导角适用于一般应力集中问题,其拱形设计可以有效分散应力,减小应力集中的程度。
2. 梯形导角:梯形导角适用于孔边缘强度较低的情况,其逐渐变宽的设计可以缓解应力集中。
3. V型导角:V型导角适用于高应力集中问题,其尖锐的V型设计可以提供更大的拱形区域,明显降低应力集中。
四、孔边导角的优势和应用范围孔边导角的优势主要体现在以下几个方面:1. 改善结构强度和耐久性:孔边导角可以降低应力集中,使结构在受力时更加均匀,提高结构的强度和耐久性。
2. 延长结构的使用寿命:通过减小应力集中,孔边导角可以延长结构的使用寿命,减少结构的疲劳损伤和断裂风险。
3. 降低结构的重量和成本:采用合理的孔边导角可以减小结构的应力集中程度,降低结构的重量和成本。
孔边导角的应用范围广泛,适用于各类开孔结构,包括但不限于:航空航天器、汽车工程、机械结构等。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
平综述摘要:在机械制造、航空、造船、建筑等领域, 开孔问题是十分普遍的。
然而, 开孔必然引起应力集中现象, 这一直是工程技术人员十分关心的问题。
对平面应力状态开孔周边应力场的研究, 掌握应力场的变化规律, 在实际工程中具有十分重要的意义.关键词:应力场开孔平面应力状态1 前言对于开口结构来说,特别突出的一个问题就是临界区域的孔边应力集中问题。
准确的求解孔周围的应力是很困难的,特别是对于一些复杂孔型。
就像人们所知道的,孔口附近往往也就是构件最薄弱的区域。
因此,对开孔及其周边应力场的研究,对于机械及相关领域来说至关重要,这将是我们必须长期坚持和努力的研究领域。
2开孔周边应力场的研究历史及现状2.1 复合材料开孔周边应力场研究吴德隆[1]在对二维平面的复合材料结构开孔分析中,得出相应的结论:开孔引起的应力扰动项是局部的,随距离的增加而迅速衰减。
最大应力集中发生在孔角处45°,并与开孔尺寸成反比。
李成[2]等为了探索出一种方法,使得在实际设计中,计算含孔的复合材料板的应力、强度时,既可以避免级数法的繁琐,又可以提高其计算精度。
于是他们以复变函数理论为基础,借助积分方程,采用多复变量应力函数对含圆孔形的复合材料板进行研究,得到了精确边界条件下的应力解析, 并用所得到的应力表达式对不同载荷的影响进行了分析、评价,同含有圆孔的均质材料板边的应力场进行比较。
得出了含复杂孔形孔边应力的解析解法。
并且得出了对带有圆形孔的复合材料板和均质材料板,在不同方向的载荷作用情况下的计算方法,这种计算方法在工程中有很高的实用价值。
2.2 平板开孔应力场的研究张涛[3]等对开椭圆孔有限板的应力集中问题进行研究。
应用弹性力学的复变函数理论,在各内边界上引入保角变换,在外边界上采用分段函数,通过傅立叶级数展开,计算整个弹性板的应力场,给出了开椭圆孔有限板的计算实例。
突破了开孔的形式、位置、载荷形式等的限制, 且充分考虑了板边界的存在, 适用于大开孔结构。
杨丽红等人[4]采用复变函数理论与保角映射技术,将含矩形孔的无限域保角映射到单位圆内,求得了含矩形孔的无限大板在单向应力状态及纯剪切状态下的孔边应力,对几种不同边长比的矩形孔进行了系列计算,并将结果图谱化。
使得结论更加系统、全面、清晰,便于工程应用。
给出了孔边峰值应力随边长比、方位角及圆角曲率半径的变化规律。
并通过光弹性实验, 验证了理论计算结果的正确性。
利用叠加原理, 将计算结果进行组合, 可以分析各种不同受力时的孔边应力。
并且由于平板弯曲边值问题的微分方程与其研究的问题相似,故他的解答又可移植到含孔无限大板的平板弯曲问题上。
杨晶[5]从弹性力学的角度入手,针对经典解法中将平板开小圆孔视为平面应力问题,采用应力法求得开孔板应力,分析了孔边应力集中的大小。
并且针对某一具体算例,将经典解与三维有限元得到的解相比较,对两种解法所得到的结果进行了比较和探讨。
他认为对于具体的平面问题,常采用直角坐标解答和极坐标解答。
而涉及平板开孔问题,分析孔边应力集中时,则采用极坐标更为方便。
于是其通过运算,得出了基尔斯解答。
杨晶针对经典解研究平板开小孔处应力集中问题时存在的缺陷,添加了对板厚影响的考虑。
由于平板开孔的应力集中问题是弹性力学平面问题中一个经典的问题,也是实际工程中常见的问题。
而作为平面问题的典型代表,圆孔应力集中问题的经典解中,考虑平面内的3个应力分量,忽略了沿厚度方向上应力的变化。
于是用有限元对小孔应力集中进行分析时,杨晶采用的是三维模型,由于三维有限元法中,考虑了厚度的影响,可分析得到各应力分量沿板厚的变化,且在各个发生应力集中的区域上,中间板厚处的应力值大于板表面的应力。
而经典解无法考虑这一变化。
这是杨晶等人取得的新进展。
2.3 连接件孔边应力场的研究高存法[6]应用直线边界上的Cauchy 积分和复应力函数Paber 级数展开的方法对被N 个任意大小,任意排布的承载螺栓孔削弱的正交异性板应力场问题的研究。
得到了确定有关复应力函数未知系数的线性方程组,进而得到了任一孔口周边应力场的表达式,并分别给出了两个自由孔和两个承载孔应力集中问题的算例。
王克峰[7]等人,则主要从细节入手,针对在机械制造业中,大量使用螺栓或铆钉等连接件以实现连接和传力功能的现象。
而连接件孔的存在又使得孔的边缘上存在应力集中。
我们知道,机械结构中,大多数损坏是由于应力集中处引起的疲劳裂纹造成的, 因此准确得到连接区的应力集中系数十分重要。
王可峰等人还引用了其他学者在相关领域的研究成果,具体有西田正孝等人[ 8 ]假设无载荷时销钉不使孔壁受到压力,而且没有间隙,不考虑接触体间的摩擦力,系统地进行了光弹性试验和光干涉试验,获得了半无限板的孔边切向应力和挤压应力的分布情况。
并给出了孔距边界的距离对孔边应力的影响。
弗罗奇特和希尔[9] 通过光弹性试验给出了销钉连接孔边应力随板宽的变化。
Iyer[10] 通过有限元计算, 得出了平面应力状态下孔的应力状态。
分析了不同的接触摩擦系数,不同的钉和板的材料,板的有限宽和无限宽对孔边的应力影响,得出了以下的结论:(1)当钉和板的材料都为金属材料,并且钉和板间的摩擦系数较小的时候,无限大板的接触压力以及板的切向应力与连接件的材料无关。
(2)当板为有限宽度时,板的应力集中系数会比相同情况下的无限宽时偏大。
(3)连接件材料,板的维度,摩擦系数这三个影响孔边应力的因素中摩擦系数的影响最大。
Yavari[11]等在Iyer 的基础之上增加了板的宽度、孔到边缘的距离、钉和孔的配合间隙对孔边应力的影响, 得出了大的摩擦系数和小的板宽会使连接更安全的结论。
颜东煌等[12] 验证了有限元模型的参数设置对结果的影响,并运用接触算法计算了轴销连接结构的接触应力分布情况,得出了材料的本构关系对轴销连接接触应力有较大的影响, 而接触区的摩擦系数对接触挤压应力几乎无影响的结论。
丁然、郭彦书、刘庆刚[13]等在最近发表的文章《压力容器开孔间距对应力集中的影响》中,采用ANSYS 有限元软件,对压力容器筒体上不同中心距L 的两相邻直径为d 的开孔周边应力场进行分析,并定义参数K =L /(2 d )。
结果表明:无接管模型开孔周边最大应力大于有接管模型,故基于无接管模型的分析结果相对安全;当K <0.9时,随着两开孔间距的增大,开孔中心线上的最小应力显著减小;当K =0.9~1.5 时,开孔中心线上的最小应力随开孔间距的增大缓慢减小;当K >1.5时,开孔中心线上的最小应力均接近筒体远离开孔部位的应力。
3 结论平面应力状态:即只在平面内有应力,与该面垂直方向的应力可忽略,例如薄板拉压,受扭的圆轴,低压容器器壁各点的应力状态等。
平面应力问题讨论的弹性体为薄板,薄壁厚度远远小于结构另外两个方向的尺度。
薄板的中面为平面,其所受外力,包括体力均平行于中面面内,并沿厚度方向不变。
而且薄板的两个表面不受外力作用。
平面应力状态在机械制造、建筑、航空航天、船舶及海洋工程等领域的应用十分广泛,为了满足工程设计的要求, 有时需要在平板上开孔。
分析由于开孔引起的应力集中,尽可能的避免材料或构件因应力集中而造成的破坏。
是我们学习和研究的重要课题。
一般情况下,孔口的应力集中区域集中在距孔边1.5 倍孔径的范围内。
从材料的各向异性和各向同性的角度,原则上孔边应力集中对于各向异性材料来说要比各向同性材料对于材料的破坏性影响要大得多, 这是由材料的各向异性性质决定的。
因此, 在情况允许的时候, 尽量使两个方向的材料性质尽可能的接近, 这样可以有效地降低孔边应力的峰值, 以尽可能的避免材料或构件因应力集中而造成的破坏。
大多数损坏是由于应力集中处引起的疲劳裂纹造成的, 因此准确得到连接区的应力集中系数十分重要。
参考文献[1] 吴德隆.复合材料结构开孔分析[J]. 导弹与航天运载技术,1994 ,(3):34—45.[2] 李成, 郑艳萍, 闫志华.不同方向载荷作用下含圆孔正交各向异性平面应力问题的弹性解[J].中国铁道科学,2007,30(2):1—4.[3] 张涛,刘土光,赵耀,刘敬喜.开孔有限板的孔边应力场分析[J]. 华中科技大学学报,2002,30(1):87—89.[4] 杨丽红,何蕴增.无限平面矩形开孔的应力场分析[J].哈尔滨工程大学学报,2002,23(2):106—110.[5] 杨晶.圆孔孔边应力集中的经典解与有限元分析[J].科技情报开发与经济,2009,19(34):163—164.[6] 高存法,类蔚勋.含孔系的正交异性半平面应力分析[J].固体力学学报,1994 ,(6):156—159.[7] 王克峰,常春雷,李丰.连接件孔边应力集中的研究进展[J].江苏航空,2010 :72—74.[8] 西田正孝.应力集中[M].李安定等,译.北京:机械工业出版社,1983:123—128.[9] 彼德森R E. 应力集中系数[M] . 杨乐民, 叶道益,译. 北京: 国防工业出版社, 1988 :88—93.[10] Iyer K. Solutio ns for co nta ct in pinned co nnectio ns[J] . Inter nat ional Jour nal of So lids and St ructures,2001, 38( 50-51) : 9133—9148.[11] Yav ari V. On the stress distribution aro und the ho lein mechanically fastenedjoints [ J ] . Mechanics Research Communicatio ns, 2008, 36( 3) : 373—380. [12] 颜东煌,刘雪锋,田仲初,等.轴销连接结构的接触应力分析[J] .工程力学,2008, 25(1) : 229—234.[13]丁然,郭彦书,刘庆刚.压力容器开孔间距对应力集中的影响[J].油汽储运,2012,31(6):432—435.。
