第15章 奇异值分解
奇异值分解

H
03 H X 01
(6.3.8)
利用式(6.3.4),不难证明
(6.3.9)
类似的其向量形式为 •
(6.3.10)
6.3.2 奇异值分解与特征值分解的关系
• 由于YHY=YYH=I,式6.3.1可以改写成
(6.3.11)
(6.3.12)
• 所以
T H 03 H 0 H 2 A A X T T Y Y X 0 2 01 0 3 01
i
(i 1,2, , r )
为矩阵A的正奇异值,简称奇异 值。
矩阵奇异值分解定理
对任意复矩阵 A C , L=N-M+1,秩为K,那么存在酉矩阵X C MXM 和 酉矩阵 Y C LXL ,使得
LXM
其中
diag 1, 2, .... K
是A的全部非零奇异值,而01,02,03分 别是(L-K)X(M-K),(L-K)XK,KX(M-K)的零矩阵。式6.3.1称为矩阵A 的奇异值分解。
• AHA是非奇异的
• 由于 AH A C MXM 是非奇异的,即AHA的秩K=M,则AHA有M个非零特征值, 或矩阵A有M个非零奇异值。此时式(6.3.11)可表示为 H A Y X 0
, M )而 • 其中,0是(L-M)XM的零矩阵, diag( 1, 2,
ˆ 的范数最小,等价于使z的范数最小。由于z是由确定量z1 这就是说,要使 w 和任意量z 2 构成的,如式(6.3.23)所示,所以,当且仅当分量z 2 =0时,向 量z的范数最小,此时的范数也将取得最小值。
• 令 •
,得方程的解为 (6.3.30)
• 利用式 得 • 将上式代入(6.3.30)得
大学《统计学习方法》第2版教学课件-第15章 奇异值分解

《统计学习方法》第2版
第十五章 奇异值分解
定义与定理
定义与定理
•
:矩阵A的奇异值分解(singular value decomposition,
SVD)
• :矩阵 A的奇异值(singular value)
• U的列向量:左奇异向量(left singular vector)
• V 的列向量:右奇异向量(right singular vector)
• 注意奇异值分解不要求矩阵A是方阵,事实上矩阵的奇异值分解 可以看作是方阵的对角化的推广。
例
• 给定一个5x4矩阵A
例
• 它的奇异值分解由三个矩阵的乘积 给出
例
• 矩阵 是对角矩阵,对角线外的元素都是0,对角线上的元素 非负,按降序排列。
• 同样,若P是n阶正交矩阵,则有 •故 •即
矩阵的最优近似
• 奇异值分解是在平方损失弗罗贝尼乌斯范数)意义下对矩阵的最 优近似,即数据压缩。
矩阵的最优近似
15.32 15.33
矩阵的最优近似
• 证明
•令
为满足式(15.32)的一个矩阵。由于
• 下面证明
于是式(15.33)成立
矩阵的最优近似
的列空间是相同的, v1, v2, …, vr是AT的一组标准正交基,因 而也是R(AT )的一组标准正交基。
标准性质
• 矩阵A的n-r个右奇异向量vr+1,vr+2, …,vn构成A的零空间N(A)的一 组 标准正交基。
• 矩阵A的r个左奇异向量u1, u2, …, ur构成值域R(A)的一组标准 正交基。
• Ur: m x r 矩阵 • Vr: n x r 矩阵 • : r阶对角矩阵
矩阵奇异值分解具体计算过程_解释说明以及概述

矩阵奇异值分解具体计算过程解释说明以及概述1. 引言1.1 概述矩阵奇异值分解(Singular Value Decomposition,简称SVD)是一种重要的矩阵分解方法,广泛应用于数据降维、图像处理、推荐系统和信号处理等领域。
通过将一个矩阵分解为三个独特的部分,即原始矩阵的奇异向量和奇异值,SVD 可以提供有关原始数据的宝贵信息。
本文旨在详细介绍矩阵奇异值分解的具体计算过程,并对其应用领域以及算法优化和改进方向进行探讨。
首先,我们将给出该方法的定义和基本原理,并描述其计算方法和数学推导。
接着,我们将深入探究矩阵奇异值分解在图像压缩与降维、推荐系统和数据挖掘以及信号处理和模式识别等方面的应用。
然后,我们将讨论近似求解算法、加速技术以及大规模矩阵奇异值分解算法的最新进展。
最后,我们还将探索结合其他矩阵分解技术发展方向。
1.2 文章结构本文共包含五个主要部分。
第一部分是引言,主要概述了本文的目的和结构。
第二部分将详细介绍矩阵奇异值分解的具体计算过程,包括定义、基本原理、计算方法和数学推导。
第三部分将解释说明矩阵奇异值分解在不同领域中的应用,如图像压缩与降维、推荐系统和数据挖掘以及信号处理和模式识别。
第四部分将讨论矩阵奇异值分解算法的优化和改进方向,包括近似求解算法、加速技术以及结合其他矩阵分解技术的发展方向。
最后一部分是结论,总结文章的主要内容和贡献,并对未来研究方向进行展望。
1.3 目的本文旨在通过详细讲解矩阵奇异值分解的具体计算过程,深入理解其原理和应用,并探讨其改进方向。
通过对该方法进行全面系统地介绍,希望能够增加读者对矩阵奇异值分解有关知识的了解,并为相关领域的研究者提供参考和启示。
同时,本文也为后续相关领域深入研究和应用提供了理论基础和开发方向。
2. 矩阵奇异值分解具体计算过程2.1 矩阵奇异值分解定义和基本原理矩阵奇异值分解(Singular Value Decomposition,简称SVD)是一种常用的矩阵分解方法。
矩阵论-奇异值分解

0
0
1
0
0 0 0
2 13 3 13
3
13
-2
13
例:求A=
-1 2
0 0
1 -2
的奇异值分解.(课本例题)
1 2
解:令B=AH
0
1
0 2
,
则BH
B=
2 -4
-4
8
,
I BHB 2
4
( 10), =10, 0
4 8
故B的奇异值为
10,B H
1
例:A=
0
2
0
1 0
,则AH
A=
5 0
0 1
,奇异值为
5,1
1 0 2
而AAH
=
0
1
0 ,I-AAH =( 1)( 5).
2 0 4
定理1:若A与B酉相抵,则A与B有相同的奇异值.
证明:因A与B酉相抵,所以存在酉阵U与V,使B=UAV. 所以BH B=VH AH UH UAV=VH AH AV, 所以BH B与AH A相似, 所以它们的特征值相同, 所以A与B有相同的奇异值.
2
0
极分解:设A Cmr n,则A有以下分解,A=GU,G为半正定 Hermite矩阵,U为酉阵,特别地,当A 满秩时,G为正定 Hermite矩阵, 且分解唯一.
证明:由奇异值分解:
1
A=U1
0
r
0 0
V1H
=
U1
1
0
r
0
U1H
U1V1H
0
同理,r( AAH ) r( AH )=r( A).
引理2:设A Cmn,则 1)AH A与AAH的特征值均为非负实数. 2)AH A与AAH的非零特征值相同且非零特征值的个数为r(A).
[整理]矩阵的奇异值分解
![[整理]矩阵的奇异值分解](https://img.taocdn.com/s3/m/afe785200a4c2e3f5727a5e9856a561253d3215f.png)
§2 矩阵的奇异值分解定义 设A 是秩为r 的m n ⨯复矩阵,T A A 的特征值为1210r r n λλλ>λλ+≥≥≥=== .则称i σ=(1,2,,)i n = 为A 的奇异值.易见,零矩阵的奇异值都是零,矩阵A 的奇异值的个数等于A 的列数,A 的非零奇异值的个数等于其秩.矩阵的奇异值具有如下性质:(1)A 为正规矩阵时,A 的奇异值是A 的特征值的模;(2)A 为半正定的Hermite 矩阵时,A 的奇异值是A 的特征值;(3)若存在酉矩阵,m m n n ⨯⨯∈∈U V C C ,矩阵m n ⨯∈B C ,使=UAV B ,则称A 和B 酉等价.酉等价的矩阵A 和B 有相同的奇异值.奇异值分解定理 设A 是秩为r (0)r >的m n ⨯复矩阵,则存在m 阶酉矩阵U 与n 阶酉矩阵V ,使得H⎡⎤==⎢⎥⎣⎦O U AV O O ∑∆. ①其中12diag(,,,)r σσσ= ∑,i σ(1,2,,)i r = 为矩阵A 的全部非零奇异值.证明 设Hermite 矩阵H A A 的n 个特征值按大小排列为1210r r n λλλ>λλ+≥≥≥=== .则存在n 阶酉矩阵V ,使得12H H()n λλ⎡⎤⎡⎤⎢⎥==⎢⎥⎢⎥⎣⎦⎢⎥⎣⎦O V A A V OO ∑. ②将V 分块为 12()=V V V ,其中1V ,2V 分别是V 的前r 列与后n r -列.并改写②式为2H⎡⎤=⎢⎥⎣⎦O A AV V O O ∑.则有H 2H 112==A AV V A AV O , ∑. ③由③的第一式可得H H 2H 1111()()r ==V A AV AV AV E , 或者∑∑∑.由③的第二式可得H 222()() ==AV AV O AV O 或者.令111-=U AV ∑,则H 11r =U U E ,即1U 的r 个列是两两正交的单位向量.记作112(,,,)r =U u u u ,因此可将12,,,r u u u 扩充成m C 的标准正交基,记增添的向量为1,,r m +u u ,并构造矩阵21(,,)r m +=U u u ,则12121(,)(,,,,,,)r r m +==U U U u u u u u是m 阶酉矩阵,且有 H H1121 r ==U U E U U O ,.于是可得H HH1121H 2()()⎡⎤⎡⎤===⎢⎥⎢⎥⎣⎦⎣⎦O U U AV U AV AV U O O O U ,,∑∑.由①式可得H H HH 111222r r r σσσ⎡⎤==+++⎢⎥⎣⎦O A U V u v u v u v O O ∑. ④称④式为矩阵A 的奇异值分解.值得注意的是:在奇异值分解中121,,,,,,r r m +u u u u u 是H AA 的特征向量,而V 的列向量是H A A 的特征向量,并且H AA 与H A A 的非零特征值完全相同.但矩阵A 的奇异值分解不惟一.证明2 设Hermite 矩阵H A A 的n 个特征值按大小排列为1210r r n λλλ>λλ+≥≥≥=== .则存在n 阶酉矩阵V ,使得12H H()n λλ⎡⎤⎡⎤⎢⎥==⎢⎥⎢⎥⎣⎦⎢⎥⎣⎦O V A A V OO ∑. ②将V 分块为12(,,,)n =V v v v ,它的n 个列12,,,n v v v 是对应于特征值12,,,n λλλ 的标准正交的特征向量.为了得到酉矩阵U ,首先考察m C 中的向量组12,,,r Av Av Av ,由于当i 不等于j 时有H H H H H (,)()()0i j j i j i j i i i j i λλ=====Av Av Av Av v A Av v v v v所以向量组12,,,r Av Av Av 是m C 中的正交向量组.又 2H H H 2||||i i i i i i iλσ===Av v A Av v v ,所以 ||||i i i σ=Av .令1i i i=u Av σ,1,2,,i r = ,则得到m C 中的标准正交向量组12,,,r u u u ,把它扩充成为m C 中的标准正交基11,,,,r r m +u u u u ,令11(,,,,)r r m +=U u u u u则U 是m 阶酉矩阵.由已知及前面的推导可得i i i σ=Av u ,1,2,,i r = ;i =Av 0,1,,i r n =+ ;从而 121(,,,)(,,,,,)n r ==AV A v v v Av Av 0011120(,,,,,)(,,,)0r m r σσσσ⎛⎫⎪ ⎪== ⎪ ⎪ ⎪⎝⎭O u u u u u O O 00 ⎛⎫= ⎪⎝⎭ΣO U O O故有=AV U Δ,即H =U AV Δ.例1 求矩阵120202⎡⎤=⎢⎥⎣⎦A 的奇异值分解.解 T52424044⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦A A 的特征值为1239,4,0λλλ===, 对应的单位特征向量依次为T T T 1231,1),(2,1,2)3==-=-v v v .所以5052643⎡-⎢=⎥⎥-⎥⎣⎦V .于是可得()2r =A ,3002∑⎡⎤=⎢⎥⎣⎦.计算111221∑-⎡⎤==⎢⎥-⎣⎦U AV ,则A 的奇异值分解为T 300020⎡⎤=⎢⎥⎣⎦A U V .在A 的奇异值分解中,酉矩阵V 的列向量称为A 的右奇异向量,V 的前r 列是H A A 的r 个非零特征值所对应的特征向量,将他们取为矩阵V 1,则12(,)=V V V .酉矩阵U 的列向量被称为A 的左奇异向量,将U 从前r 列处分块为12(,)=U U U ,由分块运算,有H H H H1111212H H H22122()⎡⎤⎛⎫⎡⎤=== ⎪⎢⎥⎢⎥⎣⎦⎣⎦⎝⎭O U U AV U AV U AV AV AV O O U U AV U AV ,∑ 从而 211=A V A V U Σ,=0.正交基;(2)1U 的列向量组是矩阵A 的列空间(){}R =A Ax 的一组标准正交基;(1)1V 的列向量组是矩阵A 的零空间(){}N ==A x Ax 0正交补H ()R A 的一组标准正交基;(1)2U 的列向量组是矩阵A 的列空间(){}R =A Ax 正交补H ()N A 的一组标准正交基.在A 的奇异值分解中,酉矩阵U 和V 不是惟一的.A 的奇异值分解给出了矩阵A 的许多重要信息.更进一步,由于12(,,)m =U u u u ,12(,,,)n =V v v v ,可借助于奇异值分解,将A 表示为H 11H 212H 0(,,,)0m r n σσ⎛⎫⎛⎫⎪ ⎪ ⎪ ⎪= ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭v O v A u u u O O v H HH 111222r r r σσσ=+++u v u v u v归纳这一结果,有如下定理.定理 设m n ⨯∈A C ,A 的非零奇异值为12r σσσ≥≥≥ ,12,,ru u u 是应于奇异值的左奇异向量,12,,,r v v v 是应于奇异值的右奇异向量,则T TT 111222r r r σσσ=+++A u v u v u v .上式给出的形式被称为矩阵A 的奇异值展开式,对一个k r ≤,略去A 的一些小的奇异值对应的项,去矩阵k A 为T T T111222k k k kσσσ=+++A u v u v u v .则k A 是一个秩为k 的m ×n 矩阵.可以证明,k A 是在所有秩为k 的m ×n 矩阵中,从Frobenius 范数的意义下,与矩阵A 距离最近的一个矩阵.这在实际中应用广泛.例如,在图像数字化技术中,一副图片可以转换成一个m ×n 阶像素矩阵来储存,存储量m ×n 是个数.如果利用矩阵的奇异值展开式,则只要存储A 的奇异值i σ,奇异向量,i i u v 的分量,总计r (m +n +1)个数.取m =n =1000,r =100作一个比较, m ×n =1000000,r (m +n +1)=100(1000+1000+1)=200100.取A 的奇异值展开式,,存储量较A 的元素情形减少了80%.另外,可取k r <,用k A 逼近A ,能够达到既压缩图像的存储量,又保持图像不失真的目的.由矩阵A 的奇异值分解可得T TT 111222r r r σσσ=+++A u v u v u v可见,A 是矩阵T TT 1122,,,r r u v u v u v 的加权和,其中权系数按递减排列120r σσσ≥≥≥> .显然,权系数大的那些项对矩阵A 的贡献大,因此当舍去权系数小的一些项后,仍然能较好的“逼近”矩阵A ,这一点在数字图像处理方面非常有用.矩阵的秩k 逼近定义为T T T111222 1k k k k r σσσ=+++≤≤A u v u v u v秩r 逼近就精确等于A ,而秩1逼近的误差最大.矩阵的奇异值分解不但在线性方程组,矩阵范数,广义逆,最优化等方面有着广泛的应用.而且在数字计算,数字图像处理,信息检索,心里学等领域也有着极重要的应用.有兴趣的读者可参阅有关教科书,如Steven J.Leon 的《线性代数》.3 矩阵A的奇异值分解与线性变换T A设A 是一个秩为r 的m ×n 复矩阵,即m n⨯∈A C,rank()r =A ,则由()T ==A A βαα可以定义线性变换:n m T →A C C .设矩阵A 有奇异值分解H=A U ΣV ,则将矩阵n n⨯∈V C 的列向量组12,,,n v v v 取作空间nC 的标准正交基;则将矩阵m m⨯∈U C的列向量组12,,m u u u 取作空间mC的标准正交基,则在所取的基下,线性变换T A 对应的变换矩阵就是Σ.设n ∈C α,α在基12,,,n v v v 下坐标向量为T12(,,,)n x x x =x ,=Vx α.那么α在线性变换T A 下的像β具有形式:11H()()()00r r x x T σσ⎛⎫ ⎪ ⎪ ⎪===== ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭A A U ΣV Vx U Σx U βαα.其中12,,,r σσσ 是A 的非零奇异值,所以,α的像()T =A βα在m C 中基12,,m u u u 下的坐标是T 11(00)r rx x σσ==y Σx .从中可以看出,当rank()r =A 时,在取定的基下,线性变换()T A α的作用是将原像坐标中的前r 个分量分别乘以A 的非零奇异值12,,,r σσσ ,后(n-r )分量化为零.如果原像坐标满足条件:222121n x x x +++= ,则像坐标满足条件:2221212()()()1rry y y σσσ+++≤ .在rank()r n ==A 时,等式成立.因此,有如下定理.定理 设H=A U ΣV 是m ×n 实矩阵A 的奇异值分解,rank()r =A ,则nR 中的单位圆球面在线性变换T A 下的像集合是:(1)若r n =,则像集合是mR 中的椭球面;(2)若r n <,则像集合是mR 中的椭球体.例2 设矩阵120202⎡⎤=⎢⎥⎣⎦A ,求3R 中的单位圆球面在线性变换:T A y =Ax 下的像的几何图形.解 由例1,矩阵A 有如下奇异值分解T5012300262102043⎛⎫⎡-⎪⎢⎛⎫⎡⎤⎡⎤⎪=⎥⎪⎢⎥⎢⎥-⎪⎣⎦⎣⎦⎥⎭⎪-⎥⎣⎦⎝⎭A. rank()23,n=<=A由定理,单位球面的像满足不等式221222132y y+≤.即单位球面的像是实心椭圆2212194y y+≤.。
奇异值分解的一些特性以及应用小案例

a11 a12
a21
a22
am
am
1 2
a11
a21
a12 a22
a1n a2n
a1n
a2n
amn
am1
am2
amn
图 2. AT A 方阵迹的形成过程
1.2 矩阵 AB 的迹等于矩阵 BA 的迹 设 A Rmn , B Rnm ,令 A (aij )mn , B (bij )nm ,则 tr( AB) tr(BA) 。
下面随机举个数据矩阵 data(12,9) ,12 行 9 列,如下所示:
1 0 0 1 0 0 0 0 0
1 0 1 0 0 0 0 0 0
1 1 0 0 0 0 0 0 0
0 1 1 0 1 0 0 0 0
0 1 1 2 0 0 0 0 0
data
0 0
aijb ji
i1 j 1
b11 b12 b1m
B
(bij )nm
b21
b22
b2m
bn1
bn2
bnm
a11 a12 a1n
A
(aij )mn
a21
a22
a2
n
am1
am 2
amn
n2
,占总信息量的
2 r 1 12
2 r 1
奇异值分解
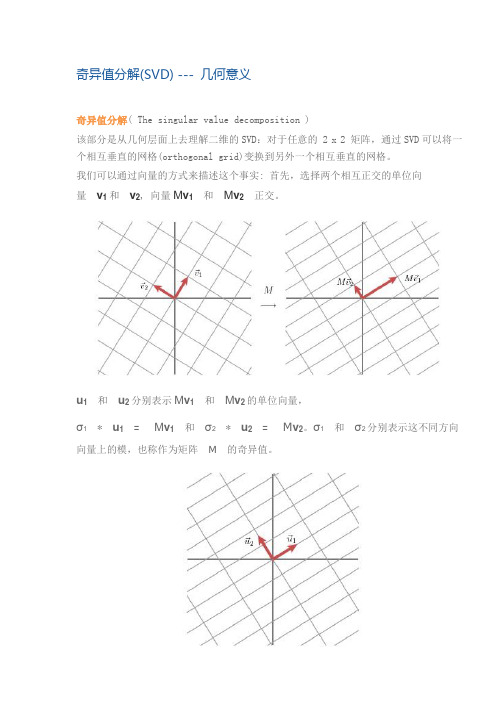
奇异值分解(SVD) --- 几何意义奇异值分解( The singular value decomposition )该部分是从几何层面上去理解二维的SVD:对于任意的 2 x 2 矩阵,通过SVD可以将一个相互垂直的网格(orthogonal grid)变换到另外一个相互垂直的网格。
我们可以通过向量的方式来描述这个事实: 首先,选择两个相互正交的单位向量v1 和v2, 向量M v1和M v2正交。
u1和u2分别表示M v1和M v2的单位向量,σ1* u1= M v1和σ2* u2= M v2。
σ1和σ2分别表示这不同方向向量上的模,也称作为矩阵M的奇异值。
这样我们就有了如下关系式M v1= σ1u1M v2= σ2u2我们现在可以简单描述下经过M线性变换后的向量x 的表达形式。
由于向量v1和v2是正交的单位向量,我们可以得到如下式子:x = (v1x) v1 + (v2x) v2这就意味着:M x = (v1x) M v1 + (v2x) M v2M x = (v1x) σ1u1 + (v2x) σ2u2向量内积可以用向量的转置来表示,如下所示v x = v T x最终的式子为M x = u1σ1v1T x + u2σ2v2T xM = u1σ1v1T + u2σ2v2T上述的式子经常表示成M = UΣV Tu 矩阵的列向量分别是u1,u2 ,Σ是一个对角矩阵,对角元素分别是对应的σ1和σ2,V 矩阵的列向量分别是v1,v2。
上角标T表示矩阵V 的转置。
这就表明任意的矩阵M是可以分解成三个矩阵。
V 表示了原始域的标准正交基,u 表示经过M 变换后的co-domain的标准正交基,Σ表示了V 中的向量与u 中相对应向量之间的关系。
(V describes an orthonormal basis in the domain, and U describes an orthonormal basis in the co-domain, and Σ describes how much the vectors in V are stretched to give the vectors in U.)如何获得奇异值分解?( How do we find the singular decomposition? ) 事实上我们可以找到任何矩阵的奇异值分解,那么我们是如何做到的呢?假设在原始域中有一个单位圆,如下图所示。
奇异值分解定理

奇异值分解定理奇异值分解(Singular Value Decomposition,简称SVD)是线性代数中一种重要的矩阵分解方法,常用于数据分析、信号处理、图像压缩等领域。
SVD的定理表明,任何矩阵都可以分解成三个矩阵的乘积,其中一个矩阵是正交矩阵,另外两个矩阵是对角矩阵,且对角线上的元素称为奇异值。
奇异值分解定理的数学概念比较复杂,需要一定的线性代数基础。
下面将对奇异值分解定理进行详细解释。
给定一个m行n列的实数矩阵A,假设rank(A)为r.那么存在两个实数方阵U(m×r)和V(n×r),使得:A = UΣV^T其中,U的每一列是A^TA的特征向量,V的每一列是AA^T的特征向量,Σ是一个对角矩阵,对角线上的元素称为奇异值。
奇异值分解定理的证明比较复杂,这里只给出一个简要的证明思路。
假设A的列向量为{a1, a2, ..., an},它们构成了一个n维向量空间的一组基。
我们可以将这组基转化为标准正交基,得到一组正交矩阵U和V。
然后我们可以通过对U和V进行一些数学操作,得到UΣV^T形式的矩阵。
最后,我们可以证明这个矩阵确实满足奇异值分解定理的要求。
奇异值分解定理在数据分析中有广泛的应用。
例如,在推荐系统中,我们可以通过SVD将用户对物品的评分矩阵分解,得到用户和物品的特征矩阵,从而进行个性化推荐。
在语音识别中,我们可以通过SVD将语音信号分解成一组基本声音的叠加,从而实现语音信号的降噪和特征提取。
在图像压缩中,我们可以通过SVD将图像分解成一组基本的图像模式,从而实现图像的降噪和压缩。
奇异值分解定理的应用不仅局限于上述领域,还可以应用于信号处理、图像处理、文本处理等其他领域。
通过奇异值分解,我们可以将复杂的问题转化为简单的线性代数运算,从而大大简化问题的求解过程。
然而,奇异值分解也有一些限制。
首先,奇异值分解是一种数值方法,对计算精度要求较高。
其次,奇异值分解的计算复杂度较高,对于大规模矩阵的分解可能会很耗时。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
• 实际应用中提到矩阵的奇异值分解时,通常指截断奇异值分解。
截断奇异值分解
例
• 矩阵A的秩为3,
• 若取k=2,则其截断奇异值分解是
几何解释
• 从线性变换的角度理解奇异值分解, m x n 矩阵A表示从n维空间Rn到 m维空间Rm的一个线性变换,
坐标系的旋转或反射变换U,得到向量
。
• 原始空间的标准正交基,
经过坐标系的旋转变换VT、 坐标轴的缩放变换刃、 坐标系的旋转变换U, 得到和经过线性变换A等价的结果。
例
• 给定一个2阶矩阵
• 其奇异值分解为
例
• 观察基于矩阵A的奇异值分解将R2的标准正交基
• 进行线性转换的情况 • 首先,VT表示一个旋转变换,将标准正交基e1, e2旋转,得到向
• 的奇异值分解
例
• (1)求ATA的特征值和特征向量
• 得到齐次线性方程组
例
• 该方程有非零解的充要条件是
• 解此方程,得矩阵ATA的特征值
和
。
• 将特征值代入线性方程组,得到对应的单位特征向量
例
• (2)求正交矩阵V • 构造正交矩阵V
• (3)求对角矩阵
• 奇异值为
和
• 构造对角矩阵
例
• (3)求 m x n 对角矩阵
• 计算A的奇异值
• 构造 m x n 矩形对角矩阵 ,主对角线元素是奇异值,其余 元素是零
奇异值分解的计算
• (4) 求m阶正交矩阵U • 对A的前r个正奇异值,令 • 得到 • 求AT的零空间的一组标准正交基
,令
• 并令
• (5)得到奇异值分解
例
• 试求矩阵
• 设矩阵A的秩是r, rank(A) = r,则矩阵ATA的秩也是r
奇异值分解基本定理
• 由于ATA是对称矩阵, 它的秩等于正的特征值的个数,所以
• 对应地有
•令
• 其中v1,… ,vr为ATA的正特征值对应的特征向量,vr+1,… ,vn为0
特征值对应的特征向量,则
15.6
• 这就是矩阵A的奇异值分解中的n阶正交矩阵V。
例
• 矩阵的奇异值分解不是唯一的。在此例中如果选择U为
• 而 和V不变,那么
也是A的一个奇异值分解
奇异值分解基本定理
• 若A为一 m x n 实矩阵,
,则A 的奇异值分解存在
• 其中U是m阶正交矩阵,V是n阶正交矩阵, 是 m x n 矩形对角 矩阵,其对角线元素非负,且按降序排列。
奇异值分解基本定理
• U的列向量u1, u2, …, um构成Rm空间的一组标准正交基,表示 Rm 中的正交坐标系的旋转或反射变换
• 的对角元素 坐标系坐标轴的
是一组非负实数,表示Rn中的原始正交 倍的缩放变换。
几何解释
• 任意一个向量
,经过基于
的线性变换,等价于
经过坐标系的旋转或反射变换VT,坐标轴的缩放变换
,以及
• 设X的奇异值分解为 • 其中
• 若令矩阵B=QTAP,则A=QBPT。由此得到
矩阵的最优近似
• 用 分块方法对B分块
• 其中B11是 k x k 子矩阵,B12是 k x (n-k) 的子矩阵,B21是(m-k) x k 子矩阵,B22 是(m-k) x (n-k)子矩阵。可得
矩阵的最优近似
• 如果将A看成是从Rn到Rm的线性变换,则A的列空间和A的值域 R(A)是相同的。因此u1, u2,…, ur 也是R(A)的一组标准正交 基。
•若
表示R(A)的正交补,则有R(A)的维数为r,
的
维数为
m – r,两者的维数之和等于m。而且有
= N(AT)成立
奇异值分解基本定理
•令
为N(AT)的一组标准正交基,并令
奇异值分解的计算
• (1)求ATA的特征值和特征向量来自• 计算对称矩阵W=ATA
• 求解特征方程
• 得到特征值 ,并将特征值由大到小排列
• 将特征值
代入特征方程求得对应的特征向量
• (2)求n阶正交矩阵V • 将交特 矩征 阵V向:量单位化,得到单位特征向量v1,v2, …,vn,构成n阶正
奇异值分解的计算
• 证明
• 证明是构造性的,对给定的矩阵A,构造出其奇异值分解的各个 矩阵。
• 为了方便,不妨假设m≥n,如果m<n证明仍然成立。
奇异值分解基本定理
• (1)确定V和 • 首先构造n阶正交实矩阵V和 m x n 矩形对角实矩阵 • 矩阵A是 m x n 实矩阵,则矩阵ATA是n阶实对称矩阵。 • 因而ATA的特征值都是实数,并且存在一个n阶正交实矩阵V实现ATA的
• 注意奇异值分解不要求矩阵A是方阵,事实上矩阵的奇异值分解 可以看作是方阵的对角化的推广。
例
• 给定一个5x4矩阵A
例
• 它的奇异值分解由三个矩阵的乘积 给出
例
• 矩阵 是对角矩阵,对角线外的元素都是0,对角线上的元素 非负,按降序排列。
• 矩阵U和V是正交矩阵,它们与各自的转置矩阵相乘是单位矩阵, 即
对角化,使得 VT(ATA)V = A 成立 • 其中A是n阶对角矩阵,其对角线元素由ATA的特征值组成。
奇异值分解基本定理
• 而且,ATA的特征值都是非负的。事实上,令 征值,x是对应的特征向量,则
是ATA的一个特
• 于是
奇异值分解基本定理
• 可以假设正交矩阵V的列的排列使得对应的特征值形成降序排列 • 计算特征值的平方根(实际就是矩阵A的奇异值)
• 其的中 奇I异k是值k分阶解单,位即矩得阵,U2,V2的分块与B的分块一致注意到B及B22 • 由此可知 的对角线元素为A的奇异值,故有 • 可证
第十五章 奇异值分解
定义与定理
定义与定理
•
:矩阵A的奇异值分解(singular value decomposition,
SVD)
• :矩阵 A的奇异值(singular value)
• U的列向量:左奇异向量(left singular vector)
• V 的列向量:右奇异向量(right singular vector)
主要性质
• (3)矩阵A的奇异值分解中,奇异值 矩阵U和V不是唯一的。
• (4)矩阵A和 的秩相等,等于正奇异值 重复的奇异值)。
是唯一的,而 的个数r(包含
主要性质
• (5) • 矩阵A的r个右奇异向量v1, v2, …, vr构成AT的值域R(AT)的一组
标准正交基。
• 因为矩阵AT是从Rm映射到砂的线性变换,则AT的值域R(AT )和AT 的列空间是相同的, v1, v2, …, vr是AT的一组标准正交基,因 而也是R(AT )的一组标准正交基。
• 由于V是正交矩阵,由式(15.6)可得
15.11
奇异值分解基本定理
• (2)确定U
• 接着构造m阶正交实矩阵
•令
15.12
• 则有
15.14
奇异值分解基本定理
• U1的列向量构成了一组标准正交集,因为
15.15
奇异值分解基本定理
• 由式(15.12)和式(15.15)可知,u1, u2,…, ur 构成A的列空 间的一组标准正交基, 列空间的维数为r。
• Ur: m x r 矩阵 • Vr: n x r 矩阵 • : r阶对角矩阵
• 矩阵Ur 由完全奇异值分解中的U的前r列、矩阵Vr的前r列、矩阵 凡由 的前r个对角线元素得到。紧奇异值分解的对角矩阵 的秩与 原始矩阵A的秩相等。
例
• 矩阵A的秩r = 3
例
• A的紧奇异值分解是
截断奇异值分解
• x和Ax分别是各自空间的向量。
• 线性变换可以分解为三个简单的变换:
• 一个坐标系的旋转或反射变换 • 一个坐标轴的缩放变换 • 另一个坐标系的旋转或反射变换
• 奇异值定理保证这种分解一定存在。这就是奇异值分解的几何解释。
几何解释
• 对矩阵A进行奇异值分解,得到
• ,V和U都是正交矩阵
• V的列向量v1, v2, …, vn构成Rn空间的一组标准正交基,表示R中 的正交坐标系的旋转或反射变换
• 奇异值分解也是一种矩阵近似的方法,这个近似是在弗罗贝尼乌 斯范数(Frobenius norm)意义下的近似。
• 矩阵的弗罗贝尼乌斯范数是向量的LZ范数的直接推广,对应着机 器学习中的平方损失函数。
• 设矩阵
,定义矩阵A的弗罗贝尼乌斯范数为
弗罗贝尼乌斯范数
• 引理15.1
弗罗贝尼乌斯范数
• 证明: • 一般地,若Q是m阶正交矩阵,则有 • 因为
• (4)求正交矩阵U • 基于A的正奇异值计算得到列向量u1
• 列向量u2, u3是AT的零空间N(AT)的一组标准正交基
例
• 求解
• 分别取(x2, x3)为(1,0)和(0,1),得到N(AT)的基 • N(AT)的一组标准正交基是 • 构造正交矩阵U
例
• (5)矩阵A的奇异值分解
弗罗贝尼乌斯范数
• 现证B12=0, B21=0。 用反证法。若B12≠0,令
•则
,且
• 这与X的定义式
• 因此B12=0, 同样可证B21=0。于是
矛盾
矩阵的最优近似
• 再证
,为此令
•则
,且
•由
知,
• 最后看B22。若(m-k) x (n-k)子矩阵B22有奇异值分解
即 ,则
矩阵的最优近似
• 证明 的对角线元素为A的奇异值。为此,令
• 同样,若P是n阶正交矩阵,则有 •故 •即
