第五章 球面透镜
八年级物理上册人教版第五章透镜及其应用知识点(超精华)
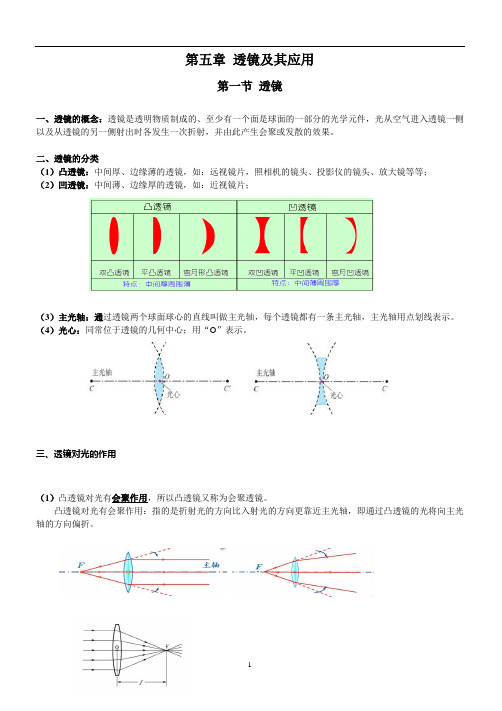
第五章透镜及其应用第一节透镜一、透镜的概念:透镜是透明物质制成的、至少有一个面是球面的一部分的光学元件,光从空气进入透镜一侧以及从透镜的另一侧射出时各发生一次折射,并由此产生会聚或发散的效果。
二、透镜的分类(1)凸透镜:中间厚、边缘薄的透镜,如:远视镜片,照相机的镜头、投影仪的镜头、放大镜等等;(2)凹透镜:中间薄、边缘厚的透镜,如:近视镜片;(3)主光轴:通过透镜两个球面球心的直线叫做主光轴,每个透镜都有一条主光轴,主光轴用点划线表示。
(4)光心:同常位于透镜的几何中心;用“O”表示。
三、透镜对光的作用(1)凸透镜对光有会聚作用,所以凸透镜又称为会聚透镜。
凸透镜对光有会聚作用:指的是折射光的方向比入射光的方向更靠近主光轴,即通过凸透镜的光将向主光轴的方向偏折。
(2)凹透镜对光有发散作用,所以凹透镜又称为发散透镜。
凹透镜对光有发散作用:指的是折射光的方向比入射光的方向更偏离主光轴,即通过凹透镜的光将向远离主光轴方向偏折。
四、焦点和焦距(1)焦点:平行于凸透镜主光轴的光线经凸透镜后会聚于主光轴上一点,这点叫焦点;用“F”表示。
(2)焦距:焦点到光心的距离(通常由于透镜较厚,焦点到透镜的距离约等于焦距)焦距用“f”表示。
如下图:注意:凸透镜和凹透镜都各有两个焦点,凸透镜的焦点是实焦点,凹透镜的焦点是虚焦点。
凸透镜:凸透镜能使跟主光轴平行的入射光线会聚于一点,叫实焦点 ,用“F”表示。
这一点到凸透镜的光心的距离叫焦距,用“f”表示。
一个凸透镜有 2 个焦点,它们位于凸透镜的两侧。
凹透镜:凹透镜能使跟主光轴平行的入射光线发散 ,且发散光的反向延长线相交在主光轴上的一点,这个点不是实际光的会聚点,所以叫做虚焦点,用F表示,凹透镜两侧各有一个虚焦点。
五、三条特殊光线(要求会画):Ⅰ凸透镜(1)平行于主光轴的光线,经凸透镜后经过焦点;(2)经过凸透镜焦点的光线经凸透镜后平行于主光轴;(3)过光心的光线经透镜后传播方向不改变。
球面透镜的像教案与实验

一、前言球面透镜是我们生活中经常使用的一种光学仪器,其具有厚透镜的特点,可以将光线折射并聚焦到一定的焦点上。
通过球面透镜,我们可以产生出清晰的像,将其应用于多个领域,如医疗、技术、工程等领域。
在本文中,我们将探讨球面透镜的像教案与实验,希望对您有所帮助。
二、球面透镜的基本原理球面透镜是由两个球面的面构成的透镜,其主要原理是根据透镜的曲率半径不同来使光线发生折射。
球面透镜的中心点即为透镜的光心,其使得通过透镜的光线可以在一定的距离内聚焦。
对于一般的凸面透镜来说,当光线从外部垂直进入时,会在透镜内部被折射,并聚焦到透镜后方的一个点上,这个点就是透镜的焦点。
同样的,当光线从外部倾斜进入时,会发生偏折,进而在透镜后方聚焦到另一个点上。
凹面透镜与凸面透镜相反,当光线从透镜内部垂直发出时,向外发散,不会聚焦于任何一个点上。
当光线倾斜入射时,也会向外发散。
三、球面透镜的像的特性球面透镜产生的像与光线的入射角度、入射的位置和透镜的曲度有关。
在本部分,我们将探讨球面透镜的像的特性。
1.像的大小像的大小决定于物体的大小、透镜的曲率和焦距的大小。
如果物体越大,透镜的曲率越小,那么产生的像也会越小。
当透镜离物体越近,产生的像也会变得更小。
2.像的清晰度像的清晰度主要取决于透镜的制造质量和曲率半径的大小。
透镜的焦距与曲度直接相关。
3.像的位置像的位置主要是由透镜的焦距和物体的位置决定的。
当物体距离透镜的距离越近时,所产生的像就会越远。
4.像的放大率像的放大率是指像与物体的大小之比。
它取决于透镜的焦距和与物体的距离。
当物体距离透镜较远时,像可以实现适当的放大。
四、球面透镜的像教案1.实验目的通过对球面透镜的实验,让学生更好的理解球面透镜的基本原理和像的特性。
2.实验设备(1) 球面透镜(2) 高亮度的小灯或其他发光物体(3) 纸板或墙壁(4) 直尺或量角器3.实验步骤(1) 将透镜放在较亮的光源上,调整透镜的位置,使光线尽量呈垂直角度照射透镜。
球面透镜知识点总结

球面透镜知识点总结一、球面透镜的定义球面透镜是一种光学元件,由凸透镜和凹透镜组成。
凹透镜的中心是一种透明介质,边缘是一种高折射率。
这种透镜的作用是集中和散焦光线,使其通过透镜的中心,并在透镜的边缘发散。
球面透镜通常用于照相机、显微镜和望远镜等设备中。
二、球面透镜的类型球面透镜根据其曲率和折射率的不同可以分为凸透镜和凹透镜。
凸透镜的中心是一种透明介质,边缘是一种高折射率。
凹透镜是一种透明介质,边缘是一种低折射率。
凸透镜具有凸面,凹透镜具有凹面。
根据透镜的应用和特性,球面透镜可以分为正透镜,负透镜和双球透镜。
正透镜的凸面是一个透明介质,边缘是一种低折射率。
负透镜的凹面是一个透明介质,边缘是一种高折射率。
双球透镜具有两个平行的球面,中间是一种透明介质,边缘是一种高折射率。
三、球面透镜的光学原理球面透镜的光学原理是利用透镜的曲率和折射率不同,使光线通过透镜的中心,并在透镜的边缘发散。
通过透镜的曲率,可以将光线折射到焦点,实现光线的聚焦和散焦。
透镜的折射率决定了光线在透镜中的折射角和折射率,影响了透镜的折射功能。
四、球面透镜的主要特性1. 焦距:球面透镜的焦距是指透镜能够使光线聚焦或散焦的距离。
焦距是球面透镜的重要参数,可以用来计算光线的折射角和折射率,以及透镜的成像功能。
2. 放大倍率:球面透镜的放大倍率是指透镜的成像功能,通过透镜的曲率和折射率,可以实现对物体的聚焦和散焦,使物体的图像变得更大或者更小。
3. 成像质量:球面透镜的成像质量是指透镜的透光性和清晰度,通过透镜的材质和加工工艺,可以改善透镜的光学性能,提高透镜的成像质量。
五、球面透镜的应用1. 光学仪器:球面透镜广泛应用于照相机、显微镜、望远镜等光学仪器中,通过透镜的成像功能,可以实现对物体的观察和测量。
2. 光学通讯:球面透镜在光学通讯中扮演着重要的角色,通过透镜的聚焦功能,可以将光信号传输到远距离的地方。
3. 医疗器械:球面透镜在医疗器械中经常使用,如眼镜、激光手术仪器等,通过透镜的放大功能,可以改善人们的视力。
第五章 透镜及其应用

F
oF
(平行于主光轴)
F
oF
(过凸透镜焦点)
F
oF
(过凸透镜光心)
F
oF
(平行于主光轴)
F
F
o
(延长线过凹透镜虚焦点)
F
oF
(过凹透镜光心)
判定凸透镜和凹透镜的方法: 1、用手摸,中间厚边缘薄的是凸透镜,
中间薄边缘厚的是凹透镜; 2、对着太阳光,如果在地面出现一个 最小最亮的光斑的则是凸透镜,没有的 则是凹透镜 3、用平行光检测,对光起会聚作用的是 凸透镜,对光起发散作用的是凹透镜; 4、用光屏检测,能在光屏上呈现像的是 凸透镜,不能在光屏上呈现像的是凹透镜。
12、夏日,某人潜水时, 眼睛能看到路灯O,能 正确的光路是哪条?OCD
13、从水面上斜着看插 在水中的筷子,情况应 该是哪种?为什么?
OA
14、放在离凸透镜20厘米处的一物体,在凸 透镜的另一侧离凸透镜5厘米的光屏上成一 清晰的像,则所成的像是__倒___立 __缩___小_的___ 像实
凸透镜的焦点、焦距
凸透镜能使平行于主光轴的光会聚 在一点,这个点叫做焦点
焦点到光心的距 离叫做焦距。
凹透镜对光有发散作用
凹透镜的焦点、焦距
凹透镜能使平行于 主光轴的光发散, 发散光线的反向延 长线交于一点,这 个点叫做焦点。 焦点到光心的距离 叫做焦距。
在图中填写上适当的光学元件
透镜的三条特殊光线
照相机内的胶卷,相当于光屏,用来承接实像 物体与实像大小比较 实像小于物体 物距与像距大小比较 像距小于物距
2、投影仪
投影仪是根据物体位于凸透镜的二倍焦距与一倍焦距
之间( 2f>u>f)成 倒立的、放大像的制、成实的。
球面透镜知识点总结高中

球面透镜知识点总结高中一、球面透镜的类型球面透镜根据其两侧曲面的凸凹性质,可以分成凸透镜和凹透镜两种类型。
凸透镜即为凸面透镜,其两侧都是凸面;凹透镜即为凹面透镜,其两侧都是凹面。
凸透镜具有聚光的作用,可以将平行光线汇聚于一点,所以也被称为“凸透镜”,而凹透镜则具有发散光线的作用,无论入射光线是经出射光线都会呈现出发散的特性。
二、主要特性1. 凸透镜的主轴、焦距和焦点:凸透镜的主轴是通过透镜的中心,并且垂直于透镜的两个面;焦距是指透镜的焦点与透镜的中心之间的距离;焦点是指凸透镜上主光线(即经过透镜中心点的光线)经折射后交于的点。
焦点有一个正焦点,位于凸透镜前方;另一个负焦点,位于凸透镜背面。
2. 凹透镜的主轴、焦距和焦点:凹透镜的主轴、焦距和焦点的概念与凸透镜类似,但由于其特性不同,凹透镜产生的焦点位置也不同。
对于凹透镜来说,其主轴也是垂直于透镜两个面的线,而焦距是指透镜的焦点与透镜中心的距离。
焦点也有正负之分,凹透镜的正焦点位于透镜的背面,负焦点位于透镜的前面。
3. 凸透镜成像规律:凸透镜在成像时,物体与凸透镜之间距离的不同,决定了其在凸透镜上的成像位置。
当光线从物体上射入凸透镜时,根据光的传播规律,可以得到物体在凸透镜上的成像位置。
4. 凹透镜成像规律:凹透镜在成像时,同样也会根据光线的传播规律产生成像。
凹透镜成像规律与凸透镜有所不同,需要根据入射光线的位置和光线的折射规律来确定成像位置。
5. 球面透镜的物像关系:根据透镜成像规律,可以得到物体、像的位置关系。
当物体位于焦点附近时,产生的像会比较特殊,需要特别注意。
6. 球面透镜的放大率计算:放大率是指成像物体的大小与实际物体大小之比,根据透镜成像规律和物像关系可以计算出物体的放大率。
三、球面透镜的成像位置计算在物理课程中,学生通常需要根据透镜成像规律和物像关系,计算出物体在透镜上的成像位置。
这个过程需要考虑入射光线的性质、透镜的焦距等因素,通过简单的几何光学原理即可求得物体的成像位置。
第五章透镜及其应用
由于甲处和蜡烛位于凸透镜的两侧,因此甲处只能成实像,故A错误;
(2)由于题干未提供物距和凸透镜的焦距,因此乙处可能成放大的实像也可能成缩小的实像,故B正确。
故选:B。
【典例7】(2022•遵义)某同学在家用一个玻璃球做成像实验,如图所示。墙上的像是实(选填“实”或“虚”)像,墙面到玻璃球球心的距离小于(选填“大于”、“小于”或“等于”)蜡烛到玻璃球球心的距离。
知识点5:显微镜和望远镜
1、显微镜:显微镜镜筒的两端各有一组透镜,每组透镜的作用都相当于一个凸透镜,靠近眼睛的凸透镜叫做目镜,靠近被观察物体的凸透镜叫做物镜。来自被观察物体的光经过物镜后成一个放大的实像,道理就像投影仪的镜头成像一样;目镜的作用则像一个普通的放大镜,把这个像再放大一次。经过这两次放大作用,我们就可以看到肉眼看不见的小物体了。
【解答】解:(1)由图甲知,焦点到凸透镜的距离为42.5cm﹣30.0cm=12.5cm,所以凸透镜的焦距为12.5cm;
(2)由图可知,此时的物距为u=50cm﹣10cm=40cm>2f时,由凸透镜成像规律可知,成倒立缩小的实像;
(3)近视眼镜为凹透镜,凹透镜对光线有发散作用,为了再次在光屏上得到清晰的像,蜡烛和透镜的位置不变,可将光屏远离透镜。
(1)u=f是成实像和虚象,像正、倒立,像物同侧和异侧的分界点。(一倍焦距分虚实)
(2)u=2f是像放大和缩小的分界点。(二倍焦距分大小)
球面透镜的成像

球面透镜的成像在光学领域中,透镜是一种重要的光学元件,它能够将光线折射并聚焦到一个点上,从而形成图像。
球面透镜作为最常见的透镜类型之一,广泛应用于照相机、眼镜、望远镜等光学仪器中。
本文将详细介绍球面透镜的成像原理及其相关性质。
一、球面透镜的基本性质球面透镜由两个球面界面组成,其中一个或两个球面可以是平面。
根据球面的曲率,透镜被分为凸透镜和凹透镜两种类型。
1. 球面透镜的主轴和焦点球面透镜的主轴是连接两个球面中心的直线,也是光线传播的方向。
主轴上的任意点都与透镜的球心对齐。
而球面透镜的焦点是主轴上与透镜对称的一点,光线经过透镜后会汇聚于该点或者看似从该点发散出来。
2. 球面透镜的焦距和焦平面焦距是描述透镜聚焦能力的重要参数,表示光线从无限远处通过透镜后的汇聚或发散程度。
焦距可正可负,正焦距表示透镜使平行光汇聚,负焦距表示透镜使平行光发散。
与焦距垂直的平面称为透镜的焦平面。
二、球面透镜的成像原理1. 凸透镜成像原理当物体距离凸透镜远于二倍焦距时,成像位置在透镜的焦点之间;当物体距离凸透镜等于二倍焦距时,成像位置在透镜的焦点上;当物体距离凸透镜小于二倍焦距时,成像位置在透镜的焦点之外。
凸透镜成像公式为:1/f = 1/v + 1/u其中 f 为焦距,v 为像距,u 为物距。
2. 凹透镜成像原理凹透镜的成像与凸透镜相反,当物体处于凹透镜的正面时,成像位置在透镜的虚焦点之间;当物体处于凹透镜的虚焦点上时,成像位置在无穷远处;当物体处于凹透镜的虚焦点之外时,成像位置在透镜的虚焦点外。
凹透镜成像公式为:1/f = 1/v - 1/u三、球面透镜的光阑和倍率1. 光阑球面透镜中,只有中心区域的光线能够通过,而朝向边缘的光线将被遮挡,这个中心区域就是光阑。
光阑的大小决定了透镜的光通量,进而影响到成像的亮度和清晰度。
2. 倍率倍率是描述透镜放大或缩小能力的参数。
对于放大(正)倍率而言,当物体距离透镜的焦点处时,成像位置将在无穷远处,此时成像尺寸相当于物体尺寸的倍数。
中学物理第五章 透镜及其应用 总结知识点
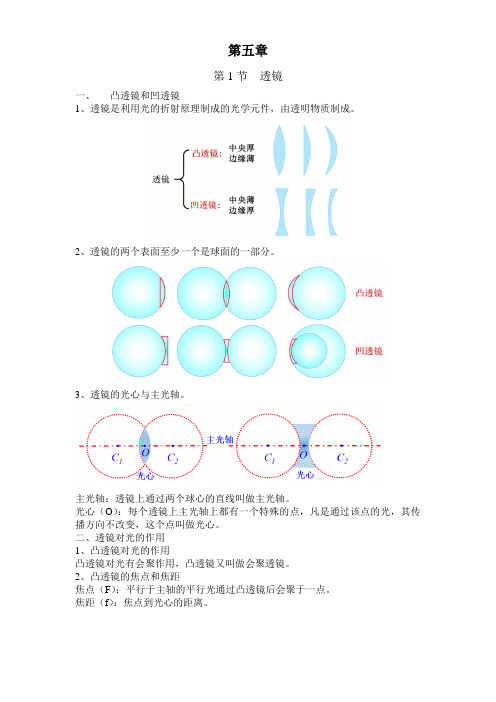
第五章第1节透镜一、凸透镜和凹透镜1、透镜是利用光的折射原理制成的光学元件,由透明物质制成。
2、透镜的两个表面至少一个是球面的一部分。
3、透镜的光心与主光轴。
主光轴:透镜上通过两个球心的直线叫做主光轴。
光心(O):每个透镜上主光轴上都有一个特殊的点,凡是通过该点的光,其传播方向不改变,这个点叫做光心。
二、透镜对光的作用1、凸透镜对光的作用凸透镜对光有会聚作用,凸透镜又叫做会聚透镜。
2、凸透镜的焦点和焦距焦点(F):平行于主轴的平行光通过凸透镜后会聚于一点。
焦距(f):焦点到光心的距离。
小结:凸透镜有两个实焦点,两侧的两个焦距相等。
小结:凸透镜的焦距越小,透镜对光的会聚作用越强。
小结:光路可逆。
小结(特殊光线):焦点处发出的一束光透过凸透镜后可以形成平行光。
小结:凸透镜对所有光都起会聚作用,但会聚后的光线不一定相交。
3、凹透镜对光的作用凹透镜对光有发散作用,凹透镜又叫做发散透镜。
4、凹透镜的焦点和焦距平行于主光轴的光线通过凹透镜后发散,发散光线的反向延长线相交于主光轴上,它不是实际光线的会聚点,叫虚焦点(F)。
小结:凹透镜有两个虚焦点。
小结:光路可逆。
小结(特殊光线):延长线在焦点处的一束光透过凹透镜后可以形成平行光。
小结:凹透镜对所有光都起发散作用,但发散后的光线不一定都散开。
三、透镜的原理通过三棱镜的光线经三棱镜两次折射后向三棱镜底部偏折。
四、透镜的三条特殊光线1.通过光心的光线:传播方向不改变。
2.平行于主光轴的光线:经凸透镜折射后通过焦点,经凹透镜折射后发散,发散光线的反向延长线通过虚焦点。
3.经过凸透镜焦点的光线:折射后平行于主光轴射出。
对着凹透镜异侧虚焦点入射的光线:折射后平行于主光轴射出。
第2节生活中的透镜一、照相机1、主要构造(1)镜头:相当于凸透镜。
(2)胶片:相当于光屏。
(3)调节控制系统:①取景窗:观察所拍景物;②光圈环:控制进入镜头的光的多少;③快门:控制曝光时间。
④调焦环:调节镜头到胶片间的距离,即像距。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
眼镜光学
1
球 面 透 镜:前后表面均为球面或一面为球面,另一面为平 面的透镜. 凸透镜(convex lens )使光线会聚 凹透镜(concave lens )使光线发散
眼镜光学
2
薄透镜的焦点
眼镜光学
3
屈光力:透镜使光束聚散度改变的程度称为透镜的镜 度或屈光力,用F来表示.
tF1 e' 7.23m m nF
放大率
• 物经透镜成像后,像与物的大小之比称为 放大率 • 放大率一般有横向线性放大率、轴向放大 率和角放大率三种,轴向放大率和角放大 率与眼镜关系较小,所以眼镜光学中所指 的放大率均指横向线性放大率。
眼镜光学
18
1、横向线性放大率 就是像高比物高,横 向放大率是随着物体位置而定的,某一 个放大率只对应一个物体的位置
Fv 眼镜的形式放大率= F 1 t t Fv (1 Fa ) 1 Fa n n Fv
眼镜光学
26
3、眼镜总的放大率 是屈光力放大率和形式放大率的乘积
1 眼镜总的放大率= 1 dF
1 t 1 Fa n
眼镜光学
27
4、眼镜的相对放大率
非正视眼戴上矫正眼镜后,远方物体在 视网膜上成像的大小,和同一位置同一 物体在标准正视模型眼眼底所成的像的 大小之比,称为眼镜的相对放大率
眼镜光学 5
问:-3.00D的薄 透镜第一焦距, 第二焦距各是多 少?
1 1 解:f 2 33.3cm F 3.00 1 1 而 f1 =- 33.3cm F 3.00 凸透镜:焦距 f 0, 屈光力 F 0 第一第二焦点为虚焦点
凹透镜:焦距 f 0, 屈光力 F 0
i f 2 Z '2 2 2 o Z f'
眼镜光学
i V 2 o U'
2
3、角放大率 当物位于无穷远时,物像 大小之比常以角放大率来表示。角放大 率即像在出射光瞳中心的夹角和物在入 射光瞳中心的夹角之比,即
i tan ' o tan
眼镜光学
21
例3-25:一个+5.
透镜的面屈光力
注意:
眼镜光学
10
眼镜光学
11
薄透镜的前后两个表面,屈光力分别为: 前表面 :F1=(n2-n1)/r1 后表面: F2=(n1-n2)/r2 1 1 总屈光力: F F2 F1 n 2 n1) ( ( ) r1 r2
通常介质1是空气,n1=1 可得:
F2= -5.00DS
t=9mm
n=1.5
t 主点屈光力:F F1 F2 F1 F2 20.75 D n F FVP 20.15 D 前顶点屈光力: t 1 F2 n
F BVP 24.41D t 后顶点屈光力: 1 F1 n
tF2 e 1.45m m nF
眼镜光学
12
眼镜光学
13
眼镜光学
14
厚透镜
薄透镜与厚透镜的区别 : 例:处方为 +10.00DS,在制作这个透镜的时候 将前表面做成+13.00DS,后表面做成-3.00DS,中 心厚度为8mm,材料的折射率为1.523。 如果将这块透镜认定为薄透镜,则薄透镜的 后顶点屈光力为+13.00+(-3.00)=+10.00DS, 但是实际测得这块透镜的后顶点屈光力为 +10.95DS,这样的误差很难被戴镜者接受,这样 如果后顶点屈光力与主点屈光力的误差大于 0.125D,戴镜者不能接受这个误差的透镜叫做厚 透镜
1
2
眼镜光学 24
眼镜的放大率
1、眼镜的屈光力放大率
• 患者戴上矫正眼镜以后,由于屈光力的 不同而导致在视网膜上成像的放大或缩 小称之为屈光力放大率 • 和矫正眼镜的性质、屈光力、镜眼距有 关
眼镜的屈光力放大倍率 =
1 1 dF
眼镜光学 25
2、眼镜的形式放大率 同一屈光力的镜片因为形式的不同放大 率也是不一样,前面所讲的屈光力,都 是指镜片的主点屈光力,但是矫正眼镜 用的都是后顶点屈光力
物聚散度 U =1/u (光束进 入透镜聚散度) 透镜屈光力F (透镜改变 光束聚散度的能力) 像聚散度 V =1/v (光束离 开透镜聚散度)
平行光入射:U=0, 可得V=F+U=F=1/v
同理可得:
眼镜光学 4
问:+4.00D 的薄透镜第 一焦距,第 二焦距各是 多少?
1 f2 0.25m 4.00 1 f1 0.25m 4.00
眼镜光学
29
• 空镜圈与眼球旋转中心的夹角称作视觉视 场
• 透镜的有效直径与眼球旋转中心共轭点的 夹角称为实际视场 • 视觉视场仅与镜框的大小和位置有关,而 实际视场除与镜片的大小、位置有关外, 还与镜片的屈光力有关。
眼镜光学
30
令:实际视场=2 视觉视场=2` 镜片半径=y 透镜至眼转动 中心距离(R)=s` 透镜至转动中心像的距离(R`)=s y yS ( y以mm为单位,S聚散度) 因为实际视场=2 tan s 1000
眼镜光学 15
后顶点屈光力BVP: 前顶点屈光力FVP:
透镜后表面顶点到第二焦点距离倒数 透镜前表面顶点到第一焦点距离倒数
眼镜光学
16
例3-24:透镜的前表面屈光力是+25.00DS,后表面屈光力是-5.00DS, 中心厚度为9mm,折射率为1.5,求透镜的每个基点的位置 ?
解:题中已知:F1=+25.00DS
' 41.99
33
视觉视场=83.97°
眼镜光学
实际视场:
y (40 F ) 22.5 35 tan 0.788 1000 1000
实际视场=76.44° 视觉视场:
38.22
y 40 22.5 40 tan ' 0.9 1000 1000
' 41.99
32
视觉视场=83.97 °
眼镜光学
因S=入射光束的聚散度,根据聚散度公式: y ( S ' F ) tan 1000 s`的平均值为+25mm,所以S`=+40.00D tan
眼镜光学
S S ' F
y (40 F ) 1000
31
例3-26:一个圆形镜圈的直径为45mm,装配上一 个+5.00DS的镜片,镜片距离眼球旋转中心的距 离为25mm,求实际视场和视觉视场是多少?
U ' V F 5 1 4D
眼镜光学
1 l ' 25cm 4
22
则横向线性放大率为:
i V 1 0.25 o U' 4
i l' 25 0.25 o l 100
i f 20 0.25 o Z 80
三种放大率之间的关系 在理想的光学系统中,同一对共轭面上的 三种放大率之间的关系为 :
i l' o l
i f Z' o Z f'
i V o U'
2、轴向放大率 轴向放大率等于横向放大率的平方,这表 明对于一个有一定轴向长度的物体,在轴 的方向上和垂直轴向上放大是不等的,会 发生变形(当轴向放大率等于+或-1时例 外)
2
i l' 2 o l
眼镜光学
7
球镜的联合
考虑: 如果 -1.50 DS/-1.00 Dc X180 联合成新透镜水平和竖直方向 上屈光度各为多少? 90度方向上-2.50;180度方向上-1.50
眼镜光学
8
球镜的识别
• 测量法:用焦度计对透镜屈光参数进行测量,得 到屈光性质。 • 薄厚法:凸透镜中间厚,边缘薄;凹透镜中间薄, 边缘厚。 • 影像法:透过凸透镜看物体,使物体变大;透过 凹透镜看物体,使物体变小。 • 像移法:透过上下左右移动的透镜看物体,凹透镜像随 透镜同向移动,称为顺动;凸透镜像随透镜反方向移动, 称为逆动。
非正视眼戴矫正眼镜后 的视网膜像大小 f z Fm 相对放大率= = 正视模型眼的视网膜像 大小 f m Fz
眼镜光学
28
视场
眼镜片的视场(视野),按通俗的话来说就是 通过镜片所能看到的空间范围,一般用角度来表 示,也就是通过透镜能看到的最大角度范围。假 设某人戴一副空镜架,其视场范围即为镜框的边 缘与眼球旋转中心的夹角(如图a)。但安装镜 片后,经过透镜折射后的光锥就有变化,通过正 镜片,光锥缩小(图b),通过负镜片,光锥扩 大(图c)。
于透镜前100cm处,求像的位置及放大率。
解:已知l=-100cm f= -20cm f′=20cm
f f' 1 l l'
20 20 1 100 l '
l′= 25cm Z′=5cm
Z 100 (20) 80cm
(80)Z ' (20) 20
1 V 1D 1
例3-27:如果将例3-26中的+5.00DS透镜换成-5.00DS的 透镜,其他已知条件不变,求视觉视场和实际视场。
实际视场:
y (40 F ) 22.5 45 tan 1.0125 1000 1000
实际视场=90.71°
45.36
视觉视场:
y 40 tan ' 22.5 40 0.9 1000
一般取 f f 2
1 简称透镜的焦距,可得F f 眼镜光学
6
透镜屈光力和处方的规范写法
表示镜片屈光力度数一般保留小数点后两位,间距通 常1/4D,即+0.25D、 +0. 50D …. 单位D, 球镜(sphere),所以用DS表示球镜度数 柱镜(cylinder),所以用Dc表示柱镜度数, 轴位(axis)用X来表示 联合时用“/ ”或者 连接。 如: -1.50 DS/-1.00 Dc X180
