分层随机抽样及其excel分析
用EXCEL数据分析工具进行抽样

用EXCEL数据分析工具进行抽样用EXCEL数据分析工具进行抽样有二种方法:第一种:举例:EXCEL表格中一列有3000多个数据,我想在这3000多个数据中随机抽取200个出来,3000多个都是文字的数据在一列里面,要随机抽取出200个出来要怎么做呢?而且要多次可以取随机的,就是200个随机数可以快捷的取多次……。
解答:数据设在a列公式c1 =rand() ,下拉至c3000,【c列可隐藏起来】(有多少数据就下拉几个)公式b1 =index(a:a,rank(c1,c:c)),下拉至b200 (抽几个就下拉几个) F9 即可多次抽取。
第二种:离如何在EXCEL进行抽样,主要利用EXCEL里的加载项“数据分析”进行介绍。
如果你的EXCEL尚未安装数据分析,请依次选择“工具”-“加载宏”,在安装光盘的支持下加载“数据分析库”。
加载成功后,可以在工具的下拉菜单中看到“数据分析”选项。
2007则需要在“EXCEL选项”--“加载项”--“分析工具库”进行加载。
操作步骤:1. 打存放需要抽样数据的EXCEL表格,本例采用手机号码进行介绍。
2. 选择“工具”—“数据分析”—“抽样”后,出现对话框,依次选择:输入区域:把原始总体数据放在此区域中,数据类型不限,数值型或者文本型均可;抽样方法:有间隔和随机两种•间隔抽样需要输入周期间隔,输入区域中位于间隔点处的数值以及此后每一个间隔点处的数值将被复制到输出列中。
当到达输入区域的末尾时,抽样将停止;•随机抽样是指直接输入样本数,电脑自行进行抽样,不用受间隔的规律限制。
样本数:在此输入需要在输出列中显示需要随机抽取总体中数据的个数。
每个数值是从输入区域中的随机位置上抽取出来的,请注意:任何数值都可以被多次抽取!所以在样本中的数据一般都会有重复现象,解决此问题有待于EXCEL软件的完善。
目前我们可以使用“高级筛选”功能进行无重复数据筛选才可得出最终数据,所以抽样所得数据实际上会有可能小于所需数量。
1000720101抽样实验四

1.设定学号顺序,单击B8单元格,在编辑栏输入“1”,选中B8单元格,单击【编辑】/【填充】/【序列】,出现【序项组中的【等差数列】单选按钮,在【步长值】文本框中输入“1”,在【终止值】文本框中输入“844”,完成后单击【完成】按钮。
2.运用抽样宏工具对女生组进行简单随机抽样,单击【工具】/【数据分析】,在【数据分析】对话框中选择【抽样】,单击【确定】按钮。
在【抽样】对话框中,单击【输入区域】后的折叠按钮,选择单元格区域,选择【抽样方法】中的【随机】,将【样本数】设为“10”,在【输出选项】中单击选中【输出区域】单选按钮,单击【输出区域】后的折叠按钮,选择E10单元格,完成后单击【确定】按钮。
附录I 实验报告的一般格式
桂林电子科技大学
数学与计算科学学院实验报告
实验室: 实验日期:2012年 12月9日
院(系)
数学与计算科学
学号
1000720101
姓名
陈斯斯
成绩
课程
名称
抽样调查实验
实验项目
名称
分层抽样
一 ,实验目的
学习利用EXCEL进行分层抽样。
二,实验原理
掌握利用EXCEL进行分层抽样的方法。
2
0
20
10
0
10
30
20
.
2
420
20
35
10
50
0
40
50
10
20
20
3
168
0
20
0
30
30
50
40
0
30
0
(1)请估计该小区居民户购买彩票的平均支出,给出估计的标准差,并与简单随机抽样进行精度比较。
抽样调查-分层抽样实验报告

实验报告实验思考题:1、某调查员欲从某大学所有学生中抽样调查学生平均生活费支出情况,假设该调查员已经完成了抽样,并获得样本情况(见样本文件),请根据此样本分别按性别、家庭所在地分层,并计算各层的样本量、平均生活费支出、生活费支出的方差及标准差。
(1)先对数据按照家庭所在地进行排序:【数据】→【排序】,选择“家庭所在地”(2)再对数据进行分类汇总:【数据】→【分类汇总】,“分类字段”选择“家庭所在地”,“汇总方式”选择“平均值”,“选定汇总项”选择“平均月生活费”,在对话框下方选择“汇总结果显示在数据下方”;再做两次分类汇总,“汇总方式”分别选择“计数”和“标准偏差”。
最后得到表1-1所示结果:表1-1家庭所在地平均月生活费大型城市平均值614.5348837大型城市计数86大型城市标准偏差300.0849173乡镇地区平均值529.4117647乡镇地区计数68乡镇地区标准偏差219.0950339中小城市平均值618.6440678中小城市计数118中小城市标准偏差202.5264159总计平均值595.0367647总计数272总计标准偏差243.4439223(3)在SPSS软件中得出的计算结果:选择————,然后在出现的对话框中分别在“Dependent list”框中选入“家庭所在地”,在“IndependentList”框中选入“平均月生活费”,得到如表1-2所示结果:表1-2Report平均月生活费家庭所在地Mean NStd. Deviation大型城市614.5386300.085乡镇地区529.4168219.095中小城市618.64118202.526Total595.04272243.444选择——,在出现的对话框中选择“function”选择估计量,得到如图1-2所示结果:图1-1图1-2选择————,出现如下图所示对话框,并按照下图1-3中所选项进行操作:得到如下图表的结果:Case Processing Summary家庭所在地CasesValid Missing TotalNPercent NPercent NPercent平均月生活费大型城市86100.0%0.0%86100.0%乡镇地区68100.0%0.0%68100.0%中小城市118100.0%0.0%118100.0%Descriptives家庭所在地Statis Std.for Mean5% Trimmed Mean518.46Median500.00Variance48002.634Std. Deviation219.095Minimum200Maximum1000Range800Interquartile Range200.00Skewness.996.291Kurtosis.172.574中小城市Mean618.6418.64495% Confidence Interval for Mean Lower Bound581.72 Upper Bound655.575% Trimmed Mean612.34 Median600.00 Variance41016.949Std. Deviation202.526 Minimum200 Maximum1200Range1000 Interquartile Range300.00 Skewness.686.223 Kurtosis.168.4421186886N =家庭所在地中小城市乡镇地区大型城市平均月生活费300020001000-10001991249789867740352462、 教材129页第3.3题层 样本1 10 102 0 20 10 0 10 30 20 220351050405010202030200303050400300(1)数据结构、运用Excel的计算步骤及结果如下:样本11010202010010302203510500405010203020030305040030m844156.70.379752.545.965 2.87769.472117241249.9404415.35520.06789.472123.077681.0483∑N S Wh h/20.29614总样本量 比例分配 185.907 奈曼分配175.381比例分配 奈曼分配奈曼分配层权 n1 56.3888 33.659 w1 0.192 n2 92.5129 98.853 w20.564 n3 37.0051 42.869 w30.244sum185.907175.381第h 层的层权:NN W hh =第h 层的样本均值:∑==hn i hihh yn y 11第h 层的样本方差: )1/()(122--=∑=h n i h hi hn y y s h总体均值方差:h 2Lh hh 2h n 1W )(ˆ)(s f y V Y V st ∑-===9.472 0483.1)96.10678.20*%10()()(222/==⋅=αu Y r y V st 下面计算两种分配方法的样本量及每层要抽的样本量:1.比例分配:比例分配的层权为:h h W w =故:n w n ⨯=21=56.3888 取整得1n =57n w n ⨯=22=92.5129 取整得2n =93 n w n ⨯=33=37.0051 取整得3n =382.奈曼分配:奈曼分配的层权为:∑==Lh hh h h h S W S W w 1/故:n w n ⨯=21=33.659 取整得1n =34n w n ⨯=22=98.853 取整得2n =99 n w n ⨯=33=42.869 取整得3n =43(2)在SPSS 中的计算均值与方差的结果如下:DescriptivesIntervalfor MeanBound5% Trimmed Mean25.00Median20.00Variance294.444Std. Deviation17.159Minimum0Maximum50Range50InterquartileRange32.50Skewness.330.687Kurtosis-1.001 1.334 3样本Mean20.00 5.96395% Confiden ce Interval for Mean LowerBound6.51 UpperBound33.495% Trimmed Mean19.44 Median25.003、教材130页第3.4题Wh ah0.18270.21280.14270.09260.16280.2229sum1165 5.50.4522220.17820.50.0003970.25838总体比例估计0.924比例分配层权总体比例估计方差0.000396981w10.18总体比例估计标准差0.019924378w20.21V 2.60308E-05w30.14w40.09w50.16总样本量w60.22比例分配 2662.655644 奈曼分配 2564.651673比例分配奈曼分配 奈曼分配层权 n1 479.278016 535.9991 w1 0.208995 n2 559.1576853 519.9509 w2 0.202737 n3 372.7717902 416.8882 w3 0.162552 n4 239.639008 303.6744 w4 0.118408 n5 426.0249031 396.1531 w5 0.154467 n6 585.7842418 391.9861 w60.152842SUM 2662.655644 2564.6521公式:(1)总体比例P 的简单估计量:P Y =,h h P Y =,h p y st =.按照总体均值估计量的公式,可推出总体比例(成数)P的估计量为:h hhh h h ˆˆp W P W P LLst ∑∑===0.924(2)总体比例P 的方差为∑---=Lst n p p f W P V hh h h h 2h 1)1()1()ˆ(ˆ=∑---Lhh h h h h h 21)1()(1n p p n N NN(3)第h 层的样本方差为:h h h h hhh q p def q p n n S 12-=(4)样本总量:若h N 较大,则2h S ≈)1(h h P P -,此时可进一步求出估计P 时对给定的分配形式(h h nw n =)有:∑∑-+-=Lhh h h hh h h P P W N V w P P W n )1(1)1(2计算抽样的样本量:在此题中,总体数量N 非常大,故,0)1(11≈-∑=Lh hhhpP W N,因此:由公式(4)得:(比例分配的层权为:h h W w =)各层的样本量为:n w n ⨯=21=479.278016 取整得1n =480n w n ⨯=22=559.1576853 取整得2n =560 n w n ⨯=33=372.7717902 取整得3n =373=⨯=n w n 44239.639008 取整得4n =240 =⨯=n w n 55426.0249031 取整得5n =427 =⨯=n w n 66585.7842418 取整得6n =586(奈曼分配的层权为:∑==Lh h h h h h S W S W w 1/)各层的样本量为:n w n ⨯=21=535.9991 取整得1n =536n w n ⨯=22=519.9509 取整得2n =520 n w n ⨯=33=416.8882 取整得3n =417=⨯=n w n 44303.6744 取整得4n =304 =⨯=n w n 55396.1531 取整得5n =397 =⨯=n w n 66391.9861 取整得6n =392。
利用EXCEL表格进行随机抽样

第二题2.使用RAND函数进行抽样:某公司需要从100名员工中随机抽取10名参加义务植树活动。
现在需要通过EXCEL选择员工的编号,并对员工的编号进行排序,写出结果:(小题解题主要步骤)工具—加载宏—分析数据库,如下图然后点击确定,数据分析选项就会出现在菜单栏的工具下,点击插入—函数—Rand函数,如下图:点击确定,在函数栏输入=RAND()*(100-1)+1,确定即可得一个数值,如选中单元格,右键单击,选择设置单元格格式,如下既得一个随机数值002,拖动填充柄,得到10个数值,再选中者10个数,选择复制,再右键单击,选择选择性粘贴—数值,如下确定,然后排序一下就可以了.3.使用RANDBETWEEN函数进行抽样:某体育彩票进行抽奖,需要从标号00001~99999的消费者中随机抽取10位中奖者,试采用RANDBETWEEN函数随机选中观众的号码,写出结果:(小题解题步骤)插入—函数—RANDBETWEEN,如下点击确定,在出现的参考函数编辑器中输入如下数据,如图:点击确定,右键单击单元格格式步骤如上一题所示,确定.4.利用“随机发生器”进行抽样:某体育彩票进行抽奖,需要从标号00001~99999的消费者中随机抽取10位中奖者,试采用随机发生器随机选中观众的号码,并对号码进行排序,写出结果:(4小题解题步骤:)工具—数据分析—随机数发生器,确定,在弹出的编辑器中输入如下数据:点击输出区域右边的指定10个单元格,确定即可,再将单元格格式设置一下,将得出的10个数值固定,和以上题相同: 确定,排序即可.5.利用抽样宏进行抽样:某图书进行推销活动,从购物清单标号001-100的消费中随机抽取10为幸运者免费赠送作何编号作为签名的图书,使用抽样宏随机抽取出幸运消费则的编号:(5小题解题步骤)先做一个表,利用填充柄会很快.如下图工具—数据分析—抽样:确定.如下图;输入区域为有100个数字的单元格(用鼠标选中即可),输出区域为任意的10个单元格,如图:确定,产生10个随机数,再固定为数值设置数字格式:确定,在排序就可以了.6.利用等距抽样进行抽样:某城市有私营企业300个,拟定样本量为7个,利用等距抽样进行企业营销状况调查,写出抽样结果:(6小题解题步骤)如图,输入一下信息:B3单元格即可得值将B3中的数值调整为整数,利用Round函数: 确定,在弹出的编辑器中进行编辑,结果如下:既得整数43.接下来用ROUNDBETWEEN函数从1-43中选出一个数,作为第一个随机数, 插入—函数—ROUNDBETWEEN如图:确定,在弹出的编辑器中输入一下信息:确定,既得第一个随机数,固定得出的第一个数为数值(方法同上) 在B6单元格输入=B5+B4,如图:将光标放在B4处,按F4键,则出现按回车键,则计算出第一个数,用填充柄进行填充得出七个数设置单元格格式,如图:确定,就可以了.如图:完成.。
用excel进行随机抽样
用excel进行随机抽样
使用excel进行抽样,首先要对各总体单位进行编号,编号可以按照随机原则,也可以按照有关标志或无关标志进行排队,完成编号后,将编号输入工作表中。
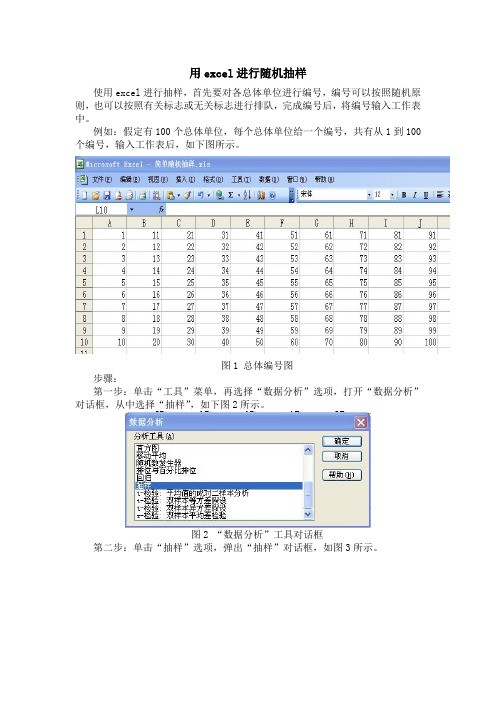
例如:假定有100个总体单位,每个总体单位给一个编号,共有从1到100个编号,输入工作表后,如下图所示。
图1 总体编号图
步骤:
第一步:单击“工具”菜单,再选择“数据分析”选项,打开“数据分析”对话框,从中选择“抽样”,如下图2所示。
图2 “数据分析”工具对话框
第二步:单击“抽样”选项,弹出“抽样”对话框,如图3所示。
图3 抽样选项对话框
第三步:在输入区域框中输入总体单位编号所在的单元格区域,如果输入区域的第一行或第一列为标志项(横行标题或纵列标题),可以选中“标志”复选框。
第四步:在抽样方法项下,有周期和随机两种抽样模式:
“周期”模式即所谓的等距抽样。
“随机”模式适用于纯随机抽样、分层抽样、整群抽样和多阶段抽样。
第五步:指定输出区域,单击“确定”后,即可得到抽样结果。
分层抽样

分层抽样————————————————————————————————作者: ————————————————————————————————日期:ﻩ分层抽样抽样技术作为现代统计学科体系的重要组成部分,被广泛运用到社会实践当中。
自从1895年挪威首任中央统计局局长凯尔在伯尔尼第五届国际统计学会会议上提出所谓“代表性调查”的抽样方法以来,经过100多年的理论探讨和时间积累,抽样理论更加科学,抽样技术日臻完善。
抽样又称取样。
其原理是从研究的全部样品中抽取一部分样品单位。
从被抽取样品单位的分析、研究结果来估计和推断全部样品特性,是科学实验、质量检验、社会调查普遍采用的一种经济有效的工作和研究方法。
基本的抽样技术包括简单随机抽样,系统抽样,分层抽样,多阶段抽样等。
在实际的抽样调查中我们常常会根据调查成本,调查规模等结合运用各种抽样方法进行实践。
分层抽样是通过对总体单位进行分类,即分成若干子总体,子总体之间比较相似,使每一个字总体的方差变小,这样只需要在子总体中抽取少量样本单位,就能很好地代表子总体的特征,从而提高对整个总体估计的精度。
分层抽样需要事先知道各层权重,但在现实情况下有些资料无法提前预知。
这时我们可以先从总体中抽取一个大的初始样本,从而获得有关的辅助信息,然后再从初始样本中抽取一个字样本,这种方法就是双重抽样。
其定义为,当简单性状与复杂性状存在关系时可用抽取简单性状来间接估计复杂性状的抽样方法。
结合分层抽样的双重抽样方法即为分层的双重抽样。
分层抽样,的主要特点就是可以提高估计精度,它不但能对总体进行估计。
同时可以对各层子总体进行估计。
如此便于实际中抽样的组织和实施。
下面我们就分层抽样方法展开讨论,运用实例分析进行比较。
一、分层抽样的原理简介在抽样之前,先将总体N 个单位划分成L个互不重复的子总体,每个子总体成为层,他们的大小分别为L N N N N ...,,,321,这L 层构成整个总体(1lh N Nh ==∑)。
如何利用Excel工具进行抽样

3
罐
≥囊 S
~
醴
魏
嚣
4
圣
1 5
1 6
o
p
擎
i
i
4
" ;
q s
2
l
黪
5
l 8
3
i
_
j
5
5
2 o
§
t
s
三、 分层抽样 , 指先将总体 的单位按某种 特征 分为若
干次级总体( )然 后再从每一层 内进 行单纯随机抽样 , 层 ,
随机化 。然后按照事前确 定的样本数量 , 按照连续的顺序 从中截 取。这里需要 注意 的是 , 由于 rn ( 函数每次计算 ad )
样, 因此使用起来不够灵活 。
工作表时都 将返回一个新 的随机实数 ,因此应 当在 编辑
其 实 , 抽样过程 中 , 完全可 以采 用 Ecl 在 我们 xe 函数 栏 中输入 “R N (” , = A D )后 保持编辑状 态 , 然后按 F 或者 9
3
5
3。
驺
l
2
f
霉 2
巷 a
i
霉
2
2
8
9
I l
h
i
k
3
唾
j 童
8i
翻 密
巍
毽
瓤
2
S
一 l 2 l 2 _源自薹 ii 1 2i  ̄ i
魏 3
l 3
1 4
I t
与其他 内置功能的结合来 实现多种抽样方法 。
一
分层随机化excel

分层随机化excel分层随机化是一种常用的实验设计方法,它能够有效地减小实验误差,提高实验结果的可靠性和可信度。
本文将介绍分层随机化的概念、原理和应用,并探讨其在Excel中的实现方式。
一、概念和原理分层随机化是一种将被试对象按照一定的特征或条件划分为不同的层次,然后在每个层次内进行随机分组的方法。
通过这种方式,可以保证实验组和对照组在不同层次的特征上保持一致,从而减小实验结果的偏差。
分层随机化的原理是基于统计学中的随机分组原则,即通过随机的方式将被试对象分配到不同的实验组和对照组中,以消除被试对象之间的差异性。
而分层随机化则是在随机分组的基础上,根据被试对象的不同特征或条件进行层次划分,以确保实验组和对照组在这些特征上具有相似性。
二、应用场景分层随机化广泛应用于各个领域的实验设计中。
例如,在医学研究中,可以将病人按照年龄、性别、病情严重程度等特征进行分层,然后在每个层次内进行随机分组,以比较不同治疗方法的疗效差异;在教育研究中,可以将学生按照学习成绩、学习动机、学习方法等特征进行分层,然后在每个层次内进行随机分组,以评估不同教学方法的效果。
三、在Excel中实现分层随机化在Excel中实现分层随机化并不复杂。
以下是一种常用的实现方式:1. 首先,将被试对象按照特征或条件进行层次划分,例如将学生按照年级进行划分,每个年级为一个层次。
2. 在Excel中,创建一个包含被试对象和其对应特征的数据表格。
每一列代表一个特征,每一行代表一个被试对象。
3. 在Excel中,使用随机数函数(如RAND())为每个被试对象生成一个随机数,并将其排序。
4. 将排序后的被试对象按照特征或条件重新分组,确保每个实验组和对照组在不同层次上的特征分布相似。
5. 最后,根据分组结果,将实验组和对照组的标识添加到Excel表格中,以便后续数据分析和结果统计。
四、总结分层随机化是一种有效的实验设计方法,可以提高实验结果的可靠性和可信度。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
课程设计任务书
案例:某公司要估计某地家用电器的潜在用户。
这种商品的消费同居民收入水平相关,因而以家庭年收入为分层基础。
假定某地居民为1,000,000户,已确定样本数为1,000户,家庭年收入分10,000元以下,10,000——30,000元;30,000——60,000元,60,000元以上四层,其中收入在10,000元以下家庭户为180,000户,收入在10,000——30,000元家庭户为350,000户,收入在30,000——60,000元家庭户为3000,000户,收入在60,000元以下家庭户为170,000户,若采取分层比例抽样法,如何抽样?
下面针对案例对分层随机抽样进行大致说明。
一.分层随机抽样定义:
分层抽样也称类型抽样或分类抽样,就是将总体单位按一定标准(调研对象的属性、特征等)分组,然后在各个类型组中用纯随机抽样方式或其他抽样方式抽取样本单位,而不是在总体中直接抽取样本单位。
二.注意事项:
分层抽样必须注意以下问题:第一,必须有清楚的分层界限,在划分时不致发生混淆;第二,必须知道各层中的单位数目和比例;第三,分层的数目不宜太多,否则将失去分层的特征,不便在每层中抽样。
三.分层抽样步骤:
分层抽样的步骤包括:
(1)确认目标总体。
(2)决定样本数。
(3)决定分层标志。
(4)将总体按照分层标志分成若干类,其中每一类称为一层。
(5)在每一层中随机抽取出足够的样本。
四.具体做法及例子说明:
分层抽样的具体做法有以下两种:
1.等比例分层抽样。
这种抽样法就是按照各层中样本单位的数目占总体单位数目的比例分配各层的样本数量。
[例]某教授对甲大学的学生消费倾向产生了兴趣,想对全校学生做抽样调查,总体有5 000人,欲抽样500人,则:
总体样本
一年级 2 000人一年级200人
二年级 1 500人二年级150人
三年级 1 000人三年级100人
四年级500人四年级50人
2.不等比例分层抽样,又称分层最佳抽样。
这种抽样法不按各层中样本单位数占总体单位数的比例分配各层样本数,而是根据各层的标准差的大小来调整各层样本数目。
该方法既考虑了各层在总体中所占比重的大小,又考虑了各层标准差的差异程度,有利于降低各层的差异,以提高样本的可信程度,故也可将不等比例分层抽样称为分层信任程度抽样。
[例]某公司要调研某地家用电器产品的潜在用户,这种产品的消费同居民收入水平有关,因
此以家庭收入为分层基础。
假定该地居民户即总体单位数为20 000户,已确定调研样本数为200户。
家庭收入分高、中、低三层,其中高档收入家庭为2 000户,占总体单位数的比重为10%;中等收入家庭为6 000户,占总体单位数的30%;低等收入家庭为12 000户,占总体单位数的60%。
现又假定各层样本标准差为:高档收入家庭是300元,中等收入家庭是200元,低等收入家庭是50元。
现要求根据分层最佳抽样法,确定各收入层家庭应抽取的户数各为多少? 公式n Si Ni Si Ni ⨯⨯⨯∑
Ni 为i 层调查单位总数;ni 为i 层应抽的样本数目;si 为i 层调查单位标准差
为了便于观察,列表1如下。
表1 调研单位数与样本标准差乘积计算表
家庭收入分层 各层调研单位数
(潜在用户数) 各层的样本标准差 乘积 样本单位数
高 2 000 300 600 000 200×600 000÷2 400 000=50
中 6 000 200 1 200 000 200×1200000÷2400 000=100
低 12 000 50 600 000 200×600 000÷2 400 000=50
合计20 000 — 2 400 000 —
如果根据等比例分层抽样的话,那么,高档收入家庭的分层样本数为20户(200×10%);中等收入家庭的分层样本数为60户(200×30%);低等收入家庭的分层样本数为120户(200 ×60%)。
将前后两种方法抽取的各层样本数做个对比,不难看出,相比于等比例分层抽样法,根据分层最佳抽样法抽取样本,则高档收入家庭的分层样本数增加了30户,中等收入家庭的分层样本数增加了40户;低等收入家庭的分层样本数则减少了70户。
由于购买家用电器同家庭收入水平是成正比例变动的,所以,增加高、中档层的样本数,相应减少低档层的样本数,将有利于提高抽样的准确性。
对案例开始进行分析:
由上述可知该案例中应采取不等比例抽样。
由公式可以求出:
收入在10000以下的家庭户的样本量应为(180000/1000000)*1000=180.
收入在10000—30000的家庭户的样本量应为(350000/1000000)*1000=350.
收入在30000—60000的家庭户的样本量应为(3000000/1000000)*1000=300.
收入在60000以上的家庭户的样本量应为(170000/1000000)*1000=170.
其分层比例抽样示意图如下所示:
分层比例抽样示意图总体
层
子样本样本
N 1000000
N1180000 N2 350000 N3300000 N4170000 n1180 n2350 n3300 n4170
n 1000
案例的excel实现过程:
因为在excel中,抽样功能是作为一种扩展功能存在的,所以在应用时就应该先加载分析工具库。
点击工具,选择加载宏,再选择分析工具库。
单击“工具”菜单,再选择“数据分析”选项,打开“数据分析”对话框,从中选择“抽样”。
单击“抽样”选项,弹出“抽样”对话框。
在输入区域框中输入总体单位编号所在的单元格区域,如果输入区域的第二行或第一列为标志项(横行标题或纵列标题),可以选中“标志”复选框。
在抽样方法项下,有周期和随机两种抽样模式:“周期”模式即所谓的等距抽样。
“随机”模式适用于纯随机抽样、分层抽样、整群抽样和多阶段抽样。
在这里我们选择随机选项。
指定输出区域,单击“确定”后,即可得到抽样结果。
点击确定,可得抽样结果,得到与计算相同数量的分层抽样。
