社会统计学第四章(一)
社会统计学-复习资料

社会统计学第一章导论一.社会统计学的产生与发展1。
国势学派:(又称记录学派或历史学派)对国家显著事迹的记录和比较。
“有名无实”代表人物:阿享瓦尔(1719—1772)“统计学之父"、康令(1606—1681)2.政治算术学派:对国家事项首创数字对比、分析。
“有实无名”代表人物:威廉 配第(1623-1687)“政治经济学之父”、格朗特(1620—1674)3。
数理统计学派:将法国古典概率论引入统计学,用纯数学的方法对社会现象进行研究。
代表人物:凯特勒(1796—1874)“现代统计学之父”4。
社会统计学派:研究社会现象代表人物:克尼斯(1821—1898)、梅尔(1841—1925)、恩格尔(1821—1896)二.社会统计学的对象和特点社会统计学:用于统计的一般原理,对社会各种静态结构和动态趋势进行定量描述或推断的一种方法与技术。
研究对象概括而言是指社会现象的数量方面。
社会统计学特点:就研究对象而言,社会统计学主要是从研究和反映一定经济基础之上的上层建筑方面去认识社会;就研究内容而言,社会统计需要对人们的态度、观念、行为进行度量,测量这些社会现象目前还没有一个精确而统一的尺度,只能以近似估算或词语表达等方式来代替;就调查方法而言,社会统计中,由于其研究对象所具有的特征,抽样调查更为常用。
三.社会统计学的方法1.大量观察法:就总体中足够多的单位进行调查和综合分析,用以反映社会总体的数量特征.2.大数定理:是随机现象出现的基本规律,一般意义为:观察过程中每次取得的结果可能不同(因为具有偶然性),但大量重复观察结果的平均值却几乎接近某个确定的数值。
3。
综合指标法4.统计推断法四.社会统计学的几个基本概念1.总体与单位总体:作为统计研究对象的,由许多具有共性的单位构成的整体。
单位:构成整体的每一个个体。
2.标志与变量,标志:总体的每个单位都具有许多属性和特性,说明总体单位属性或数量特征的名称在统计上称为标志。
社会统计学讲义

社会统计学讲义(卢淑华)第一章社会学研究与统计分析一、社会调查资料的特点(随时掌握)随机性、统计规律性;二、统计学的作用:为社会研究提供数据分析和推论的方法三、统计分析的作用及其前提。
四、统计分析方法的选择1 、全面调查和抽样调查的分析方法2 、单变量和多变量的统计分析方法五、不同变量层次的比较;定类、定序、定距、定比定义、数学特征、运算特性、涵盖关系、等第二章单变量统计描述分析一、统计图表,熟悉不同层次变量对应的分析图表,不能混淆。
尤其是直方图的意义。
二、标明组限与真实组限的换算,重要。
三、集中趋势测量法1 、定义、优缺点、注意事项;2 、众值:定义、计算公式、解释、运用,注意事项;3 、中位值:定义、计算公式(频数和比例两种公式)、解释、运用,注意事项;4 、均值:定义、计算公式(分组与加权)、解释、运用,注意事项;5 、众值、中位值和均值的关系及其相互比较,会用众值和中位值估算均值;四、离散趋势测量法1 、定义、优缺点、注意事项,与集中趋势的关系;2 、异众比例:定义、计算公式、解释、运用,注意事项;3 、质异指数:定义、计算公式、解释、运用,注意事项;4 、四分位差:定义、计算公式(频数和比例两种公式)、解释、运用,注意事项;要会举一反三,如求十分位差、以及根据数据求其在总体中的位置。
5 、方差及标准差:定义、计算公式(分组与加权)、解释、运用,注意事项;第三章概率一、概率:就是指随机现象发生的可能性大小。
随机现象具有不确定性和随机性。
二、概率的性质:1 、不可能事件的概率为O ;2 、必然事件的概率为1 ;3 、随机事件的概率在O 一1 之间;三、概率的计算方法:1 、古典法:计算等概率事件,P 一有效样本点数/样本空间数;2 、频率法:求随机事件在多次试验后的极限频率。
3 、概率是理论值,只有一个,频率是试验值,不同的试验有不同的频率。
四、概率的运算:会画文氏图1 、加法公式:两个或多个随机事件的求和概率‘2 、乘法公式:两个或多个随机时间共同发生的概率。
《统计学》第4章总体指标与相对指标

• (四)动态相对指标 • 动态相对指标又称发展速度,它是同类现象 在不同时间上变动程度的相对指标。其计算 公式为:
报告期指标数值 100% • 动态相对指标(%)= 基期指标数值
• 动态相对指标就是发展速度。
22
• 例:某大学在校生人数1990年10000人, 2000年为15000人,则该校在校生人数 2000年是1990年的150%。 • 即:动态相对指标= 15000 100% 150%
380 100 % 76% 单位成本的计划完成相对数= 500
32
(3)当计划任务数是比上期提高或降低百分 之几的形式出现时 • 计划完成程度(%)=
1 实际提高(降低)百分数 100% 1 计划提高(降低)百分数
• 该指标是用于考核社会经济现象的降低率、 增长率的计划完成程度。
25
[例3]某城市人口1000000人,零售商店3000个。则: • 该城市商业网点密度=
3000个 3个 / 千人 1000000人
• 计算结果表明,该城市每千人拥有3个商业网点, 指标数值越大,商业越发达,人民生活越方便, 表示强度越高,这是正指标。
26
• 如果把分子和分母对换,则: 1000000人 • 该城市商业网点密度= 3000个 333人 / 个 • 计算结果表明,该城市每个商业网点为333 人服务,指标数值越大,需要服务的人数 越多,商业欠发达,即表示强度越低,这 是逆指标。
• 相对指标的概念 把两个有联系的指标加 以对比而得到的统计指 标 • 相对指标的表现形式为 相对比率,相对指标也 通称为相对数。
相对指标的计量单位
无名 数 系数 或倍 数 成 百分 翻番 数 数或 千分 数
有名 将相对指标中的分子和 数 分母指标数值计量单位 同时使用的一种表示方 法,主要用于部分强度 相对指标。
《社会统计学》PPT课件(110页)

《社会统计学》PPT课件(110页)一、引言社会统计学是研究社会现象数量特征及其规律的学科,是社会学的重要组成部分。
本课件将带领大家深入了解社会统计学的定义、研究方法、数据来源以及在社会各个领域的应用。
二、社会统计学的定义社会统计学是一门应用统计学原理和方法,对社会现象进行数量分析和描述的学科。
它通过收集、整理、分析和解释社会数据,揭示社会现象的数量特征、变化规律和相互关系,为社会决策提供科学依据。
三、社会统计学的研究方法1. 调查研究法:通过问卷调查、访谈等方式,收集社会数据,了解社会现象的实际情况。
2. 实验研究法:在控制条件下,对研究对象进行实验,观察和记录实验结果,分析社会现象的因果关系。
3. 文献研究法:通过查阅相关文献,了解社会现象的历史、现状和发展趋势。
4. 案例研究法:选取具有代表性的社会现象,进行深入分析,揭示其内在规律。
5. 统计模型法:运用统计模型,对社会现象进行定量分析,预测社会现象的未来发展趋势。
四、社会统计学数据来源1. 政府统计部门:提供国家、地区和行业的社会经济数据。
2. 学术研究机构:发布学术研究报告,提供社会现象的定量分析结果。
3. 社会调查机构:开展社会调查,收集社会数据,为政府、企业和社会组织提供决策依据。
4. 新闻媒体:报道社会现象,提供社会数据的实时更新。
5. 公共图书馆和档案馆:保存历史文献,为研究社会现象提供数据支持。
五、社会统计学在社会领域的应用1. 社会经济领域:分析经济增长、就业、收入分配等社会经济现象,为国家制定经济发展政策提供依据。
3. 社会问题领域:分析社会问题,如贫困、犯罪、环境污染等,为解决社会问题提供科学依据。
4. 社会发展领域:研究社会发展规律,为推动社会进步提供理论支持。
5. 社会管理领域:分析社会管理现状,为提高社会管理水平提供数据支持。
社会统计学作为一门研究社会现象数量特征及其规律的学科,具有广泛的应用价值。
通过掌握社会统计学的定义、研究方法、数据来源及其在社会领域的应用,我们可以更好地了解社会现象,为政府、企业和社会组织提供决策依据,推动社会进步。
社会统计学基本公式及社会统计学复习整理及社会统计学复习题(有答案)
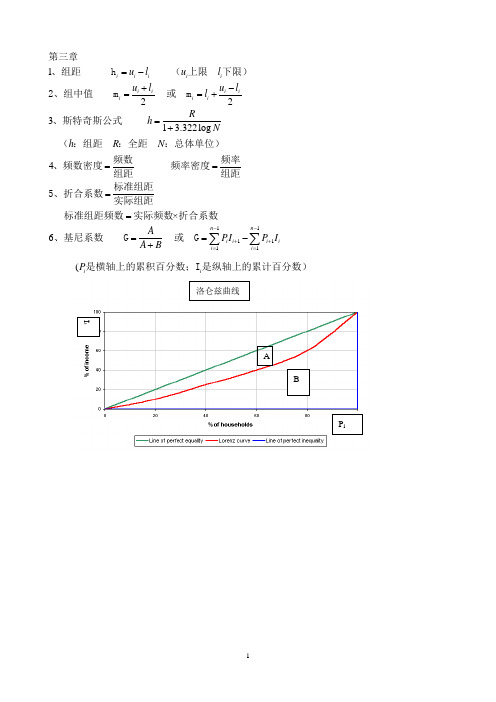
12231 3.322log 4×6i i i i i i i i i i i i u l u l u l u ll Rh N h R N AA B =-+-==+=+=====+第三章、组距 h (上限 下限)2、组中值 m 或 m 、斯特奇斯公式 (:组距 :全距 :总体单位)频数频率、频数密度 频率密度组距组距标准组距5、折合系数实际组距标准组距频数实际频数折合系数、基尼系数 G 111111n n i i i ii i PI P I --++===-∑∑ 或 G(i i P 是横轴上的累积百分数;I 是纵轴上的累计百分数)洛仑兹曲线P iI iAB1(2))(1)1221222d d X X X N fXX fN NN NN F L ==++-=+∑∑∑第四章1、算术平均数()()未分组资料 分组资料 注:对于单项数列分组,X即为变量值,若为组距式分组,则X为组中值 f:各组频数2、中位数(M 未分组资料 若N为奇数,则取第位上的变量值为中位数,若为偶数,则取第 位和第位上的两个变量值的平均数作为中位数()分组资料 M 112h h L : 2m m d m m m m m N F U f f f F F N---⨯=-⨯或 M 中位数所在组的下限: 中位数所在组的频数: 小于中位数所在组的各组频数之和(向上累计) h : 中位数所在组的组距 U: 中位数所在组的上限: 包括中位数所在组的各组频数之和(向上累计) 注: 中位数所在组由确定11111111133333334h :h 34h :N F l f F l f NF l f F l -=+⨯-=+⨯3、四分位数(1)第一四分位数 Q :小于第一四分位数所在组的各组累计频数(向上累计) 第一四分位数所在组的下限 :第一四分位数所在组的组距 :第一四分位数所在组的组距(2)第三四分位数 Q :小于第三四分位数所在组的各组累计频数(向上累计) 第三四分位数所在组的3311212h 1h :h 5o o o oo o f L L ∆=+⨯∆+∆∆∆下限 :第三四分位数所在组的组距 :第三四分位数所在组的组距4、众数(M )()未分组资料 先将所有数据顺序排列,观察某些变量值出现的次数最多,这些变量值就 是众数(2)分组资料 M 众数所在组的下限:众数所在组频数与前一组频数之差 :众数所在组频数与后一组频数之差 :众数所在组的组距、几何平均数11lg lg anti(lg )(2)1lg lg anti(lg )g g g g g gg g g X Nf X NX ========∑∑(M )()简单几何平均数 M 或 M M M 加权几何平均数M 或 M M M 注:若为组距式分组,则为组中值3112316)(1)111111...(2):312=23h h N h d o g h N Q Q NX X X X XNNf XX f X X -==++++==-≥≥-⋅∑∑、调和平均数(M 简单调和平均数(未分组) M 加权调和平均数(分组)M 注:若为组距式分组,为组中值 各组频数7、各种平均数的关系2M M M M 第五章、全距 R=X X 、四分位差 Q D、平均差=2=::X X Nf X XfX f X f -⋅-⋅∑∑(1)未分组资料 A D ()分组资料 A D 注:若为组距式分组,为组中值 各组频数4、标准差(S)(1)未分组资料(2)分组资料 注:若为组距式分组,为组中值 各组X X S-频数5、标准分 Z=社会统计学复习整理一、变量的测量层次61(2)37=1:83(o o oR R M M M o d o R X X SXN f f NNf X M X M X M S Sαα⋅⋅=-⋅=----==A D 、变异系数()全距系数 V =A D平均差系数 V =()标准差系数 V 、异众比率(非众数的频数与总体单位数的比值) V R 众数的频数、偏态系数())偏态=二、判断变量层次的技巧1.首先所有的变量都是定类变量。
社会统计学(第4章 数据的统计量描述)

三、离散性描述指标的比较
全距(四分位数) 全距(四分位数)
粗略、快捷,不稳定, 粗略、快捷,不稳定,不能用于有样本推论总体 用于定序、定距、 用于定序、定距、定比变量
标准差(方差) 标准差(方差)
精准、相对稳定, 精准、相对稳定,可以用于由样本推论总体 用于定距、 用于定距、定比变量
全距与标准差的关系
SS Σ(X − X ) 2 S = = N N
2
方差可以描述数值偏离平均值的程度。 方差可以描述数值偏离平均值的程度。 平方处理解决了绝对值的问题。 平方处理解决了绝对值的问题。 平方处理后对偏离均值的程度更加敏感。 平方处理后对偏离均值的程度更加敏感。
二、离散性的描述指标
4.标准差: 4.标准差:将方差开平方得到的数值 标准差
二、离散性的描述指标
5.分析下列4 5.分析下列4组数据的离散性 分析下列 6]、 a[6 6 6 6 6 6 6]、b[5 5 6 6 6 7 7 ] 9]、 c[3 3 4 6 8 9 9]、d[3 3 3 6 9 9 9 ]
全距=? 全距=? 四分位数=? 四分位数=? 平均离均差= 平均离均差=? 方差=? 方差=? 标准差=? 标准差=?
三、集中性描述指标的比较
1.描述不同测量等级的变量 1.描述不同测量等级的变量
定类、定序、定距、 众 数:定类、定序、定距、定比变量的描述 中位数:定序、定距、 中位数:定序、定距、定比变量的描述 平均数:定距、 平均数:定距、定比变量的描述
三、集中性描述指标的比较
2.数据的分布形状 2.数据的分布形状 中心重合
第二节 集中性的描述指标
一、数据分布的集中性 二、集中性的描述指标 三、集中性描述指标的比较
一、数据分布的集中性
《社会统计学》章节知识点——单选题

《社会统计学》章节知识点——单选题第一章总论●变量类型1.下列变量属于数值型变量的是( A )。
A.工资收入B.产品等级C.学生对考试改革的态度D.企业的类型【参考答案】A2.从变量分类看,下列变量属于定序变量的是( C )。
A.专业B.性别C.产品等级D.收入【参考答案】C●总体和样本1.某地区政府想了解全市332.1万户家庭年均收入水平,从中抽取3000户家庭进行调查,以推断所有家庭的年均收入水平,这项研究的样本是( B )。
A.332.1万户家庭B.3000户家庭C.332.1户家庭的年均收入D.3000户家庭的年均收入【参考答案】B2.学校后勤集团想了解学校22000学生的每月生活费用,从中抽取2200名学生进行调查,以推断所有学生的每月生活费用水平,这项研究的总体是( A )。
A.22000名学生B.2200名学生C.22000名学生的每月生活费用 D.2200名学生的每月生活费用【参考答案】A3.为了解某地区的消费,从该地区随机抽取5000户进行调查,其中30%回答他们的月消费在5000元以上,40%回答他们每月用于通讯、网络的费用在300元以上,此处5000户是( C )。
A.变量 B.总体 C.样本 D.统计量【参考答案】C●抽样方式4.从含有N个元素的总体中,抽取n个元素作为样本,同时保证总体中每个元素都有相同的机会入选样本,这样的抽样方式称为( A )。
A.简单随机抽样B.系统抽样 C.整群抽样D.分层抽样【参考答案】A5.某班级有60名男生,40名女生,为了了解学生购书支出,从男生中抽取12名学生,从女生中抽取8名学生进行调查,这种调查方法属于( C )。
A.简单随机抽样 B.整群抽样 C.分层抽样 D.系统抽样【参考答案】C6.先将总体按某标志分为不同的类别或层次,然后在各个类别中采用简单随机抽样或系统抽样的方式抽取子样本,最后将所有子样本合起来作为总样本,这样的抽样方式称为( D )。
社会统计学第四章相关测量法与变量层次

同分对:
Txy
n(1 n1 1) 2
n9
(n9 2
1)
例:计算G系数与dy系数
文化程度 婚姻美满
美满
大学 9
中学 16
小学 5
一般
8
30
18
不美满
3
4
7
同序对:9(30+18+4+7)+8(4+7)+16(18+7)+30(7)=1229 异序对:5(8+30+3+4)+18(3+4)+16(8+3)+30(3)=617 同分对:9(16+5)+16(5)+8(30+18)+30(18)+3(4+7)+4 (7)=1254 G系数=0.33 dy系数=0.22
E2的定义:
当已知y与x有关之后,如果再去预测y值,则可借 助x预测y。即用各类x条件下,y的条件分布中的 众值去预测y,可能性最大。
分析:
E2 = n —∑max(nij)
1)E2 = 0 (即∑max(nij) = n,即各类x条件下的 众值皆为最大值)
2)E2 = n (即∑max(nij) = 0,即各类x条件下的 众值皆为最小值)
例:对称与不对称λ系数
▪ 表 青年人与其知心朋友的志愿
自己志愿
快乐家庭
知心朋友志愿
理想工作
增广见闻
总数
快乐家庭
28
9
3
40
理想工作
2
41
7
50
增广见闻
2
4
4
10
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
5
例子1:
6
例子2:
7
λ和λy数值的含义:
①两个定类变量的相关强度。 ②用一个变量来预测另一个变量的时候,能够消减 的误差比例。
8
例子3:
9
二、tau-y相关测量法:tau-y
• • • • •
适用于分析两个定类变量的相关关系。 分析不对称关系。 具有消减误差比例的意义(PRE)。 取值范围:【0,1】。 逻辑:根据X的取值预测Y的取值时,所能 消减的误差比例。
21
本章结束!
22
3
第一节 两个定类变量: λ,tau-y
一、 Lambda相关测量法: λ和 λy
• • • • • 适用于分析两个定类变量的相关关系。 λ分析对称关系,λy分析不对称关系。 具有消减误差比例的意义(PRE)。 取值范围:【0,1】。 逻辑:根据一个变量的取值预测另一个变量的 众值时,所能消减的误差比例。
适用于分析两个定序变量的相关关系。 分析对称关系。 具有消减误差比例的意义(PRE)。 取值范围:【-1,1】。 逻辑:根据任何两个个案在某变量上的等级 来预测它们在另一个变量上的等级时,能减 少的误差比例。
20
G值的示用一个变量预测另一个变量时能够消减的误 差比例。
10
11
tau-y数值的含义:
①两个定类变量的相关强度。 ②用X来预测Y的时候,能够消减的误差比例。
12
• 对称关系可用Lambda测量法,而不对称关系最好 用tau-y测量法。
13
14
• 课堂作业: 以下是男、女青年对古典音乐是否喜爱的抽样调查: 请计算相关系数,并解释含义。
男
女
喜爱 无所谓 不喜爱
第二篇
统计叙述:单变量与双变量
1
第二章:简化一个变量之分布 简化一个变量的资料 第三章:简化两个变量之分布 简化两个变量的资料
第四章:相关测量法 描述两个变量之间的关系
2
第四章 相关测量法与测量层次
第一节 两个定类变量:Lambda,tau-y 统计相关的性质 第二节 两个定序变量: Gamma, dy 第三节 两个定距变量:简单线性回归与积矩相关r 第四节 定类变量与定距变量:相关比率与非线性相 关 第五节 定类变量与定序变量:Lambda,tau-y 第六节 定序变量与定距变量:相关比率 第七节 综合
46 10 30
20 18 50
15
第二节 两个定序变量: Gamma, dy
Gamma, dy——级序相关法:
根据任何两个个案在某变量上的相对等级 来预测它们在另一个变量上的相对等级时, 能减少的误差比例。
16
例子1:
17
• 表4-4资料
18
一、Gamma相关测量法:G
19
G的特点:
• • • • •
