自动控制原理 第五章(第二次课)
合集下载
自动控制原理第五章
1第五章 频域分析法目的：①直观，对高频干扰的抑制能力。
对快(高频)、慢(低频)信号的跟踪能力。
②便于系统的分析与设计。
③易于用实验法定传函。
§5.1 频率特性一. 定义)()()()(1n p s p s s s G +⋅⋅⋅+=θ在系统输入端加一个正弦信号：t R t r m ωsin )(⋅=))(()(22ωωωωωj s j s R s R s R m m -+⋅=+⋅=↔ 系统输出：))(()()()()(1ωωωθj s j s R p s p s s s Y m n -+⋅⋅+⋅⋅⋅+=2t j t j e A e A t y t y ωω⋅+⋅+=↔-瞬态响应)()(1 若系统稳定，即)(s G 的极点全位于s 左半平面，则 0)(l i m 1=∞→t y t 稳态响应为：t j t j ss e A eA t y ωω⋅+⋅=-)( 而)(21)()(22ωωωωωj G R j j s s R s G A m j s m -⋅-=+⋅+⋅⋅=-= )(21)()(22ωωωωωj G R jj s s R s G A m j s m ⋅=-⋅+⋅⋅== ∴t j m t j m ss e j G R je j G R j t y ωωωω⋅⋅+⋅-⋅-=-)(21)(21)( =])()([21t j t j m e j G e j G R jωωωω-⋅--⋅⋅ 又)(s G 为s 的有理函数，故)()(*ωωj G j G -=，即3φωωj e j G j G )()(=φωωj e j G j G -=-)()( ∴][)(21)()()(φωφωω+-+--⋅=t j t j m ss e e j G R jt y =)sin()(φωω+⋅⋅t j G R m=)sin(φω+⋅t Y m可见：对稳定的线性定常系统，加入一个正弦信号，其稳态响应也是一个同频率的正弦信号。
自动控制原理第五章-2
截止频率c ：开环幅相曲线上，幅值为1的频率称为截止频率。 即 |G(jwc)H(jwc)|=1。 相角裕量 ： 物理意义：若系统截止频率c处的相位迟后再增加，系统处于临界 = 180 + (c)
稳定。
Im
1 Kg
wg
Re
(wc )
wc
w
开环对数幅相曲线上的幅值裕度和相角裕度
-Kg(dB)
Kg(dB)>0
K g (dB) 20 lg
1 20 lg G ( jwg ) H ( jwg ) G ( jwg ) H ( jwg )
若系统稳定，则：Kg>1(K(dB)>0)，r>0。 一般，为确定系统的相对稳定性，描述系统的稳定程度， 需要同时给出幅值裕度和相位裕度两个量，缺一不可。 工程上，一般取：
1 T w 1
2 2
(w) arctanTw
M (0) 1, M r 1, wr 0, wb 1/ T ts 3T 3 / wb , tr 2.20T 2.20 / wb
( 0.05)
T 2
2、二阶系统 R(s)
_
2 wn s( s 2wn )
K g (dB) 10dB r 300 ~ 600
(K g (dB) 6dB)
判断系统稳定的又一方法
0
h(dB) 0
h 1
180 G( jc )H ( jc )
h 20 log G ( j g ) H ( j g )
1 h G( j g ) H ( j g )
2. 带宽频率b
当系统闭环幅频特性的幅值M()降到零频率幅值的0.707(或零分贝值以下3dB) 时，对应的频率b称为截止频率。0～b的频率范围称为带宽，它反映系统的快速 性和低通滤波特性。
稳定。
Im
1 Kg
wg
Re
(wc )
wc
w
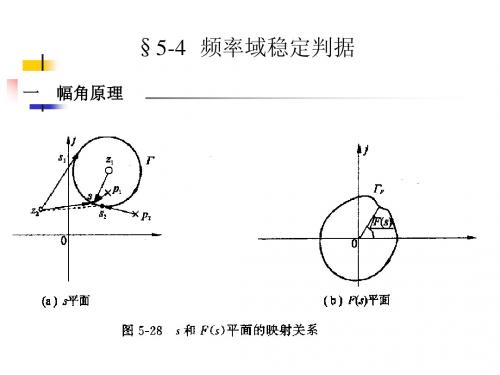
开环对数幅相曲线上的幅值裕度和相角裕度
-Kg(dB)
Kg(dB)>0
K g (dB) 20 lg
1 20 lg G ( jwg ) H ( jwg ) G ( jwg ) H ( jwg )
若系统稳定，则：Kg>1(K(dB)>0)，r>0。 一般，为确定系统的相对稳定性，描述系统的稳定程度， 需要同时给出幅值裕度和相位裕度两个量，缺一不可。 工程上，一般取：
1 T w 1
2 2
(w) arctanTw
M (0) 1, M r 1, wr 0, wb 1/ T ts 3T 3 / wb , tr 2.20T 2.20 / wb
( 0.05)
T 2
2、二阶系统 R(s)
_
2 wn s( s 2wn )
K g (dB) 10dB r 300 ~ 600
(K g (dB) 6dB)
判断系统稳定的又一方法
0
h(dB) 0
h 1
180 G( jc )H ( jc )
h 20 log G ( j g ) H ( j g )
1 h G( j g ) H ( j g )
2. 带宽频率b
当系统闭环幅频特性的幅值M()降到零频率幅值的0.707(或零分贝值以下3dB) 时，对应的频率b称为截止频率。0～b的频率范围称为带宽，它反映系统的快速 性和低通滤波特性。
北航机电控制工程基础(自动控制原理)第五章2-典型环节频率特性
北京航空航天大学
二、积分环节 Integral links 1、伯德图
机电控制工程基础
K G (s) s
Fundamentals of Mechatronic Control Engineering
K G ( j ) j
K A( )
K ( ) 0 arctan j 0 2
幅值
机电控制工程基础
袁松梅教授 Tel：82339630
下半个圆对应于正频率部分，而上 半个圆对应于负频率部分。
Email：yuansm@
北京航空航天大学
四、振荡环节Oscillation link 2、伯德图 讨论 0
机电控制工程基础
1 时的情况。当K=1时，频率特性为：
K Kn G( s ) 2 2 2 T s 2Ts 1 s 2 n s n 2
G( s) K , G( j ) K
相频特性： ( )
1、伯德图
幅频特性：A( ) K ；
0
；
L( ) / dB
20log K 20log K 20log K
K 1
对数幅频特性：
K 1 lg
0 K 1
( )
180
0 L( ) 20 lg K 0 0
1.0 -45 100 -89.4
1 1 当 0时， (0) 0;当 时， ( ) ;当 时， () 。 T T 4 2
当时间常数T 变化时，对数幅频特性和对数相频特性的形状都不变，仅仅是根据转折 频率1/T 的大小整条曲线向左或向右平移即可。而当增益改变时，相频特性不变，幅 频特性上下平移。
K P ( ) 1 T 2 2 KT Q ( ) 1 T 2 2 Q ( ) T P( )
自动控制原理第五章课后习题答案(免费)[1]
![自动控制原理第五章课后习题答案(免费)[1]](https://img.taocdn.com/s3/m/11139471f46527d3250ce001.png)
自动控制原理第五章课后习题答案（免费）5－１设单位反馈系统的开环传递函数为对系统进行串联校正，满足开环增益 及 解:① 首先确定开环增益K,00()12lim v s K SG S k →===② 未校正系统开环传函为:012()(1)G s s s =+M a g n i t u d e (d B )1010101010P h a s e (d e g )Bode DiagramGm = 70.5 dB (at 200 rad/sec) , P m = 16.5 deg (at 3.39 rad/sec)Frequency (rad/sec)③ 绘制未校正系统的开环对数频率特性,得到幅穿频率 3.4c ω=,对应相位角'0()164,16c G j ωγ∠=-∴=,采用超前校正装置,最大相角 0(180())4016630m c G j ϕγωγ=-+∠+=-+=④ 11sin ,31m αϕαα--=∴=+ 0()(1)KG s s s =+40γ=︒112K s -=⑤ 在已绘图上找出10lg 10lg3 4.77α-=-=-的频率 4.4m ω=弧度/秒 令c m ωω=⑥0.128/,0.385/m T s T s ωα=⇒==∴=校正装置的传函为:110.385()110.128Ts s G s Ts s α++==++校正后的开环传函为:012(10.39)()()()(1)(10.13)c s G s G s G s s s s +==++ 校正后1801374340γ=-=>,满足指标要求.-100-50050100M a g n i t u d e (d B )101010101010P h a s e (d e g )Bode DiagramGm = 99.2 dB (at 1.82e+003 rad/sec) , P m = 42.4 deg (at 4.53 rad/sec)Frequency (rad/sec)5－２设单位反馈系统的开环传递函数为要求 设计串联迟后校正装置。
《自动控制原理》第五章：系统稳定性
5.2 稳定的条件
当σi和λi均为负数，即特征根的 σi和λi均为负数， 均为负数 实部为负数，系统是稳定的； 实部为负数，系统是稳定的； 或极点均在左平面。 或极点均在左平面。
5.3 代数稳定性判据
定常线性系统稳定的充要条件 定常线性系统稳定的充要条件是特征方程的根具有负 充要条件是特征方程的根具有负 实部。因此，判别其稳定性，要解系统特征方程的根。为 实部。因此，判别其稳定性，要解系统特征方程的根。 避开对特征方程的直接求解，可讨论特征根的分布， 避开对特征方程的直接求解，可讨论特征根的分布，看其 是否全部具有负实部，并以此来判别系统的稳定性，这样 是否全部具有负实部，并以此来判别系统的稳定性， 也就产生了一系列稳定性判据。 也就产生了一系列稳定性判据。 其中最主要是E.J.Routh(1877 )h和Hurwitz（ 其中最主要是E.J.Routh(1877年)h和Hurwitz（1895 E.J.Routh(1877年 年）分别提出的代数判据。 分别提出的代数判据 代数判据。
习题讲解： 习题讲解：
µ
G1
Q21
G1
h2
k1 k1 G1 ( s ) = , G1 ( s ) = (T1s + 1) (T1s + 1) k1k 2 G0 ( s ) = (T1s + 1)(T2 s + 1)
kp
G0 ( s ) G(s) = 1 + G0 ( s ) K p
5.4 Nyquist稳定性判据 Nyquist稳定性判据
系统稳定的条件？ 系统稳定的条件？
5.2 稳定的条件
d n y (t ) d ( n −1) y (t ) dy (t ) 线性系统微分方程： 线性系统微分方程： n a + an −1 + L + a1 + a0 y (t ) n ( n −1) dt dt dt d m x(t ) d ( m −1) x(t ) dx(t ) = bm + bm−1 + L + b1 + b0 x(t ) m ( m −1) dt dt dt d n y (t ) d ( n −1) y (t ) dy (t ) + a( n −1) + L + a1 + a0 y (t ) = 0 齐次微分方程： 齐次微分方程： an n ( n −1) dt dt dt an s n + an −1s n −1 + L + a1s + a0 = 0 设系统k 设系统k个实根
自动控制原理(胡寿松版)完整第五章ppt课件
-20
φ (ω )
ω=0.1 L(ω )=20lg0.1=-20dB 90
对数相频特性：φ (ω )=90o 0 0.1
1
10ω
第二节 典型环节与系统的频率特性
4)．惯性环节
G(s)=Ts1+1
G(ωj
)=
jω
1 T+1
(1) 奈氏图
A(ω
)=
1 1+(ω T)2
φ (ω )= -tg-ω1 T
取特可殊以点证：绘明ω制：=0奈氏图近似方I法m : AA图心半A点(ω(ω(是 ， 圆ω，))=以 以 。惯=)0然=根ωω0(1性.171==/后据0/环2∞27为T将幅1节φ,jφo半φ它频的(ω)(ω径为(ω奈们特))=的圆)=氏平-性=09-o0滑4和o5连o相ω接频起∞特来0性-。求45ω=出T1特殊ω1=0Re
5）二阶微分环节 s 2 /n 2 2s /n 1(n 0 ,0 1 )
6）积分环节 1 / s
7）微分环节 s
第二节 典型环节与系统的频率特性
（2）非最小相位系统环节
1）比例环节 K (K0)
2）惯性环节 1/( T s1 ) (T0) 3）一阶微分环节 Ts1 (T0)
4）振荡环节 1 /( s 2 /n 2 2 s /n 1 )(n 0 ,0 1 )
第一节 频率特性
系统输入输出曲线 定义频率特性为:
r(t) c(t)
r(t)=Asinωt
G(ωj )
=|G(jω)|e j G(jω) =A(ω )e φj (ω )
A 0
幅频特性： t A(ω )=|G(jω)|
G(jω)
A G(jω )
相频特性： φ (ω )= G(jω)
自动控制原理第五章第二部分
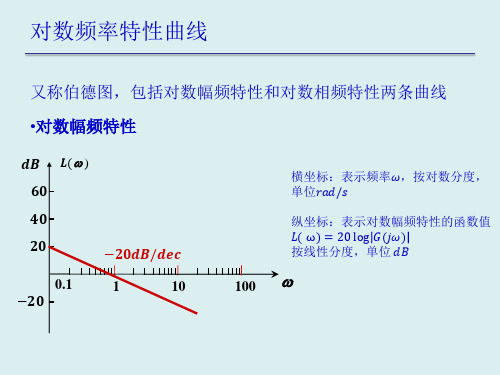
当L(w=0时：
L(w
)
20
lg
K
w
0K
wv
I型系统
斜率为-20db/dec的低频段渐近线或其延长线与横轴的 交点的频率值与开环放大系数K相等。
II型系统
斜率为-40db/dec的低频段渐近线或其延长线与横轴的 交点的频率值的平方与开环放大系数K相等。
例1:已知某最小相位系统由频率响应实验获得的对数幅 频曲线如图所示，试确定其传递函数。
3.开环对数幅频特性：
L(w)
60
40dB / dec
40
转折频率 w1 1
w2 2
w3 20
环节 惯性 一阶微分
振荡
20
60dB / dec
0
0.1
12
10 20
100 w
20
40dB / dec
40
80dB / dec
传递函数的频域实验确定
1.频率响应实验
Asinwt
L(w )
20dB / dec
0dB / dec
20
20dB / dec
0
0.1
1
20
w
40dB / dec
解： (1)确定系统积分环节的个数
低频段的渐近线为-20dB/dec 1
(2)确定系统传递函数
K ( 1 s 1)
G(s)
0.1 s(s 1)( 1
s 1)
20
L(w )
一阶微分环节 二阶微分环节
一点+一斜率确定初始段渐近线
(4)从低频渐近线开始，沿w 增大的方向，每遇到一个
转折频率改变一次渐近线斜率，直到绘出转折频率最高 的环节为止；
自动控制原理第5章
8
二、图形表示法
1.极坐标图（幅相频率特性图；奈奎斯特图） 1.极坐标图（幅相频率特性图；奈奎斯特图） 极坐标图 随着频率的变化，频率特性的矢量长度和幅角也改变。 随着频率的变化，频率特性的矢量长度和幅角也改变。 当频率ω 变化到无穷大时， 当频率ω从0变化到无穷大时，矢量的端点便在平面上画出一 条曲线，这条曲线反映出ω为参变量、模与幅角之间的关系。 条曲线，这条曲线反映出ω为参变量、模与幅角之间的关系。 通常称这条曲线叫做幅相频率特性曲线或奈奎斯特曲线。 通常称这条曲线叫做幅相频率特性曲线或奈奎斯特曲线。画 有这种曲线的图形称为极坐标图。 有这种曲线的图形称为极坐标图。
− j arctan 2 ζT ω 1−T 2ω 2
幅频特性 相频特性
A(ω ) =
ϕ (ω ) = − arctan
23
典型环节的频率特性
9
2.博德图（对数频率特性图） 博德图（对数频率特性图） 博德图 两张图构成 一张是对数幅频图 一张是对数相频图 构成： 对数幅频图， 对数相频图。 由两张图构成：一张是对数幅频图，一张是对数相频图。 两张图的横坐标都是采用了半对数坐标。 两张图的横坐标都是采用了半对数坐标。
10
对数幅频特性图的纵坐标是频率特性幅值的对数值乘20， 对数幅频特性图的纵坐标是频率特性幅值的对数值乘20， 是频率特性幅值的对数值乘20 即 L(ω ) = 20 lg A(ω ) 表示，均匀分度，单位为db。 表示，均匀分度，单位为db db。 对数相频特性图的纵坐标是相移角φ(ω)，均匀分度，单 对数相频特性图的纵坐标是相移角φ 是相移角 均匀分度， 位为“ 位为“度”。 对数幅频特性图绘的是对数幅频特性曲线， 对数幅频特性图绘的是对数幅频特性曲线， 对数相频特性图绘的是对数相频特性曲线。 对数相频特性图绘的是对数相频特性曲线。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
G( j0 ) 180 G( j) 0 90
如果 arctan arctan arctan
2
3
180 () 90
如果 arctan arctan arctan
2
3
幅相曲线会与负实轴相交
18
5-4 系统开环频率特性的绘制
自动控制原理
解方程 arctan arctan arctan
开环传递函数：G(s) G1(s) G2(s)G3(s) G4(s) 开环频率特性：G( j) G1( j)G2( j)G3( j)G4( j)
A()e j A1()e j1 A2 ()e j2 A3 ()e j3 A4 ()e j4
4
5-4 系统开环频率特性的绘制
自动控制原理
对数幅频和相频特性
20 20dB/dec
0 0.1
1
-20
10
L() 20lg
() 900
dL() d lg
20
dB dec
( ) 90
0
90
对数频率特性曲线
27
微分环节L()
自动控制原理
① G(s)= S ② G(s)= 2S ③ G(s)= 0.1S
L()dB
②与0分贝线交点频率？斜率？
自动控制原理
（2）积分环节
传递函数： GG((Ss) K1
S
频率特性： G( j) 1
j
L( ) dB
20
-20dB/dec
0 0.1
1
-20
10
对数幅频和相频特性
L（） 20lg
() 900
斜率：
dL() d lg
20 dB dec
( ) 90 0
90
25
1( )
对数频率特性曲线
积分环节L()
G(
j)
(
K (j 1) j)2 (Tj 1)
起点: G( j0 ) 180 终点: G( j) 0 180
() 180 arctg arctgT
0
T
T
j
0
15
5-4 系统开环频率特性的绘制
自动控制原理
例5.4 绘制 G ( S ) Ke s 的幅相曲线。
TS 1
①
G(s)=
1 s
②
G(s)=
10 s
自动控制原理
③
G(s)=
0.2 s
L()dB②与0分贝线交点频率？斜率？
40
20
[-20]
[-20]
0dB
0.1 0.2
12
10 20
10
-20
[-20] -40
26
5-3 典型环节的对数频率特性
自动控制原理
（3）微分环节
L() dB
G(S) S
G( j) j
G( j) 1 j 1
L() 20lg 2 1
() tg 1
()
L()
0 0.5 1 2 4 5 8 20 0 -26.60 -450 -63.40 -760 -78.70 -830 -870
00 -0.97 -3.01 -7 -12.3 -14.1 -18.1 -26
lg 7 0.845 lg 8 3lg 2 0.903 lg 9 2lg 3 0.954
21
自动控制原理
5-3 典型环节的对数频率特性
自动控制原理
对数相频特性坐标图 横坐标刻度先疏后密
N
纵坐标均按线性分度 () i () i 1
横坐标是角速率 按 lg 分度, 10倍频程，用dec 表示
S(TS 1)
解:
G( j)
K (－ j 1) j(T j 1)
K ( (T 2
T) 2 1)
K(1 T2) j (T 22 1)
相频特性为 () arctan 900 1800 arctan T
幅频特性为 A() K 22 1 T 2 2 1
0
Im
起点: G( j0 ) 270 o 终点: G( j) 0 270 o
L() dB 20 10
0
(rad / s)
-10
-20
-30
-40
10 -2
10 -1
100 2 3 4 10 1
20
5-3 典型环节的对数频率特性
对数分度： lg 2 0.301
lg 3 0.4771 lg 4 2lg 2 0.602 lg 5 0.699 lg 6 lg 3 lg 2 0.778
称为非最小相位系统。
2
5-2 典型环节的频率特性
自动控制原理
最小相位这一名称来源于通讯科学，意思是：如果有 几个稳定的传递函数，它们的幅频特性函数完全相同， 那么其中右半平面没有零点的那个函数，其相频特性 函数的绝对值必为最小。也就是输出正弦信号相对于 输入正弦信号的相移量最小。
2(2S 1) G1(S) S(5S 1)
Im
K(T1 T2)
0 Re
0
13
5-4 系统开环频率特性的绘制
自动控制原理
G(S)
S
(T1S
K 1)(T2 S
1)
14
5-4 系统开环频率特性的绘制
自动控制原理
例5.3
已知G(S)H (S)
K（ S 1）,
S 2 (TS 1)
T, , K 0
试分析并绘制>T和<T情况下的幅相曲线。
解:
1型系统
0+
10
5-4 系统开环频率特性的绘制
自动控制原理
例题2：绘制 G(S)
K
的幅相曲线。
(T1S 1)(T2S 1)
解: G( j)
K
(T1j 1)(T2j 1)
求交点：
起点: G( j0) K0 终点: G( j) 0 90 2
G(
j)
K[1T1 T2 2 j(T1 (T12 2 1)(T22 2
L()
20lg
2T 2＋1 20lg1 0(dB)
低频时的对数幅值曲线是一条0分贝的直线
29
5-3 典型环节的对数频率特性
自动控制原理
高频段 1 ， L() 20lg 2T 2 1 20lg T (dB)
T
高频时的对数幅频特性曲线是一条斜率为-20dB/dec的直线
高频段斜率： dL( )
Bode图的坐标形23 式(对数频率特性)
5-3 典型环节的对数频率特性
自动控制原理
（1）比例环节
L ( ) dB
传递函数： G(s) K
K>1
K=1
频率特性 (S j)
0
K<1
G( j) Ke j00
( )
对数幅频和相频特性
L() 20lg K
() 0
0
比例环节对数频率特性曲线
24
5-3 典型环节的对数频率特性
自动控制原理
Nyquist图
奈奎斯特图
简称奈氏图
能在一幅图上表示 出系统在整个频率范 围内的频率响应特性 (直观)。
2.缺点
不能清楚地表明 开环传递函数中每 个环节(参数)对系 统的性能影响。 (手工绘图麻烦)
Imag Axis
2
Im
1
Re[G( j)]
0 -1
A( )
3 0
()
Re
Im[G( j)]
-2
2
-3
-4
1 G( j ) A()e j ()
0
-5
-3
-2
-1
0
1
2
3
Rea l Axis
6
5-4 系统开环频率特性的绘制
自动控制原理
G(
j)
(
K (1 j 1)( 2 j 1)( m j j) (T1 j 1)(T2 j 1)(Tn
1)
j 1)
nm
▪ 幅相曲线（Nyquist)图的3个要点
Im
0 Re
0
12
5-4 系统开环频率特性的绘制
自动控制原理
G(
j)
K(T1 T2 ) (T122 1)(T222 1)
K(1T1 T2 (T122 1)(T22
2 2
)
1)
j
求与实轴交点：
令Im[G( j)] 0
x
1 T1T2
1 T1T2
G(
jx
)
KT1T2 T1 T1
G( j0 ) K (T1 T2 ) j
nm
ν＝1，I型系统
起点: 0＋ 1个积分环节项产生的相角是 90
曲线是一条渐近于平行与负虚轴的线段。 Im
终点: ＝
曲线收敛于原点， 且曲线与坐标轴相 切。
Re 0
1型系统
0+
8
5-4 系统开环频率特性的绘制
自动控制原理
2）与负实轴的交点
G ( j ) A( )e j R( ) jI ( )
K ( T )
0
Re
图 5.28 幅相曲线图
该系统为非最小相位系统
17
5-4 系统开环频率特性的绘制
自动控制原理
例题：绘制
G(s)
5(s 2)(s 3) s2 (s 1)
的幅相曲线。
解： () arctan arctan 180 arctan
2
3
A() 5 2 22 2 32 2 1
幅相曲线与实轴交点：
I() 0
x
曲线与负实轴交点：
() 180
x
R(x ) A(x )
9
5-4 系统开环频率特性的绘制