结构动力学西南交通大学
西南交通大学土木工程学院导师2009名单
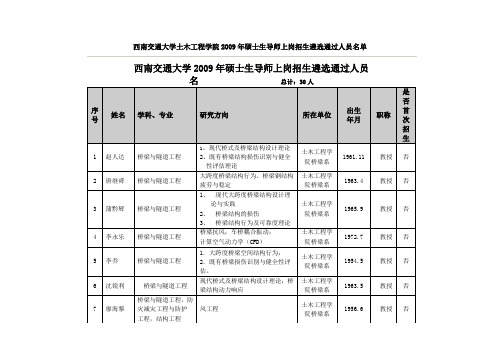
土木工程学院桥梁系
1972.7
教授
否
5
李乔
桥梁与隧道工程
1.大跨度桥梁空间结构行为;
2.既有桥梁损伤识别与健全性评估。
土木工程学院桥梁系
1954.5
教授
否
6
沈锐利
桥梁与隧道工程
现代桥式及桥梁结构设计理论;桥梁结构动力响应
土木工程学院桥梁系
1963.5
教授
否
7
廖海黎
桥梁与隧道工程,防灾减灾工程与防护工程,结构工程
土木工程学院桥梁系
1972.6
副教授
否
23
谢尚英
桥梁与隧道工程
新型桥梁结构
土木工程学院桥梁系
1963.11
副教授
否
24
成文佳
桥梁与隧道工程
1.既有桥梁受力行为及加固研究
2.现代桥式及桥梁结构设计理论
土木工程学院桥梁系
1969.8
副教授
否
25
周凌远
桥梁与隧道工程
桥梁结构行为分析
土木工程学院桥梁系
1968.1
西南交通大学土木工程学院2009年硕士生导师上岗招生遴选通过人员名单
西南交通大学2009年硕士生导师上岗招生遴选通过人员名总计:30人
序号
姓名
学科、专业
研究方向
所在单位
出生
年月
职称
是否首次招生
1
赵人达
桥梁与隧道工程
1、现代桥式及桥梁结构设计理论
2、既有桥梁结构损伤识别与健全性评估理论
土木工程学院桥梁系
土木工程学院
1963.6
教授
否
20
倾情助力中国高速动车组的发展——记西南交通大学牵引动力国家重点实验室动力学与强度研究团队

封底故事Backcover Story倾情助力中国高速动车组的发展——记西南交通大学牵引动力国家重点实验室动力学与强度研究团队 王 军到2020年年底,中国已有3700组动车组奔跑在38000公里的高铁线路上,并保持着商业运行最高时速350公里的世界纪录,日臻成熟的中国高铁正以前所未有的速度和广度走向世界。
中国高铁经历了从“跟跑”“并跑”再到“领跑”的过程。
作为“高铁梦”的牵引者之一,坐落于成都市西北角的西南交通大学牵引动力国家重点实验室的创新故事与助推中国高铁及轨道交通产业的飞速发展休戚相关。
走入实验室,机车车辆滚动振动试验台、牵引传动试验台、高频激振试验台和疲劳试验台的轰鸣声不绝于耳,犹如一首首高铁研发的交响曲。
这里有针对机车车辆动力学和结构可靠性的理论分析平台、台架试验到线路试验完整的测试系统,几乎每一种奔驰在高铁线上的动车组车型都要在这里进行仿真和台架试验,模拟动车组真实运行环境,评估其高速运行性能和安全可靠性,为高铁安全运行保驾护航。
从“和谐号”动车组走向“复兴号”动车组殊为不易,这背后是实验室多个科研劲旅的艰辛付出,动力学与强度研究团队(以下简称“动强组”)就是其中一个。
我国高速动车组经历了引进、消化、吸收再创新的发展过程,而走行部即转向架是动车组的核心,决定了动车组能否高速平稳和安全可靠运行,在引进、消化、吸收阶段,动强组是转向架技术的“接盘侠”,在再创新阶段,动强组则是中坚力量,为中车各企业的轨道车辆转向架尤其是高速转向架创新研发提供了重要技术支持。
助力“复兴号”跑出最高速2017年6月26日,由中国铁路总公司牵头组织研制、具有完全自主知识产权、达到世界先进水平的中国标准动车组“复兴号”由北京南站和上海虹桥站双向首高速列车滚振试验发。
2012年年底开始研发、2014年完成方案设计、2015年下线、2017年正式亮相,“复兴号”的诞生充满艰辛,西南交大的多个科研团队曾深度参与其中。
桥梁专业好书推荐

桥梁专业好书推荐《高等桥梁结构理论》项海帆人民交通出版社《桥梁工程》(上、下册)范立础、顾安邦主编,2001版,经典书《桥梁结构震动与稳定》李国豪著《悬索桥设计》雷俊卿:《桥梁结构分析及程序系统》,肖汝诚编著,北京:人民交通出版社,2002 《桥梁结构理论与计算方法》,贺拴海,人民交通出版社,2003.8《桥梁工程师手册》《斜拉桥建造技术(精)》《桥梁工程》李亚东《桥梁结构计算力学》《桥梁施工监测与控制》《桥梁风工程》陈政清《桥梁加固与改造》蒙云《公路小桥涵勘测设计》《桥梁结构电算程序》《桥梁抗震》《铁路桥梁》《城镇地道桥顶进施工及验收规程》《钢筋混凝土及预应力混凝土桥梁结构设计原理》作者:张树仁出版社:人民交通出版社《公路钢筋混凝土及预应力混凝土桥涵设计规范(JTG D62-2004)》《公路桥涵设计通用规范》《ansys在土木工程应用实例》――中国水利水电出版社《ansys10.0有限元分析自学教程》《ANSYS工程结构数值分析》《apdl参数化有限元分析技术及其应用实例》《ANSYS在土木工程中的应用》李权人民邮电出版社《基于有限元软件ansys7.0的结构分析》《土木工程结构分析程序设计》《Fortran 95程序设计》《结构概念和体系》(第二版)》林同炎《大跨度空间结构》张毅刚《风对结构的作用――风工程导论》《结构设计原理》叶见曙李国平《结构力学》高等教育出版社《结构力学》酒井忠明《结构力学题解精粹》《结构力学复习与习题分析》《结构动力学》杜修力《结构动力学》克拉夫和彭津《结构可靠度理论》赵国藩《混凝土结构设计基本原理》《房屋建筑学》《公路挡土墙设计》《高速公路》《公路工程地质(戴文亭)》《道路工程》(第二版)徐家钰,同济大学出版社《路基路面工程》邓学钧《土力学地基基础》清华大学出版社,陈希哲第四版《铁路站场及枢纽》《地铁与轻轨》《专业英语》《土木工程专业英语》《土木工程经济与管理》《建筑结构》《高层建筑结构》《试验应力分析》《桥梁上部构造性能(E.C.汉勃利)》《材料力学》铁摩辛柯《欧美桥梁设计思想》,王应良,高宗余《桥涵顶进设计与施工》《地道桥结构设计》《框架式地道桥》《钢筋混凝土结构裂缝与变形的验算》《曲线梁桥计算》《拱桥挠度理论》《预应力混凝土结构设计》林同炎《混凝土简支梁(板)桥》《混凝土桥梁结构》《钢筋混凝土结构的裂缝控制》《钢筋混凝土原理》《桥粱施工工程师手册》《现代桥梁建筑设计》《公路小桥涵设计示例》《钢筋混凝土及预应力混凝土简支梁桥结构设计》《杭州湾跨海大桥技术创新与应用》《混凝土结构有限元分析》《ansys操作命令与参数化编程》《ansys建模与网格划分关键技术》《钢筋混凝土结构非线性有限元理论与应用》《桥梁博士V3.0》《城市地道桥顶进施工技术及工程实例》《铁路基本规范》《芜湖长江大桥钢结构制做技术总结》大桥局《拱桥挠度理论》贺拴海人民交通出版社《桥梁工程》,大桥局,王序森等《桥梁建筑--结构构思与设计技巧》张师定著人民交通出版社《悬索桥》大桥局《桥梁力学》,胡人礼,北京:中国铁道出版社,1999《预应力混凝土结构设计》林同炎《曲线梁桥计算》孙广华《桥梁设计百问》邵旭东《科学地对待桥渡和桥梁》,钱冬生,中国铁道出版社,2003.9《桥梁建筑与小品―构思与造型》慎铁钢等编著天津大学出版社2002《桥梁结构空间分析设计方法与应用》,戴公连, 李德建著,北京:人民交通出版社,2001《混凝土结构设计》 A.H.尼尔逊著过镇海方鄂华庄崖屏等校译《桥梁与结构理论研究》李国豪上海科学技术出版社,1983《桥梁结构非线性分析》华孝良人民交通出版社《混凝土弯梁桥》邵容光夏淦人民交通出版社《组合结构桥梁》刘玉擎. 同济大学现代桥梁技术丛书《斜弯桥的广义梁格法》《电脑辅助工程分析ANSYS使用指南》《结构动力学》《铁路客运专线恰两施工技术培训班》《ANSYS土木工程应用实例》《ANSYS-APDL高级工程应用实例分析与二次开发》《一注基础复习教程》《杆系结构有限元分析与matlab应用》《origin 应用教程》《ANSYS在桥梁工程中的应用》《钢桥》;(共十一分册)小西一郎著中国铁道出版社《钢筋混凝土及预应力混凝土桥建筑原理》[联邦德国] F.莱昂哈特著《现代斜拉桥》和《现代悬索桥》; .严国敏,.(严国敏虽离我们而去,但是他的敬业精神永远激励着后人!)《斜拉桥》林元培86.577/L YP(铁道);(94年出版,但即使现在的教科书也依旧大段地摘取他的内容.现在斜拉桥发展的情况,许多方面都应证了书中的预测.)《AASHTO美国公路桥梁设计规范》;.(关于钢箱梁和剪力滞等均有详细规定,是国内现有规范和课本缺乏的.)《武汉长江二桥技术总结》大桥局;.(双壁钢围堰和前支点挂蓝等有详细介绍.) 吐血介绍大桥局的深水基础施工情况,以前我查了很多资料都含含糊糊.该书也介绍了分离双箱前支点挂篮施工也较怪异的,一般前支点挂篮施工用在边主梁桥上. (书名大致如此,内容对钢桥的材料,设计,加工,安装,监测等有详细介绍.)科技图书二库(五楼) 中文科技86.5/TDB;《斜梁桥》黄平明人民交通出版社科技图书二库(五楼) 中文科技86.571/HPM;《曲线梁》姚玲森人民交通出版社《预加应力混凝土原理》程式秋五洲出版社《斜拉桥》大桥局86.579/TDG(铁道);《桥梁工程》姚玲森《公路桥梁设计丛书》也不错分为8册⑴预应力砼连续梁桥⑵拱桥⑶桥梁通用构造及简支梁桥⑷悬索桥⑸斜拉桥⑹砼弯斜梁桥⑺组合拱桥⑻刚架桥《九江长江大桥技术总结》大桥局86.5/TDG01 (铁道);《预应力混凝土连续梁桥设计》,人民交通出版社,徐岳《桥梁简化理论-横向分布》胡肇滋86.51/HZZ ; 86.51/HZC (铁道); 86.51/HZC (铁道)《桥梁方案比选》周念先的,人民交通出版社科技图书二库(五楼) 中文科技86.5/ZNX;《结构可靠度理论及其在桥梁工程中的应用》张建仁等人民交通出版社《大跨悬索桥理论》陈仁福《大跨度桥梁设计、桥梁减隔震设计、高架桥梁抗震设计、桥梁延性抗震设计》范立础《公路桥涵设计手册》人民交通出版社《箱形梁设计理论》郭金琼科技图书二库(五楼) 中文科技86.531/GJQ;《弯梁桥设计》吴西伦科技图书二库(五楼) 中文科技86.579/WXL;《桥梁预应力技术百问》李国平主编《Algor、Ansys在桥梁工程中的应用方法与实例》《公路桥梁荷载横向分布计算》李国豪石洞86.587/TDL-2(铁道)《桥梁结构分析的数值方法及其程序:在正交桥、斜弯桥中的应用》。
西南交大-研究生课程-结构动力学-10

节点位移向量
δij δ δij 0 I G 0 δ δk i A 69δik ( 30)
3.单元力学特性矩阵
3.1.2 带刚臂的空间杆单元
根据虚功原理,可推导出
K e g[T A ]TK e[T A ] ( 3 1 )
元累加到关于i、k的节点的位
置编号的相应位置上即可。
3.单元力学特性矩阵
3.1.3 空间梁单元 采用二节点空间等参直梁单元, 每个节点包括3个线位移和3个 角位移,整个单元有12个自由 度。局部坐标系下考虑剪切变 形的空间梁单元的单元刚度矩 阵为
3.单元力学特性矩阵
3 EA.1.3 空间梁单元
3.单元力学特性矩阵
3.1单元刚度矩阵 单元刚度矩阵 K e 由下式求得
K e BTD B dv (27) V
3.单元力学特性矩阵
3.1单元刚度矩阵 3.1.1 空间杆单元
采用二节点杆单元,每个节点 有3个平移自由度,其局部坐 标系下的单元刚度矩阵如下
1 0 0 1 0 0
0
0
0
0
0
0
2.建立结构振动分析的有限元方法
2.1 连续区域的离散化 在动力问题中,因为引入了时间坐标,所以 处理的是四维 (x,y,z,t) 问题。有限元分析中一 般采用部分离散的方法,即只对空间域进行 离散,这样,此步骤与静力分析相同。
2.建立结构振动分析的有限元方法
2.2 构造插值函数 单元位移模式的选取应满足以下两个条件:
上式中 t1 t2in 1 q T i q i in 1 q T i q it t1 2 t1 t2in 1d d t q T i q id t t1 t2in 1d d t q T i q id t ( 7 )
桥梁专业好书推荐

桥梁专业好书推荐《高等桥梁结构理论》项海帆人民交通出版社《桥梁工程》(上、下册)范立础、顾安邦主编,2001版,经典书《桥梁结构震动与稳定》李国豪著《悬索桥设计》雷俊卿:《桥梁结构分析及程序系统》,肖汝诚编著,北京:人民交通出版社,2002 《桥梁结构理论与计算方法》,贺拴海,人民交通出版社,2003.8《桥梁工程师手册》《斜拉桥建造技术(精)》《桥梁工程》李亚东《桥梁结构计算力学》《桥梁施工监测与控制》《桥梁风工程》陈政清《桥梁加固与改造》蒙云《公路小桥涵勘测设计》《桥梁结构电算程序》《桥梁抗震》《铁路桥梁》《城镇地道桥顶进施工及验收规程》《钢筋混凝土及预应力混凝土桥梁结构设计原理》作者:张树仁出版社:人民交通出版社《公路钢筋混凝土及预应力混凝土桥涵设计规范(JTG D62-2004)》《公路桥涵设计通用规范》《ansys在土木工程应用实例》――中国水利水电出版社《ansys10.0有限元分析自学教程》《ANSYS工程结构数值分析》《apdl参数化有限元分析技术及其应用实例》《ANSYS在土木工程中的应用》李权人民邮电出版社《基于有限元软件ansys7.0的结构分析》《土木工程结构分析程序设计》《Fortran 95程序设计》《结构概念和体系》(第二版)》林同炎《大跨度空间结构》张毅刚《风对结构的作用――风工程导论》《结构设计原理》叶见曙李国平《结构力学》高等教育出版社《结构力学》酒井忠明《结构力学题解精粹》《结构力学复习与习题分析》《结构动力学》杜修力《结构动力学》克拉夫和彭津《结构可靠度理论》赵国藩《混凝土结构设计基本原理》《房屋建筑学》《公路挡土墙设计》《高速公路》《公路工程地质(戴文亭)》《道路工程》(第二版)徐家钰,同济大学出版社《路基路面工程》邓学钧《土力学地基基础》清华大学出版社,陈希哲第四版《铁路站场及枢纽》《地铁与轻轨》《专业英语》《土木工程专业英语》《土木工程经济与管理》《建筑结构》《高层建筑结构》《试验应力分析》《桥梁上部构造性能(E.C.汉勃利)》《材料力学》铁摩辛柯《欧美桥梁设计思想》,王应良,高宗余《桥涵顶进设计与施工》《地道桥结构设计》《框架式地道桥》《钢筋混凝土结构裂缝与变形的验算》《曲线梁桥计算》《拱桥挠度理论》《预应力混凝土结构设计》林同炎《混凝土简支梁(板)桥》《混凝土桥梁结构》《钢筋混凝土结构的裂缝控制》《钢筋混凝土原理》《桥粱施工工程师手册》《现代桥梁建筑设计》《公路小桥涵设计示例》《钢筋混凝土及预应力混凝土简支梁桥结构设计》《杭州湾跨海大桥技术创新与应用》《混凝土结构有限元分析》《ansys操作命令与参数化编程》《ansys建模与网格划分关键技术》《钢筋混凝土结构非线性有限元理论与应用》《桥梁博士V3.0》《城市地道桥顶进施工技术及工程实例》《铁路基本规范》《芜湖长江大桥钢结构制做技术总结》大桥局《拱桥挠度理论》贺拴海人民交通出版社《桥梁工程》,大桥局,王序森等《桥梁建筑--结构构思与设计技巧》张师定著人民交通出版社《悬索桥》大桥局《桥梁力学》,胡人礼,北京:中国铁道出版社,1999《预应力混凝土结构设计》林同炎《曲线梁桥计算》孙广华《桥梁设计百问》邵旭东《科学地对待桥渡和桥梁》,钱冬生,中国铁道出版社,2003.9《桥梁建筑与小品―构思与造型》慎铁钢等编著天津大学出版社2002《桥梁结构空间分析设计方法与应用》,戴公连, 李德建著,北京:人民交通出版社,2001《混凝土结构设计》 A.H.尼尔逊著过镇海方鄂华庄崖屏等校译《桥梁与结构理论研究》李国豪上海科学技术出版社,1983《桥梁结构非线性分析》华孝良人民交通出版社《混凝土弯梁桥》邵容光夏淦人民交通出版社《组合结构桥梁》刘玉擎. 同济大学现代桥梁技术丛书《斜弯桥的广义梁格法》《电脑辅助工程分析ANSYS使用指南》《结构动力学》《铁路客运专线恰两施工技术培训班》《ANSYS土木工程应用实例》《ANSYS-APDL高级工程应用实例分析与二次开发》《一注基础复习教程》《杆系结构有限元分析与matlab应用》《origin 应用教程》《ANSYS在桥梁工程中的应用》《钢桥》;(共十一分册)小西一郎著中国铁道出版社《钢筋混凝土及预应力混凝土桥建筑原理》[联邦德国] F.莱昂哈特著《现代斜拉桥》和《现代悬索桥》; .严国敏,.(严国敏虽离我们而去,但是他的敬业精神永远激励着后人!)《斜拉桥》林元培86.577/LYP(铁道);(94年出版,但即使现在的教科书也依旧大段地摘取他的内容.现在斜拉桥发展的情况,许多方面都应证了书中的预测.)《AASHTO美国公路桥梁设计规范》;.(关于钢箱梁和剪力滞等均有详细规定,是国内现有规范和课本缺乏的.)《武汉长江二桥技术总结》大桥局;.(双壁钢围堰和前支点挂蓝等有详细介绍.) 吐血介绍大桥局的深水基础施工情况,以前我查了很多资料都含含糊糊.该书也介绍了分离双箱前支点挂篮施工也较怪异的,一般前支点挂篮施工用在边主梁桥上. (书名大致如此,内容对钢桥的材料,设计,加工,安装,监测等有详细介绍.)科技图书二库(五楼) 中文科技86.5/TDB;《斜梁桥》黄平明人民交通出版社科技图书二库(五楼) 中文科技86.571/HPM;《曲线梁》姚玲森人民交通出版社《预加应力混凝土原理》程式秋五洲出版社《斜拉桥》大桥局86.579/TDG(铁道);《桥梁工程》姚玲森《公路桥梁设计丛书》也不错分为8册⑴预应力砼连续梁桥⑵拱桥⑶桥梁通用构造及简支梁桥⑷悬索桥⑸斜拉桥⑹砼弯斜梁桥⑺组合拱桥⑻刚架桥《九江长江大桥技术总结》大桥局86.5/TDG01 (铁道);《预应力混凝土连续梁桥设计》,人民交通出版社,徐岳《桥梁简化理论-横向分布》胡肇滋86.51/HZZ ; 86.51/HZC (铁道); 86.51/HZC (铁道)《桥梁方案比选》周念先的,人民交通出版社科技图书二库(五楼) 中文科技86.5/ZNX;《结构可靠度理论及其在桥梁工程中的应用》张建仁等人民交通出版社《大跨悬索桥理论》陈仁福《大跨度桥梁设计、桥梁减隔震设计、高架桥梁抗震设计、桥梁延性抗震设计》范立础《公路桥涵设计手册》人民交通出版社《箱形梁设计理论》郭金琼科技图书二库(五楼) 中文科技86.531/GJQ;《弯梁桥设计》吴西伦科技图书二库(五楼) 中文科技86.579/WXL;《桥梁预应力技术百问》李国平主编《Algor、Ansys在桥梁工程中的应用方法与实例》《公路桥梁荷载横向分布计算》李国豪石洞86.587/TDL-2(铁道)《桥梁结构分析的数值方法及其程序:在正交桥、斜弯桥中的应用》。
西南交通大学1997-2006年历年【结构力学】考研真题
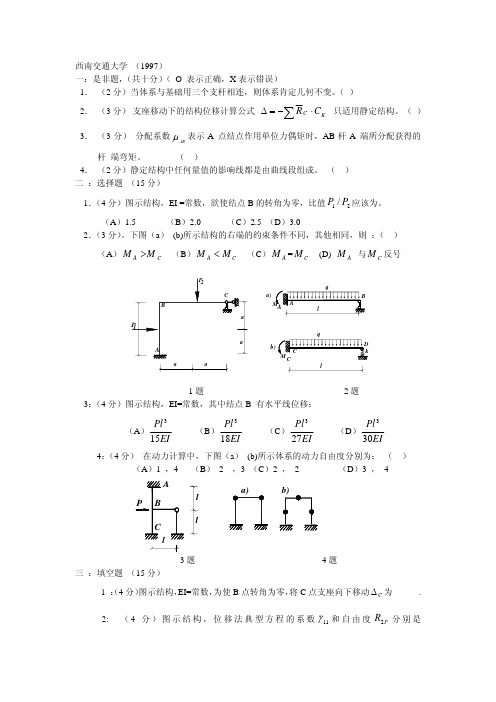
(括号内数字
(1,2,3) 3
10kN
20kN.m
(4,5,6) 4
30kN/m
3m y
1
(0,0,0)
(0,0,0) 2
x
θ
2m
2m
7: 求图示刚架的自振频率和主振型。(10 分) (横梁刚度为无限大)
m 1=m
EI
h
m2=m
EI
h
x
西南交通大学 (1999)
一:选择题:(共 15 分)
1:图示体系 A 绞可在竖直线上移动,以改变等长杆 AB ,AC 的长度,而其余结点位置不
变。当图示尺寸为那种情况时,体系为几何不变。
(A) h ≠ 2m (B) h ≠ 4m (c) h ≠ 4m 和 h ≠ ∞
4m
B
C
h
(D) h ≠ 2m 和 h ≠ ∞
6m
3m 3m 6m
2: 图示简支斜梁在荷载 P 作用下,若改变 B 支座链杆方向,则梁的内力将是:
(C) Pl 3 27EI
(D) Pl 3 30EI
4:(4 分) 在动力计算中,下图(a) (b)所示体系的动力自由度分别为: ( )
(A)1 ,4 (B) 2 ,3 (C)2 , 2
(D)3 , 4
A
PB
l
a)
b)
l C
l
3题
4题
三 :填空题 (15 分)
1 :(4 分)图示结构,EI=常数,为使 B 点转角为零,将 C 点支座向下移动 Δ C 为______.
零。 自由项_______等于零。
q
l
q
l
l K
l
l
西南交通大学专业目录
②201英语一或202俄语或203日语
③301数学一
④923材料力学
①101思想政治理论
②201英语一或202俄语或203日语
③301数学一
④923材料力学
①101思想政治理论
②201英语一或202俄语或203日语
③301数学一
④923材料力学
①101思想政治理论
②204英语二
③302数学二
081404供热、供燃气、通风及空调工程
01.空气调节技术
02.隧道与地下工程通风空调
03.暖通空调节能技术
04.暖通空调自动控制
085201◆机械工程
01.机械设计及理论
02.先进制造技术及自动化
03.机械电子工程
04.工业工程与安全工程
085203◆仪器仪表工程
01.现代测控技术及系统
02.智能化状态监测与故障诊断
081101控制理论与控制工程
01.铁路信号自动控制;
02.智能信息处理与智能控制
03.智能监控与网络信息技术
04.复杂系统控制理论
081200计算机科学与技术
01.产业链协同与信息化支撑技术
02.云计算与智能技术
03.数据库技术与数据挖掘
04.图形图像与视频处理技术
05.互联网与网络技术
06.嵌入式系统
①空气调节②工业通风
同等学力加试科目:
同学术型相关专业
同等学力加试科目:
同学术型相关专业
同等学力加试科目:
同学术型相关专业
003电气工程学院(拟招生266人,其中拟招推免生97人)
080800电气工程
01.电机与电器
02.电力系统及其自动化
高等结构动力学考试题样卷
西南交通大学研究生试试卷课程代码A11101课程名称建筑结构高等动力学考试时间150分钟阅卷教师签字:一、是非题(将判断结果填入括弧:以O 表示正确,以X 表示错误)(本大题共5小题,总计10分)1.图a 示两端固定梁的自振频率大于图b 示简支梁的自振频率。
( )2.在图示结构中,若要使其自振周期T 增大,可以增大EI 。
( )3.简谐荷载作用于单自由度体系时,干扰力频率越接近自振频率,动力系数 (绝对值)越大。
( )4.增加约束使得体系的频率减小或保持不变。
( )5.设不考虑阻尼因素,承受简谐荷载(同频率、同相角)的多自由度体系,稳态时任意一点的内力与荷载同时达到幅值。
( )二、选择题(将选中答案的字母填入括弧内)(本大题共5小题,总计15分)1.设有图示桁架,若不考虑各杆重量时,其动力自由度为:A .单自由度;B .两个自由度;C .三个自由度;D .四个自由度。
( )22.图示体系受动力荷载作用,杆重不计,不考虑阻尼,当发生共振时,θ值应为:A .()3/4ma EI ;B .()33/4ma EI ; C .()37/3ma EI ;D .()3/3ma EI 。
3. 体系的跨度、约束、质点位置不变,下列哪种情况周期最短:A .质量小 ,刚度小;B .质量大 ,刚度大 ;C .质量小 ,刚度大;D .质量大 ,刚度小 。
( )4. 多自由度体系的自振频率和振型取决于:A .干扰力的大小和方向;B .初始位移;C .结构的质量分布和刚度(或柔度)系数;D .初始速度 。
( )5.从以下三式中选一合适的曲线方程,用能量法求图示体系的第一频率。
设EI =常数。
(式中A 、f 为常数 )A .(1cos(/2))y A x l π=-;B .2334(16/5)(2)y f l l x lx x =-+;C .(/2)(1cos(2/))y f x l π=-;D .()()2242(16/5)/4y f l x x l=-。
西南交通大学结构工程(081402)专业介绍
西南交通大学结构工程(081402)专业介绍一、学科概况“结构工程”学科是土木工程中的一门应用型基础学科。
由于铁路建设发展的需要,我校于1956年在铁路院校中首先设立结构工程学科工业与民用建筑专业,几十年来连续地为铁道部门培养了成批的建设人才。
从1978年起,本学科对钢筋混凝土基本构件力学行为、结构抗震性能、型钢混凝土组合结构设计等几个重要科研方向进行了长期的系统的研究工作,参与我国混凝土结构设计规范和型钢混凝土组合结构设计规程的编制工作,使我校结构工程学科在我国工程建设标准化领域建立了重要的学术地位。
近年来本学科紧密结合工程建设实际,不断拓宽学科研究方向,在科学研究和人才培养等方面都取得了显著的成果。
结构工程学科于1986年获得硕士学位授予权,2000年获得博士学位授予权。
本学科有正教授6人,副教授13人,具有博士学位者16人,现已培养硕士150余人、博士30余人;近几年,本学科点共发表论文近190篇,3篇被收入SCI和EI,出版专著2部,教材4部;获奖或鉴定成果14项。
二、主要研究方向1.混凝土结构基本性能与设计理论该研究方向自20世纪70年代以来在钢筋混凝土偏压柱承载力及稳定性计算、钢筋混凝土框架柱抗震性能与设计方法、型钢混凝土组合结构设计方法等方面取得了一系列的研究成果,承担了多项国家和省部级科研项目,从而为我校结构工程学科的发展做出了巨大的贡献。
近年来随着新技术、新材料、新工艺、新理论的发展应用,本研究方向不断发展创新。
目前,该方向的研究重点为:型钢混凝土-钢筋混凝土混合结构基本性能与设计方法,混凝土结构性态设计理论与应用,高层建筑结构设计及理论,预应力高强混凝土、体外预应力、无粘结预应力混凝土结构性能、计算理论和抗震行为、新型预应力混凝土建筑结构体系及其计算理论的研究,既有结构的评估、诊断与加固理论研究。
2.结构抗震与隔震本研究方向将集中研究结构抗震和减振的应用理论及实用技术,具体内容涉及混凝土结构和钢结构的抗震理论;比较不同的隔震装置对于砖石结构和高层混凝土结构和钢结构的隔震效果;在两个地震水平加速度分量作用下,隔震装置对结构的扭转的影响及由于扭转引起的隔震装置的稳定性;在近源地震波作用下,具有隔震装置的结构响应;开发新的隔震和减振装置。
西南交通大学2018年硕士研究生拟录取名单(研究生院)
岩土工程 01 地基及基础
341 55 45 111 130 72.97 70.59 杨兵
岩土工程 04 岩土动力学、爆破和3抗52震5工7程65 101 129 68.47 69.44 马建林
岩土工程 01 地基及基础
341 57 68 88 128 76.27 72.24 马建林
岩土工程 04 岩土动力学、爆破和3抗41震6工1程63 75 142 76.97 72.59 魏星
081402 081402 081403 081403 081405 081406 081406 081406 081406 081406 081406 081406 081406 081406 081406 081406 081406 081406 081406 081406 081406 081406 081406 081406 081406 081406 081406 081406 081406 081406 081406 081406 081406 081406 081406 081406 081406 081406 081406
姓名
学 习 录取专 方 业代码 式
何俊松 1 梁学斌 1 陈军 1 章露露 1 王蒙婷 1 程世涛 1 李明洪 1 董琰 1 张楚 1 苏磊 1 陈壮 1 乃麒元 1 谢强 1 荆祥 1 王溢轩 1 诸洲 1 邓洋 1 周佺 1 韩莹 1 陈浩宇 1 包韵雷 1 赵一超 1 莫玉凡 1 仵振 1 李思静 1 何顺龙 1 谢鑫 1 宁杰钧 1 孙鹏 1 沈彬 1 李贞良 1 夏葳 1 张海程 1 张显昭 1 金云涛 1 杨曾 1 肖姝玮 1 骆丽茹 1 张蓝月 1
岩土工程 01 地基及基础
364 59 55 106 144 72.42 72.61 张俊云
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第十六章结构动力学【例16-1】不计杆件分布质量和轴向变形,确定图16-6 所示刚架的动力自由度。
图16-6【解】各刚架的自由度确定如图中所示。
这里要注意以下两点:1.在确定刚架的自由度时,引用受弯直杆上任意两点之间的距离保持不变的假定。
根据这个假定并加入最少数量的链杆以限制刚架上所有质量的位置,则刚架的自由度数目即等于所加链杆数目。
2.集中质量的质点数并不一定等于体系的自由度数,而根据自由度的定义及问题的具体情形确定。
【例16-2】 试用柔度法建立图16-7a 所示单自由度体系,受均布动荷载)t (q 作用的运动方程。
【解】本题特点是,动荷载不是作用在质量上的集中荷载。
对于非质量处的集中动荷载的情况,在建立运动方程时,一般采用柔度法较为方便。
设图a 质量任一时刻沿自由度方向的位移为y (向下为正)。
把惯性力I 、阻尼力R 及动荷载)(t P ,均看作是一个静荷载,则在其作用下体系在质量处的位移y ,由叠加原理(见图b 、c 、d 及e ),则)(R I y P D I P +δ+∆=∆+∆+∆=式中,)t (q EI 38454P =∆,EI483=δ。
将它们代入上式,并注意到y m I-=,y c R -=,得)(48)(384534y c y m EIt q EI y --+=图16-7经整理后可得)(t P ky y c y m E =++式中,3EI 481k =δ=,)(85)(t q k t P P E =∆=)(t P E 称为等效动荷载或等效干扰力。
其含义为:)(t P E 直接作用于质量上所产生的位移和实际动荷载引起的位移相等。
图a 的相当体系如图f 所示。
【例16-3】 图16-8a 为刚性外伸梁,C 处为弹性支座,其刚度系数为k ,梁端点A 、D 处分别有m 和3m质量,端点D 处装有阻尼器c ,同时梁BD 段受有均布动荷载)t (q 作用,试建立刚性梁的运动方程。
【解】 因为梁是刚性的,这个体系仅有一个自由度,故它的动力响应可由一个运动方程来表达,方程可以用直接平衡法来建立。
这个单自由度体系可能产生的位移形式如图b 所示,可以用铰B 的运动)t (α作为基本量,而其它一切位移均可利用它来表示。
图16-8)t (α以顺时针向为正。
则A 点有位移)t (2α 和加速度)t (2α;D 点有位移)t (23α和加速度)t (23α 及速度)t (23α ;C 点约束反力为)t (k Rc α= 。
由∑=0MB,有043)(232323221=⨯+⨯+⨯+⨯+⨯t q R R I I C 将惯性力、阻尼力及约束反力代入上式,得043)t (q 23)]t (k [23)]t (c 23[23)]t (3m 23[2)]t (m 2[2=⨯+⨯α-⨯α-⨯α-⨯α-经整理,运动方程为)t (q 89)t (k )t (c 49)t (m=α+α+α小结:∙ 例16-2及例16-3讨论的是单自由度的一般情况下的运动方程的建立。
建立方程的思路是通过分析动力平衡或考虑变形协调。
一般来说,对于单自由度体系,求11δ和11k 的难易程度是相同的,因为它们互为倒数,都可用同一方法求得。
对于多自由度体系,若是静定结构,一般情况下求柔度系数容易些,但对超静定结构就要根据情况而定。
∙ 刚度法和柔度法。
它们都是根据达朗贝尔原理和所采用的阻尼理论在体系上加惯性力和阻尼力。
刚度法是考虑质量自由度方向的平衡;柔度法是建立沿自由度方向位移的协调条件。
∙ 所谓结构振动自由度是指:确定体系全部质点位置所需的独立位移分量的个数。
在例16-3中我们选取)t (α为独立位移分量,由此得两质点处的位移、加速度及惯性力的表达式。
∙ 体系的振动自由度数目既和体系的质点数目有关,又不完全取决于质点数目,自由度还和体系的可能位移状态有关(如例题16-3),因此要根据具体问题,按自由度定义分析确定。
另一方面,自由度是确定质点空间位置的独立坐标(位移分量)个数,它和结构超静定次数或独立位移个数没有关系。
∙ 任何单自由度的振动问题,本质上都可抽象为质点、弹簧、阻尼器体系。
从实际结构到抽象模型的关键是求m 和k (或δ)。
【例16-4】试 写 出 图 16-9a 质 点 m 的 运 动 微 分 方 程 , 并 计 算 各 系 数 。
图16-9 【解】(1) 列位移方程, )()()(1111t Q t P y m y Q P ∆+∆+-=δ (2) 计算系数项(图b) , EIa a a a EI 342322211311=⎪⎭⎫ ⎝⎛⋅⋅⋅⋅⋅=δ (3) 计算自由项(图c,d )EIPa a a a a Pa a a Pa EI P1211632/2212123222121131=⎪⎭⎫ ⎝⎛⨯⨯⨯⨯+⨯⨯⨯⨯⨯=∆ 同理, EIQa Q121131=∆ (4) 将 系 数 代 入 位 移 方 程 ,)(1211)(121134333t Q EIat P EIay ym EIa+=+或)(1611)(1611433t Q t P y aEI y m +=+【例16-5】 试 按刚度法列 出 图 16-10a 所示 刚 架 在 给 定 荷 载 作 用 下 的动 力 平 衡 方 程 。
图16-10 【解】( 1 ) 考 虑 质 点 m 平 衡 (图b) 有I S = , y m I-= (2) 确 定 弹 性 力 恢 复 力 S ,弹 性 力 恢 复 力S 可 以 认 为 由 两 部 分 叠 加 而 成 。
第 一 部分 为 使 m 产 生 位 移 施 加 的 力11R ; 第 二 部 分 为 m 不 动 在 荷 载 作 用 下 产 生 的 反 力 P R 1 , 即 P R R S 111+= ,()y a l a EIy k R +==211113 , ()a l a t ql R P +=8 sin 31θ ( 3 ) 代 回 动 力 平 衡 方 程 得 ,()()a l a tql y a l a EI y m +=++8 sin 332θ 【例16-6】 图 16-11a 所示梁不计自重 ,求 自 振 频 率 ω 。
图16-11【解】由M 图(图b ),求得柔 度 为:EI l 192/53=δ 。
所以, 35/1921Wl EIg mg gm =δ=δ=ω 【例16-7】 图 16-12a 所示 单 跨 梁 不 计自重 ,杆 无 弯 曲 变 形 ,弹 性 支座 刚 度 为 k ,求 自 振 频 率 ω 。
图16-12【解】在 W 处 加 )4/(1,)2/(1,111k k P =δ=∆=()W mg gm /kg 411111=δ=δ=ω 。
【例16- 8】 图 16-13a 所示梁不计自 重 ,24m kN 102,kN 200⋅⨯==EI W ,求 自 振 圆频 率 。
【解】由于对称跨中无转角 ,求刚度k 。
2/321212331EI EIl EI k ===,则k N /m 106241⨯==k k 。
14s 2.54200/106-=⨯====ωmkN W kg mg kg m k图16- 13【例16-9】 试求图16-14a 所示结构的自振频率。
略去杆件自重及阻尼影响。
图16-14【解】图a 为一次超静定结构,用力矩分配法作出单位弯矩图(图b )。
计算质点处的柔度系数11δ(即位移计算),由图b (或图c )与图d (虚拟状态),得EIl EI l EI l l l l EI l EI 33331104219.0153623512348132221421481==⎪⎭⎫ ⎝⎛-=⎪⎪⎭⎫ ⎝⎛⨯-=δ 则,ml EIm l EI m 3311172.82315361==δ=ω。
【例16-10】作图16-15a 所示 结构的动 力 弯 矩 幅 值 图 。
已 知 质 点 重 W =1.2kN ,扰 力 幅 值 P = 75.0kN ,扰 力 频 率 -1s 177=θ,梁 的 抗 弯 刚 度 EI =4490kN ·m 2。
图16-15【解】由图b 列 幅 方 程 ,即P A m A P 1211δθδ+=,P m A P 1211)1(δθδ=-,因为 111δωm =P P m PA P P P 1122211111)1(μδδωθθδδ=-=-=,2211ωθμ-=由图c 求柔度系数11δ,即kN /000279.034311m EIm ==δ, 由图d 求柔度系数P 1δ,即kN /000408.061131m EIm P==δ, 1112s 78561-==δωm , kN37.1, m 000102.075.0000408.031, 31, 2 ,s 63.8821-=-=⨯⨯-=-===-A m A θμωθω将动荷载P 和惯性力A m 2θ加于结构上,得动力弯矩幅值图如图e 所示。
【例16-11】 图16-16a 所 示 体 系 中 ,电 机 重 kN 10=W 置 于 刚 性 横 梁 上 ,电 机 转 速 min /500r n = ,水 平 方 向 强 迫 力 为 ) sin(kN 2)(t t P θ⋅=,已 知 柱 顶 侧 移 刚 度 kN/m 1002.14⨯=k ,自 振 频 率 -1s 100=ω 。
求 稳 态 振 动 的 振 幅 及 最 大 动 力 弯 矩 图 。
图16-16【解】只有水平振动。
干扰力频率-1s 36.52=θ ,动力系数 ,378.1=μ 静位移 m 9610.1/1002.1244st -=⨯==mkN kN k P y 振 幅 mm 27.09610.1387.1 4st =⨯=μ=-m y A动 力 弯 矩 图 (图c )M M M P M D 756.22378.1=⨯⨯=μ= 。
【例16-12】 图 16-17a 所示 体 系 各 柱 EI = 常 数 ,柱 高 均 为 l ,))/(18(3ml EI =θ。
求 最 大 动 力 弯 矩 。
图16-17【解】由图b 可知,3336123l EIl EI k =⨯=,则自 振 频 率336mlEIm k ==ω。
动力系数21122=ωθ-=μ,最 大 动 力 弯 矩 M P M D μ=(max)(见图c 、d )。
【例16-13】 求 图 16-18a 所示 体 系 的 自 振 频 率 和 主 振 型 ,并 作 出 振 型 图 。
已 知 :m m m m ==21,2,EI = 常 数 。
图16-18【解】用柔度法作。
1.为求柔度系数,首先绘出单位弯矩图(图b 和c)。
由位移计算公式, 得EI 3333.111=δ,EI 5.02112-=δ=δ,EI 5833.022=δ2.求频率将它们代入频率方程,即01212222121122111=ω-δδδω-δm m m m展开上式并令λ=ω21得 ()()02121222112221112=δ-δδ+λδ+δ-λm m m m()()212112221122221112221112,1m m m m 412m m δδ+δδ-δ+δ±δ+δ=λ 两个根为 EI m 883.21=λ,EI m 366.02=λ 从而可得两个自振频率为 m EI 5889.0111=λ=ω, m EI 653.1122=λ=ω 3.求主振型下面确定相应的两个主振型。
