测距导线三角高程计算表改正数
高差改正数的公式

高差改正数的公式高差改正数是测量学中一个比较重要的概念,它在水准测量中起着关键的作用。
咱们先来说说啥是高差改正数。
比如说,咱在进行水准测量的时候,会因为各种因素产生误差。
这就好像你想做一个完美的蛋糕,但是面粉放多了或者鸡蛋大小不一样,结果就不太理想。
水准测量也是这样,因为仪器误差、观测误差、外界条件影响等等,测出来的高差可能不是那么准确。
那高差改正数就是用来对这些不太准确的高差进行修正的。
它的公式是:高差改正数 = -(∑高差观测值 - 理论高差)/ 水准路线的总测站数 ×该测段的测站数。
为了让大家更好地理解这个公式,我给大家讲讲我曾经在一次实际测量中的经历。
那是一个风和日丽的日子,我们测量小组接到了一个任务,要对学校新校区的一块地形进行水准测量。
我们拿着水准仪,兴冲冲地就出发了。
一开始,大家都信心满满,觉得这肯定是小菜一碟。
可是随着测量的进行,问题就来了。
有的同学读数读错了,有的同学忘记记录数据了,还有的同学因为仪器操作不熟练,导致测量速度很慢。
好不容易把所有的数据都测完了,回来一算,发现高差和理论值差了不少。
这可把我们急坏了,要是这个数据不准确,那后面的规划设计可就全乱套了。
于是,我们就开始用高差改正数的公式来修正这些数据。
大家分工合作,有人负责计算总测站数,有人负责计算每个测段的测站数,有人负责计算高差观测值的总和,还有人负责计算理论高差。
经过一番紧张的计算,终于得出了高差改正数。
把这些改正数加到原来的高差观测值上,得到了修正后的高差。
这时候我们才松了一口气,发现原来只要掌握了正确的方法,就算出现了问题也能解决。
在实际应用中,高差改正数的计算一定要仔细认真。
每一个数据都要准确无误,不然哪怕一个小小的错误,都可能导致最终结果的偏差。
而且,要注意的是,水准测量本身就是一个需要耐心和细心的工作。
不能马虎大意,要严格按照操作规范来进行。
总之,高差改正数的公式虽然看起来有点复杂,但只要多练习,多在实际中运用,就能熟练掌握。
三角高程测量观测与计算

三角高程测量观测与计算
(1)计算角度闭合差
A
ABB
B
3
4
CD
D
1
1
C
2
3
4
2
B1 AB 180
B
C
f 测 理
12 B1 1 8 0 1 23 12 1 8 0 2
3 4 2 3 1 8 0 3
A
1
B
5
三角高程测量观测与计算
3 4
§6.2 导线测量
一、导线测量概述 二、导线测量的外业工作 三、导线测量的内业计算 四、查找导线测量错误的方法
三角高程测量观测与计算
三、 导线测量的内业计算
思路:
①由水平角观测值β,计算方位角α; ②由方位角α、边长D,计算坐标
增量ΔX 、 ΔY; ③由坐标增量ΔX 、ΔY,计算X、Y。
目的:在国家级控制的基础上进一步 加密精度低一级而有足够数量的控制 点,供直接测图使用。
直接供地形测图使用的控制点,称为 图根控制点。
三角高程测量观测与计算
图根点的密度(包括高级点),取决于 测图比例尺和地物、地貌的复杂程度。
测图比例 尺
图跟点密 度(点
2
1: 1:1000 1:2000 1:5000
+0.03 -0.02 -17.92 +97.12 +0.04 -0.02 +30.88 +141.29 +0.03 -0.02
-0.63 +116.44 +0.05 -0.03 -13.05 +155.70
改正后增量
Δx
Δy
m
m
测距导线三角高程计算表改正数

测距导线三角高程计算表改正数
(原创实用版)
目录
1.测距导线三角高程计算表的概念
2.测距导线三角高程计算表的改正数
3.测距导线三角高程计算表改正数的应用
4.测距导线三角高程计算表改正数的重要性
正文
测距导线三角高程计算表是一种用于测量地面高程的工具,主要通过测量水平距离和竖直角度来计算地面的高程。
在测量过程中,由于各种因素的影响,测量结果往往会存在误差,因此需要对测量结果进行修正。
这个修正的过程就是通过测距导线三角高程计算表的改正数来完成的。
测距导线三角高程计算表的改正数是指在测量过程中,对水平距离和竖直角度的测量值进行修正的数值。
这个数值的大小取决于测量过程中各种因素对测量结果的影响程度,例如大气折射、地球曲率、测量仪器的精度等。
测距导线三角高程计算表改正数的应用主要体现在对测量结果的修
正上。
通过将改正数应用到测量结果中,可以得到更加准确的地面高程。
这对于地形测绘、工程建设等领域具有重要的意义,因为这些领域需要对地面高程进行精确的测量和控制。
测距导线三角高程计算表改正数的重要性不言而喻。
只有通过准确的改正数,才能保证测量结果的准确性,从而保证工程建设的顺利进行。
第1页共1页。
(整理)工程测量全站仪测距与三角高程路线高差计算表
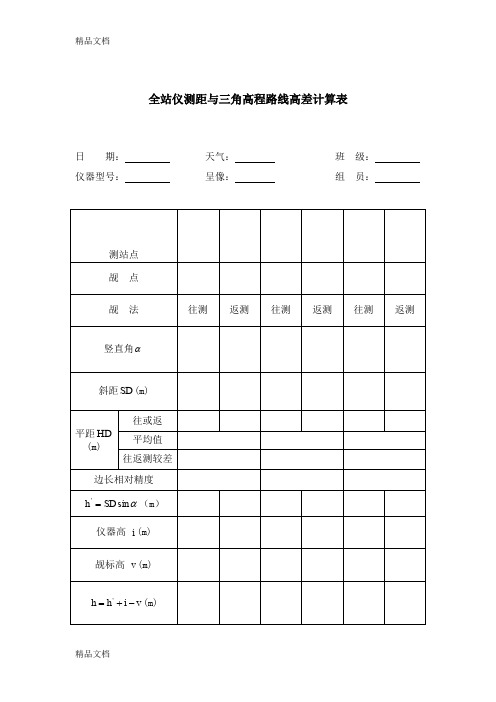
第1页
觇点
觇法
往测
返测
往测返测往测返测源自竖直角斜距 (m)
平距
(m)
往或返
平均值
往返测较差
边长相对精度
(m)
仪器高 (m)
觇标高 (m)
(m)
(m)
备注:
二、建设项目环境影响评价全站仪测距与三角高程路线高差计算表
1.环境影响评价依据的环境标准体系
日期:天气:班级:
仪器型号:呈像:组员:
1)规划实施可能对相关区域、流域、海域生态系统产生的整体影响。
『正确答案』B6.建设项目环境影响评价文件的其他要求测站点
(三)安全预评价程序
第五章 环境影响评价与安全预评价三、安全预评价报告的基本内容
三等水准计算成果改正数公式

三等水准计算成果改正数公式摘要:一、引言二、三等水准计算成果改正数公式概述1.符号表示2.公式推导3.改正数含义三、公式应用1.观测值计算2.误差处理3.成果验证四、实例分析1.数据介绍2.计算过程3.结果分析五、结论与建议正文:一、引言水准测量是工程测量中一种重要的方法,用于测定地面高程。
在三等水准测量中,计算成果的改正数是关键步骤。
本文将介绍三等水准计算成果改正数公式,并对公式进行详细解析。
二、三等水准计算成果改正数公式概述1.符号表示在公式中,以下符号表示:- H:测站高程- Z:仪器高- a:视线高- b:视准轴偏差- C:大气折光系数- δ:水准仪i角误差- ε:水准尺i段长度误差2.公式推导根据误差传播定律,水准观测高差的中误差为:mΔh = √(mh +mZ + ma + mb + mC + mδ + mε)其中,mi为各项误差的权。
3.改正数含义改正数是为了消除或减小误差而加到观测值上的值。
在三等水准计算中,改正数包括以下几类:- 仪器改正数:包括i角误差δ和视准轴偏差b的改正数- 气象改正数:大气折光系数C的改正数- 水准尺改正数:包括i段长度误差ε的改正数三、公式应用1.观测值计算根据水准观测公式,计算出各测站的高程:H1 = Z1 + a1 - δ1 - ε1H2 = Z2 + a2 - δ2 - ε22.误差处理将各项误差代入公式,计算出观测高差的改正数:mΔh_corr = √(mh + mZ + ma + mb + mC + mδ + mε) 3.成果验证将计算得到的高程值与实际值进行比较,检验测量成果的准确性。
测量学-三角高程测量

3、控制测量分类
按内容分:
平面控制测量:测定各平面控制点的坐标X、Y。 高程控制测量:测定各高程控制点的高程H。
按精度分:一等、二等、三等、四等;一级、二级、
三级
按方法分:三角网测量、天文测量、导线测量、交
会测量、卫星定位测量
按区域分:国家控制测量、城市控制测量、小区域
如图,PC为水平视线, PE 是通过P点的水准面。 由于地球曲率的影响, C、E高程不等。P、E同 高程。CE为地球曲率对 高差的影响:
P
CE
S
2 0
2R
如图,A点高程已知,测量A、B
之间的高差hAB,求B点的高程。
PC为水平视线。PM为视线未受大
气折光影响的方向线,实际照准
在N上。 视线的竖直角为 。
求: X B 、Y B
B
X AB DAB cos AB YAB DAB sin AB
Y
X B X A X AB YB YA YAB
X
坐标反算
Y
X
ab
B 已知:XA、YA、 XB、 YB
A
求:DAB、αAB
O
Y
DAB
X B X A 2 YB YA 2
x2 AB
Y
2 AB
3、大气垂直折光系数误差 大气垂直折光误差主要表现为折光系数K值测定误差。
4、丈量仪高和觇标高的误差 仪高和觇标高的量测误差有多大,对高差的影响也会有
多大。因此,应仔细量测仪高和觇标高。
控制测量
内容提要:
§7.1 控制测量概述 §7.2 导 线 测 量 §7.3 交会测量 §7.4 高程控制测量
第七章 控制测量 §7.1 概 述
三角高程计算表 带公式
90-25-59 701.177
85-04-45 414.486
94-56-16 414.493
88-24-21 338.885
复核:
往返高差 (m)
-11.641 -30.360 30.360 61.010 -61.007 22.188 -22.203 -33.647 32.403
互差 △h
(mm)
13
91-26-19
437.306
437.168 437.168
13
88-30-16
521.692
521.514 521.514
19
91-29-50
521.692
521.514 521.514
19
89-08-23
354.319
354.279 354.279
27
90-43-50 354.321 354.292 27 354.292
3
90-23-21
508.992
508.980 508.980
18
89-36-06
508.991
508.979 508.979
18
87-53-31
442.379
442.080 442.080
14
92-06-20 442.377 442.078 14 442.078
88-34-20
437.305
437.169 437.169
-918″ 1″ 3″
-866″ 20528″
8″
-21.100
1347.802
11.626
15
4″
11.633
第2页.共8页
γ 测站mz=
γ″
-2
高程误差配赋表
组号:
小组成员:
年月日
组号:
小组成员:
年月日
三角高程计算表
计算员检查员
组号:
小组成员:
导线坐标计算表
组号:
小组成员:
年月日
三(四)等水准测量手薄
自至日期时间仪器型号天气呈像
导线测量记录手薄测站
日期时间仪器高
仪器型号天气呈像
组号观测者记录者
组号小组成员
开始时间导线测量时间结束时间评委签名
日期
组号小组成员
开始时间水准测量时间结束时间评委签名
日期
内业计算评分表(140分)组号小组成员
开始时间数据计算时间
结束时间评委签名
日期。
三角高程测量高差计算表
竖直角α -2°44′33.17″ 2°45′41.33″ -4°06′18.5″ 4°08′51.7″ -2°15′50.17″ 2°16′03″ -2°09′53.83″ 2°09′56.17″ 3°57′24″ -3°57′53.33″ -6°25′56.17″ 6°31′38.17″
测站仪器高i 1.4670
11.497 12.27311
测站点
GP11
GP12
目标点
GP12
GP11
水平距离D 202.5528 202.55148
竖直角α
0°50′54″ -0°46′16.67″
测站仪器高i 1.4373
1.4303
目标棱镜高v 1.347
1.797
球气差改正f 0.00277
0.00277
单向高差h 3.09233 -3.09078
高差较差△h
-2.30889
-0.35639
0.04924
2.57790
1.81133
1.10113
限差值△h限
20.977
平均高 -
差
h
-25.49189
注:△h限=±40√D
记录:
13.775 14.11044
14.726 9.18379 计算:
15.172 -16.47160
13.077 10.12723 复核:
0.00139
0.00139
0.00084
0.00084
0.00395
0.00395
0.00207
0.00207
0.00046
0.00046
单向高差h -0.44887 0.45135 12.91050 -12.90432 -10.81016 10.81087 -6.86823 6.85952 -6.17095 6.16955 12.27352 -12.27271
三角高程测量记录及计算表
三角高程测量记录及计算表
三角高程测量记录及计算表是用于记录三角高程测量中的观测数据和计算结果的表格。
它通常包括以下内容:
1. 观测点的编号:记录测量点的编号,用于标识不同测点。
2. 观测角度:记录三角形的各个角度的观测值,包括水平角和垂直角。
3. 距离测量:记录测量点之间的距离,通常使用测距仪或测量杆进行测量。
4. 视线高差:记录测量点之间的视线高差,即测量点的垂直距离。
5. 平差高差:通过对观测角度和距离进行平差计算得到的高程差。
6. 高程值:通过测量点的已知高程和高差计算得到的绝对高程值。
7. 备注:记录测量过程中的特殊情况或其他需要备注的信息。
根据测量的具体要求,还可以在表格中添加其他需要记录的信息。
测量完成后,根据观测数据和计算结果,可以进行表格中的数据处理和检查,对测量结果进行校核和审查。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
测距导线三角高程计算表改正数
测距导线三角高程计算表是测绘工程中常用的一种测量工具,它主要用于计算地面上两点之间的高差。
然而,由于测量过程中可能存在的误差,使得计算结果并不完全准确,这时候就需要对测距导线三角高程计算表进行改正,而这个改正数就是我们要讨论的内容。
首先,我们需要明确改正数的定义。
改正数,顾名思义,就是对原有数据进行修正的数值。
在测距导线三角高程计算中,改正数主要用于修正由于测量误差导致的高程计算结果偏差。
改正数的计算方法主要依赖于测量误差的具体情况。
一般来说,如果误差是随机分布的,那么我们可以采用概率统计的方法来计算改正数;如果误差具有规律性,那么我们可以通过具体分析误差来源,采用相应的修正方法来计算改正数。
在实际应用中,改正数的使用可以大大提高测距导线三角高程计算的精度。
具体来说,首先需要根据实际情况,对测距导线三角高程计算表进行修正,然后使用修正后的计算表进行高程计算,这样可以有效提高计算结果的精度。
然而,测距导线三角高程计算表的改正数并不是一成不变的,随着测量条件的变化,改正数也需要进行相应的调整。
因此,如何优化改正数的计算,以适应不同的测量条件,是当前测绘工程中一个重要的研究课题。
