题型四规律探索题
新初一规律探索题参考答案
前言：七年级上册数学期中考试，主要考察书本前2章，想要考试取得好的成绩，首先应一般能力：①基本知识、基本技能；②计算能力；其次要想获得高分必须具备高分能力：①观察、猜想、推理、验证的能力；②数形结合思想的建立；③分类讨论思想的建立；④方程思想的建立；对于重点中学学生，尤为重要。
高分能力是今后学习领先的有力保障，需要大量练习、总结、体会，七年级涉及的仅仅是一部分。
一、规律探索类题型规律探索型问题是指在一定条件下，探索发现有关数学对象所具有的规律性或不变性的问题，它往往给出了一组变化了的数、式子、图形等条件，要求学生通过：①读题②观察③分析④猜想⑤验证，来探索对象的规律。
它体现了“特殊到一般”、“数形结合”等数学思想方法，考察学生的分析、解决问题能力。
题型可涉及填空、选择或解答。
【题型分类】【1、数字问题】最好具备数列的有关知识（小学奥数有涉及），实际考察的是：经历探索事物间的数量关系，用字母表示数和代数式表示的过程，建立初步的符号感，发展抽象思维，进一步使学生体会到代数式是刻画现实世界的有效数学模型。
如：1、正整数规律1、2、3、4、5、、、、可以表示为n （其中n 为正整数）2、奇数规律1、3、5、7、9、、、、可以表示为21n -（其中n 为正整数）3、偶数规律2、4、6、8、10、、、、可以表示为2n （其中n 为正整数）4、正、负交替规律变化一组数，不看他们的绝对值，只看其性质，为正负交替（1）、-、+、-、+、-、+、-、+可以表示为(1)n -（2）、+、-、+、-、+、-、+、-可以表示为1(1)n +-5、平方数规律1、4、9、16、、、、可以表示为2n （其中n 为正整数），能看得出：上面的规律数+1、+2、-1、-26、等差数列常识按一定次序排列的一列数就叫数列。
例如：（1）1，2，3，4，5，6，…（2）1，2，4，8，16，32；A 、一个数列中从左至右的第n 个数，称为这个数列的第n 项。
2018届中考数学专题4 规律探索题 (共28张PPT)
考点·梳理自清
考题·体验感悟
考法·互动研析
类型一
类型二
解:(1)4 17 (2)猜想:(2n+1)2-4n2=2(2n+1)-1.证明如下: 左边=(2n+1)2-4n2=4n2+4n+1-4n2=4n+1, 右边=2(2n+1)-1=4n+2-1=4n+1. 左边=右边, 故(2n+1)2-4n2=2(2n+1)-1.
考点·梳理自清
考题·体验感悟
考法·互动研析
类型一
类型二
例4(2012· 安徽,17)在由m×n(m×n>1)个小正方形组成的矩形网 格中,研究它的一条对角线所穿过的小正方形个数f, (1)当m,n互质(m,n除1外无其他公因数)时,观察下列图形并完成 下表:
考点·梳理自清考题·Fra bibliotek验感悟考法·互动研析
类型一
类型二
解析:(1)1+3+5+7=16=42, 设第n幅图中球的个数为an, 观察,发现规律:a1=1+3=22,a2=1+3+5=32,a3=1+3+5+7=42,…, 故an-1=1+3+5+…+(2n-1)=n2. (2)观察图形发现: 图中黑球可分三部分,1到n行,第n+1行,n+2行到2n+1行, 即1+3+5+…+(2n-1)+[2(n+1)-1]+(2n1)+…+5+3+1=1+3+5+…+(2n-1)+(2n+1)+(2n-1)+…+5+3+1=an2 2 2 1+(2n+1)+an-1=n +2n+1+n =2n +2n+1. 答案:(1)4 n2 (2)2n+1 2n2+2n+1
中考数学专题复习——规律探索(详细答案)
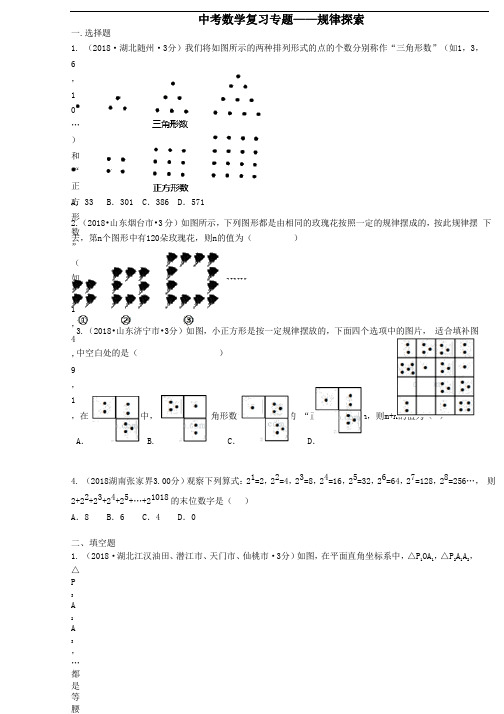
中考数学复习专题——规律探索一.选择题1. （2018·湖北随州·3 分）我们将如图所示的两种排列形式的点的个数分别称作“三角形数”（如 1，3， 6，10…）和“正方形数”（如 1，4，9，1，在小于 200 的数中，设最大的“三角形数”为 m ，最大的 “正方形数”为 n ，则 m +n 的值为（ ）A ．33B ．301C ．386D ．5712.（2018•山东烟台市•3 分）如图所示，下列图形都是由相同的玫瑰花按照一定的规律摆成的，按此规律摆 下去，第 n 个图形中有 120 朵玫瑰花，则 n 的值为（ ）3.（2018•山东济宁市•3 分）如图，小正方形是按一定规律摆放的，下面四个选项中的图片， 适合填补图中空白处的是（ ）A ．B ． B.C ．D ．4. （2018 湖南张家界 3.00 分）观察下列算式：21=2，22=4，23=8，24=16，25=32，26=64，27=128，28=256…， 则 2+22+23+24+25+…+21018 的末位数字是（ ）A ．8B ．6C ．4D ．0二、填空题 1. （2018·湖北江汉油田、潜江市、天门市、仙桃市·3 分）如图，在平面直角坐标系中，△P 1OA 1，△P 2A 1A 2， △P3A2A3，…都是等2.（2018•江苏淮安•3 分）如图，在平面直角坐标系中，直线l为正比例函数y=x 的图象，点A1的坐标为（1，，过点A1作x轴的垂线交直线l于点D1，以A1D1为边作正方形A1B1C1D1；过点C1作直线l的垂线，垂足为A2，交x 轴于点B2，以A2B2为边作正方形A2B2C2D2；过点C2作x 轴的垂线，垂足为A3，交直线l 于点D3，以A3D3为边作正方形A3B3C3D3，…，按此规律操作下所得到的正方形A n B n C n D n的面积是（92）n﹣1 ．3.（2018•山东东营市•3分）如图，在平面直角坐标系中，点A1，A2，A3，…和B1，B2，B3，…分别在直线y=15x+b和x轴上．△OA1B1，△B1A2B2，△B2A3B3，…都是等腰直角三角形．如果点A1（1，那么点A2018的纵坐标是20173()2．4.（2018•临安•3 分.）已知：2+23=22×23，3+38=32×38，4+415=42×415，5+524=52×524，…，若10+ba=102×ba符合前面式子的规律，则a+b= ．5. （2018•广西桂林•3分）将从1开始的连续自然数按如图规律排列：规定位于第m行，第n列的自然记为6. （2018•广西南宁•3 分）观察下列等式：30=1，31=3，32=9，33=27，34=81，35=243，…，根据其中规律可 得 30+31+32+…+32018 的结果的个位数字是 ．7. （2018·黑龙江龙东地区·3 分）如图，已知等边△A BC 的边长是 2，以 B C 边上的高 AB 1 为边作等边三角 形，得到第一个等边△AB 1C 1；再以等边△AB 1C 1 的 B 1C 1边上的高 AB 2 为边作等边三角形，得到第二个等边△AB 2C 2；再以等边△A B 2C 2 的B 2C 2边上的高 A B 3 为边作等边三角形，得到第三个等边△AB 3C 3；…，记△B 1CB 2 的面积为 S 1，△B 2C 1B 3 的面积为 S 2，△B 3C 2B 4 的面积为 S 3，如此下去，则 S n = ．8.（2018·黑龙江齐齐哈尔·3 分）在平面直角坐标系中，点 A （3，1）在射线 O M 上，点 B （3，3）在 射线 ON 上，以 AB 为直角边作 Rt △A BA 1，以 BA 1 为直角边作第二个 Rt △BA 1B 1，以A 1B 1 为直角边作第三个 Rt△A 1B 1A 2，…，依次规律，得到 R t △B 2017A 2018B 2018，则点 B 2018 的纵坐标为 ． 9.（2018•广东•3 分）如图，已B 1 作 B 1A 2∥OA 1 交双曲线于点 A 2，过 A 2 作 A 2B 2∥A 1B 1 交 x 轴于点 B 2，得到第二个等边△B 1A 2B 2；过 B 2 作 B 2A 3∥B 1A 2 交双曲线于点 A 3，过 A 3 作 A 3B 3∥A 2B 2 交 x 轴于点 B 3，得到第三个等边△B 2A 3B 3；以此类推，…，则点 B 6 的坐标 为 （ ） ．nn201810. （2018•广西北海•3 分）观察下列等式： 30 = 1， 31 = 3， 32 = 9 ， 33 = 27 ， 34 = 81， 35= 243，…，根据其中规律可得 01220183+3+3+...3+的结果的个位数字是 。
初一专题4,规律探究-教师版
2019-2020学年初一专题（四）——规律探索（数字类）第一部分必备知识第一：等差类如果一组数从第二项起，每一项与它的前一项的差等于同一个常数例：1，3，5，7，9，11，13，15，…____________2，5，8，11，14，17，20，23，…____________7，13，19，25，31，37，43，49，…____________第二：等比类如果一组数从第二项起，每一项与它的前一项的比等于同一个常数例：2，4，8，16，32．…________________3，9，27，54，162．…________________第三：平方类如果一组数中每一项是该项数的平方例：1，4，9，16，25…________________1，14，19，116，125…________________第四：三角形类古希腊科学家把数1，3，6，10，15，21……这些数，都可以排成三角形，像这样的数称为三角形数例：1……………第一行23……………第二行456……………第三行78910……………第四行第五：周期类如果一组数不断的循环出现的形式例：1，2，3，1，2．3．…________________（写出第2019个数是）-1，1，-1，1，-1．…________________第二部分例题精讲第一：等差类【例1】观察下列关于自然数的等式：223415⨯=-①225429⨯=-②2274313⨯-=③……根据上述规律解决下列问题：（1）完成第四个等式：294-⨯（）2=（）；（2）写出你猜想的第n 个等式（用含n 的式子表示），并验证其正确性．【分析】由①②③三个等式可得，被减数是从3开始连续奇数的平方，减数是从1开始连续自然数的平方的4倍，计算的结果是被减数的底数的2倍减1，由此规律得出答案即可．【解答】解：（1）223415-⨯=①225429-⨯=②2274313-⨯=③⋯所以第四个等式：2294417-⨯=；（2）第n 个等式为：22(21)441n n n +-=+，左边2222(21)4441441n n n n n n =+-=++-=+，右边41n =+；左边=右边22(21)441n n n ∴+-=+．【总结】此题考查数字的变化规律，找出数字之间的运算规律，利用规律解决问题【例2】阅读下面的材料：按照一定顺序排列着的一列数称为数列，数列中的每一个数叫做这个数列的项．排在第一位的数称为第一项，记为a1，排在第二位的数称为第二项，记为a2，依此类推，排在第n位的数称为第n项，记为a n．所以，数列的一般形式可以写成：a1，a2，a3，…，a n，…．一般地，如果一个数列从第二项起，每一项与它前一项的差等于同一个常数，那么这个数列叫做等差数列，这个常数叫做等差数列的公差，公差通常用d表示．如：数列1，3，5，7，…为等差数列，其中a1=1，a2=3，公差为d=2．（1）等差数列5，10，15，…的公差d为__________，第5项是__________．（2）如果一个数列a1，a2，a3，…，a n…，是等差数列，且公差为d，那么根据定义可得到：a2-a1=d，a3-a2=d，a4-a3=d，…，a n-a n-1=d，…所以a2=a1+d，a3=a2+d=（a1+d）+d=a1+2d，a4=a3+d=（a1+2d）+d=a1+3d，……由此，请你填空完成等差数列的通项公式：a n=a1+（）d（3）-4041是不是等差数列-5，-7，-9…的项？如果是，是第几项？【分析】（1）根据公差定义进行计算得d，再推算第5项便可；（2）由a2=a1+d，a3=a2+d，a4=a3+d…可知：序列号n比d的系数小1，故：a n=a1+（n-1）d．（3）先根据样例求出通项公式，再将-4041代入通项公式求出n，若n为正整数就可以断定-4041是此等差数列的某一项，反之则不是．【解答】解：（1）根据题意得，1055d =-=；315a = ，4315520a a d =+=+=，5420525a a d =+=+=，故答案为：5；25．（2）21a a d=+ 3211()2a a d a d d a d =+=++=+，4311(2)3a a d a d d a d =+=++=+，⋯⋯1(1)n a a n d∴=+-故答案为：1n -．（3）根据题意得，等差数列5-，7-，9-⋯的项的通项公式为：52(1)n a n =---，则52(1)4041n ---=-，解之得：2019n =4041∴-是等差数列5-，7-，9-⋯的项，它是此数列的第2019项．【总结】本题考查了学生的分析、阅读等自学能力，解题的关键是要认真阅读题目，理解题目呈现的数学思想及数学方法．【例3】一串数：11，12-，22，12-，13，23-，33，23-，13，14-，24，34-，44，34-，24，14-……（1）试问45-是第几个数？（2）试问711是第几个数？【分析】分母是1的分数有1个，分母是2的分数由3个，分母是3的分数有5个，……分母是n 的分数有2n -1个分数，先根据分母的变换规律，得出分母小于5的数的个数以及分母小于11的数的个数，再根据所求在分母为5的数中的位置，以及所求在分母为11的数中的位置，分别判断它们在一串数中的位置即可．【解答】解：（1）分母为1的数有1211⨯-=个，分母为2的数有2213⨯-=个，分母为3的数有2315⨯-=个，分母为4的数有2417⨯-=个，故分母小于5的数有：135716+++=个，分母为5的数有2519⨯-=个，其中的第4个和第6个为45-，45∴-是第20个数和第22个数；（2）由（1）得，分母为10的数有210119⨯-=个，故分母小于11的数有：(119)10135191002+⨯+++⋯+==个， 分母为11的数有211121⨯-=个，其中的第7个和第15个为711，∴711是第107个数和第115个数．【总结】本题主要考查了数字变化规律类问题，认真观察、仔细思考，善用联想是解决这类问题的方法．解题时注意：分子都是从1开始到与分母的数字相同连续的自然数，再递减到1，此规律是解决问题的关键．第二：等比类【例1】观察下面的一列单项式：234524816、、、、、---x x x x x 根据其中的规律，得出第10个单项式是（）A.9102-x B.992x C.992-x D.9102x 【分析】通过观察题意可得：n 为奇数时，单项式为负数．x 的指数为n 时，2的指数为（n -1）．由此可解出本题．【解答】解：依题意得：（1）n 为奇数，单项式为：(1)2n n x --；（2）n 为偶数时，单项式为：(1)2n n x -．综合（1）、（2），本数列的通式为：12()n n x -- ，∴第10个单项式为：9102x ．故选：D ．【总结】确定单项式的系数和次数时，把一个单项式分解成数字因数和字母因式的积，是找准单项式的系数和次数的关键．分别找出单项式的系数和次数的规律也是解决此类问题的关键．【例2】将一张正方形纸片剪成四个大小、形状一样的小正方形（如图所示），记为第一次操作，然后将其中的一片又按同样的方法剪成四小片，记为第二次操作，如此循环进行下去．请将下表中空缺的数据填写完整，并解答所提出的问题：操作次数1234⋯正方形个数47____________⋯（1）如果剪100次，共能得到个正方形；（2）如果剪n 次共能得到n b 个正方形，试用含有n 、n b 的等式表示它们之间的数量关系；（3）若原正方形的边长为1，设n a 表示第n 次所剪的正方形的边长，试用含n 的式子表示n a ；（4）试猜想12341n n a a a a a a -++++⋯++与原正方形边长的数量关系，并用等式写出这个关系．【分析】（1）观察图形及表格发现每多剪一刀就会增加3个小正方形，据此填表即可；（2）根据得到的规律得到通项公式，然后代入求值即可；（3）根据每次将边长一分为二即可得到答案；（4）利用发现的规律，代入数值即可求得答案．【解答】解：观察图形知道：剪一次，有4个小正方形，剪两次有7个小正方形，剪三次有10个小正方形，剪四次有13个小正方形，规律：每多剪一刀就会增加3个小正方形，故第n 个共有43(1)31n n +-=+个，（1）令100n =得313100301n +=⨯=；（2）剪n 次共能得到n b 个正方形，则用含有n 、n b 的等式表示它们之间的数量关系为31n b n =+；（3）第一次所剪的正方形的边长为12，第二次所剪的正方形的边长为21()2；第三次所剪的正方形的边长为31()2，⋯第n 次所剪的正方形的边长1()2n n a =；（4）231234111111()()()1()22222n nn n a a a a a a -++++⋯++=+++⋯+=-故答案为：（1）301；（2）31n b n =+；（3）1()2n n a =；（4）11()2n-【总结】本题考查了图形的变化类问题，找到规律并用通项公式表示出来是解决本题的关键．第三：平方类【例1】某同学在做数学题时，发现了下面有趣的结果：第1行：321-=第2行：87654+--=第3行：1514131211109++---=第4行：242322212019181716+++----=．．．．．．根据以上规律，可知第10行左起第一个数是_______．【分析】考察的数字从第一个数字开始进行判断其中的规律，3，8，15，24.....;【解答】解：3=22-1；8=32-1；15=42-1；24=52-1......第10个式子左起第一个数是112-1=120【总结】平方不仅是直观的平方类，可能在平方的基础上进行加减的过程【例2】观察下列关于自然数的等式：22222222491779213109319139425①，②，③，④-⨯=-⨯=-⨯=-⨯=L 根据上述规律解决下列问题：（1）完成第⑤个等式___________=_____________；（2）写出你猜想的第n 个等式：___________________（用含n 的式子表示）；【分析】（1）仿照以上等式确定出所求即可；（2）归纳总结得到一般性规律，写出验证即可【解答】解：（1）第五个等式：22169531-⨯=；故答案为：25；31；（2）第n 个等式：22(31)961n n n +-=+，左边22961961n n n n =++-=+=右边，则等式成立．【总结】此题考查了有理数的混合运算，熟练掌握运算法则是解本题的关键．第四：三角形类【例1】如图，是由负整数组成的“数阵”，观察规律并填空：12345678910111213141516171819202122232425-------------------------⋅⋅⋅⋅⋅⋅⋅⋅（1）第9行的最后一个数是___________，它是正整数__________的平方的_________，第9行共有____________个数；（2）第n 行的第一个数是_____________，最后一个数是_____________________，第n 行共有_____________个数．【分析】三角形的数堆需要观察边上的数字的变化规律，注意其中正负的变化【解答】观察“数阵”知第一行1个数，最后一个数是1平方的相反数第二行3个数，最后一个数是2平方的相反数第三行5个数，最后一个数是3平方的相反数...所以第九行的最后一个数是-81,9平方的相反数，共有17个数所以n 行有2n-1个数，最后一个数是n 的平方的相反数，n 行共有2n-1个数【总结】观察数字与项数之间的关系进行寻找规律即可【例2】图1是由若干个小圆圈堆成的一个形如等边三角形的图案,最上面一层有一个圆圈,以下各层均比上一层多一个圆圈,一共堆了n层.第一层第二层第三层第n层图1图2图3（1）请用含有n的式子表示出图1所有圆圈的个数；（2）如果图2的圆圈共有10层，我们自上往下，在每个圆圈中都按图2的方式填上一串连续的正整数1,2,3,4,…，则最底层最右边这个圆圈中的数是：；（3）（附加题型）我们自上往下，在每个圆圈中都按图3的方式填上一串连续的整数，1,2,2,3,3,3，…，请求出图3中所有圆圈中各数之和.【分析】（1）根据图1中所有圆圈的个数为：1+2+3+4+......+n，进行计算即可；（2）当n=10时，求得代数式的值即可；（3）图3中所有圆圈中各数之和依据平方公式进行计算即可．【解答】解：（1）图1中所有圆圈的个数为：1123(1)2n n n +++⋯+=+（个）；（2）当10n =时，11(1)10115522n n +=⨯⨯=（个）；故答案为：55；（3）图3中所有圆圈中各数之和：222221011211234103856⨯⨯++++⋯+==（个）．【总结】此题主要考查了图形的变化类，要求学生通过观察，分析、归纳发现其中的规律，并应用发现的规律解决问题第五：周期类【例1】电子跳蚤在数轴上的某点，第一步从0K 向左跳1个单位到1K ，第二步从1K 向右跳2个单位到2K ，第三步从2K 向左跳3个单位到3K ，第四步从3K 向右跳4个单位到4K ， ，按以上规律跳了100步，电子跳蚤落在数轴上的点100K ，且所表示的数恰好是2019，则电子跳蚤的初始位置0K 所表示的数是__________.【分析】规定向左跳为负数，向右跳为正数，设电子跳蚤的初始位置K 0表示的数为x ，分别表示出K 1,K 2,K 3,......K 100可以列方程求解．【解答】解：设0k点所表示的数为x，则1k，2k，3k，⋯，100k所表示的数分别为x-1，x-1+2，x-1+2-3，⋯，x-1+2-3+4....-99+100，由题意知：x-1+2-3+4....-99+100=2019，所以x=1969．答：电子跳蚤的初始位置0K点所表示的数为1969．【总结】本题考查一元一次方程的应用，实际问题中，可以用正负数表示具有相反意义的量，本题中，向左、向右具有相反意义，可以用正负数表示，并列出等量关系．【例2】如图，按大拇指，食指，中指，无名指，小指，再无名指，中指……的顺序数数，当数到2018时，对应的手指是（）A.食指B.中指C.无名指D.小指【分析】如右图可知，如果按照大拇指，食指，中指，无名指，小指，再无名指，中指的顺序数数，除第1圈是5个数外，其余各圈数内均是4个数，且每两组循环一次【解答】解：根据题意，按大拇指，食指，中指，无名指，小指，再无名指，中指⋯⋯的顺序数数，如右图，可观察出第1次数时是5个数，其余都是4个数，且每两组循环按照“无名指，中指，食指，大拇指，食指，中指，无名指，小指”循环一次，÷=⋯⋯，∴-=，201382515201852013∴对应的应是食指，5故选：A．【总结】本题考查1到2018之间的自然数数手指进行循环，然后寻找各个数排列的规律，难度适中，也检查学生的运算能力．第三部分达标练习1.一列数：0、1、2、3、6、7、14、15、30……这串数是小明按照一定规则写下来的，他第一次写下“0、1”，第二次接着写“2、3”，第三次接着写“6、7”，第四次接着写“14、15”，就这样一直接着往下写，那么这串数接下来的三个数应该是下面的（）A.30、32、64B.31、62、63C.31、32、33D.31、45、462.有若干个数,第一个数记为1a,第二个数记为2a,⋅⋅⋅,第n个数记为n a.若12a=,从第二个数起,每个数都等于“1与它前面那个数的差的倒数”.（1）试计算:2a=______,3a=______,4a=_____,5a=.a是多少?（2）这排数有什么规律吗?由你发现的规律,请计算20183.如图是由从1开始的连续自然数组成的，观察规律并填空：123456789101112131415161718192021222324252627282930313233343536⋅⋅⋅⋅⋅⋅⋅⋅（1）第8行的最后一个数是，它是自然数的平方，第8行共有个数；（2）用含n的式子表示（n为正整数）：第n行的第一个数是，最后一个数是，第n行共有个数．4.观察下列关于自然数的等式：224917①-⨯=；2279213②-⨯=；22109319③-⨯=；22139425④-⨯=； 根据上述规律解决下列问题：（1）完成第⑤个等式___________=_____________；（2）写出你猜想的第n个等式：___________________（用含n的式子表示）；5.观察下列等式：第1个等式：2241932--=，第2个等式2252962--=，第3个等式：2263992--=，第4个等式：22749122--=，按照以上规律，解决下列问题：（1）写出第5个等式：．（2）写出你猜想的第n个等式：．（用含n的等式表示），并证明．6.将正数1,2,3,4,5………按以下方式排列根据规律从2006到2008的箭头依次为（）A.↑，→B.→，↑C.↓，→D.→，↓7.观察下表三组数中每组数的规律后，回答下列问题．序号1234567⋯n A组3579111315⋯B组5813202940⋯24n+ C组48163264128256⋯（1）请填写上表中的三处空格；（2）由表可知，随着n的值逐渐变大，三组数中，最先超过10000的是组（填“A”、“B”或“C”)；（3）在A组的数中，任意圈出相邻的三个数，例如，圈出5、7、9，可求出它们的和为21．问能否圈出这样的三个数，使它们的和为607？若能，请求出这三个数；若不能，请说明理由．第三部分达标练习答案1.B2.23，3，12-；3，233.64，8，15；n 2，n 2-2n +2，2n -14.22169531-⨯=；22(31)961n n n +-=+5.解：（1） 第1个等式：2241932--=，第2个等式2252962--=，第3个等式：2263992--=，第4个等式：22749122--=，∴第5个等式：22859152--=，故答案为22859152--=，（2）第n 个等式：22(3)932n n n +--=，证明：左边226996322n n n nn ++--====右边，∴22(3)932n n n +--=，故答案为：22(3)932n n n +--=．6.A7.2n +1；53；2n +1；C ；不能。
2020年中考数学压轴题题型专练：规律探索题(含答案)
2020中考数学压轴题题型专练：规律探索题类型一数式规律1. 将一组数2，2，6，22，10，…，210，按下列方式进行排列：2，2，6，22，10；23，14，4，32，25；…若2的位置记为(1，2)，23的位置记为(2，1)，则38这个数的位置记为________．(4，4)【解析】∴当10n －2＝38时，n ＝4，∴38这个数的位置记为(4，4)． 2. 按一定规律排列的一列数：－12，1，－1， ，－911，1113，－1317，…，请你仔细观察，按照此规律方框内的数字应为________．1 【解析】将原来的一列数变形为－12，33，－55， ，－911，1113，－1317，…，观察这列数可得奇数项为负数，偶数项为正数，分子是依次从小到大排列的连续奇数，分母是依次从小到大排列的质数，故方框内填77，故答案为1.3. 观察下列数据：－2，52，－103，174，－265，…，它们是按一定规律排列的，依照此规律，第11个数据是________．－12211 【解析】∵－2＝－12＋11，52＝ 22＋12，－103＝－32＋13，174＝ 42＋14，－265＝ －52＋15，∴第11个数据是：－112＋111＝－12211.4. 已知a 1＝ t t －1，a 2＝ 11－a 1，a 3＝ 11－a 2，…，a n ＋1＝ 11－a n(n 为正整数，且t ≠0，1)，则a 2018＝ ________(用含t 的代数式表示)． 1－t 【解析】根据题意得：a 1＝ t t －1，a 2＝ 11－t t －1＝ 1－t ，a 3＝ 11－1＋t ＝ 1t ，a 4＝ 11－1t＝ t t －1， (2018)3＝ 672……2，∴a 2018的值为1－t . 5. 一列数：0，1，2，3，6，7，14，15，30，…，这列数是由小明按照一定规律写下来的，他第一次写下“0，1”，第二次接着写“2，3”，第三次接着写“6，7”，第四次接着写“14，15”，就这样一直接着往下写，那么30后三个连续数应该是________．31，62，63 【解析】通过观察可知，下一组数的第一个数是前一组数的第二个数的2倍，在同一组数中的前后两个数相差1，由此可得30后三个连续数为31，62，63.类型二 图形累加规律1. 如图，用菱形纸片按规律依次拼成如图图案，第1个图案中有5个菱形纸片，第2个图案中有9个菱形纸片，第3个图案中有13个菱形纸片，按此规律，第10个图案中有________个菱形纸片．第1题图41【解析】观察图形发现：第1个图案中有5＝4×1＋1个菱形纸片，第2个图案有9＝4×2＋1个菱形纸片，第3个图案中有13＝4×3＋1个菱形纸片，…，第n个图形中有4n＋1个菱形纸片，故第10个图案中有4×10＋1＝41个菱形纸片．2. 如图，每个图案都由大小相同的正方形组成，按照此规律，第n个图案中这样的正方形的总个数可用含n的代数式表示为________．第2题图n2＋n【解析】由题图知，第1、2、3个图案对应的正方形的个数分别为2＝1×2、6＝2×3、12＝3×4，…，∴第n个图案所对应的正方形的个数为n(n＋1)＝n2＋n.3. 下列图形都是由同样大小的小圆圈按一定规律所组成的，其中第①个图形中一共有4个小圆圈，第②个图形中一共有10个小圆圈，第③个图形中一共有19个小圆圈，…，按此规律排列下去，第⑦个图形中小圆圈的个数为________．第3题图85【解析】可以分两部分观察，上半部分小圆圈个数为：1＋2＋3＋…＋n ＋n＋1，下半部分小圆圈个数为n2，所以第⑦个图形小圆圈个数为1＋2＋3＋4＋5＋6＋7＋8＋72＝85.4. 如图是用棋子摆成的“T”字图案：从图案中可以看出，第一个“T”字图案需要5枚棋子，第二个“T”字图案需要8枚棋子，第三个“T”字图案需要11枚棋子．则摆成第n个图案需要________枚棋子．第4题图3n＋2【解析】观察图案可知，图案分成两部分，横向的横子数量依次为3，5，7，…，纵向的棋子数量依次为2，3，4，…，∴第n个图案棋子数量为2n＋1＋(n＋1)＝3n＋2.5. 如图，由若干盆花摆成图案，每个点表示一盆花，几何图形的每条边上(包括两个顶点)都摆有n(n≥3)盆花，每个图案中花盆总数为S，按照图中的规律可以推断S与n(n≥3)的关系是________．第5题图n2－n【解析】n＝3时，S＝6＝3×2，n＝4时，S＝12＝4×3，n＝5时，S ＝20＝5×4，…，依此类推，当边数为n时，S＝n(n－1)＝n2－n.类型三图形成倍递变规律1. 如图，过点A0(2，0)作直线l：y＝33x的垂线，垂足为点A1，过点A1作A1A2⊥x轴，垂足为点A2，过点A2作A2A3⊥l，垂足为点A3，…，这样依次下去，得到一组线段：A0A1，A1A2，A2A3，…，则线段A2016A2017的长为()A. (32)2015 B. (32)2016C. (32)2017 D. (32)2018第1题图B【解析】由y＝33x，得直线l的倾斜角为30°，∵点A0坐标为(2，0)，∴OA0＝2，∴OA1＝32OA0＝3，OA2＝32OA1＝32，OA3＝32OA2＝334，OA4＝32OA3＝98，…，∴OA n＝(32)n OA0＝2×(32)n.∴OA2016＝2×(32)2016，A2016A2017＝12×2×(32)2016＝(32)2016.2. 如图，在平面直角坐标系中，边长不等的正方形依次排列，每个正方形都有一个顶点落在函数y＝x的图象上，从左向右第3个正方形中的一个顶点A的坐标为(8，4)，则第4个正方形的边长为________，第n个正方形的边长为________．第2题图8，2n-1【解析】∵函数y＝x与x轴正半轴的夹角为45°，∴直线y＝x与正方形的边围成的三角形是等腰直角三角形，∵A(8，4)，∴第四个正方形的边长为8，第三个正方形的边长为4，第二个正方形的边长为2，第一个正方形的边长为1，…，第n个正方形的边长为2n－1.3. 如图，在矩形ABCD中，AD＝a，AB＝b，连接其对边中点，得到四个矩形，顺次连接矩形AEFG各边中点，得到菱形I1；连接矩形FMCH对边中点，又得到四个矩形，顺次连接矩形FNPQ各边中点，得到菱形I2，…，如此操作下去，得到菱形I2016，则I2016的面积是________．第3题图(12)4033ab 【解析】由题意得，菱形I 1的面积为：12AG ·AE ＝12×12a ×12b ＝(12)3ab ，菱形I 2的面积为：12FQ ·FN ＝12×(12×12a )×(12×12b )＝(12)5ab ；…；菱形I n 的面积为：(12)2n ＋1ab .∴当n ＝2016时，菱形I 2016的面积为(12)4033ab .4. 如图，已知∠AOB ＝30°，在射线OA 上取点O 1，以O 1为圆心的圆与OB 相切；在射线O 1A 上取点O 2，以O 2为圆心，O 2O 1为半径的圆与OB 相切；在射线O 2A 上取点O 3，以O 3为圆心，O 3O 2为半径的圆与OB 相切；…；在射线O 9A 上取点O 10，以O 10为圆心，O 10O 9为半径的圆与OB 相切．若⊙O 1的半径为1，则⊙O 10的半径长是________．第4题图29 【解析】如解图，作O 1C 、O 2D 、O 3E 分别⊥OB ，∵∠AOB ＝30°，∴OO 1＝2CO 1，OO 2＝ 2DO 2，OO 3＝2EO 3，∵O 1O 2＝DO 2，O 2O 3＝ EO 3，O 1C ＝1，∴O 2D ＝2，O 3E ＝4，∴圆的半径呈2倍递增，∴⊙On 的半径为2n －1CO 1，∵⊙O 1的半径为1，∴⊙O 10的半径长＝ 29.第4题解图类型四图形周期变化规律1. 如图，已知菱形OABC的顶点O(0，0)，B(2，2)，若菱形绕点O逆时针旋转，每秒旋转45°，则第60秒时，菱形的对角线交点D的坐标为()A. (1，－1)B. (－1，－1)C. (2，0)D. (0，－2)第1题图B【解析】∵菱形OABC的顶点O(0，0)，点B的坐标是(2，2)，∴BO与x 轴的夹角为45°，∵菱形的对角线互相垂直平分，∴点D是线段OB的中点，∴点D的坐标是(1，1) ，∵菱形绕点O逆时针旋转，每秒旋转45°，360°÷45°＝8，∴每旋转8秒，菱形的对角线交点就回到原来的位置(1，1)，∵60÷8＝7……4，∴第60秒时是把菱形绕点O逆时针旋转了7周回到原来位置后，又旋转了4秒，即又旋转了4×45°＝180°，∴点D的对应点落在第三象限，且对应点与点D关于原点O成中心对称，∴第60秒时，菱形的对角线交点D的坐标为(－1，－1)．2. 下列一串梅花图案是按一定规律排列的，请你仔细观察，在前2018个梅花图案中，共有________个“”图案．第2题图505【解析】∵2018÷4＝504……2，∴有505个．3. 如图，在平面直角坐标系中，边长为1的正方形OA1B1C1的两边在坐标轴上，以它的对角线OB1为边作正方形OB1B2C2，再以正方形OB1B2C2的对角线OB2为边作正方形OB2B3C3，以此类推…，则正方形OB2017B2018C2018的顶点B2018的坐标是________．第3题图(0，21009)【解析】点B的位置依次落在第一象限、y正半轴、第二象限、x负半轴、第三象限、y负半轴、第四象限、x正半轴…，每8次一循环.2018÷8＝252……2，所以B2018落在y轴正半轴，故B2018的横坐标是0；OB n是正方形的对角线，OB1＝2，OB2＝2＝(2)2，OB3＝22＝(2)3，…，所以OB2018＝(2)2018＝21009，所以B2018的坐标为(0，21009)．4. 如图，正△ABO的边长为2，O为坐标原点，A在x轴上，B在第二象限，△ABO沿x轴正方向作无滑动的翻滚，经一次翻滚后得△A1B1O，则翻滚3次后点B的对应点的坐标是________，翻滚2017次后AB中点M经过的路径长为________．第4题图(5，3)，(134633＋896)π 【解析】如解图，翻滚3次后点B 的对应点是B 3，作B 3E ⊥x 轴于E ，易知OE ＝ 5，B 3E ＝ 3，B 3(5，3)，观察图象可知翻滚3次为一个循环，一个循环点M 的运动路径为MM 1︵、M 1M 2︵、M 2M 3︵，120 ·π ·3180＋120 ·π ·1180＋120 ·π ·1180＝23＋43π，∵2017÷3＝672…1，∴翻滚2017次后AB 中点M 经过的路径长为672×23＋43π＋23π3＝ (134633＋896)π.第4题解图。
初中数学规律探究问题题型梳理
初中数学规律探究题型“规律探究类问题”是中考中的一棵常青树，一直受到命题者的青睐。
这类试题要求学生有一定的数感与符号感，学生通过观察、分析、比较、概括、推理、判断等探索活动，得到图形或数式内在规律的一般通式。
不仅有利于促进数学知识和数学方法的巩固和提高，也有利于自主探索，创新精神的培养。
因此规律探究类问题一直成为命题的热点。
题型一、一阶等差规律一阶等差规律意思是第一次做差差为常数。
主要考察对图形变化的规律观察，从图形变化转化为数字变化，从数字变化中去发掘规律。
这部分内容相对简单，可以直接观察图形得出规律，也可以通过套通项公式的方法找出规律，考试中单独考察这部分的概率很小，往往与其它形式一起结合考察。
1、规律分析：问题本质：前后的图形相比较，每一幅图形以恒定不变的速度保持图形增加（减少）的个数。
2、首差法通项公式（通法）（1）将题目的已知转为一组数据，第一个数记为1a 以此第n 个数记为n a （2）对这组数据两两之间做差，差为一个固定常数记为d ，即=d 后项—前项 （3）则该类型的规律为：任意的第n 项满足：d n a a n )1(1-+=（4）若记不住公式，上述数据转化为坐标点),(n a n ，设通项公式为：b kn a n +=，代入前2组数据，通过解一次函数方法，即可得到通项公式；例1、如图所示，摆第一个“小屋子”要5枚棋子，摆第二个要11枚棋子，摆第三个要17枚棋子，则摆第30个“小屋子”要（ ）枚棋子．【解析】用一阶等差实质进行分析。
根据题意分析可得：第1个图案中棋子的个数5个． 第2个图案中棋子的个数5611+=个．⋯．每个图形都比前一个图形多用6个．∴第30个图案中棋子的个数为5296179+⨯=个．答案：179例2、观察下列数：14，39，516，725，936⋯，它们按一定规律排列，那么这一组数第n 个数是( ) A ．221n n - B ．221n n + C ．221(1)n n ++ D ．221(1)n n -+ 【解析】法一：观察分析。
人教版七年级数学上册小专题练习四《有理数-探索规律题》(含答案)
人教版七年级数学上册小专题练习四《有理数-探索规律题》一、选择题1.观察下列各式： - 2x ，4x 2， - 8x 3，16x 4， - 32x 5，…则第n 个式子是( )A.- 2n - 1x nB.( - 2)n - 1x nC.- 2n x nD.( - 2)n x n2.下图是一个运算程序的示意图，若开始输入x 的值为125，则第2 016次输出的结果为( )A.125B.25C.1D.53.如图是由一些点组成的图形，按此规律，第n 个图形中点的个数为( )A.n 2＋1B.n 2＋2C.2n 2＋2D.2n 2 - 14.如图，下列每个图都是由若干个点组成的形如三角形的图案，每条边(包括两个顶点)有n 个点，每个图案的总点数是S ，按此推断S 与n 的关系式为( )A.S=3nB.S=3(n - 1)C.S=3n - 1D.S=3n ＋15.下面每个表格中的四个数都是按相同规律填写的：根据此规律确定x 的值为( )A.135B.170C.209D.2526.有一列数a 1，a 2，a 3，a 4，…，a n ，从第二个数开始，每一个数都等于1与它前面那个数的倒数的差，若a 1=2，则a 2018的值为( )A.2B.- 1C.12D.2018 7.a 是不为1的有理数，我们把称为a 的差倒数，如2的差倒数为=﹣1，﹣1的差倒数=，已知a 1=5，a 2是a 1的差倒数，a 3是a 2的差倒数，a 4是a 3的差倒数…，依此类推，a 2019的值是( )A ．5 B.﹣ C ． D ．8.如下表,从左到右在每个小格子中都填入一个整数．．，使得其中任意三个相邻．．格子中所填整数之和都相等，则第2014个格子中的数为( )A.3B.2C.0D.-19.已知一列数：1，-2，3，-4，5，-6，7，…将这列数排成下列形式：按照上述规律排下去，那么第100行从左边数第5个数是( )A.-4955B.4955C.-4950D.495010.计算：，，，，，归纳各计算结果中的个位数字规律，猜测22022-1的个位数字是（）A．1 B．3 C．7 D．5二、填空题11.填在下面各正方形中的四个数之间都有一定的规律，按此规律得出a＋b＋c=________.12.观察下列等式：1=12,1+3=22, 1+3+5=32，1+3+5+7=42,…，则1+3+5+7+…+2 015=_________.13.已知：，，，…，观察上面的计算过程，寻找规律并计算C106=.14.如图，是一个运算程序的示意图，若开始输入x的值为625，则第2020次输出的结果为．15.观察下列数据：﹣2，，﹣，，﹣，…，它们是按一定规律排列的，依照此规律，第11个数据是．16.正整数按如图的规律排列．请写出第20行，第21列的数字．参考答案1.答案为：D2.答案为：D.3.答案为：B4.答案为：B.5.答案为：C6.答案为：C7.答案为：D.8.答案为：B；解析：已知其中任意三个相邻格子中所填整数之和都相等,则3+a+b=a+b+c,a+b+c=b+c-1,所以a=-1,c=3，按要求排列顺序为，3，-1，b，3，-1，b，…，再结合已知表得：b=2，所以每个小格子中都填入一个整数后排列是：3，-1，2，3，-1，2，…，得到：每3个数一个循环，则：2014÷3=670余3，因此第2011个格子中的数为2．故选B9.答案为：B10.答案为：B11.答案为：110.12.答案为：10082.13.答案为：21014.答案为：1解析：依次求出每次输出的结果，根据结果得出规律，即可得出答案．解：当x=625时，x=125，当x=125时，x=25，当x=25时，x=5，当x=5时，x=1，当x=1时，x+4=5，当x=5时，x=1，…依此类推，以5，1循环，(2020﹣2)÷2=1010，即输出的结果是1，故答案为：115.答案为：﹣．解析：∵﹣2=﹣，，﹣，，﹣，…，∴第11个数据是：﹣=﹣．16.答案为：420；。
中考数学专题复习— 探索规律问题 完整版 后附真题剖析
解:(1)观察图 1 可知:中间的每个正方形都对应了两个等腰直角三角形, 所以每增加一块正方形地砖,等腰直角三角形地砖就增加 2 块.故答案 为 2. (2)观察图形 2 可知:中间一个正方形的左上、左边、左下共有 3 个等 腰直角三角形,它右上和右下各对应了一个等腰直角三角形,右边还有 1 个等腰直角三角形,即 6=3+2×1+1=4+2×1;图 3 和图 1 中间正方形右 上和右下都对应了两个等腰直角三角形,均有与图 2 一样的规律,图 3:8=3+2×2+1=4+2×2;归纳得:4+2n(即 2n+4); ∴若一条这样的人行道一共有 n(n 为正整数)块正方形地砖,则等腰直
中考数学专题复习
许多事物都存在着一定的规律性，只 要我们善于观察、勤于思考，就可以发现 它们，并利用它们来丰富我们的生活。
●解题思路
一、数字规律
例1
请你按照如下的数字规律,分别
写出第n个数字：（n为正整数）
① ②③ ④ ⑤
n
（1）2,4,6,8,10, … , _2_n__;
（2）1,3,5,7,9, … , 2n-1
一、选择题
1.平面上不重合的两点确定一条直线,不同三点最多可确定 3 条直线,
若平面上不同的 n 个点最多可确定 21 条直线,则 n 的值为 ( C )
A.5
B.6 C.7 D.8
2.(2021 山东临沂)实验证实,放射性物质在放出射线后,质量将减少,
减少的速度开始较快,后来较慢,实际上,物质所剩的质量与时间成某
•即时演练•
1.(2020 天水)观察等式:2+22=23-2;2+22+23=24-2;2+22+23+24=25-2;…已
2024年中考数学复习重难点题型训练—规律探索题(含答案解析)
2024年中考数学复习重难点题型训练—规律探索题（含答案解析）类型一数式规律1．（2023·云南·统考中考真题）按一定规律排列的单项式：2345,a ，第n 个单项式是（）AB1n -CnD1n -【答案】Ca ，指数为1开始的自然数，据此即可求解．【详解】解：按一定规律排列的单项式：2345,a ，第nn ，故选：C ．【点睛】本题考查了单项式规律题，找到单项式的变化规律是解题的关键．2．（2023·山东·统考中考真题）已知一列均不为1的数123n a a a a ，，，，满足如下关系：1223121111a a a a a a ++==--，34131111n n na a a a a a +++==-- ，，，若12a =，则2023a 的值是（）A ．12-B ．13C ．3-D ．2【答案】A【分析】根据题意可把12a =代入求解23a =-，则可得312a =-，413a =，52a =……；由此可得规律求解．【详解】解：∵12a =，∴212312a +==--，3131132a -==-+，411121312a -==+，51132113a +==-，…….；由此可得规律为按2、3-、12-、13四个数字一循环，∵20234505.....3÷=，∴2023312a a ==-；故选A ．【点睛】本题主要考查数字规律，解题的关键是得到数字的一般规律．3．（2023·湖南常德·统考中考真题）观察下边的数表（横排为行，竖排为列），按数表中的规律，分数202023若排在第a 行b 列，则a b -的值为()11122113223114233241……A ．2003B ．2004C ．2022D ．2023【答案】C【分析】观察表中的规律发现，分数的分子是几，则必在第几列；只有第一列的分数，分母与其所在行数一致．【详解】观察表中的规律发现，分数的分子是几，则必在第几列；只有第一列的分数，分母与其所在行数一致，故202023在第20列，即20b =；向前递推到第1列时，分数为201912023192042-=+，故分数202023与分数12042在同一行．即在第2042行，则2042a =．∴2042202022.a b -=-=故选：C ．【点睛】本题考查了数字类规律探索的知识点，解题的关键善于发现数字递变的周期性和趋向性．4．（2023·四川内江·统考中考真题）对于正数x ，规定2()1xf x x =+，例如：224(2)213f ⨯==+，1212212312f ⨯⎛⎫== ⎪⎝⎭+，233(3)312f ⨯==+，1211313213f ⨯⎛⎫== ⎪⎝⎭+，计算：11111(1)1011009932f f f f f f ⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫+++++++ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭(2)(3)(99)(100)(101)f f f f f +++++= （）A ．199B ．200C ．201D ．202【答案】C【分析】通过计算11(1)1,(2)2,(3)223f f f f f ⎛⎫⎛⎫=+=+= ⎪ ⎪⎝⎭⎝⎭，⋯可以推出11111(1)(2)(3)(99)(100)(101)1011009932f f f f f f f f f f f ⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫++++++++++++ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭结果．【详解】解：2(1)1,11f ==+ 12441212(2),,(2)2,112323212f f f f ⨯⎛⎫⎛⎫====+= ⎪ ⎪+⎝⎭⎝⎭+122331113(3),,(3)2,113232313f f f f ⨯⨯⎛⎫⎛⎫====+= ⎪ ⎪+⎝⎭⎝⎭+…2100200(100)1100101f ⨯==+，1212100()11001011100f ⨯==+，1(100)(2100f f +=，11111(1)(2)(3)(99)(100)(101)1011009932f f f f f f f f f f f ⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫++++++++++++ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭21001=⨯+201=故选：C ．【点睛】此题考查了有理数的混合运算，熟练掌握运算法则，找到数字变化规律是解本题的关键．5.（2021·湖北鄂州市·中考真题）已知1a 为实数﹐规定运算：2111a a =-，3211a a =-，4311a a =-，5411a a =-，……，111n n a a -=-．按上述方法计算：当13a =时，2021a 的值等于（）A．23-B．13C．12-D．23【答案】D 【分析】当13a =时，计算出23421,,3,32a a a ==-=⋅⋅⋅⋅⋅⋅，会发现呈周期性出现，即可得到2021a 的值．【详解】解：当13a =时，计算出23421,,3,32a a a ==-=⋅⋅⋅⋅⋅⋅，会发现是以：213,,32-，循环出现的规律，202136732=⨯+ ，2021223a a ∴==，故选：D ．【点睛】本题考查了实数运算规律的问题，解题的关键是：通过条件，先计算出部分数的值，从中找到相应的规律，利用其规律来解答．6.（2021·湖北随州市·中考真题）根据图中数字的规律，若第n 个图中的143q =，则p的值为（）A．100B．121C．144D．169【答案】B 【分析】分别分析n 的规律、p 的规律、q 的规律，再找n 、p 、q 之间的联系即可．【详解】解：根据图中数据可知：1,2,3,4n =，……22221,2,3,4,p =……222221,31,41,51,q =----……则2p n =，2(1)1q n =+-，∵第n 个图中的143q =，∴2(1)1=143q n =+-，解得：11n =或13n =-(不符合题意，舍去)∴2=121p n =，故选：B ．【点睛】本题主要考查数字之间规律问题，将题中数据分组讨论是解决本题的关键．7.（2021·山东济宁市·中考真题）按规律排列的一组数据：12，35，□，717，926，1137，…，其中□内应填的数是（）A．23B．511C．59D．12【答案】D 【分析】分子为连续奇数，分母为序号的平方1+，根据规律即可得到答案．【详解】观察这排数据发现，分子为连续奇数，分母为序号的平方1+，∴第n 个数据为：2211n n -+当3n =时W 的分子为5，分母为23110+=∴这个数为51102=故选：D ．【点睛】本题考查了数字的探索规律，分子和分母分别寻找规律是解题关键．8.（2021·湖北十堰市·）将从1开始的连续奇数按如图所示的规律排列，例如，位于第4行第3列的数为27，则位于第32行第13列的数是（）A．2025B．2023C．2021D．2019【答案】B 【分析】根据数字的变化关系发现规律第n 行，第n 列的数据为：2n(n-1)+1，即可得第32行，第32列的数据为：2×32×(32-1)+1=1985，再依次加2，到第32行，第13列的数据，即可．解：观察数字的变化，发现规律：第n行，第n列的数据为：2n(n-1)+1，∴第32行，第32列的数据为：2×32×(32-1)+1=1985，根据数据的排列规律，第偶数行从右往左的数据一次增加2，∴第32行，第13列的数据为：1985+2×(32-13)=2023，故选：B．【点睛】本题考查了数字的变化类，解决本题的关键是观察数字的变化寻找探究规律，利用规律解决问题．9.（2020•天水）观察等式：2+22＝23﹣2；2+22+23＝24﹣2；2+22+23+24＝25﹣2；…已知按一定规律排列的一组数：2100，2101，2102，…，2199，2200，若2100＝S，用含S的式子表示这组数据的和是（）A．2S2﹣S B．2S2+S C．2S2﹣2S D．2S2﹣2S﹣2【分析】根据已知条件和2100＝S，将按一定规律排列的一组数：2100，2101，2102，…，2199，2200，求和，即可用含S的式子表示这组数据的和．【解析】∵2100＝S，∴2100+2101+2102+…+2199+2200＝S+2S+22S+…+299S+2100S＝S（1+2+22+…+299+2100）＝S（1+2100﹣2+2100）＝S（2S﹣1）＝2S2﹣S．10．（2023·湖南岳阳·统考中考真题）观察下列式子：21110-=⨯；22221-=⨯；23332-=⨯；24443-=⨯；25554-=⨯；…依此规律，则第n （n 为正整数）个等式是．【答案】()21n n n n -=-【分析】根据等式的左边为正整数的平方减去这个数，等式的右边为这个数乘以这个数减1，即可求解．【详解】解：∵21110-=⨯；22221-=⨯；23332-=⨯；24443-=⨯；25554-=⨯；…∴第n （n 为正整数）个等式是()21n n n n -=-，故答案为：()21n n n n -=-．【点睛】本题考查了数字类规律，找到规律是解题的关键．11．（2023·山东临沂·统考中考真题）观察下列式子21312⨯+=；22413⨯+=；23514⨯+=；……按照上述规律，2n =．【答案】()()111n n -++【分析】根据已有的式子，抽象出相应的数字规律，进行作答即可．【详解】解：∵21312⨯+=；22413⨯+=；23514⨯+=；……∴()()2211n n n ++=+，∴()()2111n n n -++=．故答案为：()()111n n -++【点睛】本题考查数字类规律探究．解题的关键是从已有的式子中抽象出相应的数字规律．12．（2023·四川成都·统考中考真题）定义：如果一个正整数能表示为两个正整数m ，n 的平方差，且1m n ->，则称这个正整数为“智慧优数”．例如，221653=-，16就是一个智慧优数，可以利用22()()m n m n m n -=+-进行研究．若将智慧优数从小到大排列，则第3个智慧优数是；第23个智慧优数是．【答案】1545【分析】根据新定义，列举出前几个智慧优数，找到规律，进而即可求解．【详解】解：依题意，当3m =，1n =，则第1个一个智慧优数为22318-=当4m =，2n =，则第2个智慧优数为224214-=当4m =，1n =，则第3个智慧优数为224115-=，当5m =，3n =，则第5个智慧优数为225316-=当5m =，2n =，则第6个智慧优数为225221-=当5m =，1n =，则第7个智慧优数为225324-=……6m =时有4个智慧优数，同理7m =时有5个，8m =时有6个，12345621+++++=第22个智慧优数，当9m =时，7n =，第22个智慧优数为2297814932-=-=，第23个智慧优数为9,6m n ==时，2296813645-=-=，故答案为：15，45．【点睛】本题考查了新定义，平方差公式的应用，找到规律是解题的关键．13．（2023·山东聊城·统考中考真题）如图，图中数字是从1开始按箭头方向排列的有序数阵．从3开始，把位于同一列且在拐角处的两个数字提取出来组成有序数对：()3,5；()7,10；()13,17；()21,26；()31,37…如果单把每个数对中的第一个或第二个数字按顺序排列起来研究，就会发现其中的规律．请写出第n 个数对：．【答案】()221,22n n n n ++++【分析】根据题意单另把每个数对中的第一个或第二个数字按顺序排列起来研究，可发现第n 个数对的第一个数为：()11n n ++，第n 个数对的第二个位：()211n ++，即可求解．【详解】解：每个数对的第一个数分别为3，7，13，21，31，…即：121⨯+，231⨯+，341⨯+，451⨯+，561⨯+，…则第n 个数对的第一个数为：()2111n n n n ++=++，每个数对的第二个数分别为5，10，17，26，37，…即：221+；231+；241+；251+；261+…，则第n 个数对的第二个位：()221122n n n ++=++，∴第n 个数对为：()221,22n n n n ++++，故答案为：()221,22n n n n ++++．【点睛】此题考查数字的变化规律，找出数字之间的排列规律，利用拐弯出数字的差的规律解决问题．14．（2023·内蒙古通辽·统考中考真题）点Q 的横坐标为一元一次方程37322x x +=-的解，纵坐标为a b +的值，其中a ，b 满足二元一次方程组2428a b a b -=⎧⎨-+=-⎩，则点Q 关于y 轴对称点Q '的坐标为___________．【答案】()5,4--【分析】先分别解一元一次方程37322x x +=-和二元一次方程组2428a b a b -=⎧⎨-+=-⎩，求得点Q的坐标，再根据直角坐标系中点的坐标的规律即可求解．【详解】解：37322x x +=-，移项合并同类项得，525x =，系数化为1得，5x =，∴点Q 的横坐标为5，∵2428a b a b -=⎧⎨-+=-⎩①②，由2+⨯①②得，3=12b -，解得：4b =-，把4b =-代入①得，24=4a +，解得：0a =，∴=04=4a b +--，∴点Q 的纵坐标为4-，∴点Q 的坐标为()5,4-，又∴点Q 关于y 轴对称点Q '的坐标为()5,4--，故答案为：()5,4--．【点睛】本题考查解一元一次方程和解二元一次方程组、代数值求值、直角坐标系中点的坐标的规律，熟练掌握解一元一次方程和解二元一次方程组的方法求得点Q 的坐标是解题的关键．15．（2023·湖北恩施·统考中考真题）观察下列两行数，探究第②行数与第①行数的关系：2-，4，8-，16，32-，64，……①0，7，4-，21，26-，71，……②根据你的发现，完成填空：第①行数的第10个数为；取每行数的第2023个数，则这两个数的和为．【答案】1024202422024-+【分析】通过观察第一行数的规律为(2)n -，第二行数的规律为(2)1n n -++，代入数据即可.【详解】第一行数的规律为(2)n -，∴第①行数的第10个数为10(2)1024-=；第二行数的规律为(2)1n n -++，∴第①行数的第2023个数为2023(2)-，第②行数的第2023个数为2023(2)2024-+，∴202422024-+，故答案为：1024；202422024-+．【点睛】本题主要考查数字的变化，找其中的规律，是今年考试中常见的题型.16.（2021·湖南怀化市·中考真题）观察等式：232222+=-，23422222++=-，2345222222+++=-，……，已知按一定规律排列的一组数：1002，1012，1022，……，1992，若1002=m ，用含m 的代数式表示这组数的和是___________．【答案】100(21)m -【分析】根据规律将1002，1012，1022，……，1992用含m 的代数式表示，再计算0199222+++ 的和，即可计算1001011011992222++++ 的和．【详解】由题意规律可得：2399100222222++++=- ．∵1002=m∴23991000222222=2m m +++++== ，∵22991001012222222+++++=- ，∴10123991002222222=++++++ 12=2m m m m =+=．102239910010122222222+=++++++ 224=2m m m m m =++=．1032399100101102222222222=++++++++ 3248=2m m m m m m =+++=．……∴1999922m =．故10010110110199992222222m m m ++++=+++ ．令012992222S ++++= ①12310022222S ++++= ②②-①，得10021S-=∴10010110110199992222222m m m ++++=+++ =100(21)m -故答案为：100(21)m -．【点睛】本题考查规律问题，用含有字母的式子表示数、灵活计算数列的和是解题的关键．17.（2022·湖南怀化）正偶数2，4，6，8，10，……，按如下规律排列，2468101214161820……则第27行的第21个数是______．【答案】744【分析】由图可以看出，每行数字的个数与行数是一致的，即第一行有1个数，第二行有2个数，第三行有3个数••••••••第n行有n个数，则前n行共有(1)2n n+个数，再根据偶数的特征确定第几行第几个数是几．【详解】解：由图可知，第一行有1个数，第二行有2个数，第三行有3个数，•••••••第n行有n个数．∴前n行共有1+2+3+⋯+n=(1)2n n+个数．∴前26行共有351个数，∴第27行第21个数是所有数中的第372个数．∵这些数都是正偶数，∴第372个数为372×2=744．故答案为：744．【点睛】本题考查了数字类的规律问题，解决这类问题的关键是先根据题目的已知条件找出其中的规律，再结合其他已知条件求解．18.（2021·四川眉山市·中考真题）观察下列等式：1311 212x===+⨯；2711623x ===+⨯；313111234x ===+⨯；……根据以上规律，计算12320202021x x x x ++++-= ______．【答案】12016-【分析】根据题意，找到第n 个等式的左边为1与1n(n 1)+的和；利用这个结论得到原式＝112+116+1112+…+1120202021⨯﹣2021，然后把12化为1﹣12，16化为12﹣13，120152016⨯化为12015﹣12016，再进行分数的加减运算即可．【详解】11(1)n n =++，20201120202021x =+⨯12320202021x x x x ++++- ＝112+116+1112+…+1120202021⨯﹣2021＝2020+1﹣12+12﹣13+…+12015﹣12016﹣2021＝2020+1﹣12016﹣2021＝12016-．故答案为：12016-．【点睛】本题考查了二次根式的化简和找规律，解题关键是根据算式找的规律，根据数字的特征进行简便运算．19.（2022·安徽）观察以下等式：第1个等式：()()()22221122122⨯+=⨯+-⨯，第2个等式：()()()22222134134⨯+=⨯+-⨯，第3个等式：()()()22223146146⨯+=⨯+-⨯，第4个等式：()()()22224158158⨯+=⨯+-⨯，……按照以上规律．解决下列问题：(1)写出第5个等式：________；(2)写出你猜想的第n 个等式（用含n 的式子表示），并证明．【答案】(1)()()()2222516101610⨯+=⨯+-⨯(2)()[][]22221(1)21(1)2n n n n n +=+⋅+-+⋅，证明见解析【分析】（1）观察第1至第4个等式中相同位置的数的变化规律即可解答；（2）观察相同位置的数变化规律可以得出第n 个等式为()[][]22221(1)21(1)2n n n n n +=+⋅+-+⋅，利用完全平方公式和平方差公式对等式左右两边变形即可证明．(1)解：观察第1至第4个等式中相同位置数的变化规律，可知第5个等式为：()()()2222516101610⨯+=⨯+-⨯，故答案为：()()()2222516101610⨯+=⨯+-⨯；(2)解：第n 个等式为()[][]22221(1)21(1)2n n n n n +=+⋅+-+⋅，证明如下：等式左边：()2221441n n n +=++，等式右边：[][]22(1)21(1)2n n n n +⋅+-+⋅[][](1)21(1)2(1)21(1)2n n n n n n n n =+⋅+++⋅⋅+⋅+-+⋅[](1)411n n =+⋅+⨯2441n n =++，故等式()[][]22221(1)21(1)2n n n n n +=+⋅+-+⋅成立．【点睛】本题考查整式规律探索，发现所给数据的规律并熟练运用完全平方公式和平方差公式是解题的关键．20.（2021·贵州铜仁市·中考真题）观察下列各项：112，124，138，1416，…，则第n 项是______________．【答案】12nn +【分析】根据已知可得出规律：第一项：1111122=+，第二项：2112242=+，第三项：3113382=+…即可得出结果．【详解】解：根据题意可知：第一项：1111122=+，第二项：2112242=+，第三项：3113382=+，第四项：41144162=+，…则第n 项是12n n +；故答案为：12nn +．【点睛】此题属于数字类规律问题，根据已知各项的规律得出结论是解决此类题目的关键．0.618≈这个数叫做黄金比，著名数学家华罗庚优选法中的“0.618法”就应用了黄金比．设12a =，b =11111S a b =+++，2222211S a b =+++，…，10010010010010011S a b=+++，则12100S S S +++= _______．【答案】5050【分析】利用分式的加减法则分别可求S 1=1，S 2=2，S 100=100，•••，利用规律求解即可．【详解】解： 12a =，b =11122ab =⨯=∴，1112211112a ba ba b b ba bS a a ++++=+==+++++++ ，222222222222222222221112a b a b S a b a b a b a b ++++=+=⨯=⨯=+++++++，…，10101001001001010101010010011100100111a b S a b a b a b +++=+=⨯=+++++∴12100S S S +++= 121005050++⋯⋯+=故答案为：5050【点睛】本题考查了分式的加减法，二次根式的混合运算，求得1ab =，找出的规律是本题的关键．22.（2021·江西中考真题）下表在我国宋朝数学家杨辉1261年的著作《详解九章算法》中提到过，因而人们把这个表叫做杨辉三角，请你根据杨辉三角的规律补全下表第四行空缺的数字是______．【答案】3【分析】通过观察每一个数字等于它上方相邻两数之和．【详解】解：通过观察杨辉三角发现每一个数字等于它上方相邻两数之和的规律，例如：第3行中的2，等于它上方两个相邻的数1，1相加，即：211=+；第4行中的3，等于它上方两个相邻的数2，1相加，即：321=+；⋅⋅⋅⋅⋅⋅由此规律：故空缺数等于它上方两个相邻的数1，2相加，即空缺数为：3，故答案是：3．【点睛】本题考查了杨辉三角数的规律，解题的关键是：通过观察找到数与数之间的关系，从来解决问题．23.（2022·山东泰安）将从1开始的连续自然数按以下规律排列：若有序数对(),n m 表示第n 行，从左到右第m 个数，如()3,2表示6，则表示99的有序数对是_______．【答案】()10,18【分析】分析每一行的第一个数字的规律，得出第n 行的第一个数字为211n +-（），从而求得最终的答案．【详解】第1行的第一个数字：()2111=+-1第2行的第一个数字：()22121=+-第3行的第一个数字：()25131=+-第4行的第一个数字：()210141=+-第5行的第一个数字：()217151=+-…..，设第n 行的第一个数字为x ，得()211x n =+-设第1n +行的第一个数字为z ，得21z n =+设第n 行，从左到右第m 个数为y 当99y =时221(1)991n n +-≤<+∴22(1)98n n -≤<∵n 为整数∴10n =∴21182x n =+-=（）∴9982118m =-+=故答案为：()10,18．【点睛】本题考查数字规律的性质，解题的关键是熟练掌握数字规律的相关性质．24.（2022·浙江舟山）观察下面的等式：111236=+，1113412=+，1114520=+，……(1)按上面的规律归纳出一个一般的结论（用含n 的等式表示，n 为正整数）(2)请运用分式的有关知识，推理说明这个结论是正确的．【答案】(1)1111(1)n n n n =+++(2)见解析【分析】（1）根据所给式子发现规律，第一个式子的左边分母为2，第二个式子的左边分母为3，第三个式子的左边分母为4，…；右边第一个分数的分母为3，4，5，…，另一个分数的分母为前面两个分母的乘积；所有的分子均为1；所以第（n+1）个式子为1111(1)n n n n =+++．（2）由（1）的规律发现第（n+1）个式子为1111(1)n n n n =+++，用分式的加法计算式子右边即可证明．(1)解：∵第一个式子()1111123621221=+=+++，第二个式子()11111341231331=+=+++，第三个式子()11111452041441=+=+++，……∴第（n+1）个式子1111(1)n n n n =+++；(2)解：∵右边=111111(1)(1)(1)(1)n n n n n n n n n n n n ++=+==+++++=左边，∴1111(1)n n n n =+++．【点睛】此题考查数字的变化规律，分式加法运算，解题关键是通过观察，分析、归纳发现其中各分母的变化规律．类型二图形规律25．（2023·重庆·统考中考真题）用长度相同的木棍按如图所示的规律拼图案，其中第①个图案用了9根木棍，第②个图案用了14根木棍，第③个图案用了19根木棍，第④个图案用了24根木棍，……，按此规律排列下去，则第⑧个图案用的木棍根数是（）A ．39B ．44C ．49D ．54【答案】B 【分析】根据各图形中木棍的根数发现计算的规律，由此即可得到答案．【详解】解：第①个图案用了459+=根木棍，第②个图案用了45214+⨯=根木棍，第③个图案用了45319+⨯=根木棍，第④个图案用了45424+⨯=根木棍，……，+⨯=根，第⑧个图案用的木棍根数是45844故选：B．【点睛】此题考查了图形类规律的探究，正确理解图形中木棍根数的变化规律由此得到计算的规律是解题的关键．25．（2023·重庆·统考中考真题）用圆圈按如图所示的规律拼图案，其中第①个图案中有2个圆圈，第②个图案中有5个圆圈，第③个图案中有8个圆圈，第④个图案中有11个圆圈，…，按此规律排列下去，则第⑦个图案中圆圈的个数为（）A．14B．20C．23D．26【答案】B【分析】根据前四个图案圆圈的个数找到规律，即可求解.=⨯-；【详解】解：因为第①个图案中有2个圆圈，2311=⨯-；第②个图案中有5个圆圈，5321=⨯-；第③个图案中有8个圆圈，8331=⨯-；第④个图案中有11个圆圈，11341…，⨯-=；所以第⑦个图案中圆圈的个数为37120故选：B.【点睛】本题考查了图形类规律探究，根据前四个图案圆圈的个数找到第n个图案的规律为31n -是解题的关键.27．（2023·山东日照·统考中考真题）数学家高斯推动了数学科学的发展，被数学界誉为“数学王子”，据传，他在计算1234100+++++ 时，用到了一种方法，将首尾两个数相加，进而得到100(1100)12341002⨯++++++= ．人们借助于这样的方法，得到(1)12342n n n ++++++= （n 是正整数）．有下列问题，如图，在平面直角坐标系中的一系列格点(),i i i A x y ，其中1,2,3,,,i n = ，且,i i x y 是整数．记n n n a x y =+，如1(0,0)A ，即120,(1,0)a A =，即231,(1,1)a A =-，即30,a = ，以此类推．则下列结论正确的是（）A ．202340a =B ．202443a =C ．2(21)26n a n -=-D ．2(21)24n a n -=-【答案】B 【分析】利用图形寻找规律()211,1n A n n ---，再利用规律解题即可．【详解】解：第1圈有1个点，即1(0,0)A ，这时10a =；第2圈有8个点，即2A 到()91,1A ；第3圈有16个点，即10A 到()252,2A ，；依次类推，第n 圈，()211,1n A n n ---；由规律可知：2023A 是在第23圈上，且()202522,22A ，则()202320,22A 即2023202242a =+=，故A 选项不正确；2024A 是在第23圈上，且()202421,22A ，即2024212243a =+=，故B 选项正确；第n 圈，()211,1n A n n ---，所以2122n a n -=-，故C 、D 选项不正确；故选B ．【点睛】本题考查图形与规律，利用所给的图形找到规律是解题的关键．28.（2022·江西）将字母“C”，“H”按照如图所示的规律摆放，依次下去，则第4个图形中字母“H”的个数是（）A．9B．10C．11D．12【答案】B 【分析】列举每个图形中H 的个数，找到规律即可得出答案．【详解】解：第1个图中H 的个数为4，第2个图中H 的个数为4+2，第3个图中H 的个数为4+2×2，第4个图中H 的个数为4+2×3=10，故选：B．【点睛】本题考查了规律型：图形的变化类，通过列举每个图形中H 的个数，找到规律：每个图形比上一个图形多2个H 是解题的关键．29.（2022·重庆）用正方形按如图所示的规律拼图案，其中第①个图案中有5个正方形，第②个图案中有9个正方形，第③个图案中有13个正方形，第④个图案中有17个正方形，此规律排列下去，则第⑨个图案中正方形的个数为（）A．32B．34C．37D．41【答案】C 【分析】第1个图中有5个正方形，第2个图中有9个正方形，第3个图中有13个正方形，……，由此可得：每增加1个图形，就会增加4个正方形，由此找到规律，列出第n 个图形的算式，然后再解答即可．【详解】解：第1个图中有5个正方形；第2个图中有9个正方形，可以写成：5+4=5+4×1；第3个图中有13个正方形，可以写成：5+4+4=5+4×2；第4个图中有17个正方形，可以写成：5+4+4+4=5+4×3；．．．第n 个图中有正方形，可以写成：5+4（n-1）=4n+1；当n=9时，代入4n+1得：4×9+1=37．故选：C．【点睛】本题主要考查了图形的变化规律以及数字规律，通过归纳与总结结合图形得出数字之间的规律是解决问题的关键．30.（2021·广西玉林市·中考真题）观察下列树枝分杈的规律图，若第n 个图树枝数用n Y 表示，则94Y Y -=（）A．4152⨯B．4312⨯C．4332⨯D．4632⨯【答案】B【分析】根据题目中的图形，可以写出前几幅图中树枝分杈的数量，从而可以发现树枝分杈的变化规律，进而得到规律21nn Y =-，代入规律求解即可．【详解】解：由图可得到：11223344211213217211521n n Y Y Y Y Y =-==-==-==-==-则：9921Y =-，∴944942121312Y Y -=--+=⨯，故答案选：B．【点睛】本题考查图形规律，解答本题的关键是明确题意，利用数形结合的思想解答31.（2021·黑龙江大庆市·中考真题）如图，3条直线两两相交最多有3个交点，4条直线两两相交最多有6个交点，按照这样的规律，则20条直线两两相交最多有______个交点【答案】190【分析】根据题目中的交点个数，找出n 条直线相交最多有的交点个数公式：1(1)2n n -．【详解】解：2条直线相交有1个交点；3条直线相交最多有1123322+==⨯⨯个交点；4条直线相交最多有11236432++==⨯⨯个交点；5条直线相交最多有1123410542+++==⨯⨯个交点；⋯20条直线相交最多有120191902⨯⨯=．故答案为：190．【点睛】本题考查的是多条直线相交的交点问题，解答此题的关键是找出规律，即n 条直线相交最多有1(1)2n n -．32．（2023·四川遂宁·统考中考真题）烷烃是一类由碳、氢元素组成的有机化合物，在生产生活中可作为燃料、润滑剂等原料，也可用于动、植物的养护．通常用碳原子的个数命名为甲烷、乙烷、丙烷、……、癸烷（当碳原子数目超过10个时即用汉文数字表示，如十一烷、十二烷……）等，甲烷的化学式为4CH ，乙烷的化学式为26C H ，丙烷的化学式为38C H ……，其分子结构模型如图所示，按照此规律，十二烷的化学式为．【答案】1226C H 【分析】根据碳原子的个数，氢原子的个数，找到规律，即可求解．【详解】解：甲烷的化学式为4CH ，乙烷的化学式为26C H ，丙烷的化学式为38C H ……，碳原子的个数为序数，氢原子的个数为碳原子个数的2倍多2个，十二烷的化学式为1226C H ，故答案为：1226C H ．【点睛】本题考查了规律题，找到规律是解题的关键．33．（2023·山西·统考中考真题）如图是一组有规律的图案，它由若干个大小相同的圆片组成．第1个图案中有4个白色圆片，第2个图案中有6个白色圆片，第3个图案中有8个白色圆片，第4个图案中有10个白色圆片，…依此规律，第n 个图案中有个白色圆片（用含n 的代数式表示）【答案】()22n +【分析】由于第1个图案中有4个白色圆片4221=+⨯，第2个图案中有6个白色圆片6222=+⨯，第3个图案中有8个白色圆片8223=+⨯，第4个图案中有10个白色圆片10224=+⨯，⋯，可得第(1)n n >个图案中有白色圆片的总数为22n +．【详解】解：第1个图案中有4个白色圆片4221=+⨯，第2个图案中有6个白色圆片6222=+⨯，第3个图案中有8个白色圆片8223=+⨯，第4个图案中有10个白色圆片10224=+⨯，⋯，∴第(1)n n >个图案中有()22n +个白色圆片．故答案为：()22n +．【点睛】此题考查图形的变化规律，通过从一些特殊的数字变化中发现不变的因素或按规律变化的因素，然后推广到一般情况．解题关键是总结归纳出图形的变化规律．34．（2023·黑龙江绥化·统考中考真题）在求123100++++ 的值时，发现：1100101+=，299101+= ，从而得到123100++++= 101505050⨯=．按此方法可解决下面问题．图（1）有1个三角形，记作11a =；分别连接这个三角形三边中点得到图（2），有5个三角形，记作25a =；再分别连接图（2）中间的小三角形三边中点得到图（3），有9个三角形，记作39a =；按此方法继续下去，则123n a a a a ++++= ．（结果用含n 的代数式表示）【答案】22n n -/22n n -+【分析】根据题意得出()14143n a n n =+-=-，进而即可求解．【详解】解：依题意，()1231,5,9,14143n a a a a n n ===⋅⋅⋅=+-=-，，∴123n a a a a ++++= ()21432122n n n n n n +-==-=-，故答案为：22n n -．【点睛】本题考查了图形类规律，找到规律是解题的关键．35.（2022·山东泰安）观察下列图形规律，当图形中的“○”的个数和“．”个数差为2022时，n 的值为____________．【答案】不存在【分析】首先根据n=1、2、3、4时，“•”的个数分别是3、6、9、12，判断出第n 个图形中“•”的个数是3n；然后根据n=1、2、3、4，“○”的个数分别是1、3、6、10，判断出第n 个“○”的个数是()12n n +；最后根据图形中的“○”的个数和“．”个数差为2022，列出方程，解方程即可求出n 的值是多少即可．【详解】解：∵n=1时，“•”的个数是3=3×1；n=2时，“•”的个数是6=3×2；n=3时，“•”的个数是9=3×3；n=4时，“•”的个数是12=3×4；……∴第n 个图形中“•”的个数是3n；又∵n=1时，“○”的个数是1=1(11)2⨯+；n=2时，“○”的个数是2(21)32⨯+=，n=3时，“○”的个数是3(31)62⨯+=，n=4时，“○”的个数是4(41)102⨯+=，……∴第n 个“○”的个数是()12n n +，由图形中的“○”的个数和“．”个数差为2022()1320222n n n +∴-=①，()1320222n n n +-=②解①得：无解解②得：12n n ==故答案为：不存在【点睛】本题考查了图形类规律，解一元二次方程，找到规律是解题的关键．36.（2022·四川遂宁）“勾股树”是以正方形一边为斜边向外作直角三角形，再以该直角三角形的两直角边分别向外作正方形，重复这一过程所画出来的图形，因为重复数次后的形状好似一棵树而得名．假设如图分别是第一代勾股树、第二代勾股树、第三代勾股树，按照勾股树的作图原理作图，则第六代勾股树中正方形的个数为______．【答案】127【分析】由已知图形观察规律，即可得到第六代勾股树中正方形的个数．【详解】解：∵第一代勾股树中正方形有1+2=3（个），第二代勾股树中正方形有1+2+22=7（个），第三代勾股树中正方形有1+2+22+23=15（个），.....．∴第六代勾股树中正方形有1+2+22+23+24+25+26=127（个），故答案为：127．【点睛】本题考查图形中的规律问题，解题的关键是仔细观察图形，得到图形变化的规律．37.（2021·湖南常德市·中考真题）如图中的三个图形都是边长为1的小正方形组成的网格，其中第一个图形有11⨯个正方形，所有线段的和为4，第二个图形有22⨯个小正方形，所有线段的和为12，第三个图形有33⨯个小正方形，所有线段的和为24，按此规律，则第n 个网格所有线段的和为____________．(用含n 的代数式表示)【答案】2n 2+2n【分析】本题要通过第1、2、3和4个图案找出普遍规律，进而得出第n 个图案的规律为S n =4n+2n ×(n-1)，得出结论即可．【详解】解：观察图形可知：第1个图案由1个小正方形组成，共用的木条根数141221,S =⨯=⨯⨯第2个图案由4个小正方形组成，共用的木条根数262232,S =⨯=⨯⨯第3个图案由9个小正方形组成，共用的木条根数383243,S =⨯=⨯⨯第4个图案由16个小正方形组成，共用的木条根数4104254,S =⨯=⨯⨯…由此发现规律是：第n 个图案由n 2个小正方形组成，共用的木条根数()22122,n S n n n n =+=+ 故答案为：2n 2+2n．【点睛】本题考查了规律型-图形的变化类，熟练找出前四个图形的规律是解题的关键．38.（2021·黑龙江绥化市·中考真题）下面各图形是由大小相同的三角形摆放而成的，图①中有1个三角形，图②中有5个三角形，图③中有11个三角形，图④中有19个三角形…，依此规律，则第n 个图形中三角形个数是_______．【答案】21n n +-【分析】此题只需分成上下两部分即可找到其中规律，上方的规律为(n-1)，下方规律为n 2，结合两部分即可得出答案．【详解】解：将题意中图形分为上下两部分，则上半部规律为：0、1、2、3、4……n-1，下半部规律为：12、22、32、42……n 2，∴上下两部分统一规律为：21n n +-．故答案为：21n n +-．【点睛】本题主要考查的图形的变化规律，解题的关键是将图形分为上下两部分分别研究．类型三与函数有关规律39．（2023·山东烟台·统考中考真题）如图，在直角坐标系中，每个网格小正方形的边长均为1个单位长度，以点P 为位似中心作正方形123PA A A ，正方形456,PA A A ⋯，按此规律作下去，所作正方形的顶点均在格点上，其中正方形123PA A A 的顶点坐标分别为()()()123,0,2,1,1,0P A A ---，()32,1A --，则顶点100A 的坐标为（）。
中考数学复习指导：探索规律型问题归类解析
探索规律型问题归类解析探索规律型问题是历年中考数学试题中的重要题型之一，其特点是给出一组变化了的数字、式子、表格、图形等，要求学生通过观察、归纳、猜想、验证、类比，探求其内在规律．1.通用的解题策略解答规律型问题一般要从特殊情况入手→探索发现规律→综合归纳→猜想得出结论→验证结论．这种“特殊——一般——特殊”的解题模式，体现了总结归纳的数学思想，也正是人们认识新事物的一般过程．具体来说，就是先写出开头几个数式的基本结构，然后通过横比或纵比找出各部分的特征，写出符合要求的结果．例1 如图1，房间地面的图案是用大小相同的黑、白正方形镶嵌而成．图中，第1个黑色“L”形由3个正方形组成，第2个黑色“L”形由7个正方形组成，…那么组成第6个黑色“L”形的正方形个数是( )(A)22 (B)23 (C)24 (D)25解析从特例入手：如图1．纵比正方形的个数3，7，11，15中，后一个数比前一个大4（即相邻两数的差为4），猜想与4有关．横比3与1，7与2，11与3，15与4之间有何关系？联想到与4有关，故改写为：3＝4×1－1，7＝4×2－1．11＝4×3－1，15＝4×4－1．猜想组成第6个黑色L形的正方形个数是4 ×6－1＝23个．故选B．点评考察相邻两数的差（或商）是探究数字规律的常用手段．常见的类型有：相邻两数的差（或商）相等或成倍数关系，相邻两数的差相等与商相等交替出现等．2.关注特殊数列(1)斐波那契数列：1，1，2，3，5，8，13，21…（其规律为：从第三项开始，每一项都等于前两项之和）；(2)平方数数列：1，4，9，16，25，36…（其规律为：n2，即每一项都等于项数的平方）．例2 有一组数：1，2，5，10，17，26…请观察这组数的构成规律，用你发现的规律确定第8个数为_______．解析规律为：n2＋1（n＝0，1，2…）．答案：50．点评此类题要注意n2，n2＋1，n2－1等(3)三角形数列：1，3，6，10，15，21，…（其规律为1＋2＋3＋…＋n）例3 世界上著名的莱布尼茨三角形如图2所示，则排在第10行从左边数第3个位置上的数是：( )（A）（B）（C）（D）解析从第3行起，从左边数第3位置上的数分别为，，，，…它们的分母可分别改写为：1×3，3×4，6×5，10×6，15×7，21×8，…，而1，3，6，10，15，21，…，正是三角形数，故答案为：．选B．(4)杨辉三角形，杨辉三角形斜边上1以外的各数，都等于它“肩上”的两数之和，如图3．(5)与等差等比数列有关的数列．如例1中3，7，11，15…就是一个等差数列．例4 数字解密：第一个数是3＝2＋1，第二个数是5＝3＋2，第三个数是9＝5＋4，第四个数是17＝9＋8，……观察并猜想第六个数应是_______．解析第二个加数1，2，4，8…规律为2n（为一等比数列，也要关注这一数列），第一个加数2，3，5，9…比第二个加数大1．所以第六个数为(25＋1)＋25＝65．例5 一组按规律排列的数：…请你推断第9个数是________．解析这列数的分母为2，3，4，5，6…的平方数，分子形成二阶等差数列，依次相差2，4，6，8…故第9个数分子为1＋2＋4＋6＋8＋10＋12＋14＋16＝73，分母为100，故答案为．(6)与循环有关的问题例6 让我们轻松一下，做一个数字游戏：第一步：取一个自然数n1＝5，计算n12＋1得a1；第二步：算出a1的各位数字之和得n2，计算n22＋1得a3；第三步：算出a2的各位数字之和得n3，再计算n32＋1得a3；……依此类推，则a2008＝_______．解析根据题意可算出a1＝26，a2＝65，a3＝122，a4＝26，a5＝65，a6＝122，…发现每3个数就出现一次循环．所以由2008＝669×3＋1，可得a2008＝a1＝26．点评一列数由某m个数循环出现组成，可依据同余等值(由n＝p·m＋r得a n＝a r)实施转换．(7)分奇数项偶数项的问题例7 一组按规律排列的式子：，…(a b≠0)，其中第7个式子是________，第n个式子是_(n为正整数)．解析6的指数2，5，8，11…，相邻两数差为3，是等差数列，其规律为3n－1；再注意到奇数项为负，偶数项为正，则第n个式子为第七个式子为3.特殊数列的迁移例8 把数字按如图4所示排列起来，从上开始，依次为第一行、第二行、第三行、…，中间用虚线围的一列，从上至下依次为1.5.13.25.…，则第10个数为_______．解析1 中间框出的一列数的规律为：第n个数为1＋4＋8＋12＋…＋4（n－1）．所以第10个数为1＋4＋8＋12＋…＋36＝．解析2 用虚线圈出的一列数1，5，13，25可改写为：02＋12，12＋22，22＋32，32＋42，猜想第10个数为92＋102＝181．点评此列数可看成是平方数数列的迁移．例9 图5中是与杨辉三角有类似性质的三角形数垒．a，b，c，d是相邻两行的前四个数，那么当a＝8时，c＝_______，d＝_______．解析除两边外，中间的每个数等于肩上两数的和．答案：9；32．点评此列数可看成是杨辉三角形的迁移．4.关注中考新题型例10 观察图6所示表格，依据表格数据排列的规律，数2008在表格中出现的次数共有_______次．解析从特例入手，通过扩充表格可得：数1，2，3，4，5，6，7，8，9，10出现次数分别为1，2，2，3，2，4，2，4，3，4．出现的次数恰为给定数的所有因数的个数，而2008的因数为1，2，4，8，251，502，1004，2008等8个．故答案为8．点评本例中新产生的数为自然数的倍数，因此，其出现的次数与其因数的多少有关，仔细观察便会发现，其出现次数就是给定数所有因数的个数，本题规律的隐蔽性较强，因而有一定的难度．。
中考数学《规律探索》专题复习试题含解析
中考数学《规律(Lv)探索》专题复习试题含解析一(Yi)、选择题1. 如图，将一张等边(Bian)三角形纸片沿中位线剪成4个小三角形，称为第一次操作；然后，将其中的一个三角形按(An)同样方式再剪成4个小三(San)角形，共得到7个小(Xiao)三角形，称为第二次操作；再将其中一个三角形按同样方式再剪成4个小三角形，共得(De)到10个小三角形，称为第三次操(Cao)作；…根据以上操作，若要得到100个小三角形，则需要操作的次数是（）A．25 B．33 C．34 D．50【考点】规律型：图形的变化类．【分析】由第一次操作后三角形共有4个、第二次操作后三角形共有（4+3）个、第三次操作后三角形共有（4+3+3）个，可得第n次操作后三角形共有4+3（n﹣1）=3n+1个，根据题意得3n+1=100，求得n的值即可．【解答】解：∵第一次操作后，三角形共有4个；第二次操作后，三角形共有4+3=7个；第三次操作后，三角形共有4+3+3=10个；…∴第n次操作后，三角形共有4+3（n﹣1）=3n+1个；当3n+1=100时，解得：n=33，故选：B．2.观察图中正方形四个顶点所标的数字规律，可知，数2016应标在（）A．第504个正方形的左下角B．第504个正方形的右下角C．第505个正方形的左上角D．第505个正方形的右下角【考点】规律型：点的坐标．【分(Fen)析】根据图形中对应的数字和各个(Ge)数字所在的位置，可以推出数2016在第多少个正方形和它所在的位置，本(Ben)题得以解决．【解(Jie)答】解(Jie)：∵2016÷4=504，又(You)∵由题目中给出的几个(Ge)正方形观察可知，每个正方形对应四个数，而第一个最小的数是0，0在(Zai)右下角，然后按逆时针由小变大，∴第504个正方形中最大的数是2015，∴数2016在第505个正方形的右下角，故选D．3．（2016.山东省临沂市，3分）用大小相等的小正方形按一定规律拼成下列图形，则第n个图形中小正方形的个数是（）A．2n+1 B．n2﹣1 C．n2+2n D．5n﹣2【考点】规律型：图形的变化类．【分析】由第1个图形中小正方形的个数是22﹣1、第2个图形中小正方形的个数是32﹣1、第3个图形中小正方形的个数是42﹣1，可知第n个图形中小正方形的个数是（n+1）2﹣1，化简可得答案．【解答】解：∵第1个图形中，小正方形的个数是：22﹣1=3；第2个图形中，小正方形的个数是：32﹣1=8；第3个图形中，小正方形的个数是：42﹣1=15；…∴第n个图形中，小正方形的个数是：（n+1）2﹣1=n2+2n+1﹣1=n2+2n；故选：C．【点评】本题主要考查图形的变化规律，解决此类题目的方法是：从变化的图形中发现不变的部分和变化的部分及变化部分的特点是解题的关键．二、填空题1．如图，①是一个三角形，分别连接这个三角形三边中点得到图②，再连接图②中间小三角形三边的中点得到图③，按这样的方法进行下去，第n个图形中共有三角形的个数为4n﹣3 ．【考点】规律型：图形的变化类．【分析】结合题意，总结可知，每(Mei)个图中三角形个数比图形的编号的(De)4倍(Bei)少(Shao)3个三角形，即可(Ke)得出结果．【解(Jie)答】解：第(Di)①是(Shi)1个三角形，1=4×1﹣3；第②是5个三角形，5=4×2﹣3；第③是9个三角形，9=4×3﹣3；∴第n个图形中共有三角形的个数是4n﹣3；故答案为：4n﹣3．【点评】此题主要考查了图形的变化，解决此题的关键是寻找三角形的个数与图形的编号之间的关系．2．如图，直线l：y=－x，点A1坐标为（－3，0）. 过点A1作x轴的垂线交直线l于点B1，以原点O为圆心，OB1长为半径画弧交x轴负半轴于点A2，再过点A2作x 轴的垂线交直线l于点B2，以原点O为圆心，OB2长为半径画弧交x轴负半轴于点A 3，…，按此做法进行下去，点A2016的坐标为 .【考点】一次函数图像上点的坐标特征，规律型：图形的变化类．【分析】由直线l：y=－x的解析式求出A1B1的长，再根据勾股定理，求出OB1的长，从而得出A2的坐标；再把A2的横坐标代入y=－x的解析式求出A2B2的长，再根据勾股定理，求出OB2的长，从而得出A3的坐标；…，由此得出一般规律．【解(Jie)答】解(Jie)：∵点(Dian)A1坐(Zuo)标为（－3，0），知(Zhi)O A1=3，把(Ba)x=－3代入(Ru)直线(Xian)y=－x中，得y= 4 ，即A1B1=4.根据勾股定理，OB1===5，∴A2坐标为（－5，0），O A2=5；把x=－5代入直线y=－x中，得y=，即A2B2=.根据勾股定理，OB2====，∴A3坐标为（－3512，0），O A3=3512；把x=－3512代入直线y=－x中，得y=，即A3B3=.根据勾(Gou)股定理，OB 3====，∴A 4坐标(Biao)为（－3523，0），O A 4=3523；……同理(Li)可得(De)A n 坐(Zuo)标为（－，0），O A n =3521--n n ；∴A 2016坐(Zuo)标为（－，0）故(Gu)答案为：（− 3520142015，0）【点(Dian)评】本题是规律型图形的变化类题是全国各地的中考热点题型，考查了一次函数图像上点的坐标特征. 解题时，要注意数形结合思想的运用，总结规律是解题的关键. 解此类题时，要得到两三个结果后再比较、总结归纳，不要只求出一个结果就盲目的匆忙得出结论。
2024辽宁中考数学二轮专题训练 题型四 规律探索题 (含答案)
2024辽宁中考数学二轮专题训练题型四规律探索题类型一图形递推变化典例精讲例1如图，∠MON ＝45°，正方形ABB 1C ，正方形A 1B 1B 2C 1，正方形A 2B 2B 3C 2，正方形A 3B 3B 4C 3，…，的顶点A ，A 1，A 2，A 3，…，在射线OM 上，顶点B ，B 1，B 2，B 3，B 4，…，在射线ON 上，连接AB 2交A 1B 1于点D ，连接A 1B 3交A 2B 2于点D 1，连接A 2B 4交A 3B 3于点D 2，…，连接B 1D 1交AB 2于点E ，连接B 2D 2交A 1B 3于点E 1，…，按照这个规律进行下去，设△ACD 与△B 1DE 的面积之和为S 1，△A 1C 1D 1与△B 2D 1E 1的面积之和为S 2，△A 2C 2D 2与△B 3D 2E 2的面积之和为S 3，…，若AB ＝2，则S n 等于______．(用含有正整数n 的式子表示)例1题图基本模型【解题步骤】分析图形可知，所有图形都是由如图所示的基本模型构成，故求出S 1，S 2，S 3的面积可类比出S n 的面积．①求S 1的面积：根据题意可得：∠AOB ＝45°，∠ABO ＝90°，∴OB ＝AB ，∵AB ＝AC ＝B 1C ＝BB 1＝______，AB ∥A 1B 1，∴A 1B 1＝2AB ＝________，∴A 1B 1＝A 1C 1＝B 2C 1＝B 1B 2＝________，∵AC ∥ON ，∴CD DB 1＝AC B 1B 2＝____，∴CD ＝________B 1C ＝________，B 1D ＝__________B 1C ＝__________．同理可得，B 2D 1＝________B 2C 1＝________．∵B 1D ∥B 2D 1，∴DE B 2E ＝B 1D B 2D 1＝________，∴S △B 1DE ＝________S △B 1B 2D ＝________，∵S △ACD ＝____，∴S 1＝________；②求S 2，S 3，…的面积：A 2B 2＝________，S △B 2D 1E 1＝________S △B 2B 3D 1＝________，∵S △A 1C 1D 1＝________，∴S 2＝________；S 3＝________；③总结，类比可得：S n ＝________．例2如图，在平面直角坐标系中，△ABC ，△A 1B 1C 1，△A 2B 2C 2，△A 3B 3C 3，…，△A n B n C n 都是等腰直角三角形，点B ，B 1，B 2，B 3，…，B n 都在x 轴上，点B 1与原点重合，点A ，C 1，C 2，C 3，…，C n 都在直线l ：y ＝13x ＋43上，点C 在y 轴上，AB ∥A 1B 1∥A 2B 2∥…∥A n B n ∥y 轴，AC ∥A 1C 1∥A 2C 2∥…∥A n C n ∥x 轴，若点A 的横坐标为－1，则点C n 的纵坐标是________．例2题图基本模型【解题步骤】分析图形可知，所有图形都是由如图所示的基本模型构成，故求出点C 1，C 2，C 3，C 4的纵坐标可类比出点C n 的纵坐标．①求点C 1的坐标：∵点C 1在直线y ＝13x ＋43上，∴设点C 1的坐标为(t ，______)．∵△B 1B 2C 1是等腰直角三角形，且点B 1与原点O 重合，∴B 1B 2＝B 2C 1，即t ＝______，解得t ＝2.∴点C 1的纵坐标为________；②求点C 2，C 3，C 4的坐标：设点C 2的坐标为(m ，______)，∵△B 2B 3C 2是等腰直角三角形，∴m －2＝________，解得m ＝________，∴点C 2的纵坐标为________．同理可得，点C 3的纵坐标为_________；点C 4的纵坐标为________；③总结，类比可得：点C n 的纵坐标为________．辽宁近年中考真题精选1.如图，四边形ABCD 是矩形，延长DA 到点E ，使AE ＝DA ，连接EB ，点F 1是CD 的中点，连接EF 1,BF 1，得到△EF 1B ；点F 2是CF 1的中点，连接EF 2，BF 2，得到△EF 2B ；点F 3是CF 2的中点，连接EF 3，BF 3，得到△EF 3B ；…；按照此规律继续进行下去，若矩形ABCD 的面积等于2，则△EF n B 的面积为_________________________．(用含正整数n 的式子表示)第1题图基本模型：____________________2.如图，在△A 1C 1O 中，A 1C 1＝A 1O ＝2，∠A 1OC 1＝30°，过点A 1作A 1C 2⊥OC 1，垂足为C 2，过点C 2作C 2A 2∥C 1A 1交OA 1于点A 2，得到△A 2C 2C 1；过点A 2作A 2C 3⊥OC 1，垂足为C 3，过点C 3作C 3A 3∥C 1A 1交OA 1于点A 3，得到△A 3C 3C 2；过点A 3作A 3C 4⊥OC 1，垂足为C 4，过点C 4作C 4A 4∥C 1A 1交OA 1于点A 4，得到△A 4C 4C 3；…；按照上面的作法进行下去，得到△A n ＋1C n ＋1C n 的面积为________．(用含正整数n 的代数式表示)第2题图基本模型：__________________3.如图，等边△A 1C 1C 2的周长为1，作C 1D 1⊥A 1C 2于D 1，在C 1C 2的延长线上取点C 3，使D 1C 3＝D 1C 1，连接D 1C 3，以C 2C 3为边作等边△A 2C 2C 3；作C 2D 2⊥A 2C 3于D 2，在C 2C 3的延长线上取点C 4，使D 2C 4＝D 2C 2，连接D 2C 4，以C 3C 4为边作等边△A 3C 3C 4；…；且点A 1，A 2，A 3，…都在直线C 1C 2同侧，如此下去，则△A 1C 1C 2，△A 2C 2C 3，△A 3C 3C 4，…，△A n C n C n ＋1的周长和．．．为________．(n ≥2，且n 为整数)第3题图基本模型：__________________4.如图，点B 1在直线l ：y ＝12x 上，点B 1的横坐标为2，过B 1作B 1A 1⊥l ，交x 轴于点A 1，以A 1B 1为边，向右作正方形A 1B 1B 2C 1，延长B 2C 1交x 轴于点A 2；以A 2B 2为边，向右作正方形A 2B 2B 3C 2，延长B 3C 2交x 轴于点A 3；以A 3B 3为边，向右作正方形A 3B 3B 4C 3，延长B 4C 3交x 轴于点A 4；…；按照这个规律进行下去，点C n 的横坐标为________(结果用含正整数n 的代数式表示)．第4题图基本模型：__________________5.如图，直线l 1的解析式是y ＝33x ，直线l 2的解析式是y ＝3x ，点A 1在l 1上，A 1的横坐标为32，作A 1B 1⊥l 1交l 2于点B 1，点B 2在l 2上，以B 1A 1，B 1B 2为邻边在直线l 1，l 2间作菱形A 1B 1B 2C 1，分别以A 1，B 2为圆心，以A 1B 1为半径画弧得扇形B 1A 1C 1和扇形B 1B 2C 1，记扇形B 1A 1C 1与扇形B 1B 2C 1重叠部分的面积为S 1；延长B 2C 1交l 1于点A 2，点B 3在l 2上，以B 2A 2，B2B3为邻边在l1，l2间作菱形A2B2B3C2，分别以A2，B3为圆心，以A2B2为半径画弧得扇形B2A2C2和扇形B2B3C2，记扇形B2A2C2与扇形B2B3C2重叠部分的面积为S2；…；按照此规律继续作下去，则S n＝__________________________(用含有正整数n的式子表示)．第5题图基本模型：________________针对训练1.如图，在平面直角坐标系中，第一次将△OAB变换成△OA1B1，第二次将△OA1B1变换成△OA2B2，第三次将△OA2B2变换成△OA3B3，已知A(1，3)，A1(2，3)，A2(4，3)，A3(8，3)，B(2，0)，B1(4，0)，B2(8，0)，B3(16，0)．将△OAB进行n次变换得到△OA n B n，则△OA n B n 的面积为________．第1题图2.如图，∠MON＝30°，点A1在ON上，点C1在OM上，OA1＝A1C1＝2，C1B1⊥ON于点B1，以A1B1和B1C1为邻边作矩形A1B1C1D1，点A1，A2关于点B1对称，A2C2∥A1C1交OM 于点C2，C2B2⊥ON于点B2，以A2B2和B2C2为邻边作矩形A2B2C2D2，连接D1D2，点A2，A3关于点B2对称，A3C3∥A2C2交OM于点C3，C3B3⊥ON于点B3，以A3B3和B3C3为邻边作矩形A3B3C3D3，连接D2D3，…，依此规律继续下去，则D2021D2022＝________．第2题图3.如图，直线y＝－x＋1分别交x轴、y轴于点A、B，点O1、A1分别是BO、BA的中点，连接A1O1、AO1；O2、A2分别是BO1、BA1的中点，连接A2O2、A1O2，…，按此规律进行下去，则S△A n A n＋1O n＋1的面积是________．第3题图4.如图，四边形OAA1B1是边长为1的正方形，以对角线OA1为边作第二个正方形OA1A2B2，连接AA2，得到△AA1A2；再以对角线OA2为边作第三个正方形OA2A3B3，连接A1A3，得到△A1A2A3；再以对角线OA3为边作第四个正方形OA3A4B4，连接A2A4，得到△A2A3A4，…，则△A n A n＋1A n＋2的面积等于________．第4题图5.如图，n个腰长为1的等腰直角三角形(Rt△B1AA1，Rt△B2A1A2，Rt△B3A2A3，…)有一条腰在同一直线上，设△A1B2C1的面积为S1，△A2B3C2的面积为S2，△A3B4C3的面积为S3，…，则S n＝________．(用含n的代数式表示)第5题图6.如图，分别过x 轴上点A 1(1，0)，A 2(2，0)，…，A n (n ，0)作x 轴的垂线，与反比例函数y ＝6x(x ＞0)的图象的交点分别为B 1，B 2，…，B n ，若△A 1B 1A 2的面积为S 1，△A 2B 2A 3的面积为S 2，…，△A n B n A n ＋1的面积为S n ，则S n ＝________．(用含n 的式子表示)第6题图7.已知直线m ：y ＝12x ＋12与直线n ：y ＝－12x ＋12交于点A ，直线n 与x 轴交于点B 1，过B 1作B 1C 1⊥x 轴，交直线m 于点C 1，作菱形AB 1D 1C 1得点D 1，过D 1作B 2C 2⊥x 轴，分别与直线n 和直线m 交于点B 2，C 2，作菱形AB 2D 2C 2得点D 2，过点D 2作B 3C 3⊥x 轴，分别与直线n 和直线m 交于点B 3，C 3，作菱形AB 3D 3C 3得点D 3，…，设△B 1C 1D 1的面积为S 1，△B 2C 2D 2的面积为S 2，△B 3C 3D 3的面积为S 3，…，依次类推，则△B 2022C 2022D 2022的面积S 2022的值是________．第7题图8.如图，△ABC 中，AB ＝AC ，∠BAC ＝30°，作BC 1⊥AC ，垂足为C 1，作CB 1⊥AB ，垂足为B 1，BC 1与CB 1交于点A 1；作B 1C 2⊥AC ，垂足为C 2，作C 1B 2⊥AB ，垂足为B 2，B 1C 2与C 1B 2交于点A 2；作B 2C 3⊥AC ，垂足为C 3，作C 2B 3⊥AB ，垂足为B 3，B 2C 3与C 2B 3交于点A 3；…；若△A 1BC 的面积为1，则四边形A n B n A n ＋1C n 的面积为________．第8题图9.如图，∠MON＝90°，点A1，A2，A3，….A n＋1在射线OM上，点B1，B2，B3，…，B n＋1在射线ON上，连接A1B2，A2B1，∠A1B2O＝∠B1A2O＝30°，A1B2∥A2B3∥A3B4…∥A n B n＋1，A2B1∥A3B2∥A4B3…∥A n＋1B n，A1B2与A2B1相交于点C1，A2B3与A3B2相交于点C2，A3B4与A4B3相交于点C3，…，A n B n＋1与A n＋1B n相交于点C n，OA1＝OB1＝1，则四边形A n C n B n O的周长为________．第9题图10.如图，∠MON＝45°，正方形ABB1C，正方形A1B1B2C1，正方形A2B2B3C2，正方形A3B3B4C3，…的顶点A，A1，A2，A3，…在射线OM上，顶点B，B1，B2，B3，B4，…在射线ON上，连接AB2交A1B1于点D，连接A1B3交A2B2于点D1，连接A2B4交A3B3于点D2，…，连接B1D1交AB2于点E，连接B2D2交A1B3于点E1，…，按照这个规律进行下去，设四边形A1DED1的面积为S1，四边形A2D1E1D2的面积为S2，四边形A3D2E2D3的面积为S3，…，若AB＝2，则S n等于________．(用含有正整数n的式子表示)第10题图11.正方形A1B1C1A2，A2B2C2A3，A3B3C3A4，…，按如图所示的方式放置，点A1，A2，A3，…和点B1，B2，B3，…分别在直线y＝－x＋2和x＝1上，且A1在x轴上，则点C2022的横坐标是________．第11题图12.如图，在平面直角坐标系中，点A(－2，0)，直线l：y＝33x＋33与x轴交于点B，以AB为边作等边△ABA1，过点A1作A1B1∥x轴，交直线l于点B1，以A1B1为边作等边△A1B1A2，过点A2作A2B2∥x轴，交直线l于点B2，以A2B2为边作等边△A2B2A3，以此类推，连接AB1，与A1B交于点C1，连接A1B2，与A2B1交于点C2，以此类推，则点C2022的纵坐标是________．第12题图类型二图形周期变化典例精讲例3如图，△A1A2A3，△A4A5A6，△A7A8A9，…，△A3n－2A3n－1A3n(n为正整数)均为等边三角形，它们的边长依次为2，4，6，…，2n，顶点A3，A6，A9，…，A3n均在y轴上，点O 是所有等边三角形的中心，则点A2016的坐标为________．例3题图【解题步骤】①确认周期：观察图形可知，三角形的顶点______个为一个循环；②确定A2016的位置：∵2016÷______＝______，∴点A2016在y轴上，且是第________个三角形的顶点；③求A2016的坐标：在△A1A2A3中，A1A2＝2，∴△A1A2A3的高为________．∵点O是△A1A2A3的中心，∴OA3＝________，同理得OA6＝________，OA9＝________，…，∴点A2016的坐标为________．辽宁近年中考真题精选1.如图①，边长为1的正三角形ABC放置在边长为2的正方形内部，顶点A在正方形的一个顶点上，边AB在正方形的一边上，将△ABC绕点B顺时针旋转，当点C落在正方形的边上时，完成第1次无滑动滚动(如图②)；再将△ABC绕点C顺时针旋转，当点A落在正方形的边上时，完成第2次无滑动滚动(如图③)；…；每次旋转的角度都不大于120°，依次这样操作下去，当完成第2016次无滑动滚动时，点A经过的路径总长为________．第1题图针对训练1.如图，在平面直角坐标系xOy中，第一象限内有一条折线，构成这条线段的端点的坐标是这样的：A1(1，1)、A2(1，2)、A3(2，2)、A4(2，3)、A5(3，3)、A6(3，4)、A7(4，4)，…，依此规律，点A71的坐标为________．第1题图2.如图，多边形A1A2A3A4A5A6、多边形A7A8A9A10A11A12、…、多边形A6n－5A6n－4A6n－3A6n－2A6n A6n(n为正整数)均为正六边形，它们的边长依次是2、4、…、2n，顶点A6、A12、…、A6n －1均在x轴上，点O是所有正六边形的中心，则A2021的坐标是________．第2题图3.如图，四边形OA1B1C1是边长为1的正方形，点A1、C1分别在x轴、y轴的负半轴上，连接OB1，以OB1的长为边长向右侧作正方形OA2B2C2，点A2在y轴的负半轴上，点C2在x轴的正半轴上，连接OB2，以OB2的长为边长向上方作正方形OA3B3C3，点A3、C3分别在x轴、y轴的正半轴上，…，按照这个规律进行下去，点B2021的坐标为________．第3题图4.如图，在直角坐标系中，以原点O为圆心的同心圆的半径由内向外依次为1，2，3，4，…，同心圆与直线y＝x和y＝－x分别交于A1，A2，A3，A4，…，则点A30的坐标是________．第4题图5.如图，在平面直角坐标系中，等腰Rt△OA1A2的直角边OA1在y轴的正半轴上，且OA1＝A1A2＝1，以OA2为直角边作第二个等腰Rt△OA2A3，以OA3为直角边作第三个等腰Rt△OA3A4，…，依此规律，得到等腰Rt△OA2021A2022，则点A2022的坐标为________．第5题图6.如图，在平面直角坐标系中，△A1A2A3，△A3A4A5，△A5A6A7，△A7A8A9，…，都是等边三角形，且点A1，A3，A5，A7，A9的坐标分别为A1(3，0)，A3(1，0)，A5(4，0)，A7(0，0)，A9(5，0)，依据图形所反映的规律，则A100的坐标为________．第6题图7.如图，边长为4的等边△ABC，AC边在x轴上，点B在y轴的正半轴上，以OB为边作等边△OBA1，边OA1与AB交于点O1，以O1B为边作等边△O1BA2，边O1A2与A1B交于点O2，以O2B为边作等边△O2BA3，边O2A3与A2B交于点O3，…，依此规律继续作等边△O n BA n，则A2020的横坐标为________．－1第7题图参考答案类型一图形递推变化典例精讲例17×22n－19【解题步骤】①2，4，4，12，13，23，23，43，23，83，12，13，13×12×43×4＝89，12×2×23＝23，23＋89＝149；②8，13，13×12×83×8＝329，12×4×43＝83，83＋329＝569，2249；③7×22n －19.例23n －12n －2【解题步骤】①13t ＋43，13t ＋43，2；②13m ＋43，13m ＋43，5，3，92，274；③3n －12n －2.辽宁近年中考真题精选1.2n ＋12n 【解析】设AB ＝CD ＝a ，AD ＝CB ＝EA ＝b ，则DE ＝2b ，DF 1＝CF 1＝12a ，CF 2＝14a ，CF 3＝18a ，∴S △EF 1B ＝S 四边形BCDE －S △DEF 1－S △CBF 1＝12(2b ＋b )a －12×2b ×12a －12×12ab ＝34ab ＝34×2＝32；S △EF 2B ＝S 四边形BCDE －S △DEF 2－S △CBF 2＝12(2b ＋b )a －12×2b ×34a －12×14ab ＝58ab ＝58×2＝54；S △EF 3B ＝S 四边形BCDE －S △DEF 3－S △CBF 3＝12(2b ＋b )a －12×2b ×78－12×18ab ＝916ab ＝916×2＝98；…；由面积变化规律可知S △EF n B ＝2n ＋12n .基本模型：2.34n 【解析】∵A 1O ＝A 1C 1＝2，∠A 1OC 1＝30°，A 1C 2⊥OC 1，∴A 1C 2＝12A 1O ＝1，C 1C 2＝C 2O ＝3，又∵A 2C 3⊥OC 1，∴A 2C 3∥A 1C 2，∴A 2C 3是△A 1C 2O 的中位线，∴A 2C 3＝12A 1C 2＝12，S △A 2C 2C 1＝12C 1C 2·A 2C 3＝34；以此类推，S △A 3C 3C 2＝342；S △A 4C 4C 3＝343；…；∴S △A n ＋1C n ＋1C n ＝34n.基本模型：3.2n －12n －1【解析】∵△A 1C 1C 2是等边三角形，∴∠A 1C 2C 1＝60°，∵C 1D 1⊥A 1C 2，∴D 1C 2＝12C 1C 2，∠D 1C 1C 2＝30°，∵C 1D 1＝D 1C 3，∴∠D 1C 3C 2＝∠D 1C 1C 2＝30°，∴∠C 2D 1C 3＝∠C 2C 3D 1＝30°，∴C 2C 3＝C 2D 1＝12C 1C 2，∴C △A 2C 2C 3＝12C △A 1C 1C 2＝12，同理C △A 3C 3C 4＝12C △A 2C 2C 3＝122，∴△A n C n C n ＋1的周长为12n －1，∴这些三角形的周长和为1＋12＋122＋…＋12n －1＝2n －12n －1.基本模型：4.7×3n －12n 【解析】如解图，过点B 1作B 1M ⊥x 轴于点M ，过点C 1作C 1N ⊥x 轴于点N ，∵点B 1的坐标为(2，1)，∴点M 的坐标为(2，0)，即B 1M ＝1，OM ＝2，由△A 1MB 1∽△B 1MO可得A 1M ＝12，又∵△C 1NA 1≌△A 1MB 1，∴A 1N ＝1，C 1N ＝12，∴点C 1的横坐标为72；同理可得，点C 2的横坐标为72×32；点C 3的横坐标为72×(32)2；…；∴点C n 的横坐标为7×3n －12n .第4题解图基本模型：5.(π3－32)×(32)2n －2【解析】∵直线l 1∶y ＝33x ，∴∠A 1Ox ＝30°，∵直线l 2∶y ＝3x ，∴∠B 1Ox ＝60°，∴∠A 1OB 1＝30°.∵A 1B 1⊥l 1，∴∠OB 1A 1＝60°，∵四边形A 1B 1B 2C 1是菱形，∴A 1C 1∥B 1B 2，∴∠B 1A 1C 1＝∠A 1B 1O ＝60°，∵A 1B 1＝A 1C 1，∴△A 1B 1C 1是等边三角形，∴S 1＝2(S 扇形A 1B 1C 1－S △A 1B 1C 1).∵点A 1的横坐标为32，∴点A 1的纵坐标为32，OA 1＝3.如解图，过点A 1作A 1D ⊥x 轴于点D ，则△A 1OB 1∽△DOA 1，∴A 1B 1DA 1＝A 1O DO ，即A 1B 132＝332，∴A 1B 1＝1，∴S 1＝2×(π6－34)＝π3－32.在△A 2A 1C 1中，A 1C 1＝A 1B 1＝1，∠C 1A 1A 2＝30°，∴A 2C 1＝12A 1C 1＝12，∴A 2B 2＝A 2C 1＋B 2C 1＝32，∴S 2＝2[(π6×(32)2－12×32×(32)2]＝(π3－32)×(32)2，同理S 3＝(π3－32)×(32)4，S 4＝(π3－32)×(32)6，∴S n ＝(π3－32)×(32)2(n －1)＝(π3－32)×(32)2n －2.第5题解图基本模型：针对训练1.3·2n 【解析】∵A ，A 1，A 2…A n 都在平行于x 轴的直线上，点的纵坐标都相等，∴A n 的纵坐标是3，这些点的横坐标有一定的规律A n ＝2n ；B ，B 1，B 2，…，B n 都在x 轴上，B n 的纵坐标是0，这些点的横坐标也有一定的规律B n ＝2n ＋1，点A n 的坐标是(2n ，3)，B n 的坐标是(2n ＋1，0)，∴△OA n B n 的面积＝12×3×OB n ＝3·2n .2.22020·7【解析】由题意得D 1D 2＝22＋（3）2＝7＝20·7，D 2D 3＝42＋（23）2＝27＝21·7，D 3D 4＝82＋（43）2＝47＝22·7，…，∴D n D n ＋1＝2n －1·7.∴D 2021D 2022＝22020·7.3.122n ＋3【解析】把x ＝0代入y ＝－x ＋1得，y ＝1，∴OB ＝1，把y ＝0代入y ＝－x ＋1得，x ＝1，∴OA ＝1，∴OA ＝OB ，∵点O 1、A 1分别是BO 、BA 的中点，∴OO 1＝12OB ＝12，O 1A 1是△OAB 的中位线，∴O 1A 1∥OA ，O 1A 1＝12OA ＝12，如解图，连接OA 1，O 1A 2，∵O 1A 1∥OA ，∴S △AO 1A 1＝S △OO 1A 1＝12×12×12＝123，同理，O 2A 2＝12O 1A 1＝14，O 2O 1＝12BO 114，S △A 1O 2A 2＝S △O 1O 2A 2＝12×14×14＝125，…，∴S △A n A n ＋1O n ＋1＝122n ＋3.第3题解图4.2n －1【解析】设△AA 1A 2、△A 1A 2A 3、△A 2A 3A 4的面积分别为S 1、S 2、S 3，∵四边形OAA 1B 1是正方形，∴OA ＝AA 1＝A 1B 1＝1，∴S 1＝12，∵∠OAA 1＝90°，∴OA 21＝12＋12＝2，∴OA 2＝A 2A 3＝2，∴S 2＝1，同理可求：S 3＝2，S 4＝4，…，∴S n ＝2n －2，∴△A n A n ＋1A n ＋2的面积S n ＋1＝2n －1.5.n2n ＋2【解析】如解图，连接B 1B 2，B 2B 3，B 3B 4，∵n 个腰长为1的等腰三角形有一条腰在同一直线上，∴B 1B 2＝B 2B 3＝B 3B 4＝1，∴△A 1B 1B 2的面积＝12，∵B 1B 2∥AA 4，∴B 1B 2AA 1＝1，B 2B 3AA 2＝12，B 3B 4AA 3＝13，∴S 1＝12×11＋1＝14，∵S 2＝12×21＋2＝13，S 3＝12×33＋1＝38，∴S n ＝12×n n ＋1＝n 2n ＋2.第5题解图6.3n【解析】如解图，分别连接OB 1，OB 2，…，OB n ，∵点A 1(1，0)，A 2(2，0)，…，A n (n ，0)，∴OA 1＝A 1A 2＝A 2A 3＝A 3A 4＝…，∵B 1，B 2，…，B n 在反比例函数y ＝6x(x ＞0)的图象上，∴S △A n OB n ＝12×6＝3，∴S 1＝S △A 1OB 1＝3，S 2＝12S △A 2OB 2＝32，S 3＝13S △A 3OB 3＝33，…，S n ＝1n S △A n OB n ＝3n .第6题解图7.24041【解析】由12x ＋12＝－12x ＋12得x ＝0，则A (0，12)，令y ＝0，由y ＝－12x ＋12＝0得x ＝1，则B 1(1，0)，C 1(1，1)，∴B 1C 1＝1，如解图，连接AD 1，D 1D 2，D 2D 3，由菱形的对称性可得AD 1＝2，∴S 菱形AB 1D 1C 1＝12AD 1·B 1C 1＝12×2×1＝1，∴S 1＝12S 菱形AB 1D 1C 1＝12，把x ＝2分别代入y ＝12x ＋12与y ＝－12x ＋12得y ＝32和y ＝－12，∴B 2(2，－12)，C 2(2，32)，∴B 2C 2＝2，由菱形的对称性得AD 2＝4，∴S 2＝12S 菱形AB 2D 2C 2＝12×12×4×2＝2，把x ＝4分别代入y ＝12x ＋12与y ＝－12x ＋12得y ＝52和y ＝－32，∴B 3(4，－32)，C 3(4，52)，∴B 3C 3＝4，由菱形的对称性得AD 3＝8，∴S 3＝12S 菱形AB 3D 3C 3＝12×12×8×4＝8，同理可得S 4＝32，S 5＝128，…，由上可知S n ＝22n －3，∴S 2022＝24041.第7题解图8.3n22n －1【解析】∵∠A ＝30°，AB ＝AC ，∴∠ABC ＝∠ACB ＝75°，∵BC 1⊥AC ，∴∠CBA 1＝15°，同理可得∠BCB 1＝15°，∴∠CA 1C 1＝30°，A 1B ＝A 1C ，∴CC 1＝12A 1C ，∵△A 1BC 的面积为1，∴12A 1B ·CC 1＝1，即12A 1C ·12A 1C ＝1，∴A 1C ＝2，∴A 1C 1＝32A 1C ＝3，∵A 1C 1⊥AC ，B 1A 2⊥AC ，∴A 1C 1∥B 1A 2，同理，A 1B 1∥A 2C 1，∴四边形A 1B 1A 2C 1是平行四边形，∵∠B 1BC ＝∠C 1CB ，∠BB 1C ＝∠CC 1B ＝90°，BC ＝CB ，∴△BB 1C ≌△CC 1B (AAS)，∴BC 1＝CB 1，∵A 1B ＝A 1C ，∴A 1B 1＝A 1C 1，∴四边形A 1B 1A 2C 1是菱形，∴A 1C 1＝A 2C 1，∵CB 1∥C 1B 2，∴∠A 2C 1A 1＝∠CA 1C 1＝30°，如解图，过点A 1作A 1M ⊥A 2C 1于M ，∴A 1M ＝12A 1C 1＝123，∴菱形A 1B 1A 2C 1的面积＝A 2C 1·A 1M ＝32＝3122×1－1；同理可得，菱形A 2B 2A 3C 2的面积＝98＝3222×2－1；菱形A 3B 3A 4C 3的面积＝2732＝3322×3－1；…；由上可知四边形A n B n A n ＋1C n 的面积＝3n 22n －1.第8题解图9.2(3)n 【解析】∵OA 1＝OB 1＝1，∠A 1B 2O ＝∠B 1A 2O ＝30°，∴OA 2＝1tan ∠OA 2B 1＝1tan30°＝3，∴A 1A 2＝OA 2－OA 1＝3－1，∵∠A 1B 2O ＝∠B 1A 2O ＝30°，∴∠B 2A 1O ＝60°，∵∠B 2A 1O ＝∠B 1A 2O ＋∠A 1C 1A 2，∴∠A 1C 1A 2＝30°，∴∠B 1A 2O ＝∠A 1C 1A 2＝30°，∴A 1A 2＝A 1C 1＝3－1，同理OB 2＝3，B 1B 2＝B 1C 1＝3－1，∴四边形A 1C 1B 1O 的周长为1＋1＋3－1＋3－1＝23，∵A 1B 2∥A 2B 3，A 2B 1∥A 3B 2，∴∠OA 1B 2＝∠OA 2B 3，∠OB 1A 2＝∠OB 2A 3，∴四边形OA 1C 1B 1∽四边形OA 2C 2B 2，且相似比为OA 2OA 1＝3，同理四边形OA 2C 2B 2∽四边形OA 3C 3B 3，且相似比为3；以此类推，四边形OA n －1C n －1B n －1∽四边形OA n C n B n ，且相似比为3；∴四边形OA 1C 1B 1∽四边形OA n C n B n ，且相似比为(3)n －1，∴四边形OA 1C 1B 1的周长四边形OA n C n B n 的周长＝1（3）n －1，∴四边形A n C n B n O 的周长为23×(3)n －1＝2(3)n .10.19×4n ＋2【解析】设△ADC 的面积为S ，由题意得，AC ∥B 1B 2，AC ＝AB ＝2，B 1B 2＝4，∴△ACD ∽△B 2B 1D ，∴S △ADC S △B 1B 2D ＝(AC B 1B 2)2＝14，∴S △B 1B 2D ＝4S ，∵CD DB 1＝AC B 1B 2＝12，CB 1＝2，∴DB 1＝43，同理D 1B 2＝83，设△B 1DE 的边B 1D 上的高为h 1，△B 2D 1E 的边B 2D 1上的高为h 2，∵B 1D ∥B 2D 1，∴△B 1DE ∽△D 1B 2E ，∴h 1h 2＝B 1D B 2D 1＝4383＝12，又∵h 1＋h 2＝4，∴h 1＝43，S 1＝12(B 1B 2)2－12B 1D ·h 1＝19×43，同理可得S 2＝19×44，…，S n ＝19×4n ＋2.11.22021＋1【解析】如解图，令y ＝0，则y ＝－x ＋2＝0，得x ＝2，∴点A 1的坐标为(2，0)．令x ＝0，则y ＝－x ＋2＝2，∴M (0，2)，∴OM ＝OA 1＝2，∴∠MA 1O ＝45°，∴∠A 1PN ＝45°，∵四边形A 1B 1C 1A 2为正方形，∴∠MA 1B 1＝90°，∴∠NA 1B 1＝45°，∴∠A 1B 1N ＝45°，∴A 1N ＝B 1N ＝2－1＝1，∴A 1P ＝A 1B 1＝A 1A 2＝A 2C 1＝B 1C 1＝2，B 1(1，－1)，如解图，连接A 2B 1，A 1C 1，则∠A 1B 1A 2＝∠C 1A 1B 1＝45°，∴∠A 2B 1N ＝∠C 1A 1N ＝90°，∴点C 1的横坐标与A 1的横坐标相等为2，A 2与B 1的纵坐标相等为－1，当y ＝－1时，y ＝－x ＋2＝－1，得x ＝3，∴点A 2的坐标为(3，－1)．∵四边形A 2B 2C 2A 3为正方形，∴∠PA 2B 2＝90°，∵∠A 1PN ＝45°，∵A 2B 2＝A 2P ＝22，∴PB 2＝2A 2B 2＝4，∴B 2(1，－3)，如解图，连接A 3B 2，A 2C 2，则A 3B 2∥x 轴，A 2C 2∥y 轴，∴点C 2的横坐标与A 2的横坐标相等为3，A 3与B 2的纵坐标相等为－3，当y ＝－3时，y ＝－x ＋2＝－3，得x ＝5，∴点A 3的坐标为(5，－3)．∴点C 3的横坐标为5.同理可得，C 4的横坐标为9，C 5的横坐标为17，…，由上可得规律，C n 的横坐标为2n －1＋1(n ≥2)，∴点C 2022的纵坐标为22021＋1.第11题解图12.22023－363【解析】∵直线l ：y ＝33x ＋33与x 轴交于点B ，∴B (－1，0)，∴OB ＝1，∵A (－2，0)，∴OA ＝2，∴AB ＝1，∵△ABA 1是等边三角形，∴A 1(－32，32)，把y ＝32代入y ＝33x ＋33，求得x ＝12，∴B 1(12，32，∴A 1B 1＝2，设C 1到x 轴的距离为h 1，C 1到A 1B 1的距离为h 1′，∴h 1＋h 1′＝yA 1＝123，∵A 1B 1//AB ，∴△A 1B 1C 1∽△BAC 1，∴h 1h 1′＝BA A 1B 1＝12，∴h 1＝13(h 1＋h 1′)＝13×123＝163，∴C 1的纵坐标为163；∵A 1B 1＝2，∴A 2(－12，332，将y ＝332代入y ＝33x ＋33中，得33x ＋33＝332，求得x ＝72，∴B 2(72，332)，∴A 2B 2＝4，设C 2到A 1B 1的距离为h 2，C 2到A 2B 2的距离为h 2′，∴h 2＋h 2′＝12A 1B 1·3＝3，∵A 1B 1//A 2B 2，∴△A 1B 1C 2∽△B 2A 2C 2，∴h 2h 2′＝A 1B 1A 2B 2＝12，∴h 2＝13(h 2＋h 2′)＝13×3＝133，∴C 2的纵坐标为yA 1＋h 2＝123＋133＝563；同理可得，C 3的纵坐标为1363；C 4的纵坐标为2963；…，∴C n 的纵坐标为2n ＋1－36 3.∴点C 2022的纵坐标是22023－363.第12题解图类型二图形周期变化典例精讲例3(0，4483)【解题步骤】①3；②3，672,672；③3，233，433，23，(0，4483)辽宁近年中考真题精选1.560π【解析】第一次操作：A 点运动路径长为l 1＝120×π×1180＝23π，第二次操作：A 点运动路径长为l 2＝30×π×1180＝16π，第三次操作：A 点运动路径长为l 3＝0，第四次操作：A 点运动路径长为l 4＝30×π×1180＝16π，第五次操作：A 点运动路径长为l 5＝120×π×1180＝23π，第六次操作：A 点运动路径长为l 6＝0，第七次操作：A 点运动路径长为l 7＝120180×π×1＝23π，…，以此类推，不难发现每三次操作，A 点的运动路径总长相同，即为l ＝23π＋16π＋0＝56π，又∵2016÷3＝672刚好整除，∴A 点的运动总路径长为l 总＝672×56π＝560π.针对训练1.(36，36)【解析】观察这些端点的坐标，有以下规律：当n 为奇数时，第n 个点的坐标为(n ＋12，n ＋12)；当n 为偶数时，第n 个点的坐标为(12n ，12n ＋1)．由此可知，点A 71的坐标为(36，36)．2.(337，－3373)【解析】观察图形可知，六边形的顶点是6个为一个循环，∵2021÷6＝336……5，∴点A 2021是第337个正六边形的顶点，且在第四象限，如解图连接OA 5，A 5，A 11，并延长至A 2021，∵点O 是所有正六边形的中心，易得△OA 5A 6、△OA 11A 12…，都是等边三角形，∴OA 5＝2、OA 11＝4、…，OA 2021＝337×2＝674，作A 2021P ⊥x 轴于点P ，∵∠A 2021OP ＝60°，∴A 2021P ＝OA 2021·sin60°＝3373，OP ＝OA 2021·cos60°＝337，∴点A 2021的坐标是(337，－3373)．第2题解图3.(－21010，－21010)【解析】由题意得，点B 1，B 2，B 3，B 4分别在第三象限，第四象限，第一象限，第二象限的角平分线上，且点B 5与点B 1在一条直线上，∴周期为4.∵2021÷4＝505……1，∴点B 2021在第三象限的角平分线上．∵四边形OA 1B 1C 1是边长为1的正方形，∴OA 1＝1，∴OB 1＝2.∵正方形OA 2B 2C 2的边长等于OB 1，∴OA 2＝2，∴OB 2＝2OA 2＝2＝(2)2.∵正方形OA 3B 3C 3的边长等于OB 2，∴OA 3＝2，∴OB 3＝2OA 3＝22＝(2)3.同理可得，OB 2021＝(2)2021，∴点B 2021的横坐标为－(2)2021×cos45°＝－（2）20222＝－210112＝－21010，纵坐标为－(2)2021×sin45°＝－（2）20222＝－210112＝－21010，∴点B 2021的坐标为(－21010，－21010)．4.(－42，42)【解析】观察题图可知，每4个点在一个图上，∴周期为4，∵30÷4＝7……2，∴A 30在直线y ＝－x 上，且在第二象限第8个圆上，即射线OA 30与x 轴的夹角是45°，∵在直角坐标系中，以原点O 为圆心的同心圆的半径由内向外依次为1，2，3，4，…，∴OA 30＝8，如解图，OA ＝8，∠AOB ＝45°，∵sin45°＝AB 8，cos45°＝OB 8，∴AB ＝42，OB ＝42，∵A 30在第二象限，∴A 30的横坐标是－42，纵坐标是42，即A 30的坐标是(－42，42)．第4题解图5.(－21010，－21010)【解析】∵等腰Rt △OA 1A 2的直角边OA 1在y 轴的正半轴上，且OA 1＝A 1A 2＝1＝(2)°，以OA 2为直角边作第二个等腰Rt △OA 2A 3，以OA 3为直角边作第三个等腰Rt △OA 3A 4，…，∴OA 1＝1＝(2)°，OA 2＝2，OA 3＝(2)2，…，OA 2022＝(2)2021，∵A 1、A 2、A 3、…，每8个一循环，再回到y 轴的正半轴，2022÷8＝252……6，∴点A 2022在第三象限对角线上，∵OA 2022＝(2)2021，∴点A 2022的坐标为(－21010，－21010)．6.(52，－5132)【解析】观察，发现规律：A 2(2，3)，A 4(52，－332)，A 6(2，23)，A 8(52，－532)，…，∴A 4n ＋2(2，3n ＋3)，A 4n ＋4(52，－（2n ＋3）32)(n 为自然数)，∵100＝4×24＋4，∴A 100的坐标为(52，－5132)．7.－3101022019【解析】∵边长为4的等边△ABC ，AC 边在x 轴上，点B 在y 轴的正半轴上，OB ⊥AC ，∴∠BAC ＝∠ABC ＝60°，∠ABO ＝12∠ABC ＝30°，∴AO ＝12AB ＝2，OB ＝3AO ＝23；∵以OB 为边作等边△OBA 1，边OA 1与AB 交于点O 1，以O 1B 为边作等边△O 1BA 2，边O 1A 2与A 1B 交于点O 2，∴∠BA 1O ＝∠A 1OB ＝∠A 2O 1B ＝60°，∠A 1BO 1＝∠OBO 1＝12∠A 1BO＝30°，∴∠AOO 1＝∠A 1O 1O 2＝90°－60°＝30°，在△OO 1A 与△O 1O 2A 1OAO 1＝∠A 1AOO 1＝∠A 1O 1O 2，∴△OO 1A ∽△O 1O 2A 1，同理，可得△OO 1A ∽△O 1O 2A 1∽△O 2O 3A 2∽…∽△O n －1O n A n －1，相似比O 1A 1OA ＝O 1O 2OO 1＝sin60°＝32，∴O 1A 1＝32OA ，同理O 2A 2＝32O 1A 1＝(32)2OA ，…，O n A n ＝(32)n OA ∵∠OBA ＝∠O 1BA 1＝∠O 2BA 2＝∠O 3BA 3＝…＝∠O n －2BA n －2＝∠O n －1BA n －1＝30°，360°÷30°＝12，∴这些点所在的位置以12个为一个周期依次循环，∵2020÷12＝168……4，∴O 2020A 2020为4÷2×(32)2020＝3101022019.∴△O 2019BA 2020的边长为2O 2020A 2020＝2×(3101022019)＝3101022018，∵点A 2020与点A 4位置类似，∴点A 2020的横坐标为－3101022019·sin30°＝－3101022019.。
中考数学题型四 规律探索题
考法
类型1 数与式的规律探索
例2
高分技法
思路分析
观察每个等式可知,第n个等式中,第1个分 数的分母为n,分子为1,第2个分数的分母 为n+1,分子为n-1,据此规律即可解决问题 .
考法 类型 1 数与式的规律探索
例2
高分技法
解决数式类规律探究问题,一般要抓住所给式子的特点,通过对简单、
特殊情况或部分情况的观察,利用列举归纳法或观察归纳法猜想得到
边数第2个数为n-1;观察前5行数字,分析每行所有数字之和与行数之间的关系,即可得
到第n行中所有数字之和.
考法 类型1 数与式的规律探索
例1
高分技法
解答数字规律探索题的一般步骤
在解答数字规律探索题时,分三种情况.
1.若题中给出的是一组数字且这组数字均为整数,则一般步骤如下. (1)得出数字规律:观察这组数字是自然数列、正整数列、奇数列、偶数列还是整数列经过和、差、平方、 平方和、平方差、平方和加1、平方和减1等运算后得到的数列;观察每个数字与其对应的序号、相邻两个 数字之间的关系; (2)得出符号规律:看这组数字的符号,判断是正负号交替出现,还是只出现一个符号,如果是交替出现,若奇 数项为负,则用(-1)n表示数字的符号;若偶数项为负,则用(-1)n+1表示数字的符号;
(2)第n行中从左边数第2个数为 n-1 ;第n行中所有数字之和为 2n-1 .
思路分析 (1)先观察前7行中数字的排列情况,可发现从第2行起,每行数字左右对称,且第n(n≥3)
行中,第2~n-1个数都等于各数上方左右两侧的两数之和,由此可推出第9行的数字.(2)
第2行从左边数第2个数为1,第3行从左边数第2个数为2,以此类推,即可得到第n行从左
平面直角坐标系重难点题型(四大题型)(解析版)—2024-2025学年八年级数学上册(北师大版)
平面直角坐标系重难点题型（四大题型）【题型1 两点间距离】【题型2 求平面直角坐标系中动点问题的面积】【题型3 平面直角坐标系中规律题探究】【题型4 等腰三角形个数讨论问题】【题型1 两点间距离】1．在平面直角坐标系中，A，B两点的坐标分别为(5,―1)，(5,2)，则A，B两点间的距离为.2．已知平面直角坐标系中有一点M(3―2m,3m+2)．(1)存在点N(2,―3)，当MN平行于y轴时，求点M的坐标：(2)当点M在x轴上方，且到x轴的距离是到y轴距离的两倍时，求点M的坐标．3．已知点P(2m―1,m+3)．(1)若点P在y轴上，求m的值；(2)若点P在第一象限，且点P到x轴的距离是到y轴的距离的4倍，求点P的坐标．4．阅读理解：如何根据坐标求出两点之间的距离？如图，在坐标系中A(2,1)，B(6,4)，构造Rt△ACB，则AC=6―2=4，BC=4―1=3，∴AB===5若A(x1,y1)，B(x2,y2)，则AC=|x2―x1|BC=|y2―y1|∴AB==这就是两点间的距离公式，例如E(0,1)，D(4,0)∴ED===(1)+A(12,3)与点C(x,0)点B(0,2)与点C(x,0)的距离．请完成如下填空：作点B关于x轴的对称点B′（____，___），当A、C、B′三点共线时AC+BC最小，连接AB′，则AC+BC 的最小值等于AB′，由两点间的距离公式得AB′=______________，_____________．(2)借助上面的思考过程，画图说明并求出代数式：②的最大值．，当A、C、B′三点共线时AC+AB′=(12―0)2+(3+2)的最小值是13．1)，当A、C、B′三点共线时AC+BC5．阅读材料：两点间的距离公式：如果平面直角坐标系内有两点A(x1,y1)、B(x2,y2)，那么A、B两点的距离AB=AB2=(x1―x2)2+(y1―y2)2．例如：若点A(4,1),B(3,2)，则AB==若点A(a,1),B(3,2)，且AB=2=(a―3)2+(1―2)2．a的值．根据上面材料完成下列各题：(1)若点A―2，3，B m，2①若m=1，则A、B两点间的距离是______．②若AB∥y轴，则A、B两点间得距离是______．(2)若点A―2，3，点B在x轴上，且A、B两点间的距离是5，求B点坐标．【题型2 求平面直角坐标系中动点问题的面积】6．如图，在平面直角坐标系中，已知A(a,0)，B(b,0)，其中a，b(b―2)2=0．(1)填空：a=______，b=_______；(2)如果在第三象限内有一点M(―3,m)，请用含m的式子表示△ABM的面积；(3)在（2）的条件下，当m=―3时，在y轴上有一点P，使得△ABP的面积是△ABM的面积的2倍，请求出点P的坐标．7．已知在平面直角坐标系中有点A(―2，1)，B(3,1)，C(2，3)，D(―1，5)．(1)在坐标系内描出△ABC的位置；(2)求出△ACD的面积；(3)在y轴上是否存在一点P使得以A、B、P三点为顶点的三角形面积为10，若存在，请直接写出点P 的坐标，若不存在，请说明理由．，D(―1，5)，在平面直角坐标系中顺次连接得到△ACD，3×12―2×4×12=16―2―3―4=7三点为顶点的三角形面积为10，，在平面直角坐标系顺次连接A、B、P，三点围成的三角形高为ℎ，=y，即P(0,5)，=y，即P(0,―3)，8．在平面直角坐标系中，A(a,0)，C(b,2)，满足(a+1)2=0，过点C作CB⊥x轴于点B．(1)如图1，连接AC，求三角形ABC的面积．(2)如图2，连接AC，若过点B作BD∥AC交y轴于点D，且AE，DE分别平分∠CAB，∠ODB，求∠AED？(3)如图3，过C作CD垂直于点D，连接AD，点P从D点出发，沿“DC→CB”移动，若点P的速度为每秒1个单位长度，运动时间t秒，当P运动到什么位置时，直线OP将四边形ABCD面积分为3:11两部分？求出P的坐标？=∠2，×2，2，9．如图，已知A(―4,0)，B(4,0)，C(3,2)，D(―2,4)．(1)求四边形ABCD的面积；(2)在y轴上存在一点P APB的面积等于四边形ABCD面积的一半，求P点的坐标．【答案】(1)20(2)P点的坐标(0,2.5)或(0,―2.5)．【分析】此题主要考查了多边形面积及坐标系的基础知识，解题关键是熟练掌握基础图形面积公式．（1）观察图形，用分割法求解，分别过C、D两点作x轴的垂线，将图形分割为两个直角三角形和一个直角梯形，再根据直角三角形和直角梯形的面积公式求面积和即可；（2）P点的纵坐标到原点的距离就是△APB的AB边上的高，根据（1）P点到原点的距离，再根据P点分别在y轴正负半轴，写出P点的坐标即可．【详解】（1）解：分别过C、D两点作x轴的垂线，垂足分别为E、F，如下图：D(―2,4)，BE=1，CE=2，CDFE+S△BCE+12×1×210．如图，在直角坐标平面内，已知A(―1,2)，B(1,―2)，C(4,0)，线段AB经过原点O．(1)求△ABC的面积；(2)在x轴上是否存在一点D，使S△ACD=S△ABC，如果存在，求出点D的坐标，如果不存在说明理由．【答案】(1)8(2)(―4,0)或(12,0)【分析】本题考查了求平面直角坐标系中三角形的面积；【题型3 平面直角坐标系中规律题探究】11．如图，在平面直角坐标系中，每个最小方格的边长均为1个单位长，P1，P2，P3，…，均在格点上，其顺序按图中“→”方向排列，如：P1(0，0)，P2(0，1)，P3(1，1)，P4(1，―1)，P5(―1，―1)，P6(―1，2)…根据这个规律，点P2019的坐标为（）A．(―505,505)B．(505,―505)C．(505,―506)D．(505,505)【答案】D【分析】本题考查了规律型：点的坐标，根据前几个点的坐标，总结出规律是解题的关键．根据各个点的位置关系，可得出从P3(1,1)开始，下标为4的倍数的点在第四象限的角平分线上，被4除余1的点在第三象限的角平分线上，被4除余2的点在第二象限的角平分线上，被4除余3的点在第一象限的角平分线上，所以点P2019的在第四象限的角平分线上，然后根据规律求解即可．【详解】解：∵P1(0,0),P2(0,1),P3(1,1),P4(1,―1),P5(―1,―1),P6(―1,2),...，∴从P3(1,1)开始，P4n(n,―n)在第四象限的角平分线上，P4n+1(―n,―n)在第三象限的角平分线上，P4n+2(―n,n+1)在第二象限的角平分线上，P4n+3(n+1,n+1)在第一象限的角平分线上，∵2019=4×504+3，∴点P2019的在第一象限的角平分线上，n=504，∴点P2019坐标为(505,505)故选D．12．如图，动点P在平面直角坐标系中按图中箭头所示方向运动，第一次从原点O运动到点P1(1,2)，第二次运动到点P2(2,0)，第三次运动到P3(3,―1),…，按这样的运动规律，第23次运动后，动点P23的纵坐标是（ ）A．―1B．0C．1D．2【答案】C【分析】本题考查了规律型点的坐标，数形结合并从图象中发现循环规律：纵坐标每6次运动组成一个循环是解题的关键．由图得点的纵坐标变化每6次一循环，23÷6=3......5，点P23的纵坐标为符合第5个点的纵坐标为1．【详解】解：由图得，点每运动一次横坐标就增加1，∴P23的横坐标为23，点的纵坐标变化每6次一循环，23÷6=3......5，∴点P23的纵坐标为1．故选：C．13．在一单位为1的方格纸上，有一列点A1,A2,A3,⋯,A n,⋯,（其中n为正整数）均为网格上的格点，按如图所示规律排列，点A1(2,0),A2(1,―1),A3(0,0),A4(2,2),⋯⋯，则A2024的坐标为（）A．(―1010,0)B．(2,1012)C．(1012,2)D．(1014,0)14．如图，在平面直角坐标系中，一动点从原点出发，沿着箭头所示方向，每次移动1个单位，依次得到点P1(1,0),P2(1,1),P3(0,1),P4(0,2),P5(1,2)，…，根据这个规律，点P28的坐标为（）A．(0,14)B．(1,7)C．(0,8)D．(1,8)【答案】A【分析】本题主要考查了点的坐标规律探索，根据题意可得规律每四次移到为一个循环，横坐标为1，1，0，0依次出现，纵坐标每2次移到增加1，据此规律求解即可．【详解】解：P1(1,0)，P2(1,1)，P3(0,1)，P4(0,2)，P5(1,2)，……，以此类推可知，每四次移到为一个循环，横坐标为1，1，0，0依次出现，纵坐标每2次移到增加1，∵28÷4=7，28÷2=14，∴点P28的横坐标为0，纵坐标为14，∴点P28的坐标为(0,14)，故选：A．15．如图，平面直角坐标系中，x轴负半轴上有一点A(―1,0)．点A第一次向上平移1个单位至点A1(―1,1)，接着又向右平移1个单位至点A2(0,1)，然后再向上平移1个单位至点A3(0,2)，向右平移1个单位至点A4(1,2)，…，照此规律平移下去，点A2024的坐标是（）A．(1010,1011)B．(1011,1012)C．(1010,1012)D．(1011,1013)16．如图，点A在y轴正半轴及x轴正半轴上交替运动，点A从原点出发，依次跳动至点A1(0,1)，A2 (1,0)，A3(2,0)，A4(0,2)，A5(0,3)，A6(3,0)，A7(4,0)，A8(0,4)，…，按此规律，则点A2024的坐标是（）A．(0,1011)B．(1011,0)C．(0,1012)D．(1012,0)【答案】C【分析】本题考查规律探索，根据已知的点坐标，对点分组找出规律是解题的关键．根据已知点的坐标特征，将连续的4个点看成一组，由第1组，第2组确定组内点的位置特征、点坐标与组序数的联系；以此类推，2023=4×505+3，故点A2024是第506组的第4个点，则A2024在y 轴上，其非零坐标即横坐标为2×506=1012．【详解】解：根据题意，将连续的4个点A看成一组，第1组：A1(0,1)，A2(1,0)，A3(2,0)，A4(0,2)，其位置分别为y轴、x轴、x轴、y轴，前两个点的非零坐标为1，后两个点的非零坐标为2；其中，1=2×1―1，2=2×1；第2组：A5(0,3)，A6(3,0)，A7(4,0)，A8(0,4)，其位置分别为y轴、x轴、x轴、y轴，前两个点的非零坐标为3，后两个点的非零坐标为4；其中，3=2×2―1，4=2×2；……以此类推，2024=4×506，则点A2024是第506组的第4个点，则A2024在y轴上，其非零坐标即横坐标为1012，故点A2024的坐标是(0,1012)，故选：C．17．如图，在一个单位为1的方格纸上，△A1A2A3，△A3A4A5，△A5A6A7，是斜边在x轴上，斜边长分别为2，4，6的等腰直角三角形．若△A1A2A3的顶点坐标分别为A1(2,0)，A2(1,―1)，A3(0,0)，则依图中所示规律，A2024的横坐标为．18．如图所示，在平面直角坐标系中，A(1,1)，B(―1,1)，C(―1,―2)，D(1,―2)．把一条长为2019个单位长度且没有弹性的细线（线的粗细忽略不计）的一端固定在点A处，并按A→B→C→D→A→…的规律紧绕在四边形ABCD的边上，则细线另一端所在位置的点的坐标是（）A．(1,0)B．(0,1)C．(0,―2)D．(1,―2)【答案】A【分析】本题考查的是坐标规律的探究，先求解四边形ABCD的周长为2(AB+BC)=10．结合2019÷10=201……9，从而可得答案．【详解】解：∵A(1,1)，B(―1,1)，C(―1,―2)，D(1,―2)，∴AB=2，BC=3，∴四边形ABCD的周长为2(AB+BC)=10．∵2019÷10=201……9，∴细线另一端所在位置的点的坐标为(1,0)．故选A．19．如图，在平面直角坐标系上有点A(1,―1)，点A第一次向左跳动至A1(―1,0)，第二次向右跳动至A2 (2,0)，第三次向左跳动至A3(―2,1)，第四次向右跳动至A4(3,1)…依照此规律跳动下去，点A第2021次跳动至A2021的坐标（）A．(―1011,1010)B．(―1011,1009)C．(1012,1010)D．(1012,1009)20．如图，在平面直角坐标系中，有若干个整数点，其顺序按图中“→”方向排列，如(0,1),(―1,2),(0,2),(1,2) ,(2,3),(1,3),(0,3)，……，根据这个规律探索可得第2024个点的坐标是（）A．(43,45)B．(44,45)C．(―43,45)D．(―42,45)【答案】C【分析】本题考查了点的坐标规律探索，探索出点的坐标规律是解题的关键；按点的纵坐标分类：纵坐标是1的点有1个，纵坐标是2的点有3个，纵坐标是3的点有5个，纵坐标是4的点有7个，……，一般地，纵坐标为n的点有(2n―1)个；考虑点排列方向：纵坐标是1、3、5、7，……，点是从右往左的方向，纵坐标是2、4、6，……，点是从左往右排列的方向；而452=2025，当纵坐标是45时，这样的点共有89个，且点是从右往左方向，则可得第2024个点的坐标．【详解】解：纵坐标是1的点有1个，纵坐标是2的点有3个，纵坐标是3的点有5个，纵坐标是4的点有7个，……，一般地，纵坐标为n的点有(2n―1)个，且这n个点的横坐标从左往右依次是―n+1,―n+2,⋯,―1,0,1,⋯,n―1；考虑点排列方向：纵坐标是1、3、5、7，……，点是从右往左的方向，纵坐标是2、4、6，……，点是从左往右排列的方向；∵452=2025，当纵坐标是45时，这样的点共有89个，且点是从右往左方向，∴最左边的点坐标为(―44,45)，即第2025个点的坐标，∴第2024个点的坐标为(―43,45)．故选：C．21．如图，在平面直角坐标系中，一点自P0(1,0)处向上运动1个单位长度至P1(1,1)，然后向左运动2个单位长度至P2处，再向下运动3个单位长度至P3处，再向右运动4个单位长度至P4处，再向上运动5个单位长度至P5处，…，按此规律继续运动，则P2024的坐标是（）A．(―1011,―1012)B．(1013,―1012)C．(―1011,1012)D．(1013,1012)【答案】B【分析】本题考查坐标系下点的规律探究．解题的关键是找到点的横纵坐标的数字规律．先确定点P2024在第三象限，根据第三象限各点横坐标、纵坐标的数据得出规律P2n(n+1,―n)，进而得出答案即可．【详解】解：∵2024÷4=506，则P2024在第四象限，由题意，第四象限的点为P4(3,―2)，P8(5,―4)，……，P2n(n+1,―n)∴P2024(1013,―1012)．故选：B．22．平面直角坐标系中有若干点，按照如图所示的方式排列，其坐标依次为A1(1,0)，A2(1,1)，A3(―1,1)，A4(―1,―1)，A5(2,―1)，…按此规律，点A2024的坐标为（）A．(―505,―505)B．(―505,506)C．(―506,―506)D．(507,―506)23．将从1开始的连续自然数按以下规律排列：若有序数对(n,m)表示第n行，从左到右第m个数，如(3,2)表示6，则252表示的有序数对是（）A．(14,16)B．(14,24)C．(16,27)D．(16,29)【答案】C【分析】本题考查数字规律的性质，解题的关键是熟练掌握数字规律的相关性质．分析每一行的第一个数字的规律，得出第n行的第一个数字为1+(n―1)2，从而求得最终的答案．【详解】第1行的第一个数字：1=1+(1―1)2第2行的第一个数字：2=1+(2―1)2第3行的第一个数字：5=1+(3―1)2第4行的第一个数字：10=1+(4―1)2第5行的第一个数字：17=1+(5―1)2…..，设第n行的第一个数字为x，得x=1+(n―1)2设第n+1行的第一个数字为z，得z=1+n2设第n行，从左到右第m个数为y当y=252时1+(n―1)2≤252<1+n2∴(n―1)2≤251<n2∵n为整数∴n=16∴x=1+(n―1)2=226∴m=252―226+1=27，∴252表示的有序数对是(16,27)故选：C．24．如图，在平面直角坐标系中，动点A从1，0出发，向上运动1个单位长度到达点B1，1，分裂为两个点，分别向左、右运动到点C0，2，D2，2，此时称动点A完成第一次跳跃；再分别从C，D 点出发，每个点重复上面的运动，到达点G―1，4，H1，4，I3，4，此时称动点A完成第二次跳跃；依此规律跳跃下去，动点A完成第2023次跳跃时，最右边一个点的坐标是（ ）A．2023，4046B．2023，22023C．2024，4046D．2024，22023【答案】C【分析】根据题意找到点坐标变化的规律即可．【详解】解：由题意可得：A1，0、D2，2、I3，4．．．每完成一次跳跃，最右边一个点的纵坐标增加2，到达点的横坐标增加1，则动点A完成第2023次跳跃时，最右边一个点纵坐标为2023×2=4046，横坐标为：2023+1=2024故选：C．【点睛】本题考查了点坐标规律的探索．根据题意寻找变化规律是解题关键．【题型4 等腰三角形个数讨论问题】25．在平面直角坐标系中，O为坐标原点，点A(―4，4―5a)位于第二象限，点B(―4,―a―1)位于第三象限，且a为整数．（1）求点A和点B的坐标．（2）若点C(m,0)为x轴上一点，且△ABC是以BC为底的等腰三角形，求m的值．26．如图1，在平面直角坐标系中，A，B在x轴上，C在y轴上，BC2+CO2=AC2.（1）求证：AO=BC；（2）如图2，若点A(―5,0)，C(0,4)，现有一个动点P从点A出发，沿着x轴正方向运动，连结PC，当ΔPCB为等腰三角形时，求点P的坐标；（3）如图3，若AB=AC，点B1,0)，过O作OE//BC交AC于E，求OE的长.27．长方形ABCO在平面直角坐标系的位置如左图所示，A、C两点分别在x、y轴上，且B点的坐标为(8,6)，P为射线AO上的一动点，点O关系直线PC的对称点为D.（1）当ΔOPC的面积为12时，则点P坐标为_______________.（2）当ΔAPC为等腰三角形时，求点P坐标.（3）如图所示，若点O关于直线PC的对称点为点D，当ΔAPD为直角三角形时，请直接写出点P坐标.∠P1D1C=∠P1OC=∠P1D1A，AC=10，设OP1=x，则P1D1=x，2+16=(8―x)2∴x=3∴P1（3,0）OP2=P2D2=6∴P2(6,0)OP3=P3D3=6∴P3(―6,0)∠P4D4C=90∘，AD4=10+6=16，设OP4=x，则P4D4=x，AP8)2∴x=12∴P(―12,0)分类讨论思想；3.数形结合思想.28．如图，在平面直角坐标系中，A(0,a)为y轴正方向上一点，B(b,0)为x轴正方向上一点，(b―6)2=0．(1)求线段AB的长；(2)点C是线段AC上一点，如果BC平分∠ABO，求点C的坐标；(3)点P是x轴上一动点，且△PAB为等腰三角形，直接写出所有符合条件的点P的坐标．时，如图；OP′=OB+P′B=6+10=16，P(x,0)，=(6―x)2，股定理，灵活运用这些知识是关键．。
2020年中考数学一轮专项复习——规律探索(含答案)
2020年中考数学一轮专项复习——规律探索中考备考攻略规律探索型问题是根据已知条件或题干所提供的若干特例，通过观察、类比、归纳，发现题目所蕴含的数字或图形的本质规律与特征的一类探索性问题.纵观宜宾近五年中考，往往以选择题、填空题形式出现，这类问题在素材的选取、文字的表述、题型的设计等方面都比较新颖.其目的是考查收集、分析数据、处理信息的能力.所以规律探索型问题备受命题专家的青睐，逐渐成为中考数学的热门考题.规律探索型问题是指在一定条件下，探索发现有关数学对象所具有的规律性或不变性的问题，它往往给出了一组变化了的数、式子、图形或条件，要求通过阅读、观察、分析、猜想来探索规律.它体现了“特殊到一般”的数学思想方法，既考查分析、解决问题能力，也考查观察、联想、归纳能力以及探究能力和创新能力.题型可涉及填空题、选择题或解答题.中考重难点突破数与式变化规律【典例1】（2019·达州中考）a 是不为1的有理数，我们把11－a 称为a 的差倒数，如2的差倒数为11－2＝－1，－1的差倒数11－（－1）＝12.已知a 1＝5，a 2是a 1的差倒数，a 3是a 2的差倒数，a 4是a 3的差倒数，…，依此类推，a 2 019的值是（ ）A .5B .－14C .43D .451.一组按规律排列的多项式：a ＋b ，a 2－b 3，a 3＋b 5，a 4－b 7，…，其中第10个式子是（ ）A. a 10＋b 19 B .a 10－b 19 C .a 10－b 17 D .a 10－b 212.有一组数：12，35，510，717，926，…，请观察它们的构成形式，用你发现的规律写出第n （n 为正整数）个数： .3.已知：1＋112＋122＝112，1＋122＋132＝116，1＋132＋142＝1112，…，根据此规律1＋192＋1102＝ .4.（2019·自贡中考）阅读下列材料：小明为了计算1＋2＋22＋…＋22 017＋22 018的值，采用以下方法：设S＝1＋2＋22＋…＋22 017＋22 018，①则2S＝2＋22＋…＋22 018＋22 019.②②－①，得2S－S＝S＝22 019－1.∴S＝1＋2＋22＋…＋22 017＋22 018＝22 019－1.请仿照小明的方法解决以下问题：（1）1＋2＋22＋…＋29＝；（2）3＋32＋…＋310＝；（3）求1＋a＋a2＋…＋a n的和（a＞0，n是正整数，请写出计算过程）.点阵变化规律【典例2】如图，在一个三角点阵中，从上向下数有无数多行，其中各行点数依次为2、4、6、…、2n、…，若前n行点数和为930，则n＝（）A.29B.30C.31D.325.将全体正奇数排成一个三角形数阵：13 57911131517192123252729………………根据以上排列规律，数阵中第25行的第20个数是（）A.639B.637C.635D.633循环排列规律【典例3】观察下列图形，并判断照此规律从左向右第2 018个图形是（）A B C D6.如图是一列用若干根火柴棒摆成的由正方形组成的图案.（1）完成下表的填空：正方形个数 1 2 3 4 5 6 … 火柴棒根数4710131619…（2）某同学用若干根火柴棒按如图的方式摆图案，摆完了第1个后，摆第2个，接着摆第3个，第4个，…，当他摆完第n 个图案时剩下了20根火柴棒，要刚好摆完第（n ＋1）个图案还差2根.问最后摆的图案是第几个图案？图形生长变化规律【典例4】（2019·内江中考）如图，将△ABC 沿着过BC 的中点D 的直线折叠，使点B 落在AC 边上的B 1处，称为第一次操作，折痕DE 到AC 的距离为h 1；还原纸片后，再将△BDE 沿着过BD 的中点D 1的直线折叠，使点B 落在DE 边上的B 2处，称为第二次操作，折痕D 1E 1到AC 的距离记为h 2；按上述方法不断操作下去……经过第n 次操作后得到折痕D n －1E n －1，到AC 的距离记为h n .若h 1＝1，则h n 的值为（ ）A .1＋12n －1 B .1＋12nC .2－12n －1 D .2－12n7.（2019·广元中考）如图，过点A 0（0，1）作y 轴的垂线交直线l ：y ＝33x 于点A 1，过点A 1作直线l 的垂线，交y 轴于点A 2，过点A 2作y 轴的垂线交直线l 于点A 3，…，这样依次下去，得到△A 0A 1A 2、△A 2A 3A 4、△A 4A 546、…，其面积分别记为S 1、S 2、S 3、…，则S 100为（ ）A .⎝⎛⎭⎫332100B .（33）100C .33×4199D .33×2395与坐标有关的规律【典例5】如图，已知A 1（1，0），A 2（1，1），A 3（－1，1），A 4（－1，－1），A 5（2，－1），…，则点A 2018的坐标为 .8.（2019·攀枝花中考）正方形A 1B 1C 1A 2、A 2B 2C 2A 3、A 3B 3C 3A 4、…按如图所示的方式放置，点A 1、A 2、A 3、…和点B 1、B 2、B 3、…分别在直线y ＝kx ＋b （k ＞0）和x 轴上.已知点A 1（0，1），点B 1（1，0），则点C 5的坐标是 .中考备考过关1.某校数学课外小组，在坐标纸上为学校的一块空地设计植树方案如下：第k 棵树种植在点P k （x k ，y k ）处，其中x 1＝1，y 1＝1，当k ≥2时，⎩⎨⎧x k ＝x k －1＋1－5⎝⎛⎭⎫⎣⎡⎦⎤k －15－⎣⎡⎦⎤k －25，y k ＝y k －1＋⎣⎡⎦⎤k －15－⎣⎡⎦⎤k －25，[a]表示非负实数a 的整数部分，如[2.6]＝2，[0.2]＝0.按此方案，第2 019棵树种植点的坐标为（ ）A .（5，2 019）B .（6，2 020）C .（3，403）D .（4，404）2.正方形A 1B 1C 1O 、A 2B 2C 2C 1、A 3B 3C 3C 2、…按如图所示的方式放置，点A 1、A 2、A 3、…和点C 1、C 2、C 3、…分别在直线y ＝kx ＋b （k ＞0）和x 轴上，已知B 1（1，1），B 2（3，2），则点B n 的坐标是 .,（第2题图）) ,（第3题图）)3. 我国古代《易经》一书中记载，远古时期，人们通过在绳子上打结来记录数量，即“结绳记数”.如图，一位妇女在从右到左依次排列的绳子上打结，满六进一，用来记录采集到的野果数量，由图可知，她一共采集到的野果数量为 个.4.（2019·广安中考）如图，在平面直角坐标系中，点A 1的坐标为（1，0），以OA 1为直角边作Rt △OA 1A 2，并使∠A 1OA 2＝60°；再以OA 2为直角边作Rt △OA 2A 3，并使∠A 2OA 3＝60°；再以OA 3为直角边作Rt △OA 3A 4，并使∠A 3OA 4＝60°……按此规律进行下去，则点A 2 019的坐标为 .5.符号“f ”表示一种运算，它对一些数的运算结果如下：（1）f （1）＝0，f （2）＝1，f （3）＝2，f （4）＝3，…；（2）f ⎝⎛⎭⎫12＝2，f ⎝⎛⎭⎫13＝3，f ⎝⎛⎭⎫14＝4，f ⎝⎛⎭⎫15＝5，…. 利用以上规律计算：f ⎝⎛⎭⎫12 019－f （2 019）＝ .6.用同样大小的黑色棋子按如图所示的方式摆图形，按照这样的规律摆下去，则第n 个图形需棋子 枚（用含n 的代数式表示）.7.观察下列图中所示的一系列图形，它们是按一定规律排列的，依照此规律，第2 019个图形共有 个○.8.如图，阶梯图的每个台阶上都标着一个数，从下到上的第1个至第4个台阶上依次标着－5、－2、1、9，且任意相邻四个台阶上数的和都相等.尝试 （1）问前4个台阶上数的和是多少？ （2）问第5个台阶上的数x 是多少？应用 求从下到上前31个台阶上数的和；发现 试用含k （k 为正整数）的式子表现出数“1”所在的台阶数.9.观察： 11×2＝1－12，12×3＝12－13，13×4＝13－14，….解答下面的问题：（1）若n 为正整数，请你猜想1n ×（n ＋1）＝ ；（2）若n 为正整数，请你猜想11×2＋12×3＋13×4＋…＋1n ×（n ＋1）＝ ；（3）若x －1＋（xy －2）2＝0，求1xy ＋1（x ＋1）（y ＋1）＋1（x ＋2）（y ＋2）＋…＋1（x ＋2 017）（y ＋2 017）的值.10.一列火车自A 城驶往B 城，沿途有n 个车站（包括起点站A 和终点站B ），该列火车挂有一节邮政车厢，行驶时需要在每个车站停靠，每停靠一站不仅要卸下已经通过的各车站发给该站的邮包一个，还要装上该站发给后面行程中每个车站的邮包一个.例如，当列车停靠在第x 个车站时，邮政车厢上需要卸下已经通过的（x －1）个车站发给该站的邮包（x －1）个，还要装上后面行程中要停靠的（n －x ）个车站的邮包（n －x ）个.（1）根据题意，完成下表：车站序号 在第x 个车站启程时邮政车厢上的邮包总个数1 n －12 （n －1）－1＋（n －2）＝2（n －2）3 2（n －2）－2＋（n －3）＝3（n －3）4 3（n －3）－3＋（n －4）＝4（n －4）5 … … n 0（2）根据上表写出列车在第x 个车站启程时，邮政车厢上共有的邮包个数y （用x 、n 表示）； （3）当n ＝18时，列车在第几个车站启程时邮车上的邮包个数最多？参考答案中考重难点突破数与式变化规律【典例1】（2019·达州中考）a 是不为1的有理数，我们把11－a 称为a 的差倒数，如2的差倒数为11－2＝－1，－1的差倒数11－（－1）＝12.已知a 1＝5，a 2是a 1的差倒数，a 3是a 2的差倒数，a 4是a 3的差倒数，…，依此类推，a 2 019的值是（ D ）A .5B .－14C .43D .45【解析】∵a 1＝5，a 2＝11－a 1＝11－5＝－14，a 3＝11－a 2＝11－⎝⎛⎭⎫－14＝45，a 4＝11－a 3＝11－45＝5，…，∴数列以5、－14、45三个数依次不断循环.∵2 019÷3＝673，∴a 2 019＝a 3＝45.1.一组按规律排列的多项式：a ＋b ，a 2－b 3，a 3＋b 5，a 4－b 7，…，其中第10个式子是（ B ）A .a 10＋b 19B .a 10－b 19C .a 10－b 17D .a 10－b 212.有一组数：12，35，510，717，926，…，请观察它们的构成形式，用你发现的规律写出第n （n 为正整数）个数：2n －1n 2＋1Ｗ. 3.已知：1＋112＋122＝112，1＋122＋132＝116， 1＋132＋142＝1112，…，根据此规律1＋192＋1102＝ 1190 Ｗ. 4.（2019·自贡中考）阅读下列材料：小明为了计算1＋2＋22＋…＋22 017＋22 018的值，采用以下方法： 设S ＝1＋2＋22＋…＋22 017＋22 018，① 则2S ＝2＋22＋…＋22 018＋22 019.② ②－①，得2S －S ＝S ＝22 019－1.∴S ＝1＋2＋22＋…＋22 017＋22 018＝22 019－1. 请仿照小明的方法解决以下问题： （1）1＋2＋22＋…＋29＝ ； （2）3＋32＋…＋310＝ ；（3）求1＋a ＋a 2＋…＋a n 的和（a ＞0，n 是正整数，请写出计算过程）.解：（1）210－1；（2）311－12； （3）设S ＝1＋a ＋a 2＋…＋a n ，①则aS ＝a ＋a 2＋a 3＋…＋a n ＋a n ＋1.②②－①，得（a －1）S ＝a n ＋1－1.∴S ＝a n ＋1－1a －1，即1＋a ＋a 2＋…＋a n ＝an ＋1－1a －1.点阵变化规律【典例2】如图，在一个三角点阵中，从上向下数有无数多行，其中各行点数依次为2、4、6、…、2n 、…，若前n 行点数和为930，则n ＝（ B ）A .29B .30C .31D .32【解析】设前n 行的点数和为S ，则S ＝2＋4＋6＋…＋2n ＝（2n ＋2）n2＝n （n ＋1）. 若S ＝930，则n （n ＋1）＝930，即（n ＋31）（n －30）＝0，∴n 1＝－31（不合题意，舍去），n 2＝30.5.将全体正奇数排成一个三角形数阵：1 3 5 7 9 11 13 15 17 19 21 23 25 27 29 … … … … … …根据以上排列规律，数阵中第25行的第20个数是（ A ） A .639 B .637 C .635 D .633循环排列规律【典例3】观察下列图形，并判断照此规律从左向右第2 018个图形是（ B ）A B C D【解析】根据题意可知前面4个笑脸循环出现，因为2 018÷4＝504……2，所以第2 018个图形是循环出现到第2个图形.6.如图是一列用若干根火柴棒摆成的由正方形组成的图案.（1）完成下表的填空：正方形个数 1 2 3 4 5 6 … n火柴棒根数4 7 10 13 16 19 … 3n ＋1（2）某同学用若干根火柴棒按如图的方式摆图案，摆完了第1个后，摆第2个，接着摆第3个，第4个，…，当他摆完第n 个图案时剩下了20根火柴棒，要刚好摆完第（n ＋1）个图案还差2根.问最后摆的图案是第几个图案？解：（1）见上表；（2）由3（n ＋1）＋1＝22，解得n ＝6. ∴这位同学最后摆的图案是第7个图案.图形生长变化规律【典例4】（2019·内江中考）如图，将△ABC 沿着过BC 的中点D 的直线折叠，使点B 落在AC 边上的B 1处，称为第一次操作，折痕DE 到AC 的距离为h 1；还原纸片后，再将△BDE 沿着过BD 的中点D 1的直线折叠，使点B 落在DE 边上的B 2处，称为第二次操作，折痕D 1E 1到AC 的距离记为h 2；按上述方法不断操作下去……经过第n 次操作后得到折痕D n －1E n －1，到AC 的距离记为h n .若h 1＝1，则h n 的值为（ C ）A .1＋12n －1 B .1＋12nC .2－12n －1 D .2－12n【解析】根据相似三角形的性质，对应高的比等于相似比，得出h 2＝1＋12h 1，依次得出h 3、h 4、…、h n ，再对h n 进行计算变形即可.,7.（2019·广元中考）如图，过点A 0（0，1）作y 轴的垂线交直线l ：y ＝33x 于点A 1，过点A 1作直线l 的垂线，交y 轴于点A 2，过点A 2作y 轴的垂线交直线l 于点A 3，…，这样依次下去，得到△A 0A 1A 2、△A 2A 3A 4、△A 4A 546、…，其面积分别记为S 1、S 2、S 3、…，则S 100为（ D ）A .⎝⎛⎭⎫332100B .（33）100C .33×4199D .33×2395与坐标有关的规律【典例5】如图，已知A 1（1，0），A 2（1，1），A 3（－1，1），A 4（－1，－1），A 5（2，－1），…，则点A 2018的坐标为 （505，505） .【解析】根据各个点（点A 1和第四象限内的点除外）分别位于象限的角平分线上，逐步探索出下标和各点坐标之间的关系，根据规律推出点A 2 018的坐标.通过观察可得序号是4的倍数的点在第三象限，由2 018÷4＝504……2，得点A 2 018在第一象限，其横、纵坐标都为（2 018－2）÷4＋1＝505.,8.（2019·攀枝花中考）正方形A 1B 1C 1A 2、A 2B 2C 2A 3、A 3B 3C 3A 4、…按如图所示的方式放置，点A 1、A 2、A 3、…和点B 1、B 2、B 3、…分别在直线y ＝kx ＋b （k ＞0）和x 轴上.已知点A 1（0，1），点B 1（1，0），则点C 5的坐标是 （47，16） Ｗ.中考备考过关1.某校数学课外小组，在坐标纸上为学校的一块空地设计植树方案如下：第k 棵树种植在点P k （x k ，y k ）处，其中x 1＝1，y 1＝1，当k ≥2时，⎩⎨⎧x k ＝x k －1＋1－5⎝⎛⎭⎫⎣⎡⎦⎤k －15－⎣⎡⎦⎤k －25，y k ＝y k －1＋⎣⎡⎦⎤k －15－⎣⎡⎦⎤k －25，[a]表示非负实数a 的整数部分，如[2.6]＝2，[0.2]＝0.按此方案，第2 019棵树种植点的坐标为（ D ）A .（5，2 019）B .（6，2 020）C .（3，403）D .（4，404）2.正方形A 1B 1C 1O 、A 2B 2C 2C 1、A 3B 3C 3C 2、…按如图所示的方式放置，点A 1、A 2、A 3、…和点C 1、C 2、C 3、…分别在直线y ＝kx ＋b （k ＞0）和x 轴上，已知B 1（1，1），B 2（3，2），则点B n 的坐标是 （2n －1，2n －1） Ｗ.,（第2题图）) ,（第3题图）)3. 我国古代《易经》一书中记载，远古时期，人们通过在绳子上打结来记录数量，即“结绳记数”.如图，一位妇女在从右到左依次排列的绳子上打结，满六进一，用来记录采集到的野果数量，由图可知，她一共采集到的野果数量为 1 838 个.4.（2019·广安中考）如图，在平面直角坐标系中，点A 1的坐标为（1，0），以OA 1为直角边作Rt △OA 1A 2，并使∠A 1OA 2＝60°；再以OA 2为直角边作Rt △OA 2A 3，并使∠A 2OA 3＝60°；再以OA 3为直角边作Rt △OA 3A 4，并使∠A 3OA 4＝60°……按此规律进行下去，则点A 2 019的坐标为 （－22 017，22 0173） Ｗ.5.符号“f ”表示一种运算，它对一些数的运算结果如下：（1）f （1）＝0，f （2）＝1，f （3）＝2，f （4）＝3，…；（2）f ⎝⎛⎭⎫12＝2，f ⎝⎛⎭⎫13＝3，f ⎝⎛⎭⎫14＝4，f ⎝⎛⎭⎫15＝5，…. 利用以上规律计算：f ⎝⎛⎭⎫12 019－f （2 019）＝ 1 Ｗ.6.用同样大小的黑色棋子按如图所示的方式摆图形，按照这样的规律摆下去，则第n 个图形需棋子 （3n ＋1） 枚（用含n 的代数式表示）.7.观察下列图中所示的一系列图形，它们是按一定规律排列的，依照此规律，第 2 019个图形共有 6 058 个○.8.如图，阶梯图的每个台阶上都标着一个数，从下到上的第1个至第4个台阶上依次标着－5、－2、1、9，且任意相邻四个台阶上数的和都相等.尝试 （1）问前4个台阶上数的和是多少？ （2）问第5个台阶上的数x 是多少？应用 求从下到上前31个台阶上数的和；发现 试用含k （k 为正整数）的式子表现出数“1”所在的台阶数.解：尝试 （1）由题意，得－5－2＋1＋9＝3，故前4个台阶上的数字的和是3； （2）由题意，得－2＋1＋9＋x ＝3，所以x ＝－5；应用 由题意知台阶上的数从下到上每4个循环，因为31÷4＝7……3，所以7×3＋1－2－5＝15， 即从下到上前31个台阶上数的和是15. 发现 “1”所在的台阶数为4k －1.9.观察： 11×2＝1－12，12×3＝12－13，13×4＝13－14，….解答下面的问题：（1）若n 为正整数，请你猜想1n ×（n ＋1）＝ ；（2）若n 为正整数，请你猜想11×2＋12×3＋13×4＋…＋1n ×（n ＋1）＝ ；（3）若x －1＋（xy －2）2＝0，求1xy ＋1（x ＋1）（y ＋1）＋1（x ＋2）（y ＋2）＋…＋1（x ＋2 017）（y ＋2 017）的值.解：（1）1n －1n ＋1；（2）1－1n ＋1；[原式＝1－12＋12－13＋13－14＋…＋1n －1n ＋1＝1－1n ＋1.]（3）∵x －1＋（xy －2）2＝0，∴x －1＝0，xy －2＝0， 解得x ＝1，y ＝2.则原式＝11×2＋12×3＋13×4＋…＋12 018×2 019＝1－12 019＝2 018 2 019.10.一列火车自A城驶往B城，沿途有n个车站（包括起点站A和终点站B），该列火车挂有一节邮政车厢，行驶时需要在每个车站停靠，每停靠一站不仅要卸下已经通过的各车站发给该站的邮包一个，还要装上该站发给后面行程中每个车站的邮包一个.例如，当列车停靠在第x个车站时，邮政车厢上需要卸下已经通过的（x－1）个车站发给该站的邮包（x－1）个，还要装上后面行程中要停靠的（n－x）个车站的邮包（n－x）个.（1）根据题意，完成下表：（2（3）当n＝18时，列车在第几个车站启程时邮车上的邮包个数最多？解：（1）见上表；（2）y＝x（n－x）；（3）当n＝18时，y＝x（18－x）＝－x2＋18x＝－（x－9）2＋81.当x＝9时，y取最大值，所以列车在第9个车站启程时，邮政车厢上的邮包个数最多.。
小升初必考题探索规律-可能性
可能性题型1：事件的确定性与不确定性例1：选择“一定”“可能”或“不可能”填空。
①地球________绕着太阳转。
②在装有5个白球和3个红球的袋子里，________摸到黑球。
③明天________会下雨。
【分析】地球绕着太阳转是不可改变的现象，袋子里没有黑色球，所以不可能摸到黑色球，明天是否会下雨并不确定，可能会下雨，也可能不会下雨。
①地球一定绕着太阳转。
②在装有5个白球和3个红球的袋子里，不可能摸到黑球。
③明天可能会下雨。
【答案】一定；不可能；可能例2：在括号里填上“一定”“可能”或“不可能”．（1）长方形的四个角是90度．（2）离开了水，金鱼就存活．（3）一次抽奖活动的中奖率是50%，张老师抽了2张奖券，他中奖．【分析】根据事件的确定性和不确定性，并结合题意，进行依次分析，解答即可．解：（1）长方形的四个角一定是90度；属于确定事件中的必然事件；（2）离开了水，金鱼就不可能存活；属于确定事件中的不可能事件；（3）一次抽奖活动的中奖率是50%，只是有中奖的可能，属于不确定事件；故答案为：一定，不可能，可能．【答案】一定，不可能，可能题型2：可能性的大小例3：桌子上有一些反扣的扑克牌，其中红桃有3张，黑桃有9张，方块有6张，随意摸一张摸出（____）的可能性最大，摸出（____）的可能性最小。
【答案】黑桃红桃例4：从（）号布袋里摸到红球和白球的可能性差不多。
1号袋 2号袋 3号袋A． 1 B． 2 C． 3【答案】C例5：盘上放着4个苹果，2个桃子，7个梨，随便拿一个水果，有（_______）种可能，拿到（_______）的可能性最小，要想拿到这种水果的可能性最大，至少还要加（________）个。
【答案】3桃子6题型3：事件发生的可能性大小语言描述例6：一个正方体，六个面上分别写着数字1～6，掷一次，可能会出现哪些结果，请你列举出来．【分析】正方体6个面上共有6个数字，掷一次，哪个面都有可能朝上，根据这些数字确定可能会出现的结果即可. 共有6个数字，掷一次，哪个数字都有可能出现.【答案】会出现6种可能性，可能是1、2、3、4、5或6.例7：按要求给袋子里的球涂上颜色。
探索规律专项练习(含答案)
探索规律练习专题（含答案）1、（2015•山东临沂,第11题3分）观察下列关于x的单项式，探究其规律：x，3x2，5x3，7x4，9x5，11x6，….按照上述规律，第2015个单项式是（）(A) 2015x2015. (B) 4029x2014. (C) 4029x2015. (D) 4031x2015. 【答案】C【解析】试题分析：根据这组数的系数可知它们都是连续奇数，即系数为（2n －1），而后面因式x的指数是连续自然数，因此关于x的单项式是，所以第2015个单项式的系数为2×2015－1=4029，因此这个单项式为. 故选C考点：探索规律2、（2015•四川省内江市，第16题，5分）如图是由火柴棒搭成的几何图案，则第n个图案中有根火柴棒．（用含n的代数式表示）考点：规律型：图形的变化类．. 专题：压轴题．分析：本题可分别写出n=1，2，3，…，所对应的火柴棒的根数．然后进行归纳即可得出解答：解：依题意得：n=1，根数为：4=2×1×（1+1）；n=2，根数为：12=2×2×（2+1）；n=3，根数为：24=2×3×（3+1）；…n=n时，根数为：2n（n+1）．点评：本题是一道找规律的题目，这类题型在中考中经常出现．对于找规律的题目首先应找出哪些部分发生了变化，是按照什么规律变化的．3、(2015·深圳，第15题分)观察下列图形，它们是按一定规律排列的，依照此规律，第5个图形有个太阳。
【答案】21【解析】第一行的规律是1，2，3，4，…，故第五个数是5；第二行的规律是1，2，4，8，…，故第五个数是16；故第五个图中共有21个太阳。
4、(2015·南宁，第18题3分)如图9，在数轴上，点A表示1，现将点A沿x轴做如下移动，第一次点A向左移动3 个单位长度到达点A1，第二次将点A1向右移动6个单位长度到达点A2，第三次将点A2向左移动9个单位长度到达点A3，按照这种移动规律移动下去，第n次移动到点A N，如果点A N与原点的距离不小于20，那么n的最小值是．考点：规律型：图形的变化类；数轴．.分析：序号为奇数的点在点A的左边，各点所表示的数依次减少3，序号为偶数的点在点A的右侧，各点所表示的数依次增加3，于是可得到A13表示的数为﹣17﹣3=﹣20，A12表示的数为16+3=19，则可判断点A n与原点的距离不小于20时，n的最小值是13．解答：解：第一次点A向左移动3个单位长度至点A1，则A1表示的数，1﹣3=﹣2﹣2；第2次从点A1向右移动6个单位长度至点A2，则A2表示的数为﹣2+6=4；第3次从点A2向左移动9个单位长度至点A3，则A3表示的数为4﹣9=﹣5；第4次从点A3向右移动12个单位长度至点A4，则A4表示的数为﹣5+12=7；第5次从点A4向左移动15个单位长度至点A5，则A5表示的数为7﹣15=﹣8；…；则A7表示的数为﹣8﹣3=﹣11，A9表示的数为﹣11﹣3=﹣14，A11表示的数为﹣14﹣3=﹣17，A13表示的数为﹣17﹣3=﹣20，A6表示的数为7+3=10，A8表示的数为10+3=13，A10表示的数为13+3=16，A12表示的数为16+3=19，所以点A n与原点的距离不小于20，那么n的最小值是13．故答案为：13．点评：本题考查了规律型，认真观察、仔细思考，找出点表示的数的变化规律是解决本题的关键．5、（2015·湖北省孝感市，第15题3分）观察下列等式：1=12；1+3=22；1+3+5=32；1+3+5+7=42；…，则1+3+5+…+2015＝．考点：规律型：数字的变化类分析：根据1=12；1+3=22；1+3+5=32；1+3+5+7=42；…，可得1+3+5+…+（2n ﹣1）=n2，据此求出1+3+5+…+2015的值是多少即可．解答：解：因为1=12；1+3=22；1+3+5=32；1+3+5+7=42；…，所以1+3+5+…+2015=1+3+5+…+（2×1008﹣1）=10082=1016064 故答案为：1016064．点评：此题主要考查了探寻数列规律问题，注意观察总结规律，并能正确的应用规律，解答此题的关键是判断出：1+3+5+…+（2n﹣1）=n2．6、（2015·湖南省益阳市，第13题5分）如图是用长度相等的小棒按一定规律摆成的一组图案，第1个图案中有6根小棒，第2个图案中有11根小棒，…，则第n个图案中有有根小棒．考点：规律型：图形的变化类．分析： 由图可知：第1个图案中有5+1=6根小棒，第2个图案中有2×5+2﹣1=11根小棒，第3个图案中有3×5+3﹣2=16根小棒，…由此得出第n 个图案中有5n +n ﹣（n ﹣1）=5n +1根小棒．解答： 解：∵第1个图案中有5+1=6根小棒，第2个图案中有2×5+2﹣1=11根小棒， 第3个图案中有3×5+3﹣2=16根小棒， …∴第n 个图案中有5n +n ﹣（n ﹣1）=5n +1根小棒．故答案为：5n +1．点评： 此题考查图形的变化规律，找出图形之间的联系，得出数字之间的运算规律，利用规律解决问题．7、(2015·黑龙江绥化，第20题分)填在下面各正方形中的四个数之间都有一定的规律 ，按此规律得出a +b +c =__________考点：规律型：数字的变化类．分析：观察不难发现，左上角+4=左下角，左上角+3=右上角，右下角的数是左下角与右上角两个数的乘积减去1的差，根据此规律列式进行计算即可得解． 解答：解：根据左上角+4=左下角，左上角+3=右上角，右下角的数是左下角与右上角两个数的乘积减去1的差，可得6+4=a ，6+3=c ，ac +1=b ，可得：a =10，c =9，b =91，所以a +b +c =10+9+91=110，故答案为：110点评：本题是对数字变化规律的考查，仔细观察前三个图形，找出四个数之间的变化规律是解题的关键．8、（2015•广东省,第15题，4分）观察下列一组数：13，25，37，49，511，…，根据该组数的排列规律，可推出第10个数是 . 【答案】1221. 【考点】探索规律题（数字的变化类）. 【分析】观察得该组数的排列规律为：分母为奇数，分子为自然数，第n 个数为21+n n ，所以，第10个数是1012210121=⨯+。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
类型1数与式的规律探索1.[2019安徽中考]下面两个多位数1248624…、6248624…,都是按照如下方法得到的:将第一位数字乘以2,若积为一位数,将其写在第2位;若积为两位数,则将其个位数字写在第2位.对第2位数字再进行如上操作得到第3位数字……,后面的每一位数字都是由前一位数字进行如上操作得到的.当第一位数字是3时,仍按如上操作得到一个多位数,则这个多位数前100位的所有数字之和是A.495B.497C.501D.5032.[2019合肥蜀山区二模]观察下列等式:① 1=12;② 2+3+4=32;③ 3+4+5+6+7=52;④ 4+5+6+7+8+9+10=72;请根据上述规律判断下列等式正确的是()A.1 008+1 009+…+3 025=2 0162B.1 009+1 010+…+3 026=2 0172C.1 009+1 010+…+3 027=2 0182D.1 010+1 011+…+3 028=2 01923.[2019安徽中考]观察下列关于自然数的等式:32-4×12=5;①52-4×22=9;②72-4×32=13;③根据上述规律解决下列问题:(1)完成第四个等式:92-4×()2=();(2)写出你猜想的第n个等式(用含n的式子表示),并验证其正确性.4.[2019合肥包河区二模]观察下列式子:①2×0+1=12;②4×2+1=32;③8×6+1=72;④16×14+1=152;(1)请按规律写出第⑤个式子: ;(2)根据你发现的规律写出第个式子(n为正整数),并验证其正确性.5.[2019芜湖二模]观察下列各个等式的规律:第1个等式:=1;第2个等式:=2;第3个等式:=3;请用上述等式反映出的规律解决下列问题:(1)直接写出第4个等式;(2)猜想第n个等式(用含n的代数式表示),并证明你猜想的等式是正确的.6.[2019合肥45中三模]已知一定数量的石子可以摆成如图所示的三角形和四边形,古希腊科学家把数1,3,6,10,15,21,…称为“三角形数”,把1,4,9,16,25,…称为“正方形数”.同样,可以把数1,5,12,22,…称为“五边形数”.将“三角形数”、“正方形数”、“五边形数”按从小到大的顺序依次填在下面表格里:三角形数136101521a…正方形数1491625b49…五边形数151222c5170…(1)按照规律,表格中a=,b=,c=;(2)观察表中规律,第n(n为正整数)个“五边形数”是.7.[2019安庆模拟]特殊两位数乘法的速算——如果两个两位数的十位数字相同,个位数字相加为10,那就能立即说出这两个两位数的乘积.如果这两个两位数分别写作AB和AC(即十位数字为A,个位数字分别为B,C,且B+C=10,A>3),那么它们的乘积是一个四位数,前两位数字是A和(A+1)的乘积,后两位数字是B和C的乘积.如47×43=2 021,61×69=4 209.(1)请你直接写出83×87的值;(2)设这两个两位数的十位数字为x(x>3),个位数字分别为y和z(y+z=10),通过计算验证这两个两位数的乘积为100x(x+1)+yz;99 999=.(3)99 991×8.[2019宣城模拟]阅读下列材料,并解决相关的问题.按照一定顺序排列着的一列数称为数列,排在第一位的数称为第1项,记为a1,依此类推,排在第n 位的数称为第n项,记为a n.一般地,如果一个数列从第2项起,每一项与它前一项的比等于同一个常数,那么这个数列叫做等比数列,这个常数叫做等比数列的公比,公比通常用字母q表示(q≠0),如:数列1,3,9,27,…为等比数列,其中a1=1,公比q=3.(1)等比数列3,6,12…的公比q为,第4项是;(2)如果一个数列a1,a2,a3,a4,…是等比数列,且公比为q,那么根据定义可得到=q,=q,=q,…,=q,所以a2=a1q,a3=a2q=a1q·q=a1q2,a4=a3q=a1q2·q=a1q3,由此可得a n=(用含a1,n和q的代数式表示);(3)若一个等比数列的公比q=,第2项a2=,求它的第1项与第4项.9.[2019合肥高新区模拟]我们学习了勾股定理后,都知道“勾三、股四、弦五”.观察:3,4,5;5,12,13;7,24,25;9,40,41;发现:这些勾股数的勾都是奇数,从3起就没有间断过,而且股和弦是两个连续整数.(1)请你根据上述的规律写出下一组勾股数:;(2)若第一个数用字母n(n为奇数,且n≥3)表示,写出后两个数(用含n的代数式表示),并用所学知识说明它们是一组勾股数.类型2图形中的规律探索10.[2019六安地区二模]观察下列n×n的点阵与等式的关系,并填空:(1)根据你发现的规律,在(n×n)图的后面的横线上填上所对应的等式,并证明等式成立.(2)根据等式的性质,将上图所对应的前4个已知等式的左侧和右侧式子分别相加,等式依然成立,即(22-12)+(32-22)+(42-32)+(52-42)=(1+2×1)+(1+2×2)+(1+2×3)+(1+2×4).经化简,变形后得到52-12=4+2×(1+2+3+4),即1+2+3+4=,这种方法叫等式叠加法.如果将上图(2×2)到(n×n)所对应的(n-1)个等式进行叠加,经化简,变形后可以得到1+2+3+…+(n-1)=.11.[2019合肥瑶海区二模](1)观察下面的图案与等式的关系,并填空.(2)通过猜想,写出第n个图案相对应的等式.12.[2019安徽中考]【阅读理解】我们知道1+2+3+…+n=,那么12+22+32+…+n2的结果等于多少呢?在图(1)所示三角形数阵中,第1行圆圈中的数为1,即12;第2行两个圆圈中数的和为2+2,即22……第n行n个圆圈中数的和为,即n2.这样,该三角形数阵中共有个圆圈,所有圆圈中数的和为12+22+32+…+n2.图(1)【规律探究】将三角形数阵经两次旋转可得如图(2)所示的三角形数阵,观察这三个三角形数阵各行同一位置圆圈中的数(如第n-1行的第一个圆圈中的数分别为n-1,2,n),发现每个位置上三个圆圈中数的和均为.由此可得,这三个三角形数阵所有圆圈中数的总和为3(12+22+32+…+n2)=.因此,12+22+32+…+n2=.图(2)【解决问题】根据以上发现,计算的结果为.13.[2019安徽中考]在由m×n(m×n>1)个小正方形组成的矩形网格中,研究它的一条对角线所穿过的小正方形个数 f.(1)当m,n互质(m,n除1外无其他公因数)时,观察下列图形并完成下表:m n m+n f123213432354257347猜想:当m,n互质时,在m×n的矩形网格中,一条对角线所穿过的小正方形的个数f与m,n的关系式是(不需证明);(2)当m,n不互质时,请画图验证你猜想的关系式是否仍然成立.参考答案1.A2.D【解析】由①~④的等式规律可知,第n个等式的结果为(2n-1)2,故A,C中的等式错误.第n 个等式中等号左边的项数为2n-1,故B中的等式错误,D中的等式正确.3.(1)417(2)第n个等式为(2n+1)2-4×n2=4n+1.∵左边=4n2+4n+1-4n2=4n+1=右边,∴第n个等式成立.30+1=3124.(1)32×(2)第个等式为:2n(2n-2)+1=(2n-1)2.验证:左边=2n×2n-2n×2+1=(2n)2-2×2n+1=(2n-1)2=右边,故2n(2n-2)+1=(2n-1)2是成立的.5.(1)第4个等式是=4.(2)第n个等式是=n.证明:∵===n=右边,∴第n个等式是=n.6.(1)283635解法提示:第n(n为正整数)个“三角形数”为,故a==28;第n(n为正整数)个“正方形数”为n2,故b=62=36;第n(n为正整数)个“五边形数”为n2-n,故c=×25-=35.(2)n2-n7.(1)7 221.(2)验证:(10x+y)(10x+z)=100x2+10xz+10xy+yz=100x2+10x(y+z)+yz=100x2+100x+yz=100x(x+1)+yz.(3)9 999 000 009解法提示:由题中规律可得,如果两个n位数分别写作AB和AC(即前n-1位数字部分均可表示为A(A>3),个位数字分别为B,C,且B+C=10),那么它们的乘积是一个2n位数,前2n-2位数字是A和(A+1)的乘积,后两位数字是B和C的乘积. 故99 991×99 999=9 999 000 009.8.(1)224(2)a1q n-1(3)第1项a1==÷=,第4项a4=a1·q3=×()3=.9.(1)11,60,61(2),说明:∵n2+()2=n2+===()2,∴由勾股定理的逆定理可知,n,,是一组勾股数.10.(1)n2-(n-1)2=1+2(n-1).证明:∵左边=n2-n2+2n-1=2n-1,右边=1+2n-2=2n-1=右边,∴左边=右边,即n2-(n-1)2=1+2(n-1).(2)11.(1)22323242(2)1+3+5+…+(2n-1)+(2n+1)+(2n-1)+…+5+3+1=n2+(n+1)2.12.2n+1 1 34513.(1)6 6f=m+n-1注:若猜想出的是其他关系式,只要这个关系式对表中5种情况都成立即可.(2)当m,n不互质时,f与m,n的关系式f=m+n-1不成立.例如:当m=2,n=2时,图形如图.对角线所穿过的小正方形的个数f=2,而m+n=4,等式f=m+n-1不成立.。