巧解数学题集
四年级数学总复习习题集巧妙运用解题技巧

四年级数学总复习习题集巧妙运用解题技巧数学是一门需要不断巩固和复习的学科,而解题技巧又是提高数学解题能力的关键。
为了帮助四年级的小朋友们更好地复习数学知识,本文将为大家提供一份巧妙运用解题技巧的数学总复习习题集。
希望通过这份习题集的训练,能够帮助大家更好地掌握解题技巧,提高数学成绩。
一、四则运算题1. 计算下列各题:(1) 13 + 25 - 8 = ?(2) 37 - 15 + 4 = ?(3) 9 × 6 - 3 = ?(4) 48 ÷ 6 × 2 = ?解题技巧1: 从左到右依次计算运算符两边的数字。
解题技巧2: 首先计算乘法和除法,再计算加法和减法。
2. 将下列各题用竖式计算:(1) 63 + 25 - 9 = ?(2) 174 - 57 + 19 = ?(3) 45 × 6 - 12 = ?(4) 378 ÷ 6 × 2 = ?解题技巧: 竖式计算可以帮助小朋友们更好地理解每一步的运算过程。
二、数的认识和比较1. 按要求填写下列各题:(1) 2134的千位数是_______,百位数是_______,十位数是_______,个位数是_______。
(2) 用<、>、=填空:2 356 ______ 2 3652 710 ______ 2 7017 456 ______ 9 465解题技巧1: 将数字拆分成个位、十位、百位、千位等,通过理解每个位上的数字来解答问题。
解题技巧2: 比较大小时,从左至右依次比较每一位的大小。
三、整数的加减法1. 计算下列各题:(1) 25 + 37 - 18 = ?(2) 49 - 35 + 12 = ?(3) 15 - 7 + 20 - 8 = ?解题技巧: 在加减法中,可以先进行加法运算,再进行减法运算。
2. 将下列各题用括号表示加法和减法运算:(1) 28 + 17 - 12 = ?(2) 56 - 23 + 15 = ?(3) 35 - 7 + 12 - 5 = ?解题技巧: 用括号表示加法和减法运算可以帮助小朋友们更好地理解运算顺序。
整体代入法巧解数学难题+整体法与隔离法练习题

初中数学思想方法专题讲座——整体思想解题策略整体思想,就是在研究和解决有关数学问题时,通过研究问题的整体形式、整体结构、整体特征,从而对问题进行整体处理的解题方法.从整体上去认识问题、思考问题,常常能化繁为简、变难为易,同时又能培养学生思维的灵活性、敏捷性.整体思想的主要表现形式有:整体代入、整体加减、整体代换、整体联想、整体补形、整体改造等等.在初中数学中的数与式、方程与不等式、函数与图象、几何与图形等方面,整体思想都有很好的应用,因此,每年的中考中涌现了许多别具创意、独特新颖的涉及整体思想的问题,尤其在考查高层次思维能力和创新意识方面具有独特的作用. 一.数与式中的整体思想【例1】 已知代数式3x 2-4x+6的值为9,则2463x x -+的值为 ( ) A .18 B .12 C .9 D .7相应练习:1. 若代数式2425x x -+的值为7,那么代数式221x x -+的值等于( ).A .2B .3C .-2D .42.若3a 2-a-2=0,则 5+2a-6a 2=3.先化简,再求值222142442a a a a a a a a +--⎛⎫-÷ ⎪--+-⎝⎭,其中a 满足a 2-2a -1=0.总结:此类题是灵活运用数学方法解题技巧求值的问题,首先要观察已知条件和需要求解的代数式,然后将已知条件变换成适合所求代数式的形式,运用主题带入法即可得解。
【例2】.已知114a b -=,则2227a ab ba b ab---+的值等于( ) A.6 B.6- C.125 D.27-分析:根据条件显然无法计算出a ,b 的值,只能考虑在所求代数式中构造出11a b-的形式,再整体代入求解.【例3】已知2002007a x =+,2002008b x =+,2002009c x =+,求多项式222a b c ab bc ac ++---的值.总结:在进行条件求值时,我们可以根据条件的结构特征,合理变形,构造出条件中含有的模型,然后整体代入,从整体上把握解的方向和策略,从而使复杂问题简单化.【例4】逐步降次代入求值:已知m 2-m -1=0,求代数式m 3-2m +2005的值.相应练习:1、已知m 是方程2250x x +-=的一个根,求32259m m m +--的值.2、已知m 是方程2310x x -+=的根,求代数式10214+-m m 的值.总结:此类题目通常为初中阶段很少接触到得三次方程甚至更高次的方程,那么用初中阶段的知识直接解题时肯定行不通的,所以这个时候我们就要考虑如何降次的问题。
以形助数 巧解数学竞赛题
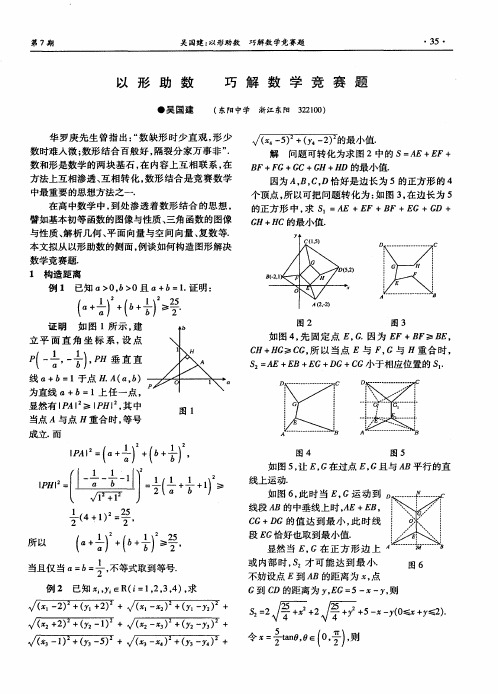
AO B 和 AO D 的 费 马 点 时 , E +E +E 与 A C O A B
>
。
图 1
如图 4 先 固定点 , . , G 因为 F+ F≥B B E, C ≥C , 以 当点 E与 F G与 日重合 时 , H+ G所 , S = E+ B+E DG+C 2 A E G+ G小于 相应 位置 的 S. 1
为直线 口+ 1上任一点 , b= 显然 有 IAI l I 其 中 P ≥ ,
第 7期
吴 国建 : 以形助数
巧解数 学竞赛题
・3 5・
以 形 助 数
●吴 国建
巧 解 数 学 竞 赛 题
( 东阳中学 浙江东阳 320 ) 21 0
华 罗 庚 先 生 曾指 出 : 数 缺形 时 少 直 观 , 少 “ 形
√( 一 )+ y — ) 5 ( 2 4 的最/值. J 、
解 问题 可 转 化 为求 图 2中的 S= E+E A F+ B F+F G+I 5 l 的最 ,值. : C+I 日+i D J 、
数时难人微 ; 数形结合百般好 , 隔裂分家万事非 ” . 数和形是数学的两 块基 石 , 内容上互相联系 , 在 在 方法上互相渗透、 互相转化 , 数形结合是竞赛数学
CO SO
,
解 考 曲 Y詈 坐 轴 围 区 内 虑 线 与 标 所 成 域
的格点 ( 坐标 为 整数 的点 ) 设 k为 自然 数 , 图 8 . 如 ,
≥ ,≥ 4£
小学数学趣题巧解

小学数学趣题巧解篇一:趣题巧解趣题巧解(十一)姓名1、一张长方形纸片有四个角,用剪刀沿直线剪掉一个角后,还剩几个角?2 、37个同学要坐船过河,渡口处只有一只能载5人的小船(无船工)。
他们要全部渡过河去,至少要使用这只小船渡河多少次?3、右图是10枚硬币,移动其中1枚硬币,使每一行上都有6枚硬币。
4、有一个村子里有6个小矮人,他们总是为了不能平分土地吵架。
现在,聪明的小朋友,你能帮助他们解决这个问题吗?六个小矮人的要求是把空白部分分成大小相等、形状相同的6块。
5、一把钥匙只能开一把锁,现在有10把钥匙和10把锁,但不知哪把钥匙开哪把锁,最多试多少次就能配好全部的钥匙和锁?6、小A、小B、小C、小D、小E五名同学参加了跳绳比赛的决赛,比赛前每两个小选手都要握一次手表示友好。
当小A握了4次手,小B握了3次手、小C握了2次手、小D握了1次手的时候,小E握了几次手?最后这五名小选手一共要握多少次手?7、用6根长短、粗细一样的火柴棍拼出四个等边三角形(即三边相等的三角形),如何拼?篇二:趣题巧解1、有一堆夹心糖,如果平均分成8份,最后多余2块;如果平均分成9份,(来自: 小龙文档网:小学数学趣题巧解)最后多余3块;如果平均分成10份,最后多余4块。
这堆糖至少有多少块?古希腊一位将军要从A地出发到河边(如下图MN)去饮马,然后再回到驻地B。
问怎样选择饮马地点,才能使路程最短?图1,电子跳蚤每跳一步,可从一个圆圈跳到相邻的圆圈,现在一只红跳蚤从标有数字“0”的圆圈按顺时针方向跳了1991步,落在一个圆圈里。
一只黑跳蚤也从标有数字“0”的圆圈起跳,但它是沿着逆时针方向跳了1949步,落在另一个圆圈里。
问:这两个圆圈里数字的乘积是多少?图1从一盒火柴中取出15根,排成图1所示的“弓”字形。
只许移动其中的4根,要用这些火柴排成两个正方形,怎样移动?一队士兵行军到河边,他们想渡过河去,可是河水又深又急不能泅渡。
忽然,看到河对岸有两个孩子摇来一条小船。
小学五年级数学思维训练(奥数)《巧解方程》讲解及练习题(含答案)

巧解方程专题简析:学习解方程。
首先,我们要对方程进行观察,将能够先计算的部分先计算或合并,使其化简,然后再求出x的值。
例1:解方程:6x+9x-13=17分析与解答方程左边的6x与9x可以合并为15x,因此,可以将原方程转化成15x-13=17,从而顺利地求出方程的解。
解:6x+9x-13=17,15x-13=1715x=30x= 2随堂练习:解方程7.5x-4.1x+1.8=12例2 解方程:8x-16=4x分析与解答方程胡两边都有X,运用等式的性质,我们先将方程两边同时减去4x,然后再方程两边同时加上16变为8x-4x=16.8x-16=4x解:8x-4x=164x= 16x=4随堂练习:解方程10x-7=4.5x+20.5 16-2x=6x例3 解方程:4(4x-11)=3(22-2x)分析与解答第一步先运用乘法分配律去掉括号;第二步,运用等式的性质,便未知数和已知数分别在等号的两边;第三步把等号两边的未知数与数合并;第四步求出方程的解4(4x-11)=3(22-2x)解:16x-44=66-6x 去括号16x+6x=66+44 等式的性质22x=110x=5随堂练习解方程7(2x-6)=84 15(22-x)+2=68x例4 解方程:x÷3=(2x-11) ÷5分析与解答我们先根据等式的性质,在方程的两边同时乘3和5的最小公倍数,然后再运用前面的方法进行求解。
解:x÷3×15=(2x-11)÷5×155x=3(2x-11)5x=6x-33x=33随堂练习:解方程:2x÷3=(2x-5)÷2 (3x-0.5)÷2=2x÷3拓展应用1、解方程5x+0.7x-3x=10-1.92、解方程7(2x-6)=843、解方程5(x-8)=3x4、解方程5.9x-9=4.2x+2.95、解方程9(2x-3)-2=5(2x-1)6、解方程:x÷5+0.5=x÷47、在下面的□内填入相同的数,使等式成立。
小学数学世界名题巧解(7)

小学数学世界名题巧解
﹙真假硬币的问题﹚
有这么一道题:
27枚硬币中混有一枚较轻的假币,请你用一架没有砝码的天平最多称三次,将它找出来。
解:第一次将硬币分成三堆,每堆9枚,把其中的两堆分别放到天平的两个托盘上,若天平平衡,则假币在第三堆中;若不平衡,则假币在较轻的那一堆里。
第二次将有假币的那一堆9枚硬币分成三小堆,每一小堆3枚硬币,把其中两小堆分别放到天平的两个托盘中,同上一次一样,天平平衡则假币在第三小堆中;若不平衡则假币在较轻的那一小堆里。
第三次从含有假币的那一小堆的3枚硬币中,取出两枚硬币分别放到天平的两个托盘上,若天平平衡,则剩下的那一枚硬币是假币;若不平衡,那么较轻的一枚硬币是假币。
小学数学世界名题巧解(51)

小学数学世界名题巧解
﹙兔跳的问题﹚
19世纪俄国女数学家柯瓦列夫斯卡娅,还是在童年的时候,就解开过妈妈给她编的兔跳的问题。
题目如下:
森林里有一对兔兄弟,它们在进行跳跃比赛。
兔弟弟说,应该先让它跳10次,哥哥才可以起步。
假如在同样的时间内,兔弟弟每跳4次,兔哥哥只能跳3次,而兔哥哥跳5次的距离相当于兔弟弟跳7次那样远。
那么这样下去,兔哥哥能追上兔弟弟吗?如果能,它要在跳多少次以后才能追上兔弟弟呢?
解:在同样的时间内,兔哥哥跳了3次,兔弟弟跳了4次,但兔哥哥跳5次的距离相当于兔弟弟跳7次的距离。
为了便于分析比较,假设兔哥哥每次都是连续跳15次﹙15次是3次的5倍﹚,那么在相同的时间内,兔弟弟要跳的次数应是20次﹙20次是4次的5倍﹚:
4×5=20﹙次﹚
因为兔哥哥跳5次的距离相当于兔弟弟跳7次的距离,看15中包含几个5,兔哥哥跳的就是兔弟弟所跳几个7次的距离:
7×﹙15÷5﹚=21﹙次﹚
而实际上,兔弟弟只跳了4×5=20﹙次﹚,这就是说,兔哥哥每跳15次,就超过兔弟弟:
21-20=1﹙次﹚
这也就是说,兔哥哥每跳15次,才可以追上兔弟弟跳20次的距离,并且,超过兔弟弟跳1次的距离,而兔弟弟先跳了10次,所以,兔哥哥追上兔弟弟要跳的次数是:
15×﹙10÷1﹚=150﹙次﹚
解:﹙略﹚。
5学通数学小学奥数数字谜专题-12 数论巧解数字谜 课后习题

数论巧解数字谜
主讲:五豆
【练习】用1、2、3、4、5、6、7这七个数字恰好组成一个一位数和两个三位数,每个数字只用一次,使得这三个数两两互质。
已知其中一个三位数是714,那么其他两个数是多少?
答案:263、5
数论巧解数字谜
【练习】在下面的乘法算式中,相同的汉字表示相同的数字,不同的汉字表示不同的数字。
那么“好棒”所代表的两位数是多少?
数好×学好=棒棒棒
【练习】在横线上填上适当的质数,使得算式:
△○□△○□÷(××)=66成立,且六位数“△○□△○□”尽量小,其中“△”、“○”、“□”代表不同的数字,这时三位数“△○□”是多少?
【练习】将1、2、3、4、5、6、7、8、9这9个数字分别填入下式的各个方
框中,使等式成立。
答案:54×93=27×186=5022数论巧解数字谜
□□×□□=□□×□□□=5022
【练习】在乘法算式“清清×楚楚=明明白白”中,相同的汉字表示相同的数字,不同的汉字表示不同的数字。
那么“明明白白”所表示的四位数是多少?答案:3388数论巧解数字谜。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1、有只猴子在树林采了100根香蕉堆成一堆,猴子家离香蕉堆50米,猴子打算把香蕉背回家,每次最多能背50根,可是猴子嘴馋,每走一米要吃一根香蕉,问猴子最多能背回家几根香蕉?要想猴子背回家最多香蕉,就要背着香蕉走的路尽量少,因此安排猴子先背50个香蕉到25米处,此时只剩25个香蕉,再回去背50个到25米处,此时在25米处有50个香蕉,一次全部背回家,能够剩余25个香蕉。
(在这种情况下,猴子后25米只走了一次,走的路程最少。
如果最后走一次的路程大于25米,那么吃掉的香蕉就要多于25个,剩下的香蕉就要少于25个。
)另:此题应该是16根。
在剩余香蕉大于50根之前,猴子每走1米要吃3根香蕉,因为他走1米吃掉1根后,还得往回走1米抱剩下的香蕉,这又得吃1根,然后再回到原位置需要走1米,再吃1根,所以实际上猴子走1米需要消费3个香蕉当走到17米的时候,猴子一共吃了17*3=51个香蕉,还剩49,这样猴子就可以一次性搬回家了,不用往回去搬香蕉,离家还剩下50-17=33米,需要吃33根香蕉,所以到家时还剩下49-33=16根例题】有a ,b,c,d 四条直线,依次在a线上写1,在b 线上写2,在c 线上写3,在d 线上写4,然后在a 线上写5,在b 线,c 线和d 线上写数字6,7,8……按这样的周期循环下去,问数2008 在哪条线上?A.a 线 B .b 线 C.C 线D.d 线【解析】abcd分别代表每个数除以4的余数,每条线上的余数相同,分别是1,2,3,0,因为2008除以4余0,所以在d线上,选D【例题】小王工作一年酬金是1800元和一台全自动洗衣机。
他干了7个月,得到560元和一台洗衣机,问这台洗衣机价钱为多少元()A.1176 B.1144 C.1200 D.1154【解析】小王做12个“7个月”要得到560*12+12台洗衣机,跟干7年共1800*7+7台洗衣机应该是相等的。
即5台洗衣机=1800*7-560*12,1台洗衣机=360*7-112*12,尾数应该是6,选A【例题】15克盐放入135克水中,放置一段时间后,盐水重量变为100克,这时盐水的浓度是多少?浓度比原来提高了百分之几()A.75%,12.5% B.25%,12.5% C.15%,50% D.50%,62.5%【解析】盐的重量是不变的,因此浓度=15/100*100%=15%,选C【例题】小张和小王两人比赛珠算,共有1200题,小张每分钟算出20题,小王每算出80题比小张算同样多的题少用2秒,问:小王做完1200题时,小张还有多少题没做()A.10B.15C.20D.5【解析】小张3秒做一道题,小王每算240道题要比小张少用6秒,即小张还差2道题,于是1200/240=5,小张还有5*2=10道题没做,选A【例题】某校二年级全部共3个班的学生排队.每排4人,5人或6人,最后一排都只有2人.这个学校二年级有()名学生。
A.120 B.122 C.121 D.123【解析】本题即4,5,6的任意公倍数+2,此题采用最小公倍数=1222、旅客在车站候车室等车,并且排队的乘客按一定速度增加,检查速度也一定,当车站放一个检票口,需用半小时把所有乘客解决完毕,当开放2个检票口时,只要10分钟就把所有乘客OK了求增加人数的速度还有原来的人数?牛吃草问题:公式法(牛的头数-每天长草量)×天数=草原原有草量(1-x)*30=y(2-x)*10=y即y/10-y/30=1,解得y=15,x=0.5(其中x表示增加人数的速度,y表示原来的人数)3、某单位有78人,站成一排,从左到右数,小王是第50个,从右往左,小张是第48个,则小王和小张之间有多少人?A,16 B,17 C,18 D,20容斥原理问题,加上小王、小张和中间的人,共有50+48-78=20人,所以小王和小张之间共有18个人。
4、人们将1/10表示为1月10日,也有人将1/10表示为10月1日,这样一年中就有不少混淆不清的日期了,当然,8/15和15/8只能表示为8月15日,那么一年中像这样不会搞错的日期最多会有多少天?不会搞错的有这么几种类型:类型一:前后两个数字相同:1/1,2/2,3/3,……,12/12,共12天,类型二:有一个数字大于12,其中1、3、5、7、8、10、12月有31-12=19天,4、6、9、11有30-12=18天,2月在平年中有28-12=16天,闰年有17天。
于是类型二共有7*19+4*18+16=221天,或者闰年222天综上,共有12+221=233或234天。
5、某地区2009年全年实现工业增加值3107亿元,同比增长8.7%第四季度实现工业增加值828亿元,同比增长12.5%问:前三个季度的工业增加值,同比增长率为多少?A 7.4%B 8.8%C 9.6%D 10.7%8.7%应该介于12.5%和前三个季度的工业增长率之间(因为8.7%是两个数值加权平均出来的),选A关于加权平均,举个例子,X=a*p1+b*p2,其中p1+p2=1,p1,p2均为正数,a<b,那么a<X<b6、现要挂号邮寄120本书,每11本重2千克,邮局规定(为计算方便,略有改动):印刷品的邮费是每千克0.8元,不足1千克的以1千克计,每件限重5千克,挂号费每件0.6元(含手续费0.3元),试问:这批书最省的邮费为多少元?( )A.20.6 B.20 C.19.6 D.19.2为使邮费最省,则每次尽量装满,5千克只能装11+11+5=27本,于是120本书应该分为27+27+27+27+12每包邮费=5*0.8+0.6=4.6元12本书的邮费=3*0.8+0.6=3元于是120本书=4.6*4+3=21.4元,无答案所以考虑把最后一个装满4千克,这样就还可以装10本,从前面的2包中取出10本,于是4千克的邮费=4*0.8+0.6=3.8最省邮费=3.8*3+2*4.6=20.6,选a7、一次测验中共有10道问答题,每题评分标准时:回答完全正确,得5分;回答不完全正确,得3分;回答完全错误或不回答,得0分。
那么,至少()人参加这次测验,才能保证至少有3人的得分相同?将这10道题分为0,3,5三类,那么用插空法,有C(12,2)=66种方法。
但是3个5分的与5个3分的得分相同,于是当有5道题得了3分时,此时剩下的5道题还有C(7,2)=21种方法,要减掉于是有66-21=45种不同的分数于是至少要45*2+1=91人参加考试才行。
8、插板法就是在n个元素间的(n-1)个空中插入若干个(b)个板,可以把n个元素分成(b+1)组的方法。
应用插板法必须满足三个条件:(1)这n个元素必须互不相异(2)所分成的每一组至少分得一个元素(3) 分成的组别彼此相异举个很普通的例子来说明把10个相同的小球放入3个不同的箱子,每个箱子至少一个,问有几种情况?问题的题干满足条件(1)(2),适用插板法,c9 2=36下面通过几道题目介绍下插板法的应用===================================================a 凑元素插板法(有些题目满足条件(1),不满足条件(2),此时可适用此方法)例1 :把10个相同的小球放入3个不同的箱子,问有几种情况?3个箱子都可能取到空球,条件(2)不满足,此时如果在3个箱子种各预先放入1个小球,则问题就等价于把13个相同小球放入3个不同箱子,每个箱子至少一个,有几种情况?显然就是c12 2=66-------------------------------------------------例2:把10个相同小球放入3个不同箱子,第一个箱子至少1个,第二个箱子至少3个,第三个箱子可以放空球,有几种情况?我们可以在第二个箱子先放入10个小球中的2个,小球剩8个放3个箱子,然后在第三个箱子放入8个小球之外的1个小球,则问题转化为把9个相同小球放3不同箱子,每箱至少1个,几种方法?c8 2=28==================================================b 添板插板法例3:把10个相同小球放入3个不同的箱子,问有几种情况?-o - o - o - o - o - o - o - o - o - o - o表示10个小球,-表示空位11个空位中取2个加入2块板,第一组和第三组可以取到空的情况,第2组始终不能取空此时若在第11个空位后加入第12块板,设取到该板时,第二组取球为空则每一组都可能取球为空c12 2=66--------------------------------------------------------例4:有一类自然数,从第三个数字开始,每个数字都恰好是它前面两个数字之和,直至不能再写为止,如257,1459等等,这类数共有几个?因为前2位数字唯一对应了符合要求的一个数,只要求出前2位有几种情况即可,设前两位为ab显然a+b<=9 ,且a不为01 -1- 1 -1 -1 -1 -1 -1 -1 - - 1代表9个1,-代表10个空位我们可以在这9个空位中插入2个板,分成3组,第一组取到a个1,第二组取到b个1,但此时第二组始终不能取空,若多添加第10个空时,设取到该板时第二组取空,即b=0,所以一共有c10 2=45-----------------------------------------------------------例5:有一类自然数,从第四个数字开始,每个数字都恰好是它前面三个数字之和,直至不能再写为止,如2349,1427等等,这类数共有几个?类似的,某数的前三位为abc,a+b+c<=9,a不为01 -1- 1 -1 -1 -1 -1 -1 -1 - - -在9个空位种插如3板,分成4组,第一组取a个1,第二组取b个1,第三组取c个1,由于第二,第三组都不能取到空,所以添加2块板设取到第10个板时,第二组取空,即b=0;取到第11个板时,第三组取空,即c=0。
所以一共有c11 3=165============================================c 选板法例6:有10粒糖,如果每天至少吃一粒(多不限),吃完为止,求有多少种不同吃法?o - o - o - o - o - o - o - o - o - o o代表10个糖,-代表9块板10块糖,9个空,插入9块板,每个板都可以选择放或是不放,相邻两个板间的糖一天吃掉这样一共就是2^9= 512啦=============================================d 分类插板例7:小梅有15块糖,如果每天至少吃3块,吃完为止,那么共有多少种不同的吃法?此问题不能用插板法的原因在于没有规定一定要吃几天,因此我们需要对吃的天数进行分类讨论最多吃5天,最少吃1天1:吃1天或是5天,各一种吃法一共2种情况2:吃2天,每天预先吃2块,即问11块糖,每天至少吃1块,吃2天,几种情况?c10 1=103:吃3天,每天预先吃2块,即问9块糖,每天至少1块,吃3天? c8 2=284:吃4天,每天预先吃2块,即问7块糖,每天至少1块,吃4天?c6 3=20所以一共是2+10+28+20=60 种=================================e 二次插板法例8 :在一张节目单中原有6个节目,若保持这些节目相对次序不变,再添加3个节目,共有几种情况?-o - o - o - o - o - o - 三个节目abc可以用一个节目去插7个空位,再用第二个节目去插8个空位,用最后个节目去插9个空位所以一共是c7 1×c8 1×c9 1=504种插板法另一模型a+b+c<=na+b+c<=10 ,a+b+c+d<=10a+b+c<=10 ,a+b+c+d<=10以上两个不等式的非负整数解各有几种?没事做做----------------------------------------------------------------x=a+1,y=b+1,z=c+1,则x,y,z为正整数x+y+z<=130- 0- 0- 0- 0 -0 -0 -0 -0 -0- 0- 0 -0- 0代表13个1,-代表空位13个空选3个插入3板,13个1被分成4部分,前3部分分别对应x,y,z满足x,y,z>=1,且x+y+z<=13, 共有c13 3=286种一个xyz与一个abc唯一对应,所以共有286个abcp.s 这里取3个空,而不取2个空,是由于前三个数和可以小于13------------------------------------------------------a+b+c+d<=10x=a+1,y=b+1,z=c+1,t=d+1,x,y,z,t为正整数,x+y+z+t<=14分析方法同上,需要从14个空选4个c14 4=1001-----------------------------模型应用举例有一类自然数,从第三个数字开始,每个数字都恰好是它前面两个数字之和,直至不能再写为止,如257,1459等等,这类数共有几个?10、一只船从甲码头往返一次共用4小时,回来时顺水比去时每小时多行12千米,因此后2小时多行16千米。
