树的概念和定义
分别简述树、树枝、连支的概念

树、树枝、连支的概念树(Tree)是一种抽象的数据类型,通常用于表示具有层次结构的数据。
树由一个根节点和若干个子节点组成,每个子节点可以进一步分解为更小的子树。
树的概念可以广泛应用于各种领域,如计算机科学、图形学、人工智能等。
在计算机科学中,树通常被用于表示具有层次结构的数据,例如文件系统、组织结构、XML文档等。
树可以表示为一种特殊的图(Graph),其中每个节点都有一个父节点,除了根节点外。
树中的每个节点可以有多个子节点,但只有一个父节点。
这种结构使得树在处理具有层次结构的数据时非常方便。
树的定义和性质:每个节点都有一个值。
根节点的值是唯一的。
每个子节点的值都是唯一的。
每个子节点可以进一步分解为更小的子树。
树中的每个节点只有一个父节点,但可以有多个子节点。
树可以表示为一种特殊的图,其中每个节点都有一个父节点。
树可以用于表示具有层次结构的数据,例如文件系统、组织结构等。
树枝(Branch)是树的一部分,它从树的根节点开始,经过若干个子节点,最终到达一个叶子节点。
树枝由根节点、若干个子节点和连接这些节点的边组成。
在树中,根节点没有父节点,叶子节点没有子节点。
树枝的概念可以用于表示树的结构和层次关系。
连支(Connected Component)是指图形中相互连接的顶点组成的子图。
在一个无向图中,如果任意两个顶点之间都存在一条路径相连,则称该图为连通的。
在连通图中,任意两个顶点之间都存在一条路径,因此连支可以被定义为连通图的子图。
在非连通图中,连支可以被定义为与连通图的连通分量相对应的子图。
树的概念和定义

第十四讲
性质5: 对于具有n个结点的完全二叉树, 如果按照从上到 下和从左到右的顺序对二叉树中的所有结点从1开始顺序编号, 则对于任意的序号为i的结点有:
(1) 如i=1,则序号为i的结点是根结点, 无双亲结点; 如 i>1, 则序号为i的结点的双亲结点序号为[i/2]。
(2) 如2×i>n,则序号为i的结点无左孩子;如2×i≤n,则 序号为i的结点的左孩子结点的序号为2×i。
第十四讲 树的概念与定义
精选完整ppt课件
1
第十四讲
树是n(n≥0)个结点的有限集合T。当n=0时,称为空树; 当n>0时, 该集合满足如下条件:
(1) 其中必有一个称为根(root)的特定结点,它没有直接 前驱,但有零个或多个直接后继。
(2) 其余n-1个结点可以划分成m(m≥0)个互不相交的有限 集T1,T2,T3,…,Tm,其中Ti又是一棵树,称为根root的子 树。 每棵子树的根结点有且仅有一个直接前驱,但有零个或 多个直接后继。
精选完整ppt课件
13
第十四讲
(6) Parent(bt, x):求双亲函数。求二叉树bt中结点x的双 亲结点。若结点x是二叉树的根结点或二叉树bt中无结点x, 则返回“空”。
(7) LeftChild(bt, x):求左孩子。 若结点x为叶子结点或x 不在bt中, 则返回“空”。
(8) RightChild(bt, x):求右孩子。 若结点x为叶子结点或x 不在bt中, 则返回“空”。
(11) TraverseTree(Tree,Visit()): 树Tree存在,Visit() 是对结点进行访问的函数。按照某种次序对树Tree的每个结点调 用Visit()函数访问一次且最多一次。若Visit()失败, 则操 作失败。
数据结构树的知识点总结

数据结构树的知识点总结一、树的基本概念。
1. 树的定义。
- 树是n(n ≥ 0)个结点的有限集。
当n = 0时,称为空树。
在任意一棵非空树中:- 有且仅有一个特定的称为根(root)的结点。
- 当n>1时,其余结点可分为m(m>0)个互不相交的有限集T1、T2、…、Tm,其中每个集合本身又是一棵树,并且称为根的子树(sub - tree)。
2. 结点的度、树的度。
- 结点的度:结点拥有的子树个数称为结点的度。
- 树的度:树内各结点的度的最大值称为树的度。
3. 叶子结点(终端结点)和分支结点(非终端结点)- 叶子结点:度为0的结点称为叶子结点或终端结点。
- 分支结点:度不为0的结点称为分支结点或非终端结点。
- 除根结点之外,分支结点也称为内部结点。
4. 树的深度(高度)- 树的层次从根开始定义起,根为第1层,根的子结点为第2层,以此类推。
树中结点的最大层次称为树的深度(或高度)。
二、二叉树。
1. 二叉树的定义。
- 二叉树是n(n ≥ 0)个结点的有限集合:- 或者为空二叉树,即n = 0。
- 或者由一个根结点和两棵互不相交的、分别称为根结点的左子树和右子树的二叉树组成。
2. 二叉树的特点。
- 每个结点最多有两棵子树,即二叉树不存在度大于2的结点。
- 二叉树的子树有左右之分,次序不能颠倒。
3. 特殊的二叉树。
- 满二叉树。
- 一棵深度为k且有2^k - 1个结点的二叉树称为满二叉树。
满二叉树的特点是每一层上的结点数都是最大结点数。
- 完全二叉树。
- 深度为k的、有n个结点的二叉树,当且仅当其每一个结点都与深度为k的满二叉树中编号从1至n的结点一一对应时,称之为完全二叉树。
完全二叉树的叶子结点只可能在层次最大的两层上出现;对于最大层次中的叶子结点,都依次排列在该层最左边的位置上;如果有度为1的结点,只可能有一个,且该结点只有左孩子而无右孩子。
三、二叉树的存储结构。
1. 顺序存储结构。
- 二叉树的顺序存储结构就是用一组地址连续的存储单元依次自上而下、自左至右存储完全二叉树上的结点元素。
树的基本概念与特点

树的基本概念与特点树,被广泛应用于生物学、计算机科学、数学等领域,是一种重要的数据结构。
本文将介绍树的基本概念与特点,并对其进行详细论述。
一、概念树是一种由节点和边组成的非线性数据结构。
它以一个称为根节点的特殊节点作为起点,每个节点可以有零个或多个子节点,且子节点之间没有任何顺序关系。
二、特点1. 分层结构:树的节点可以按照层次分布。
根节点处于第一层,根节点的子节点处于第二层,依次类推。
2. 唯一路径:树中的任意两个节点之间只存在唯一的路径。
即从根节点到任意一个节点,只有一条路径可达。
3. 无环结构:树是无环的,即不存在环形路径。
每个节点只能通过一条路径与其他节点相连。
4. 子树概念:树中的每个节点都可以看作是一个子树的根节点。
子树是由其下属的节点及其子节点构成的一颗完整树。
三、常见类型树有许多常见的类型,每种类型都有其特定的应用场景和特点。
以下列举几种常见的树类型:1. 二叉树:每个节点最多只有两个子节点的树称为二叉树。
二叉树有许多变种,例如满二叉树、完全二叉树等。
2. 二叉搜索树:在二叉搜索树中,每个节点的值都大于其左子树中的任意节点的值,小于其右子树中的任意节点的值。
这个特性使得查找、插入和删除操作具有较高的效率。
3. 平衡二叉树:平衡二叉树是一种特殊的二叉搜索树,它的左右子树的高度差不超过1。
这保证了树的整体高度较低,提高了查找、插入和删除操作的效率。
4. B树:B树是一种自平衡的搜索树,它可以拥有多个子节点。
它的出色特性使得它被广泛应用于文件系统和数据库的设计中。
5. 红黑树:红黑树是一种特殊的二叉搜索树,具有一些平衡性质。
红黑树的高度近似于log(n),使得它的查找、插入和删除操作具有较好的性能。
四、应用场景树的应用场景非常广泛。
下面列举几个常见的应用场景:1. 文件系统:文件系统通常使用树的结构来组织文件和目录。
每个目录可以包含多个子目录或文件。
2. 数据库:数据库中的索引通常使用树的结构,如B树和红黑树,以提高查询效率。
数据结构第七章 树和森林

7.5 树的应用
➢判定树
在实际应用中,树可用于判定问题的描述和解决。
•设有八枚硬币,分别表示为a,b,c,d,e,f,g,h,其中有一枚且 仅有一枚硬币是伪造的,假硬币的重量与真硬币的重量不同,可能轻, 也可能重。现要求以天平为工具,用最少的比较次数挑选出假硬币, 并同时确定这枚硬币的重量比其它真硬币是轻还是重。
的第i棵子树。 ⑺Delete(t,x,i)在树t中删除结点x的第i棵子树。 ⑻Tranverse(t)是树的遍历操作,即按某种方式访问树t中的每个
结点,且使每个结点只被访问一次。
7.2.2 树的存储结构
顺序存储结构 链式存储结构 不管哪一种存储方式,都要求不但能存储结点本身的数据 信息,还要能够唯一的反映树中各结点之间的逻辑关系。 1.双亲表示法 2.孩子表示法 3.双亲孩子表示法 4.孩子兄弟表示法
21
将二叉树还原为树示意图
A BCD
EF
A
B
C
E
D
F
A
B
C
E
D
F
22
练习:将下图所示二叉树转化为树
1 2
4
5
3
6
2 4
1 53
6
23
7.3.2 森林转换为二叉树
由森林的概念可知,森林是若干棵树的集合,只要将森林中各棵树 的根视为兄弟,森林同样可以用二叉树表示。 森林转换为二叉树的方法如下:
⑴将森林中的每棵树转换成相应的二叉树。 ⑵第一棵二叉树不动,从第二棵二叉树开始,依次把后一棵二叉树 的根结点作为前一棵二叉树根结点的右孩子,当所有二叉树连起来 后,此时所得到的二叉树就是由森林转换得到的二叉树。
相交的集合T1,T2,…,Tm,其中每一个集合Ti(1≤i≤m)本身又是 一棵树。树T1,T2,…,Tm称为这个根结点的子树。 • 可以看出,在树的定义中用了递归概念,即用树来定义树。因此, 树结构的算法类同于二叉树结构的算法,也可以使用递归方法。
图论中的树与树的性质

图论中的树与树的性质图论是数学中的一个分支,研究各种图形的结构和性质。
其中,树是图论中非常重要的一个概念。
本文将介绍树的定义和性质,并探讨它在图论中的应用。
一、树的定义在图论中,树是一种特殊的无向图,它是一个连通的无环图。
这意味着树中的任意两个顶点之间都存在唯一的路径,并且不存在回路。
在树中,有一个特殊的顶点被称为“根”,其他顶点都与根有一条直接的路径相连。
根据根与其他顶点之间的距离可以将树分为不同的层次。
二、树的性质1. 顶点数与边数关系在一个树中,边的数量等于顶点数减1。
这可以通过归纳证明来证明。
2. 树的层次关系在树中,从根开始,每一层的顶点都与上一层的顶点相连。
树的层次关系可以用来刻画树中的信息流动或者依赖关系。
3. 叶子节点在树中,没有子节点的顶点被称为叶子节点。
树的叶子节点是最末端的节点,它们没有子节点与之相连。
4. 子树在一个树中,任意一个顶点都可以看作是一个树的根。
以某个顶点为根的子树包含了该顶点以及与之直接相连的所有顶点。
5. 树的深度树的深度是指树中从根到最深的叶子节点的层数。
树的深度也可以看作是树的高度,表示树的层数。
三、图论中树的应用图论中的树在很多问题中起到了重要的作用,下面列举几个常见的应用。
1. 最小生成树最小生成树是指在一个连通的带权无向图中选择一棵边的子集,使得这棵子树包含了图中的所有顶点,并且权重之和最小。
最小生成树常被用于网络设计、电路布局等问题中。
2. 网络路由在一个网络中,通过树的结构可以确定数据的传输路径,有效地避免了数据的冗余和混乱。
树结构的拓扑设计对于确定最短路径、避免环路等问题非常有帮助。
3. 数据压缩树结构可以用于数据的压缩和解压缩。
通过构建哈夫曼树,可以实现对数据的高效压缩,去除冗余信息,提高存储和传输效率。
4. 优先级队列优先级队列常通过堆这种数据结构来实现,而堆可以看作是一种特殊的树。
通过构建堆结构,可以高效地实现插入和删除操作,常被用于任务调度、最短路径算法等场景。
山东科技大学 离散数学7-6对偶图与着色7-7 树+复习

7-8 根树及其应用
一、根树
1、有向树 定义7-8.1 如果一个有向图在不考虑边的方向时
是一棵树,那么,该有向图称为 有向树。
2、根树
定义7-8.2 一棵有向树,如果恰有一个 结点的入度为0,其余所有结点的入度都为1, 则称为根树(rooted tree)。 入度为0的结点称为T的树根。 出度为0的结点称为树叶。 出度不为0的结点称为分支点或内点。
7. 设a和b是格<A, ≤>中的两个元素,证明 (1)a∧b=b 当且仅当a∨b=a (2) a∧b < b和a∧b <a 当且仅当a与b是不可比较的 证明: (1)在格中吸收律满足, 则 由a∧b=b, a∨b=a∨(a∧b)=a 反之, 若a∨b=a, 则a∧b= (a∨b)∧b=b (2)若a∧b < b和a∧b <a, 即表明a∧b ≠b和a∧b ≠a, 用反证法: 假设a与b是可比较的, 则 a≤b,a∧b=a,矛盾; b≤a,a∧b=b,矛盾 因此a与b是不可比较的。 反之, a与b是不可比较的, 则a≤b和b≤a均不成立, 即a∧b ≠b和a∧b ≠a 根据∧的定义:a∧b≤a 和 a∧b≤b, 故 a∧b < b和a∧b <a
点中的某一个称为根,其他所有结点被分成有限个
在有向树中,结点的出现次序是没有意义的。 但实际应用中,有时要给出同一级中结点的相对 次序,这便导出有序树的概念。 4、有序数:在根树中规定了每一层上结点的次 序,称为有序树。
为表示结点间的关系,有时借用家族中的术语。
定义 在以v0为根的树中, (1)v1,v2,…,vk称为v0的 儿子,v0称为它们的 父亲。vi,vj 同为一顶点v的儿子时,称它们为兄弟。 (2)顶点间的父子关系的传递闭包称为顶点间
树的有关概念
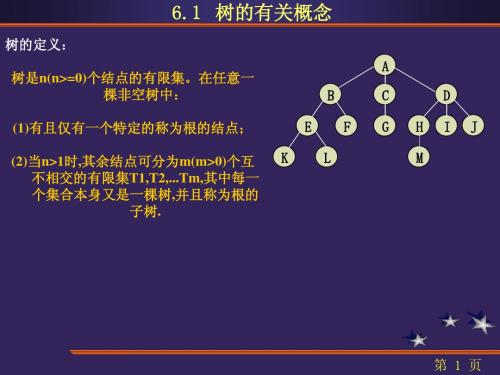
树的定义: 树的定义: 树是n(n>=0)个结点的有限集。在任意一 个结点的有限集。 树是 个结点的有限集 棵非空树中: 棵非空树中: (1)有且仅有一个特定的称为根的结点; 有且仅有一个特定的称为根的结点; 有且仅有一个特定的称为根的结点 (2)当n>1时,其余结点可分为 当 其余结点可分为m(m>0)个互 时 其余结点可分为 个互 不相交的有限集T1,T2,...Tm,其中每一 不相交的有限集 其中每一 个集合本身又是一棵树,并且称为根的 个集合本身又是一棵树 并且称为根的 子树. 子树 K E L A B F C G H M D I J
第 1 页
6.1 树的有关概念
树的 基本术语 树的结点:包含一个数据元素及若干指 树的结点: 向子树的分支; 向子树的分支; 孩子结点: 孩子结点:结点的子树的根称为该结点 的孩子; 的孩子; 双亲结点: 结点是A 结点的孩子, 双亲结点:B 结点是 结点的孩子,则A K B E L F A C G H M D I J
结点是B 结点的双亲; 结点是 结点的双亲; 兄弟结点:同一双亲的孩子结点; 兄弟结点:同一双亲的孩子结点; 堂兄结点:同一层上结点; 堂兄结点:同一层上结点; 祖先结点: 祖先结点 从根到该结点的所经分支上的所有结点 子孙结点: 子孙结点:以某结点为根的子树中任一结点都称为该结点的子 孙
第 2 页
D H M I J
6.1 树的有关概念
树的 基本术语 结点层:根结点的层定义为 ;根的孩子为第二层结点, 结点层:根结点的层定义为1;根的孩子为第二层结点,依此 类推; 类推; A 树的深度: 树的深度:树中最大的结点层 结点的度: 结点的度:结点子树的个数 B C 树的度: 树中最大的结点度。 树的度: 树中最大的结点度。 叶子结点:也叫终端结点,是度为 0 的结点; 叶子结点:也叫终端结点, 的结点; E F G 分枝结点:度不为0的结点 的结点; 分枝结点:度不为 的结点; K L 有序树:子树有序的树, 有序树:子树有序的树,如:家族树; 家族树; 无序树:不考虑子树的顺序; 无序树:不考虑子树的顺序; 森林;互不相交的树集合;森林和树之间的联系是: 森林;互不相交的树集合;森林和树之间的联系是:一棵树去 其子树构成一个森林; 掉根 ,其子树构成一个森林;一个森林增加一个根 结点成为树。 结点成为树。 第 3 页
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
