图与网络分析64777
合集下载
第八章图与网络分析-PPT精选文档

v1 v3 v5 v2 v4 v6
图及 其分 类
X:{v1, v3, v5} Y:{v2, v4, v6}
定义5
以点v为端点的边的个数称为点v 的度 (次),记作 d (。 v) 图中d(v1)= 4,d(v6)= 4(环计两度)
顶点 的次
度为零的点称为弧立点,度为1的点称为悬挂 点。悬挂点的关联边称为悬挂边。度为奇数的 点称为奇点,度为偶数的点称为偶点。
定义7
图G=(V,E),若E′是E的子集,V′是V的子集,且E′ 中的边仅与V′中的顶点相关联,则称G′=(V′,E′)是G 的一个子图。特别是,若V′=V,则G′称为G的生成 子图(支撑子图)。
子图
v1 e1 e6
v2 e7
e2
e8 e9
v3 e3 v1
e1 e6
v2 e7
e8 v7 v5 (b)
定义8
无向图G=(V,E),若图G中某些点与边的交替序列 可以排成(vi0,ei1,vi1,ei2,…,vik-1,eik,vik)的形式,且 eit=(vit-1,vit)(t=1,…,k),则称这个点边序列为连接vi0 与vik的一条链,链长为k。 点边列中没有重复的点和重复边者为初等链。
对于有向图可以类似于无向图定义链和圈,初等 链、圈,此时不考虑边的方向。而当链(圈)上的 边方向相同时,称为道路(回路)。 对于无向图来说,道路与链、回路与圈意义相同。
v2 v4 v6
图及 其分 类
A = {(v1 , v3 ) , (v2 , v1) , (v2 , v3 ) , v1
( v2 , v5 ) , ( v3 , v5 ) , ( v4 , v5 ) ,
( v5 , v4 ) , ( v5 , v6 ) }
图及 其分 类
X:{v1, v3, v5} Y:{v2, v4, v6}
定义5
以点v为端点的边的个数称为点v 的度 (次),记作 d (。 v) 图中d(v1)= 4,d(v6)= 4(环计两度)
顶点 的次
度为零的点称为弧立点,度为1的点称为悬挂 点。悬挂点的关联边称为悬挂边。度为奇数的 点称为奇点,度为偶数的点称为偶点。
定义7
图G=(V,E),若E′是E的子集,V′是V的子集,且E′ 中的边仅与V′中的顶点相关联,则称G′=(V′,E′)是G 的一个子图。特别是,若V′=V,则G′称为G的生成 子图(支撑子图)。
子图
v1 e1 e6
v2 e7
e2
e8 e9
v3 e3 v1
e1 e6
v2 e7
e8 v7 v5 (b)
定义8
无向图G=(V,E),若图G中某些点与边的交替序列 可以排成(vi0,ei1,vi1,ei2,…,vik-1,eik,vik)的形式,且 eit=(vit-1,vit)(t=1,…,k),则称这个点边序列为连接vi0 与vik的一条链,链长为k。 点边列中没有重复的点和重复边者为初等链。
对于有向图可以类似于无向图定义链和圈,初等 链、圈,此时不考虑边的方向。而当链(圈)上的 边方向相同时,称为道路(回路)。 对于无向图来说,道路与链、回路与圈意义相同。
v2 v4 v6
图及 其分 类
A = {(v1 , v3 ) , (v2 , v1) , (v2 , v3 ) , v1
( v2 , v5 ) , ( v3 , v5 ) , ( v4 , v5 ) ,
( v5 , v4 ) , ( v5 , v6 ) }
新编第6章图与网络分析精选文档PPT课件
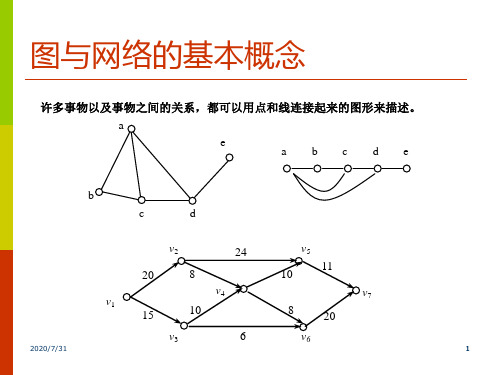
有向图
由点和弧组成的图称为有向图。
有向图是一个有序二元组(V,A),记为 D=(V,A),其中 V=(v1,v2,…….vp)是 p 个点 的集合,A={a1,a2,……aq}是 q 条弧的集合,并且 ai 是一个有序二元组,记为 aij=(vi,vj)≠ (vj,vi),vi,vj∈V,并称 aij 是以 vi 为始点,vj 为终点的弧, i, j 的顺序不能颠倒,图中弧的方 向用箭头标识。
上图中的{ v1,v2,v3 },{ v2,v4,v5},{ v1,v2,v4,v5}都是链。 闭链或圈:两个端点重合的链,称为圈。上图中的{ v1,v2,v3 , v1}就是圈。 简单链与初等链:若链μ中,若含的边数均不相同,则称之为简
单链;若链μ中,顶点 vi1,vi2,…,vik 都不相同,则称此链为初等链。 除非特别交代,以后我们讨论的均指初等链。
V=(v1,v2,v3,v4,v5) E={e1,e2,e3,e4,e5,e6,e7,e8}
e1
v2
e2
v1
e6
e4
e5
e3 v3
e7
2020/7/31
v4
e8
v5
4
无向图
点集 V 中元素的个数成为图 G 的点数,记为 p(G)=| V |。如上图中,p(G)=5。 边集 E 中元素的个数成为图 G 的边数,记为 q(G)=| E |。如上图中,q(G)=8。 边 e=[vi,vj]∈E,称 vi,vj 为 e 的端点,e 为 vi,vj 的关联边。上图中,v1,v2 为 e2 的端点,e2 为 v1,v2 的关联边。 若边 ei,ej 有一公共端点,则称 ei,ej 相邻。如上图中中,e7,e8 相邻。 若点 vi,vj 有边相连,即[vi,vj]∈E,则称 vi,vj 相邻。如上图中中,v3,v5 相 邻。
8图和网络分析-文档资料77页

4
7
5
6
5
2
3
4
6
7
4
8 8
min {c12,c16,c42,c47}=min {0+2,0+3,1+10,1+2}=min {2,3,11,3}=2 X={1,2,4}, p2=2
(vi ,vj)E (vi ,vj)E
称矩阵A为网络G的权矩阵。
设图G=(V,E)中顶点的个数为n,构造一个
矩阵 A(aij)nn ,其中:
aij 01
称矩阵A为网络G的邻接矩阵。
(vi ,vj)E (vi ,vj)E
v1 4
v2
例
36
72
v6 4
3
3
v3
5
2
v5
v4
权矩阵为:
(一)、 狄克斯屈拉(Dijkstra)算法 适用于wij≥0,给出了从vs到任意一个点vj的最短路。
算法步骤: 1.给始点vs以P标号 P(vs) 0,这表示从vs到 vs的最短距离 为0,其余节点均给T标号,P (v i) (i 2 ,3 , ,n )。 2.设节点 vi 为刚得到P标号的点,考虑点vj,其中
v2 2
3
v1
1
2
5 v3 4
v4
4
2
v6
2 v5
(5) P(v3) 4 (6) T ( v 5 ) m i n [ T ( v 5 ) , P ( v 3 ) l 3 5 ] m i n [ 5 , 4 4 ] 5 (7) P(v4)5 P(v5) 5 (8) T ( v 6 ) m T ( v 6 ) i ,P ( n v 4 ) l 4 [ ] 6 m ,5 i 4 n ] 9 [
第八章 图与网络分析
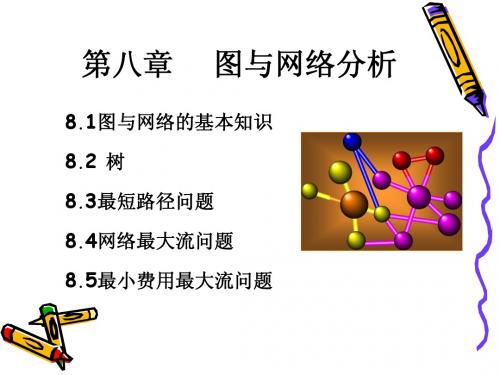
[解]设以vi(i=1,2,3,4,5)表示“第i年初购进一台新设备”这 种状态,以v6表示“第5年末”这种状态;以弧(vi, vj)表示 “第i年初购置的一台设备一直使用到第j年初”这一方案,以 wij表示这一方案所需购置费和维护费之和。
(21,V1) v2
32 63
(44,V1) v4 27
37 (78,V3)
例9:(图8-31)
步骤 v1 v2 v3 v4 v5 v6 v7 v8 最短 前向 路 结点
1
2 3
0*
∞
4*
∞
6 6*
∞
∞ 9 9 9*
∞
∞ 8 8*
∞
∞ ∞ ∞ 13 13 *
∞
∞ ∞ ∞ 14 14 14*
∞
∞ ∞ ∞ ∞ ∞ 17
0
4 6 8 9 13 14 15 v1 v1 v2 v2 v5 v5
w(T)=Σwij
(vi,vj)∈T
如果支撑树T*的权w(T*)是G的所有支撑树的权中最小者,则称T*是G的 最小生成树(最小支撑树,简称最小树) w(T*)=min w(T)
2)求最小树的方法: 方法一(避圈法) 开始选一条最小权的边,以后每一步中,总从未被 选取的边中选一条权最小的边,并使之与已选取的边不构成圈。 方法二(破圈法) 任取一个圈,从圈中去掉一条权最大的边。在余下 的图中,重复这个步骤,一直到一个不含圈的图为止,这时的图便是 最小树。 例 用破圈法求下图的最小树
2、中国邮路问题:给定一个连通图G,每边有非负权l(e),要求一 条回路过每边至少一次,且满足总权最小。
8.2 树(是最简单又十分重要的图)
例如:比赛中的相遇情况、组织结构图、家庭树
1、定义:一个无圈的连通图称为树。
第6章 图与网络分析――基础知识PPT课件

D
E
F
甲
√
√
√
乙
√
√
√
丙
√
√
丁
√
√
戊
√
√
√
己
√
√
√
将研究对象用点表示。对象与对象之间用边表示。依题意,找出不相邻的顺序。
B
C
ACBFED
A
D
36
F
E
类型2. 求最小部分树。避圈法和破圈法
基本定理:图中任一个点i,若j是与i相邻点 中距离最短的,则边[i,j]一定含在该图的 最小部分树内。
推论:把图的所有点分成集合V和它的补集两 个集合,则两集合之间连线的最短边一定 包含在最小部分树内。
A
7
2 2
S
5
B
5
D
5
T
1
1
4
3
7
C
E
4
39
[例2]如图6-2,SABCDET代表村镇,它们中间 连线表明各村镇间现有道路交通情况,连线旁 数字代表道路的长度。现要求沿图中道路架设 电线,使上述村镇全部通上电,应如何架设使 总的长度为最短。
A
7
2 2
S
5
B
5
D
5
T
1
1
4
3
7
C
E
4
40
[例2]如图6-2,SABCDET代表村镇,它们中间 连线表明各村镇间现有道路交通情况,连线旁 数字代表道路的长度。现要求沿图中道路架设 电线,使上述村镇全部通上电,应如何架设使 总的长度为最短。
点边交替序列,点边均不重 复。
点边交替序列,起点和终点 不重复。 点边交替序列,起点和终点 重复。
运筹学图与网络分析

第5章 图论与网络分析
网络分析
➢ 图的基本概念 ➢最小支撑树问题 ➢ 最短路径问题 ➢网络最大流问题
图论起源:哥尼斯堡七桥问题
A
A
C
D
C
D
B
B
问题:一个散步者能否从任一块陆地出发;走过七 座桥;且每座桥只走过一次;最后回到出发点
结论:每个结点关联的边数均为偶数
§1 图的基本概念
1图
由点和边组成;记作G=V;E;其中 V=v1;v2;……;vn为结点的集 合;E=e1;e2;……;em 为边的集合; 点表示研究对象 边表示研究对象之间的特定关系
例 : G1为不连通图; G2为连通图
G1
G2
5 支撑子图
图G=V;E和G'=V ' ;E ';若V =V ' 且E ' E ;则 称G' 为
G的支撑子图;
例 :G2为G1的支撑子图
v5
v5
v1
v4 v1
v4
v2
v3
G1
v2
v3
G2
例 : G2 是G1 的子图;
v2
e1 v1
e6 e7
e2
v3
e8 e9
两条以上的边都是权数最大的边;则任意去掉其 中一条: ③若所余下的图已不含圈;则计算结束;所余下的图 即为最小支撑树;否则;返问①;
例 求上例中的最小支撑树
v1
5
v2
7.5 4
5.5
3
v5
2
解:
v3 3.5 v4 v1
5
v2
75 4
55
3
v5
2
v3 3 5 v4
算法2避圈法:从某一点开始;把边按权从小到大 依次添入图中;若出现圈;则删去其中最大边;直至 填满n1条边为止n为结点数 ;
网络分析
➢ 图的基本概念 ➢最小支撑树问题 ➢ 最短路径问题 ➢网络最大流问题
图论起源:哥尼斯堡七桥问题
A
A
C
D
C
D
B
B
问题:一个散步者能否从任一块陆地出发;走过七 座桥;且每座桥只走过一次;最后回到出发点
结论:每个结点关联的边数均为偶数
§1 图的基本概念
1图
由点和边组成;记作G=V;E;其中 V=v1;v2;……;vn为结点的集 合;E=e1;e2;……;em 为边的集合; 点表示研究对象 边表示研究对象之间的特定关系
例 : G1为不连通图; G2为连通图
G1
G2
5 支撑子图
图G=V;E和G'=V ' ;E ';若V =V ' 且E ' E ;则 称G' 为
G的支撑子图;
例 :G2为G1的支撑子图
v5
v5
v1
v4 v1
v4
v2
v3
G1
v2
v3
G2
例 : G2 是G1 的子图;
v2
e1 v1
e6 e7
e2
v3
e8 e9
两条以上的边都是权数最大的边;则任意去掉其 中一条: ③若所余下的图已不含圈;则计算结束;所余下的图 即为最小支撑树;否则;返问①;
例 求上例中的最小支撑树
v1
5
v2
7.5 4
5.5
3
v5
2
解:
v3 3.5 v4 v1
5
v2
75 4
55
3
v5
2
v3 3 5 v4
算法2避圈法:从某一点开始;把边按权从小到大 依次添入图中;若出现圈;则删去其中最大边;直至 填满n1条边为止n为结点数 ;
图与网络分析

end;
例 1 中 1 到 7 点的最短路是 1-2-5-7
查伴随矩阵 E 的第一行
1234567
10020255 19
hw
小结
• 最短路有广泛的应用 (P176案例) • 最短路的多种形式:无向图,有向图无循环圈,有向
图,混合图,无负边权,有负边权,有负回路,k-最 短路等 • 当存在负权值边时,Floyd算法比Dijkstra算法效率高, 且程序极简单。但Dijkstra算法灵活 • 若图是前向的,则Dijkstra算法也可以求两点间最长路 • 一般情况下,两点间最长路是 NP-complete,但最短 路是 P算法 • 两点间k-最短路:分为边不相交的和边相交的 求边不相交的k-最短路非常容易:先求最短路,将该 最短路中的边从网路删去,再用Dijkstra算法可求次最 短路,以此类推
hw
6.1.4 链,圈,路径,回路,连通图
• 走过图中所有边且每条边仅走一次的闭行走称为欧拉 回路
定理 2:偶图一定存在欧拉回路(一笔画定理) 6.1.4 连通图,子图,成分
• 设有两个图 G1(V1, E1), G2(V2, E2), 若V2 V1, E2 E1, 则 G2 是 G1 的子图
• 无向图中,若任意两点间至少存在一条路径,则称为 连通图(connected graph),否则为非连通图( disconnected graph);非连通图中的每个连通子图称为成分 (component)
线表示实体间的关联
A
A D
C
C
D
B
B
2
hw
6.1 图与网络的基本概念
6.1.1图与网络 • 节点 (Vertex)
– 物理实体、事物、概念 – 一般用 vi 表示
《图与网络分析》课件

广度优先搜索
2
历图中的节点。
通过按逐层扩展的方式,搜索和遍历图 中的节点。
最短路径算法
1
Dijkstra算法
寻找两个节点之间最短路径的一种算法,适用于无负权重边的情况。
2
Floyd算法
寻找所有节点之间最短路径的一种算法,适用于有向图和无向图。
最小生成树算法
1
Prim算法
找出连接所有节点的最小成本树的算法。
Kruskal算法
2
找出连接所有节点的最小成本树的另一 种算法。
应用案例
1 社交网络分析
通过图与网络分析方法, 揭示社交网络中的关键人 物和社群结构。
2 物流网络优化
使用图与网络分析技术来 优化物流网络的路径和资 源分配。
3 路网分析
通过图与网络分析,提高 交通规划和城市布局的效 率。
网络分析的思路
顶点
网络中的数据节点或实体。
边
连接顶点的关系或连接。
权重
边的属性或度量,用于表示连接的强度或重要性。
图的分类与存储结构
有向图
边具有方向性,表ห้องสมุดไป่ตู้顶点之间 的单向关系。
无向图
边没有方向性,表示无序关系。
加权图
边具有权重,表示连接的强度 或重要性。
图搜索算法
1
深度优先搜索
通过探索尽可能深入的路径,搜索和遍
网络分析的思路是通过对网络结构和属性的分析,揭示出潜在的模式、关系和洞察力,帮助我们洞悉复杂系统 的运作。
《图与网络分析》PPT课 件
欢迎来到《图与网络分析》PPT课件!本课程将帮助您深入了解图网络分析的 概念和应用。准备好探索各种令人兴奋的网络分析方法和工具了吗?让我们 开始吧!
