5 粘性流体运动的基本性质解析
粘性流体的名词解释

粘性流体的名词解释粘性流体是一类特殊的物质,其在受力作用下会表现出类似于黏稠的流动特性。
与非粘性流体相比,粘性流体的分子有更强的相互作用力,导致其流动时呈现出一定的粘性效应。
粘性流体在日常生活和工业生产中都有广泛的应用,如润滑剂、食品、医药、等等。
本文将从不同角度对粘性流体进行详细解释和解剖。
一、粘性流体的特性粘性流体的流动特性主要由两个方面影响:剪切力和黏滞系数。
剪切力是指应用在流体上的力,而黏滞系数则是描述流体抵抗剪切力的能力。
黏滞系数越大,流体越粘稠。
粘性流体在受力作用下会发生形变,当受力作用停止时则会恢复原状。
这种特性称为流变特性,包括弹性应变、塑性流动和粘弹性等。
二、粘性流体的分类根据粘性流体在外力作用下形变的特点,可以将粘性流体分为牛顿流体和非牛顿流体两类。
牛顿流体的黏滞系数与剪切力成线性关系,即剪切应力与剪切速率成正比。
水和某些溶液就是典型的牛顿流体。
而非牛顿流体则不符合这种关系,其黏滞系数会随剪切应力或剪切速率的变化而变化。
例如,血液、牙膏以及液态塑料都属于非牛顿流体。
三、粘性流体的应用1. 医药领域:粘性流体在医药领域具有重要应用价值。
例如,制药工业中的药品、注射剂、多种胶囊等,都需要粘性流体的理解和控制。
此外,粘性流体还被用于人体内部的诊断和治疗技术,如胶囊内摄像头、可溶性药丸等。
2. 食品工业:粘性流体在食品加工中发挥着关键作用。
许多食品的口感和质地都与粘性流体的特性相关。
例如,面团的柔软和口感,果酱和酱料的黏稠度,甚至是巧克力的顺滑质地,都与粘性流体的黏度有关。
3. 石油工业:石油粘度是指石油流动的阻力和油品的黏稠度。
粘性流体的分析可以帮助石油工业确定石油的流动性能和适用性,从而更好地控制石油的开采和加工过程。
4. 汽车工业:粘性流体在汽车工业中的应用也是不可忽视的。
例如,引擎油、润滑剂和制动液都属于粘性流体,它们在汽车的正常运行和维护中起着关键作用。
四、粘性流体的研究领域粘性流体的研究领域包括流变学、纳米流体力学和自由表面流体等。
粘性流体运动微分方程(了解性学习)讲解

一、粘性流体的特点
粘性流体运动微分方程
(1)粘性流体的表面力包括:压应力和粘性引起的切应力。
xy ( yz ( zx (
u x y u y z u z x
u y x u z y
) yx ) zy ) xz
二阶非线性非齐次偏微分方程组
四个未知量ux,uy,uz和 p
N-S方程与连续性微分方程4个
理论上可 以求解
只能对一些简单的流动问题,如圆管中的层流 等,求得精确解。 对于大多数较复杂的不可压缩粘性流体的流动问 题,难以用该方程求出精确解。
计算流体力学的发展,可以用该方程求得许多复 杂流动的近似解。
无法求解
z方向
9个应力,3个速度分量,共12个未知数
3个方程加上连续性方程,共4个方程
补充关系式: 1、切应力和角变形速度的关系
yz zx xy
u z u y zy y z u x u z xz x z u y u x yx x y
u x t u y t u z t
u u u
u x x x
u u u
u x y y
u u u
u x z z
v u y
2
u y x x
u y y y
u y z z
v u
2
u z x x
u z y y
u z z z
zx z
dz )dxdy]
化简后得 x方向 y方向
1 pxx 1 yx zx dux X x y z dt 1 p yy 1 zy xy duy Y y z x dt 1 pzz 1 xz yz duz Z z x y dt
5-6黏性流体
p1 + ρ gh1 = p2 + ρ gh2 + w
或
( p1 p2 ) + ρ g(h1 h2 ) = w
可见,由于黏力的存在 可见,由于黏力的存在, 要流体在管道中作定 常流动, 常流动 须保证管道两端的压强差 (p1p2) 或保证 或者两者兼而有之. 管道两端的高度差 (h1h2) 或者两者兼而有之.
Rec η vc = ρr
如果流速从低于v 增大到高于v 如果流速从低于 c增大到高于 c,那么流动将 会从层流转变为湍流. 会从层流转变为湍流.
9
*五,斯托克斯黏性公式 五 (Stokes' viscosity resistance formula ) 当固体物在黏性流体中作相对运动时, 当固体物在黏性流体中作相对运动时,将受到流 体的阻力作用. 体的阻力作用. 斯托克斯黏性公式 固体小球以不大的速率在流 体中运动时, 体中运动时,所受黏性阻力大小为
y
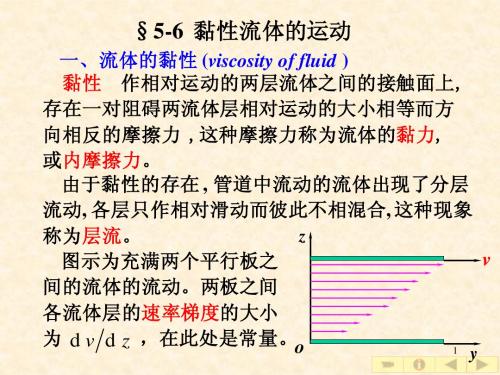
一般情况下, 速率梯度的大小不是常量, 一般情况下 速率梯度的大小不是常量 z0 处速 率梯度的大小为 dv ( ) z0 dz 实验表明, 实验表明 流体内部相邻两流体层间黏力的大小 正比于接触面积, 正比于该处速率梯度的大小, 正比于接触面积 正比于该处速率梯度的大小,即
dv f = ±η( )z0 S dz
温 度/℃ 20 20 20 15 23 23
水的黏度随温度的变化 20 40 60 80 100
η / (10-3 Pas) 1.792 1.0050 0.6560 0.4688 0.3565 0.2838
表 3 气 体 温 度 /℃ ℃
几种气体的黏度随温度的变化 空 气 0 20 671 18 18.1 42 二氧化碳 0 20 302 14 14.8 27 氢 气 -1 20 251 8.3 8.8 13
流体力学中的黏性流体

流体力学中的黏性流体黏性流体是流体力学中的重要概念之一,它在实际生活和工程应用中有着广泛的应用。
本文将探讨黏性流体的基本特性、黏性流体的模型以及黏性流体在工程中的应用案例。
1. 黏性流体的基本特性黏性流体是一种具有内部黏性阻力的流体。
与无黏性流体(如理想气体)不同,黏性流体具有以下基本特性:1.1 流体的黏度黏度是黏性流体最重要的特性之一。
它描述了黏性流体内部分子之间相互作用的强度。
黏度越大,流体的黏性就越高,即流动阻力越大。
1.2 流体的粘性黏性流体具有粘性,即常常会产生阻力和内摩擦力。
当流体流动时,流体分子之间会发生相互作用,导致流动速度的差异。
这种相互作用会导致黏性流体内部的能量耗散。
1.3 流体的剪切应力黏性流体在流动过程中会受到剪切应力的作用。
剪切应力描述了流体内部不同层次之间的相对运动情况。
当黏性流体受到剪切应力时,会发生流体的变形和能量的耗散。
2. 黏性流体的模型为了研究黏性流体的性质和行为,研究者们提出了多种黏性流体模型。
下面介绍两种常用的模型:2.1 牛顿流体模型牛顿流体模型是最简单且最常用的黏性流体模型。
根据该模型,流体内部的黏性阻力与剪切速率成正比。
这意味着牛顿流体的黏度在不同的剪切速率下保持不变。
2.2 非牛顿流体模型非牛顿流体模型适用于一些特殊流体,如液晶、聚合物溶液等。
与牛顿流体不同,非牛顿流体的黏度会随着剪切速率的变化而发生改变。
这种流体模型在实际应用中更加复杂,但也更加接近真实的流体行为。
3. 黏性流体在工程中的应用案例黏性流体在工程领域中有着广泛的应用。
以下是几个黏性流体在工程中的应用案例:3.1 润滑油润滑油是黏性流体的典型应用之一。
黏性流体的黏度可以调整,使其在机械设备中形成一层薄膜,减小设备零件之间的摩擦和磨损。
3.2 高分子聚合物高分子聚合物是一种非牛顿流体,常用于涂料、胶水等领域。
通过调整聚合物的黏度和流变性能,可以实现不同的涂覆和粘附效果。
3.3 食品加工在食品加工过程中,黏性流体的应用非常广泛。
5 粘性流体运动的基本性质

2
2
5.2.1 不可压缩粘性流体流动的涡量方程
N-S方程变成
u tu Ω f 1 p 2u u 2 2
对上式两端进行旋度运算,可得
u t u Ω f 1 p 2 u u 2 2
5.2.1 不可压缩粘性流体流动的涡量方程
设在t=0时刻外加能量突然中断,现分析t >0时该微小直 涡管旋涡强度的扩散(衰减)情况以及旋涡的扩散规律。
5.2.2 粘性流体流动中旋涡的扩散性
在圆柱坐标系中,初始时刻t=0且r >0处,有
Ωr = 0, Ωθ = 0, Ωz = Ω,
(ur)t=0 =0,(uz)t=0 =0,
u
t0
u t0
高等流体力学
5 粘性流体运动 的基本性质
5 粘性流体运动的基本性质
粘性流体的运动特征与理想流体运动存 在着巨大的差别。
从数学角度看,N-S方程与Euler方程的 阶数不同,前者为二阶非线性偏微分方程, 后者为一阶非线性偏微分方程,这个差别导 致所要求的定解条件的个数以及解法不同。
5 粘性流体运动的基本性质
2r 动。
5.2.2 粘性流体流动中旋涡的扩散性
在理想流体中,由于没有粘性,该微小直涡管的强度守 恒,且不会向周围流体扩散,不需要外加能量来维持流体质 点的定常圆周运动。
在粘性流体中,由于存在粘性,旋涡强度将会衰减并扩 散,要维持流体质点的定常圆周运动,就需要有外加的能量 供给微小直涡管,使其保持涡管强度Γ0。
求解热传导方程的方法很多,现采用相似变换法进行求 解。相似变换法:引进由变量组合成的相似变量,将偏微分 方程化成常微分方程进行求解。这种方法能使变量数目减少 一个或更多,它在流体力学和传热学中应用较多。
粘性流体力学讲解

z
-px
、v、px、p y、pz、f
牛顿第二定律:
x -py
z
M
z
y
py
p y y
y
ma F
x
y
px
p x x
x
-pz
Dv Dt
x
y
z
f
x
y
z
p x
y
z
(p x
p x x
x)
y
z
p y
x
z
(p
y
p y y
y)
x
z
Dv Dt
fy
1
p y
2v
Dw Dt
fz
1
p z
2w
Discussion:
Dv f 1 p 2 v v
Dt
3
1. 物理意义:单位质量流体惯性力、质量力、压力合力和 粘性力平衡。粘性力包括剪应力与附加法向应力。
0
du
dy
yh
dp h dx
y
h
o -h
umax x
dp 0 dx
压力梯度使速度剖面为抛物型——层流运动的特征。
7.3.2往复振荡平板引起的层流流动
平板运动引起粘性效应的扩散。 流场速度分布:
y o u=Ucos t
u U eky cosky t ——粘性扰动波。 y 2
dp 0 dx
速度分布: (Couette流动)
第3章:粘性流体运动

p x dp dx L
1 h h 2 p v x vx dy h 0 12 L
Wh 3 p 流量 Q 12 L
(a)情形的流量是(b)情形和(c)情形的流量之和
圆管内的一维稳态流动分析。
不可压缩流体在水平 圆管内作一 维稳态层流流动。试写出该条件下的连 续性方程和运动微分方程。并证明管道 截面上任一点的总势能和轴向压力梯度 为常数。
re10510re1010re102580455lgre紊流边界层内沿平板壁面发向截面上的速度比层流边界层的速度增加得快在其它条件相同的情况下平板壁面上的切向应力沿着壁面的减小在紊流边界层中要比层流边界层减小得在同一下紊流边界层得摩擦阻力系数比层流边界层的大得多实际情况下边界层是层流和紊流同时存在的混合边界层re37re0462re036re0289re036re84re752re686re343re686re372re074边界层的基本特性速度分布规边界层厚度位移厚度动量损失厚切向应力总摩擦力摩擦阻力系以如图所示的圆柱绕流为例在势流流动中流体质点从d到e是加速的为顺压强梯度
Dv y
2 y 2 y 2 y 1 p fy 2 2 2 Dt y x y z
2 z 2 z 2 z Dvz 1 p fz 2 2 2 Dt z x y z
一 速度势函数
V 0 ,由矢量分析知,任一标 对于无旋流场,处处满足:
量函数梯度的旋度恒为零,所以速度 数 的梯度,即: V
连续方程和N-S方程是粘性流体流动应遵循的质量守恒和 动量守恒的数学表达式。
N-S方程应用概述
封闭条件:理论上方程是封闭的,但若要考虑到物性参数 的变化,应将物性变化的关系作为补充方程。
第五章 实际(粘性)流体动力学基础解剖

2 uz dz )
0
或
d (U
p
u2 2
)
( 2 ux dx
2uy dy
2 uz dz )
(5.4)
上式仍假定质量力为有势力,流动是恒定的,并且沿流
线积分。
(5.4)式表明,实际(粘性)流体在同一流线(或元流) 上的机械能是不断变化的。这是由于当粘性流体向前流动时, 需不断克服因粘滞性作用产生的内摩擦力,因而一部分机械 能将转化为热能而消耗于流体中。
几何意义:总流各过流断面上的 总水头沿程下降,所下降的高度 即为平均水头损失;同时,各水 头之间可以相互转化,平均总水 头线沿程下降,平均测压管水头 线可以上升,可以下降。
总水头线的坡度叫做水力坡度,表示单位重力流体在 单位长度的流程上所损失的平均水头。
以H表示总流的平均总水头,则水力坡度为
J dH dhw (5.21) ds ds
Z
1
p z
2uz
uz t
ux
uz x
uy
uz y
uz
uz z
N-S方程的推导中,应用了牛顿内摩擦定律。对于二元
平行直线流动有
du
dy
(5.2)
所以N-S方程仅适用于牛顿流体。
此外,N-S方程中的动水压强 p 的推导,应用了不可压缩 流体的连续性方程,得出结论:在不可压缩实际流体中,任 意一点的任何三个相互垂直面上的法向应力的平均值为一常 数,并定义此常数为该点的动水压强
A
(z
p )udA
(z
p
)A
udA
(
z
p
)Q
(5.11)
Q
(
z
p)dQ
(z
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1 u2 u 2 p u uΩ f t 2
5.2.1 不可压缩粘性流体流动的涡量方程
根据向量分析,有
uΩ Ω u Ω u u Ω u Ω
由以上方程组及其边界条件可以解出速度场u和压强场p。
5.1 粘性流体运动的有旋性
先假设流动无旋,然后证明基本方程组与边界条件相 矛盾,则可证明粘性流体流动通常是有旋流动。 如果运动是无旋的,则必存在速度势函数φ,且 u 连续性方程变成
2 0
N-S方程变成
Du 1 f p 2 Dt
5.1 粘性流体运动的有旋性
由上述的分析可以说明,只有在粘性项 ν2u=0,且流动边界是运动的这种极个别的 情况下,粘性流体运动才可能是无旋的。 例如:①不可压缩粘性流体绕旋转圆柱 体的定常流动;②不可压缩粘性流体在两个 共轴旋转的圆柱面之间作定常流动,且两旋 转圆柱面的角速度刚好调整到使其间的流速 分布为uθ1/r的情况。
流体在一般情况下,是不可能作无旋流动的。这 就从反面证明了粘性流体运动总是有旋的。
5.1 粘性流体运动的有旋性
此外,还可以从物理概念上来理解。对于不 可压缩粘性流体,如假设它作无旋流动,则在N-S 方程中将不出现粘性项 ν2u ,这意味着粘性将不
影响速度场与压力场,显然,这是与实际流动相
矛盾的。这从另一个侧面说明了粘性流体作无旋
u2 u2 u u u u uΩ 2 2
5.2.1 不可压缩粘性流体流动的涡量方程
N-S方程变成
对上式两端进行旋度运算,可得
u 1 u2 2 uΩ f p u t 2
高等流体力学
5 粘性流体运动 的基本性质
5 粘性流体运动的基本性质
粘性流体的动特征与理想流体运动存 在着巨大的差别。 从数学角度 看,N-S方程与Euler方程的 阶数不同,前者为二阶非线性偏微分方程, 后者为一阶非线性偏微分方程,这个差别导 致所要求的定解条件的个数以及解法不同。
5 粘性流体运动的基本性质
5.1 粘性流体运动的有旋性
粘性流体运动必然有旋的情形分析: (2) 若 N-S 方程中的粘性项 ν2u0 ,则粘性流 体运动必然有旋。
用反证法证明:假设不可压缩粘性流体流动 是无旋的,则有u=φ,于是
2 u 2 2 0
由此可见,若流动无旋,则粘性项 ν2u 必为 零。因此,若粘性项 ν2u0 ,则粘性流体运动必 有旋。
而
2 2 0
5.1 粘性流体运动的有旋性
这样,在无旋流动的假设下,不可压缩粘性流体的基 本方程组变为速度势方程(Laplace方程)和欧拉运动方程
2 0
Du 1 f p Dt 它与不可压缩理想流体的基本方程组完全相同。现在 的问题是方程组完全相同,而在固体壁面处的边界条件却 不一样。对于不可压缩粘性流体沿固体壁面流动,应满足 无滑移条件,即 un=0 , ut=0 ;而不可压缩理想流体,在固 体壁面处, un=0,ut一般不等于零。
5.1 粘性流体运动的有旋性
虽然流体是否具有粘性与流体运动是否有旋是从不同 的角度提出来的,但是这两者之间有一定的联系。一般说 来,粘性流体运动总是有旋的。因此,处理势流的一整套 方法不再适用于粘性流体。下面用反证法证明这一性质。 对于不可压缩粘性流体的基本方程组是 u 0 Du 1 f p 2 u Dt 当边界为静止的固体壁面时,上述方程组的边界条件为 u n 0 , ut 0
运动的不可能性。
5.1 粘性流体运动的有旋性
粘性流体运动必然有旋的情形分析: (1) 若流动边界为静止固体壁面,则粘性流体 运动必然有旋。
用反证法证明:假设不可压缩粘性流体流动 是无旋的,则连续性方程为
2 0
而粘性流体流动时静止固体壁面的边界条件为 u=0 或φ=0,因此,边界上的速度势函数φb为常数。
5.1 粘性流体运动的有旋性
Navier-Stokes方程是二阶偏微分方程,加上无 旋流动条件以后,方程中的二阶偏导数项消失, 变成了一阶偏微分方程。因此,粘性流体流动的
无滑移边界条件(ut=0)就多余了。也就是说,对于
不可压缩理想流体流动的基本方程,其满足无滑
移边界条件的解一般是不存在的。或者说,粘性
从 物理角度 看:①粘性流体运动时,由于流 体与静止固体壁面的相互作用,总是会产生旋涡; ②由于流体所具有的粘性,在其运动过程中不遵 循理想流体运动时的涡量守恒规律;③由于粘性 流体运动中存在不可逆过程,流体运动的机械能 并不守恒。
因此,与非粘性流体运动相比较,粘性流体 运动具有三个方面的基本性质:运动的有旋性、 涡旋的扩散性与能量的耗散性。
5.2 粘性流体运动的旋涡扩散性
流体具有粘性是旋涡产生和消失的原因, 通过涡量输运方程可以说明旋涡的扩散性。 5.2.1 不可压缩粘性流体流动的涡量方程
不可压缩粘性流体的运动微分方程(N-S 方程)为 Du u 1 u u f p 2 u
Dt t
根据向量分析,有
5.1 粘性流体运动的有旋性
粘性流体运动必然有旋的情形分析: 满足Laplace方程的函数φ称为调和函数,由调 和函数 φ 的极值原理可知, φ 在求解域内不可能有 极值,又由于流动边界为静止固体壁面,因而速 度势函数方程2φ=0只有常数解。在求解域内速度 势函数φ处处为常数,即流体的流动速度为零,流 体是静止的。这一结论与粘性流体是运动的这一 前提相矛盾,从而证明了在这种情况下粘性流体 运动必然有旋。
