求一均匀带电球面的电场能量
大学物理常用公式(电场磁场 热力学)
第四章 电 场一、常见带电体的场强、电势分布2）均匀带电球面（球面半径 ）的电场：3）无限长均匀带电直线（电荷线密度为）: E = ，方向：垂直于带电直线。
2r( rR ) 4）无限长均匀带电圆柱面（电荷线密度为）:E =2r (rR )5）无限大均匀带电平面（电荷面密度为）的电场: E =/20 ，方向：垂直于平面。
二、静电场定理 1、高斯定理：e = ÑE v dS v = q 静电场是有源场。
Sq 指高斯面内所包含电量的代数和；E 指高斯面上各处的电场强度，由高斯面内外的全 部电荷产生； Ñ E vdS v 指通过高斯面的电通量，由高斯面内的电荷决定。
2、环路定理： Ñ E v dl v =0 静电场是保守场、电场力是保守力，可引入电势能三、求场强两种方法1、利用场强势叠加原理求场强 分离电荷系统： E v = E v i ；连续电荷系统： E v = dE v i =12、利用高斯定理求场强 四、求电势的两种方法n1、利用电势叠加原理求电势 分离电荷系统：U =U i ；连续电荷系统： U = dU i =1电势零点v v 2、利用电势的定义求电势 U =电势零点Edl五、应用vv b点电荷受力： F = qE电势差： U ab =U a -U b = b EdraE =1 qU =q4r 24r1）点电荷：E =0 (rR ) q2 (rR ) 4r 2U =q (r R ) 4r q (r R ) 4Ra 点电势能：W a = qU a由 a 到 b 电场力做功等于电势能增量的负值 A ab = -W = -（W b -W a ）六、导体周围的电场1、静电平衡的充要条件： 1）、导体内的合场强为 0，导体是一个等势体。
2）、导体表面的场强处处垂直于导体表面。
E v ⊥表面。
导体表面是等势面。
2、静电平衡时导体上电荷分布： 1）实心导体： 净电荷都分布在导体外表面上。
大学物理试题及参考答案
大学物理?试题及参考答案一、填空题〔每空1分、共20分〕1．某质点从静止出发沿半径为m R 1=的圆周运动，其角加速度随时间的变化规律是t t 6122-=β(SI) ，那么该质点切向加速度的大小为 。
2．真空中两根平行的无限长载流直导线，分别通有电流1I 和2I ,它们之间的间隔 为d ，那么每根导线单位长度受的力为 。
3．某电容器电容F C μ160=，当充电到100V 时，它储存的能量为____________焦耳。
4．一个均匀带电球面，半径为10厘米，带电量为2×109-库仑。
在距球心6厘米处的场强为__________。
5．一平行板电容器充电后切断电源。
假设使两极板间间隔 增加，那么两极板间场强E __________，电容C__________。
〔选填：增加、不变、减少〕6．一质量为m ，电量为q 的带电粒子以速度v 与磁感应强度为B 的磁场成θ角进入时，其运动的轨迹为一条等距螺旋，其盘旋半径R 为____________ ，周期T 为__________，螺距H 为__________。
7. 真空中一个边长为a 的正方体闭合面的中心，有一个带电量为Q 库仑的点电荷。
通过立方体每一个面的电通量为____________。
8．电力线稀疏的地方，电场强度 。
稠密的地方，电场强度 。
9. 均匀带电细圆环在圆心处的场强为 。
10.一电偶极子，带电量为q=2×105-库仑，间距L ＝0.5cm ，那么它的电距为________库仑米11.一空心圆柱体的内、外半径分别为1R ,2R ,质量为m 〔SI 单位〕.那么其绕中心轴竖直轴的转动惯量为____________。
12.真空中的两个平行带电平板，板面面积均为S ，相距为d 〔S d 〈〈〕，分别带电q + 及q -，那么两板间互相作用力F 的大小为____________。
13．一个矩形载流线圈长为a 宽为b ，通有电流I ，处于匀强磁场B 中。
《大学物理》课后习题答案
《大学物理》课后习题答案习题４-12HLh4-12 一个器壁竖直的开口水槽，如图所示，水的深度为H =10m ，在水面下h =3m 处的侧壁开一个小孔。
试求：（1）从小孔射出的水流在槽底的水平射程L 是多少？（2）h 为何值时射程最远？最远射程是多少？ 解：（１）设水槽表面压强为p 1，流速为v 1，高度为h 1，小孔处压强为p ２，流速为v ２，高度为h ２，由伯努利方程得：222212112121gh v p gh v p ρρρρ++=++ 根据题中的条件可知： 21121,0,h h h v p p p -==== 由上式解得：gh v 22=由运动学方程：221gt h H =-，解得: gh H t )(2-=水平射程为:)(m 17.9)310(34)(42=-⨯⨯=-==h H h t v L(2)根据极值条件，令0=dhdL ，Ｌ出现最大值， 即22=--hhH h H ，解得：h=5m此时Ｌ的最大值为10m 。
4-14 水在粗细不均匀的水平管中作稳定流解：刚性双原子气体分子的自由度5i = （1）氧气分子的平均平动动能 2321k331.3810(2730) 5.710J 22kT ε--==⨯⨯⨯+≈⨯ 平均转动动能2321t 22 1.3810(2730) 3.810J22kT ε--==⨯⨯⨯+≈⨯ （2）34.010kg-⨯氧气的内能323' 4.01058.312737.110J 232102m i E RT M --⨯==⨯⨯⨯≈⨯⨯ 34.010kg-⨯氦气的内能333' 4.01038.31273 3.410J 24102m i E RT M --⨯==⨯⨯⨯≈⨯⨯5-17 储有1mol 氧气（可视为刚性分子），容积为31m 的容器以110m s υ-=⋅速度运动，设容器突然停止，其中氧气的80%的机械运动动能转化为气体分子热运动动能。
试求气体的温度及压强各升高了多少？解：分子热运动增加的能量为23211'80%32101080% 1.28J 22E m v -∆=⨯=⨯⨯⨯⨯= 又由理想气体内能公式2i E RT ν=可得2iE R T ν∆=∆,则222 1.286.1610K 558.31E T R -∆⨯∆==≈⨯⨯由理想气体状态方程pV RT ν=可得28.31 6.16100.51Pa1R Tp V ν-∆⨯⨯∆==≈6-10 一压强为51.010Pa ⨯,体积为331.010m -⨯的氧气自0C 加热到100C ，问：（1）当压强不变时，需要多少热量？当体积不变时，需要多少热量？（2）在等压和等体过程中各作了多少功？ 解：（1）压强不变，即等压过程：对初状态应用理想气体状态方程111p V RT ν= ,代入到p()2iQR R Tν=+∆中，得5311p 1 1.010 1.0105()()(1)100222732pV i i Q R R T R R T RT ν-⨯⨯⨯=+∆=+∆=⨯+⨯21.2810J=⨯体积不变时，即等体过程：对初状态应用理想气体状态方程111p V RT ν= ,代入到V2iQR T ν=∆中，得5311V 1 1.010 1.010510091.6J222732pV i i Q R T R T RT ν-⨯⨯⨯=∆=∆=⨯⨯≈（2）等体过程，系统对外不做功，即0J W =；r R r RE Or(D) E ∝1/r 222等压过程：内能的变化量91.6J 2iE R T ν∆=∆=,由热力学第一定律可得12891.636.4JW Q E =-∆=-=6-12 2mol 的理想气体在300K 时，从33410m -⨯等温压缩到33110m -⨯，求气体所做的功和放出的热量？ 解：等温过程：E ∆=；3211ln28.31300ln 6.910J 4T T V Q W RT V ν===⨯⨯⨯≈-⨯ 6-17 一卡诺热机的低温热源温度为7C ，效率为40%，若要将其效率提高到50%，问高温热源的温度应提高多少？解：由21-1=T Tη得原高温热源的温度为 21280467K 110.4T T η===--50%η=时对应的高温热源的温度为21280'560K 1'10.5T T η===-- 高温热源应提高的温度为560K 467K =93K -7-2 半径为R 的均匀带电球面的静电场中各点的电场强度的大小E 与距球心的距离r 之间的关系曲线为[ ]。
电场习题及答案
真空静电场(一)一．选择题1. 一均匀带电球面，电荷面密度为σ，球面内电场强度处处为零，球面上面元dS 的一个带电量为dS σ的电荷元，在球面内各点产生的电场强度 [ ]（A ） 处处为零 （B ）不一定都为零 （C ）处处不为零 （D ）无法判断2. 设有一“无限大”均匀带负电荷的平面，取X 轴垂直带电平面，坐标原点位于带电平面上，则其周围空间各点的电场强度E 随距离平面的位置坐标X 变化的关系曲线为（规定场强方向沿X 轴方向为正，反之为负） []3. 下面列出的真空中静电场的场强公式，其中哪个是正确的？ [ ]（A ） 点电荷Q 的电场: 204QE r πε=（B ） 无限长均匀带电直线（线密度λ）的电场： 302E r rλπε= （C ） 无限大均匀带电平面（面密度σ）的电场：02E σε= （D ） 半径为R 的均匀带电球面（面密度σ）外的电场：230R E r r σε= 4. 将一个试验电荷Q （正电荷）放在带有负电荷的大导体附近P 点处，测得它所受的力为F 。
若考虑到电量Q 不是足够小，则 [ ](A) F/Q 比P 点处原先的场强数值大(B) F/Q 比P 点处原先的场强数值小(C) F/Q 与P 处原先的场强数值相等(D) F/Q 与P 处原先的场强数值关系无法确定。
5. 根据高斯定理的数学表达式0s q E dS ε=∑⎰可知下列各种说法中，正确的是 [ ] （A ） 闭合面内的电荷代数和为零时，闭合面上各点场强一定为零（B ） 闭合面内的电荷代数和不为零时，闭合面上各点场强一定处处不为零（C ） 闭合面内的电荷代数和为零时，闭合面上各点场强不一定处处为零（D ） 闭合面上各点场强均为零时，闭合面内一定处处无电荷6. 当带电球面上总的带电量不变，而电荷的分布作任意改变时，这些电荷在球心处产生的电场强度E 和电势U 将 [ ]（A ）E 不变，U 不变； （B ）E 不变，U 改变；（C ）E 改变，U 不变 （D ） E 改变，U 也改变7. 在匀强电场中，将一负电荷从A 移至B ，如图所示，则： [ ]（A ） 电场力作正功，负电荷的电势能减少（B ） 电场力作正功，负电荷的电势能增加（C ） 电场力作负功，负电荷的电势能减少（D ） 电场力作负功，负电荷的电势能增加8. 真空中平行放置两块大金属平板，板面积均为S ，板间距离为d ，（d 远小于板面线度），板上分别带电量＋Q 和－Q ，则两板间相互作用力为 [ ]（A ）2204Q d πε （B ）220Q S ε （C ）2205k Q S ε+ （D ）2202Q S ε 二．填空题1 带有N 个电子的一个油滴，其质量为m ，电子的电量的大小为e ，在重力场中由静止开始下落（重力加速度为g ），下落中穿越一均匀电场区域，欲使油滴在该区域中匀速下落，则电场的方向为________________，大小为____________________。
川师大学物理第十章 静电场中的导体和电介质习题解
第十章 静电场中的导体和电介质10–1 如图10-1所示，有两块平行无限大导体平板，两板间距远小于平板的线度，设板面积为S ，两板分别带正电Q a 和Q b ，每板表面电荷面密度σ1= ，σ2= ，σ3= ，σ4= 。
解：建立如图10-2所示坐标系，设两导体平板上的面电荷密度分别为σ1，σ2，σ3，σ4。
由电荷守恒定律得12a S S Q σσ+= （1）34b S S Q σσ+= （2）设P ，Q 是分别位于二导体板内的两点，如图10-2所示，由于P ，Q 位于导板内，由静电平衡条件知，其场强为零，即3124000002222P E σσσσεεεε=---= （3）3124000002222Q E σσσσεεεε=++-= （4） 由方程（1）~（4）式得142abQ Q Sσσ+== （5） 232a bQ Q Sσσ-=-= （6） 由此可见，金属平板在相向的两面上（面2，3），带等量异号电荷，背向的两面上（面1，4），带等量同号电荷。
10–2 如图10-3所示，在半径为R 的金属球外距球心为a 的D 处放置点电荷+Q ，球内一点P 到球心的距离为r ，OP 与OD 夹角为θ，感应电荷在P 点产生的场强大小为 ，方向 ；P 点的电势为 。
解：（1）由于点电荷+Q 的存在，在金属球外表面将感应出等量的正负电荷，距+Q 的近端金属球外表面带负电，远端带正电，如图10-4所示。
P 点的场强是点电荷+Q 在P 点产生的场强E 1，与感应电荷在P 点产生的场强E 2的叠加，即E P =E 1+E 2，当静电平衡时，E P =E 1+E 2=0，由此可得21r 2204π(2cos )Qa r ar εθ=-=-+-E E e其中e r 是由D 指向P 点。
因此，感应电荷在P 点产生的场强E 2的大小为图10–4xσ2 4σQQ aQ b 图10-2σ1σ2 σ4σ3 Q a Q b图10-1图10-322204π(2cos )QE a r ar εθ=+-方向是从P 点指向D 点。
大学物理常用公式(电场磁场-热力学)
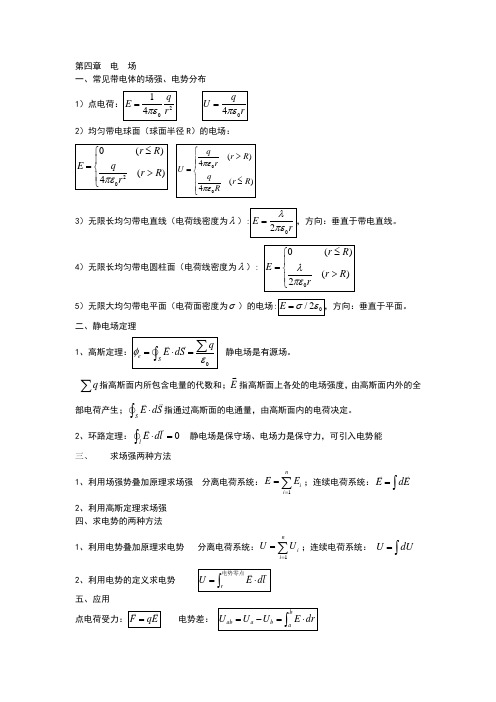
第四章 电 场一、常见带电体的场强、电势分布 1）点电荷：2014q E r πε=04q U rπε=2）均匀带电球面（球面半径R ）的电场：200()()4r R E qr R r πε≤⎧⎪=⎨>⎪⎩00()4()4qr R r U q r R R πεπε⎧>⎪⎪=⎨⎪≤⎪⎩3）无限长均匀带电直线（电荷线密度为λ）:02E rλπε=，方向：垂直于带电直线。
4）无限长均匀带电圆柱面（电荷线密度为λ）: 00()()2r R E r R rλπε≤⎧⎪=⎨>⎪⎩5）无限大均匀带电平面（电荷面密度为σ）的电场:0/2E σε=，方向：垂直于平面。
二、静电场定理 1、高斯定理：0e Sq E dS φε=⋅=∑⎰静电场是有源场。
q ∑指高斯面内所包含电量的代数和；E指高斯面上各处的电场强度，由高斯面内外的全部电荷产生；SE dS ⋅⎰指通过高斯面的电通量，由高斯面内的电荷决定。
2、环路定理：0lE dl⋅=⎰ 静电场是保守场、电场力是保守力，可引入电势能三、求场强两种方法1、利用场强势叠加原理求场强 分离电荷系统：1ni i E E ==∑；连续电荷系统：E dE =⎰2、利用高斯定理求场强 四、求电势的两种方法1、利用电势叠加原理求电势 分离电荷系统：1nii U U==∑；连续电荷系统： U dU =⎰2、利用电势的定义求电势 rU E dl =⋅⎰电势零点五、应用点电荷受力：F qE = 电势差： bab a b aU U U E dr =-=⋅⎰a由a 到b六、导体周围的电场1、静电平衡的充要条件： 1）、导体内的合场强为0，导体是一个等势体。
2）、导体表面的场强处处垂直于导体表面。
E ⊥表表面。
导体表面是等势面。
2、静电平衡时导体上电荷分布： 1）实心导体： 净电荷都分布在导体外表面上。
2）导体腔内无电荷： 电荷都分布在导体外表面，空腔内表面无电荷。
3）导体腔内有电荷+q ，导体电量为Q ：静电平衡时，腔内表面有感应电荷-q ，外表面有电荷Q ＋q 。
大学物理答案详解
10-15 三个半径分别为321R R R 、、的同心导体球壳，带电量依次为321q q q 、、。
求：（1）这个带电体系的总电能；（2）当内、外两球壳共同接地时，体系的电容和各球壳的带电量。
解：由高斯定律可以求得 0ε∑⎰=∙iqS d Er>R 3时有 032124επq q q r E ++=203214rq q q E πε++=R 3 >r>R 2时有 20214r q q E πε+=R 2 >r>R 1时有2014rq E πε=r<R 1时有 E=0 电场能量：dr r r q q q dr r r q q dr r r q W R R R R R 22203210222021022201044244244233221ππεεππεεππεε⎪⎪⎭⎫ ⎝⎛+++⎪⎪⎭⎫ ⎝⎛++⎪⎪⎭⎫ ⎝⎛=⎰⎰⎰∞302321320221210218)(118)(118R q q q R R q q R R q πεπεπε+++⎪⎪⎭⎫ ⎝⎛-++⎪⎪⎭⎫ ⎝⎛-=内外半径分别为21,R R 的球面电容由下式求得（设球面带电q ）：电势差⎪⎪⎭⎫⎝⎛-=210114R R q V πε 电容为122104R R R R V q C -==πε 则内侧两球面电容12210114R R R R V q C -==πε 同样得到外侧两球面的电容 23230224R R R R V q C -==πε 内外球都接地则中间的球壳对地电容是上面两个电容并联，总电容为))(()(423121322021R R R R R R R C C C ---=+=πε 这时内球与外球带电量与中间球面带电量等值异号，设带电量大小分别为/3/1,q q 。
有/3/12q q q +=再由中间那个球面电势V 可以表示为：2/31/1C q C q V == 解得：)()(1/12311232122/1R R R R R R q C C q q -++=+=，)()(1/11232312212/2R R R R R R q C C q q +-+=+= 10-16 一个充有各向同性均匀介质的平行板电容器，充电到1000V 后与电源断开，然后把介质从极板间抽出，此时板间的电势差升高到3000V 。
大学物理 答案
10-15 三个半径分别为321R R R 、、的同心导体球壳，带电量依次为321q q q 、、。
求：（1）这个带电体系的总电能；（2）当内、外两球壳共同接地时，体系的电容和各球壳的带电量。
解：由高斯定律可以求得 0ε∑⎰=∙iqS d Er>R 3时有 032124επq q q r E ++=203214rq q q E πε++=R 3 >r>R 2时有 20214r q q E πε+=R 2 >r>R 1时有2014rq E πε=r<R 1时有 E=0 电场能量：dr r r q q q dr r r q q dr r r q W R R R R R 22203210222021022201044244244233221ππεεππεεππεε⎪⎪⎭⎫ ⎝⎛+++⎪⎪⎭⎫ ⎝⎛++⎪⎪⎭⎫ ⎝⎛=⎰⎰⎰∞302321320221210218)(118)(118R q q q R R q q R R q πεπεπε+++⎪⎪⎭⎫ ⎝⎛-++⎪⎪⎭⎫ ⎝⎛-=内外半径分别为21,R R 的球面电容由下式求得（设球面带电q ）：电势差⎪⎪⎭⎫ ⎝⎛-=210114R R q V πε 电容为122104R R R R V q C -==πε 则内侧两球面电容12210114R R R R V q C -==πε 同样得到外侧两球面的电容 23230224R R R R V q C -==πε 内外球都接地则中间的球壳对地电容是上面两个电容并联，总电容为))(()(423121322021R R R R R R R C C C ---=+=πε这时内球与外球带电量与中间球面带电量等值异号，设带电量大小分别为/3/1,q q 。
有/3/12q q q +=再由中间那个球面电势V 可以表示为：2/31/1C q C q V ==解得：)()(1/12311232122/1R R R R R R q C C q q -++=+=，)()(1/11232312212/2R R R R R R q C C q q +-+=+=10-16 一个充有各向同性均匀介质的平行板电容器，充电到1000V 后与电源断开，然后把介质从极板间抽出，此时板间的电势差升高到3000V 。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
W
R
0
内 4r 2 dr
3Q 2 20 o R
例: 半径为R的雨点带有电量q．现将其打破，在保持总体积不
变的情况下分成完全相同的两点，并拉开到“无限远”．此系 统的电能改变量是多少? 解释出现这个结果的原因． 解:将雨点视为导体，其电荷分布在表面，所以静电能为
1 1 q q2 W U dq dq 2 q 2 q4 π 0 R 8 π0R
qi dq
φi φ
φi
qi
V
1 W φ dq 2V
式中dq处的电势为
φ
例题１、如图所示，边长为a的立方体的每一边顶点上方
放有一点电荷 -e,立方体中心处放有一正点电荷 ＋2e,
求此系统的相互作用能 。 解：（１）、八个顶点上的负 电荷 分别与相邻的负电荷之
-e -e
+2e
a
-e
q
Q
0.63Q
q
q Q(1 e
t RC
RC 时间常数
t RC q 0.63Q
t 3 5
RC大充电时间长
0
t
放电过程
dq q R dt C
K
R
t RC
q Qe
c q
q
Q
0.37Q
q
U U 0e
放电时间
t RC
t 2 3
0
t
五、静电场的能量
Q E 4 0 r 2
ε
0
dV 4 r dr
2
Q
1 WE 0 E 2 dV 2 V
1 Q 2 0 4 r dr 2 2 4 0 r R
Q2 8 0 R
2
dr
+r
+
+ + + + +
+ + +R
静电能就是电荷产生的电场的能量
1 1 W ( A B )Q Ed S 2 2 1 1 2 0 E dS 0 E 2V WE 2 2
电场能量密度
E 0
?
1 2 wE 0 E 2
电场的能量
1 WE 0 E 2 dV 2 V
V是场所在的空间
[例4]求一均匀带电球面的电场能量。
均匀带电球面和均匀带电球外的电场分布相同，因此后者的 静电能大于前者的静电能.
例6、从场的角度谈谈自能、相互作用能和静电能
E2 E E1 E 2
WE
E1
１
0
２
E EdV
1 ε 2
0
V
1 2 E dV ε 2
V
2 2 1 1 0 E1 dV 0 E 2 dV 0 E1 E 2 dV 2 V 2 V V
2 1 1 1 W互 A A1 A2 q1φ 1 q 2φ 2 q iφ i 2 2 2 i 1
式中 i是 qi 以外的电荷在 qi 处的电势
2、三个点电荷 组成的系统的相互作用能
r13
q3
A1 0
q1
r23
r12
q2
q1q2 A2 4 0 r12 q1q3 q2 q3 q1 q2 A3 ( )q3 4 0 r13 4 0 r23 4 0 r13 4 0 r23
W W W WE 互 W静 E1 E2
例7. 真空中一半径为a，带电量为Q 的均匀球体的静电场能。
解： 球内场强：
球外场强：
Qr E1 4o a 3 Q E2 4o r 2
a 0
Q
a
WE wedV
a o
1 1 2 o E1 dV o E22dV a 2 2
2 2
1 Q 1 Qr 2 2 o 4 r d r 4 r dr o 3 2 a 2 2 4 o a 4 o r
3Q 2 20 o a
利用静电能公式如何推导?
Q(3R 2 r 2 ) 内 (r ) 8 π 0 R 3
3
其原因是：两雨点电荷相同，在分开时相互排斥，电场力对
外作了功．
4 3 4 R 3 2 π r π R r 3 3 3 2
电势能之和
3 ( q / 2) 2 q2 2q 2 W 2 8 π 0 r 16 π 0 r 16 π 0 R
3 2 q2 2q 2 q2 W W W 1 0 16 π 0 R 8 π 0 R 2 8 π0R
1 φ dq 2 S q 8π ε 0R
2
＋
＋ ＋ ＋
＋ dq
φ
R
＋
＋
例题３、求电容器的能量
+ +
_ dq u _
R
dq
ε 解法：（１）、将dq从负极搬到正极，电源克服电场力作功
q dA udq dq C
A udq
Q
0
Q2 q 1 1 2 dq CU QU 2C 2 2 C
静电场能量
一、带电体之间的相互作用能
q1
Ａ
Wa 0
Ｂ
q2
（a）
r
Ａ
（ b） Ｂ
Wb
4 0r q1q2
W互 Wb Wa
二、带电体的静电能
定义： 如图设想构成带电体的无限多的元电荷开始处于彼此相距无 穷远的分散状态。现将这些分散的元电荷聚集起来，在此过 程中外界做的功就是这个带电体的静电能。
2、三个点电荷 组成的系统的相互作用能
q1 q 3 q2 q3 q1 q 2 A A1 A2 A3 4 π ε 0 r12 4 π ε 0 r13 4 π ε 0 r23
q3 1 q2 q3 q1 ( ) 1 q2 ( q1 ) 2 4 0 r12 4 0 r13 2 4 0 r12 4 0 r23 q1 q2 1 q3 ( ) 2 4 π ε 0 r13 4 π ε 0 r23
间的相互作用能为Ｗ１
e2 W1 12 4 π ε 0a
-e
-e -e
-e
（２）、６个面上其有１２对 顶点负电荷 之间的相互作用 的相互作用能为Ｗ２
-e -e -e
a
-e
+2e -e -e
W 2 12
e2 4π ε
0
2a
（３）、立方体对角线上四对负 电荷 的相互作用能Ｗ３
-e
W3 4
e2 4 π ε 0 3a
思考题
有一半径为R的导体球,开始不带电,现将分散在无限远处
的元电荷聚集到导体球上,则当导体球上带有Q电量时,外 力做的功是多少? 同学们推导.
q 4 0 R
dW dA dq
W
q 4 0 R
q
dq
dq
Q
0
dq
Q2
Q
0
4 0 R
8 0 R
试比较均匀带电球面和均匀带电球的静电能
i3 1 1 1 1 W互 A q11 q2 2 q3 3 qi i 2 2 2 2 i 1
3、n个点电荷组成的系统的相互作用能？
1 n W 互 A q iφ i 2 i 1
无限多元电荷dq的相互作用能?
四 、连续分布的电荷系统的静电能
W互 1 in q i i 2 i 1
二、带电体的静电能
dq 5
dq1
dq 4
dq 2
dq 3
三、带电体系的静电能
2
1 3
W静＝Ｗ互＋Ｗ自
???
三、点电荷系之间的相互作用1q2 1 q2 1 q1 A2 q1 q2 4 0 r12 2 4 0 r12 2 4 0 r12
解法：（２）利用静电能公式？
1 1 1 W dq dq dq 2V 2A 2B
1 1 1 AQ B ( Q ) ( A B)Q 2 2 2
1 Q2 UQ 2 2C
电容器的充放电过程
充电过程
K
R
dq q R dt C
)
c q
（４）、中心点电荷与八个顶点 上的负电荷 的相互作用能Ｗ４为
-e -e
a
-e
W4 8
2e 2 4π ε
0
3 a 2
+2e
-e
-e -e
-e
0.34e 2 W互 Wi 0a i 1
4
例题２、求均匀带电 球面的静电能
解：
Q 4 0R
Q
1 W dq 2