组合结构3章
合集下载
结构力学第三章静定结构组合结构及拱
0 FNJ 右 FQJ 右 sin FH cos (7.5) (0.447) 10 0.894
3.35 8.94 12.29kN (压)
二、三较拱的压力线
如果三铰拱某截面D以左(或以右)所有外力的 合力FRD已经确定，则该截面的弯矩、剪力、轴 力可按下式计算：
15kN K右
Fº ＝－2.5kN QK右
0 0 (FH 10kN , FQK左 12.5kN , FQK右 2.5kN )
(sin 0.447, cos 0.894)
0 FQK 左 FQK 左 cos FH sin 12.5 0.894 10 0.447
67.5kN
50
A F C G E
B
30
D
M图
kN.m
求AC杆和BC杆剪力
F
FQAC
y
0, FQAC 7.5kN
22.5kN 7.5 32.5 10kN/m FNAD
FAy
+ _
15
+
7.15 67.5kN 35 FQ图 kN
作业
3-20
§3-6 三铰拱受力分析
拱 (arch)
FN DE 135kN ,
FNDF FN EG =-67.5kN
FAy
D
FCx 135kN , FCy 15kN
FNDA
FNDF
D
FN DA FN EB＝ kN 151
FNDE
2m
F
50kN.m
求AC杆和BC杆弯矩
22.5kN 5kN.m
20kN.m 10kN/m
30kN.m
MD FRD
3.35 8.94 12.29kN (压)
二、三较拱的压力线
如果三铰拱某截面D以左(或以右)所有外力的 合力FRD已经确定，则该截面的弯矩、剪力、轴 力可按下式计算：
15kN K右
Fº ＝－2.5kN QK右
0 0 (FH 10kN , FQK左 12.5kN , FQK右 2.5kN )
(sin 0.447, cos 0.894)
0 FQK 左 FQK 左 cos FH sin 12.5 0.894 10 0.447
67.5kN
50
A F C G E
B
30
D
M图
kN.m
求AC杆和BC杆剪力
F
FQAC
y
0, FQAC 7.5kN
22.5kN 7.5 32.5 10kN/m FNAD
FAy
+ _
15
+
7.15 67.5kN 35 FQ图 kN
作业
3-20
§3-6 三铰拱受力分析
拱 (arch)
FN DE 135kN ,
FNDF FN EG =-67.5kN
FAy
D
FCx 135kN , FCy 15kN
FNDA
FNDF
D
FN DA FN EB＝ kN 151
FNDE
2m
F
50kN.m
求AC杆和BC杆弯矩
22.5kN 5kN.m
20kN.m 10kN/m
30kN.m
MD FRD
组合结构桥梁第1～3章
无 连 接 件
有 连 接 件
• 作用1：连接件承担了混凝土板与钢梁界面的剪力，协调混 凝土板与钢梁的变形，将混凝土板与钢梁组合在一起共同 工作，是组合梁得以实现的关键
三、抗剪连接件（shear connector）
3.1 抗剪连接件的基本受力性能
局部放大
由于混凝土板与钢梁刚度不同， 混凝土板
导致其变形的曲率不同，在局部
心线至自由边的距离 • （2）l：对于悬臂梁取悬臂长度；对于一般情况取支座间
距 • （3）同时明确指出，不适用于受压的情况
三、抗剪连接件（shear connector）
3.1 抗剪连接件（也称剪力键，传剪器）的基本受力性能
• 1.抗剪连接件的作用及要求
无
• 混凝土板的I=0.000667，EI=23000
重庆观音岩长江大桥
叠合梁
一、组合结构入门
1.叠合梁
就截面形式而言可分为：板梁、箱梁、桁架梁
组合板梁
• 由至少2片钢主梁和混凝土板构成，横梁一般采用钢结构 ，主要有梁式和桁架式两种，需注意的是混凝土顶板既 是主梁的一部分，也是桥面板
一、组合结构入门
1.叠合梁
单箱双室
单箱双室带挑臂
组合箱梁
混凝土
双箱截面 多箱截面
闭口钢箱
开口钢箱
互通匝道桥采用的 斜置双向截面
• 由至少1片钢主梁和混凝土板构成，钢主梁可为开口箱也 可为闭口箱，可根据需要设置成多种截面形式，十分灵 活，同样地混凝土顶板既是主梁的一部分，也是桥面板
一、组合结构入门
1.叠合梁
混凝土板
钢桁架
组合桁架梁
• 与组合箱梁相比，只是将钢箱换为了桁架，由于桁架的 用钢梁较大，目前一般在公、铁两用桥中使用，但桁架 可以散件拼装，适应山区不便于大件运输的特点，在山 区大跨度桥梁中有发展潜力。
有 连 接 件
• 作用1：连接件承担了混凝土板与钢梁界面的剪力，协调混 凝土板与钢梁的变形，将混凝土板与钢梁组合在一起共同 工作，是组合梁得以实现的关键
三、抗剪连接件（shear connector）
3.1 抗剪连接件的基本受力性能
局部放大
由于混凝土板与钢梁刚度不同， 混凝土板
导致其变形的曲率不同，在局部
心线至自由边的距离 • （2）l：对于悬臂梁取悬臂长度；对于一般情况取支座间
距 • （3）同时明确指出，不适用于受压的情况
三、抗剪连接件（shear connector）
3.1 抗剪连接件（也称剪力键，传剪器）的基本受力性能
• 1.抗剪连接件的作用及要求
无
• 混凝土板的I=0.000667，EI=23000
重庆观音岩长江大桥
叠合梁
一、组合结构入门
1.叠合梁
就截面形式而言可分为：板梁、箱梁、桁架梁
组合板梁
• 由至少2片钢主梁和混凝土板构成，横梁一般采用钢结构 ，主要有梁式和桁架式两种，需注意的是混凝土顶板既 是主梁的一部分，也是桥面板
一、组合结构入门
1.叠合梁
单箱双室
单箱双室带挑臂
组合箱梁
混凝土
双箱截面 多箱截面
闭口钢箱
开口钢箱
互通匝道桥采用的 斜置双向截面
• 由至少1片钢主梁和混凝土板构成，钢主梁可为开口箱也 可为闭口箱，可根据需要设置成多种截面形式，十分灵 活，同样地混凝土顶板既是主梁的一部分，也是桥面板
一、组合结构入门
1.叠合梁
混凝土板
钢桁架
组合桁架梁
• 与组合箱梁相比，只是将钢箱换为了桁架，由于桁架的 用钢梁较大，目前一般在公、铁两用桥中使用，但桁架 可以散件拼装，适应山区不便于大件运输的特点，在山 区大跨度桥梁中有发展潜力。
3-5组合结构(结构力学第3章)
FN图(kN )
例3-13 分析图示组合结构的内力。
M 图(kN m)FQ图源自kN )FN图(kN )例3-14 计算图示组合结构中链杆的轴力, 并作出受弯杆的M图。
MJ 0 :
M图, FN
FNHG 3a FNHC 2a FNDG 2a q 2a a 2qa 2a 0
FNHG a FNHC 2a 0
再考虑HBF部分对F点的力矩平衡, 有：
结合 FNHC FNDG ,可得：
FNHG 2qa, FNHC FNDG 2qa
若将铰F的位置上移, 则结构的受力状态不再对称。
(c )
可将刚片EAG和HBF视作链杆, 将链杆GH视作刚片, 然后按三刚 片问题进行求解; 即用m-m截断形成无穷远处虚铰的链杆CH和EG, 由 刚片Ⅲ对虚铰(Ⅱ, Ⅲ)和刚片Ⅱ、Ⅲ联合体对虚铰(Ⅰ, Ⅱ)的力矩平衡 方程联立解得以上两链杆的轴力, 问题便可以得到解决。 其中, EAG部分的弯矩可根据虚拟链杆EG的轴力, 按图3-55c求得。
析：因DE杆与受弯杆平行，链杆DF和EG又与之垂 直，可判定受弯杆全长受轴向压力90kN。
FN图(kN )
例3-13 分析图示组合结构的内力。
M 图(kN m)
MF FyA 2.5m FNDE 1m 30kN 1m 20kN m MG FyB 2.5m FNDE 1m 40kN m
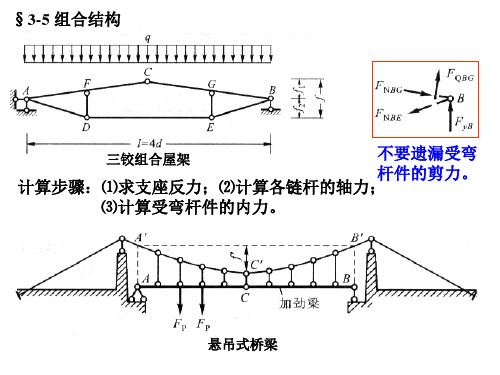
§3-5 组合结构
不要遗漏受弯 杆件的剪力。 计算步骤：⑴求支座反力；⑵计算各链杆的轴力； ⑶计算受弯杆件的内力。
三铰组合屋架
悬吊式桥梁
例3-13 分析图示组合结构的内力。
解：⑴求支座反力。 ⑵计算各链杆的轴力。
第三章 静定结构的内力计算(组合结构)
A A A A 0 0 0 0
0 0 0 0
8 8 8 8
HC
3、求梁式杆内力 处理结点A处力
结构力学
第3章静定结构的内力计算
静定结构特性
结构力学
第3章静定结构的内力计算
静定结构特性 静定结构特性 一、结构基本部分和附属部分受力影响
A
F1
B
C
F2
D
E
F3
F
如只有 F1 作用。则Ⅱ、Ⅲ无内力和反力； Ⅰ Ⅱ Ⅲ 如只有 F1 作用。则Ⅱ、Ⅲ无内力和反力； 如只有 F1 作用。则Ⅱ、Ⅲ无内力和反力； 如只有 F3 作用。则Ⅰ、Ⅱ均有内力和反力； 如只有 F3 作用。则Ⅰ、Ⅱ均有内力和反力； 如只有 F3 作用。则Ⅰ、Ⅱ均有内力和反力； 如只有 F2 作用。则Ⅲ无内力和反力，但Ⅰ有内力和反力。 如只有 F2 作用。则Ⅲ无内力和反力，但Ⅰ有内力和反力。 特性一、静定结构基本部分承受荷载作用，只在基本部分上产 如只有 F2 作用。则Ⅲ无内力和反力，但Ⅰ有内力和反力。 生反力和内力；附属部分上承受荷载作用，在附属部分和基本 部分上均产生反力和内力。
第3章静定结构的内力计算
q = 1 kN/m A FR Ax FR Ay FNDA F C FNFD VC
8 8 8 8
M M图 图 （ m M图 （kN· kN· m） ） M 图 （kN· m） （kN· m） F 图 FQ 图 Q （ ） FkN 图 （ kN Q ） FkN 图 （ Q ） （kN） F 图 FN N图 （ ） FkN （ kN ） N图 FkN N图 （ ） （kN）
结构力学
第3章静定结构的内力计算
二、平衡荷载的影响
F C B D
A B q C
组合结构 各章小结汇总
受构造等原因的影响，剪切连接件的设置数量少于完全剪切连接所需的剪切连接件数量时，可采用部分剪切连接设计法。对于连续组合梁的正弯矩区段，它不仅可以减少剪切连接件的数量，方便施工，而且不会显著降低截面的受弯承载力
采用柔性剪切连接件的简支组合梁中，钢与混凝土之间粘结滑移对组合梁挠度的影响已经较大，不能忽略，这时应考虑粘结滑移效应的折减钢度法进行挠度计算。连续组合梁应按变截面刚度梁进行计算
影响型钢混凝土梁柱剪切性能有诸多因素，其中剪跨比与轴压比的影响明显，必须考虑。剪切破坏主要有三种破坏形态，由于粘结滑移的影响，容易发生剪力粘结破坏。通过实验，取三种破坏形态中剪切强度较低的破坏形态作为梁柱剪切强度的计算依据而得出型钢混凝土梁柱斜截面剪切承载力计算公式
影响型钢混凝土柱的强度有诸多因素，其中偏心距是主要因素之一。主要与偏心距有关，型钢混凝土柱正截面破坏有两种破坏形态，即大偏心受压与小偏心受压。可以根据两种破坏形态各自的应力图得出型钢混凝土柱正截面承载能力计算公式
组合梁应按两个受力阶段分别进行承载力计算和变形验算。第一受力阶段，即楼板的混凝土达到强度设计值以前，混凝土板只能作为外加荷载来考虑。第二受力阶段，楼板的混凝土已达到强度设计值，钢梁与混凝土之间存在组合作用，可以按组合梁进行计算
组合梁按弹性理论的计算，截面的应力和变形都可按照材料力学的公式进行。必要时还应考虑荷载长期作用时混凝土徐变的影响，以及温度应力和混凝土收缩引起的应力
施工阶段组合板的变形计算，不考虑压型钢板与混凝土的组合效应，应取压型钢板有效截面的抗弯刚度，按弹性力学的方法计算。使用阶段组合板的变形计算，可采用换算截面法，分别按荷载效应的标准组合和准永久组合进行计算，其较大值应满足变形控制的要求
小结
1，组合梁是指通过剪切连接件将钢梁与混凝土板连成整体共同工作的受弯构件。当组合梁承受正弯矩时，混凝土板处于受压区，钢梁的大部分处于受拉区，因而能够充分发挥两种材料各自的强度优势。与钢筋混凝土梁相比，它具有承载力高，自重小，便于施工的特点，与钢构件相比，它又具有抗弯刚度大，变形小，稳定性好的优点，
采用柔性剪切连接件的简支组合梁中，钢与混凝土之间粘结滑移对组合梁挠度的影响已经较大，不能忽略，这时应考虑粘结滑移效应的折减钢度法进行挠度计算。连续组合梁应按变截面刚度梁进行计算
影响型钢混凝土梁柱剪切性能有诸多因素，其中剪跨比与轴压比的影响明显，必须考虑。剪切破坏主要有三种破坏形态，由于粘结滑移的影响，容易发生剪力粘结破坏。通过实验，取三种破坏形态中剪切强度较低的破坏形态作为梁柱剪切强度的计算依据而得出型钢混凝土梁柱斜截面剪切承载力计算公式
影响型钢混凝土柱的强度有诸多因素，其中偏心距是主要因素之一。主要与偏心距有关，型钢混凝土柱正截面破坏有两种破坏形态，即大偏心受压与小偏心受压。可以根据两种破坏形态各自的应力图得出型钢混凝土柱正截面承载能力计算公式
组合梁应按两个受力阶段分别进行承载力计算和变形验算。第一受力阶段，即楼板的混凝土达到强度设计值以前，混凝土板只能作为外加荷载来考虑。第二受力阶段，楼板的混凝土已达到强度设计值，钢梁与混凝土之间存在组合作用，可以按组合梁进行计算
组合梁按弹性理论的计算，截面的应力和变形都可按照材料力学的公式进行。必要时还应考虑荷载长期作用时混凝土徐变的影响，以及温度应力和混凝土收缩引起的应力
施工阶段组合板的变形计算，不考虑压型钢板与混凝土的组合效应，应取压型钢板有效截面的抗弯刚度，按弹性力学的方法计算。使用阶段组合板的变形计算，可采用换算截面法，分别按荷载效应的标准组合和准永久组合进行计算，其较大值应满足变形控制的要求
小结
1，组合梁是指通过剪切连接件将钢梁与混凝土板连成整体共同工作的受弯构件。当组合梁承受正弯矩时，混凝土板处于受压区，钢梁的大部分处于受拉区，因而能够充分发挥两种材料各自的强度优势。与钢筋混凝土梁相比，它具有承载力高，自重小，便于施工的特点，与钢构件相比，它又具有抗弯刚度大，变形小，稳定性好的优点，
结构力学第三章静定结构的受力分析
例2： MA
A
MA
FP L/2 L/2
FP
MB
B 结论
把两头的弯矩标在杆
端，并连以直线，然
后在直线上叠加上由
节间荷载单独作用在
简支梁上时的弯矩图
MB MA
FPL/4
FPL/4
2020年5月29日星期五7时56分M25秒B
§3-1 梁的内力计算的回顾
3）画剪力图
要求杆件上某点的剪力，通常是以弯矩图为
C
B FQBA
由： MA 0 FQBA (81 26) 2 9kN
也可由： Y 0 FQCA 17 8 9kN
剪力图要注意以下问题： ▲ 集中力处剪力有突变； ▲ 没有荷载的节间剪力是常数； ▲ 均布荷载作用的节间剪力是斜线； ▲ 集中力矩作用的节间剪力是常数。
2020年5月29日星期五7时56分25秒
L/2
M/2
FPL/4
L/2
M
M/2
2020年L5/月229日星期五L7/时2 56分25秒
§3-1 梁的内力计算的回顾
2）用叠加法画简支梁在几种简单荷载共同作用下 的弯矩图
例1： MA
q
MB
q
A
B=
qL2/8
MA
MB
+
+
MA
=A
qL2/8
MB
B
2020年5月29日星期五7时56分25秒
§3-1 梁的内力计算的回顾
2020年5月29日星期五7时56分25秒
§3-1 梁的内力计算的回顾
正 MAB
杆端内力
FNAB
A端 FQAB
MBA 正
B端
FNBA
FQBA
第3章 桁架、组合结构计算
线上的两杆的内力
相等且性质相同。
例1 用结点法计算图中所示桁架在 半跨集中荷载作用下各杆的内力。
10kN 20kN 10kN
4 1
5
2
2m
H1=0
1
3
2
6 5 7 4 2m=8m
8
V1
V8
(1) 计算桁架的支座反力
X=0
H1=0
H1=0
10kN
20kN
4
10kN
1
1
5
2
2m
3
2
6 5 7 4 2m=8m
根据比例关系 求出 N25 。
计算3-4杆内力N34 ：
o
a
M2 =0
V25 Ⅰ H25 2 5 r1 N34 H24 4 1 3 V1 P1 V24
Ⅰ
V1 d N34 h1=V1 d N34 = h1
计算2-4杆内力N24 ：
Mo =0
o
a
V25 Ⅰ H25 2 5 r1 N34 H24 4 1 3 V1 P1 V24
10kN
20kN
10kN
4
1
5
2
H1=0
1
3
2
6 5 7 4 2m=8m
2m
8
V1
V8
V34
20kN
4
H34
3
40kN
H35
2
M5 =0
1
5
20kN
V35
H34 2 + 20 4 H34 = 20kN 20 2=0
利用比例关系
V34 = 10kN
N34 = 5 V34 = 5 ( 10) = 22.36kN
结构力学I-第三章 静定结构的受力分析(桁架、组合结构)
FNEC FNED 33.54 kN
Y 0 FNEC sin FNED sin FNEA sin 10 kN 0
联立解出
FNEC FNED 10 5 33.5 思考：能否更快呢？ FNEC 22.36 kN， FNED 11.18 kN
00:44
静定平面桁架
• 桁架的内力计算
由力矩平衡方程 ∑ ME = 0，可求CD杆内力。
FA×d - FNCD×h = 0
FNCD = FAd / h = M0E / h
F1 F2 F3 F4 F5
M0E FA
6d
M FB
若M0E > 0，则FNCD >0 (下弦杆受拉 )
M0E是什么？
00:44
I
II
静定平面桁架
I
II
• 桁架的内力计算
简支梁
悬臂梁
伸臂梁
刚架：受弯构件，由若干直杆联结而成的结构，其中全部或部份 结点为刚结点；
A
D
B
C
简支刚架
悬臂刚架
三铰刚架
00:44
回顾
• 结构内力图
M–AB (表0) 示结构上各截面内力值的图形：弯矩图、M剪BA (0)
力图、A端轴力图；
A
B
FNA横B 坐标 -- 截面位置；
内力图 - 弯矩
A
FA
FB
– 截面法
• 例1：试求图示桁架中杆EF、ED，CD，DG的内力。
解: ⑶ 求上弦杆EF内力，力矩法；
取 ED 和 CD 杆 的 交 点 D 为 矩 心 ， 先 求 EF 杆 的 水 平 分 力
FxEF，由力矩平衡方程∑MD = 0，
FA×2d - F1×d + FxEF×H = 0
Y 0 FNEC sin FNED sin FNEA sin 10 kN 0
联立解出
FNEC FNED 10 5 33.5 思考：能否更快呢？ FNEC 22.36 kN， FNED 11.18 kN
00:44
静定平面桁架
• 桁架的内力计算
由力矩平衡方程 ∑ ME = 0，可求CD杆内力。
FA×d - FNCD×h = 0
FNCD = FAd / h = M0E / h
F1 F2 F3 F4 F5
M0E FA
6d
M FB
若M0E > 0，则FNCD >0 (下弦杆受拉 )
M0E是什么？
00:44
I
II
静定平面桁架
I
II
• 桁架的内力计算
简支梁
悬臂梁
伸臂梁
刚架：受弯构件，由若干直杆联结而成的结构，其中全部或部份 结点为刚结点；
A
D
B
C
简支刚架
悬臂刚架
三铰刚架
00:44
回顾
• 结构内力图
M–AB (表0) 示结构上各截面内力值的图形：弯矩图、M剪BA (0)
力图、A端轴力图；
A
B
FNA横B 坐标 -- 截面位置；
内力图 - 弯矩
A
FA
FB
– 截面法
• 例1：试求图示桁架中杆EF、ED，CD，DG的内力。
解: ⑶ 求上弦杆EF内力，力矩法；
取 ED 和 CD 杆 的 交 点 D 为 矩 心 ， 先 求 EF 杆 的 水 平 分 力
FxEF，由力矩平衡方程∑MD = 0，
FA×2d - F1×d + FxEF×H = 0
结构力学T-第3章 静定结构的受力分析(II)
理想约束的解释
理想约束是指其约束力在可能位移上所作的功恒等于零的那种约束。如光滑铰、 刚性链杆。
图中的约束为铰C，体系可能的位 移为绕铰C转动，约束力为X、Y两 个方向的分力，但体系转动时，在 C处并无X、Y方向的位移，故约束 力所做的功为零，铰C为理想约束。
图中的约束为铰A、滑动支座B，体系可能的 位移为点C绕铰A转动、点B水平移动，约束 力为A铰X、Y两个方向的分力、支座B竖向反 力，但体系位移时，在A处并无X、Y方向的 位移，在B处并无竖向位移，故约束力所做 的功为零，铰A、支座B为理想约束。
合理拱线通式：
三铰拱
三铰拱的合理轴线
上式两侧对x两次求导得：
因：
推导合理拱线 通式的y值以支 座连线为0起点
所以有： 拱计算简图 （ 此处y值以拱顶C铰为0起点） 求解思路： 在本题中，因为荷载与拱线形状有 关，故拱线的变化会引起荷载的变 体，不能事先确定对应简支梁的弯 矩值。故合理拱线不直接利用 y=M0/FH来求解，而是利用dM/dx=q 的微分关系，通过建立y与荷载q的 关系来求解合理拱线。 因本题与推导全理拱线通式的y值反号，换号后得： 由x=0,y=0得： 把q=qc+γy代入上式得： 由x=0,dy/dx=0得： 悬链线 最终合理拱线方程为：
拱微段隔离体
例3-13 均匀水压力下的合理拱线-由微元的微分关系导出
微元力矩平衡方程为：
三铰拱
三铰拱的合理轴线
即： 所有内力的平衡微分方程写在一起为：
拱计算简图
当R->∞时， 变为直杆公式
对水压力，qs=0，qr=q（常数），上式变为：
水压力下微元所 有内力平衡微分 方程通式的推导
拱微段隔离体
例3-13 均匀水压力下的合理拱线-由微元的微分关系导出
3第三章 压型钢板与混凝土组合板解析
以上两类均属于非组合板。
③考虑组合作用的压型钢板混凝土组合板。施工阶段压型钢板作为模 板及浇注混凝土的作业平台。使用阶段，压型钢板相当于钢筋混凝土 板中的受拉钢筋，在全部静载及活载作用下，考虑二者的组合作用。
本章主要讲第三类，即组合楼板。
2.组合板优点
1) 压型钢板作为浇灌混凝土的模板，节省了大量木模板及其支撑。 2) 压型钢板工厂生产、运输、堆放方便，节省大量支模工作，并且改善 了施工条件。 3) 在使用阶段，由于组合作用，可代替受拉钢筋。减少了钢筋的制作与 安装工作。
4) 刚度大，自重轻。
5) 便于敷设通信、电力、采暖等管线。 6) 便于立体作业，加快施工进度，缩短工期。 7) 可直接做顶棚。 8) 减小了发生火灾的可能性。
பைடு நூலகம்
3.2 压型钢板的型式及要求
3.2.1 压型钢板的形式：
(1)闭口形槽口的压型钢板(图3.1a) (2)轧齿槽或开小孔的压型钢板 (图3.1b) (3)加焊钢筋的压型钢板(图3.1c) 国内生产的压型钢板仅适用于直接作用于非组合板，如果用于组合板中 ，必须在板的翼缘上采取措施，以保证组合效应。
当压型钢板顶面以上的混凝土厚度大于 100mm时，组合板 的挠度应按强边方向的简支单向板计算。当 0.5 e 2.0 时，应按双向板计算内力；当 e 0.5 或 e 2.0 时，应 按单向板计算内力。其中 （3.3） l x
e
ly
式中 ； lx—组合板强边（顺肋）方向的跨度； ly—组合板弱边（垂直肋）方向的跨度； Ix、Iy—分别为组合板强边和弱边方向的截面惯性矩（计算 Iy时只考虑压型钢板顶面以上的混凝土厚度hc， 即 I y Bhc3 / 12 ，其中B为压型钢板的计算宽度，通常取
组合结构课件
20世纪80年代我国在组合楼板技术方面的研究和应用发展迅速。 1984年，冶金工业部冶金建筑研究总院对压型钢板的选型、加 工工艺、抗剪连接件等配套技术进行了大量的开发、研究与应用 工作，制定了冶金行业标准《钢-混凝土组合楼盖结构设计与施 工规程》YB9238-92。 国家标准《钢结构设计规范》GB50017-2003、电力行业标准 《钢-混凝土组合楼盖结构设计规程》DL/T5085-1999等对压型钢 板-混凝土组合楼盖的设计作了规定。
深圳赛格大厦
钢管混凝土结构在桥梁结构中的应用形式如图所示。
钢管混凝土结构桥梁结构
图为钢管混凝土拱肋的截 面形式。1990年，钢管混 凝土技术首次成功应用于 跨度115m的四川省旺苍东 河大桥。
钢管混凝土拱肋结构 截面形式
四川省旺苍东河大桥
5.外包钢混凝土组合结构
外包钢混凝土结构是指外部配钢的钢筋混凝土结构，简 称外包钢结构。应用较多的是四角配置角钢的钢筋混凝土 结构，角钢的外表面与混凝土表面取平或稍突出表面0.51.5mm。横向箍筋与角钢焊接成骨架，为了满足箍筋保护 层的要求，可将箍筋两端墩成球状再与角钢内侧焊接。
钢管混凝土柱可分为（圆）钢管混凝土柱和方钢管混凝土 柱。一般在钢管中浇注混凝土，并不另配钢筋。
（ 1 ）圆钢管混凝土柱的特点：利用钢管约束混凝土，将 混凝土由单向受压转变为三向受压。钢管混凝土结构充分发 挥混凝土和钢材各自的优点，避免了钢材特别是薄壁钢材容 易失稳的缺点，所以受力合理，大大节省材料由于其是圆形 截面，而且断面高度较小，所以在受弯矩作用时显然并无优 越可言，而且是不利的，因此常常将其作为高层建筑中的下 面数层的柱是最合适的。圆钢管混凝土结构的最大弱点是圆 形截面的柱与矩形截面的梁连接比较复杂，是推广圆钢管混 凝土结构的一大障碍。
结构力学 第三章桁架讲解
上弦杆
腹杆
下弦杆
理想与实际的偏差：并非理想铰接， 并非理想直杆， 并非为二力杆。
主内力:按计算简图计算出的内力，次内力:实际内力与主内力的差值
2.桁架的分类
按几何组成分类：
简单桁架—在基础或一个铰结三角形上依次加二元体构成 联合桁架—由简单桁架按基本组成规则构成 复杂桁架—非上述两种方式组成的静定桁架
第三章 静定结构受力分析
§3-4 静定桁架受力分析
(Statically determinate trusses)
1. 桁架的特点
（1）桁架的结点都是光滑无摩擦的铰结点； 理想桁架：
（2）各杆的轴线都是直线，并通过铰的中心；
结论：理想桁 架中的杆件均
（3）荷载和支座反力都作用在结点上。
是“二力杆”
对称,方向反对称的荷载
Fp
Fp
Fp
Fp
对称荷载
反对称荷载
对称结构的受力特点:在对称荷载作用下内力是对称的, 在反对称荷载作用下内力是反对称的。
Fp
Fp
Fp
Fp
E
D
0
A
B
C
Fp
Fp
E
D
A
B
C
既对称 又平衡 NCE NCD 0
E
D
既反对称
E
D
NED 0
又平衡
例:试求图示桁架A支座反力.
B
F
0, NDF
N DA
Fp
其它杆件轴力求 法类似.
求出所有轴力后, 2 / 2 应2把2F轴p 力标在杆件旁.
F
0, N DE
2Fp / 2
对于简单桁架,若与组成顺序相反依 次截取结点,可确保求解过程中一个方程 只包含一个未知力。
外包钢混凝土梁-钢管混凝土柱组合结构技术规程
外包钢混凝土梁-钢管混凝土柱组合结构技术规程第一章引言1.1技术规程的目的与依据本技术规程是为规范外包钢混凝土（以下简称外包PV）梁-钢管混凝土柱组合结构设计和施工而制定的。
依据国家有关建筑法规、规范和标准，结合实际工程，制定本技术规程。
1.2适用范围本技术规程适用于外包PV梁-钢管混凝土柱组合结构的设计和施工。
第二章术语和定义2.1术语第三章组合结构的基本要求3.1构件材料的要求3.1.2钢管混凝土柱应采用强度等级不小于Q345B的钢管，并符合GB/T1591-XXXX《低合金高强度结构钢技术条件》中有关要求。
3.2构件连接方式3.2.1外包PV梁与钢管混凝土柱连接应采用搭接连接方式，梁端与柱端设置钢筋连接件，连接件应符合设计要求并具备必要的延性。
3.3砌体填充要求3.3.1PV梁与钢管混凝土柱之间的空间可用轻质砌体填充，填充材料需符合设计要求，并保证填充密实度。
3.3.2砌体填充高度可根据设计要求灵活确定，并应符合相关规范要求。
第四章施工工艺与质量控制4.1施工工艺要求4.1.1外包PV梁与钢管混凝土柱的制作、运输和安装过程中应严格按照相关规范和设计要求进行。
4.1.2构件连接应符合设计要求，安装过程中应注意梁与柱之间的水平、垂直和轴线位置控制。
4.1.3砌体填充时要求填充材料的均匀性、密实性和符合设计要求。
4.2质量控制要求4.2.1施工过程中，对外包PV梁和钢管混凝土柱的材料、制作和安装过程进行质量控制，确保符合相关规范和设计要求。
4.2.2施工中的关键节点应进行质量检查，包括梁端和柱端连接件的设置、砌体填充的均匀性和密实度等。
4.2.3完工后进行结构整体验收，并编制验收报告。
第五章设计要求与设计步骤5.1设计要求5.1.1外包PV梁-钢管混凝土柱组合结构的设计应符合国家相关规范和标准的要求，并根据工程实际情况进行合理设计和优化布置。
5.1.2设计应考虑组合结构的荷载特点、构造性能和耐久性等因素，保证结构的安全和可靠性。
第3章 组合逻辑电路
例3-5的真值表 C 0 0 1 1 0 0 1 1 0 0 1 1 0 0 1 1 D 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 F1 F2 0 0 0 0 0 0 0 0 1 1 1 1 1 1 0 0 0 0 1 1 1 1 1 1 1 1 0 0 0 0 0 0
图3－9
3.2.2 组合逻辑电路设计举例 例3-3 设计一个三人按少数服从多数的表决电路。并用与 非门实现。 解：（1）由题意可知，三人代表三个输入变量，通过与 否的结果为一个输出变量。三个输入变量用字母A、B、 C表示，输出用F表示。列出真值表，见表3－2，输入变 量“1”表示同意，“0”表示不同意；输出变量“1”表示通 过，“0”表示不通过。 （2）对真值表用卡诺图化简，如图3－4所示，得到化简 函数 F=AB+BC+AC （3）把化简的与或式转换成“与非－与非”表达式`
_ I7 X 1 0 1 1 1 1 1 1 1
表3－6 表3-6 74148的真值表 输 入 输 _ _ _ _ _ _ _ _ _ _ I 6 I5 I4 I3 I2 I 1 I0 Y2 Y 1 Y0 X X X X X X X 1 1 1 1 1 1 1 1 1 1 1 1 1 X X X X X X X 0 0 0 0 X X X X X X 0 0 1 1 0 X X X X X 0 1 0 1 1 0 X X X X 0 1 1 1 1 1 0 X X X 1 0 0 1 1 1 1 0 X X 1 0 1 1 1 1 1 1 0 X 1 1 0 1 1 1 1 1 1 0 1 1 1
S ABC ABC ABC ABC
C′= A B + A C + B C （3）把表达式转化为“与非－与非”表达式
2-钢-混凝土组合梁 . 3章解析
取1.05、1.2，箱形截面均取1.05；
f ——钢材的抗弯强度设计值。
52
2、钢梁正应力计算
当钢梁当受压翼缘的自由外伸宽度与其厚度比值 b / t 13 235 / f y （图3.4.4 ），但能满足下列公式要求时， x 1.0 应取 。 对于工字截面梁
b 235 15 t fy
22
3.1.4
施工阶段在组合梁下设置临时支撑，临时支撑的数量根据组合梁的跨度大小
来确定，当跨度L大于7m时，支撑不应少于3个，当跨度L小于7m时，可设置 1~2个支撑。支撑设置的精确数量应根据施工阶段的变形来确定。这时，组合梁 不必进行施工阶段的计算，按使用阶段进行计算，全部荷载均由组合梁承受。设 置临时支撑可以减少组合梁在使用阶段的挠度，但需要较多的连接件来抵抗钢梁 与混凝土板之间的相对滑移。
23
§ 3.2 构造要求 3.2.1 材料
1.混凝土 强度等级不低于C20。
2.钢筋
混凝土板中一般采用HPB235与HRB335。 3.钢材 宜采用Q235与Q345。
24
3.2.2
截面尺寸
1、组合梁的截面高度 简支梁组合梁的高跨比为1/18~1/12,一般取1/15. 2、混凝土楼板的厚度 当楼板采用压型钢板组合板时 , 压型钢板凸肋顶 至混凝土板顶混凝土板厚度不应小于50mm. 当楼板采用普通钢筋混凝土板时,混凝土板的厚度 不应小于100mm. 组合梁混凝土板厚，一般以10mm为模数，经常采 用的板厚为100mm、120mm、140mm、160mm 。 3、混凝土板的有效宽度 be b0 b1 b2
42
3、荷载短期效应组合下截面弹性抵抗矩
（1）中和轴在板内（见图3.4.2）
43
f ——钢材的抗弯强度设计值。
52
2、钢梁正应力计算
当钢梁当受压翼缘的自由外伸宽度与其厚度比值 b / t 13 235 / f y （图3.4.4 ），但能满足下列公式要求时， x 1.0 应取 。 对于工字截面梁
b 235 15 t fy
22
3.1.4
施工阶段在组合梁下设置临时支撑，临时支撑的数量根据组合梁的跨度大小
来确定，当跨度L大于7m时，支撑不应少于3个，当跨度L小于7m时，可设置 1~2个支撑。支撑设置的精确数量应根据施工阶段的变形来确定。这时，组合梁 不必进行施工阶段的计算，按使用阶段进行计算，全部荷载均由组合梁承受。设 置临时支撑可以减少组合梁在使用阶段的挠度，但需要较多的连接件来抵抗钢梁 与混凝土板之间的相对滑移。
23
§ 3.2 构造要求 3.2.1 材料
1.混凝土 强度等级不低于C20。
2.钢筋
混凝土板中一般采用HPB235与HRB335。 3.钢材 宜采用Q235与Q345。
24
3.2.2
截面尺寸
1、组合梁的截面高度 简支梁组合梁的高跨比为1/18~1/12,一般取1/15. 2、混凝土楼板的厚度 当楼板采用压型钢板组合板时 , 压型钢板凸肋顶 至混凝土板顶混凝土板厚度不应小于50mm. 当楼板采用普通钢筋混凝土板时,混凝土板的厚度 不应小于100mm. 组合梁混凝土板厚，一般以10mm为模数，经常采 用的板厚为100mm、120mm、140mm、160mm 。 3、混凝土板的有效宽度 be b0 b1 b2
42
3、荷载短期效应组合下截面弹性抵抗矩
（1）中和轴在板内（见图3.4.2）
43
第三章 机构组合与创新设
第三章 机构组合与创新设计
基本机构及其运动特性 基本机构及其组合的概念 机构组成原理与机构创新设计 机构的串联组合与创新设计 机构的并联组合与创新设计 机构的叠加组合与创新设计 机构的封闭组合与创新设计 其它类型的机构组合与创新设计
§3-1 基本机构及其运动特性
一、基本机构的概念
本章把连杆机构、凸轮机构、齿轮机构、间 歇运动机构等结构最简单且不能再进行分割的闭
第十二章 机构组合与创新设计
简单机械的示意图
第十二章 机构组合与创新设计
复杂的机械装置
第十二章 机构组合与创新设计
常用的机构组合方法如下:
1. 利用机构的组成原理，不断连接各类杆组，可得到复杂的
机构系统。
2. 按照串联规则组合基本机构，可得到复杂的机构系统。 3. 按照并联规则组合基本机构，可得到复杂的机构系统。 4. 按照叠加规则组合基本机构，可得到复杂的机构系统。 5. 按照封闭规则组合基本机构，可得到复杂的机构系统。
1.基本概念
前一个机构的输出构件与后一个机构 的输入构件刚性连接在一起，称之为串联 组合。 前一个机构称为前置机构，后一个机 构称为后置机构。其特征是前置机构和后 置机构都是单自由度机构。
第十二章 机构组合与创新设计
2.分类
机构1 前置机构
机构2 后置机构 (a) I型串联
机构1
前置机构
机构2
后置机构 ( b) II型串联
第十二章 机构组合与创新设计
第五节 机构的并联组合与创新设计
一、机构的并联组合方法 二、并联组合的基本思路
第十二章 机构组合与创新设计
一、机构的并联组合方法
1. 基本概念 2. 分类
3. 组合示例
第十二章 机构组合与创新设计
基本机构及其运动特性 基本机构及其组合的概念 机构组成原理与机构创新设计 机构的串联组合与创新设计 机构的并联组合与创新设计 机构的叠加组合与创新设计 机构的封闭组合与创新设计 其它类型的机构组合与创新设计
§3-1 基本机构及其运动特性
一、基本机构的概念
本章把连杆机构、凸轮机构、齿轮机构、间 歇运动机构等结构最简单且不能再进行分割的闭
第十二章 机构组合与创新设计
简单机械的示意图
第十二章 机构组合与创新设计
复杂的机械装置
第十二章 机构组合与创新设计
常用的机构组合方法如下:
1. 利用机构的组成原理，不断连接各类杆组，可得到复杂的
机构系统。
2. 按照串联规则组合基本机构，可得到复杂的机构系统。 3. 按照并联规则组合基本机构，可得到复杂的机构系统。 4. 按照叠加规则组合基本机构，可得到复杂的机构系统。 5. 按照封闭规则组合基本机构，可得到复杂的机构系统。
1.基本概念
前一个机构的输出构件与后一个机构 的输入构件刚性连接在一起，称之为串联 组合。 前一个机构称为前置机构，后一个机 构称为后置机构。其特征是前置机构和后 置机构都是单自由度机构。
第十二章 机构组合与创新设计
2.分类
机构1 前置机构
机构2 后置机构 (a) I型串联
机构1
前置机构
机构2
后置机构 ( b) II型串联
第十二章 机构组合与创新设计
第五节 机构的并联组合与创新设计
一、机构的并联组合方法 二、并联组合的基本思路
第十二章 机构组合与创新设计
一、机构的并联组合方法
1. 基本概念 2. 分类
3. 组合示例
第十二章 机构组合与创新设计
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
18/163
1. 适用范围
符合下列情况之一的组合梁，应按弹性理论进 行截面分析和截面应力力计算。 (1) 组合梁内钢梁翼缘或腹板的板件的宽厚比值 大于表3.2.1规定的限值，且其组合梁截面的中和 轴位于钢梁腹板内。
(2)在设计荷载作用下，可能因交替发生受拉、受 压屈服使材料产生低周期疲劳破坏的构件。
(2)组合梁中钢梁,在出现全截面塑性化之前,受 压翼缘和腹板不发生板件的局部屈曲; (3)应设置侧向支承杆,以控制钢梁的侧向变形和 弯扭变形.
34/163
• 3.5.1 组合梁受弯承载力计算
1.计算假定
（1）塑性中和轴以下的型钢截面，其压应力 全部达到钢材抗压强度设计值； （2）塑性中和轴以上的型钢截面，其拉应力 也全部达到钢材的抗拉设计强度； （3）塑性中和轴以上的混凝土截面均匀受压 ，其压应力全部达到混凝土的抗压强度设计值； （4）塑性中和轴以下的混凝土截面，假定全 部开裂而不再受力；
21/163
对钢梁上翼缘
0t
b 0
M f t W0
M f W0b
对钢梁下翼缘
对组合梁顶部混凝土 b）中和轴在钢梁内 对钢梁上翼缘 对钢梁下翼缘 对组合梁顶部混凝土
0c
M fc c W0
t 0
M f t W0
b 0
M f b W0
0c
20/163
3)截面应变符合平截面假定; 4)不考虑组合梁混凝土翼缘板内钢筋; 5)不考虑混凝土开裂影响； 6)当钢筋混凝土楼板下边设置板托时，截面计 算时不考虑混凝土板托影响。 (2)组合梁正应力计算 1)当组合梁下设置临时支撑时，按一阶段受力 设计，梁上的荷载全部由组合截面承担。不考虑 混凝土徐变的影响时，其截面应力可按下式计算 a）中和轴在混凝土板内
(b) 两根材料、断面、刚度完全相同的矩形梁，叠在 一起，可靠连接。 3 2 b 2h Mymax ql 3 ql 2 正应力 max I 8 h / 12 16 bh2 剪应力
max
3 V 3 ql 1 3 ql 2 b 2h 2 2 b 2h 8 bh
3) 总的剪应力 a） 当组合截面的中和轴0--0位于钢梁截面内 时，钢梁总剪应力按 1 2 见图3.4.6(d); b）当组合截面的中和轴0—0位于混凝土翼缘 或板托内时，钢梁剪应力的验算截面，取钢梁腹 板与翼缘的交接面，此处钢梁的剪应力最大。
28/163
(3) 抗剪强度验算
b 0 1 x nx 2 b 0
对组合梁顶部混凝土
0c
M2 fc c EW0
24/163
式中 M 1 ---施工阶段的永久荷载对组合梁产生的弯矩设计值 M 2 ---使用阶段的永久荷载与可变荷载对组合梁产生 的弯矩设计值。
4. 组合梁竖向受剪承载力计算 (1) 计算原则 1)计算组合梁的剪应力时，应考虑施工阶段和 使用阶段不同工作截面和受力特点： 2)在楼板混凝土未硬化之前,施工阶段的全部荷 载由组合梁的钢梁承担，钢梁的剪应力按钢梁截 面进行计算，当楼板的强度达到混凝土的设计强 度后，后加的使用阶段荷载由组合梁来承担，其 钢梁的剪应力按组合截面计算；
8/163
• 5. 钢梁 （1）截面尺寸 钢梁截面高度h≥1/2.5组合梁截面高度H 即 h ≥0.4 H （2）板件宽厚比
9/163
• 3.3 组合梁的正截面受力性能
1. 弹性阶段 2. 弹塑性阶段 3. 塑性阶段
10/163
• 3.4 组合梁按弹性理论计算
• 3.4.1 截面的几何特性 1. 换算截面 原则：截面应变相同且总内力不变 (1) 荷载的短期效应组合
(1)在设计荷载作用下,不会因交替发生受拉屈 服和受压屈服使材料低周疲劳破坏的构件. (2)组合梁的中和轴位于混凝土受压翼缘板面 内, (3)组合梁的塑性中和轴虽位于其钢梁部件的 截面内,但钢梁翼缘和腹板的板件宽厚比均满足表 3.2.1的要求.
33/163
2.适用条件
(1)塑性设计的前提条件是，组合梁截面应全截 面塑性。因此，其钢材的力学性能应满足以下条 件： 1)强屈比： f u / f y 1.2 2)伸长率： 5 15% 3)极限应变： u 20 y y 和 u分别为钢材的屈服点应变和对应抗拉强度f u的应变
25/163
3)组合梁的钢梁的实际剪应力，等于钢梁分别 按两阶段产生的剪应力之和。 (2) 剪应力计算公式 1) 第一受力阶段 在施工荷载作用下,钢梁截面剪应力分布见图 3.4.6(b)，剪应力按下式计算：
1
V1 S1 I stw
式中 V1----施工阶段的可变荷载和永久荷载在钢梁上产生 的剪应力设计值; S 1----剪应力验算截面以上的钢梁截面面积对钢梁 中和轴S--S的面积矩. ----钢梁的腹板厚度和毛截面的惯性矩 tw I w
（3）组合楼板 notes：压型钢板肋与钢梁平行----考虑板肋贡献
14/163
4. 考虑混凝土徐变的截面抵抗矩
中和轴位于钢梁内，将αE → 2 αE
• 3.4.2 施工阶段组合梁计算 第一受力阶段：钢梁正应力、剪应力、整体稳 定和挠度计算。 可不验算整体稳定情况
15/163
1. 荷载计算
（1）永久荷载---压型钢板、混凝土自重；
（2）中和轴在型钢内
换算后的面积A0 惯性矩为I0 对钢梁上翼缘W0t 对钢梁下翼缘W0b 对组合梁上翼缘W0c
A0 beq hc1 A beq hc31 2 2 I0 beq hc1 y0 0.5hc1 I A y y0 12 I0 t W0 y0 hc1 I0 b W0 H y0 I W0c 0 y0
第3章 组合梁设计
• 3.1 概述 • 3.1.1 组合梁的特点及类型
图3.1 压型钢板组合梁
1/163
• 3.1.2 组合梁的工作原理
(a) 两根材料、断面、刚度完全相同的矩形梁， 叠在一起，无连接、忽略摩擦。
2/163
3/163
Mymax ql 2 h bh3 3 ql 2 正应力 max I 16 2 / 12 8 bh2 3 V 3 ql 1 3 ql max 剪应力 2bh 2 4 bh 8 bh q 4 q 4 l l 5 2 5 2 5 ql 4 跨中挠度 f 3 384 EI 384 bh 64 Ebh3 E 12
35/163
（5）组合梁受到负弯矩作用时，混凝土翼缘板 有效宽度内的纵向钢筋，其拉应力全部达到钢筋 的抗拉强度设计值； （6）若钢筋混凝土板的支座处设置了混凝土板 托,确定组合梁截面尺寸时，混凝土板托的截面不 计。 2. 正弯矩作用区段承载力计算公式 （1）塑性中轴位于混凝土受压翼板内(图 3.5.1),即 A f be hc1 f c 时
19/163
2. 适用条件
(1) 当钢梁部件拉应力小于钢材的屈服强度，混 凝土最大压应力小于0.5倍轴心抗压强度。 (2)若钢梁宽厚比较大,钢梁受力后，截面尚未出 现塑性化以前，受压翼缘和腹板有可能发生局部 屈曲，这时不应按塑性理论计算，而应按弹性理 论进行截面计算。 3. 组合梁正应力计算 (1)计算假定 1)钢材和混凝土均为理想的弹性材料； 2)钢梁和混凝土板之间的相对滑移很小，可以 忽略不计，接截面在弯曲后仍保持平面；
换算后的面积A0 惯性矩为I0 对钢梁上翼缘W0t 对钢梁下翼缘W0b 对组合梁上翼缘W0c
A0 beq hc1 A beq hc31 2 2 I0 beq hc1 y0 0.5hc1 I A y y0 12 I0 t W0 hc1 y0 I0 b W0 H y0 I0 c W0 y0 13/163
5/163
• 2. 混凝土楼板的厚度 压型钢板组合楼板---不应小于50mm 钢筋混凝土楼板---不应小于100mm • 3. 混凝土楼板的有效宽度 计算宽度be值与梁的高跨比、荷载形式、翼缘板 厚度与梁高的比值、钢梁间距有关，具体：
6/163
7/163
• 4. 板托尺寸 板托顶部宽度与板托高度hc2之比不应小于1.5， 且板托的高度不应大于混凝土板厚度hc1的1.5倍。
跨中挠度
5 ql 4 5 f 384 EI 384
ql 4 b 2h E 12
3
5 ql 4 256 Ebh3
4/163
• 3.1.3 组合梁的计算方法
(1) 弹性理论 (2) 塑性理论
• 3.2 构造要求
• • • • • • 3.2.1 材料 1. 混凝土 2. 钢筋 3. 连接件 3.2.2 截面尺寸 1. 梁高 高跨比1/18~1/12，常用1/15
bc 0 g q bc 0 b 0
对组合梁顶部混凝土
cc 0
Mg 2 EW
cc 0
Mq
EW
c 0
fc
23/163
b）中和轴在混凝土板下 对钢梁下翼缘 对组合梁顶部混凝土
W W Mg Mq 0cc fc 2 EW0cc EW0c
bc 0
Mg
bc 0
beq be / E
(2) 荷载的长期效应组合
beq be / 2 E
11/163
2. 换算截面中和轴位置
短期荷载作用下
长期荷载作用下
y0 y 0c
Ay A Ay A
i i i i
i
i
12/163
3. 荷载短期效应组合下截面弹性抵抗矩
（1）中和轴在混凝土板内 换算后的组合截面面积为A0，惯性矩为I0 ， 对钢梁上翼缘、下翼缘的抵抗矩为W0t 、 W0b ， 对组合梁截面顶的抵抗矩为W0c ，按下式计算：
M fc c EW0
22/163
1. 适用范围
符合下列情况之一的组合梁，应按弹性理论进 行截面分析和截面应力力计算。 (1) 组合梁内钢梁翼缘或腹板的板件的宽厚比值 大于表3.2.1规定的限值，且其组合梁截面的中和 轴位于钢梁腹板内。
(2)在设计荷载作用下，可能因交替发生受拉、受 压屈服使材料产生低周期疲劳破坏的构件。
(2)组合梁中钢梁,在出现全截面塑性化之前,受 压翼缘和腹板不发生板件的局部屈曲; (3)应设置侧向支承杆,以控制钢梁的侧向变形和 弯扭变形.
34/163
• 3.5.1 组合梁受弯承载力计算
1.计算假定
（1）塑性中和轴以下的型钢截面，其压应力 全部达到钢材抗压强度设计值； （2）塑性中和轴以上的型钢截面，其拉应力 也全部达到钢材的抗拉设计强度； （3）塑性中和轴以上的混凝土截面均匀受压 ，其压应力全部达到混凝土的抗压强度设计值； （4）塑性中和轴以下的混凝土截面，假定全 部开裂而不再受力；
21/163
对钢梁上翼缘
0t
b 0
M f t W0
M f W0b
对钢梁下翼缘
对组合梁顶部混凝土 b）中和轴在钢梁内 对钢梁上翼缘 对钢梁下翼缘 对组合梁顶部混凝土
0c
M fc c W0
t 0
M f t W0
b 0
M f b W0
0c
20/163
3)截面应变符合平截面假定; 4)不考虑组合梁混凝土翼缘板内钢筋; 5)不考虑混凝土开裂影响； 6)当钢筋混凝土楼板下边设置板托时，截面计 算时不考虑混凝土板托影响。 (2)组合梁正应力计算 1)当组合梁下设置临时支撑时，按一阶段受力 设计，梁上的荷载全部由组合截面承担。不考虑 混凝土徐变的影响时，其截面应力可按下式计算 a）中和轴在混凝土板内
(b) 两根材料、断面、刚度完全相同的矩形梁，叠在 一起，可靠连接。 3 2 b 2h Mymax ql 3 ql 2 正应力 max I 8 h / 12 16 bh2 剪应力
max
3 V 3 ql 1 3 ql 2 b 2h 2 2 b 2h 8 bh
3) 总的剪应力 a） 当组合截面的中和轴0--0位于钢梁截面内 时，钢梁总剪应力按 1 2 见图3.4.6(d); b）当组合截面的中和轴0—0位于混凝土翼缘 或板托内时，钢梁剪应力的验算截面，取钢梁腹 板与翼缘的交接面，此处钢梁的剪应力最大。
28/163
(3) 抗剪强度验算
b 0 1 x nx 2 b 0
对组合梁顶部混凝土
0c
M2 fc c EW0
24/163
式中 M 1 ---施工阶段的永久荷载对组合梁产生的弯矩设计值 M 2 ---使用阶段的永久荷载与可变荷载对组合梁产生 的弯矩设计值。
4. 组合梁竖向受剪承载力计算 (1) 计算原则 1)计算组合梁的剪应力时，应考虑施工阶段和 使用阶段不同工作截面和受力特点： 2)在楼板混凝土未硬化之前,施工阶段的全部荷 载由组合梁的钢梁承担，钢梁的剪应力按钢梁截 面进行计算，当楼板的强度达到混凝土的设计强 度后，后加的使用阶段荷载由组合梁来承担，其 钢梁的剪应力按组合截面计算；
8/163
• 5. 钢梁 （1）截面尺寸 钢梁截面高度h≥1/2.5组合梁截面高度H 即 h ≥0.4 H （2）板件宽厚比
9/163
• 3.3 组合梁的正截面受力性能
1. 弹性阶段 2. 弹塑性阶段 3. 塑性阶段
10/163
• 3.4 组合梁按弹性理论计算
• 3.4.1 截面的几何特性 1. 换算截面 原则：截面应变相同且总内力不变 (1) 荷载的短期效应组合
(1)在设计荷载作用下,不会因交替发生受拉屈 服和受压屈服使材料低周疲劳破坏的构件. (2)组合梁的中和轴位于混凝土受压翼缘板面 内, (3)组合梁的塑性中和轴虽位于其钢梁部件的 截面内,但钢梁翼缘和腹板的板件宽厚比均满足表 3.2.1的要求.
33/163
2.适用条件
(1)塑性设计的前提条件是，组合梁截面应全截 面塑性。因此，其钢材的力学性能应满足以下条 件： 1)强屈比： f u / f y 1.2 2)伸长率： 5 15% 3)极限应变： u 20 y y 和 u分别为钢材的屈服点应变和对应抗拉强度f u的应变
25/163
3)组合梁的钢梁的实际剪应力，等于钢梁分别 按两阶段产生的剪应力之和。 (2) 剪应力计算公式 1) 第一受力阶段 在施工荷载作用下,钢梁截面剪应力分布见图 3.4.6(b)，剪应力按下式计算：
1
V1 S1 I stw
式中 V1----施工阶段的可变荷载和永久荷载在钢梁上产生 的剪应力设计值; S 1----剪应力验算截面以上的钢梁截面面积对钢梁 中和轴S--S的面积矩. ----钢梁的腹板厚度和毛截面的惯性矩 tw I w
（3）组合楼板 notes：压型钢板肋与钢梁平行----考虑板肋贡献
14/163
4. 考虑混凝土徐变的截面抵抗矩
中和轴位于钢梁内，将αE → 2 αE
• 3.4.2 施工阶段组合梁计算 第一受力阶段：钢梁正应力、剪应力、整体稳 定和挠度计算。 可不验算整体稳定情况
15/163
1. 荷载计算
（1）永久荷载---压型钢板、混凝土自重；
（2）中和轴在型钢内
换算后的面积A0 惯性矩为I0 对钢梁上翼缘W0t 对钢梁下翼缘W0b 对组合梁上翼缘W0c
A0 beq hc1 A beq hc31 2 2 I0 beq hc1 y0 0.5hc1 I A y y0 12 I0 t W0 y0 hc1 I0 b W0 H y0 I W0c 0 y0
第3章 组合梁设计
• 3.1 概述 • 3.1.1 组合梁的特点及类型
图3.1 压型钢板组合梁
1/163
• 3.1.2 组合梁的工作原理
(a) 两根材料、断面、刚度完全相同的矩形梁， 叠在一起，无连接、忽略摩擦。
2/163
3/163
Mymax ql 2 h bh3 3 ql 2 正应力 max I 16 2 / 12 8 bh2 3 V 3 ql 1 3 ql max 剪应力 2bh 2 4 bh 8 bh q 4 q 4 l l 5 2 5 2 5 ql 4 跨中挠度 f 3 384 EI 384 bh 64 Ebh3 E 12
35/163
（5）组合梁受到负弯矩作用时，混凝土翼缘板 有效宽度内的纵向钢筋，其拉应力全部达到钢筋 的抗拉强度设计值； （6）若钢筋混凝土板的支座处设置了混凝土板 托,确定组合梁截面尺寸时，混凝土板托的截面不 计。 2. 正弯矩作用区段承载力计算公式 （1）塑性中轴位于混凝土受压翼板内(图 3.5.1),即 A f be hc1 f c 时
19/163
2. 适用条件
(1) 当钢梁部件拉应力小于钢材的屈服强度，混 凝土最大压应力小于0.5倍轴心抗压强度。 (2)若钢梁宽厚比较大,钢梁受力后，截面尚未出 现塑性化以前，受压翼缘和腹板有可能发生局部 屈曲，这时不应按塑性理论计算，而应按弹性理 论进行截面计算。 3. 组合梁正应力计算 (1)计算假定 1)钢材和混凝土均为理想的弹性材料； 2)钢梁和混凝土板之间的相对滑移很小，可以 忽略不计，接截面在弯曲后仍保持平面；
换算后的面积A0 惯性矩为I0 对钢梁上翼缘W0t 对钢梁下翼缘W0b 对组合梁上翼缘W0c
A0 beq hc1 A beq hc31 2 2 I0 beq hc1 y0 0.5hc1 I A y y0 12 I0 t W0 hc1 y0 I0 b W0 H y0 I0 c W0 y0 13/163
5/163
• 2. 混凝土楼板的厚度 压型钢板组合楼板---不应小于50mm 钢筋混凝土楼板---不应小于100mm • 3. 混凝土楼板的有效宽度 计算宽度be值与梁的高跨比、荷载形式、翼缘板 厚度与梁高的比值、钢梁间距有关，具体：
6/163
7/163
• 4. 板托尺寸 板托顶部宽度与板托高度hc2之比不应小于1.5， 且板托的高度不应大于混凝土板厚度hc1的1.5倍。
跨中挠度
5 ql 4 5 f 384 EI 384
ql 4 b 2h E 12
3
5 ql 4 256 Ebh3
4/163
• 3.1.3 组合梁的计算方法
(1) 弹性理论 (2) 塑性理论
• 3.2 构造要求
• • • • • • 3.2.1 材料 1. 混凝土 2. 钢筋 3. 连接件 3.2.2 截面尺寸 1. 梁高 高跨比1/18~1/12，常用1/15
bc 0 g q bc 0 b 0
对组合梁顶部混凝土
cc 0
Mg 2 EW
cc 0
Mq
EW
c 0
fc
23/163
b）中和轴在混凝土板下 对钢梁下翼缘 对组合梁顶部混凝土
W W Mg Mq 0cc fc 2 EW0cc EW0c
bc 0
Mg
bc 0
beq be / E
(2) 荷载的长期效应组合
beq be / 2 E
11/163
2. 换算截面中和轴位置
短期荷载作用下
长期荷载作用下
y0 y 0c
Ay A Ay A
i i i i
i
i
12/163
3. 荷载短期效应组合下截面弹性抵抗矩
（1）中和轴在混凝土板内 换算后的组合截面面积为A0，惯性矩为I0 ， 对钢梁上翼缘、下翼缘的抵抗矩为W0t 、 W0b ， 对组合梁截面顶的抵抗矩为W0c ，按下式计算：
M fc c EW0
22/163