电路分析基础第7章 互感和变压器
合集下载
第七章 -互感耦合与变压器
.
L1 R1
- d
U ab 10 / 0oV
. .
.
U ab 10 / 0 I1 R jL1 3 j 4 2 / 53.1o A
o
U cd jM I 1 U ab j 2 / 53.1o 10 4 / 36.9o 10 13.4 / 10.3oV
M k L1L 2
L1
N1
L2
N2
11
21
i1
自感磁通链为
互感磁通链为
线圈1中的磁通为11 交链线圈2的磁通为21
11 L1i1 21 M 21i1
互感系数
思考:若线圈2中通过电流i2,则自感磁通链为? 互感磁通链为?
22 L2i2
12 M12i2
M12 M 21
.
US 4 j2 ( j10 j 5) (30 j 30) 1 j j 20 ( j10 j 5) (30 j 30)
.
应用阻抗并联分流关系求得流
. j10 j 5 I2 I 1 245o ( j10 j 5) (30 j30) .
M
I2
+ jL2 U 2 –
U1 jL1 I1 jMI 2
U 2 jL2 I 2 jMI1
理想变压器的阻抗变换质
一、互感线圈的串联
互感的线圈串联时有两种接法——顺向串 联(异名端相连)和反向串联(同名端连)。
1. 顺向串联
异名端联在一起的串联方式,顺向串联。
Ls ( )2 R 2 (
Ls 18 0.057 2 50
反向串联时,线圈电阻不变,由已知条件可求出反 向串联时的等效电感:
互感电路分析

第7章 互感电路分析 1. 在图7-1-6(a)中,磁通相助,若i1(t)≠0,i2(t) = 0,则
di1 (t ) u1 (t ) L1 u1 dt di1 (t ) u2 (t ) M u2 dt
(7-1-11
若i1(t) = 0, i2(t) ≠0,
di2 (t ) u1 (t ) M u1 dt di2 (t ) u2 (t ) L2 u2 dt
(7-1-8)
第7章 互感电路分析 式(7-1-8)中第一项是由自感而产生的自感电压,用 u′ 表 示 ;第 二 项 是由 于 耦 合而 产 生 的互 感 电 压 ( mutual induced voltage ),用u″表示。即两耦合线圈的自磁通与互 磁通相助时,线圈端电压等于自感电压 u′与互感电压 u″之和。 同理,两耦合线圈的自磁通与互磁通相反时,磁通相消,
第7章 互感电路分析
i2(t)
11
i1(t)
22
图 7-1-2
第7章 互感电路分析
i1(t)
i2(t)
图7-1-3
第7章 互感电路分析 7.1.2 耦合电感线圈上的电压、电流关系当两个耦合电 感线圈上都有电流流过时,与L1交链的磁通为φ11与φ12 之和,与L2交链的磁通为φ22与φ21之和。 在L1中, 若 φ11 与φ12方向相同,则磁通相助; 同理, 在L2中,若 φ22与φ21方向相同,磁通也相助,如图7-1-4所示。
如图7-1-5所示。在这种情况下, 耦合线圈的磁通链分别为
对L1 ψ1=ψ11-ψ12=L1i1(t)-Mi2(t) 对L2 ψ2=ψ22-ψ21=L2i2(t)-Mi1 (t)
(7-1-9)
第7章 互感电路分析 如图 7-1-5所示,设 u1(t) 与i1(t) 、 u2(t) 与 i2(t) 参考方 向关联,则两线圈上电压与电流的关系为 对L1 对L1
第七章 含有互感电路的分析图文模板

我们把这种两个线圈间 磁场产生的相互联系的现象称为互 感(或磁耦合),将这对电感线圈 有称时作,耦耦合合电电感感(不或只互有感两元个件电)感。元件, 但只要它们之间彼此存在着磁耦合, 我们就可以把它们整体的称作一个耦 合电感(互感元件)。
现在,我们若在线
圈2中通以电流
i2 ,则i2同样在 自身线圈中产生自
其相量形式为: Uሶ L = jωLIሶ
其相量形式为: Uሶ L = jωLIሶ
该式中,
ZL = jωL 称为自感阻抗
XL = ωL 称为自感 抗
电压uL的参 考极性如下
图中所示。
互感
互感元 件
若在一个电感线圈附近放置另一个电感线圈。
此时,线圈1中电流i1产生的自感磁通ϕ11 (或 磁链ψ11)除与自身线圈1交链外,其中还有一部分或 全部与线圈2交链,这部分磁通我们称为互感磁通,用 ϕ21表示,这部ψ分2磁1 =链N我2们ϕ2称1 为互感磁链,用ψ21 表 示,且有
圈的绕向都有关系。若不知道线圈的绕向,就无法判断
互感电压的参考方向。
绕向被隐去的线圈
封装线圈 为了解决这一问题,引入同名端的概念。
THANK YOU 谢谢观看
同名端 7.2
同名端的定义: 我们将耦合电感中一个电感线圈施感 电流的进端与其在另一个电感线圈产 生的互感电压的正极性端,称为一对 同名端。
感磁通及自感磁链,
同时在线圈1中也
会产生ϕ2互2 感磁通ψ及22 分别是线圈2自身产生的自感磁通
互感磁及ϕ1链自2 ,感i磁2的链ψ变12 分别是线圈2在线圈1中产生的互感磁
化且会,在通两线及个圈互耦2感中合磁产线链圈中的磁通存在以下关系:
生自感电ϕ压21。≤ϕ11
第7章 互感耦合电路与变压器

1.顺向串联:
将耦合电感两个线圈的异名端串联连接,即电流由同名端流入
M
i
i L1 M
L1
L2
u
u
L2 M
(a)
(b)
图7-8 顺向串联及去耦合等效电路
M
•
I
L1
L2
•
•
jL1 I jM I
•
jL2 I
•
jM I
•
U
图7-8 (a) 顺向串联顺向串联
•
I
L1 M
•
U
L2 M
去耦图合7等-8效(b电) 去路耦合等效电路
I1 0.28A
I2 0.2A U2 2V
电路吸收的功率就是电阻R吸收的功率
P
I
2 2
R
பைடு நூலகம்
0.22
10
0.4W
【例7-5】 如图7-17(a)所示电路,已知U• S 2e j45 V,L1 L2 3,
M
1,R
1,1
C
2。求
I1、
I2、U2 和电路吸收的功率
P。
jM
•
•
I1
I2
•
I1
•
•
U jL2 I 2 jM I1
•• •
I I1 I2
•
•
•
I
j
U L1L2 M 2
U
jL
L1 L2 2M
等效电感
L L1L2 M 2 L1 L2 2M
4.异侧并联
将耦合电感两个线圈的异名端分别连接一起
•
I
•
I
-M
•
•
•
U
jL1 I 1
电路分析基础马颖-西电版第7章-互感与变压器ppt课件.ppt

11
在整堂课的教学中,刘教师总是让学 生带着 问题来 学习, 而问题 的设置 具有一 定的梯 度,由 浅入深 ,所提 出的问 题也很 明确
第7章互感与变压器
图7-3 磁通相消电路图
12
在整堂课的教学中,刘教师总是让学 生带着 问题来 学习, 而问题 的设置 具有一 定的梯 度,由 浅入深 ,所提 出的问 题也很 明确
为了表示两线圈耦合的紧密程度,引入了一个新的参 数——耦合系数,用字母k表示,定义为
k 21 12 11 22
(7-3)
5
在整堂课的教学中,刘教师总是让学 生带着 问题来 学习, 而问题 的设置 具有一 定的梯 度,由 浅入深 ,所提 出的问 题也很 明确
第7章互感与变压器
由自感系数和互感系数的定义可得
图7-2 磁通相助电路图
9
在整堂课的教学中,刘教师总是让学 生带着 问题来 学习, 而问题 的设置 具有一 定的梯 度,由 浅入深 ,所提 出的问 题也很 明确
第7章互感与变压器
对于电感L2 Ψ2=Ψ22+Ψ21=L2i2+Mi1
如图7-2所示,设i1与u1、i2与u2参考方向关联,根据电
对于电感L1,有
7-5
16
在整堂课的教学中,刘教师总是让学 生带着 问题来 学习, 而问题 的设置 具有一 定的梯 度,由 浅入深 ,所提 出的问 题也很 明确
第7章互感与变压器
图7-4 磁通相助同名端标定示意图
17
在整堂课的教学中,刘教师总是让学 生带着 问题来 学习, 而问题 的设置 具有一 定的梯 度,由 浅入深 ,所提 出的问 题也很 明确
7
在整堂课的教学中,刘教师总是让学 生带着 问题来 学习, 而问题 的设置 具有一 定的梯 度,由 浅入深 ,所提 出的问 题也很 明确
第7章 互感耦合电路与变压器

1和2是一对同名端!线圈串联、并联时的处理方法
,熟练写出互感元件两端的电压表达式,了解互感线 圈T型等效的方法。
6.2.1 互感线圈的串联
互感线圈L1和L2相串联时有两种情况:(1)一对异 名端相联,另一对异名端与电路相接,这种连接方法 称为顺接串联(顺串),下左图所示;
M
di1 , dt
uM1
M
di2 dt
L1
L2
ψ1
uL1
uM2
依据图中所示参考方向可
ψ21 列出两线圈端电压的相量表达
ψψ122
式分别为:
•
•
•
U 1 j I 1 X L1 j I 2 X M
i1 uM1
i2 uL2
•
•
•
U 2 j I 2 X L2 j I1 X M
自感电压总是与本线圈中通过的电流取关联参考
在本线圈中相应产生的感应电压
L1
L2
称为自感电压,用uL表示;在
相邻线圈中产生的感应电压
ψ1
ψ12
称为互感电压,用uM表示。
uL1
uM2
注脚中的12是说明线圈1的磁 i1
场在线圈2中的作用。
6.1.2 互感电压
通过两线圈的电流是交变 的电流,交变电流产生交变的 磁场,当交变的磁链穿过线圈
L1
L2
ψ1
i1
uL1 uM1
ψ1 uL2 uM2
ψ12 i2
互感现象的应用和危害
• 互感现象在电工电子技术中有着广泛的应用,变 压器就是互感现象应用的重要例子。
• 变压器一般由绕在同一铁芯上的两个匝数不同的 线圈组成,当其中一个线圈中通上交流电时,另 一线圈中就会感应出数值不同的感应电动势,输 出不同的电压,从而达到变换电压的目的。利用 这个原理,可以把十几伏特的低电压升高到几万 甚至几十万伏特。如高压感应圈、电视机行输出 变压器、电压、电流互感器等。
电路分析基础~~第七章 耦合电感与理想变压器

11
21
i1 + u1
i2 + u2
1 (t ) 11 (t ) 12 (t ) 2 (t ) 22 (t ) 21 (t )
-
-
12
22
自感磁链与互感磁链的方向可能相同也可能相反,由线圈 电流方向、线圈绕向等因素决定。因此广义的讲,每一个线圈 的总磁链又可表示为
初级回路的自阻抗 次级回路的自阻抗
jωM +
I1 R1
R2
jωL2
I2
RL
US
jωL1
US I1 (M ) 2 Z11 Z 22
-
(b)
j M I I2 1 Z 22
(M ) 2 Z i Z11 Z 22
空芯变压器从电源端看进去的输入阻抗为
次级回路在初级回 路的反映阻抗
7-3 空芯变压器
变压器也是电路中常用的一种器件,其电路模型由耦 合电感构成。
空芯变压器:耦合电感中的两个线圈绕在非铁磁性材料的 芯子上,则构成空芯变压器 铁芯变压器:耦合电感中的两个线圈绕在铁芯上,则构成
铁芯变压器
空芯变压器和铁芯变压器的主要区别: 前者属松耦合,耦合系数K较小, 后者属紧耦合,耦合系数K接近于1。
( R1 jL1 ) I 1 jMI 2 U S jMI 1 ( R2 RL jL2 ) I 2 0
令 Z11 R1 jL1 Z 22 R2 RL jL2 则上式可变换为 Z11 I 1 jMI 2 U S jMI 1 Z 22 I 2 0 求解以上方程可得:
a
j2Ω b
1Ω
US 100 I1 4.38 38 A 4 (M ) 2 1 j3 Z11 1 j2 Z 22
21
i1 + u1
i2 + u2
1 (t ) 11 (t ) 12 (t ) 2 (t ) 22 (t ) 21 (t )
-
-
12
22
自感磁链与互感磁链的方向可能相同也可能相反,由线圈 电流方向、线圈绕向等因素决定。因此广义的讲,每一个线圈 的总磁链又可表示为
初级回路的自阻抗 次级回路的自阻抗
jωM +
I1 R1
R2
jωL2
I2
RL
US
jωL1
US I1 (M ) 2 Z11 Z 22
-
(b)
j M I I2 1 Z 22
(M ) 2 Z i Z11 Z 22
空芯变压器从电源端看进去的输入阻抗为
次级回路在初级回 路的反映阻抗
7-3 空芯变压器
变压器也是电路中常用的一种器件,其电路模型由耦 合电感构成。
空芯变压器:耦合电感中的两个线圈绕在非铁磁性材料的 芯子上,则构成空芯变压器 铁芯变压器:耦合电感中的两个线圈绕在铁芯上,则构成
铁芯变压器
空芯变压器和铁芯变压器的主要区别: 前者属松耦合,耦合系数K较小, 后者属紧耦合,耦合系数K接近于1。
( R1 jL1 ) I 1 jMI 2 U S jMI 1 ( R2 RL jL2 ) I 2 0
令 Z11 R1 jL1 Z 22 R2 RL jL2 则上式可变换为 Z11 I 1 jMI 2 U S jMI 1 Z 22 I 2 0 求解以上方程可得:
a
j2Ω b
1Ω
US 100 I1 4.38 38 A 4 (M ) 2 1 j3 Z11 1 j2 Z 22
第8章互感与变压器图文模板
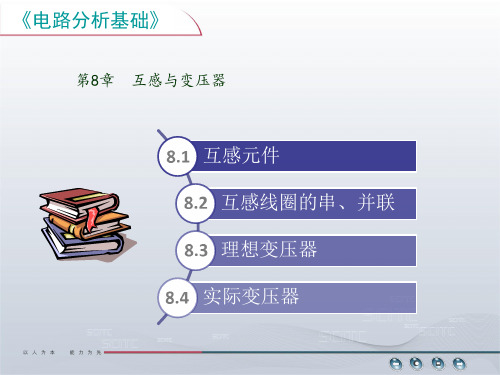
铁芯材料的磁导率μ无穷大。 理想变压器的电路模型: 初级线
n: + i *1 * i +
u1 1 N1
N2 2 u2
-
-
次级线
圈
圈
《电路分析基础》
2.理想变压器的主要性能
(1)变压关系
+ i1
Φ11=Φ21 i2 +
U1 N1 n
u1
U2 N2
u2
‒
‒
n称做匝数比或变压比。
Φ22=Φ12
理想变压器结构示意图
当两耦合线圈的自磁通与互磁通相消时,线圈电压等 于自感电压u′与互感电压u″之差。
《电路分析基础》
8.1.2 互感线圈的同名端 为什么要引入同名端的概念?
《电路分析基础》
安培定则
安培定则,也叫右手螺旋定则,是表示电流和电流激 发磁场的磁感线方向间关系的定则。
通电螺线管中的安培定则:用右手握住通电螺线管,让 四指指向电流的方向,那么大拇指所指的那一端是通电螺 线管的N极。
路中信号的传输质量。
《电路分析基础》
(3)互感系数
ψ21
L1
i1
uL1
uM1
L2 ψ22
ψ11 uM2 uL2
ψ12 i2
定义互磁通链Ψ21与 i1的比值为线圈L1对线圈L2的 互感系数,用M表示。单位和
自感系数L相同,都是亨利[H]。
M 21 M12
Ψ 21 i1
Ψ12 i2
N 2Φ21 i1
解:(a)图为顺向串联 Lab L1 L2 2M 10H
(b)图为反向串联 Lcd L1 L2 2M 4H
《电路分析基础》
8.2.2 互感线圈的并联等效 1.同侧并联
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
对于电感L1,有
u1dd t1L1d dit1Md dit2u'1u"1
对于电感L2,有
u2dd t2L2d d it2M d dit1u'2u"2
(7-5a) (7-5b)
11
第7章互感与变压器 式(7-5)中第一项是由自感产生的自感电压,第二项是由 耦合产生的互感电压。即两耦合线圈的自磁通与互磁通相助 时,线圈电压等于自感电压u′与互感电压u″ 同理,当两耦合线圈的自磁通与互磁通方向相反时,即 在L1中,自磁通Φ11与互磁通Φ12方向相反,则称为磁通相消; 在L2中,自磁通Φ22与互磁通Φ21方向相反,磁通也相消,如 图7-3所示。
称为两互感线圈反向串联时的等效电感,因此可画出图7-
9(a)所示电路的等效电路图,如图7-9(b)所示。
30
第7章互感与变压器 【例7-2】计算图7-10所示电路中的等效电感Lab。 解 根据式(7-8)、式(7-9) 对于图7-10(a)
Lab=L1+L2+2M=10H 对于图7-10(b)
Lab=L1+L2-2M=4H
17
第7章互感与变压器
图7-4 磁通相助同名端标定示意图
18
第7章互感与变压器
图7-5 磁通相助电路模型
19
第7章互感与变压器 2.同名端的实验判定方法 (1)直流法。如图7-6(a)所示,给线圈L1的两个端钮1和2 之间接直流电压源,线圈L2的两个端钮3和4之间接直流检流 计G。当开关S闭合瞬间检流计G正向偏转(右偏),则1和3为 同名端;若检流计G反向偏转,则1和4 (2)交流法。如图7-6(b)所示,给线圈L1的两个端钮1和2 之间接交流电压源u(t),用万用表分别测量各接线端的电压 (有效值)U12、U13和U34,若U12=│U13-U34│,则1和3为同名 端;若U12=U13+U34,则1和4
称为两互感线圈异侧并联时的等效电感,因此可画出图7-
5
第7章互感与变压器
线圈L1和L2在电的方面是相互独立的,它们的相互影响 是靠磁场相互联系起来,称为磁耦合。线圈L1中电流i1产生 的磁通与L2相交链的部分Φ21总是小于或等于产生的自磁通 Φ11,线圈L2中电流i2产生的磁通与L1相交链的部分Φ12总是 小于或等于产生的自磁通Φ22。即互磁通总是小于或等于自 磁通,若自磁通中的一部分不与另一线圈相交链,则该部分
25
第7章互感与变压器
7.2.1 图7-8(a)所示电路中,两电感线圈L1、L2串联,它们相
连的端钮是异名端,这种形式的串联称为顺向串联。 根据电路中所设电压、电流参考方向及互感线圈上的电
压、电流关系,可得
u
u1
u2
(L1
di dt
M
di dt
)
(L2
di dt
M
di dt
)
di (L1 L2 2M) dt
为了表示两线圈耦合的紧密程度,引入了一个新的参 数——耦合系数,用字母k表示,定义为
k 21 12 1 1 2 2
(7-3)
6
第7章互感与变压器
由自感系数和互感系数的定义可得
L1
N 1 11 i1
11
L 1 i1 N1
L2
N 2 22 i2
22
L 2i2 N2
式中
ZU I jL1L 1LL 22M 2M 2 jLAB
LAB
L1L2 M2 L1 L2 2M
(7-12)
35
第7章互感与变压器
称为两互感线圈同侧并联时的等效电感,因此可画出图7-
11(a)所示电路的等效电路图,如图7-11(b)所示。
如图7-12(a)所示电路中,两电感线圈L1、L2并联,它们 相连的端钮是异名端,这种形式的并联称为异侧并联。
20
第7章互感与变压器
图7-6 实验法判定同名端电路图
21
第7章互感与变压器 【例7-1】 写出图7-7所示互感线圈端电压u1和u2的表达
解 对于图7-7(a),两耦合线圈的自磁通与互磁通相助,
u1
L1
di1 dt
Mdi2 dt
u2
L2
di2 dt
Mdi1 dt
对于图7-7(b),两耦合线圈的自磁通与互磁通相消,有
电路中电压、电流参考方向如图7-12(a)
KCL
i=i1+i2
(7-13)
u u 1 u 2 L 1d d it1 M d d it2 L 2d d it2 M d d it1
(7-14)
36
第7章互感与变压器
图7-12 电感线圈异侧并联电路图
37
第7章互感与变压器
设外加正弦交流电压u=Umsinωt,则式(7-13)、式(7-14) 可改写成相量形式,即
12
第7章互感与变压器
图7-3 磁通相消电路图
13
第7章互感与变压器
对于电感L1 Ψ1=Ψ11-Ψ12=L1i1-Mi2
对于电感L2 Ψ2=Ψ22-Ψ21=L2i2-Mi1
如图7-3所示,设i1与u1、i2与u2参考方向关联,根据电
对于电感L1
u1dd t1L1d dit1Md dit2u'1u"1
它所产生的变化磁场,将使位于它附近的另一线圈中的磁通 量发生变化,从而激发起感应电压。这种由一个线圈的交变 电流在另一个线圈中产生感应电压的现象叫做互感现象。由
2
第7章互感与变压器 设有相邻放置的两个电感线圈L1、L2,如图7-1所示, 匝数分别为N1和N2,通过的交变电流分别为i1和i2。i1在线圈 L1中产生的自磁通为Φ11,则线圈L1的自磁通链Ψ11=N1Φ11, 同时Φ11的一部分通过线圈L2,称为互磁通Φ21,则线圈L1与 线圈L2的互磁通链Ψ21=N2Φ21。同理有i2在线圈L2中产生的自 磁通为Φ22,自磁通链Ψ22=N2Φ22,与线圈L1的互磁通为Φ12, 互磁通链Ψ12=N1Φ12
31
第7章互感与变压器
图7-10 例7-2图
32
第7章互感与变压器
7.2.2
如图7-11(a)所示电路中,两电感线圈L1、L2并联,它们 相连的端钮是同名端,这种形式的并联称为同侧并联。
电路中电压、电流参考方向如图7-11(a)
KCL
i=i1+i2 根据互感的电压、电流关系,可得
(7-10)
u u 1 u 2 L 1d d it1 M d d it2 L 2d d it2 M d d it1
M N 1 12 N 2 21
i2
i1
代入式(7-3)可得
k M L1 L 2
7
(7-4)
第7章互感与变压器
所以耦合系数为互感系数与两线圈自感系数几何平均值 的比值,是一个无量纲参数。理想情况下无漏磁通,Φ21 =Φ11,Φ12=Φ22,k=1。所以,一般有
k M 1 L1L2
(7-6a)
14
第7章互感与变压器
对于电感L2,有
u2dd t2L2d d it2M d dit1u'2u"2
(7-6b)
所以,当两耦合线圈的自磁通与互磁通相消时,线圈电
压等于自感电压u′与互感电压u″
15
第7章互感与变压器 7.1.2
综上所述,耦合电感线圈上的电压等于自感电压与互感 电压的代数和。在上述内容中,分析电压、电流关系时,给 定了两个条件:①规定了电压与电流的参考方向关联;②已 知线圈的绕向,通过安培定则确定磁通的方向。但是在工程 实践中,线圈的绕制方向从外观上无法看出;且无法画出耦 合电感线圈电路模型,很不方便。所以,为了表示线圈的相 对绕向以确定互感电压的极性,常采用标记同名端的方法。
第7章互感与变压器
第7章 互感与变压器
7.1 互感元件 7.2 互感线圈的串、并联 7.3 理想变压器 7.4 实际变压器 本章小结 阅读材料:涡流现象及其应用 实验11 单相铁芯变压器特性的测试
1
第7章互感与变压器
7.1 互感元件
7.1.1 1.互感的基本概念 两个相邻的载流线圈,当任一线圈中的电流发生变化时,
8
第7章互感与变压器
2.耦合电感线圈上的电压、电流关系
当两个耦合电感线圈上都有电流通过时,在L1中,若自 磁通Φ11与互磁通Φ12方向相同,则称为磁通相助;同理,在 L2中,若自磁通Φ22与互磁通Φ21方向相同,磁通也相助。即 两耦合线圈的自磁通与互磁通方向相同,如图7-2所示。
根据自感和互感的定义,有以下关系式
16
第7章互感与变压器 1 如图7-4(a)所示,i1与u1、i2与u2参考方向关联,两个电 感线圈L1、L2磁通相助,所产生的磁通是相互增强的,那么, 两电流同时流入(或流出)的端钮a和c就是同名端,用标记“·” 或“*”表示。当电感线圈L2的绕制方向发生变化时,要使 两线圈的磁通相助,则电压、电流方向应如图7-4(b)所示。 根据上述分析,同名端的定义为自感电压与互感电压极 性相同的端钮。因此,可将图7-4所示的耦合电感线圈用图 7-5
LAB
di dt
(7-7)
26
第7章互感与变压器
图7-8 电感顺向串联电路图
27
第7章互感与变压器
式(7-7)中
Lab=L1+L2+2M
(7-8)
称为两互感线圈顺向串联时的等效电感,因此可画出图7-
8(a)所示电路的等效电路图,如图7-8(b)
图7-9(a)所示电路中,两电感线圈L1、L2串联,它们相
L1i1 11,L2i2 2
2,M 21 12 i1 i2
对于电感L1
Ψ1=Ψ11+Ψ12=L1i1+Mi2
