电路分析第11章 耦合电路和理想变压器
电路分析 耦合电路和理想变压器36页PPT

6
、
露
凝
无
游
氛
,
天
高
风
景
澈
。
7、翩翩新 来燕,双双入我庐 ,先巢故尚在,相 将还旧居。
8
、
吁
嗟
身
后
名
,
于
我
若
浮
烟
。
9、 陶渊 明( 约 365年 —427年 ),字 元亮, (又 一说名 潜,字 渊明 )号五 柳先生 ,私 谥“靖 节”, 东晋 末期南 朝宋初 期诗 人、文 学家、 辞赋 家、散
1
0
、
倚
南
窗
以
寄
傲
,
审
容
膝
之
易
安
。
61、奢侈是舒适的,否则就不是奢侈 。——CocoCha nel 62、少而好学,如日出之阳;壮而好学 ,如日 中之光 ;志而 好学, 如炳烛 之光。 ——刘 向 63、三军可夺帅也,匹夫不可夺志也。 ——孔 丘 64、人生就是学校。在那里,与其说好 的教师 是幸福 ,不如 说好的 教师是 不幸。 ——海 贝尔 65、接受挑战,就可以享受胜利的喜悦 。——杰纳勒 尔·乔治·S·巴顿
文 家 。汉 族 ,东 晋 浔阳 柴桑 人 (今 江西 九江 ) 。曾 做过 几 年小 官, 后辞 官 回家 ,从 此 隐居 ,田 园生 活 是陶 渊明 诗 的主 要题 材, 相 关作 品有 《饮 酒 》 、 《 归 园 田 居 》 、 《 桃花 源 记 》 、 《 五 柳先 生 传 》 、 《 归 去来 兮 辞 》 等 。
谢谢!
Hale Waihona Puke
第11章 耦合电感和理想变压器PPT课件

u1
2 2221
i2 u2
11、 22为自感磁通链,21、 12为互感磁通链。 L1、L2分别为线圈1和线圈2的自感,M21、 M12为耦 合电感的互感。可以证明M21=M12=M。
第1个线圈总的磁通链为 1= 11+ 12=L1 i1+M i2 第2个线圈总的磁通链为 2= 22+ 21 =L2 i2+M i1
第十一章 耦合电感和理想变压器
• 11.1 耦合电感元件 • 11.2 含耦合电感正弦稳态电路的分析 • 11.3 空芯变压器 • 11.4 理想变压器 • 11.5 铁芯变压器的模型 • 11.6 例题
返回目录
11.1 耦合电感元件
1
一. 互感和互感压降 11
11 L 1 i1, 21 M 2i112 22 L 2 i2, 12 M 1i2 2 i1
u 2 L 2d 2d i M t d 1d i t
6
例2:右图电路中,已知L1=4H, L2=3H,M=2H ,求
以下3种情况的 u2 。
+ i1
i2
+
M
( 1 )i1 5 e 4 t(A ),i2 0 (A )u 1 L 1
L2 u2
( 2 )i1 0 (A ),i2 3 e 4 t(A ) -
2
若取各线圈电压与电流为关联参考方向,则:
u 1 d 1d L t 1 d 1d i M td 2d i t u 2 d 2d L t 2 d 2d i M td 1 d i t
自感压降
互感压降
二. 互感压降的正负号 11 1
12
1= 11- 12=L1 i1-M i2 2= 22- 21 =L2 i2-M i1
李瀚荪《电路分析基础》(第4版)章节题库-第11章 耦合电感和理想变压器【圣才出品】

第11章 耦合电感和理想变压器一、选择题1.如图11-1所示是一个全耦合的耦合电感元件,其两个绕组L1=L2=1H,两绕组串联连接,通过的电流i=1 A,耦合电感元件所储磁能为()J。
图11-1A.0.5B.1C.2D.0【答案】D2.如图11-2所示耦合电感电路中,其去耦等效电路为()。
图11-2A.B.C.D.【答案】B3.如图11-3所示含理想变压器的电路中,欲使负载电阻R。
获得最大功率,则变比n和所获得的最大功率值为()。
图11-3【答案】A【解析】欲使负载电阻R。
获得最大功率,则负载电阻折算到理想变压器原边后的等效电阻应等于电源内阻,即故可求出n=2。
此时负载电阻所获得的最大功率为4.两个自感系数为L1、L2的耦合电感,其互感系数M的最大值为()。
A.L1L2B.C.D.【答案】D5.如图11-4所示含理想变压器电路的输入电阻为()Ω。
图11-4【答案】C【解析】设参考电流如图11-5所示。
由图11-5有所以 图11-5二、填空题1.如图11-6所示电路中,已知线性非时变耦合电感L1=4 H,L2=3 H,M=2 H,则从A、B端看进去的等效电感L AB为______H。
图11-6【答案】38【解析】对图11-6所示电路进行互感去耦等效,可得如图11-7所示的等效电路,有等效电感L AB=5×(-2)/5+(-2)+6=8/3H。
图11-72.如图11-8所示电路的等效电感L ab=______H。
图11-8【答案】73.如图11-9所示含耦合电感的电路中,若L=M,则电路的入端(复)阻抗为______。
图11-9【答案】三、计算题1.如图11-10所示含耦合电感电路中,互感M=30H,t=0时S闭合,试求t≥0时的一次电流i1和二次电流i2。
图11-10解:如图11-10所示电路中的耦合电感为全耦合电感,其等效电路如图11-18.1所示,其中图11-11(a )可表示成图11-11(b )所示等效电路。
电路分析第11章耦合电路和理想变压器

M
i2
2H 1
+ u1 –
1H
M 0.5 2
列回路方程
I1
I2
j2 1 + jMI1 –
jI1 j0.5 2I 2 U (1 j 2 ) I2 j0.5 2I1 0
j 1.5 2 U ( ) I1 1 j 2 U j 1.5 2 I 1 j 2
R1 I1 jM
US
+ – jL1
1 jC
I 2 R2
解:回路法
( R1 jL1 1 ) I1 jMI 2 U S jC 1 ( R2 jL2 ) I 2 jMI1 0 jC
jL2 1 jC
R1 I1
US
jL1 – – jMI 2 + +
uM 2
di1 dt
uM 2 di1 M 21 dt
4
di M 21 1 dt
2.互电感 i1
+
Φ12
i2
+
自感电压
uL 2
di2 L2 dt
dt
u1
-
Φ 22 Φ22
u2
-
互感电压 u M di2 M1 12
uM 1 M 12 di2 dt
i2 流过第二个线圈产生自感磁通Φ22, 其磁链Ψ22=L2i2且 在第一个线圈产生互感磁通Φ12, 其磁链Ψ12=M12i2 M12=M21=M
M称为互电感,单位亨利(H)
5
2.互电感 i1
+
Φ12 i2
+ +
Φ21 i1
u2
-
电路分析基础ppt第11章 耦合电感

j ( L1 L2 2 M ) I Z I jLI L
+
U
I
. . jL jL
1
jM
2
等效电感
L L1 L2 2 M
等效感抗 Z L jL
通过测量顺接串联和反接串联时的电流I ,可判别同名端。 .
第十一章 耦合电感和理想变压器
§11-1 §11-2 基本概念 耦合电感的VCR 耦合系数
电路分析基础
§11-3
§11-4
空心变压器的电路分析 反映阻抗
耦合电感的去耦等效电路
§11-5
§11-6 §11-7 §11-8
理想变压器的VCR
理想变压器的阻抗变换性质 理想变压器的实现 铁心变压器的模型
§11-2耦合电感的VCR 耦合系数 …. 电路分析基础
第十一章 耦合电感和理想变压器
§11-2耦合电感的VCR 耦合系数 …. 电路分析基础
3. 耦合系数
1 2 w L (t ) Li L (t ) 0 2 L1 L2 M 2 L 0 L1 L2 M 2 0 L1 L2 2 M
M L1 L2
M L1 L2 1
1
第十一章
耦合电感和理想变压器
电路分析基础 §11-3 空心变压器电路的分析 反映阻抗…..
二、反映阻抗法
若令
则
.. 初级自阻抗 次级自阻抗 ①
Z 11 R1 jL1 Z 22 R2 jL2 Z L jMI U Z I
11 1 2 S
+
i1
M
u1
. . L L
1
第十一章 耦合电感和理想变压器

§11-5 理想变压器的VCR
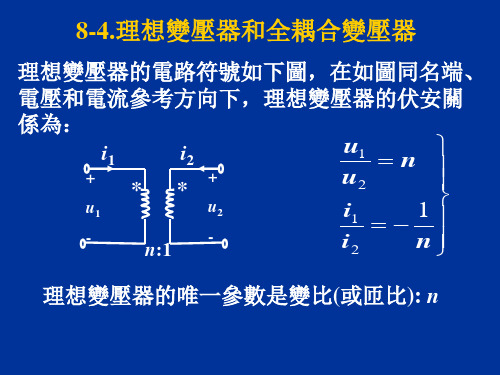
一.理想变压器的概念:实际铁心变压器的理想化模型。 1、理想变压器满足三个条件: 1)变压器本身无损耗;这意味着绕线圈的金属导线无任何电 阻,做芯的铁磁材料的磁导率μ无穷大。 2)耦合系数k=1。 3)L1,L2,M趋于无穷大,但L1/L2为常数。 2、理想变压器的电路符号:理想变压器的定义式(VCR):
作业:P183 11-8
§11-4 耦合电感的去耦等效电路
对于在一个公共端钮相连接的一对耦合电感,如图(a)所示, 可以用三个电感组成的T形网络来作等效替换,如图(b)所示。 下面来推导这种网络等效替换的关系。 1.同侧连接——同名端相连时等效的推导:
图(a)所示耦合电感,其端钮的VCR为:
而在T形等效电路中,由KVL得:
比较 值应为
前面的系数,即可求得T形等效电路中各电感
2.异侧连接-异名端相连:
La L1 M L M b L L M 2 c
小结:上述的这种等效消除了原电路中的感应耦合——互 感,称为去耦等效。替换后的电路即可作为一般无互感电路 来分析计算,但使用范围有限,需记忆公式。
故得 由此可见,把电阻RL接在理想变压器的次级,变压器初级
端的输入电阻即为RL /n2。理想变压器起着改变电阻大小的作用, 把RL变换为RL/ n2 。
正弦稳态时,若次级所接阻抗为ZL(jω),则初级的输入阻 抗,或次级ZL 对初级的折合阻抗为
因此,理想变压器有改变电阻或阻抗的性质。
二.阻抗变换性质的应用
3、掌握理想变压器的变压、变流、变阻抗的三个主要
性能,熟练求解含有理想变压器的电路。
磁耦合线圈在电子工程、通信工程和测量仪 器等方面得到了广泛应用。为了得到实际耦合线 圈的电路模型,现在介绍一种动态双口元件—— 耦合电感,并讨论含耦合电感的电路分析。 在介绍耦合电感元件以前,下面先用示波
李瀚荪 电路分析基础第十一章(耦合电感和理想变压器)

例题
11-13
已知U S 150 V, I 1、I 2 。 求
I 1 15Ω j5Ω I2 j15Ω -j20Ω
I1
15Ω
+
US
+
j10Ω
j 10Ω
-
-
Us
Zref
解 (a) 求 I 1 2M 2 回路2对回路1 Z ref
Z 22
52 25 j5 j15 j20 j5
§2-2 耦合系数
1
11-8 (b)
φ12
i1
(a)
φ21
+
+
φs1
2
1
i2 N2
+
2
u1 N1
1'
N2 u(开路) 2
开路
N1
线圈Ⅰ
φs2
-
-2
线圈Ⅰ 线圈Ⅱ
'
1'
-2
线圈Ⅱ
'
11 21 S1 22 12 S 2 当 S1、 S 2 均为零时全耦合——耦合的上限,M的上限。
2 2
' i 1 i1 + + u1 L1 u1 - iφ -
+
1:n
i2
R
u2
-
U1 1 I I I1 I2 1 jL1 n 0.24 j0.2 0.312 39.8A
d u1 N1 dt 故得 u2
11 22 d u N
2 2
nu1
dt
(11-31)
11-23
(b)理想变压器 u1并不取决于 i1或 i2,只取决于 u2。 同样, i1只取决于 i2,与u1 、u2无关。 设想在一次侧施加电压u1,并使二次侧开路,则i2=0 从而i1也必须为零。在非零u1下,L1应→∞。类似地可说 明L2→∞。 (c)采取技术措施可力争实现上述两条件。 设计精良的变压器可认为是理想的; 一般变压器 也可用理想变压器为核心构成它的模型。
电路课件-理想变压器和全耦合变压器
1 n2
Z1
1 n2 Z2
N
b n:1
d
由理想變壓器
c Z3
的VCR,簡化 -
成沒有變壓器 的電路。
1 n
U+S
1 n2 Z1
1 n2 Z2
N
d
理想變壓器還可由一個初級線圈與多個次級 線圈構成。
i1 n1:1 * i2 +
+
N2 u2
*
-
u1 - N1
* i3 +
n2:1 N3
u3 -
在圖示電壓,電流參考 R2方向下,有
1. 並聯阻抗可以從次級搬移到初級; 2.串聯阻抗可以從初級搬移到次級。 阻抗可以從初級與次級之間來回搬移。
1. 並聯阻抗可以從次級搬移到初級;
a I1
I2 I2 ' c
+
U1
*
*U+ 2
I2"
Z2
N
-
-
b n:1
d
a I1 I1'
I2 ' c
+
U1 n2 Z2
-
*
*
+
U 2
-
N
b
n:1 d
(a)
I2(
ZL '
cosL )
( RS
ZL'
U
2 S
ZL'
cos L
cosL )2 ( XS
ZL'
sin L )2
要使P達到最大,必須
dP d( ZL
')
0,即
Z
L
'=
ZS
這時,負載獲得最大功率。這種情況稱為 “模匹配”。模匹配時負載中電阻吸收的功 率一般比達到共軛匹配時的功率小。這時
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
二பைடு நூலகம் 耦合系数
i1在线圈L1产生自感磁链 Ψ11= N111= L1i1 在线圈L2产生互感磁链 Ψ21= N221= Mi1 1 +
i1
M
i2
+
2
i2 在线圈L2产生自感磁链 Ψ22 = N222= L2i2 – 在线圈L1产生互感磁链 Ψ12 = N112= Mi2 1´ 在极限情况下, 21= 11, 12= 22,即每一线圈产 生的磁通全部与另一线圈交链,这种耦合称为全耦合。
第11章 耦合电感和理想变压器
§11-1 §11-2 §11-3 §11-4 §11-5 基本概念 耦合电感的VCR 耦合系数 空心变压器电路的分析 反映阻抗 耦合电感的去耦等效电路 理想变压器的VCR
§11-6 理想变压器的阻抗变换性质 §11-7 理想变压器的实现 §11-8 铁心变压器的模型
di2 di M M 1 – dt – – dt – 2´ 1´
u1
u2
1 +
I1
I2 0
+
2
1 +
I1
I2
+
2
U1 jL1 – 1´
jL2 U 2 – 2´
jL1 U1 + jMI 2 – – 1´
jL2 U 2 + jMI1 – 2´ –
U 1 jL1 I1 jMI 2
– 初级回路
2M 2
Z22
2 M 2 称为次级回路在初
Z22
级回路的反映阻抗
2.用反映阻抗计算
Z11=R1+jL1 Z22=R2+ RL+ jL2 Z12= Z21= jM
R1
R2 jL2 RL + jMI1 –
jL1 Us + – jMI 2 –
+ Z11
I1
§11-1 基本概念
一.电感元件 N i + u – + u –
i
磁链 =N =L i
– i eL L 单位: —韦伯(Wb), + i—安培,L—亨利(H)
自电感 L= N
L称为自电感或自感。线圈的匝数N 越多,其电感 越大;线圈中单位电流产生的磁通越大,电感也越大。 在图示u、i、e假定参考方向的前提下,当通过线 圈的磁通或i 发生变化时,线圈中产生感应电动势为
I2
I1
Us Z11
2M 2
Z22
I1
+
Us
– 初级回路
2M 2
Z22
次级电流和初级电流的关系
jMI1 ( R2 RL jL2 ) I2 0
jMI1 I2 Z22
3.用戴维南定理分析
将RL断开, I2 0
I10 R1 jL1 Us U OC jMI10
绕组的同名端
同名端:绕在同一铁心上的两个绕组,在工作磁通作 用下,在任何瞬时感应电动势的极性都相同的两个对 应端。用“● ”标出。
① ② ③ Ⅱ ④ ⑤ Ⅲ ⑥
●
●
●
绕组的同名端
对于绕向已知的两个绕组,可以根据右手螺旋法 则判别。如果电流在铁心中所产生的磁通方向一致, 这两端便是同名端。
i A
X a x • i •
k=0.5
–
j2I1
•
+
I1
6
=5×1.09cos 17.6°
=5.19W
50oV
j2 –j5 –
1 I
•
I2 +
•
U
4 –
•
+
耦合电感串联联接时的等效电感 (见P156 例11-3) 1. 顺接串联:异名端相接 i a i
a + M +
u L1
b –
u
L2
M
L1 di +
dt –
–
L2
•
6
5
50 V
j2I2 – +
•
–j5 – o +
1
+
4 U –
•
•
5
•
I1
6
j2
I1=(0.49+j0.46)A
• I2=(0.55–j0.13)A
•
50oV
–j5 – +
– j8 1
j2I1
+
I2 +
•
U
4 –
•
例:图示正弦稳态电路中,k为耦合系数,求(1)U; (2)电路消耗的功率P。(12分)
I 10
+
R1 jL1 Us + – jMI 2 – R1
R2 I 2
+
将uS置零,在开路处外加电压源, 可等效看作初级与次级颠倒。
M
2
2
Z11
为初级回路在次级 回路的反映阻抗
I1
jL2 U OC + jMI10 – – R2 I 2 +
jL2 U + jMI1 – –
1
A • •
X a
x
同名端
2
绕组的同名端
对于绕向已知的两个绕组,可以根据右手螺旋法 则判别。如果电流在铁心中所产生的磁通方向一致, 这两端便是同名端。
i • i •
1
A •
A X a
X a
同名端
•
x
2
x
二. 根据同名端确定互感电压的正负 如果电流的参考方向由线圈 的同名端指向另一端, 那么由这个电流在另一个线圈中产生的互感电压的 参 考方向也应该由线圈的同名端指向另一端。 i1
jL2 U 2 – jMI1 – + 2´
di1 di2 u1 L1 M dt dt di2 di1 u2 L2 M dt dt
U 1 jL1 I1 jMI 2 U 2 jL2 I 2 jMI1
例:求图示电路中的开路电压Uab。(4分)
•
解: I1=(0.49+j0.46)A
• I2=(0.55–j0.13)A
•
• 6
U=
• •
•
• –4I2=(– •
2.2+j0.52)V
I=I1+I1=(1.04+j0.33)A
=1.09∠17.6°A P =USIcos
j2I2 – +
• •
• j8 j2 + 1 • –j5 4 U – – 50oV + j8
0≤k≤1:
k >0.5 紧耦合 k=0 无耦合
例:图示正弦稳态电路中,k为耦合系数,求(1)U; (2)电路消耗的功率P。(12分) —— k=0.5 解: M=k√L1L2 • • ——— j8 j2 jM=jk√L1L2=j0.54=j2 用网孔分析法
• • • (7+j2–j5)I1+(1–j5)I2+j2I2= • • • (1–j5)I1+j2I1+(5+j8–j5)I2= • • (7–j3)I1+(1–j3)I2= 5 • • (1–j3)I1+(5+j3)I2= 5
d eL = N dt = L di dt
u= – eL = L di dt
变压器的工作原理
i1 +
2
S +e + – 2 +e2 – u2 –
i2 |Z |
u1
–
– e1+ e1– +
1
N1
N2
→e1
u1 → i1( i1N1)
1→ e1
e2
i2 (i2N2 ) → 2→ e2
di M dt +
b–
di di di di di uab L1 M L2 M ( L1 L2 2 M ) dt dt dt dt dt
di uab L dt
等效电感 L=L1+L2+2M
正弦稳态时,顺接等效阻抗 Z=jω(L1+L2+2M )
耦合电感串联联接时的等效电感 (见P156 例11-3) 2. 反接串联:同名端相接 i i a M a +
u1
1´
di2 + + di1 M M – dt – – dt – 2´
u2
di1 di2 u1 L1 M dt dt di2 di1 u2 L2 M dt dt
一.耦合电感的VCR M i2 i1
1 + –
1
i1
+ L1 ++ L2
i2
+
+
2
2
u1 L1
1´
L2 u2 – 2´ jM
U 2 jL2 I 2 jMI1
一.耦合电感的VCR
1
i1
+ –
M i 2 +
2
u1 L1
1´ 1
L2 u2 – 2´
i1
+ L1
L2
i2
+
2
1 +
I1
I2
+
2
u1
1´
di2 – – di1 M M – dt + + dt – 2´
u2
jL1 U1 – jMI 2 – + 1´
di1 u2 M dt
三. 互感电压用附加的电压源代替
1
i1
+ –
M
