2017年秋冀教版七年级上2.6角的大小同步练习及答案

合集下载

冀教版初中数学七年级上册《2.6 角的大小》同步练习卷

冀教新版七年级上学期《2.6 角的大小》同步练习卷一．选择题（共50小题）1．如图，∠AOB是平角，∠AOC＝50°，∠BOD＝60°，OM平分∠BOD，ON 平分∠AOC，则∠MON的度数是（）A．135°B．155°C．125°D．145°2．如图，将一副三角板叠放在一起，使直角的顶点重合于O，则∠AOC+∠DOB ＝（）A．90°B．120°C．160°D．180°3．如图，OB是∠AOC的角平分线，OD是∠COE的角平分线，如果∠AOB＝40°，∠COE＝60°，则∠BOD的度数为（）A．50°B．60°C．65°D．70°4．如图，点B，O，D在同一直线上，若∠1＝15°，∠2＝105°，则∠AOC的度数是（）A．75°B．90°C．105°D．125°5．若一个60°的角绕顶点旋转15°，则重叠部分的角的大小是（）A．15°B．30°C．45°D．75°6．已知∠AOB＝70°，以O为端点作射线OC，使∠AOC＝42°，则∠BOC的度数为（）A．28°B．112°C．28°或112°D．68°7．已知∠AOB＝30°，又自∠AOB的顶点O引射线OC，若∠AOC：∠AOB＝4：3，那么∠BOC＝（）A．10°B．40°C．70°D．10°或70°8．把两块三角板按如图所示那样拼在一起，则∠ABC等于（）A．90°B．100°C．105°D．120°9．如图，OC是∠AOB的平分线，OD是∠AOC的平分线，且∠COD＝25°，则∠AOB等于（）A．50°B．75°C．100°D．120°10．把两块三角板按如图所示那样拼在一起，则∠ABC等于（）A．70°B．90°C．105°D．120°11．如图，一副三角板（直角顶点重合）摆放在桌面上，若∠AOD＝150°，则∠BOC等于（）A．30°B．45°C．50°D．60°12．如图，∠AOC和∠DOB都是直角，如果∠AOB＝150°，那么∠DOC＝（）A．30°B．40°C．50°D．60°13．如图所示，已知O是直线AB上一点，∠1＝40°，OD平分∠BOC，则∠2的度数是（）A．20°B．25°C．30°D．70°14．如图，∠AOB是一直角，∠AOC＝40°，OD平分∠BOC，则∠AOD等于（）A．65°B．50°C．40°D．25°15．如图，点C、O、B在同一条直线上，∠AOB＝90°，∠AOE＝∠DOB，则下列结论：①∠EOD＝90°；②∠COE＝∠AOD；③∠COE＝∠DOB；④∠COE+∠BOD＝90°．其中正确的个数是（）A．1B．2C．3D．416．如图，点O在直线AB上，若∠AOD＝159.5°，∠BOC＝51°30′，则∠COD的度数为（）A．30°B．31°C．30°30′D．31°30′17．如图，小明将自己用的一副三角板摆成如图形状，如果∠AOB＝155°，那么∠COD等于（）A．15°B．25°C．35°D．45°18．如图，已知∠AOB是直角，∠AOC是锐角，ON平分∠AOC，OM平分∠BOC，则∠MON是（）A．45°B．45°+∠AOC C．60°﹣∠AOC D．不能计算19．已知∠AOB＝70°，以O端点作射线OC，使∠AOC＝28°，则∠BOC的度数为（）A．42°B．98°C．42°或98°D．82°20．如图，已知∠COB＝2∠AOC，OD平分∠AOB，且∠COD＝20°，则∠AOB ＝（）A．40°B．60°C．120°D．135°21．如图，已知直线AB和CD相交于O点，∠COE是直角，OF平分∠AOE，∠COF＝34°，则∠BOD的大小为（）A．22°B．34°C．56°D．90°22．如图是我们常用的一副三角板．用一副三角板可以拼出的角度是（）A．70°B．135°C．140°D．55°23．如图，已知∠AOC＝∠BOD＝90°，∠AOD＝150°，则∠BOC的度数为（）A．30°B．45°C．50°D．60°24．如图，∠AOC＝∠BOD＝80°，如果∠AOD＝140°，那么∠BOC等于（）A．20°B．30°C．50°D．40°25．用一副三角尺，你能画出下面那个度数的角（）A．65度B．105度C．85度D．95度26．用一副三角板不能画出下列那组角（）A．45°，30°，90°B．75°，15°，135°C．60°，105°，150°D．45°，80°，120°27．一副三角板如图所示放置，则∠AOB等于（）A．120°B．90°C．105°D．60°28．已知∠AOB＝3∠BOC，若∠BOC＝30°，则∠AOC等于（）A．120°B．120°或60°C．30°D．30°或90°29．已知∠AOB＝30°，∠BOC＝50°，那么∠AOC＝（）A．20°B．80°C．20°或80°D．30°30．如图，点O在直线AB上，若∠AOD＝160°，∠BOC＝60°，则∠COD的度数为（）A．20°B．30°C．40°D．50°31．如图所示，已知∠AOC＝∠BOD＝70°，∠BOC＝30°，则∠AOD的度数为（）A．100°B．110°C．130°D．140°32．若∠1＝40.4°，∠2＝40°4′，则∠1与∠2的关系是（）A．∠1＝∠2B．∠1＞∠2C．∠1＜∠2D．以上都不对33．如图．∠AOB＝∠COD，则（）A．∠1＞∠2B．∠1＝∠2C．∠1＜∠2D．∠1与∠2的大小无法比较34．在∠AOB的内部任取一点C，作射线OC，则一定存在（）A．∠AOB＞∠AOC B．∠AOB＜∠BOC C．∠BOC＞∠AOC D．∠AOC＞∠BOC35．已知∠1＝17°18′，∠2＝17.18°，∠3＝17.3°，下列说法正确的是（）A．∠1＝∠2B．∠1＝∠3C．∠1＜∠2D．∠2＞∠3 36．若∠1＝20°18′，∠2＝20°15′30′′，∠3＝20.25°，则（）A．∠1＞∠2＞∠3B．∠2＞∠1＞∠3C．∠1＞∠3＞∠2D．∠3＞∠1＞∠2 37．如图，在此图中小于平角的角的个数是（）A．9B．10C．11D．1238．下列说法正确的个数是（）（1）连接两点之间的线段叫两点间的距离；（2）两点之间，线段最短；（3）若AB＝2CB，则点C是AB的中点；（4）角的大小与角的两边的长短无关．A．1个B．2个C．3个D．4个39．如图，如果∠CAE＞∠BAD，那么下列说法中一定正确的是（）A．∠BAC＞∠CAD B．∠DAE＞∠CADC．∠CAE＜∠BAC+∠DAE D．∠BAC＜∠DAE40．如图，AOE是一条直线，图中小于平角的角共有（）A．4个B．8个C．9个D．10个41．若∠A＝30°18′，∠B＝30°15′30″，∠C＝30.25°，则这三个角的大小关系正确的是（）A．∠C＞∠A＞∠B B．∠C＞∠B＞∠A C．∠A＞∠C ＞∠B D．∠A＞∠B＞∠C42．已知α＝76°5′，β＝76.5°，则α与β的大小关系是（）A．α＞βB．α＝βC．α＜βD．以上都不对43．若∠A＝20°18′，∠B＝1212′，∠C＝20.25°，则（）A．∠A＞∠B＞∠C B．∠B＞∠A＞∠C C．∠A＞∠C ＞∠B D．∠C＞∠A＞∠B44．已知∠A＝40°18′，∠B＝40°17′30″，∠C＝40.18°，则（）A．∠A＞∠B＞∠C B．∠B＞∠A＞∠C C．∠C＞∠A ＞∠B D．∠A＞∠C＞∠B45．如图，若∠AOB＝∠COD，那么（）A．∠1＞∠2B．∠1＜∠2C．∠1＝∠2D．∠1、∠2的大小不确定46．如图，∠AOB＝∠COD，则∠AOC与∠DOB的大小关系是（）A．∠AOC＞∠DOBB．∠AOC＜∠DOBC．∠AOC＝∠DOBD．∠AOC与∠DOB无法比较大小47．如图，若∠AOC＝∠BOD，那么∠AOD与∠BOC的关系是（）A．∠AOD＞∠BOC B．∠AOD＜∠BOC C．∠AOD＝∠BOC D．无法确定48．如果∠α＝55.5°，∠β＝55°5′，那么∠α与∠β之间的大小关系是（）A．∠α＞∠βB．∠α＜∠βC．∠α＝∠βD．无法确定49．下列角度中，比20°小的是（）A．19°38′B．20°50′C．36.2°D．56°50．若∠A＝20°18′，∠B＝20°16″，∠C＝20.25°，则有（）A．∠A＞∠B＞∠C B．∠B＞∠A＞∠C C．∠A＞∠C ＞∠B D．∠C＞∠A＞∠B冀教新版七年级上学期《2.6 角的大小》2018年同步练习卷参考答案与试题解析一．选择题（共50小题）1．如图，∠AOB是平角，∠AOC＝50°，∠BOD＝60°，OM平分∠BOD，ON 平分∠AOC，则∠MON的度数是（）A．135°B．155°C．125°D．145°【分析】根据条件可求出∠COD的度数，利用角平分线的性质可求出∠MOC与∠DON的度数，最后根据∠MON＝∠MOC+∠COD+∠DON即可求出答案．【解答】解：∵∠AOC+∠COD+∠BOD＝180°，∴∠COD＝180°﹣∠AOC﹣∠COD＝70°，∵OM、ON分别是∠AOC、∠BOD的平分线，∴∠MOC＝∠AOC＝25°，∠DON＝∠BOD＝30°，∴∠MON＝∠MOC+∠COD+∠DON＝125°，故选：C．【点评】本题考查角度计算，解题的关键是熟练利用角分线的性质，本题属于基础题型．2．如图，将一副三角板叠放在一起，使直角的顶点重合于O，则∠AOC+∠DOB ＝（）A．90°B．120°C．160°D．180°【分析】因为本题中∠AOC始终在变化，因此可以采用“设而不求”的解题技巧进行求解．【解答】解：设∠AOD＝a，∠AOC＝90°+a，∠BOD＝90°﹣a，所以∠AOC+∠BOD＝90°+a+90°﹣a＝180°．故选：D．【点评】本题考查了角度的计算问题，在本题中要注意∠AOC始终在变化，因此可以采用“设而不求”的解题技巧进行求解．3．如图，OB是∠AOC的角平分线，OD是∠COE的角平分线，如果∠AOB＝40°，∠COE＝60°，则∠BOD的度数为（）A．50°B．60°C．65°D．70°【分析】先根据OB是∠AOC的角平分线，OD是∠COE的角平分线，∠AOB ＝40°，∠COE＝60°求出∠BOC与∠COD的度数，再根据∠BOD＝∠BOC+∠COD即可得出结论．【解答】解：∵OB是∠AOC的角平分线，OD是∠COE的角平分线，∠AOB＝40°，∠COE＝60°，∴∠BOC＝∠AOB＝40°，∠COD＝∠COE＝×60°＝30°，∴∠BOD＝∠BOC+∠COD＝40°+30°＝70°．故选：D．【点评】本题考查的是角的计算，熟知角平分线的定义是解答此题的关键．4．如图，点B，O，D在同一直线上，若∠1＝15°，∠2＝105°，则∠AOC的度数是（）A．75°B．90°C．105°D．125°【分析】由图示可得，∠2与∠BOC互补，结合已知可求∠BOC，又因为∠AOC ＝∠COB+∠1，即可解答．【解答】解：∵∠2＝105°，∴∠BOC＝180°﹣∠2＝75°，∴∠AOC＝∠1+∠BOC＝15°+75°＝90°．故选：B．【点评】本题考查了角的计算，解决本题的关键是利用补角求出∠BOC．5．若一个60°的角绕顶点旋转15°，则重叠部分的角的大小是（）A．15°B．30°C．45°D．75°【分析】先画出图形，利用角的和差关系计算．【解答】解：∵∠AOB＝60°，∠BOD＝15°，∴∠AOD＝∠AOB﹣∠BOD＝60°﹣15°＝45°，故选：C．【点评】本题考查了角的计算，注意先画出图形，利用角的和差关系计算．6．已知∠AOB＝70°，以O为端点作射线OC，使∠AOC＝42°，则∠BOC的度数为（）A．28°B．112°C．28°或112°D．68°【分析】根据题意画出图形，利用数形结合求解即可．【解答】解：如图，当点C与点C1重合时，∠BOC＝∠AOB﹣∠AOC＝70°﹣42°＝28°；当点C与点C2重合时，∠BOC＝∠AOB+∠AOC＝70°+42°＝112°．故选：C．【点评】本题考查的是角的计算，在解答此题时要注意进行分类讨论，不要漏解．7．已知∠AOB＝30°，又自∠AOB的顶点O引射线OC，若∠AOC：∠AOB＝4：3，那么∠BOC＝（）A．10°B．40°C．70°D．10°或70°【分析】OC可以在OA的外侧，也可以在OB的外侧，所以要分两种情况考虑．【解答】解：∵∠AOB＝30°，∠AOC：∠AOB＝4：3，∴∠AOC＝40°当OC在OA的外侧时，∠BOC＝∠AOC+∠AOB＝40°+30°＝70°；当OC在OB的外侧，∠BOC＝∠AOC﹣∠AOB＝40°﹣30°＝10°．故选：D．【点评】解答本题要注意注意两种情况的考虑：OC可以在OA的外侧，也可以在OB的外侧．8．把两块三角板按如图所示那样拼在一起，则∠ABC等于（）A．90°B．100°C．105°D．120°【分析】∠ABC等于30度角与直角的和，据此即可计算得到．【解答】解：∠ABC＝30°+90°＝120°．故选：D．【点评】本题考查了角度的计算，理解三角板的角的度数是关键．9．如图，OC是∠AOB的平分线，OD是∠AOC的平分线，且∠COD＝25°，则∠AOB等于（）A．50°B．75°C．100°D．120°【分析】根据角的平分线定义得出∠AOD＝∠COD，∠AOB＝2∠AOC＝2∠BOC，求出∠AOD、∠AOC的度数，即可求出答案．【解答】解：∵OC是∠AOB的平分线，OD是∠AOC的平分线，∠COD＝25°，∴∠AOD＝∠COD＝25°，∠AOB＝2∠AOC，∴∠AOB＝2∠AOC＝2（∠AOD+∠COD）＝2×（25°+25°）＝100°，故选：C．【点评】本题考查了对角平分线定义和角的计算等知识点的应用，主要考查学生运用角平分线定义进行推理的能力和计算能力，题目较好，难度不大．10．把两块三角板按如图所示那样拼在一起，则∠ABC等于（）A．70°B．90°C．105°D．120°【分析】∠ABC等于30度角与直角的和，据此即可计算得到．【解答】解：∠ABC＝30°+90°＝120°．故选：D．【点评】本题考查了角度的计算，理解三角板的角的度数是关键．11．如图，一副三角板（直角顶点重合）摆放在桌面上，若∠AOD＝150°，则∠BOC等于（）A．30°B．45°C．50°D．60°【分析】从如图可以看出，∠BOC的度数正好是两直角相加减去∠AOD的度数，从而问题可解．【解答】解：∵∠AOB＝∠COD＝90°，∠AOD＝150°∴∠BOC＝∠AOB+∠COD﹣∠AOD＝90°+90°﹣150°＝30°．故选：A．【点评】此题主要考查学生对角的计算的理解和掌握，解答此题的关键是让学生通过观察图示，发现几个角之间的关系．12．如图，∠AOC和∠DOB都是直角，如果∠AOB＝150°，那么∠DOC＝（）A．30°B．40°C．50°D．60°【分析】根据图象∠AOB等于两个直角的和减去∠COD计算．【解答】解：∠DOC＝90°+90°﹣∠AOB＝180°﹣150°＝30°．故选A．【点评】本题注意，∠COD是两个直角重叠的部分．13．如图所示，已知O是直线AB上一点，∠1＝40°，OD平分∠BOC，则∠2的度数是（）A．20°B．25°C．30°D．70°【分析】先根据平角的定义求出∠COB的度数，再由OD平分∠BOC即可求出∠2的度数．【解答】解：∵∠1＝40°，∴∠COB＝180°﹣40°＝140°，∵OD平分∠BOC，∴∠2＝∠BOC＝×140°＝70°．故选：D．【点评】本题考查的是平角的定义及角平分线的定义，熟知以上知识是解答此题的关键．14．如图，∠AOB是一直角，∠AOC＝40°，OD平分∠BOC，则∠AOD等于（）A．65°B．50°C．40°D．25°【分析】由∠AOB是一直角，∠AOC＝40°，可知∠COB＝50°，又知OD平分∠BOC，故可知∠AOD的度数．【解答】解：∵∠AOB是一直角，∠AOC＝40°，∴∠COB＝50°，∵OD平分∠BOC，∴∠COD＝25°，∵∠AOD＝∠AOC+∠COD，∴∠AOD＝65°．故选：A．【点评】本题考查角与角之间的运算，注意结合图形，发现角与角之间的关系，进而求解．15．如图，点C、O、B在同一条直线上，∠AOB＝90°，∠AOE＝∠DOB，则下列结论：①∠EOD＝90°；②∠COE＝∠AOD；③∠COE＝∠DOB；④∠COE+∠BOD＝90°．其中正确的个数是（）A．1B．2C．3D．4【分析】结合图形，根据平角的定义、余角的性质和等量代换可以进行判断，注意运用角的和差的运算．【解答】解：∵∠AOB＝90°∴∠AOD+∠BOD＝90°∵∠AOE＝∠DOB∴∠AOE+∠AOD＝90°，即∠EOD＝90°∴∠COE＝∠AOD，∠COE+∠BOD＝90°∴①②④正确．故选：C．【点评】解题时注意运用余角的性质：同角的余角相等．16．如图，点O在直线AB上，若∠AOD＝159.5°，∠BOC＝51°30′，则∠COD的度数为（）A．30°B．31°C．30°30′D．31°30′【分析】将∠AOD转化成159°30′，将其代入∠COD＝∠AOD+∠BOC﹣∠AOB 中，即可求出结论．【解答】解：∵∠AOD＝159.5°＝159°30′，∴∠COD＝∠AOD+∠BOC﹣∠AOB＝159°30′+51°30′﹣180°＝31°．故选：B．【点评】本题考查了角的计算以及度分秒的换算，牢记“将高级单位化为低级单位时乘以60，将低级单位转化为高级单位时除以60”是解题的关键．17．如图，小明将自己用的一副三角板摆成如图形状，如果∠AOB＝155°，那么∠COD等于（）A．15°B．25°C．35°D．45°【分析】利用直角和角的组成即角的和差关系计算．【解答】解：∵三角板的两个直角都等于90°，所以∠BOD+∠AOC＝180°，∵∠BOD+∠AOC＝∠AOB+∠COD，∵∠AOB＝155°，∴∠COD等于25°．故选：B．【点评】本题是对三角板中直角的考查，同时也考查了角的组成．18．如图，已知∠AOB是直角，∠AOC是锐角，ON平分∠AOC，OM平分∠BOC，则∠MON是（）A．45°B．45°+∠AOC C．60°﹣∠AOC D．不能计算【分析】结合图形，根据角的和差，以及角平分线的定义，找到∠MON与∠AOB 的关系，即可求出∠MON的度数．【解答】解：∵OM平分∠BOC，ON平分∠AOC，∴∠MOC＝∠BOC，∠NOC＝∠AOC，∴∠MON＝∠MOC﹣∠NOC＝（∠BOC﹣∠AOC），＝（∠BOA+∠AOC﹣∠AOC），＝∠BOA，＝45°．故选：A．【点评】本题考查了角的计算，属于基础题，此类问题，注意结合图形，运用角的和差和角平分线的定义求解．19．已知∠AOB＝70°，以O端点作射线OC，使∠AOC＝28°，则∠BOC的度数为（）A．42°B．98°C．42°或98°D．82°【分析】根据题意画出图形，利用分类讨论思想求解即可．【解答】解：如图，当点C与点C1重合时，∠BOC＝∠AOB﹣∠AOC＝70°﹣28°＝42°；当点C与点C2重合时，∠BOC＝∠AOB+∠AOC＝70°+28°＝98°．故选：C．【点评】本题考查的是角的计算，在解答此题时要注意进行分类讨论，不要漏解．20．如图，已知∠COB＝2∠AOC，OD平分∠AOB，且∠COD＝20°，则∠AOB ＝（）A．40°B．60°C．120°D．135°【分析】设∠AOC＝x，则∠BOC＝2x，则∠AOD＝1.5x，最后，依据∠AOD﹣∠AOC＝∠COD列方程求解即可．【解答】解：设∠AOC＝x，则∠BOC＝2x，则∠AOD＝1.5x．∵∠AOD﹣∠AOC＝∠COD，∴1.5x﹣x＝20°，解得：x＝40°．∴∠AOB＝3x＝120°．故选：C．【点评】本题主要考查的是角的计算，角平分线的定义，方程思想的应用是解题的关键．21．如图，已知直线AB和CD相交于O点，∠COE是直角，OF平分∠AOE，∠COF＝34°，则∠BOD的大小为（）A．22°B．34°C．56°D．90°【分析】先根据∠COE是直角，∠COF＝34°求出∠EOF的度数，再根据OF 平分∠AOE求出∠AOC的度数，根据对顶角相等即可得出结论．【解答】解：∵∠COE是直角，∠COF＝34°，∴∠EOF＝90°﹣34°＝56°，∵OF平分∠AOE，∴∠AOF＝∠EOF＝56°，∴∠AOC＝56°﹣34°＝22°，∴∠BOD＝∠AOC＝22°．故选：A．【点评】本题考查的是角的计算，熟知角平分线的定义、直角的定义等知识是解答此题的关键．22．如图是我们常用的一副三角板．用一副三角板可以拼出的角度是（）A．70°B．135°C．140°D．55°【分析】一副三角板的度数为30°，60°，90°.45°，可以拼出的角度都是15的倍数，进而可得答案．【解答】解：A、不能拼出70°的角，故此选项错误；B、可以利用90°和45°的角拼出135°的角，故此选项正确；C、不能拼出140°的角，故此选项错误；D、不能拼出55°的角，故此选项错误；故选：B．【点评】此题主要考查了角的计算，关键是掌握三角板各角的度数．23．如图，已知∠AOC＝∠BOD＝90°，∠AOD＝150°，则∠BOC的度数为（）A．30°B．45°C．50°D．60°【分析】由∠AOC＝∠BOD＝90°，∠AOD＝150°，可求出∠BOC的度数，再根据角与角之间的关系求解．【解答】解：∵∠AOC＝∠BOD＝90°，∠AOD＝150°，∴∠BOC＝∠AOC+∠BOD﹣∠AOD＝180°﹣150°＝30°，故选：A．【点评】此题考查的知识点是角的计算，注意此题的解题技巧：两个直角相加和∠BOC相比，多加了∠BOC一次．24．如图，∠AOC＝∠BOD＝80°，如果∠AOD＝140°，那么∠BOC等于（）A．20°B．30°C．50°D．40°【分析】先求出∠COD的度数，然后根据∠BOC＝∠BOD﹣∠COD，即可得出答案．【解答】解：∵∠AOC＝80°，∠AOD＝140°，∴∠COD＝∠AOD﹣∠AOC＝60°，∵∠BOD＝80°，∴∠BOC＝∠BOD﹣∠COD＝80°﹣60°＝20°．故选：A．【点评】本题主要考查了角的计算能力，熟练掌握角相互间的和差关系是基础．25．用一副三角尺，你能画出下面那个度数的角（）A．65度B．105度C．85度D．95度【分析】首先判断出一副三角尺的各个角的度数分别为多少，然后将各个角相加或相减，逐一判断出用一副三角尺能画出的角是多少度即可．【解答】解：用一幅三角尺可以直接画出的角的度数有：30°、45°、60°、90°．A：65度的角不能用一副三角尺画出．B：因为105度＝45度+60度，所以105度的角能用一副三角尺画出．C：85度的角不能用一副三角尺画出．D：95度的角不能用一副三角尺画出．故选：B．【点评】此题主要考查了角的计算，要熟练掌握，解答此题的关键是要明确一副三角尺的各个角的度数，并能根据角的加减法，判断出一个角能不能用一副三角尺画出．26．用一副三角板不能画出下列那组角（）A．45°，30°，90°B．75°，15°，135°C．60°，105°，150°D．45°，80°，120°【分析】A、45°30°90°，可以，B、75°15°135，可以，C、60°105°150，可以，D、45°80°120°，其中80°、120°不能．【解答】解：A、45°，30°，90°，可以，B、75°，15°，135，可以，C、60°，105°，150，可以，D、45°，80°，120°，其中80°、120°不能．故选：D．【点评】本题考查的是角的计算，根据题意提供的角度，画出图形即可解答．27．一副三角板如图所示放置，则∠AOB等于（）A．120°B．90°C．105°D．60°【分析】根据三角板的度数可得：∠2＝45°，∠1＝60°，再根据角的和差关系可得∠AOB＝∠1+∠2，进而算出角度．【解答】解：根据三角板的度数可得：∠2＝45°，∠1＝60°，∠AOB＝∠1+∠2＝45°+60°＝105°，故选：C．【点评】此题主要考查了角的计算，关键是掌握角之间的关系．28．已知∠AOB＝3∠BOC，若∠BOC＝30°，则∠AOC等于（）A．120°B．120°或60°C．30°D．30°或90°【分析】此题需要分类讨论，共两种情况．先作图后计算．【解答】解：∵∠BOC＝30°，∠AOB＝3∠BOC，∴∠AOB＝3×30°＝90°（1）当OC在∠AOB的外侧时，∠AOC＝∠AOB+∠BOC＝90°+30°＝120度；（2）当OC在∠AOB的内侧时，∠AOC＝∠AOB﹣∠BOC＝90°﹣30°＝60度．故选：B．【点评】此题考查的知识点是角的计算，此题计算量不大，但是不能忽略有两种情况．29．已知∠AOB＝30°，∠BOC＝50°，那么∠AOC＝（）A．20°B．80°C．20°或80°D．30°【分析】本题是角的计算的多解问题，求解时要注意分情况讨论，可以根据OA 在∠BOC的位置关系分为OA在∠BOC的内部和外部两种情况求解．【解答】解：①如图1，当OA在∠BOC内部，∵∠AOB＝30°，∠BOC＝50°，∴∠AOC＝∠BOC﹣∠AOB＝20°；②如图2，当OA在∠BOC外部，∵∠AOB＝30°，∠BOC＝50°，∴∠AOC＝∠AOB+∠BOC＝80°；综上所述，∠AOC为20°或80°．故选：C．【点评】本题考查了角的计算，本题只是说出了两个角的度数，而没有指出OC 与∠AOB的位置关系，因此本题解题的关键是根据题意准确画出图形．30．如图，点O在直线AB上，若∠AOD＝160°，∠BOC＝60°，则∠COD的度数为（）A．20°B．30°C．40°D．50°【分析】将∠AOD代入∠COD＝∠AOD+∠BOC﹣∠AOB中，即可求出结论．【解答】解：∵∠AOD＝160°，∠BOC＝60°，∴∠COD＝∠AOD+∠BOC﹣∠AOB＝160°+60°﹣180°＝40°．故选：C．【点评】本题考查了角的计算，将∠AOD代入∠COD＝∠AOD+∠BOC﹣∠AOB 是解题的关键．31．如图所示，已知∠AOC＝∠BOD＝70°，∠BOC＝30°，则∠AOD的度数为（）A．100°B．110°C．130°D．140°【分析】根据图形和题目中的条件，可以求得∠AOB的度数和∠COD的度数，从而可以求得∠AOD的度数．【解答】解：∵∠AOC＝70°，∠BOC＝30°，∴∠AOB＝40°；同理可得，∠COD＝40°．∴∠AOD＝∠AOB+∠BOC+∠COD＝40°+30°+40°＝110°，故选：B．【点评】本题考查角的计算，解答本题的关键是明确角之间的关系，利用数形结合的思想解答．32．若∠1＝40.4°，∠2＝40°4′，则∠1与∠2的关系是（）A．∠1＝∠2B．∠1＞∠2C．∠1＜∠2D．以上都不对【分析】首先同一单位，利用1°＝60′，把∠α＝40.4°＝40°24′，再进一步与∠β比较得出答案即可．【解答】解：∵∠1＝40.4°＝40°24′，∠2＝40°4′，∴∠1＞∠2．故选：B．【点评】此题考查角的大小比较和度分秒之间的换算，在比较角的大小时有时可把度化为分来进行比较．33．如图．∠AOB＝∠COD，则（）A．∠1＞∠2B．∠1＝∠2C．∠1＜∠2D．∠1与∠2的大小无法比较【分析】根据∠AOB＝∠COD，再在等式的两边同时减去∠BOD，即可得出答案．【解答】解：∵∠AOB＝∠COD，∴∠AOB﹣∠BOD＝∠COD﹣∠BOD，∴∠1＝∠2；故选：B．【点评】本题考查了角的大小比较，此题较简单，培养了学生的推理能力．34．在∠AOB的内部任取一点C，作射线OC，则一定存在（）A．∠AOB＞∠AOC B．∠AOB＜∠BOC C．∠BOC＞∠AOC D．∠AOC＞∠BOC【分析】利用角的大小进行比较．【解答】解：射线OC在∠AOB的内部，那么∠AOC在∠AOB的内部，且有一公共边；则一定存在∠AOB＞∠AOC．故选：A．【点评】本题考查角的大小比较，比较简单．35．已知∠1＝17°18′，∠2＝17.18°，∠3＝17.3°，下列说法正确的是（）A．∠1＝∠2B．∠1＝∠3C．∠1＜∠2D．∠2＞∠3【分析】根据1°＝60′把∠1＝17°18′化成度数再进行解答即可．【解答】解：∵1°＝60′，∴18′＝（）°＝0.3°，∴∠1＝17°18′＝17.3°，∴B正确．故选：B．【点评】此题比较简单，解答此题的关键是熟知1°＝60′．36．若∠1＝20°18′，∠2＝20°15′30′′，∠3＝20.25°，则（）A．∠1＞∠2＞∠3B．∠2＞∠1＞∠3C．∠1＞∠3＞∠2D．∠3＞∠1＞∠2【分析】∠1、∠2已经是度、分、秒的形式，只要将∠3化为度、分、秒的形式，即可比较大小．【解答】解：∵∠1＝20°18′，∠2＝20°15′30′′，∠3＝20.25°＝20°15′，∴∠1＞∠2＞∠3．故选：A．【点评】主要考查了两个角比较大小．在比较时要注意统一单位后再比较．37．如图，在此图中小于平角的角的个数是（）A．9B．10C．11D．12【分析】根据角的定义，找出图中小于平角的角．【解答】解：由图可知：∠CAB、∠CAE、∠BAE、∠AEB、∠CED、∠D、∠DCE、∠DCA、∠ECA、∠EBA、∠ABC小于平角，共11个．故选：C．【点评】除了注意角要小于平角外，还要注意同一顶点处的角要全部找出来．38．下列说法正确的个数是（）（1）连接两点之间的线段叫两点间的距离；（2）两点之间，线段最短；（3）若AB＝2CB，则点C是AB的中点；（4）角的大小与角的两边的长短无关．A．1个B．2个C．3个D．4个【分析】根据两点之间的距离的定义，线段的中点的定义以及角的定义即可作出判断．【解答】解：（1）连接两点之间的线段的长度叫两点间的距离，则命题错误；（2）两点之间，线段最短，正确；（3）当C在线段AB上，且AB＝2CB时，点C是AB的中点，当C不在线段AB上时，则不是中点，故命题错误；（4）角的大小与角的两边的长短无关，正确．故正确的有（2）、（4）．故选：B．【点评】本题考查了两点之间的距离、线段中点的定义、以及角的大小的定义，正确理解定义是关键．39．如图，如果∠CAE＞∠BAD，那么下列说法中一定正确的是（）A．∠BAC＞∠CAD B．∠DAE＞∠CADC．∠CAE＜∠BAC+∠DAE D．∠BAC＜∠DAE【分析】先由∠CAE＞∠BAD，根据角的和差可得∠CAD+∠DAE＞∠BAC+∠CAD，再利用不等式的性质得出∠DAE＞∠BAC，即∠BAC＜∠DAE．【解答】解：∵∠CAE＞∠BAD，∴∠CAD+∠DAE＞∠BAC+∠CAD，∴∠DAE＞∠BAC，即∠BAC＜∠DAE．故选：D．【点评】本题考查了角的大小比较，角的和差，不等式的性质，根据角的和差结合图形得出∠CAE＝∠CAD+∠DAE，∠BAD＝∠BAC+∠CAD是解题的关键．40．如图，AOE是一条直线，图中小于平角的角共有（）A．4个B．8个C．9个D．10个【分析】根据角的定义分别表示出各角即可．【解答】解：图中小于平角的角共有：∠AOB，∠AOC，∠AOD，∠BOC，∠BOD，∠BOE，∠COD，∠DOE，∠COE，共9个．故选：C．【点评】此题主要考查了角的定义，熟练掌握角定义是解题关键．41．若∠A＝30°18′，∠B＝30°15′30″，∠C＝30.25°，则这三个角的大小关系正确的是（）A．∠C＞∠A＞∠B B．∠C＞∠B＞∠A C．∠A＞∠C＞∠B D．∠A＞∠B＞∠C【分析】先把∠C的度数化成度、分、秒，再比较即可，也可把∠A和∠B的度数化成度，再进行比较．【解答】解：∵∠C＝30.25°＝30°+0.25°0.25°＝0.25×60′＝15′，∴∠C＝30°15′，∵∠A＝30°18′，∠B＝30°15′30″，∴∠A＞∠B＞∠C．故选：D．【点评】本题考查了度分秒的换算和角的大小比较，主要考查学生能否正确进行度分秒之间的换算．42．已知α＝76°5′，β＝76.5°，则α与β的大小关系是（）A．α＞βB．α＝βC．α＜βD．以上都不对【分析】根据度分秒转化得出76.5°＝76°30′，进而得出α与β的大小关系．【解答】解：∵α＝76°5′，β＝76.5°＝76°30′，∴α＜β．故选：C．【点评】此题主要考查了角的比较以及度分秒的转化，正确进行度分秒转化是解题关键．43．若∠A＝20°18′，∠B＝1212′，∠C＝20.25°，则（）A．∠A＞∠B＞∠C B．∠B＞∠A＞∠C C．∠A＞∠C＞∠B D．∠C＞∠A＞∠B【分析】先把∠B和∠C用度、分、秒表示，再比较即可．【解答】解：∵∠A＝20°18′，∠B＝1212′＝20°12′，∠C＝20.25°＝20°15′，∴∠A＞∠C＞∠B，故选：C．【点评】本题考查了度、分、秒之间的换算，角的大小比较的应用，能理解度、分、秒之间的关系是解此题的关键．44．已知∠A＝40°18′，∠B＝40°17′30″，∠C＝40.18°，则（）A．∠A＞∠B＞∠C B．∠B＞∠A＞∠C C．∠C＞∠A ＞∠B D．∠A＞∠C＞∠B【分析】先统一单位，再根据角的大小比较的方法进行比较即可求解．【解答】解：∵∠C＝40.18°＝40°10′48″，40°18′＞40°17′30″＞40°10′48″，∴∠A＞∠B＞∠C．故选：A．【点评】考查了度分秒的换算和角的大小比较，度、分、秒是常用的角的度量单位．1度＝60分，即1°＝60′，1分＝60秒，即1′＝60″．注意要统一单位．45．如图，若∠AOB＝∠COD，那么（）A．∠1＞∠2B．∠1＜∠2C．∠1＝∠2D．∠1、∠2的大小不确定【分析】根据图形可知∠1+∠COB＝∠AOB，∠COB+∠2＝∠COD，由∠AOB ＝∠COD，从而可以判断∠1与∠2的关系．【解答】解：由图可知：∠1+∠COB＝∠AOB，∠COB+∠2＝∠COD，∵∠AOB＝∠COD，∴∠1+∠COB＝∠COB+∠2．∴∠1＝∠2．故选：C．【点评】本题考查角的大小的比较，解题的关键是数形结合，找出其中相等的量．46．如图，∠AOB＝∠COD，则∠AOC与∠DOB的大小关系是（）A．∠AOC＞∠DOBB．∠AOC＜∠DOBC．∠AOC＝∠DOBD．∠AOC与∠DOB无法比较大小【分析】先根据∠AOB＝∠COD得出∠AOB+∠BOC＝∠COD+∠BOC，故可得出结论．【解答】解：∵∠AOB＝∠COD，∴∠AOB+∠BOC＝∠COD+∠BOC，即∠AOC＝∠DOB．故选：C．【点评】本题考查的是角的大小比较，熟知角比较大小的法则是解答此题的关键．47．如图，若∠AOC＝∠BOD，那么∠AOD与∠BOC的关系是（）A．∠AOD＞∠BOC B．∠AOD＜∠BOC C．∠AOD＝∠BOC D．无法确定【分析】根据题意∠AOC＝∠BOD，再根据图得知∠COD为∠AOD与∠BOC的公共角，从而得出答案．【解答】解：∵∠AOC＝∠BOD，∠COD为∠AOD与∠BOC的公共角，∴∠AOC+∠COD＝∠BOD+∠COD，∴∠AOD＝∠BOC，故选：C．【点评】本题考查了角的大小比较，解题的关键是根据图得知∠COD为∠AOD 与∠BOC的公共角，再解题就容易了．48．如果∠α＝55.5°，∠β＝55°5′，那么∠α与∠β之间的大小关系是（）A．∠α＞∠βB．∠α＜∠βC．∠α＝∠βD．无法确定【分析】首先根据1°＝60′，将∠α转化为55°30′，再比较即可．【解答】解：∵∠α＝55.5°＝55°30′，∠β＝55°5′，∴∠α＞∠β．故选：A．【点评】此题考查角的大小比较及度分秒的换算，注意统一单位，掌握1°＝60′，1′＝60″．49．下列角度中，比20°小的是（）A．19°38′B．20°50′C．36.2°D．56°【分析】根据角的大小比较方法分别与20°进行比较，即可得出答案．【解答】解：∵19°38′＜20°，20°50′＞20°，36.2°＞20°，56°＞20°，∴比20°小的是19°38，故选：A．【点评】此题考查了角的大小比较，根据角的比较方法进行比较，是一道基础题，比较简单．50．若∠A＝20°18′，∠B＝20°16″，∠C＝20.25°，则有（）A．∠A＞∠B＞∠C B．∠B＞∠A＞∠C C．∠A＞∠C＞∠B D．∠C＞∠A＞∠B【分析】根据度分秒之间的换算，先把∠C的度数化成度、分、秒的形式，再根据角的大小比较的法则进行比较，即可得出答案．【解答】解：∵∠A＝20°18′，∠B＝20°16″，∴∠A＞∠B，∵∠C＝20.25°＝20°15′，∴∠B＜∠C∴∠A＞∠C＞∠B．故选：C．【点评】此题考查了角的大小比较，先把∠C的度数化成度、分、秒的形式，再进行比较是本题的关键．。

2017年秋冀教版七年级上2.5角以及角的度量同步练习及答案

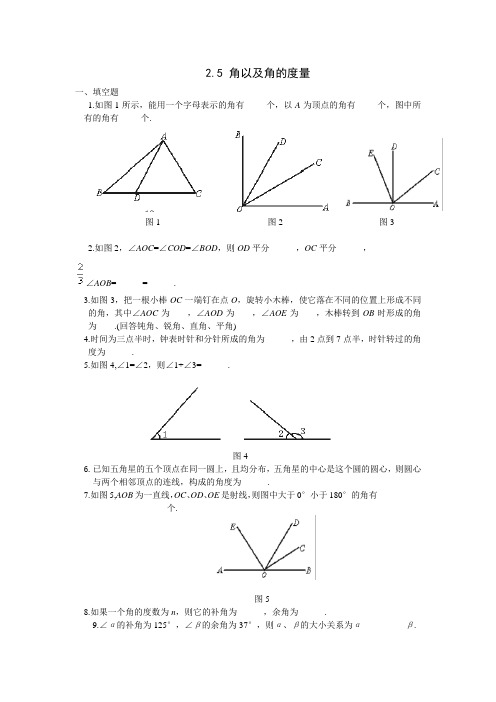
2.5 角以及角的度量一、填空题1.如图1所示，能用一个字母表示的角有_____个，以A为顶点的角有_____个，图中所有的角有_____个.图1 图2 图32.如图2，∠AOC=∠COD=∠BOD，则OD平分______，OC平分______，∠AOB=______=______.3.如图3，把一根小棒OC一端钉在点O，旋转小木棒，使它落在不同的位置上形成不同的角，其中∠AOC为____，∠AOD为____，∠AOE为____，木棒转到OB时形成的角为____.(回答钝角、锐角、直角、平角)4.时间为三点半时，钟表时针和分针所成的角为______，由2点到7点半，时针转过的角度为______.5.如图4,∠1=∠2，则∠1+∠3=______.图46.已知五角星的五个顶点在同一圆上，且均分布，五角星的中心是这个圆的圆心，则圆心与两个相邻顶点的连线，构成的角度为______.7.如图5,AOB为一直线，OC、OD、OE是射线，则图中大于0°小于180°的角有__________个.图58.如果一个角的度数为n，则它的补角为______，余角为______.9.∠α的补角为125°，∠β的余角为37°，则α、β的大小关系为α__________β.11.由_______的_______射线组成的图形叫做角.12.一条以一个角的_______为_______的射线把这个角分成_______的角，这条射线叫做这个角的_______.13.一副三角板的六个角各是_______、_______、_______、_______、_______、_______.14.一个周角是一个平角的_________倍，一个平角是一个直角的_________倍.15.根据右图，比较∠AOC、∠BOD、∠BOC、∠COD、∠AOD的大小，它们从小到大排列为___________.二、选择题10.一个角等于它的补角的5倍，那么这个角的补角的余角是（）A.30°B.60°C.45°D.150°11.两个锐角的和（）A.一定是锐角B.一定是钝角C.一定是直角D.以上三种情况都有可能12.互为补角的两个角度比是3∶2，这两个角是（）A.108°,72°B.95°，85°C.108°，80°D.110°，70°13.下列各角中是钝角的为（）A.周角B.平角C.直角D.直角14.如果角α和角β互为余角,角α与角γ互为补角,角β和角γ的和等于周角的，那么此三个角分别为（）A.75°,15°,105°B.60°,30°, 120°C.50°, 30°,130°D.70°, 20°, 110°15.如图6，图形表示的是（）A.直线B.射线C.平角D.周角图616.船的航向从正北按顺时针方向转到东南方向，它转了（）A.135°B.225°C.180°D.90°17.有两个角，它们的比为7∶3，它们的差为72°，则这两个角的关系是（）A.互为余角B.互为补角C.相等D.以上答案都不对三、解答题18.四个角的和是180°，其中有三个角相等，且都是第四个角的，求这四个角.19.如图7，已知∠AOC=∠BOD=75°，∠BOC=30°，求∠AO D.图7 图820.如图8，已知O是直线AB上的点，OD是∠AOC的平分线，OE是∠COB的平分线，求∠DOE的度数.四、读图填空1.如图1，∠BDC=_______+_______，∠CDA=_______－_______.2.如图2，OC⊥AB，OE为∠COB的平分线，∠AOE的度数为_______.图1 图23.如图3，BD与CE分别是∠ABC和∠ACB的平分线，如果∠DBC=∠ECB，那么∠ABC=∠ACB吗？_______.4.如图4，OB是∠AOC的平分线，OD是∠COE的平分线，若∠AOC=70°，∠COE=40°,那么∠BOD=_______°.2.5 角以及角的度量一、1. 2 3 72.∠BOC∠AOD∠AOD∠BOC3.锐角直角钝角平角4.75°165°5.180°6.72°7.9 8.180°－n90°－n9.＞二、10.B 11.D 12.A 13.B 14.A 15.D16.A 17.B三、18.40°，40°，40°，60°19.120°20.90°。

新冀教版数学七年级上册同步练习：2.6 角的大小

2.6角的大小知识点1角的比较1．用一个放大镜去观察一个角，下列说法正确的是()A．角的度数扩大了B．角的度数缩小了C．角的度数没有变化D．以上选项都不对2．∠ABC与∠MNP相比较，若顶点B与N重合，且BC与MN重合，BA在∠MNP的内部，则它们的大小关系是()A．∠ABC＞∠MNP B．∠ABC＝∠MNPC．∠ABC＜∠MNP D．不能确定3．一副三角尺有6个角，这6个角中最小角的度数是()A．15°B．30°C．45°D．60°4．如图2－6－1所示，其中最大的角是________，∠DOC，∠DOB，∠DOA的大小关系是________________(用“＞”连接)．图2－6－15．如图2－6－2，直线AB和CD相交于点O.(1)分别测量∠AOC，∠AOD，∠BOD和∠BOC的度数；(2)∠AOC和∠BOD相等吗？∠AOD和∠BOC呢？图2－6－26．如图2－6－3，回答下列问题：(1)比较∠FOD与∠FOE的大小；(2)借助三角尺比较∠DOE与∠BOF的大小；(3)借助量角器比较∠AOE与∠FOD的大小．图2－6－3 知识点2角的画法7．如图2－6－4，已知∠1，用直尺和圆规求作一个角，使它等于∠1.(不写作法，保留作图痕迹)图2－6－48．已知∠A＝18°18′，∠B＝18.18°，∠C＝18.3°，则下列选项正确的是()A．∠A＝∠B B．∠A＝∠CC．∠A<∠B D．∠A>∠C9．在图2－6－5所示的4×4的方格中，记∠ABD＝∠α，∠DEF＝∠β，∠CGH＝∠γ，则()图2－6－5A．∠β<∠α<∠γB．∠β<∠γ<∠αC．∠α<∠γ<∠βD．∠α<∠β<∠γ10．比较两个角的大小，有以下两种方法：方法一：用量角器量出两个角的度数，则度数大的角大；方法二：构造图形，若一个角包含(或覆盖)另一个角，则这个角大．对于如图2－6－6给定的∠ABC与∠DEF，用以上两种方法分别比较它们的大小．(注：构造图形时，用尺规作图作出示意图)图2－6－6教师详解详析【备课资源】【详解详析】1．C[解析] 用放大镜观察一个角时，角的度数不会发生变化．2．C[解析] 根据题意画出图形，比较出两角的大小关系即可得出∠ABC＜∠MNP.故选C.3．B[解析] 一副三角尺共两块(缺少一块就不成“副”了)，一块是三个内角分别为45°，45°，90°；另一块是三个内角分别为30°，60°，90°，所以最小的角度为30°.故选B.4．∠DOA∠DOA>∠DOB>∠DOC5．解：(1)∠AOC＝30°，∠AOD＝150°，∠BOD＝30°，∠BOC＝150°.(2)∠AOC＝∠BOD，∠AOD＝∠BOC.6．解：(1)因为OD在∠FOE的内部，所以∠FOD＜∠FOE.(2)用含有45°角的三角尺比较，可得∠DOE＞45°，∠BOF＜45°，则∠DOE＞∠BOF.(3)用量角器度量得∠AOE＝30°，∠FOD＝30°，则∠AOE＝∠FOD.7．解：如图，∠ABC即为所求作的角．8．B[解析] 将其都化成“度”的形式，再比较大小．∠A＝18°18′＝18.3°＝∠C.故选B.9．B10．解：方法一：测量得∠ABC＝45°，∠DEF＝65°，所以∠ABC<∠DEF.方法二：以E为顶点，EF为一边，作∠FEA′，使∠FEA′＝∠ABC，且EA′与ED在EF 的同侧，如图，则∠FEA′<∠DEF.又因为∠FEA′＝∠ABC，所以∠ABC<∠DEF.。

2017年七年级数学上2.6角的大小(冀教版)最新版

E
C
D
A
O
B
∠ECD＞∠AOB
或 ∠AOB <∠ECD
E
C
D
A
O
B
∠ECD =∠AOB
∠ABC > ∠DEF 或∠DEF <∠ABC
D
B
C
E
F
例1 根据如图所示，点A、O、E在一条直线上。
解答下列问题：
（1）图中直角有 3
个，
A
B
分 ∠AOC、∠BOD、∠COE
别
是
4
O
C
∠AO；B、∠BOC、∠COD、∠DOE
回顾总结：
通过本节课的学习，你对角又多了哪些认识？
记得一个基本图形；学会有关角的计算的分析方法。
现代人每天生活在纷繁、复杂的社会当中，紧张、高速的节奏让人难得有休闲和放松的时光。人们在奋斗事业的搏斗中深感身心的疲惫。然而，如果你细心观察，你会发现作为现代人，其实人们每天都在尽可能的放松自己，调整生活节奏，追求充实快乐的人生。看似纷繁的社会里，人们的生活方式其实也不复杂。大家在忙忙碌碌中体味着平凡的人生乐趣。由此我悟出一个道理，那就是----生活简单就是幸福。生活简单就是幸福。一首优美的音乐、一支喜爱的歌曲，会让你心境开朗。你可以静静地欣赏你喜爱的音乐，可以在流荡的旋律中回忆些什么，或者什么都不去想；你可以一个人在房间里大声的放着摇滚，也可以在网上用耳麦与远方的朋友静静地共享；你还可以一边放送着音乐，一边做着家务....生活简单就是幸福。一杯清茶，或一杯咖啡，放在你的桌边，你的心情格外的怡然。你可以浏览当天的报纸，了解最新的国内外动态，哪怕是街头趣闻；或者捧一本自己喜欢的杂志、小说，从字里行间获得那种特别的轻松和愉悦....生活简单就是幸福。经过精心的烹制，一桌可心的菜肴就在你的面前，你招呼家人快来品尝，再备上最喜欢的美酒，这是多么难得的享受！生活简单就是幸福。春暖花开的季节，或是清风送爽的金秋，你和家人一起，或是朋友结伴，走出户外，来一次假日的郊游，享受大自然带给你的美丽、芬芳。吸一口新鲜的空气，忘却都市的喧嚣，身心仿佛受到一番洗涤，这是一种什么样的轻松感受！生活简单就是幸福。你参加朋友们的一次聚会，那久违的感觉带给你温馨和激动，在觥酬交错之间你享受与回味真挚的友情。朋友，是那样的弥足珍贵....生活简单就是幸福。周末的夜晚，一家老小围坐在电视机旁，尽享团圆的欢乐现代人越来越会生活，越来越会用各种不同的方式来放松自己。垂钓、上网、打牌、玩球、唱卡拉OK、下棋.....不一而足。人们根据自己的兴趣爱好寻找放松身心的最佳方式，在相对固定的社交圈子里怡然的生活，而且不断的扩大交往的圈子，结交新的朋友有时，你会为新添置的一套漂亮时装而快乐无比；有时，你会为孩子的一次小考成绩优异而倍感欣慰；有时，你会为刚参加的一项比赛拿了名次而喜不自胜；有时，你会为完成了上司交给的一个任务而信心大增生活简单就是幸福！生活简单就是幸福，不意味着我们放弃了对目标的追逐，是在忙碌中的停歇，是身心的恢复和调整，是下一步冲刺的前奏，是以饱满的精力和旺盛的热情去投入新的“战斗”的一个“驿站”；生活简单就是幸福，不意味着我们放弃了对生活的热爱，是于点点滴滴中去积累人生，在平平淡淡中寻求充实和快乐。放下沉重的负累，敞开明丽的心扉，去过好你的每一天。生活简单就是幸福！我的心徜徉于春风又绿的江南岸，纯粹，清透，雀跃，欣喜。原来，真正的愉悦感莫过于触摸到一颗不染的初心。人到中年，初心依然，纯真依然，情怀依然，幸甚至哉。生而为人，芳华刹那，真的不必太多要求，一盏茶，一本书，一颗笃静的心，三两心灵知己，兴趣爱好一二，足矣。亦舒说：“什么叫做理想生活？不用吃得太好穿得太好住得太好，但必需自由自在，不感到任何压力，不做工作的奴隶，不受名利的支配，有志同道合的伴侣，活泼可爱的孩子，丰衣足食，已经算是理想。”时间如此猝不及防，生命如此仓促，忠于自己的内心才是真正的勇敢，以不张扬的姿态，将自己活成一道独一无二的风景，才是最大的成功。试问，你有多久没有靠在门槛上看月亮了，你有多久没有在家门口的那棵大树下乘凉了，你有多久没有因为一个人一件事而心生感动了，你又有多久没有审视自己的内心了？与命运的较量中，我们被迫前行，却忘记了来时的方

冀教版七年级数学上册《2.6角大小的比较》同步测试题及答案

冀教版七年级数学上册《2.6角大小的比较》同步测试题及答案学校:___________班级：___________姓名：___________考号：___________一、选择题1．用10倍的放大镜看30︒的角，看到的角的度数是（）A ．300︒B ．10︒C ．30︒D ．不确定2．如图，利用一副三角板比较AOB ∠与CPD ∠的大小，两角顶点均与三角板某一顶点重合．已知图1中射线OB 经过60︒角的一边，图2中射线PC 经过45︒角的一边，则下列判断正确的是（）A ．CPD AOB ∠>∠ B ．AOB CPD ∠>∠C ．AOB CPD ∠=∠ D ．无法判断 3．杨老师到几何王国去散步，刚走到“角”的家门，就听到∠A 、∠B 、∠C 在吵架，∠A 说：“我是3015'︒，我应该最大!”∠B 说：“我是30.3°，我应该最大!”．∠C 也不甘示弱：“我是30.15°，我应该和∠A 一样大!”听到这里，杨老师对它们说：“别吵了，你们谁大谁小，由我来作评判!”，杨老师评判的结果是（） A ．∠A 最大 B ．∠B 最大 C ．∠C 最大 D ．∠A ＝∠C4．若3218A '∠=︒ 321530B '''∠=︒ 32.25C ∠=︒则（）．A ．ABC >>∠∠∠B ．B AC ∠>∠>∠ C ．A C B ∠>∠>∠D ．C A B ∠>∠>∠5．如图所示，正方形网格中有∠α 和∠β，如果每个小正方形的边长都为1，估测∠α 与∠β 的大小关系为（）A ．∠α< ∠βB ．∠α= ∠βC ．∠α> ∠βD ．无法估测6．用叠合的方法比较AOB ∠和A O B '''∠两个角的大小，先将A O B '''∠的顶点O ＇与AOB ∠的顶点O 重合，边O A ''与边OA 重合，边O B ''落在了AOB ∠的内部，则AOB ∠和A O B '''∠的关系是（）A ．AOB A O B '∠'>'∠B ．AOB A O B '∠'<'∠C ．AOB AO B '''∠=∠D ．不确定7．如图AOB COD ∠=∠，则AOC ∠与DOB ∠的大小关系是（）A ．AOC DOB ∠>∠B ．AOC DOB ∠<∠ C ．AOC DOB ∠=∠D ．AOC ∠与DOB ∠无法比较大小8．图中哪一个角的度数最接近45°（）A ．1∠B ．2∠C ．3∠D ．4∠9．如图，已知∠AOB 与∠EO ′F ，分别以O ，O ′为圆心，以同样长为半径画弧，分别交OA ，OB 于点A ′，B ′，交O ′E ，O ′F 于点E ′，F ′．以B ′为圆心，以E ′F ′长为半径画弧，交弧A ′B ′于点H ．下列结论不正确的是（）A ．∠AOH =∠AOB −∠EO ′F B ．∠AOB >∠EO ′FC ．∠HOB =∠EO ′FD ．∠AOB =2∠EO ′F10．如图，已知∠AOB ，用尺规作∠AOD =2∠AOB ，第一步的作法：以点О为圆心，任意长为半径画弧∠，分别交OA ，OB 于点E ，F ，第二步的作法是（）A ．以点E 为圆心，OE 长为半径画弧，与弧∠相交于点DB ．以点E 为圆心，EF 长为半径画弧，与弧∠相交于点DC ．以点F 为圆心，OE 长为半径画弧，与弧∠相交于点DD ．以点F 为圆心，EF 长为半径画弧，与弧∠相交于点D11．下面是黑板上出示的尺规作图题，需要回答符号代表的内容（）如图，已知∠AOB ，求作：∠DEF ，使∠DEF ＝∠AOB作法：（1）以●为圆心，任意长为半径画弧，分别交OA 、OB 于点P 、Q（2）作射线EG ，并以点E 为圆心∠长为半径画弧交EG 于点D（3）以点D 为圆心∠长为半径画弧交（2）步中所画弧于点F（4）作∠，∠DEF 即为所求作的角A ．●表示点EB ．∠表示PQC ．∠表示OQD ．∠表示射线EF二、填空题12．比较大小：38.15︒ 3815'︒(用>、=、<填空)13．小正方形网格如图所示，点A 、B 、C 、D 、O 均为格点，那么AOB ∠ COD ∠（填“＞”“＜”或“＝”）三、解答题14．对于如图所示的各个角，用“>”、“<”、“=”填空：(1)AOB ∠___________AOC ∠；(2)DOB ∠___________BOC ∠；(3)BOC ∠___________AOD ∠；(4)AOD ∠___________BOD ∠．15．如图，小华在街心花园的步道AB 上观看宣传画廓MN ，他发现在点C 处观看效果最佳．(1)请测量BCN ∠ MCA ∠ CMN ∠ MNC ∠的度数，发现哪两个角近似相等？(2)请在步道AB 上点C 的两边分别任意取一点D ，E ，画出MDN ∠，MEN ∠测量MDN ∠ MCN ∠ MEN ∠的度数，并指出它们中的最大角．16．如图所示表示两块三角板．（1）用叠合法比较∠1，∠α，∠2的大小；（2）量出图中各角的度数，并把图中的6个角从小到大排列，然后用“＜”或“＝”连接．17．如图，已知∠AOB ，求作∠ECF ，使∠ECF=∠AOB ．（要求：尺规作图，保留作图痕迹，不写作法）18．已知∠α、∠β，求作：∠AOB ，使∠AOB=∠α+∠β（保留作图痕迹）．参考答案：1．C2．B3．B4．A5．A6．A7．C8．D9．D10．D11．D12．<13．＞14．(1)<(2)>(3)<(4)>15．（1）解：如图所示测量发现：BCN ∠ MCA ∠ CMN ∠ MNC ∠的度数分别约为67,42,67,42︒︒︒︒∠BCN ∠与CMN ∠近似相等MCA ∠与MNC ∠近似相等（2）解：如图所示测量MDN ∠ MCN ∠ MEN ∠的度数约为547164︒︒︒，，∠最大的角是MCN．16．解：（1）如图所示，把两块三角板叠在一起，可得∠1＞∠α，用同样的方法可得∠α＜∠2．所以∠2＝∠1＞∠α．（2）用量角器量出图中各个角的度数，分别是∠1＝∠2＝45°，∠3＝90°，∠α＝30°，∠β＝60°，∠γ＝90°把它们从小到大排列，有∠α＜∠1＝∠2＜∠β＜∠3＝∠γ．17．解：如图所示：∠ECF即为所求．18．解：。

初中数学冀教版七年级上册第二章2.6角的大小-普通用卷

初中数学冀教版七年级上册第二章2.6角的大小一、选择题1.∠α=40.4°，∠β=40°4′，则∠α与∠β的关系是()A. ∠α=∠βB. ∠α>∠βC. ∠α<∠βD. 以上都不对2.已知∠AOB和∠DEF，如果移动∠DEF使得顶点O与顶点E重合，边ED与边OA叠合，边EF在∠AOB内部，那么∠AOB和∠DEF大小关系是()A. ∠AOB>∠DEFB. ∠AOB<∠DEFC. ∠AOB=∠DEFD. 不能确定3.若∠A=18°18′，∠B=18°19′，∠C=18.19°，则有()A. ∠A>∠B>∠CB. ∠B>∠A>∠CC. ∠A>∠C>∠BD. ∠C>∠A>∠B4.若∠1=40.4°，∠2=40°4′，则∠1与∠2()A. ∠1<∠2B. ∠1>∠2C. ∠1=∠2D. 无法确定5.若∠A=20°18′，∠B=20°15″，∠C=20.25°，则有()A. ∠A>∠B>∠CB. ∠B>∠A>∠CC. ∠A>∠C>∠BD. ∠C>∠A>∠B6.若∠A=30°18′，∠B=30°15′30″，∠C=30.25°，则这三个角的大小关系正确的是()A. ∠C>∠A>∠BB. ∠C>∠B>∠AC. ∠A>∠C>∠BD. ∠A>∠B>∠C7.已知∠1=25∘12′，∠2=25.12∘，∠3=25.2∘，下列说法正确的是()A. ∠1=∠3B. ∠3=∠2C. ∠1=∠2D. 三个角互不相等8.若∠1=75°24′，∠2=75.3°，∠3=75.12°，则()A. ∠1=∠2B. ∠2=∠3C. ∠1>∠3D. 以上都不对9.如图，射线OC、OD分别在∠AOB的内部、外部，下列各式错误的是()A. ∠AOB<∠AODB. ∠BOC<∠AOBC. ∠COD>∠AODD. ∠AOB>∠AOC10.已知∠α=39°18′，∠β=39.18°，∠γ=39.3°，下面结论正确的是()A. ∠α<∠γ<∠βB. ∠γ>∠α=∠βC. ∠α=∠γ>∠βD. ∠γ<∠α<∠β二、填空题11.如图，∠AOB=90°，OD平分∠BOC，∠DOE=45°，则∠AOE______∠COE(填“<”“>”或“=”号)12.∠α=10.5°，∠β=10°20′，则∠α，∠β的大小关系是∠α______∠β(在横线上填“>”，“<“或“=“)．13.比较大小：30.15°30°15′(用>、=、<填空)14.比较两个角的大小关系：小明用度量法测得∠AOB=45°，∠COD=50°；小丽用叠合法比较，将两个角的顶点重合，边OB与OD重合，边OA和OC置于重合边的同侧，则边OA______.(填序号：①“在∠COD的内部”；②“在∠COD的外部”；③“与边OC重合”)15.下列说法：①连接两点间的线段叫这两点的距离；②木匠师傅锯木料时，一般先在模板上画出两个点，然后过这两点弹出一条墨线，这样做的原理是：两点之间，线段最短；③若A、B、C三点在同一直线上，且AB=2CB，则C是线段AB的中点；④若∠A=20°18′，∠B=20°28″，∠C=20.25°，则有∠A>∠C>∠B．其中一定正确的是______.(把你认为正确结论的序号都填上)三、解答题16.如图，以学校为参照点，请用方位角和实际距离分别表示新华书店、少年官和超市的位置．17.如图，P，Q是∠MON内的两点，请由点P，Q分别向∠MON的两边画垂线PA，PB和QC，QD，垂足分别为A，B，C，D.通过观察与测量，对∠APB和∠CQD的大小关系提出你的猜想．18.观察图中的∠AOB和∠CO′D，你认为哪一个角大？用量角器量一量，并和你观察得出的结论进行比较．答案和解析1.【答案】B【解析】解：∵∠α=40.4°=40°24′，∠β=40°4′，∴∠α>∠β．故选：B．首先同一单位，利用1°=60′，把∠α=40.4°=40°24′，再进一步与∠β比较得出答案即可．此题考查角的大小比较的方法和度分秒之间的换算．2.【答案】A【解析】解：如图，由叠合法可得，∠AOB>∠DEF，故选：A．依据叠合法，即将两个角叠合在一起比较，使两个角的顶点及一边重合，观察另一边的位置．本题主要考查了角的大小的比较，将两个角叠合在一起比较，使两个角的顶点及一边重合，观察另一边的位置即可．3.【答案】B【解析】解：∵∠A=18°18′，∠B=18°19′，∴∠A<∠B，∵∠C=18.19°=18°11′24″，∴∠C<∠A<∠B，∴∠B>∠A>∠C．故选：B．根据度分秒之间的换算，先把∠C的度数化成度、分、秒的形式，再根据角的大小比较的法则进行比较，即可得出答案．此题考查了角的大小比较，先把∠C的度数化成度、分、秒的形式，再进行比较是本题的关键．4.【答案】B【解析】解：∵∠1=40.4°=40°24′，∠2=40°4′，∴∠1>∠2．故选：B．首先统一单位，利用1°=60′，可得∠1=40.4°=40°24′，再进一步与∠2比较得出答案即可．此题考查角的大小比较和度分秒之间的换算，在比较角的大小时有时可把度化为分来进行比较．5.【答案】C【解析】解：∵∠A=20°18′，∠B=20°15″，∴∠A>∠B，∵∠C=20.25°=20°15′，∴∠B<∠C<∠A，∴∠A>∠C>∠B．故选：C．根据度分秒之间的换算，先把∠C的度数化成度、分、秒的形式，再根据角的大小比较的法则进行比较，即可得出答案．此题考查了角的大小比较，先把∠C的度数化成度、分、秒的形式，再进行比较是本题的关键．6.【答案】D【解析】解：∵∠C=30.25°=30°+0.25°0.25°=0.25×60′=15′，∴∠C=30°15′，∵∠A=30°18′，∠B=30°15′30″，∴∠A>∠B>∠C．故选：D．先把∠C的度数化成度、分、秒，再比较即可，也可把∠A和∠B的度数化成度，再进行比较．本题考查了度分秒的换算和角的大小比较，主要考查学生能否正确进行度分秒之间的换算．7.【答案】A【解析】【分析】本题考查了度分秒的换算，角的大小比较．根据小单位化大单位除以进率，可得答案．【解答】解：∠1=35°12′=25.2°=∠3>∠2，故选A．8.【答案】C【解析】【分析】本题考查角的大小比较和度分秒之间的换算，此题比较简单，解答此题的关键是熟知1°=60′.根据1°=60′把∠1=75°24′化成度数再进行解答即可．【解答】解：∵1°=60′，)°=0.4°，∴24′=(2460∴∠1=75°24′=75.4°，∵∠2=75.3°，∠3=75.12°，∴∠1>∠2>∠3．故选：C．9.【答案】C【解析】【分析】本题主要考查了角的大小比较，比较简单，主要培养了学生的推理能力．根据所给出的图形，再利用图形中角的和差关系，分别进行解答即可．【解答】解：A、∵OD在∠AOB的外部，∴∠AOB<∠AOD；故本选项正确；B、∵OC在∠AOB的内部，∴∠BOC<∠AOB；故本选项正确；C、∵OC在∠AOD的内部，∴∠COD<∠AOD；故本选项错误；D、∵OC在∠AOB的内部，∴∠AOB>∠AOC；故本选项正确；故选：C．10.【答案】C【解析】【分析】本题考查了角的大小比较、度分秒的换算．度、分、秒是常用的角的度量单位．1度=60分，即1°=60′，1分=60秒，即1′=60″．首先把∠α转化为39.3°，然后再来比较它们的大小．【解答】解：∵∠α=39°18′=39.3°，39.18°<39.3°，∴∠α=∠γ>∠β．故选C．11.【答案】=【解析】解：∵∠AOB=90°，∠DOE=∠DOC+∠COE=45°，∴∠BOD+∠AOE=45°，∵OD平分∠BOC，∴∠BOD=∠COD，∴∠AOE=∠COE，故答案为：=根据角的和差得出∠BOD+∠AOE=45°，再利用角平分线的定义得出∠BOD=∠COD，即可得到答案．此题考查角的大小比较，关键是利用角的和差得出∠BOD+∠AOE=45°．12.【答案】>【解析】解：∵∠α=10.5°=10°30′，∠β=10°20′，∴∠α>∠β．故答案为：>．根据1°=60′先换算单位，再根据角的大小比较的方法进行比较即可求解．考查了角的大小比较，关键是先统一单位再比较大小．13.【答案】<【解析】【分析】本题主要考查了度、分、秒的转化运算以及角的大小比较，注意以60为进制，比较简单.先进行度、分、秒的转化运算，注意以60为进制，然后对比即可得出答案．【解答】解：∵30.15°=30°9′，∴30°9′<30°15′，故答案为<．14.【答案】①【解析】解：如图，由于∠AOB<∠COD，因此OA在∠COD的内部，故答案为：①；根据题意画出图形，由∠AOB<∠COD，图形直观得出答案．考查角的大小比较的方法，度量法、叠合法是常用的方法，叠合法的前提是使两个角的一条边重合，两个角的另一条边都在重合边的同侧．15.【答案】④【解析】解：①连接两点间的线段的长度叫这两点的距离，故①错误；②木匠师傅锯木料时，一般先在模板上画出两个点，然后过这两点弹出一条墨线，这样做的原理是：两点确定一条直线，故②错误；③若A、B、C三点在同一直线上，且AB=2CB，则C不一定是线段AB的中点，故③错误；④若∠A=20°18′，∠B=20°28″，∠C=20.25°=20°15′，则有∠A>∠C>∠B，故④正确．故答案为：④．依据两点间的距离，直线的性质以及度分秒的换算，即可得出结论．本题主要考查了两点间的距离，直线的性质，线段的性质以及度分秒的换算，解题时注意：经过两点有且只有一条直线．简称：两点确定一条直线．16.【答案】解：如图，新华书店在学校的北偏西40°方向1.6cm处；少年官在学校的南偏西20°方向3.2cm处；超市在学校的北偏东60°方向2.2cm处．【解析】确定物体的位置要有三个步骤：(1)定观察点，(2)量角度，(3)算距离，据此即可进行解答．此题主要考查依据方向(角度)和距离判定物体位置的方法．17.【答案】解：∠APB和∠CQD的大小关系是相等，理由如下：如图，∵PA⊥OM，PB⊥ON，∴∠PAO=∠PBO=90°，∴∠APB=180°−∠O，∵QC⊥OM，QD⊥ON，∴∠QCO=∠QDO=90°，∴∠CQD=180°−∠O，∴∠APB=∠CQD．【解析】根据题意画出图形，再利用四边形内角和定理即可得∠APB和∠CQD的大小关系．本题考查了角的大小比较，解决本题的关键是掌握四边形内角和定理．18.【答案】解：分别用量角器量出∠AOB和∠CO′D，得到∠AOB=∠CO′D，根据观察发现OA//O′C，OB//O′D，得到∠AOB=∠CO′D．【解析】用用量角器量后，得出结论即可．本题考查了角的大小比较，正确使用量角器是解题的关键．第11页，共11页。

冀教版-数学-七年级上册-同步练习：2.6 角的大小

自我小测基础巩固JICHU GONGGU1．如图，在此图中小于平角的角的个数是()A．9 B．10 C．11 D．122．用量角器测量下列图中每两个角，然后比较它们的大小：(1)∠1__________∠2(2)∠3__________∠4(3)∠5__________∠63．如图，用“＜”把∠AOD，∠BOD，∠COD连接起来：______＜______＜______.4．如果∠1＝4°18′，∠2＝3°79′，∠3＝4.4°，则∠1，∠2，∠3的大小顺序是__________．(由大到小排列)5．已知射线BC和∠α，用直尺、圆规作∠ABC，使∠ABC＝∠α.6．如图，已知O是直线AD上的点，∠AOB，∠BOC，∠COD三个角从小到大依次相差25°，求这三个角的度数．能力提升NENGLI TISHENG7．在∠AOB的内部任取一点C，作射线OC，则一定存在()A．∠A O B＞∠A O C B．∠B O C＞∠A O BC．∠B O C＞∠A O C D．∠A O C＞∠B O C8．如图，∠AOD＞∠BOC，则下列说法中正确的是()A．∠C O D＞∠A O B B．∠A O B＞∠C O DC．∠C O D＝∠A O B D．∠A O B与∠C O D的大小关系不能确定9．如图，在一张透明纸上画∠AOB，能否折出一条射线，使这条射线把∠AOB平均分为2份？参考答案1．C2．(1)＜(2)＞(3)＝3．∠COD∠BOD∠AOD4．∠3＞∠2＞∠1点拨：∵∠2＝3°79′＝4°19′，∠3＝4.4°＝4°24′，故∠3＞∠2＞∠1. 5．略6．解：设∠AOB的度数为x，由题意得：x＋(x＋25°)＋(x＋50°)＝180°，解得x＝35°，则x＋25°＝60°，x＋50°＝35°＋50°＝85°.即∠AOB＝35°，∠BOC＝60°，∠COD＝85°.7．A8．B点拨：∠AOD＝∠AOB＋∠BOD，∠BOC＝∠COD＋∠BOD，因为∠AOD＞∠BOC，所以∠AOB＋∠BOD＞∠COD＋∠BOD，所以∠AOB＞∠COD.9．解：能．把∠AOB对折，使OA，OB重合，则折痕可把∠AOB平分．。

冀教版七年级上册数学2.6 角的大小

冀教版七年级上册数学2.6 角的大小基础闯关全练知识点一角的大小的比较方法1．如图2-6-1，射线OC 、OD 分别在∠AOB 的内部、外部，下列各式错误的是 ( )A. ∠AOB<∠AODB.∠BOC<∠AOBC. ∠ COD> ∠AODD. ∠AOB>∠AOC2．如图2-6-2所示，将∠AOB ，∠BOC ，∠AOC 用“>”连接起来： .知识点二作一个角等于已知角3．在利用圆规和直尺作一个角等于已知角( ∠EOF)时，第一步可以为 ( )A ．以O 点为圆心，以3 cm 为半径画弧B ．以O 点为圆心，分别以3 cm 和5 cm 为半径画弧与OE ，OF 相交C ．以O 点为圆心，以任意长为半径画弧与OE ．OF 相交D ．以任意一点为圆心，以3 cm 为半径画弧与OE ，OF 相交4．如图2-6-3所示，已知∠AOB ，点P 在OA 上，请以P 为顶点，PA 为一边在∠AOB 内部作∠APC=∠D ．（不写作法，但必须保留作图痕迹）能力提升全练1．用一个放大镜去观察一个角的大小，正确的说法是( )A ．角的度数扩大了B ．角的度数缩小了C ．角的度数没有变化D ．以上都不对2．如果∠1=21∠a, ∠2=21∠α( ∠α≠00)，那么∠1和 ∠2的大小关系是 . 3．图2-6-4是部分节目的播出时间，分别确定出钟表上时针与分针所成的较小的角的度数．三年模拟全练选择题（2017河北秦皇岛抚宁期末，11，★☆☆）若∠1= 40.4°，∠2= 40°4'，则∠1与∠2的关系是( )A．∠1= ∠2B．∠1>∠2C.∠2<∠2D．以上都不对五年中考全练选择题（2016湖北宜昌中考改编，9，★★☆）已知M，N，P，Q四点的位置如图2-6-5所示，下列结论中，正确的是( )A.∠NOQ=42°B.∠NOP= 132°C.∠PON比∠MOQ大D.∠NOQ 比∠MOP小核心素养全练1．李老师到数学王国去散步，刚走到“角”的家门口，就听到∠A，∠B，∠C在吵架，∠A 说：“我是37°18'，我应该最大！”∠B说：“我是37.2°，我应该最大！”∠C也不甘示弱：“我是37.18°，我应该和∠A 一样大！”听到这里，李老师对它们说：“别吵了，你们谁大谁小，由我来评判！”你知道李老师是怎样评判的吗？2．比较两个角的大小，有以下两种方法（规则）．①用量角器度量两个角的大小，用度数表示，则角度大的角大；②构造图形，如果一个角包含（或覆盖）另一个角，则这个角大.对于如图2-6-6所示的∠ABC 与∠DEF,用以上两种方法分别比较它们的大小，注：构造图形时，作示意图（草图）即可．答案基础闯关全练1．C解析：由题图易知∠CDD<∠ AOD ，故C 不正确，故选C ．2．答案 ∠A0C>∠ AOB>∠BOC3．C解析：由教材中给出的作图步骤可知选C ．4．解析如图所示．能力提升全练1．C解析：用放大镜看一个角时，角的度数不会发生变化，故选C ．2．答案∠1>∠2解析因为21∠α>∠10：，所以∠1>∠2．3．解析新闻联播：30°×5=150°；新闻30分：0°；今日说法：30°×56035= 167.5°；电视剧：30°×4= 120°，三年模拟全练选择题B解析：因为∠1= 40.4°= 40°24'，∠2=40°4'，所以∠1>∠2．故选B. 五年中考全练选择题C解析：∠NOQ= 138°，故选项A 错误；∠NOP=48°，故选项B 错误；∠PON=48°，∠MOQ= 42°，故∠PON 比∠MOQ 大，故选项C 正确；∠NOQ=138°，∠MOP=132°，所以∠NOQ 比∠MOP 大，故选项D 错误．故选C ．核心素养全练1.解析∵∠A= 37°18',∠B=37. 2°= 37°12', ∠C= 37. 18°=37°10.8'= 37°10'48",∴∠C<∠B<∠A.2．解析用方法①：∠ABC=46°,∠DEF=67°.即∠DEF> ∠ABC.用方法②：如图.把∠ABC放在∠DEF上，使B和E重合，边EF和BC重合，DE和BA在EF的同侧，从图形可以看出∠DEF>∠ABC．。

冀教版-数学-七年级上册-2.6 角的大小练习

角的大小一、选择：1.下列关于角的说法正确的个数是( )①角是由两条射线组成的图形;②角的边越长,角越大; ③在角一边延长线上取一点D;④角可以看作由一条射线绕着它的端点旋转而形成的图形.A.1个B.2个C.3个D.4个2.下列4个图形中,能用∠1,∠AOB,∠O三种方法表示同一角的图形是( )3.下列说法中正确的是（）A .直线是平角B.角的大小与角的两边长有关C.角的两边是两条射线D. 用放大镜看一个角，角的度数变大了4.把10.26°用度分秒表示为（）A.10°15′36"B.10°20′6"C. 10°14′6"D. 10°26"5.若∠P=25°12" ，∠Q=25.12°,∠R=25.2°，则（）A. ∠P=∠QB.∠Q=∠RC.∠P=∠RD.∠P=∠Q=∠R6.如图所示，射线OB，OC将∠AOD分为三部分，如果∠AOC>∠BOD，那么∠AOB与∠COD的大小关系是( )A. ∠AOB>∠CODB. ∠AOB<∠CODC. ∠AoB=∠CODD.无法判断二、填空：7.30.6°=_____°_____′=______′;30°6′=_____′=______°.8.（1）由一点引出2条射线，共有_____个角；（2）由一点引出3条射线，共有_____个角；（3）由一点引出4条射线，共有_____个角；（4）由一点引出n条射线，共有_____个角；三．解答题：9.如图，O为直线AB上一点，∠AOD=90°.回答下列问题：(1)试比较∠AOB，∠AOD，∠AOE，∠AOC的大小.(2)在如图的角中找出三个等量关系.参考答案：1.A2.B3.C4.A5.A6.A7.30 36 1836 18068. （1）1 （2）3 （3）6 （4）()12 n n-9.(1)∠AOB>∠AOC>∠AOD>∠AOE(2)∠COE=∠DOE+∠COD，∠AOB=2∠AOD=∠AOE+∠BOE，∠DOB=∠COD+∠BOC.。

冀教版数学七年级上册 2.6角的大小同步测试(含答案)

冀教版数学七年级上册第二章几何的初步认识同步测试2.6角的大小本次测试共计分为三部分，单选、填空和解答题，总分100分，时间为60分钟。

一、选择题（共计10题，每题5分，共计50分）1、下列说法错误的是（）A．角的大小与角的边画出的部分的长短无关B．角的大小和它们度数的大小是一致的C．角的平分线是一条线段D．角的和差倍分的度数等于它们的度数的和差倍分2、下列四个选项中，表示的角最大的是( )3、借助一副三角尺,你能画出下面哪个度数的角( )A.65°B.75°C.85°D.95°4、下列说法:①角是由两条射线组成的图形;②角的边越长,角也越大;③以A为顶点的角可以表示为∠A;④一个角只有一个顶点.其中正确的个数为( )A.1B.2C.3D.45、已知∠MON与∠MOP，若OP在∠MON的内部，且∠MON＝60°，则∠MOP( )A. 一定是锐角 B．一定是直角 C．一定是钝角 D．可能是锐角6、40°15′的一半是 ( )A.20°B.20°7′C.20°8′D.20°7′30″7、如图，∠α的另一种正确的表示方法是：（）A、∠1B、∠CC、∠ACBD、∠ABC8、用一个放大10倍的放大镜看一个30°的角,看到的角的度数是( )A.300°B.30°C.3°D.无法确定9、时钟的分钟走过5分钟的角度是（）A、30°B、13°C、12°D、5°10、已知∠AOB=20°,∠BOC=65°,∠AOC=45°,那么( )A.射线OB在∠AOC外部B.射线OB在∠AOC内部C.射线OB与射线OA重合D.射线OB与射线OC重合二、填空题（共计5题，每题4分，共计20分）1、时钟4点15分时，时针和分针所成的角为_________2、一副三角板中，最大的角为________度，最小的角为________度3、3、如图，OC是∠AOB的平分线，那么，∠AOC=______=12_______，∠AOB=2_______=2_______4、从1时5分到1时35分，时钟的分针转了________º时针转了_______º5、一个角为N，则它的余角可以表示成_______；它的补角可以表示成_______三、解答题（共计2题，第1题10分，第2题20分，共计30分）1、请你试着做一做，作一个角等于∠MON．（用直尺和圆规）NOM2、如图所示,∠BOD=90°,∠COE=90°,解答下列问题:(1)图中有哪些小于平角的角?用适当的方法表示出它们;(2)比较∠AOC,∠AOD,∠AOE,∠AOB的大小,并指出其中的锐角、钝角、直角、平角;(3)找出图中所有相等的角.答案：一、选择题1—5 C D B A A6—10 D C B A A二、填空题1、37.5°2、90°30°3、∠BOC，∠AOB，∠AOC，∠BOC4、180°15°5、90°-N 180°-N三、解答题1、略3、解:(1)图中小于平角的角有∠AOC,∠AOD,∠AOE,∠COD,∠COE,∠COB,∠DOE,∠DOB,∠EOB.(2)由图可知,∠AOC<∠AOD<∠AOE<∠AOB其中∠AOC为锐角,∠AOD为直角,∠AOE为钝角,∠AOB为平角(3)∠AOC=∠DOE,∠COD=∠BOE,∠AOD=∠BOD=∠COE。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

2.6 角的大小同步练习
第1题. 一个角的补角的
1
3
等于它的余角，则这个角是度．第2题. 一个角的补角加上14°，等于这个角的余角的5倍，这个角的度数是．
第3题. 如果两个角互补，并且它们的差是30°，那么较大的角是 °．
第4题. 若90A B ∠+∠=︒，90B C ∠+∠=︒，那么____A C ∠∠，理由是．第5题. 已知：12201552'''∠-∠=︒，且122∠=∠，求1∠和2∠．
第6题. 如图，点O 是直线AD 上的点，AOB ∠，BOC ∠，COD ∠三个角从小到大依次相差25°，则这三个角的度数是．
第7题. 如图，78AOC BOD ∠=∠=︒，35BOC ∠=︒，则____AOD ∠=．
第8题. 某火车站的钟楼上装有一电子报时钟，在钟面的边界上每一分钟的刻度处都装有一只小彩灯，晚上九点三十五分二十秒时，时针与分针所夹的角α内装有只小彩灯．
第9题. 如图，O 是直线AB 上的点，OD 是AOC ∠的平分线，OE 是COB ∠的平分线，求DOE ∠的度数．
⑴一变：如图，90DOE ∠=︒，OD 平分AOC ∠，问OE 是否平分BOC ∠？ ⑵二变：如图，点O 在直线AB 上，且AOC BOC ∠≠∠，OD 平分AOC ∠，90DOE ∠=︒，下面四个结论，错误的有（） ①图中必有3个钝角； ②图中只有3对既相邻又互补的角； ③图中没有45°的角； ④OE 是BOC ∠的平分线．
A
B
C
D
O
A
B
C
D
O
A
B
C D E
O
Ａ．0个Ｂ．1个Ｃ．2个Ｄ．3个
第10题. 已知40AOB ∠=︒，OC 是AOB ∠的平分线，则AOC ∠的余角等于．
第11题. 如图，3540AOB '∠=︒，5030BOC '∠=︒，2118DOC '∠=︒，OE 平分AOD ∠，求BOE ∠的度数．
第12题. 若把一个平角三等分，则两旁的两个角的平分线所组成的角等于（）Ａ．
1
3
平角Ｂ．
1
2
平角Ｃ．
2
3
平角Ｄ．
3
4
平角
第13题. 已知AOB ∠和BOC ∠之和为180︒，这两个角的平分线所成的角（）Ａ．一定是直角Ｂ．一定是锐角Ｃ．一定是钝角Ｄ．是直角或锐角
第14题. 如图，O 是直线AB 上一点，120AOD ∠=︒，90AOC ∠=︒，OE 平分BOD ∠，则图中和为180︒的两个角有（）Ａ．3对Ｂ．4对Ｃ．5对Ｄ．6对
第15题. 已知：170AOB ∠=︒，70AOC ∠=︒，60BOD ∠=︒，求COD ∠的大小．第
16题. 互余且相等的两个角都是 °．
第17题. 一个锐角的补角比这个角的余角大 °．
第18题. 如图，已知2COB AOC ∠=∠，OD 平分AOB ∠，且20COD ∠=︒，求AO B ∠的度数．
A
B
C
D
E O
A
B
C D
E
O
A
B
C
D
O
第19题. 下列说法中错误的个数是（） ①线段有两个端点，直线有一个端点； ②角的大小与我们画出的角的两边的长短无关；③线段上有无数个点； ④同角或等角的补角相等； ⑤两锐角的和一定大于直角．Ａ．1个Ｂ．2个Ｃ．3个Ｄ．4个
第20题. 如图，平原上有A ，B ，C ，D 四个村庄，为解决当地缺水问题，政府准备投资修建一个蓄水池．
⑴不考虑其他因素，请你画图确定蓄水池H 点的位置，使它与四个村庄的距离之和最小． ⑵计划把河中的水引入蓄水池H 中，怎样开的渠最短？并说明根据．
第21题. 下列说法中正确的是（）
Ａ．一条射线把一个角分成两个角，这条射线是这个角的角平分线Ｂ．点到直线的距离是指从直线外一点到这条直线的垂线的长度Ｃ．若2MN MC =，则点C 是线段MN 的中点
Ｄ．有AB MA MB =+，AB NA NB <+，则点M 在线段AB 上，点N 在线段AB 外第22题. 已知线段AB ，在AB 的延长线上取一点C ，使2AC BC =，在AB 的反向延长线上取一点D ，使2D A A B =，那么线段AC 是线段DB 的（）Ａ．
1
3
Ｂ．
23
Ｃ．
12
Ｄ．
32
第23题. 已知∠α与∠β互余，且∠α=40°，则∠β的补角为度．第24题. 请你用三角板、圆规或量角器等工具，画∠P OQ =60°，在它的边OP 上截取OA =50 mm ，OQ 上截取OB =70 mm ，连结AB ，画∠AOB 的平分线与AB 交于点C ，并量出AC 和OC 的长．(结果精确到1 mm ，不要求写作法).
第25题. 已知α50∠=，那么它的补角等于．
第26题.
图中给出的各角中，哪些互为余角？哪些互为补角？
A B C
D
E
F
10°
30°
60°
80°
100°
120°
150° 170°
参考答案
1.答案：45．
2.答案：64°．
3.答案：105．
4.答案：＝；同角的余角相等．
5.答案：解：设2∠为x ︒，则1∠为2x ︒，则 2201552x x '''︒-︒=︒
201552x '''︒=︒， 2403144x '''︒=︒，
答：2∠为201552'''︒，1∠为403144'''︒． 6.答案：35°，60°，85°． 7.答案：121°． 8.答案：12．
9.答案：解：由题意可知12DOC AOC ∠=∠，1
2
EOC BOC ∠=∠．因为AB 是一条直线，所以180AOB ∠=︒，也就是180AOC BOC ∠+∠=︒，
11
9022
DOE DOC EOC AOC BOC ∠=∠+∠=∠+∠=︒．
⑴解：因为180AOC BOC ∠+∠=︒，90DOE ∠=︒，
所以1()2DOE AOC BOC ∠=∠+∠11
22
AOC BOC =∠+∠，
而DOE DOC EOC ∠=∠+∠，1
2
DOC AOC ∠=∠，
所以1
2
COE BOC ∠=∠，即OE 平分BOC ∠．
⑵Ａ．
10.答案：70° 11.答案：解：
35405030211810728AOD AOB BOC COD ''''
∠=∠+∠+∠=︒+︒+︒=︒1
53442
AOE AOD '∠=∠=︒
53443540184BOE AOE AOB '''∠=∠-∠=︒-︒=︒
12.答案：Ｃ． 13.答案：Ａ． 14.答案：Ｄ．
15.答案：40°或60°或160°或180°． 16.答案：45 17.答案：90
18.答案：120°19答案：Ｂ．
20答案：解：⑴连结AD ，BC ，交于点H ，则H 为所求的蓄水池点．
⑵过H 作HK EF 于K ，沿HK 开挖，可使开挖的渠最短，依据是：“点与直线的连线中，垂线段最短”．（如图）
21.答案：Ｄ． 22.答案：Ｂ． 23.答案：130
24.答案：画出图形(基本正确即可)AC =26 mm ，OC =50 mm. 25.答案：130．
26.答案：互余：10°和80°；30°和60°．
互补：100°和80°；120°和60°；150°和30°；170°和10°．
A B C
D
E
F
H K。