线性模型参数的估计理论(陈希孺[等]著)思维导图
合集下载
一元线性回归模型参数的最小二乘估计 课件 (共27张PPT) 人教A版(2019)选择性必修第三册
R2 = 1-
(yi -
i )2 = 1-
残差平方和
(yi - y)2
总偏差平方和
①和②的R2分别为0.7325和0.9983
R2越大 ，表示残差平方和越小 ，即模型的拟合效果越好； R2越小 ，表示残差平方和越大 ，即模型的拟合效果越差. 显然0≤R2 ≤1 ， R2越接近1 ，则线性回归刻画的效果越好.
2 ≈ 0 .669, Q 2 =
2 ≈ 0 .004
Q2明显小于Q1 ，说明非线性回归方程的拟合效果 要优于线性回归方程.
探究新知
思考 ：对于通过创纪录时间预报世界纪录的问题 ，我们建立了两个回归模型， 得到了两个回归方程 ，你能判断哪个回归方程拟合的精度更好吗？
（3) 利用决定系数R2刻画回归效果.
1.残差等于观测值减预测值 = y -
2.残差的平方和越小越好； 3.原始数据中的可疑数据往往是残差绝对值过大的数据； 4. 对数据刻画效果比较好的残差图特征:残差点比较均匀的集 中在水平带状区域内 .
一般地, 建立经验回归方程后,通常需要对模型刻画数据的效 果进行分析.借助残差分析还可以对模型进行改进,使我们能根据改 进模型作出更符合实际的预测与决策.
探究新知
思考: 儿子身高与父亲身高的关系 ，运用残差分析所得的一元线性回归模型的 有效性吗？
: 作图时纵坐标为残差, 横坐标可以选为样本编号, 或身高数据 或体重估计值等 ，这样作出的图形称为残差图 .
探究新知
为了使数据更加直观 ，用父亲身高作为横坐标 ，残差作为 纵坐标 ，可以画出残差图 ，如下图所示：
再根据求解线性回归模型的方法求出a, b. 求解线性回归模型的方法求出a, b.
1.残差平方和
第四章线性系统参数估计的最小二乘法
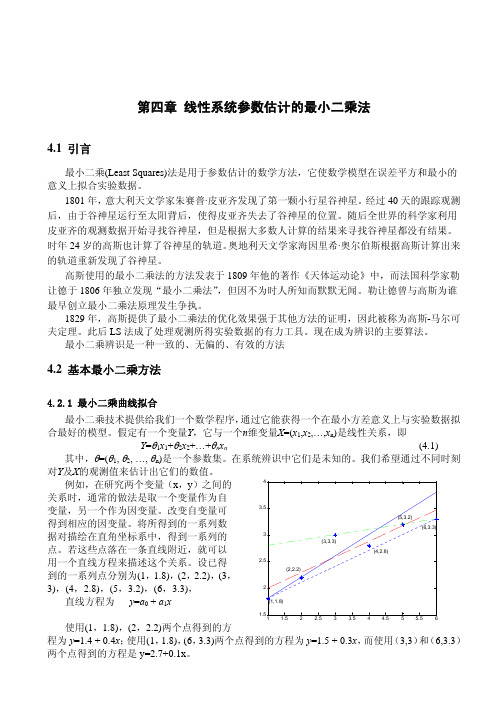
下面讨论更为一般的情况。 假设在t1, t2, …, tm时刻对Y及X的观测值序列已经被我们获得，并且用
y(i), x1(i), x2(i), x3(i), … i = 1,2, …, m 来表示这些观测数据。显然，可以用 m 个方程组来表示量测数据与估计值之间的关系
⎧ y(1) = θ1x1(1) +θ 2 x2 (1) +L+θ n xn (1)
从图中可看到，前两条线都仅能满足两个点的要求，而对其它点的误差都很大，其 6 个点的 误差平方累计分别为 0.49 和 0.42。第三条线能满足三个点的要求，但误差平方累计更大，为 1.58。 显然我们需要找到一条更为理想的直线来取得较小的误差。例如图中的红色短划线，它的方程 为 y=1.697 + 0.294x，误差平方累计为 0.25。这条线是怎样得到的呢？它是用最小二乘法得到的。
z
−2
，在其输入端加入 M 序列输入后
所得到的输出输入数据见下表，请利用这些数据辨识出系统的传递函数的系数。
k
1
2
3
4
5
6
7
8
9
10
输入 u
1
0
1
1
0
0
1
1
1
0
输出 y -0.45 -0.01
1.15
2.56
1.92
-0.30 -0.80 0.91 2.92 2.40
解： 已知系统阶数 n=2，有 4 个未知数。将式（4.4）展开 y(k) = −a1 y(k −1) − a2 y(k − 2) + b0u(k) + b1u(k −1) 根据要求，观测次数 N>2n+1，取 N 为 6，k=3
第2章古典线性回归模型-59页PPT文档资料
E(β XX1Xε -β )(β XX1Xε -β )
E X X 1 X ε ε X X X 1 X X 1 X E ε ε ( ) X X X 1
X X 1 X E2 I ( n ) X X X 1 2 X X 1
三、 参数估计量的性质
性质1 βˆ 是随机向量y的一个线性变换。
β ˆ (XX)-1Xy 性质2 βˆ 是β的无偏估计。
E(βˆ ) E ((X X)-1 Xy) (X X)-1XE(y) (X X)-1XE( Xβε) (X X)-1X Xββ
性质 3 D（βˆ )=σ 2(X′X)-1
Lxx
x 2
Lxx
2
L xx
性质四（高斯-马尔可夫定理）
在假设 E( y) X ，D( y) 2In 下， 的任一线性函数 的 最小方差线性无偏估计为 ˆ ，其中 是任一不为零的 p 1 维向量， ˆ 是 最小二乘估计。 证明：（1）ˆ ( X X )1 X y 是 y 的线性函数，所以是线性估计。
D(β ˆ)coβ vˆ,β (ˆ)
E(β ˆ(Eβ ˆ)β (ˆEβ ˆ))E(β ˆ(β )β (ˆβ ))
EXX1XyβXX1Xyβ
EXX1X(Xβ ε )β XX1X(Xβ ε )β
在正态假定下:
y～N(Xβ, 2In)
E(y)=Xβ
var(y)= 2In
3. 多元线性回归方程的解释
例1
y表示空调机的销售量,
x1表示空调机的价格, x2表示消费者可用于支配的收入。
y=β0+β1x1+β2x2+ε
8.2.1一元线性回归模型-高二数学精品课件(人教A版2019选择性必修第三册)
，得到的数据如下表所示.
编号
1
2
3
4
5
6
7
8
9
10
11
12
13
14
父亲身高/cm 174 170 173 169 182 172 180 172 168 166 182 173 164 180
儿子身高/cm 176 176 170 170 185 176 178 174 170 168 178 172 165 182
下面，我们用散点图对上面的数据进行分析。
新知讲解
问题1 这是上述的数据画出来的散点图，你发现了什么？
如图所示.可以发现，散点大致分布在一条
从左下角到右上角的直线附近，表明儿子
身高和父亲身高线性相关.
利用统计软件，求得样本相关系数为 ≈
. ，表明儿子身高和父亲身高正线性
相关，且相关程度较高.
如母亲身高、生活环境、饮食习惯等作为随机误差，得到刻画两个
变量之间关系的线性回归模型.其中，随机误差是一个随机变量.
概念生成
用表示父亲身高，表示儿子身高，表示随机误差.假定随机误差
的均值为，方差为与父亲身高无关的定值 ，则它们之间的关系
= + + ，
可以表示为
() = ，() = .
的没有线性相关关系；当||＝时，成对数据都落在一条直线上.
新课导入
通过前面的学习，我们已经了解到，根据成对样本数据的散点图和样本相关
系数，可以推断两个变量是否存在相关关系、是正相关还是负相关，以及线
性相关程度的强弱等.
进一步地，如果能像建立函数模型刻画两个变量之间的确定性关系那样，通
过建立适当的模型刻画两个随机变量的相关关系，那么我们就可以利用这个
编号
1
2
3
4
5
6
7
8
9
10
11
12
13
14
父亲身高/cm 174 170 173 169 182 172 180 172 168 166 182 173 164 180
儿子身高/cm 176 176 170 170 185 176 178 174 170 168 178 172 165 182
下面，我们用散点图对上面的数据进行分析。
新知讲解
问题1 这是上述的数据画出来的散点图，你发现了什么？
如图所示.可以发现，散点大致分布在一条
从左下角到右上角的直线附近，表明儿子
身高和父亲身高线性相关.
利用统计软件，求得样本相关系数为 ≈
. ，表明儿子身高和父亲身高正线性
相关，且相关程度较高.
如母亲身高、生活环境、饮食习惯等作为随机误差，得到刻画两个
变量之间关系的线性回归模型.其中，随机误差是一个随机变量.
概念生成
用表示父亲身高，表示儿子身高，表示随机误差.假定随机误差
的均值为，方差为与父亲身高无关的定值 ，则它们之间的关系
= + + ，
可以表示为
() = ，() = .
的没有线性相关关系；当||＝时，成对数据都落在一条直线上.
新课导入
通过前面的学习，我们已经了解到，根据成对样本数据的散点图和样本相关
系数，可以推断两个变量是否存在相关关系、是正相关还是负相关，以及线
性相关程度的强弱等.
进一步地，如果能像建立函数模型刻画两个变量之间的确定性关系那样，通
过建立适当的模型刻画两个随机变量的相关关系，那么我们就可以利用这个
广义线性模型_九_陈希孺
文章编号:1002—1566(2004)01—0077—04广义线性模型(九)陈希孺(中国科学院研究生院,北京100039)摘要:本讲座是广义线性模型这个题目的一个比较系统的介绍。
主要分3部分:建模、统计分析与模型选择和诊断。
写作时依据的主要参考资料是L .F ahrmeir 等人的《M ultivariate Statistical M od -eling Based o n Generalized Linear M odels 》。
关键词:广义线性模型;建模;统计分析;模型选择和诊断中图分类号:O212文献标识码:AGeneralized Linear ModelsCHEN Xi -ru(Graduate school of Chinese academia of science ,Beijing 100039,China )A bstract :This set of articles gives an introduction to generalized linear models .T hey can be divided into three parts ;M odel building ,statistical inference and M odel diagnostics .The presentation is mainly based on L .Fahrmeir et al .《M ultivariate Statistical M odeling Based on G eneralized Linear M odels 》.Key words :g eneralized linear models ;model building ;statistical inference ;model diagnostics3.2 模型选择(一)从若干个备选模型中选取一个模型选择包含以下一些方面·因变量Y 分布的选择;·联系函数的选择;·自变量的选择;·z (x )的选择。
程老师计量经济学线性回归模型概述和一元模型参数估计.pptx
5
2024/11/25
P(Y 65 X 80) P(Y 70 X 80) P(Y 75 X 80) 1 .
5
5
第6页/共25页
• 对于同一等级收入水平，消费支出Y的平均值称
为条件期望，记为E（Y｜X）。
例如: E(Y X 80) 55 1 60 1 65 1 70 1 75 1 65 55555
身高的趋势，而矮个子父母的子女身高有高于其父母身
高的趋势，结论：父母所生子女有回归于人类平均身高 的趋势，故某人种的平均身高是相当稳定的。
——见1889年F.Gallton的论文《普用回归定律》。
回归的含义：任何变异的东西总有趋向于一般、平稳 的势头。
后来人们将此种方法普遍用于寻找变量之间的规律 。
1997 1904 8651 645.1429 3151 1962.851 -58.85057 -3.09%
2024/11/2平5 均百分误差在10%以内，表第明22页是/共一25个页 拟合得比较好的模型
21
拟合优度R2
1、作业记录
2.估计结果：系数、标准误差、 T统计量、显著性水平prob
残差标准差SE
边际消费<消费与收 入的比重。
y
y y
实际上消费与收入之间的关系式并不是准确的。 原因在于：
（1）消费还受到除收入以外的因素的影响； （2）线性关系是一种近似关系； （3）收入、消费数据也是一个近似 。
2024/11/25
3
第4页/共25页
• 为了更准确、符合实际地描述消费与收 入间的关系，必须引入随机误差μ。
随机扰动项是不可观察的，但可通过残差 （实际值与拟合值的差）进行估计。
2024/11/25
9
2024/11/25
P(Y 65 X 80) P(Y 70 X 80) P(Y 75 X 80) 1 .
5
5
第6页/共25页
• 对于同一等级收入水平，消费支出Y的平均值称
为条件期望，记为E（Y｜X）。
例如: E(Y X 80) 55 1 60 1 65 1 70 1 75 1 65 55555
身高的趋势，而矮个子父母的子女身高有高于其父母身
高的趋势，结论：父母所生子女有回归于人类平均身高 的趋势，故某人种的平均身高是相当稳定的。
——见1889年F.Gallton的论文《普用回归定律》。
回归的含义：任何变异的东西总有趋向于一般、平稳 的势头。
后来人们将此种方法普遍用于寻找变量之间的规律 。
1997 1904 8651 645.1429 3151 1962.851 -58.85057 -3.09%
2024/11/2平5 均百分误差在10%以内，表第明22页是/共一25个页 拟合得比较好的模型
21
拟合优度R2
1、作业记录
2.估计结果：系数、标准误差、 T统计量、显著性水平prob
残差标准差SE
边际消费<消费与收 入的比重。
y
y y
实际上消费与收入之间的关系式并不是准确的。 原因在于：
（1）消费还受到除收入以外的因素的影响； （2）线性关系是一种近似关系； （3）收入、消费数据也是一个近似 。
2024/11/25
3
第4页/共25页
• 为了更准确、符合实际地描述消费与收 入间的关系，必须引入随机误差μ。
随机扰动项是不可观察的，但可通过残差 （实际值与拟合值的差）进行估计。
2024/11/25
9
一元线性回归模型参数的最小二乘估计 第1课时-高二数学课件(人教A版2019选择性必修第三册)
2
i =1
n
=b
2
( x - x)
i
i =1
n
2
n
2b ( xi - x )( yi y ) + ( yi y ) .
2
i =1
i =1
上式是关于b的二次函数，因此要使Q取得最小值，
当且仅当b的取值为 n
( xi - x )( yi y )
bˆ = i =1 n
.
2
( xi - x )
174.943
171.587
174.104
170.748
181.655
173.256
179.977
173.256
169.909
168.231
181.655
174.104
166.553
179.977
残差/cm
1.057
4.413
−4.104
−0.748
3.345
2.735
−1.977
0.735
0.091
−0.231
−3.655
−2.104
−1.553
2.023
为了使数更加直观，用父亲身高作为横坐标，残差作
为纵坐标，可以画出残差图，如下图所示.
残差 / cm
5
4
3
2
1
0 160 165
-1
-2
-3
-4
-5
170
175
180
父亲身高 / cm
185
观察残差表可以看到，残差有正有负，残差的绝对值
最大是4.413. 观察残差的散点图可以发现，残差比较均匀
i =1
综上，当a, b的取值为
i =1
n
=b
2
( x - x)
i
i =1
n
2
n
2b ( xi - x )( yi y ) + ( yi y ) .
2
i =1
i =1
上式是关于b的二次函数，因此要使Q取得最小值，
当且仅当b的取值为 n
( xi - x )( yi y )
bˆ = i =1 n
.
2
( xi - x )
174.943
171.587
174.104
170.748
181.655
173.256
179.977
173.256
169.909
168.231
181.655
174.104
166.553
179.977
残差/cm
1.057
4.413
−4.104
−0.748
3.345
2.735
−1.977
0.735
0.091
−0.231
−3.655
−2.104
−1.553
2.023
为了使数更加直观，用父亲身高作为横坐标，残差作
为纵坐标，可以画出残差图，如下图所示.
残差 / cm
5
4
3
2
1
0 160 165
-1
-2
-3
-4
-5
170
175
180
父亲身高 / cm
185
观察残差表可以看到，残差有正有负，残差的绝对值
最大是4.413. 观察残差的散点图可以发现，残差比较均匀
i =1
综上，当a, b的取值为
选择性必修第三册8.2.2一元线性回归模型参数的最小二乘估计课件(人教版)(1)
编号 胸径/cm 树高/cm
1 2 3 4 5 6 7 8 9 10 11 12 18.1 20.1 22.2 24.4 26.0 28.3 29.6 32.4 33.7 35.7 38.3 40.2 18.8 19.2 21.0 21.0 22.1 22.1 22.4 22.6 23.0 24.3 23.9 24.7
yˆ2 0.4264398 ln(t 1895) 11.8012653.
②
在同一坐标系中画出成对数据散点图、非线性经验回归方程②的图象(蓝色) 以及经验回归方程①的图象(红色)，如图(5)所示. 我们发现，散点图中各散点都 非常靠近②的图象，表明非线性经验回归方程②对于原始数据的拟合效果远远 好于经验回归方程①.
问题人”. 下表给
出了1968年之前男子短跑100m世界纪录产生的年份和世界纪录的数据. 试
根据这些成对数据，建立男子短跑100m世界纪录关于纪录产生年份的经验
回归方程.
编号
12345678
年份
1896 1912 1921 1930 1936 1956 1960 1968
两个经验回归方程的残差(精确到0.001)如下表所示.
编号
t
eˆ uˆ
1 1896 0.591 -0.001
2 1912 -0.284 0.007
3
4
1921 1930
-0.301 -0.218
-0.012 0.015
5 1936 -0.196 -0.018
6 1956 0.111 0.052
7 1960 0.092 -0.021
i 1
i 1
∴ R2 1 0.01318 0.9991. 14.6784
0.025 2.31
一元线性回归模型及参数估计ppt课件
X
i
i
可见，在满足一系列基本假设的情况下，模
型结构参数的最大或然估计量与普通最小二乘估 计量是相同的。
15
但是，随机误差项的方差的估计量是不同的。
解或然方程
s
2 m
L*
=
n
2s
2 m
+
1
2s
4 m
S(Yi
bˆ0
bˆ1 X i )2
=
0
即可得到sm2 的最大或然估计量为：
sˆ
2 m
22
3、有效性：在所有线性无偏估计量中，最 小二乘参数估计量具有最小方差。
23
（1）先求bˆ0 和bˆ1 的方差
Var(bˆ ) = Var( k Y ) =
1
ii
k 2Var(b
i
0
+b X
1i
+
m
i
)
=
x
i
x2
i
2
s
2 m
=
s
2 m
Sx2
i
Var(bˆ ) = Var w Y
条件 ，当
Q
对
b$ 0
、
b$ 1
的一阶偏导数为
0 时， Q 达到最小。即
Q
bˆ0 Q
bˆ1
=0 =0
(bˆ0 (bˆ0 +
+ bˆ1 bˆ1 X
X i
i
Yi) Yi) X
=
i
0 =
0
S Yi = nbˆ0 + bˆ1S X i
广义线性模型_三_陈希孺
大多数有序模型是按下述机制产生 : 有一个( 或几个 , 此处只考虑一个的情形) 明显或潜在 ( 1. 70)
此处 Y 记样品的序值( 勿与前面的 Y = ( Y( ) ′ 混淆) 。 而 U 则是从该样品测 1), …, Y ( q) 得的值 。 例如 , 学生的考试成绩分不及格( 1) , 中( 2) , 良( 3) , 优( 4) 4 个等级 , U 为其考试分数 。
+x′ β r P( Y > r | x )= 1 -F ( θ β)= exp( - eθ ) r + x′
( 1. 76) ( 1. 77)
因此 log ( -log P ( Y > r |x ) )= θ β r + x′ 3 . 极大值分布模型 F 为极大值分布 : F( t) = exp( -e -t ) ,有 P( Y ≤ r |x )= exp( -e ) -log ( -log P ( Y ≤ r | x) )= θ β r + x′ 78) 知
年龄 吸烟史 从不吸 以前吸 现在吸 结果( 人数) 正常 边缘 不正常 577 192 682 27 20 46 4 15 47 7 3 11 0 7 27
〈40
调查某大学心理系即将毕业的学生对照工作前景的预 从不吸 164 期反应分 3 种 : 1. 不预期能找到合适工作 。 2 . 不清楚 。 3 . 40 -59 以前吸 145 预期毕业后可立即找到工作 。 数据 : 现在吸 245 的变量 U 及门限 -∞=θ 0 <θ 1 <… <θ k -1 <θ k =∞, 而定 Y = r , 当且仅当 θ r1 <U ≤θ r , r =1, …, k
( 四) 状态有序的情况 在旅行交通工具的例中 , 火车 、 汽车 、 轮船 、 飞机等状态 , 可以认为是 “ 无序” 的 。 一则因为 对其优劣次序的看法因人而异 , 二则即使同一个人 , 在不同情况下的排序也不同 。 在有些问题 中 , 目标状态有公认的优劣次序 , 如病情分 1 、 2、 3 期 , 产品品质分 1 、 2、 3 和等外等等级 , 都是公 认的由好到不好的次序 。 注意 : 即使在这种场合 , 其序号( 1 , 2 , …) 也无数量意义 。 例 1. 7 呼吸测验 : 目标 Y 分 3 状态 : 正常 、 边缘 、 不正 常 。 自变量 2 个 : 年龄 , 分〈40 和 40 -59 两级 , 吸烟史 : 分 “ 从不吸烟” 、 “以前级” 、 “ 现在吸” 3 级 , 数据 : 例 1. 8 找工作前景的调查