数字化信息编码与数制转换
数制与编码

第一章数制与编码1.1 数制数制是计数的方法,通常采用进位计数制。
在进位计数制的多位编码中,数制是:⏹ 每一位的构成方法,以及⏹ 从低位到高位的进位规则。
常用的数制:⏹ 二进制(Binary )、 ⏹ 八进制(Octal )、 ⏹ 十进制(Decimal )、 ⏹ 十六进制(Hex-decimal )。
例如:十进制:⏹ 每一位——十进制数由0~9个数字符号(数码)和小数点组成, ⏹进位规则——“逢十进一”(基数为10)。
1.1.1 记数法和分析方法记数法——位置记数法, 分析方法——按权展开式。
例如:十进制数(652.5)10=6×102+5×101+2×100+5×10-1左边为“位置记数法”,右边为“按权展开式”。
代数式为:∑⨯=iiikD 10说明:每一个数位上的数码有不同的权值, ⏹ 权值从左到右以基数的幂次由大到小, ⏹ 数位从左到右由高位到低位排列。
例如:二进制数(101.11)2 = 1×22+0×21+1×20+1×2-1+1×2-2任意进制(基数为R )记数法:∑--=----==110121).()(n mi iiR m n n R R kk k k k k k D八进制和十六进制的按权展开式以此类推。
位置记数法 按权展开式1.1.2 数制转换数值相等,记数方法(数值)不同的数之间的转换。
数制转换的本质是——权值的转换。
1.1.2.1 任意进制到十进制的转换利用任意进制数的按权展开式,可以将一个任意进制数转换成等值的十进制数。
例如:(1011.01)2 =1×23+0×22+1×21+1×20+0×2-1+1×2-2=(11.25)10例如:(8FA.C)16=8×162+F ×161+A ×160+C ×16-1=2048+240+10+0.75=(2298.75)101.1.2.2 “十 二”进制转换考查整数部分,数的二进制按权展开式:设:(D )10可以由n 位二进制数表示,即 (D )10=(k n -1k n -2,…,k 1k 0)2 存在:(D )10=k n -1×2n -1+k n -2×2n -2+…+k 1×21+k 0×20 (D )10/2= k n -1×2n -2+k n -2×2n -3+…+k 1×20 + k 0 / 2((D )10/2商的整数部分)/2= k n -1×2n -3+k n -2×2n -4+…+k 2×20 + k 1 / 2“孤立”余数后,整数的商再除以基数2,依次类推;余数依次为从低到高位的二进制数位。
数制的转换与编码

数制的转换十进制数和二进制,八进制,十六进制数的转换。
1将二进制,八进制,十六进制数转换为10进制数。
用对应的数位的值乘以进制的权值,然后累加。
(前面讲过)2 将十进制数转换为二进制,八进制,十六进制数。
将十进制数除以对应的进制,取其余数,然后逆序陈列即可。
(辗转相除法)例如将十进制数194进行转换成二进制。
194除以2得到97余097除以2得到48 余148除以2 得到24 余024除以2 得到12 余012除以2 得到6 余06除以2得到3 余03除以 2 得到1 余 11除以2 得到0 余1 逆序即可得到11000010同理可以得到八进制数为302Q可以得到十六进制数位D2H上面讲述的都是针对整数的情况,非整数,也可以用同样的方法,只是把除变为乘,逆序变为正序即可,可以根据精确到的位数求对应的进制数。
如将十进制234.56转换为2进制,精确到小数点后第5位小数点前面可以同上,对于小数点后用0.56*2(二进制)若是八进制则乘以8,十六进制则乘以16(这里转换为2进制为例)得到1.12取整数部分1 余下0.12用0.12乘以 2 得到0.24取整数部分0用0.24乘以 2得到 0.48取整数部分为0用0.48乘以 2得到 0.96取整数部分为 0用0.96乘以 2得到 1.92取整数部分为 1用0.92乘以 2得到 1.84取整数部分为 1…所以结果为 11101010.10001。
3 将十六进制,八进制,转换成二进制的转换。
①十六进制数是四位二进制数,将八进制数是三位二进制数。
将十六进制数转换为二进制,只需用四位二进制表示十六进制的一个数,例如0用0000表示,1用0001表示,2用0010表示,…A用1010表示,B用1011表示,C 用1100表示,D用1101表示,E用1110表示,F用1111表示。
(0—15)如12FB3H用二进制表示为0001 0010 1111 1011 0011同理八进制的数也可以表示(0—7)如将13507Q转换为二进制001 011 110 000 111②将二进制转换成为八进制,十六进制,只需将二进制数进行三位(八进制),四位(十六进制)划分即可例如1101011000111010 转换成八进制先划分从低位开始划分不够位数的补01/ 101/ 011/ 000/ 111/ 010补0为001/ 101/ 011/ 000/ 111/ 010变换成八进制的数即为153072Q同理转换成十六进制的数为1101/0110/0011/1010 转换成十六进制的数字即为D63AH4 将十六进制数转换为八进制的转换。
计算机《数制和编码进制转换》公开课教案设计

数制与编码——进制变换【学情剖析】本课内容是在学生已经学习了计算机发展与应用、计算机系统的组成等知识的基础长进行,已经初步知道了人与计算机进行信息互换往常使用程序设计语言,程序设计语言经历了三个阶段:机器语言、汇编语言和高级语言。
机器语言是机器指令序列,是一串 0 和 1 构成的二进制编码,是独一能被计算机识其余语言。
那么要认识计算机是怎样将我们发出的信息变换成数字编码以前,我们一定先认识掌握各样数制及互相间的变换。
这节课内容许多,学生理解起来比较困难,依据讲堂需要和学生特色,既要让学生有信心、热忱地学习新知识,又要让他们主动踊跃地参加到整个教课活动中来。
【课时安排】 2 课时【讲课形式】讲解、多媒体教课【教课方法】讲解法、练习法、问答法、演示法【教课器具】计算机、黑板、多媒体、课件【教课目的】知识目标 : 1、认识数制、基、基数及位权的观点;2、掌握二进制、十进制、八进制、十六进制的表示方法;3、掌握二进制与十进制间互相变换的方法。
技术目标 : 1、培育学生逻辑运算能力;2、培育学生剖析问题、解决问题的能力;3、培育学生独立思虑问题的能力。
感情目标:经过数制变换的学习培育学生的计算机科学修养 , 同时,让学生领会到仔细的学习态度,谨慎仔细的学习习惯。
【教课要点】1、进制、基数、位权的观点。
2、二进制与十进制间互相变换方法。
【教课难点】二进制与十进制间互相变换【教课过程】一、师生问好,考勤二、复习旧识,导入新课(以下教师的语言、活动简称“师” ,学生的活动简称“生” )前引入:师:我想大家做一道算:110+110= ?(学生几乎都回答等于220)。
师:那么 220 个答案是不呢?能够,也能够不。
在学本以前,回答220 是正确的,但是,在我学完今日的知后,答案就不一是220了。
什么呢?( 设疑,学生思虑,教师点名个别学生回答)师:到数字,有好多同学可能会的很可笑,不就是1234⋯⋯是的,在生活中,我用的一般都是十制。
数字电路_2数制和编码

? 区位码——GB 2312的所有字符分布在一个94行×94列的二维平面内,行号称为区号,列号称 为位号。区号和位号的组合就可以作为汉字字符的编码,称为汉字的区位码。
加法
减法
十六进制
? 由于二进制数在使用时位数太长,不容易记忆,所以又推出了十六进制数。 ? 十六进制数有两个基本特点:
? 它由十六个字符 0~9以及A,B,C,D,E,F组成(它们分别表示十进制数 10~15);
? 十六进制数运算规律是逢十六进一,即基 R=16=2 4,通常在表示时用尾部标志 H或下标 16以示区别。 例如:十六进制数 4AC8可写成( 4AC8 )16,或写成 4AC8H 。
B表示。 例如:二进制数 10110011 可以写成( 10110011 )2,或写成 10110011B ? 对于十进制数可以不加注基数;
十进制
(D) 0 1 2 3 4
56
7
8
9 10
二进制 (B) 0 1 10 11 100 101 110 111 1000 1001 1010
计算机采用二进制数
(101.11)B= 1×22 +0×21+1×20+1×2-1+1×2-2 =(5.75)D
各数位的权是2的幂
十进制数 →二进制数 将整数部分和小数部分分别进行转换。
整数部分 ---除2取余,逆序排列 ; 合并
小数部分 ---乘2取整,顺序排列。
? 十进制数 44.375 转换成二进制等于多少?
(44.375)D=(?)B
十六进制数 →二进制数
? 十六进制数转换为二进制数时正好与上面所述相反,只要将每位的十六进制数对应的 4 位二进制写出来就行了。
计算机中的数制及其编码

一、计算机中的数制及其转换
2. 数制之间的转换
(4) 二、十六进制之间的转换
二进制十六进制: 以小数点为界,分别向左、向右四位一组分段,不足四位 补0(整部在前,小数部分在后),然后将每段换成对应的十 六进制数码。 十六进制二进制: 将每位十六进制数码换成对应的四位二进制数,然后去前 后无效的0。 例7 (10110101.10101011)2 =(1011 0101. 1010 1011)2 =(B5.AB)16 (56A.C4)16 =(0101 0110 1010. 1100 0100)2
一、计算机中的数制及其转换
2. 数制之间的转换
(2) 十进制数转换为非十进制数
例4 (123.45)10 =(? 2 123……..1 2 61…….1 2 30……0 2 15…...1 2 7…..1 2 3…..1 2 1….1 0 )2 低位
0
1
高位
除 到 商 为 0 时 停 止
1
1 0 0 1
一、计算机中的数制及其转换
2. 数制之间的转换
(1) 非十进制数转换为十进制数
例2:(345.67)8 = 3*82 + 4*81 + 5*80 + 6*8-1 + 7*8-2 = 192 + 32 + 5 + 0.75 + 0.109375 = (229.859375)10
例3: (2FA.D)16 = 2*162 + 15*161 + 10*160 + 13*16-1 = 512 + 240 + 10 + 0.8125 = (762.8125)10
+101.0001 1111.0001 10.1 ×100 000 000 +101 10100 101.0001 11001.0101 101 101 101
第二讲(数制转换与码制)

将(376.4)8转换为十进制数。
1
3 64 7 8 6 1 4 0 . 125 ( 254 . 5 ) 10
将(3AB.11)16转换为十进制数。
( 3 AB . 11 ) 16 3 16 10 16 11 16 1 16
3 2 1 0
将(207)8转换为十进制数。
( 207 ) 8 2 8
2
08 78
1
0
2 64 7 1
135
将(7F)16转换为十进制数
1 0 ( 7 F ) 16 7 16 15 16 7 16 15 1 127
§3.1非十进制数转换为十进制数
§3.3二进制数、八进制数、十六进制数间的转换
八进制数、十六进制数转换为二进制数 将(764.23)8、(F09.B8)16转换为二进制数
八进制 7
6
4
.
2
3
二进制 111 110 100 . 010 011 所以(764.23)8=(111110100.010011)2 十六进制 F 0 9 . B 8
若十进制数较大时,不必逐位去除2,可算出2的幂与十 进制对比,如: (261)10 =(?)2 ∵28 =256 而 261 – 256 = 5 ,(5)10=(101)2
∴(261)10=(100000101)2 将(0.25)10转换为二进制数。
0.25 2 0.50 2 1.00
……..取出整数0作为小数部分的最高位 ……..取出整数1作为小数部分的最低位
由于最后的小数小于0.5,根据“四舍五入”的原则,应为0。
所以,(382.45) 10=(17E.73) 16。
1-2计算机的数制与编码
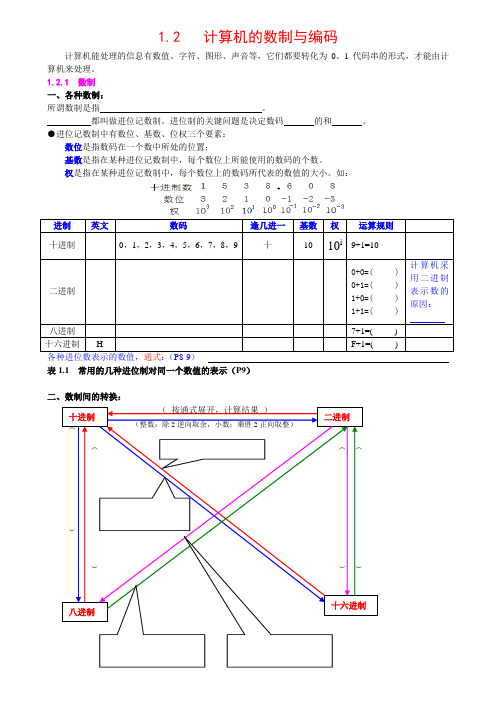
1.2 计算机的数制与编码计算机能处理的信息有数值、字符、图形、声音等,它们都要转化为0、1代码串的形式,才能由计算机来处理。
1.2.1 数制 一、各种数制:所谓数制是指 。
都叫做进位记数制。
进位制的关键问题是决定数码 的和 。
●进位记数制中有数位、基数、位权三个要素: 数位是指数码在一个数中所处的位置;基数是指在某种进位记数制中,每个数位上所能使用的数码的个数。
权是指在某种进位记数制中,每个数位上的数码所代表的数值的大小。
如:表1.1 常用的几种进位制对同一个数值的表示(P9)二、数制间的转换:例:(重点:十进制与二进制的互相转换)●各种进制转十进制●十进制转各种进制●二进制转八进制、八进制转二进制与二进制转十六进制、十六进制转二进制练习:P39:20、21、22、23、24、25、26、27、28、29(写在课本上)如何检查?(计算器!)1.2.2 ASCII码●通称为字符。
字符没有数值意义。
为了便于计算机的应用推广,这些字符必须用统一的规定编码方式来表示。
目前在国际上广泛采用“”表示、和作为使用的等。
●ASCII码的英文全称:,中文。
●ASCII码用位0、1代码串来编码一个符号,每个符号占的存储空间,字节最高位(左)为,作奇偶校验用。
(注:1字节= 位,一个字符的ASCII码占位,余下位用作)●ASCII码给出了个数码,个英文字母,个通用符号,个动作控制符的编码标准。
◆例:查表P308(1)字母“A”的ASCCII的二进制表示为:,十六进制表示为:,十进制表示为:(2)将字符“2”的ASCII码当成数值,转换为十进制数得到50,数字字符“5”的ASCII码转换为十进制数应得到●ASCII码的比较:(详见附录1:P308)空格(space)的ASCCII码是32‘0’~‘9’的ASCCII码是48~57‘A’~‘Z’的ASCCII码是65~90‘a’~‘z’的ASCCII码是97~1221.2.3 汉字编码1.国标码GB 2312-80《》1级汉字个,按顺序排列、2级汉字个,按排列,汉字有6763个,常用符号、字母、图形符号等682个,共计7445个。
中职计算机应用基础(计算机常用数制转换与信息编码)逐字稿(数制转换超级简单易懂)
计算机常用数制转换与信息编码逐字稿一、数制概念及特点(一)数制相关概念1.数码数制中表示基本数值大小的不同数字符号。
十进制的数码为0~9共10个;二进制的数码为0、1共2个;八进制的数码为0~7共8个;十六进制的数码为0~9,A、B、C、D、E、F共十六个,其中A-F分别代表十进制数10-15(理解:就和我们做选择题一样A-D 四个选项是1.2.3.4;而这里的A是从10开始数,所以就是10、11、12、13、14、15)。
2.基数基数即数制所使用的数码个数。
二进制的基数为2;十进制的基数为10;八进制的基数为8;十六进制的基数为16;3.位权(这个比较重要)数制中的每一固定位置对应的单位值称为“位权”(理解:4123,3在这个位置上是3,3*1;2在这个位置上是20,2*10;1在这个位置上是100,1*100;4在这个位置上是4000,4*1000;这个“个十百千”就是它的位权;也就相当于个位上的位权是10^0,十位上的位权10^1,百位上的位权是10^2)。
对于二进制来说,整数部分的第i位的位权就是2^(i-1);对于N进制来说,整数部分的第i位的位权就是N^(i-1);(二)常见数制的表示法及计算规则1.十进制(1)表示法十进制数用D表示,如十进制数15,可表示成15D、(15)D或(15)10(2)计算规则进位规则是“逢十进一”,借位规则是“借一当十”。
(计算机直接表现在你面前的一般不会是二进制,它会转成八进制、十进制、十六进制给你展示,一般十进制、十六进制比较多,这样比较直观,不会是一长串的0101数字)我们来看一下“二进制”、“八进制”、“十六进制”,感觉有种倍数的关系,都是2的倍数,21、23、24、那我们分别介绍一下,这个“11”这个数字在各个数制中怎么表示呢常见数制的位权(三)二进制与十进制的相互转换1.二进制化为十进制例1:10110B转换成十进制数例2:一个字节等于8位(1B=8bit)11110011B转换成十进制数2.十进制数转二进制数方法:除2取余法,商作为下次的被除数,直到被除数为0停止,最后将余数按从下由上的顺序写出来即可。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
教学目标
• 理解并掌握进位计数制概念 • 掌握数制的转换 • 掌握计算机中数据的表示方法 • 了解常用信息编码的分类
重点难点
• 掌握二进制与十进制的相互转换 • 掌握二进制与八进制的相互转换 • 掌握二进制与十六进制的相互转换 • 掌握十进制与十六进制的相互转换
教学内容
D
图1-2 将二进制数转变成十六进制数
3、十六进制与十进制的相互转换
十六进制数与十进制数相互转换时,可以分 成两步完成:将待转换的十六进制数转换成二进 制,然后再将二进制数转换成十进制。
四、计算机中的存储单位
1.位 计算机中所有的数据都是以二进制来表示的,
一个二进制代码称为一位,记为bit。位是计算机 中最小的信息单位。
一、数字化信息编码的概念 二、进位计数制 三、不同进制之间的转换 四、计算机中数据的表示方法 五、常用信息编码
一、数字化信息编码的概念
计算机中的信息也称为数据。由于二进 制电路简单、可靠且具有很强的逻辑功能, 因此数据在计算机中均以二进制表示,并用 它们的组合表示不同类型的信息。
二、进位计数制
1.十进制 日常生活中最常见的是十进制数,用十个不同的符号来表示:0、1、
八进制的数较二进制的数书写方便,常应用在电子计算机的计算中。
三、不同进制之间的转换
1.二进制与十进制的相互转换 二进制数要转换成十进制数非常简单,只需
将每一位数字乘以它的权2n,再以十进制的方法 相加就可以得到它的十进制的值(注意,小数点 左侧相邻位的权为20,从右向左,每移一位,幂 次加1)。
【例1】(10110.011) B=1×24+0×23+1×22+1×21+0×20+0×2-1 +1×2-2+1×23=(22.375)余”的方法。具体过程介绍如下:
1.将十进制数除2,保存余数。
2.若商为0,则进行第三步,否则,用商代替 原十进制数,重复第1步。
3.将所有的余数找出,最后得到的余数作为 最高位,最先得出的余数作为最低位,由各余数 依次排列而成的新的数据就是转换成二进制的结 果。
2、二进制数与十六进制数的相互转换
由于16=24,所以在将二进制数转换成十 六进制数时,从最右侧开始,每四位二进制 数划为一组,用一位十六进制数代替,也称 为“以四换一”;十六进制数转换成二进制 数时正好相反,一位十六进制数用四位二进 制数来替换,也称“以一换四”。
0110 0101 1101
6
5
常用的存储存容量单位有B、KB、MB、GB, TB它们之间的关系是:
1KB=1024B, 1MB=1024KB, 1GB=1024MB ,1TB=1024GB。
五、常用信息编码
1.ASCII码 2.国标码 3.汉字字模
小结
• 理解信息在计算机中的表示方法 • 理解二进制、十六进制 • 掌握不同进制间数据的转换方法 • 理解并掌握信息在计算机中的存储方式 • 了解常用信息编码
2、3、4、5、6、7、8、9,称为代码。
2.二进制 二进制数只有两个代码“0”和“1”,所有的数据都由它们的组合
来实现。二进制数据在进行运算时,遵守“逢二进一,借一当二”的 原则。 3.十六进制
十六进制数采用0~9和A、B、C、D、E、F六个英文字母一 起构成十六个代码。 (半斤八两)
4.八进制 八进制数采用0,1,2,3,4,5,6,7八个数码,逢八进位。
2.字节 在对二进制数据进行存储时,以八位二进制
代码为一个单元存放在一起,称为一个字节,记 为Byte。字节是计算机中次小的存储单位。
3.字 一条指令或一个数据信息,称为一个字。字是
计算机进行信息交换、处理、存储的基本单元。
4.字长 CPU中每个字所包含的二进制代码的位数,
称为字长。字长是衡量计算机性能的一个重要 指标。
【例2】将(236)D转换成二进制。 转换过程如图1-1所示。
2 2 36 2 118 2 59 2 29 2 14 27 23 21 0
…………… 0 …………… 0 …………… 1 …………… 1 …………… 0 …………… 1 …………… 1 …………… 1
二进制数的低位 二进制数的高位
图1-1 将十进制数转变成二进制数
作业
1.(100101)2=( 2.(64)10=( 3.(25)10=( 4.(3C)16=( 5. (41)8=( 6.(17)10=(
)8=(
)16
)2
)8=(
)16
)2=(
)8
)2
)2=(
)16
