导弹比例导引Matlab编程
导弹最优导引律仿真分析(例子)
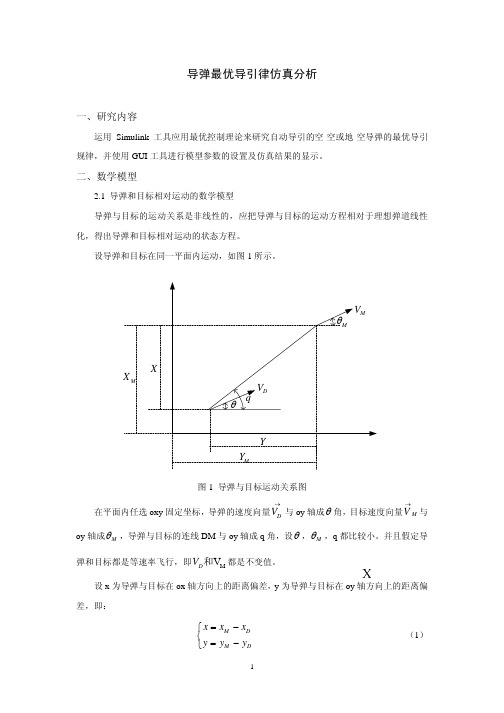
到限制,导弹结构能承受的最大过载也受到限制,所以控制信号 u 应该受到限制,因此,选
择下列形式的二次型指标函数
( ) ( ) ∫ ( ) J = 1 X T 2
tf
CX t f
+ 1 tf 2 t0
X T QX + U T RU dt
⎡c1 0 0 0 ⎤ ⎡0 0 0 0⎤
式中,
C
=
⎢ ⎢
0
c2
0
0
⎥ ⎥
,
Q
=
⎢⎢0
0
0
0⎥⎥
⎢0
⎢ ⎣
0
0 0
c3 0
0⎥
c4
⎥ ⎦
⎢0 0 0 0⎥ ⎢⎣0 0 0 0⎥⎦
2.2.2 最优导引律
(11)
完全考虑弹体二阶振荡环节时,假定目标不机动,导弹运动的状态方程见式(8),即
•
X = AX + Bu
(12)
⎡0 1 0 0 ⎤ ⎡ 0 ⎤
式中, A = ⎢⎢0 0 VD ⎢0 0 0
]
2(t f − t)2 + 6(t f − t)
ω
ω2
−
15 4ω
2
3
]
K3 (t) =
KDVD [(t f
− t)3
3 ω2 3 −
(t f
−t −
3 )2 ω
2(t f ω
− t)2
+
6(t f − t) ω2
−
15 4ω
2
3
]
最优导引方框图如图 3 所示。
6
u(σ )
KDω 2
+
1 s x4 1 s x3 VD +
导弹拦截制导的建模与仿真matlab-概述说明以及解释

导弹拦截制导的建模与仿真matlab-概述说明以及解释1.引言1.1 概述导弹拦截制导技术作为现代军事领域中的重要一环,对于保障国家安全和维护世界和平具有重要意义。
随着科技的不断发展和武器系统的日益进步,导弹拦截制导技术也不断得到改进和完善。
本文旨在通过使用MATLAB进行建模与仿真,对导弹拦截制导系统进行研究。
通过建模与仿真,可以模拟真实环境中导弹与目标之间的相互作用,以及制导系统的性能表现。
这种方法可以更好地理解导弹拦截制导的原理和机制,为相关研究提供有效的工具和方法。
本文的结构如下:首先,我们将概述导弹拦截制导技术的基本原理和应用领域。
其次,我们将介绍导弹拦截制导的建模方法,包括数学建模和计算机仿真技术。
然后,我们将总结现有的研究成果,并展望未来导弹拦截制导技术的发展方向。
我们相信,通过对导弹拦截制导系统的建模与仿真研究,可以更好地提高导弹拦截效果,保护国家安全。
通过本文的阐述,我们希望读者能够对导弹拦截制导技术有一个全面的了解,并了解到利用MATLAB进行建模与仿真的重要性。
同时,我们也希望通过本文的研究成果,能够为相关领域的科研人员提供一定的参考和借鉴。
最终,我们期待本文的研究成果能够推动导弹拦截制导技术的进一步发展,为维护世界和平做出更大的贡献。
文章结构部分是用来介绍整篇文章的框架和组织方式,可以包括章节标题及其内容简介。
对于本篇文章的结构,可以编写如下内容:1.2 文章结构本文的结构按照以下几个部分来组织和呈现:第一部分为引言。
在引言部分,首先对导弹拦截制导的背景和重要性进行简要说明,然后介绍文章的研究目的,即针对导弹拦截制导问题进行建模与仿真。
最后,概述了本文的整体结构和各个部分的内容安排。
第二部分是正文部分。
在正文部分,首先对导弹拦截制导的概述进行详细介绍,包括导弹拦截制导的基本原理、目标追踪与识别方法以及导弹拦截制导中常用的技术和算法等。
接着,介绍了导弹拦截制导的建模方法,具体包括建立导弹、目标和拦截器的数学模型,以及制导控制算法的设计和仿真等。
轨迹控制算法比例导引法

比例导引法(Proportional Navigation,简称PN)是一种常用于飞行器、导弹、火箭等动态系统的控制算法,用于实现目标追踪和控制。
它是一种基于相对速度的导引法,通过比较控制器的输出信号和目标的相对速度,计算控制指令,从而实现目标追踪和控制。
PN算法的核心思想是:保持自身和目标的相对速度矢量不变,即使目标在运动,也能够始终指向目标。
具体而言,PN算法的控制指令与目标的相对速度矢量成比例,即控制器输出的指令大小与目标的角度偏差成正比。
在轨迹控制中,PN算法可以用于实现飞行器或导弹的目标追踪和控制。
例如,在空中追踪一架移动的目标飞机时,飞行器可以根据目标的相对速度矢量计算出控制指令,使自身的运动轨迹始终与目标保持一定的相对位置关系,从而实现目标的跟踪和攻击。
需要注意的是,PN算法通常用于实现快速响应和高精度控制,但也有一定的局限性,例如对于目标突然变化或运动不规律的情况,可能会导致控制系统失效或效果不佳。
因此,在实际应用中,需要综合考虑PN算法的特点和局限性,选择合适的控制算法,并进行必要的参数优化和测试。
导弹追击模型-matlab求解

《数学软件与数学实验》课程设计实验题目导弹追击问题数学实验报告实验导弹追击问题课程设计名称问题背景描述:某军的一导弹基地发现正北方向200 km处海面上有敌舰一艘以100 km/h的速度向正东方向行驶. 该基地立即发射导弹跟踪追击敌舰, 导弹速度为500 km/h,自动导航系统使导弹在任一时刻都能对准敌舰.实验目的与任务:(1)试问导弹在何时何处击中敌舰?(2)如果当基地发射导弹的同时,敌舰立即由仪器发觉. 假定敌舰为一高速快艇,它即刻以150 km/h的速度与导弹方向垂直的方向逃逸,问导弹何时何地击中敌舰?(3)如果敌舰以150 km/h的速度与导弹方向成固定夹角的方向逃逸, 问导弹何时何地击中敌舰?试建立数学模型.并选择若干特殊角度进行计算.试确定敌舰与导弹方向的最佳逃逸夹角?实验原理与数学模型:(含模型的假设、符号说明、模型的建立)实验原理:根据题意,导弹在任一时刻都能对准敌舰,可知导弹飞行方向会随t 而改变,因此导弹的轨迹是一条斜率随着时间变化的曲线,且曲线上每一点的斜率方向都指向敌舰.故可以建立坐标轴进行分析。
实验中考虑到敌艇体积大小,当导弹与敌艇距离小于10米时,视为追击成功.因实验所列方程较为复杂,所以本实验采用龙格-库塔方法求得数值解(matlab命令:ode45).第一题:根据快艇的定向运动,在t时刻竖直距离200km,水平距离150t km,可以建立根据分速度的合成,纵向距离为定值,水平方向距离等于敌舰打中后的距离来建模。
因此,每一点的速度可进行正交分解,从而联立微分方程组求解.第二题:由题意可知,敌舰任意时刻的速度方向都与导弹飞行方向垂直,即两者斜率关系呈负倒数关系,由此列方程组进行求解.第三题:实际上第二问是第三问的一个特殊情况,可以由类似方法得到导弹追击所用时间,通过对逃逸角度和追击时间作图分析,可以确定最优逃逸角.符号说明:导弹的位置为敌艇的位置为v:速度:比例系数st:快艇逃逸角度代码中方便起见,y1,y2分部由x(3),x(4)表示实验所用软件及版本:【实验环境】MATLAB主要内容(要点):(模型的求解原理、公式、推导、基本求解步骤、算法的流程图等)本文解决的是对导弹追击的问题:对于问题一:设坐标系如下,取基地为O(0,0),导弹的位置为,船的位置为,导弹时时刻刻指向船,可以得到运动轨迹的斜率为 ,即=。
(518618873) 典型导引规律三维弹道仿真分析

总第164 期200 8年第2期舰船电子工程Vo l.28No. 211 0Sh i p E lec tron ic En gin ee ringt3典型导引规律三维弹道仿真分析周纪元 1 ) 童幼堂2) 张磊1) 王亚1)(海军大连舰艇学院研究生1队1 )大连11 601 8)( 海军大连舰艇学院舰载武器系2 )大连11 601 8)摘要介绍几种典型导弹导引规律及其约束方程,运用MA T L AB 语言对纯追踪法、平行接近法和比例导引法的理想弹道进行了三维仿真。
绘制导弹速度和目标速度变化时,其对应的三维理想弹道,并进行比较分析。
关键词导引规律;弹道;仿真; MA T LAB中图分类号TP391. 91 引言导弹在攻击目标时,为了使导弹稳定的跟踪并命中目标,导引系统必须及时准确地提供导引信号,而导引信号又必须严格遵循某种规律,这种规律就是导引规律。
导引规律一般分为两大类,即两点法和三点法。
两点法又包括纯追踪法、比例导引法和平行接近法及固定前置角法等[ 1 ] 。
目前,大多数文献给出的两点法的运动学弹道多为导弹和目标在同一平面内的二维弹道,本文使用 MA T LAB 语言,对两点法前三种导引规律的理想弹道进行了三维仿真。
绘制出了三维仿真弹道,分析比较了不同导引规律对应的导弹和目标运动参数变化时的弹道变化特性。
2 两点法导引规律式中: r = d r/ d t:距离变化率;θ: V 与目标视线的夹角, 即目标运动前置角;β: Vm与目标视线的夹角;即导弹运动前置角;φ: 目标视线与x 轴夹角, 即视线角; r:目标与导弹之间的距离。
如图1所示。
图1导弹与目标相对关系图由图1可得各夹角之间的相互关系为:φ= η+θ (3)φ= β+γ(4)将( 3) 、( 4 )式代入(1)、( 2 ) 式可得:r = V t co s(φ- η) - V m co s(φ- γ) (5)两点法是确定导弹与目标两点在空间相对位置的方法。
matlab los制导编程

matlab los制导编程在MATLAB中进行LOS(Line-of-Sight)制导编程涉及到利用MATLAB来实现导弹或者飞行器等载具的制导系统。
这涉及到数学建模、控制理论和仿真等方面的知识。
下面我将从多个角度来谈谈MATLAB中的LOS制导编程。
首先,实现LOS制导编程的第一步是建立载具的动力学模型和环境模型。
这包括载具的运动方程、姿态动力学方程以及环境因素如风速、重力等的影响。
在MATLAB中,可以利用ODE(Ordinary Differential Equations)求解器来建立和求解这些动力学模型。
其次,制导算法是实现LOS制导的关键。
常见的LOS制导算法包括PN(Proportional Navigation)导引律和PPN(Pure Pursuit Navigation)算法等。
这些算法涉及到目标跟踪、姿态控制和导航等方面的知识。
在MATLAB中,可以利用控制系统工具箱来设计和实现这些制导算法。
此外,仿真是LOS制导编程过程中必不可少的一部分。
利用MATLAB的Simulink工具箱,可以建立载具的动力学仿真模型,并结合制导算法进行闭环仿真。
这有助于评估制导算法的性能,并进行调试和优化。
另外,MATLAB提供了丰富的绘图和可视化工具,可以用来可视化导弹或飞行器的轨迹、目标的运动轨迹以及制导算法的性能等。
这对于分析和展示LOS制导系统的工作原理和性能非常有帮助。
最后,要注意在编写MATLAB代码时要考虑代码的可重用性和可扩展性,这样可以更好地应对不同的制导场景和需求。
综上所述,MATLAB中的LOS制导编程涉及到建立动力学模型、设计制导算法、进行仿真和可视化等多个方面,需要综合运用数学建模、控制理论和编程技能。
希望这些信息能够对你有所帮助。
制导律实验报告

导弹自寻的制导律实验报告报告人:刘军学号:030710218一、实验目的通过本实验加深了解导弹制导律的设计、实现,从而加深对导弹制导律的理解。
二、实验要求1、实验准备理论基础:学习过导弹制导与控制系统原理等相关课程。
软件基础:熟悉Matlab 等相关软件。
2、实验要求熟练应用Matlab 编程语言设计各种形式的制导律,不少于3 种。
三、实验原理相对运动方程是指描述导弹、目标、制导站之间相对运动关系的方程、建立相对运动方程是导引弹道运动学分析方法的基础。
相对运动方程习惯上建立在极坐标系中,其形式最简单。
下面分别建立自动瞄准制导的相对运动方程。
自动瞄准制导的相对运动方程实际上是描述导弹与目标之间相对运动关系的方程。
图1 导弹、目标间相对运动关系r=。
其中r表示导弹相对目标的距离,当导弹命中目标时0q目标线与基准线之间的夹角,称目标线方位角(简称目标线角)。
若从基准线逆时针—1——2—转到目标线上时,则q 为正。
σ、M σ分别为导弹、目标速度矢量与基准线之间的夹角,称之为导弹弹道角和目标航向角。
分别以导弹、目标所在位置为原点,若由基准线逆时针旋转到各自的速度矢量上时,则σ、M σ为正,当攻击平面为铅垂面时,σ就是弹道倾角 θ;当攻击平面为水平面时,θ就 是弹道偏V ψ。
η、M η分别为导弹、目标速度矢量与目标线之间的夹角,相应称之为导弹速度矢量前置角和目标速度矢量前置角(简称为前置角)。
分别以导弹、目标为原点,若从各自的速度矢量逆时针旋转到目标线上时,η、M η则为正。
考虑到上图所示角度间的几何关系,以及导引关系方程,就可以得到自动瞄准制导的相对运动方程组为:1cos cos sin sin 0M M D D M M M Mdr V V dtdq r V V dtq q ηηηησησηξ=−=−=+=+= 上面方程组中,10ξ=为描述导引方法的导引关系方程(或称理想控制关系方程)。
在自动瞄准制导中常见的导引方法有:追踪法、平行接近法,比例导引法等,相应的导引关系方程为:追踪法:0η=,10ξη==;平行接近法:0q q const ==,10dq dt ξ==; 比例导引法:d dq K dt dt σ=,10d dq K dt dtσξ=−=; 上述方程组中;()D V t 、()M V t 、()M t η(或()M t σ)为已知,方程组中只含有5 个未知参数:()r t 、()q t 、()M t σ(或()M t η)、()t σ、()t η因此方程组是封闭的,可以求得确定解。
导弹姿态控制及其matlab源码

导弹姿态控制是导弹制导系统的重要组成部分,它涉及到导弹的飞行姿态、速度和位置等参数的精确控制。
在导弹制导系统中,导弹姿态控制通常通过惯性导航系统、雷达测距系统和激光测距系统等传感器获取导弹的姿态信息,然后通过控制系统对导弹的发动机进行控制,以实现导弹的姿态调整。
在Matlab中,可以使用Simulink工具箱进行导弹姿态控制的建模和仿真。
下面是一个简单的导弹姿态控制系统的Matlab源码示例:matlab% 导入Simulink库from Simulink.BlockDiagram import BlockDiagram% 创建导弹姿态控制系统模型bd = BlockDiagram()% 添加输入模块bd.add('Input', 'Input')% 添加姿态传感器模块bd.add('Inertial Navigation System', 'Inertial Navigation System')% 添加控制系统模块bd.add('Control System', 'Control System')% 添加发动机控制模块bd.add('Thrust Control', 'Thrust Control')% 添加输出模块bd.add('Output', 'Output')% 连接模块之间的信号线bd.connect('Input', 'Inertial Navigation System')bd.connect('Inertial Navigation System', 'Control System')bd.connect('Control System', 'Thrust Control')bd.connect('Thrust Control', 'Output')% 运行仿真并显示结果bd.run(100)bd.plot()上述代码创建了一个简单的导弹姿态控制系统模型,包括输入模块、姿态传感器模块、控制系统模块、发动机控制模块和输出模块。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
导弹比例导引Matlab 编程
一、比例导引
比例制导律产生加速度指令,方向垂直于目标线的瞬时方向。
和目标线方向角变化率、导弹和目标接近速度成正比。
可用一下方程表示
'
C C n NV λ=
(1)
C n 为控制加速度;'N 是无量纲设计参数,称为有效制导系数,通常取为3-5;C V 为导弹-目标接近速度;λ为目标线方向角变化率。
二、运动方程的建立
1
2
为更方便的理解比例制导,我们将运动方程限制在二维剖面内,采用惯性坐标系,忽略地球曲率的影响。
在并且假设导弹和目标为质点,忽略重力作用和空气阻力。
上图中,M V 、T V 分别为导弹和目标的速度; T n 为目标的加速度,方向垂直于目标速度矢量。
λ为目标线与水平参考线的夹角;β为目标速度矢量与水平参考线的夹角。
TM R 为目标-导弹相隔距离。
L 为相撞角,即当导弹速度矢量与目标线夹角为此值时,导弹和目标保持当前速度飞行,将恰好相撞。
HE 为方向误差,表示导弹初始飞行方向与相撞角的偏差。
关于目标线的运动方程:
111TM T M R R R =-
(2)
222TM T M R R R =-
(3)
TM R =(4) 111TM T M V V V =- (5) 222TM T M V V V =-
(6)
1122()
TM TM TM TM C TM TM
R V R V V R R -+=-=
(7)
关于目标的运动方程: 11T T R V = (8) 22T T R V =
(9) 11T T V a = (10) 22T T V a =
(11) 1cos T T V V β=-
(12) 2sin T T V V β= (13) 1sin T T a n β= (14) 2cos T T a n β=
(15)
T
T
n V β=
(16)
关于导弹的运动方程 11M M R V = (17) 22M M R V = (18) 11M M V a = (19) 22M M V a =
(20) 1sin M C a n λ=- (21)
2cos M C a n λ=
(22)
1
2
1
tan TM TM R R λ-= (23)
1221
2TM TM TM TM TM
R V R V R λ-=
(24)
1
sin()
sin T M
V L V βλ-+=
(25)
1(0)cos()M M V V L HE λ=++ (26)
2(0)sin()M M V V L HE λ=++
(27)
三、Matlab 仿真
对初始航向角偏差-20度、目标存在3g 机动、初始航向角偏差-10度,目标存在1g 机动三种情况进行了仿真,有效制导系数取4和5两种值,以验证比例导引的效果。
对于微分方程的求解,采用了二阶龙格-库塔方法。
1[(,)(,)]2
K K h
x x f x t f x t h +=+++
(28)
其中h 为时间步长,()(,)x t f x t =。
对于(,)f x t h +的求法,以导弹速度为例。
假设目前进行到i 步,要求1(1)M V i +、
2(1)M V i +。
求解方程为
1111(1)()[()(1)]2
M M M M h
V i V i a i a i +=+++
(29)
但是,从1(1)(1)sin (1)M C a i n i i λ+=-++可以看出,在求出M V 之前,1(1)M a i +是不可能求出的。
所以,我们将用1(1)M a i +的欧拉求解值(0)1
(1)M a i +近似代替1(1)M a i +。
欧
拉法的方程为
1(,)K K x x hf x t +=+
(30)
所以,需要先求出(0)1M R
、
(0)2M R 、(0)1T R 、(0)2T R 、(0)1M V 、(0)2M V 、(0)1T V 、(0)2T V 、
(0)λ。
接着代入一下方程
(0)1111(1)()[()(1)]2
M M M M h
V i V i a i a i +=+++
(31)
1、 -20 DEG Heading Error
图1初始航向角存在偏差仿真运动轨迹
图2初始航向角存在偏差仿真需用过载曲线
从上图可以看出,在存在初始航向角偏差的情况下,有效制导系数越大,导弹运动轨迹越紧促,飞行开始阶段所需的过载越大。
最大需用过载出现在初始阶段,目的是校正初始航向角。
2、3G Target Maneuver
图3目标存在机动仿真运动轨迹
图4目标存在机动仿真需用过载曲线
可以看出,在目标存在机动情况下,最大需用过载出现在飞行中段。
且有效制导系数为5时,末端需用过载小于有效制导系数为4的情况。
3、-10DEG Heading Error and1G Target Maneuver
图5初始航向角存在偏差和目标机动仿真运动轨迹从上面的仿真结果可以看出,比例导引法适用于多种拦截情况。
四、Matlab程序。
