p-n_结电流电压特性(精选)
合集下载
第二章 p-n结
d 2ψ qN D =− 2 dx εs
0 < x ≤ xn
半导体的总电荷中性要求p侧每单位面积总负空间电荷必须 精确地和n侧每单位面积总正空间电荷相同：
N A x p = N D xn
总耗尽层宽度W即为
W = x p + xn
由
耗尽区 d ψ qN
2
dx
2
=
εs
A
− xp ≤ x < 0 和
d 2ψ qN =− D dx 2 εs
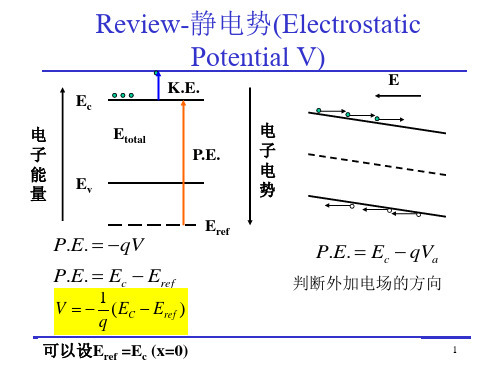
静 电 势 Ψ 电 子 势 能 Ei qψ p
qψ a qVbi EC EF Ei EV
（b） 在热平衡下突变结的能带图
Ei − E F p = ni exp( ) kT kT NA 1 ψ p ≡ − ( Ei − EF ) x≤− x p = − ln( ) 得到 q q ni
同理，可得n型中性区相对于费米能级的静电势为
热平衡状态下的p-n结
1 kT ND ψ n ≡ − ( Ei − EF ) x≥ xn = ln( ) q q ni
由上二式可计算出在不同掺杂浓度时，硅和砷化镓的 ψ p 和ψn 值的大小，如图所示．对于一给定掺杂的浓度，因为砷化镓有 较小的本征浓度，其静电势较高． 0.8
Ψ p 或Ψn / V
在热平衡时，p型和n型中性 区的总静电势差即为内建电 势Vbi
E ( x ) = − Em + qN D x
− xp ≤ x < 0
0 < x ≤ xn
εs
=
qN D
εs
( x − xn )
对耗尽区积分，可得到总电势变化，此即内建电势Vbi：
Vbi = −∫ E( x)dx = − ∫ E( x)dx
pn结
注入的非平衡载流子与 外加电压以及平衡时的少子浓度有关
第六章2 第六章 18
同理可得注入n区边界的非平衡载流子浓度为： 同理可得注入n区边界的非平衡载流子浓度为：
qV ∆pn ( xn ) = pn ( xn ) − pn 0 = pn 0 [exp( ) − 1] (6 − 24) k0T
第六章2 第六章
第六章2 第六章
4
电子通过势垒区扩散入p区 在边界 电子通过势垒区扩散入 区，在边界pp‘ (x=xp)处形成电子的积累，成为 区的非平衡少 处形成电子的积累， 处形成电子的积累 成为p区的非平衡少 数载流子，结果使pp’处电子浓度比 处电子浓度比p区内部 数载流子，结果使 处电子浓度比 区内部 形成了从pp’处向 区内部的电子扩散流。 处向p区内部的电子扩散流 高，形成了从 处向 区内部的电子扩散流。 非平衡少子边扩散边与p区的空穴复合 区的空穴复合， 非平衡少子边扩散边与 区的空穴复合，经过 比扩散长度大若干倍的距离后，全部被复合。 比扩散长度大若干倍的距离后，全部被复合。 这一段区域称为扩散区。 这一段区域称为扩散区。
d 2 ∆pn d ∆pn d ε x ∆pn Dp − µ pε x − µ p pn − = 0 (6 − 25) 2 dx dx dx τ p
第六章2 第六章
21
dε x 因为外加电压主要加在势垒区，所以扩散区中 以及ε x 取为0 dx d 2 ∆pn ∆pn 所以，D p − = 0 (6 − 26)，即 2 τp dx d 2 ∆pn ∆pn − 2 = 0, L p = D pτ p 2 dx Lp
第六章2 第六章 11
因为少子浓度很低，而扩散长度基本不变化， 因为少子浓度很低，而扩散长度基本不变化， 所以反向偏压时少子的浓度梯度也较小;当反 所以反向偏压时少子的浓度梯度也较小 当反 向电压很大时，边界处的少子可以认为是零。 向电压很大时，边界处的少子可以认为是零。 这时少子的浓度梯度不再随电压变化， 这时少子的浓度梯度不再随电压变化，因此 扩散流也不随电压变化，所以在反向偏压下， 扩散流也不随电压变化，所以在反向偏压下， pn结的电流较小并且趋于不变。 结的电流较小并且趋于不变。 结的电流较小并且趋于不变
5.半导体物理：p-n结
5.2 p-n结伏安特性
1.非平衡状态下的p-n结
(1)外电压下p-n结势垒的变化及载流子的运动
正向偏压 (如何分布)
正反偏压时势垒变化
扩散大于漂移
与内建电场相反
势垒区电场
宽度 高度
扩散大于漂移
n区电子通过势垒区流入p区 非平衡少数载流子
p区空穴通过势垒区流入n区
的电注入
电子积累
p区电子扩散流 与p区空穴复合
电子（扩散）电流 p区扩散到势垒区
p’ n’ pn
空穴（扩散）电流 n区扩散到势垒区
反向p-n结电流分布 反向总电流：势垒区边界nn’ 和pp’附近的少数载流子扩散电流之和
n(x)
nn 0
exp
Ecn E(x) k0T
nn 0
exp
qV
(x) k0T
qVD
p(x)
pno
exp
qVD
qV (x) k0T
---
+++
---
+++
空间电荷 区
内建电场
V
内建电场：
空间电荷区中的正、负电荷间产生的电场，其方向由n区指向p区。
平衡p-n结：
载流子在内建电场的作用下，漂移运动和扩散运动相抵时，所达到 的动态平衡（p-n结的净电流为零）。
2.p-n结能带图
平衡p-n结的能带图
电子
n区
费米能级高
p区 空穴 费米能级低
p’ n’
p n
n区空穴扩散流与
n区电子复合
空穴积累
p区空穴 p区电子
n区电子 n区空穴
扩散区
如何变化的？ 代表什么？
正向偏压下载流子分布
第五章-PN-结
（1）势垒电容 （2）扩散电容
（a）平衡p-n结势垒区； （b）正偏时，势垒区变窄； （c）正偏时，p-n结载流子变化
PN结电容的计算
突变结势垒电容公式
①突变结的势垒电容和结的面积以及轻掺杂一边的杂质浓度的平方根成正比，因此减小结面积以及降低轻掺杂一边的杂质浓度是减小结电容的途径； ②突变结势垒电容和电压（VＤ—V）的平方根成反比，反向偏压越大，则势垒电容越小，若外加电压随时间变化，则势垒电容也随时间而变，可利用这一特性制作变容器件。以上结论在半导体器件的设计和生产中有重要的实际意义。
图5－14反向偏压下p－n结的费米能级（非常重要）
8·理想p-n结模型及其电流电压方程
符合以下假设条件的p-n结称为理想p-n结模型： （1）小注入条件 即注入的少数载流子浓度比平衡多数载流子浓度小得多； （2）突变耗尽层条件即外加电压和接触电势差都降落在耗尽层上，耗尽层中的电荷是由电离施主和电离受主的电荷组成，耗尽层外的半导体是电中性的。因此，注入的少数载流子在p区和n区是纯扩散运动； （3）通过耗尽层的电子和空穴电流为常量，不考虑耗尽层中载流子的产生及复合作用； （4）玻耳兹曼边界条件即在耗尽层两端，载流子分布满足玻耳兹曼统计分布。
外电场与自建场方向相反，外电场减弱PN结区的电场，使原有的载流子平衡受到破坏
—— 非平衡载流子 —— PN结的正向注入
电子扩散电流密度
—— 外加电场使边界处电子的浓度提高 倍
和
比较得到
正向注入，P区边界电子的浓度变为
边界处非平衡载流子浓度
—— 正向注入的电子在P区边界积累，同时向P区扩散 —— 非平衡载流子边扩散、边复合形成电子电流
(3)．热电击穿
当p-n结上施加反向电压时，流过p-n结的反向电流要引起热损耗。反向电压逐渐增大时，对应于一定的反向电流所损耗的功率也增大，这将产生大量热能。如果没有良好的散热条件使这些热能及时传递出去，则将引起结温上升。 反向饱和电流密度随温度按指数规律上升，其上升速度很快，因此，随着结温的上升，反向饱和电流密度也迅速上升，产生的热能也迅速增大，进而又导致结温上升，反向饱和电流密度增大。如此反复循环下去，最后使Js无限增长而发生击穿。这种由于热不稳定性引起的击穿，称为热电击穿。对于禁带宽度比较小的半导体如锗p-n结，由于反向饱和电流密度较大，在室温下这种击穿很重要。
（a）平衡p-n结势垒区； （b）正偏时，势垒区变窄； （c）正偏时，p-n结载流子变化
PN结电容的计算
突变结势垒电容公式
①突变结的势垒电容和结的面积以及轻掺杂一边的杂质浓度的平方根成正比，因此减小结面积以及降低轻掺杂一边的杂质浓度是减小结电容的途径； ②突变结势垒电容和电压（VＤ—V）的平方根成反比，反向偏压越大，则势垒电容越小，若外加电压随时间变化，则势垒电容也随时间而变，可利用这一特性制作变容器件。以上结论在半导体器件的设计和生产中有重要的实际意义。
图5－14反向偏压下p－n结的费米能级（非常重要）
8·理想p-n结模型及其电流电压方程
符合以下假设条件的p-n结称为理想p-n结模型： （1）小注入条件 即注入的少数载流子浓度比平衡多数载流子浓度小得多； （2）突变耗尽层条件即外加电压和接触电势差都降落在耗尽层上，耗尽层中的电荷是由电离施主和电离受主的电荷组成，耗尽层外的半导体是电中性的。因此，注入的少数载流子在p区和n区是纯扩散运动； （3）通过耗尽层的电子和空穴电流为常量，不考虑耗尽层中载流子的产生及复合作用； （4）玻耳兹曼边界条件即在耗尽层两端，载流子分布满足玻耳兹曼统计分布。
外电场与自建场方向相反，外电场减弱PN结区的电场，使原有的载流子平衡受到破坏
—— 非平衡载流子 —— PN结的正向注入
电子扩散电流密度
—— 外加电场使边界处电子的浓度提高 倍
和
比较得到
正向注入，P区边界电子的浓度变为
边界处非平衡载流子浓度
—— 正向注入的电子在P区边界积累，同时向P区扩散 —— 非平衡载流子边扩散、边复合形成电子电流
(3)．热电击穿
当p-n结上施加反向电压时，流过p-n结的反向电流要引起热损耗。反向电压逐渐增大时，对应于一定的反向电流所损耗的功率也增大，这将产生大量热能。如果没有良好的散热条件使这些热能及时传递出去，则将引起结温上升。 反向饱和电流密度随温度按指数规律上升，其上升速度很快，因此，随着结温的上升，反向饱和电流密度也迅速上升，产生的热能也迅速增大，进而又导致结温上升，反向饱和电流密度增大。如此反复循环下去，最后使Js无限增长而发生击穿。这种由于热不稳定性引起的击穿，称为热电击穿。对于禁带宽度比较小的半导体如锗p-n结，由于反向饱和电流密度较大，在室温下这种击穿很重要。
pn结(2)
E Fn E Fp V np n e
2 V / k BT i
半导体器件物理
N型一侧
• 空穴分布连续性方程
p 2 pn pn pn 0 Dp 2 t x p
• 边界条件
x= Wn, pn =pn0; x=xn,
pn pn 0 exp(qV / kBT )
• 空穴扩散长度 Lp • 解(Wn -xn>>Lp)
半导体器件物理
pn结二极管(二)
理想pn结电流特性 实际电流曲线相对理想的偏离 二级管的温度特性
半导体器件物理
pn结二极管电流特性曲线
半导体器件物理
理想pn结电流特性
• 基本假设
– – – – 外加偏置电压全部降落在耗尽区 均匀掺杂突变结，载流子非简并 小注入电流 不考虑耗尽区载流子产生－复合
半导体器件物理
半导体器件物理
半导体器件物理
半导体器件物理
定性分析结果
半导体器件物理
准费米能级
• 载流子分布偏离平衡，存在 过剩载流子
– 假定电子在导带内平衡，空 穴在价带内平衡 – 电子和空穴各自平衡的时间 远小于产生－复合时间
n ni e
EFn Ei / kBT
• 电子、空穴的分布仍然满足 费米分布
np np0 np0 e
J n qDn
qV / kBT
1 e
x x p / Lp
d (n p n p 0 ) dx
xp
qDn n p 0 e qV / kBT 1 Ln
半导体器件物理
总电流
• 理想二极管方程（Shockley方程）
J J n J p J s eqV / kBT 1 Js qDp Lp qDn pn 0 np0 Ln qD p ni2 qDn ni2 Lp N D Ln N A
微电子学 半导体物理学 第六章pn结
(N
2 x 2 + N D xn ) A p
x D = xn + x p N A x p = N D xn
NA ND xn = xD x p = xD NA + ND NA + ND
1/ 2
1/ 2
2ε 0ε r 2ε ε N + N D 代入 VD 得 x D = 0 r A VD = qN VD N AN D q eff q2 N A (x + x p )2 (-xp<x<0) EC ( x ) = EC ( p ) − 2ε 0ε r q2 N D ( x − xn )2 − 2011 EC ( x ) = E复旦大学半导体物理 -qV D (0<x<xn) + C ( p) 2ε 0ε r
复旦大学半导体物理 - 2011
14
平衡时的费米能级
J n = J n扩 + J n漂 = 0
dn 0 J n = qn 0 µ n E + qDn dx
dn0 1 dEi 1 dE F = − n0 + n0 dx k BT dx k BT dx dV ( x ) 1 dEi E=− = dx q dx
NDNA越大，VD越大；Eg越大，ni越小，VD越大。 NA=1017cm-3, ND=1015cm-3, Si的VD＝0.70V. 复旦大学半导体物理 - 2011
17
平衡时，
qVD = Ecp − Ecn = E g + ( EFn − Ec ) + ( Ev − EFp )
对于非简并半导体，势垒高度会大于禁带宽度Eg吗？
耗尽层近似
从N区到P区，随着电子势能的升高，电子浓度 迅速下降，由于Vd（~1V），在势垒区的大部 分范围内，电子极为稀少，可视为电子耗尽， N侧空间电荷区的电荷基本是由电离施主贡献 的。同理，P侧空间电荷区的电荷有电离受主 贡献。 认为，在空间电荷区载流子被耗尽了
PN结的特性(8)
扩散运动>漂移运动
扩散电流占主导： 形成正向电流IF
正向电流IF随VF增加 很快，PN结表现为一 个很小的电阻(R小)
电位 V
VF VO-VF VO
PN结的特性
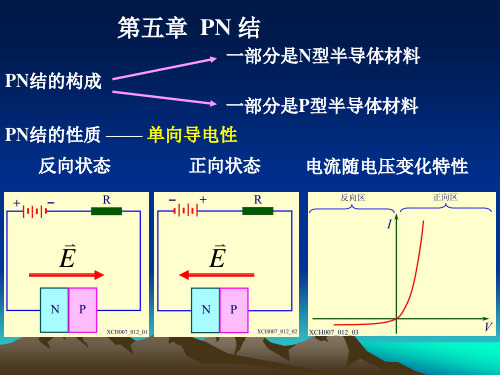
1. PN结的单向导电性——外加反向电压 (反偏)
多子扩散困难，
21 P
VR 12
N
扩散电流≈0
IR
少子漂移占主导 形成反向电流IR
反向电流IR很小，
PN结的特性
反向饱和电流
2. PN结的(10V-8-~I1特0-1性4A)
PN结的V-I 特性表达式:
反向饱和电流
iD IS (evD VT 1)
VT ——温度的电压当量
VT
kT q
波耳兹曼常数 1.38*10-23J/K
T=300k时，VT＝26mV
死区电压 （门坎电压）
正偏: v D
VT，iD
模拟电子技术
知识点：PN结的特性
1. PN结的单向导电性 2. PN结的V-I特性 3. PN结的反向击穿
PN结的特性
1. PN结的单向导电性
• 没有偏置
• 正偏
• 反偏
PN结的3种工作模式
PN结的特性
1. PN结的单向导电性——外加正向电压 (正偏)
PN结的平衡状态被打破
IF
12
P
VF 21
N 内电场ε0 外电场εF
➢ 2种：雪崩击穿和齐纳击穿
知识点：PN结的特性
1. PN结的单向导电性 2. PN结的V-I特性 3. PN结的反向击穿
R很大！
内电场ε0 外电场εR
IR的大小取决于温度！ 而与外加反压几乎无关！
电位 V
PN结及其特性详细介绍
P N结及其特性详细介绍结的形成在一块本征半导体在两侧通过扩散不同的杂质,分别形成N型半导体和P型半导体。
此时将在N型半导体和P型半导体的结合面上形成如下物理过程:扩散到对方的载流子在P区和N区的交界处附近被相互中和掉，使P区一侧因失去空穴而留下不能移动的负离子，N区一侧因失去电子而留下不能移动的正离子。
这样在两种半导体交界处逐渐形成由正、负离子组成的空间电荷区（耗尽层）。
由于P区一侧带负电，N区一侧带正电，所以出现了方向由N区指向P区的内电场PN结的形成当扩散和漂移运动达到平衡后，空间电荷区的宽度和内电场电位就相对稳定下来。
此时，有多少个多子扩散到对方，就有多少个少子从对方飘移过来，二者产生的电流大小相等，方向相反。
因此，在相对平衡时，流过PN结的电流为0。
对于P型半导体和N型半导体结合面，离子薄层形成的空间电荷区称为PN结。
在空间电荷区，由于缺少多子，所以也称耗尽层。
由于耗尽层的存在，PN结的电阻很大。
PN结的形成过程中的两种运动：多数载流子扩散少数载流子飘移PN结的形成过程（动画）结的单向导电性PN结具有单向导电性，若外加电压使电流从P区流到N区，PN结呈低阻性，所以电流大；反之是高阻性，电流小。
如果外加电压使PN结中：P区的电位高于N区的电位，称为加正向电压，简称正偏；P区的电位低于N区的电位，称为加反向电压，简称反偏。
(1)PN结加正向电压时的导电情况PN结加正向电压时的导电情况如图所示。
外加的正向电压有一部分降落在PN结区，方向与PN结内电场方向相反，削弱了内电场。
于是,内电场对多子扩散运动的阻碍减弱，扩散电流加大。
扩散电流远大于漂移电流，可忽略漂移电流的影响，PN结呈现低阻性。
PN结加正向电压时的导电情况(2)PN结加反向电压时的导电情况外加的反向电压有一部分降落在PN结区，方向与PN结内电场方向相同，加强了内电场。
内电场对多子扩散运动的阻碍增强，扩散电流大大减小。
此时PN结区的少子在内电场的作用下形成的漂移电流大于扩散电流，可忽略扩散电流，PN结呈现高阻性。