第三讲组合图形面积(一)
《组合图形的面积》PPT课件经典.ppt

6cm
3cm
7cm
课件
练一练 分成两个长方形
4cm 6cm
4×3+3×7 =12+21 =33(cm2)
3cm 3cm
7cm
课件
练一练 分割成一个长方形和一个正方形
4cm 3cm
6cm 7cm
3cm
4×6+3×3 =24+9 =33(cm2)
课件
练一练 分割成两个梯形
4cm
(3+7)×3÷2+(3+6)×4÷2
组合图形的面积
新安小学 徐国权
课件
已经学过的几种平面图形的面积计算公 式
b
a
S=ab
aห้องสมุดไป่ตู้
a
S=a×a
h
a
S=ah
h a
S=ah÷2
a
b
h
ba
S=(a+b)h÷2
课件
课件
课件
课件
组合图形是由几个简单的图形组合而成的。
课件
课件
我们身边的组合图形
课件
课件
课件
课件
组合图形面积怎样计算?
是由哪些简单图形组成的?同学们分组讨 论,四人一组。
3cm
3cm
6cm 3cm
7cm
课件
练一练 添补一个正方形成一个长方形
3cm 3cm
4cm 3cm 6cm
7×6-3×3 =42-9 =33(cm2)
7cm
课件
4c m
6c m
7cm
4c
3cm
m
6c m
7cm
3cm 3cm
3cm 3cm
4cm 6cm
7cm 分割法
添补法
六上第三讲:扇形的面积 组合图形的面积计算
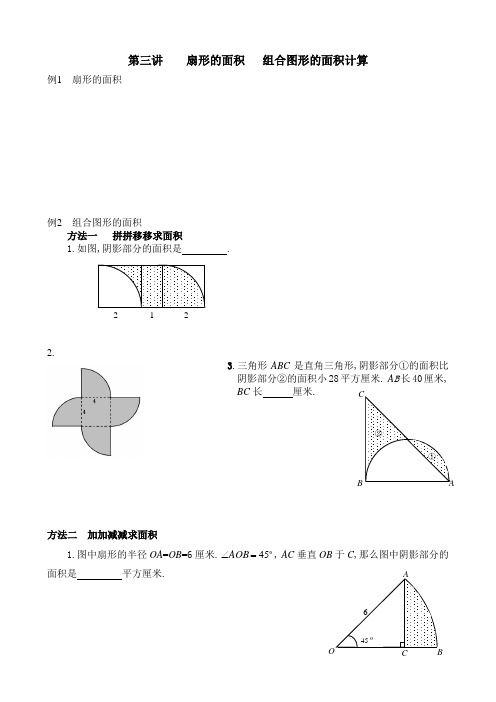
第三讲 扇形的面积 组合图形的面积计算
例1 扇形的面积
例2 组合图形的面积
方法一 拼拼移移求面积
1.如图,阴影部分的面积是 .
3.三角形ABC 是直角三角形,阴影部分①的面积比
阴影部分②的面积小
BC 长 厘米.
方法二 加加减减求面积
1.图中扇形的半径OA =OB =6厘米.45=∠AOB , AC 垂直OB 于C ,那么图中阴影部分的面积是 平方厘米.
45
2.在下图中(单位:厘米),两个阴影部分面积
的和是平方厘米.
3.右图中三角形是等腰直角三角形,阴影部
分的面积是 (平方厘米).
4.
5.
6.如图所求
,圆的周长是16.4厘米,圆的面
积与长方形的面积正好相等.图中阴影部分
的周长是厘米.
7.如图所示,以B、C为圆心的两个半圆的直
径都是2厘米,则阴影部分的周长是
厘米.(保留两位小数)
8.右图是一个直角等腰三角形,直角边长2
厘米,图中阴影部分面积是
平方厘米.
15。
第3讲:组合图形面积

组合图形面积(一)知识梳理:组合图形是由两个或两个以上的简单的几何图形组合而成的。
组合的形式分为两种:一是拼合组合,二是重叠组合。
由于组合图形具有条件相等的特点,往往使得问题的解决无从下手。
要正确解答组合图形的面积,应该注意以下几点:1、切实掌握有关简单图形的概念、公式,牢固建立空间观念;2、仔细观察,认真思考,看清所求图形是由哪几个基本图形组合而成的;3、适当采用增加辅助线等方法帮助解题;4、采用割、补、分解、代换等方法,可将复杂问题变得简单。
典型例题:例1:一个等腰直角三角形,最长的边是12厘米,这个三角形的面积是多少平方厘米?练习:已知,一个等腰直角三角形,最长的边是16厘米,这个等腰直角三角形的面积是多少平方厘米?例2:求四边形ABCD的面积。
(单位:厘米)练习:已知一个五边形的三条边的长和四个角的度数,如图所示,那么,它的面积是多少?例3:已知正方形ABCD的边长是7厘米,求正方形EFGH的面积。
练习:如下图、已知大正方形的边长是12厘米,求中间最小正方形的面积。
例4:正图正方形中套着一个长方形,正方形的边长是12厘米,长方形的四个角的顶点把正方形的四条边各分成两段,其中长的一段是短的2倍。
求中间长方形的面积。
练习:如图,一个正方形中套着一个长方形,已知正方形的边长是16分米,长方形的四个角的顶点恰好把正方形四条边都分成两段,其中长的一段是短的3倍.长方形的面积是多少?例5:正图长方形ABCD的面积是16平方厘米,E、F都是所在边的中点,求三角形AEF的面积。
练习:如图,在长方形ABCD中,BD长18cm,AB长15cm,E是BC中点,F是CD中点,求三角形AEF的面积例6:四边形ABCD和四边形DEFG都是正方形,已知三角形AFH的面积是7平方厘米。
三角形CDH的面积是多少平方厘米?练习:图中两个正方形的边长分别是6厘米和4厘米,求阴影部分的面积。
例7:下图中正方形的边长为8厘米,CE为20厘米,梯形BCDF的面积是多少平方厘米?练习:如下图,正方形ABCD中,AB=4厘米,EC=10厘米,求阴影部分的面积。
北师大版五年级数学上册 (组合图形的面积)组合图形的面积教学课件

①
拼成长方形 拼成的长方形面积
草坪通过分割、平移后,可看成一个长方形.
(16-2)×(12-2) =14×10 =140(平方米) 答:草坪的面积是140平方米.
1
一块菜地的形状如右图,你知道这 5
块菜地的面积是多少吗?(单位:米) 1
7
错解:(1+7)×5÷2+1×7 =40÷2+7 =27(平方米)
答:这块菜地的面积是27平方米.
正解:(1+7)×(5-1)÷2+1×7 =32÷2+7 =23(平方米)
答:这块菜地的面积是23平方米.
错解错在计算时误把梯形的高看成了5米, 实际应该是5-1=4(米). 此题是把组合图形分成一 个梯形和一个长方形. 计算组合图形的面积时,要 找准每个简单图形的相应数据.
组合图形的面积
什么是组合图形
有些图形是由几个简单的 图形组合而成的,这样的图形 叫作组合图形.
组合图形面积的计算方法
二计算:分别计算 出简单图形的面积.
三求和:对这些简 单图形的面积求和.
一分割:根据已知条件对 图形进行分割,转化成已
学过的几个简单图形.
例1 求出下面组合图形的面积. 2 cm
它表示( 百 )分之( 十七)。 0.009里面有( 9 )个千分之一,
推进新课
1
1 =1 20=0.05, 20 因为0.06 > 0.05, 所以0.06 > 1 。
0.06= 6 , 1 = 5 , 100 20 100
因为 6 5 , 100 100 10.5 0.7 0 Nhomakorabea87 55
×
0.4
×
1 20
×
1 50
5.在生活中寻找用分数或小数表示的信息,并与同 伴交流。
-组合图形的面积优秀课件1

术》影响、支配中国古代数学的发展1000
余年。
1.中国少年先锋队的中队旗是五角星加火炬 的红旗,如下图。(单位:cm) ⑴估一估,这面中队旗的面积大约有多大?
与同伴交流你的想法。 ⑵计算中队旗的面积,说一 说你是怎么想的。
2.把下面各个图形分成已学过的图形,并与同伴交流你的想法。
3.如图一张硬纸板剪下4个边长是4cm的小正方形 后。可以做成一个没有盖子的盒子。你知道剪后 的硬纸板面积是多少吗?
4.学校要给30扇教室门的正面刷漆。(单位:m) ⑴需要刷漆的面积一共是多少?
⑵如果刷漆每平方米需要花费5元,那么刷漆共要花费多少元?
5
刘徽
中国数学史上一个非常伟大
的数学家,在世界数学史上,也占有重要
的地位.割补法就是他的著作——《九章
算术》中首先系统提出的。公元元年前后
,盛极一时的古希腊数学走向衰微,“九
章算术”的出现,标志着世界数学研究中
心从地中海沿岸转到了中国,开创了东方
以应用数学为中心占据世界数学舞台主导
地位千余年的局面。经他注释的《九章算
北师大版 五年级上册 第六单元 组合图形的面积
看一看,想一想,怎样计算下列图形的面积(只列式不计算)。
3
3
3
3
3
3
3554 Nhomakorabea5
图1:
图4:
图2:
图5:
图3:
学习目标:
(1)选择合适的方法计算组合图形的面积;
(2)应用组合图形面积的计算方法解决实际 问题。
智慧老人的客厅
4m
6m 3m
7m
1
2
34
《组合图形面积》优秀课件(共20张PPT)

3、等底等高的两个三角形的面积一定相等. ( ∨ )
4,、周长相等的长方形和平行四边形,他们的面积一定
相等.
(× )
5、底和高都是0.2厘米的三角形的面积是0.2平方厘米.
( ×)
6、下图中,两个完全一样的长方形中有 ① 、 ②两个
三角形,比较①和②的面积是 ①>②. ( ×)
①
②
练一练
求下列图形的面积。 (单位:cm)
27
10
下图是一个机器零件横截面图,
求黑色部分的面积。
20毫米
54×27—(20+30)×10÷2 =1458—50×10÷2 =1458—250
毫
米
30毫米
毫
米
=1208(平方毫米)
54毫米
答:黑色部分的面积是1208平方毫米。
判断
1、面积相等的两个梯形一定可以拼成一个平行四边形.
( ×) 2、面积相等的两个三角形形状也相同. (× )
15、最终你相信什么就能成为什么。因为世界上最可怕的二个词,一个叫执着,一个叫认真,认真的人改变自己,执着的人改变命运。只要在路上,就没有到不了的地方。 16、你若坚持,定会发光,时间是所向披靡的武器,它能集腋成裘,也能聚沙成塔,将人生的不可能都变成可能。 17、人生,就要活得漂亮,走得铿锵。自己不奋斗,终归是摆设。无论你是谁,宁可做拼搏的失败者
2、人生就有许多这样的奇迹,看似比登天还难的事,有时轻而易举就可以做到,其中的差别就在于非凡的信念。 3、影响我们人生的绝不仅仅是环境,其实是心态在控制个人的行动和思想。同时,心态也决定了一个人的视野和成就,甚至一生。
4、无论你觉得自己多么了不起,也永远有人比更强;无论你觉得自己多么不幸,永远有人比你更不幸。 5、也许有些路好走是条捷径,也许有些路可以让你风光无限,也许有些路安稳又有后路,可是那些路的主角,都不是我。至少我会觉得,那些路不是自己想要的。 6、在别人肆意说你的时候,问问自己,到底怕不怕,输不输的起。不必害怕,不要后退,不须犹豫,难过的时候就一个人去看看这世界。多问问自己,你是不是已经为了梦想而竭尽全力了?
组合图形面积ppt课件
CHAPTER 06
练习与思考
练习题一:三角形与梯形面积计算
总结词
掌握基本图形面积计算方法
VS
详细描述
本练习题旨在帮助学员掌握三角形和梯形 面积的基本计算方法,包括三角形面积的 公式以及梯形面积的公式,并了解如何应 用这些公式进行实际计算。
练习题二:组合图形面积分解与计算
总结词
掌握组合图形面积的分解与计算方法
计算完成后,需要对答 案进行验证,确保计算 的准确性。可以通过重 新计算或者与同学互相 检查来提高答案的可靠 性。
组合图形面积计算的总结与回顾
掌握基本公式
在计算组合图形面积时,需要熟练掌握基 本图形的面积计算公式,例如矩形、三角 形、圆形等。
加强练习
要提高组合图形面积的计算能力,需要加 强练习,多做相关题目,提高熟练度和准 确性。
组合图形面积的计算步骤
步骤1
将组合图形分解为多个三角形和 梯形
步骤2
分别计算每个三角形和梯形的面积
步骤3
将各个面积相加,得到组合图形的 总面积
CHAPTER 04
组合图形面积的应用举例
三角形与梯形面积的应用举例
三角形面积计算
在三角形面积计算中,可以使用以下 公式:A = 1/2 × 底 × 高。这个公 式可以帮助学生计算不同形状的三角 形面积,例如直角三角形、等腰三角 形等。
理解分割思想
对于较复杂的组合图形,可以采用分割思 想,将复杂图形分解为多个基间观念
通过组合图形面积的计算,可以培养空间 观念和几何思维能力,提高对几何图形的 认识和理解。
掌握整体计算方法
对于某些组合图形,可以采用整体计算方 法,即不分割图形,而是根据图形的整体 特征直接计算面积。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第三讲组合图形面积(一)
专题简析:
组合图形是由两个或两个以上的简单的几何图形组合而成的。
组合的形式分为两种:一是拼合组合,二是重叠组合。
由于组合图形具有条件相等的特点,往往使得问题的解决无从下手。
要正确解答组合图形的面积,应该注意以下几点:1,切实掌握有关简单图形的概念、公式,牢固建立空间观念;
2,仔细观察,认真思考,看清所求图形是由哪几个基本图形组合而成的;
3,适当采用增加辅助线等方法帮助解题;
4,采用割、补、分解、代换等方法,可将复杂问题变得简单。
例1 一个等腰直角三角形,最长的边是12厘米,这个三角形的面积是多少平方厘米?
分析与解答由于此三角形中只知道最长的边是12厘米,所以,不能用三角形的面积公式来计算它的面积。
我们可以假设有4个这样的三角形,且拼成了下图正方形。
显然,这个正方形的面积是12×12,那么,一个三角形的面积就是12×12÷4=36平方厘米。
练习一
1,求四边形ABCD的面积。
(单位:厘米)
2,已知正方形ABCD的边长是7厘米,求正方形EFGH的面积。
3,有一个梯形,它的上底是5厘米,下底7厘米。
如果只把上底增加3厘米,那么面积就增加4.5平方厘米。
求原来梯形的面积。
例2 正图正方形中套着一个长方形,正方形的边长是12厘米,长方形的四个角的顶点把正方形的四条边各分成两段,其中长的一段是短的2倍。
求中间长方形的面积。
分析与解答图中的两个小三角形平移后可拼得一个小正方形,两个大三角形平移后可拼得一个大正方形。
这两个正方形的边长分别是12÷(1+2)=4(厘米)和4×2=8(厘米)。
中间长方形的面积只要用总面积减去这两个拼起来的正方形的面积就可以得到。
即:
12×12-(4×4+8×8)=64(平方厘米)
练习二
1,(如下图)已知大正方形的边长是12厘米,求中间最小正方形的面积。
2,如下图长方形ABCD的面积是16平方厘米,E、F都是所在边的中点,求三角形AEF的面积。
3,求下图长方形ABCD的面积(单位:厘米)。
例3 四边形ABCD和四边形DEFG都是正方形,已知三角形AFH的面积是7平方厘米。
三角形CDH的面积是多少平方厘米?
分析设大正方形的边长是a,小正方形的边长是b。
(1)梯形EFAD的面积是(a+b)×b÷2,三角形EFC的面积也是(a+b)×b÷2。
所以,两者的面积相等。
(2)因为三角形AFH的面积=梯形EFAD的面积-梯形EFHD的面积,而三角形CDH的面积=三角形EFC的面积-梯形EFHD的面积,所以,三角形CDH的面积与三角形AFH的面积相等,也是7平方厘米。
练习三
1,图中两个正方形的边长分别是6厘米和4厘米,求阴影部分的面积。
2,下图中两个完全一样的三角形重叠在一起,求阴影部分的面积。
(单位:厘米)
3,下图中,甲三角形的面积比乙三角形的面积大多少平方厘米?
例4 下图中正方形的边长为8厘米,CE为20厘米,梯形BCDF的面积是多少平方厘米?
分析要求梯形的面积,关键是要求出上底FD的长度。
连接FC后就能得到一个三角形EFC,用三角形EBC的面积减去三角形FBC的面积就能得到三角形EFC的面积:8×20÷2-8×8÷2=48平方厘米。
FD=48×2÷20=4.8厘米,所求梯形的面积就是(4.8+8)×8÷2=51.2平方厘米。
练习四
1,如下图,正方形ABCD中,AB=4厘米,EC=10厘米,求阴影部分的面积。
2,在一个直角三角形铁皮上剪下一块正方形,并使正方形面积尽可能大,正方形的面积是多少?(单位:厘米)
3,图中BC=10厘米,EC=8厘米,且阴影部分面积比三角形EFG的面积大10平方厘米。
求平行四边形的面积。
例5 图中ABCD是长方形,三角形EFD的面积比三角形ABF的面积大6平方厘米,求ED的长。
分析因为三角形EFD的面积比三角形ABF的面积大6平方厘米,所以,三角形BCE的面积比长方形ABCD的面积大6平方厘米。
三角形BCE的面积是6×4+6=30平方厘米,EC的长则是30×2÷6=10厘米。
因此,ED的长是10-4=6厘米。
练习五
1,如图,平行四边形BCEF中,BC=8厘米,直角三角形中,AC=10厘米,阴影部分面积比三角形ADH的面积大8平方厘米。
求AH长多少厘米?
2,图中三个正方形的边长分别是1厘米、2厘米和3厘米,求图中阴影部分的面积。
3,正方形的边长是2(a+b),已知图中阴影部分B的面积是7平方厘米,求阴影部分A和C的和是多少平方厘米?
基础练习
1.如图所示,两个完全一样的直角三角形重叠在一起,求阴
影部分的面积。
(单位:cm)
2.把边长是10cm的正方形卡片按下图的方法重叠起来,3张这样的卡片重叠以后
组成的图形的面积是多少?
3.有一块长方形草地,长16m,宽12m,中间有一条宽2m的小路,求草地(阴影
部分)的面积。
4.如图所示,三角形ABC被分为四个小三角形,其中三个
三角形的面积分别为8cm2、6cm2、12cm2,求阴影部分的
面积。
5.已知正方形EFGH的边长是4cm,求正方形ABCD的面积。
6.如图所示,长方形的长是8cm,宽是6cm,A、B是宽的中点,求长方形内阴影
部分的面积
提高练习
1.在腰长为10cm,面积为34cm2的等腰三角形的底边上任取一点,设这个点到两
腰的垂线分别长acm、bcm,那么a+b的长度是多少厘米?
2.如图所示,ABCD是正方形,三角形DEF的面积比三角形ABF的面积大6cm2,
CD长4cm,求DE的的长度。
3.如图所示,大正方形和小正方形的边长分别是4cm,3cm,求阴影部分的面积。
4.长方形ABCD的周长是16cm,在它的每条边上各画一个以该边为边长的正方形,
已知这四个正方形的面积和是68cm2,求长方形ABCD的面积。
5.如图所示,在边长为12cm的正方形ABCD中,E、F是BC边上的三等分点,M、
N是对角线BD上的三等分点,邱三角形EMN的面积。
6.梯形ABCF的下底BC是12cm,高AB是18cm,CE=2DE,求DF。
AB⊥BC,DC⊥BC,AB=CD=18(厘米)CE的长度是ED的2倍CE=18×2/(2+1)=12(厘米)ED=12÷2=6(厘米)S△BCF=BC×AB÷2=12×18÷2=108(平方厘米)S△BCE=BC×CE÷2=12×12÷2=72(平方厘米)阴影部分的面积=S△BCF-S△BCE=108-72=36(平方厘米)S△DEF=S阴影÷2=36÷2=18(平方厘米)DF=2×18÷ED=2×18÷6=6(厘米)。
