力法 PPT课件
合集下载
大学《结构力学》第6章 力法课件

超超静静定定次次数数==33××51==135
? 超超静静定定次次数数==33××52-=356=120
结构超静定次数的判定方法(拆除约束法)
一般从约束数少的约束开始拆(截断),直到使结构成为一个
无多余约束的几何不变体系(静定结构)为止。
1)去掉一根支座链杆或截断一根桁架杆,相当拆除1个约束;
2)去掉一个固定铰支座或切开一个单铰,相当拆除2个约束;
•
荷载作用下超静定结构的力法计算及内力图绘制与校核;
• (2)难点:根据已知变形条件建立力法典型方程;
•
利用对称性取等效半结构;
§6-1 超静定结构的组成和超静定次数
一、超静定结构 几何特征:多余约束
静力特征:多余力
组成 :有多余联系的几何不变体系。注意多余联系是对几何不变 体而言,可在结构内部或外部,多余联系中产生的力称为多余力。 如果一个结构的支座反力和各截面内力都可以由静力平衡
l
MP
M1
3、力法基本方程-
11 1p 0
11 11 X 1
11 X 1 1P 0
X1 1
4、系数与自由项 1P ,11
1P
M1M P dx ql4
EI
8 EI
5、解方程
l3 3EI
X1
ql 4 8EI
0
11
M1M1 dx l3
EI
3EI
X1
3 8
ql
8
X1
3 8
ql
4
3次超静定
P
X
X
3
2
X
3
X1
X
X
2
1
3.切断一根梁式杆等于去掉三个约束
力法知识讲解PPT89页

↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓B
Δ1P
Δ1=δ11X1 + Δ1P=0
= X1=-Δ1P / δ11 3ql/8
↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓ M图
3ql/8
17
d X D 0
11 1
1P
D1P
512 EI1
d11
288 k 144 k EI1
X1
-
D1P
d11
-
320k
92k 1
X1
k1 2
- 80 kN 9
由上述,力法计算步骤可归纳如下: 影响。
1)确定超静定次数,选取力法基本体系;
2)按照位移条件,列出力法典型方程;
3)画单位弯矩图、荷载弯矩图,用(A)式求系数和自由项;
4)解方程,求多余未知力;
5)叠加最后弯矩图。M M i X i M P
25
§6.4 超静定梁、刚架和排架
FP
例 . 求解图示两端固支梁。
d12 X 2 d 22 X 2
D1P D2P
0 0
图乘求得位移系数为
d 11
d 22
2d 12
l 3EI
D1P
-
FPab(l b) 6EIl
D2 P
-
FPab(l a) 6EIl
X 1
FPab2 l2
X
2
FP a 2b l2
可代 得入
并 求 解
FPab2 l2
FPab l
FPa2b l2
11
EI
X1=1
求l X1方 E向1I 的 l位22 移23l 虚 拟3的lE3I力状P=态1
ql2/2 ↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓
MP
第十二章-力法及正则方程(材料力学课件)

a2 2
2a
3
2a 3 3EI
1P
1 EI
2 3
qa 2 8
a
a
2
qa 4 24 EI
由 11 X1
1P
0得
X1
qa 16
XB
qa 16
,
YB
9qa 16
X
A
qa 16
,
YA
7qa 16
等截面梁的受力情况如图所示。试求A、 B、C三处的约束力。
CL12TU85
M10 图
CL12TU83
11
1 EI
l 1
l EI
M10 图
1P
1 EI
Pl 2 8
1
Pl 2 8EI
由 11 X1
1P
0得X 1
Pl 8
MP图
vC
Pl 3 48EI
Pl l 2 2 8
16EI
Pl 3 192EI
求图示刚架的支反力。
CL12TU84
M10 图
MP图
11
2 EI
CL12TU86
解:载荷关于对角线AC 和BD反对称。
由平衡条件可得:
Q P cos45 2 P 2
M max
Pa 2
M max 发生在外载荷P作用点处
0 j
实际载荷引起的弯矩为M P
则: ii
l
M
0 i
M
0 i
EI
dx,
i j
l
M
0 i
M
0 j
EI
dx
i P
l
M
0 i
MP
EI
dx
平面刚架受力如图,各杆 EI=常数。试求 C处的约束力、支座反力。
结构力学课件--6力法
2m 2m
4m
1
4m
125
15
11.3
15
M kN m
Q kN
3.7 75
200
15 147.5
11.3 22.5
11.3 3.7
22.5
2021/4/9竖向力不平衡
147.5
N kN
二、变形条件的校核
25
200
100 60
2
2 30
1
40
1
150
4m
1
1
20 2m 2m
15 4m
11
M kN m
2) 3
4a 3EI
X2 1
22
1 EI
(1 2
a 1
2) 3
a 3EI
M2
12
1 EI
(1 2
a 1 1) 3
a 6EI
1 1 Pa
1 Pa 2 5Pa2
1P
EI
( 2
2
a1 2
2
a ) 3 12EI
2P
1 EI
1 2
Pa 2
a
1) 3
Pa 2 12EI
Pa 2
P 2 MP 1
X1 1 M1
EA
0 E1A1
1P
M1M P EI
ds
=
1P
l N12 dx l 12 dx l
0 E1A1
0 E1A1
E1 A1
11
M12 ds EI
N12 ds EA
l E1 A1
11
l E1 A1
两类拱的比较: 无拉杆 H 1P
11
E1A1 H H 相当于无拉杆
力法—力法的基本原理和典型方程(工程力学课件)

——
M
i、M
图互乘
j
iP
M
i
MP EI
ds
——
M
i、M
图互乘
P
力法又称为柔度法,力法方程称为柔度方程。
11X1 12 X 2 1i X i 1n X n 1P 0 21 X1 22 X 2 2i X i 2n X n 2P 0
n1 X1 n2 X 2 ni X i nn X n nP 0
物理意义:基本结构在全部多余力和荷载共同作用 下,在去掉各多余联系处沿各多余力方向的位移,与 原结构相应的位移相等。
δij X j 1 单独作用下引起的 Xi 方向的位移;
iP 外荷载单独作用下引起的Xi 方向的位移
主系数:δ11、δ22、δ33恒大于零。
副系数:δij (i≠j)可能>、=或<0。 δij=δji
➢ 力法的典型方程
一般情况下,一个 n 次超静定结构,则有n 个多余未 知力,而每个多余力都对应一个多余联系,相应就有一 个位移条件,故可据此建立 n 个方程,这 n 个方程为:
X3=1 B
δ13
➢ 力法的典型方程
q
C
D
FP 基本体系
11 X1 12 X2 13 X3 1P BH 0 21 X1 22 X2 23 X3 2P BV 0 31 X1 32 X2 33 X3 3P B 0
A
X3
i 表示位移的因。
X2
力法的基本原理
超静定结构
力法
超静定次数较低时
位移法
超静定次数较高时
➢ 力法的基本概念
待解的未知问题
基本体系
1 0
变形条件
X1
力法基本 未知量
10力法--习题ppt课件

A
B
l
C M1 X1 1
2
11
M1 dx 1 1 l l l 2 1 1 l l l 2
EI
EI1 2
3 EI2 2
3
A
B
C MP
(1 k )l3 3kEI2
ql2/8
结构力学电子教程
10 力法
A
B
l
A
B
ql2/8
ql 2 8(1 k)
A
(ql2/8)
(1 2k)ql2B
10 力法
(c) I1=kI2
q A
I1 B l
① k=10,② k=0.1
【解】
I2
C
l
一、取力法基本体系 二、列力法基本方程
q A
B
C
X1
力法基本体系
11X1+1P=0 三、计算Байду номын сангаас数11和自由项1P
1P
M1MP dx
1
2 ql 2 1 l l
ql 4
EI
EI1 3 8 2 24kEI2
MP (kN·m)
得
X1 X2
9.375 6.429
五、作M图
104.46
47.41
36.96
M (kN·m)
180
M M1X1 M2 X2 MP
结构力学电子教程
10 力法
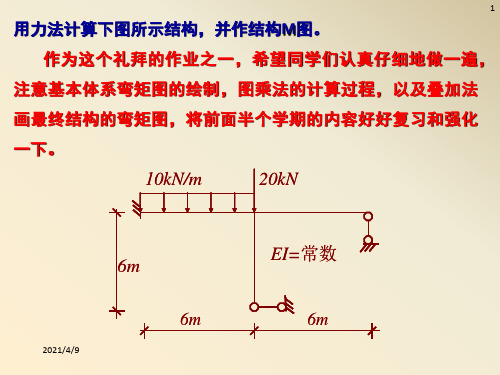
10.5 用力法计算下列排架,作M图,
(a)
20kN/m EA
C
D
I
I
A
B
6m
6m
6m
【解】 一、取力法基本体系 二、列力法基本方程
力法方程代表变形条件----位移应与原结构在相应处的 位移相等。
力法 ppt课件

力法课件包含了大量的信息和内容,可能 导致学生无法消化和理解,造成信息过载 。
替代传统教学
技术更新快
力法课件虽然可以辅助教学,但不能完全 替代传统的教学方式,过分依赖课件可能 影响学生的思考能力和实践能力。
力法课件所依赖的技术更新换代较快,导 致课件的维护和更新成本较高,对学校和 教师提出了更高的要求。
扩展应用领域
随着研究的深入和技术的发展,展望
更高效的求解算法
针对大规模、复杂问题,寻 求更快速、稳定的求解算法 是力法未来的重要研究方向 。
跨学科交叉融合
力法将与其它工程学科、数 学方法及计算科学进一步交 叉融合,形成更综合、系统 的分析方法。
力法的基本原理
总结词
力法的基本原理包括虚功原理、虚位移原理和最小势能原理。
详细描述
力法的基本原理包括虚功原理、虚位移原理和最小势能原理。虚功原理是力法的基本依据,它表明在平衡状态下 ,实功和虚功相等;虚位移原理表明在平衡状态下,虚位移和外力所做的虚功相等;最小势能原理则表明结构的 平衡状态对应于势能的最小值。
结果分析
解析解的意义
对求解得到的力学模型结果进行深入分析,理解其物理意义 ,并评估其对实际问题的指导价值。这一步骤有助于将力学 模型解转化为实际应用的指导。
03
力法的应用实例
桥梁结构的力法分析
总结词
桥梁结构的力法分析是利用力学原理对桥梁结构进行受力 分析和评估的过程。
计算模型
力法分析基于力学原理建立计算模型,通过计算和分析桥 梁结构的内力和变形,评估其承载能力和稳定性。
详细描述
通过力法分析,可以确定桥梁结构的承载能力、稳定性以 及在不同载荷下的变形情况。这对于确保桥梁安全运行和 预防潜在的损坏至关重要。
结构力学力法PPT_图文

q EI 1次超静定
一个无铰封闭圈有三个多余联系
q
q
q
q
第8章
2、去掉多余联系的方法
(1)去掉支座的一根支杆或切断一根链杆相当于去掉一个联系。 (2)去掉一个铰支座或一个简单铰相当于去掉两个联系。 (3)去掉一个固定支座或将刚性联结切断相当于去掉三个联系。 (4)将固定支座改为铰支座或将刚性联结改为铰联结相当于 去掉一个联系。
1、解题思路
q
2
1
l
原结构
q
x1 基本结构
位移条件: 1P+ 11=0 因为 11= 11X1 ( 右下图) 所以 11X1 +1P =0 X1= -1P/ 11
q 1P
11 x1
11 x1=1
第8章
2、解题步骤
(1)选取力法基本结构; (2)列力法基本方程; (3)绘单位弯矩图、荷载弯矩图; (4)求力法方程各系数,解力法方程; (5)绘内力图。
X1
X2
基本结构(1)
第8章
对应不同的基本结构有不同的力法方程:
A
B
C
D
C1
C2
l A X1
l
l
原结构
B
C
D
C1
C2
X2
解:力法方程:
基本结构(2)
第8章
对应不同的基本结构有不同的力法方程:
A
B
C
D
C1
C2
l
l
原结构
A
B
C
l D
C1
X1
X2
解:力法方程:
基本结构(3)
第8章
四、如何求
A
以基本结构(2)为例:
一个无铰封闭圈有三个多余联系
q
q
q
q
第8章
2、去掉多余联系的方法
(1)去掉支座的一根支杆或切断一根链杆相当于去掉一个联系。 (2)去掉一个铰支座或一个简单铰相当于去掉两个联系。 (3)去掉一个固定支座或将刚性联结切断相当于去掉三个联系。 (4)将固定支座改为铰支座或将刚性联结改为铰联结相当于 去掉一个联系。
1、解题思路
q
2
1
l
原结构
q
x1 基本结构
位移条件: 1P+ 11=0 因为 11= 11X1 ( 右下图) 所以 11X1 +1P =0 X1= -1P/ 11
q 1P
11 x1
11 x1=1
第8章
2、解题步骤
(1)选取力法基本结构; (2)列力法基本方程; (3)绘单位弯矩图、荷载弯矩图; (4)求力法方程各系数,解力法方程; (5)绘内力图。
X1
X2
基本结构(1)
第8章
对应不同的基本结构有不同的力法方程:
A
B
C
D
C1
C2
l A X1
l
l
原结构
B
C
D
C1
C2
X2
解:力法方程:
基本结构(2)
第8章
对应不同的基本结构有不同的力法方程:
A
B
C
D
C1
C2
l
l
原结构
A
B
C
l D
C1
X1
X2
解:力法方程:
基本结构(3)
第8章
四、如何求
A
以基本结构(2)为例:
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
F
6、叠加法内力并作内力图
M M 1 X1 M F FQ F Q1 X 1 FQ F
X 1 =1
M1
Fl 2
FN F N1 X1 FN F
11 16 F
MF
3 l 16 Fl M Fl 4
FQ 5 16 F
M AB FNAB A FQ AB
F B X1
作FQ、 FN图
杆端弯矩 作M图 M AB M 1AB X1 M FAB 5 Fl 3 Fl Fl (上拉) 16 2 16 M BA M 1BA X1 M FBA 0
3次超静定
6次超静定
4次超静定
15次超静定
10次超静定
7次超静定
§6-2 力法基本原理 一、力法基本思路 根据已掌握的静定结构的内力和位移计算知识,将静定结构转 化为静定结构来求解,先求出多余未知力。 二、力法基本原理
F A EI C l B
F
F
A
C
B X1
A
B X1
静定结构
原超定结构
基本体系(基本结构)
基本体系 (基本结构)
F
变形协调条件 X1
1 11 1F 0
11:X1引起X1方向的位移 1F:F引起X1方向的位移 11:X1 =1引起X1方向的位移
X 1 =1
M1
Fl 2
MF
l
3、典型方程
基本未知量
11 X1 1F 0
X1
1F
11=11 X1
自由项
(4)超静定拱; (5)超静定组合结构等。
三、超静定次数 超静定次数=多余约束的个数 超静定次数确定方法:解除约束法 解除超静定结构中的多余约束,使之成为静定结构。解除约束 的个数即为超静定的次数 截断一根连杆=解除1个约束;(支座连杆) 解除一个单铰=解除2个约束;(固定铰支座) 截断一受弯杆=解除3个约束;(刚结点、固定端) 单刚变为单铰=解除1个约束。
力法典型方程 力法基本方程 补充方程 4、作M 1、M F图并求11、1F
11
柔度系数
图乘法或 积分法计算
图乘法计算柔度系数和自由项
F A EI C l B
F A C B X1
A
F B
Δ1F Δ11
原超定结构
基本体系 (基本结构)
F
变形协调条件 X1
1 11 1F 0
1 1 2 l3 11 l l l EI 2 3 3EI 1 1 l Fl 5 1F l EI 2 2 2 6 5Fl 3 48EI
( 3)作M 1、 M 2及M F图 自由项 (4)求柔度系数和自由项 M iMF iF ds s EI (5)回代求未知力 (6)叠加法作内力图 11 1F M M 1 X 1 M 2 X 2+M F 12 2 F X2 FQ F Q1 X 1 F Q2 X 2+FQ F 11 12 21 22 FN F N1 X 1 F N2 X 2 FN F
变形协调条件
ห้องสมุดไป่ตู้
关键求X1 ?
1、问题转化 超静定结构 2、等效
变形协调条件 解除多余约束代之 以多余约束力作用
1 11 1F 0 11=? 1F=?
荷载作用 F
静定结构
未知力作用 X 1
Δ1F Δ11
F A EI C l B
F A C B X1
A
F B
Δ1F Δ11
原超定结构
MF
解除多余约束代之以多余约束力作用 荷载作用 F 静定结构 超静定结构 未知力作用 X 1 变形协调条件 基本体系(基本结构) (1)建立基本体系 (2)列力法典型方程 (5)回代求未知力
5 16 F
11 X1 1F 0
( 3)作M 1、M F图
(6)叠加法作内力图
(4)求11、1F
X 1 =1
M1
Fl 2
MF
l
3、典型方程
11 X1 1F 0
X1
1F
11
4、作M 1、M F图并求11、1F
5、求X1
X1
1F
11
5 F 16
F A EI C l B
F A C B X1
X1
1F
11
5 F 16
原超定结构
基本体系 (基本结构)
A a
B EI 1
X1
X1
C
B EI 1 C X2
基本系无穷多个
q
EI 2
悬臂结构
q
EI 2
三铰结构
悬臂结构、简支结构较简单
三铰结构、组合结构较复杂
A X2
X1
A
二、典型方程
B EI 1 C
EI 2
超定结构
A a
B EI 1 C
多次超静定结构内力计算步骤 (1)建立基本体系(两次超静定结构) 2 (2)列力法典型方程 Mi ds ii + 0 s 1 11 12 1 F EI 变形 条件 2 21 22 + 2 F 0 主系数 ii>0 典型 方程
§6-3 力法基本未知量、基本系和典型方程 一、力法基本未知量和基本系
基本未知量的个数=超静定次数=多余约束的个数=补充方程的个数
解除约束的位置和方法不同,基本系也不同。
B EI 1 C
B EI 1 X2 C X1
X1 EI 1 C
B X1
X2
q
q
EI 2
a
超定结构
A
EI 2
q
简支结构
A
EI 2
三铰结构
q
a
MiM j 11 X 1 12 X 2 +1F 0 ij ji ds s EI 21 X 1 22 X 2 + 2 F 0 副系数(> 0、<0、=0) ij
EI 2
基本系
A X2
X1
X1
1F 2F
11 21
12 22 12 22
第六章 力法
§6-1 概述 超静定结构:是指在荷载等因素作用下,其支座反力和内力不能 仅由平衡条件全部确定的结构。 特点:整体性好,有较大的强度、刚度和稳定性,工程应用广泛。 一、几何组成特性和解答唯一性定理
几何组成特性:有多余约束的几何不变体系
唯一性定理:超静定结构在荷载等因素作用下,同时满足平衡条 件和位移协调条件的支座反力和内力的解答是确定的、有限的和 唯一的。 二、超静定结构形式 (1)超静定梁;(2)超静定刚架;(3)超静定桁架;
作FQ、 FN图回归到静定结构作图方法 计算机编程计算用叠加公式
小结
A EI C l
F B
F A C B
A
F B
Δ1F Δ11
原超定结构
X1 静定结构 基本体系(基本结构)
F
X 1 =1
变形协调条件
3 16 Fl M
1 11 1F 0
X1
M1
Fl 2
11 16 F FQ
Fl 4
l
6、叠加法内力并作内力图
M M 1 X1 M F FQ F Q1 X 1 FQ F
X 1 =1
M1
Fl 2
FN F N1 X1 FN F
11 16 F
MF
3 l 16 Fl M Fl 4
FQ 5 16 F
M AB FNAB A FQ AB
F B X1
作FQ、 FN图
杆端弯矩 作M图 M AB M 1AB X1 M FAB 5 Fl 3 Fl Fl (上拉) 16 2 16 M BA M 1BA X1 M FBA 0
3次超静定
6次超静定
4次超静定
15次超静定
10次超静定
7次超静定
§6-2 力法基本原理 一、力法基本思路 根据已掌握的静定结构的内力和位移计算知识,将静定结构转 化为静定结构来求解,先求出多余未知力。 二、力法基本原理
F A EI C l B
F
F
A
C
B X1
A
B X1
静定结构
原超定结构
基本体系(基本结构)
基本体系 (基本结构)
F
变形协调条件 X1
1 11 1F 0
11:X1引起X1方向的位移 1F:F引起X1方向的位移 11:X1 =1引起X1方向的位移
X 1 =1
M1
Fl 2
MF
l
3、典型方程
基本未知量
11 X1 1F 0
X1
1F
11=11 X1
自由项
(4)超静定拱; (5)超静定组合结构等。
三、超静定次数 超静定次数=多余约束的个数 超静定次数确定方法:解除约束法 解除超静定结构中的多余约束,使之成为静定结构。解除约束 的个数即为超静定的次数 截断一根连杆=解除1个约束;(支座连杆) 解除一个单铰=解除2个约束;(固定铰支座) 截断一受弯杆=解除3个约束;(刚结点、固定端) 单刚变为单铰=解除1个约束。
力法典型方程 力法基本方程 补充方程 4、作M 1、M F图并求11、1F
11
柔度系数
图乘法或 积分法计算
图乘法计算柔度系数和自由项
F A EI C l B
F A C B X1
A
F B
Δ1F Δ11
原超定结构
基本体系 (基本结构)
F
变形协调条件 X1
1 11 1F 0
1 1 2 l3 11 l l l EI 2 3 3EI 1 1 l Fl 5 1F l EI 2 2 2 6 5Fl 3 48EI
( 3)作M 1、 M 2及M F图 自由项 (4)求柔度系数和自由项 M iMF iF ds s EI (5)回代求未知力 (6)叠加法作内力图 11 1F M M 1 X 1 M 2 X 2+M F 12 2 F X2 FQ F Q1 X 1 F Q2 X 2+FQ F 11 12 21 22 FN F N1 X 1 F N2 X 2 FN F
变形协调条件
ห้องสมุดไป่ตู้
关键求X1 ?
1、问题转化 超静定结构 2、等效
变形协调条件 解除多余约束代之 以多余约束力作用
1 11 1F 0 11=? 1F=?
荷载作用 F
静定结构
未知力作用 X 1
Δ1F Δ11
F A EI C l B
F A C B X1
A
F B
Δ1F Δ11
原超定结构
MF
解除多余约束代之以多余约束力作用 荷载作用 F 静定结构 超静定结构 未知力作用 X 1 变形协调条件 基本体系(基本结构) (1)建立基本体系 (2)列力法典型方程 (5)回代求未知力
5 16 F
11 X1 1F 0
( 3)作M 1、M F图
(6)叠加法作内力图
(4)求11、1F
X 1 =1
M1
Fl 2
MF
l
3、典型方程
11 X1 1F 0
X1
1F
11
4、作M 1、M F图并求11、1F
5、求X1
X1
1F
11
5 F 16
F A EI C l B
F A C B X1
X1
1F
11
5 F 16
原超定结构
基本体系 (基本结构)
A a
B EI 1
X1
X1
C
B EI 1 C X2
基本系无穷多个
q
EI 2
悬臂结构
q
EI 2
三铰结构
悬臂结构、简支结构较简单
三铰结构、组合结构较复杂
A X2
X1
A
二、典型方程
B EI 1 C
EI 2
超定结构
A a
B EI 1 C
多次超静定结构内力计算步骤 (1)建立基本体系(两次超静定结构) 2 (2)列力法典型方程 Mi ds ii + 0 s 1 11 12 1 F EI 变形 条件 2 21 22 + 2 F 0 主系数 ii>0 典型 方程
§6-3 力法基本未知量、基本系和典型方程 一、力法基本未知量和基本系
基本未知量的个数=超静定次数=多余约束的个数=补充方程的个数
解除约束的位置和方法不同,基本系也不同。
B EI 1 C
B EI 1 X2 C X1
X1 EI 1 C
B X1
X2
q
q
EI 2
a
超定结构
A
EI 2
q
简支结构
A
EI 2
三铰结构
q
a
MiM j 11 X 1 12 X 2 +1F 0 ij ji ds s EI 21 X 1 22 X 2 + 2 F 0 副系数(> 0、<0、=0) ij
EI 2
基本系
A X2
X1
X1
1F 2F
11 21
12 22 12 22
第六章 力法
§6-1 概述 超静定结构:是指在荷载等因素作用下,其支座反力和内力不能 仅由平衡条件全部确定的结构。 特点:整体性好,有较大的强度、刚度和稳定性,工程应用广泛。 一、几何组成特性和解答唯一性定理
几何组成特性:有多余约束的几何不变体系
唯一性定理:超静定结构在荷载等因素作用下,同时满足平衡条 件和位移协调条件的支座反力和内力的解答是确定的、有限的和 唯一的。 二、超静定结构形式 (1)超静定梁;(2)超静定刚架;(3)超静定桁架;
作FQ、 FN图回归到静定结构作图方法 计算机编程计算用叠加公式
小结
A EI C l
F B
F A C B
A
F B
Δ1F Δ11
原超定结构
X1 静定结构 基本体系(基本结构)
F
X 1 =1
变形协调条件
3 16 Fl M
1 11 1F 0
X1
M1
Fl 2
11 16 F FQ
Fl 4
l
