反比例函数中“K”与面积专题
八年级数学专题 已知面积求反比例函数比例系数k
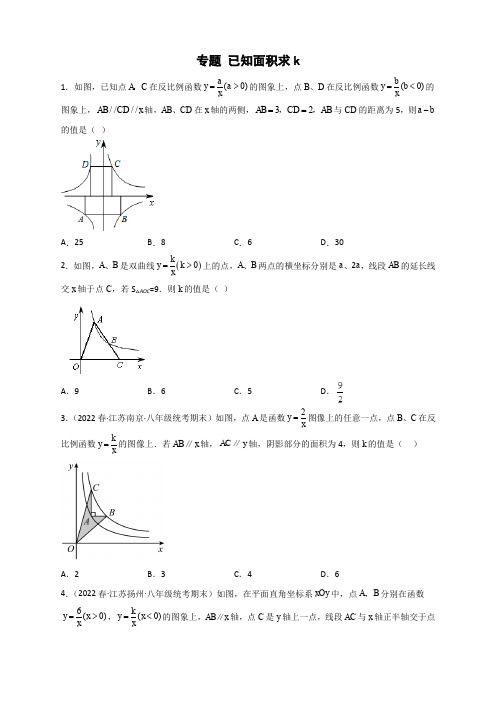
A.9 B.6 C.5 D.2x2AD,若ABO的面积为6\kkxDE OC,FG的面积为10,则kmx在平面直角坐标系中,ABO的边若O A B的面积为6,则x,将ABO向右平移到CDE位置,C和DE的中点,则k的值是k(1)设2a =,点(4,2)B 在函数12,y y 的图象上. ①分别求函数12,y y 的表达式;②直接写出使120y y >>成立的x 的范围;(2)如图,设函数12,y y 的图象相交于点B ,点B 的横坐标为3a ,AA B '∆的面积为16,求k 的值. 25.六•一儿童节,小文到公园游玩.看到公园的一段人行弯道MN (不计宽度),如图,它与两面互相垂直的围墙OP 、OQ 之间有一块空地MPOQN (MP ⊥OP ,NQ ⊥OQ ),他发现弯道MN 上任一点到两边围墙的垂线段与围墙所围成的矩形的面积都相等,比如:A 、B 、C 是弯道MN 上的三点,矩形ADOG 、矩形BEOH 、矩形CFOI 的面积相等.爱好数学的他建立了平面直角坐标系(如图),图中三块阴影部分的面积分别记为S 1、S 2、S 3,并测得S 2=6(单位:平方米).OG=GH=HI . (1)求S 1和S 3的值;(2)设T (x ,y )是弯道MN 上的任一点,写出y 关于x 的函数关系式;(3)公园准备对区域MPOQN 内部进行绿化改造,在横坐标、纵坐标都是偶数的点处种植花木(区域边界上的点除外),已知MP=2米,NQ=3米.问一共能种植多少棵花木?A.9 B.6 C.5 D.x22km m m ⎛⎫- ⎪⎝⎭6k =.D .2ADBCDBDASS=【详解】解:如图,过点6kBCDBDASS=ADB=61,若ABO的面积为628AB OA =根据EAB ∠EAB ∴∠=E k x y =⋅设(712E m ,EOF S ∴=△\DBO DBE S S =,根据反比例函数,AD AC =BDA S ∴=△EDB S ∴=△AB AC =AD AB ∴=DBA ∴∠=DBA ∠+ABD ∴∠+D在第一象限,∴=k43故答案为:AOE S =-OBF S =-1+k 2-2k 的值. AOE S +OBF S +S 三点分别在反比例函数y=1k x (x<0AOE S =12OBF S =12△ABC =(,x y=,2∵点A在第二象限,则=-=x y xy2xy=-,即∴反比例函数的解析式为:故答案为:y=、OABC的DE OC,FG 的面积为10,则∴两三角形的相似比为,∵双曲线,可知,,由,得,解得m(,)A a b、∴点O在线段(,)A a b是反比例函数mba∴=,AC∥y轴,∴点C的坐标为|mACa ∴=x【点睛】本题主要考查菱形的性质及反比例函数的比例系数k的几何意义.反比例函数图象上的点与原点所连的线段、坐标轴、向坐标轴作垂线所围成的直角三角形面积S的关系,即S=|k|.在平面直角坐标系中,ABO的边x若O A B的面积为6,则根据OAB的面积为的坐标,从而得出结论.【详解】解:如图,延长∵OAB的面积为1 2AB OD⋅(1 2AB x⋅-CBDS =,证明BFG BCD ∽,可得BFGS =2k=解方程即分别作x 轴的垂线,垂足分别为四边形Rt Rt OAE CBD ≌CBDS=若点为BC 的中点,△FG CD ∥BFG BCD ∴∽,12BF BC =, 21BFG BCGS BF S⎛⎫∴== ⎪BFGS=OBF +△8k .故答案为:8.【点睛】本题考查了平行四边形的性质,相似三角形的性质与判定,反比例函数与数形结合是解题的关键.,将ABO 向右平移到CDE 位置,C 和DE 的中点,则k 的值是AOD AOB BOC ADCB SS S S +=+四,,2AOD BOC k S S ==AOB S ,列出方程,解出即可.【详解】解:过点,2AOD BOC k S S ==AOD AOB BOC ABCO ADCB S S S S S =+=+四四,AOB ADCB S S ∴=四,2,4,24k k A B ⎛⎫⎛⎫ ⎪ ⎝⎭⎝1222k ⎛∴⨯ ⎝4.k ∴=2a =∴点A 坐标为把()4,2BO 为AA '12AOB S ∆=点A 、36。
专题01 用几何意义探究反比例函数中k值问题的多种解法(解析版)

专题01 用几何意义探究反比例函数中k 值问题的多种解法如图,反比例函数k y x =(k >0),A 、C 是第一象限上两点,S △OAB =S △OCD =2k ;S △OAC =S 梯形ABDC 在已知面积或比例线段解答反比例函数的问题中,善于利用k 与面积的关系,往往可以事半功倍.典例1.知面积比值,求k 值(2022•山东聊城中考真题)如图,直线与反比例函数在第一象限内的图象交于点,与y 轴交于点B ,过双曲线上的一点C 作x 轴的垂线,垂足为点D ,交直线于点E ,且.()30y px p =+¹()0k y k x=>()2,A q 3y px =+:3:4AOB COD S S =△△(1)求k ,p 的值;(2)若OE 将四边形BOCE 分成两个面积相等的三角形,求点C 的坐标.【答案】(1),;(2)点C 的坐标为(4,2)【解析】【方法一】坐标法(1)解:∵直线与y 轴交点为B ,∴,即.∵点A 的横坐标为2,∴.∵,∴△COD 的面积为4,设,∴,解得.∵点在双曲线上,∴,把点代入,得,∴,;8k =12p =3y px =+()0,3B 3OB =13232AOB S =´´=V :3:4AOB COD S S =△△,k C m m æöç÷èø142k m m×=8k =()2,A q 8y x=4q =()2,4A 3y px =+12p =8k =12p =(2)解:由(1)得8,C m m æöç÷èø,∴.∵OE 将四边形BOCE 分成两个面积相等的三角形,∴,∵32BOE S m =△,,∴,解得或(不符合题意,舍去),∴点的坐标为(4,2).【方法二】k 的几何意义法解:(1)由题意知,△ABO 的面积为3,又,得:△OCD 的面积为4,故k =2S △OCD =8,所以,A (2,4),把点代入,得(2)如图,过A ,E 作y 轴垂线,垂足为M ,N则四边形ODEN 为矩形,所以,S △OEN =S △OED ,又S △OBE =S △OCE ,所以S △BEN =S △OCD =4,1,32E m m æö+ç÷èøBOE COE S S =△△13422COE m S m æö=+-ç÷èø△3134222m m m æö=+-ç÷èø4m =4m =-C :3:4AOB COD S S =△△()2,4A 3y px =+12p =所以S △ABM =1,∵AM ∥NE ,∴△ABM ∽△EBN ,其面积比为1:4,∴AM :NE =1:2,即NE =4,∴C 点坐标为(4,2)典例2.知比例线段,求k 值(2022•贵州铜仁中考真题)如图,点A 、B 在反比例函数k y x=的图象上,AC y ^轴,垂足为D ,BC AC ^.若四边形AOBC 的面积为6,12AD AC =,则k 的值为_______.【答案】3.【解析】【方法一】坐标法设点,k A a a æöç÷èø,∵AC y ^轴,∴AD a =,k OD a =,∵12AD AC =,∴AC 2a =,∴CD =3a ,∵BC AC ^.AC y ^轴,∴BC ∥y 轴,∴点B 3,3æöç÷èøk a a ,∴233k k k BC a a a=-=,∵AOD AOBC OBCD S S S =+V 四边形梯形,四边形AOBC 间面积为6,∴12136232k k a k a a æö+´=+ç÷èø,解得:3k =.【方法二】k 的几何意义法如图,连接OC ,延长CB 交x 轴于E ,则S △AOD =S △BOE =12k ,因为AD :AC =1:2,所以S △AOC =2S △AOD =k ,S △BOC =6-k ,又四边形DOEC 为矩形,OC 为对角线,所以,S △COD =S △COE ,所以12k +k =6-k +12k ,解得:k =3.典例3.知面积值,求k 值(2022•内蒙古呼伦贝尔中考真题)如图,在平面直角坐标系中,Rt OAB △的直角顶点B 在x 轴的正半轴上,点O 与原点重合,点A 在第一象限,反比例函数k y x=(0x >)的图象经过OA 的中点C ,交AB 于点D ,连接CD .若ACD △的面积是1,则k 的值是_________.【答案】43.【解析】【方法一】坐标法解:设C (m ,k m),因为C 为OA 中点,所以A (2m ,2k m),则D (2m ,2k m ),又△ACD 的面积为1,所以12122k k m m m æö×-=ç÷èø,解得:k =43【方法二】k 的几何意义法解:连接OD ,过C 作CE AB ∥,交x 轴于E ,∵∠ABO =90°,反比例函数k y x =(x >0)的图象经过OA 的中点C ,1ACD S =V ,∴12COE BOD S S k ==△△,1ACD OCD S S ==V V ,2OC =OA ,∵CE AB ∥,∴△OCE ∽△OAB ,∴221124OCE S OC S OA æöæö===ç÷ç÷èøèø△△O A B ,∴4OCE OAB ACD OCD OBD S S S S S ==++V V V V V ,∴1141122k k ´=++,∴k =43,故答案为:43.1.(2022•辽宁锦州中考真题)如图,在平面直角坐标系中,△AOB 的边OB 在y 轴上,边AB 与x 轴交于点D ,且BD =AD ,反比例函数y =k x(x >0)的图像经过点A ,若S △OAB =1,则k 的值为___________.【答案】2.【解析】【方法一】坐标法解:设A(a,b) ,如图,作A过x轴的垂线与x轴交于C,则:AC=b,OC=a,AC∥OB,∴∠ACD=∠BOD=90°,∠ADC=∠BDO,∴△ADC≌△BDO,∴S△ADC=S△BDO,∴S△OAC=S△AOD+ S△ADC=S△AOD+ S△BDO= S△OAB=1,∴12×OC×AC=12ab=1,∴ab=2,∵A(a,b) 在y=kx上,∴k=ab=2 .【方法二】k的几何意义法由上知,S△AOC=1,所以,k=2S△AOC=2故答案为:2.2.(2022•辽宁鞍山中考真题)如图,在平面直角坐标系中,O 是坐标原点.在Rt OAB V 中,90OAB Ð=°,边OA 在y 轴上,点D 是边OB 上一点,且:1:2OD DB =,反比例函数()0ky x x=>的图象经过点D 交AB 于点C ,连接OC .若4OBC S =△,则k 的值为_________.【答案】1.【解析】【方法一】坐标法解:∵反比例函数()0k y x x=>的图象经过点D ,∠OAB =90°,∴D (m ,k m ),∵OD :DB =1:2,∴B (3m ,3k m),∴AB =3m ,OA =3k m ,∴反比例函数()0k y x x =>的图象经过点D 交AB 于点C ,∠OAB =90°,∴12AOC S k =△,∵4OBC S △=,∴4AOB AOC S S -△△=,即1313422k m k m ´×-=,解得k =1【方法二】k 的几何意义法如图,过D 作DE ⊥x 轴,则DE ∥AB ,因为OD :BD =1:2,所以DE :AB =1:3,所以S △ODE :S △OAB =1:9,又S △ODE =S △OAC =12k ,所以12k +4=92k ,解得:k =13.(2022•江苏南通中考真题)平面直角坐标系中,已知点是函数图象上的三点.若,则k 的值为___________.【答案】【解析】【方法一】坐标法解:∵点是函数图象上的三点,∴,,∴m =n ,∴,,∴点B 、C 关于原点对称,∴设直线BC 的解析式为,代入得:,解得:,∴直线BC 的解析式为,xOy (,6),(3,2),(3,2)--A m m B m n C m n (0)k y k x=¹2ABC S =△34(,6),(3,2),(3,2)--A m m B m n C m n (0)k y k x =¹260k m =>6k mn =(3,2)B m m (3,2)C m m --()0y kx k =¹(3,2)B m m 23m mk =23k =23y x =不妨设m >0,如图,过点A 作x 轴的垂线交BC 于D ,把x =m 代入得:,∴D (m ,),∴AD =,∴,∴,∴,而当m <0时,可得,故答案为:.【方法二】由题意知,S △OAB =12632m n m m ×-×,O 为BC 中点,因为所以,S △OAB =12632m n m m ×-×=1,即291mn m -=①,又632m m m n k ×=×=②,23y x =23y m =23m 216633m m m -=()11633223ABC S m m m =´×+=V 218m =2136684k m ==´=34k =342ABC S =△由①②可得:4.(2022•湖北十堰中考真题)如图,正方形ABCD 的顶点分别在反比例函数()110k y k x=>和()220k y k x =>的图象上.若BD y ∥轴,点D 的横坐标为3,则12k k +=( )A .36B .18C .12D .9【答案】B .【解析】【方法一】解:连接AC ,与BD 相交于点P ,设PA =PB =PC =PD =t (t ≠0).∴点D 的坐标为(3,23k ),∴点C 的坐标为(3-t ,23k +t ).∵点C 在反比例函数y =2k x 的图象上,34k=∴(3-t )(23k +t )=k 2,化简得:t =3-23k ,∴点B 的纵坐标为23k +2t =23k +2(3-23k )=6-23k ,∴点B 的坐标为(3,6-23k ),∴3×(6-23k )=1k ,整理,得:1k +2k =18.【方法二】先利用D 点坐标,表示出A 和C 点坐标,再根据四边形ABCD 为正方形,BD 与y 轴平行,知AC 平行于x 轴,那么,A 和C 点的纵坐标相等,进而求解23,3k D æöç÷èø,13,3k B æöç÷èø,122123,636k k k C k k æöç÷--ç÷-ç÷-èø,121123,636k k k A k k æöç÷-+ç÷-ç÷+èø所以2112123366k k k k k k =---+,整理得:()212212180k k k k ---=即()()1212108k k k k -+=-因为()120k k -¹所以()12018k k +-=,即1218k k +=5.(2022•黑龙江龙东中考真题)如图,在平面直角坐标系中,点O 为坐标原点,平行四边形OBAD 的顶点B 在反比例函数3y x =的图象上,顶点A 在反比例函数k y x=的图象上,顶点D 在x 轴的负半轴上.若平行四边形OBAD 的面积是5,则k 的值是( )A .2B .1C .1-D .2-【答案】D .【解析】解:设B点坐标为3,mmæöç÷èø,则A3,3kmmæöç÷èø,因为平行四边形OBAD的面积是5,所以353kmmmæö-×=ç÷èø,解得k=-2【方法二】解:如图,连接OA,设AB交y轴于点C,∵四边形OBAD是平行四边形,平行四边形OBAD的面积是5,∴1522AOB OBADS S==V Y,AB∥OD,∴AB⊥y轴,∵点B在反比例函数3yx=的图象上,顶点A在反比例函数kyx=的图象上,∴3,22 COB COAkS S==-V V,∴35222 AOB COB COAkS S S=+=-=V V V,解得:2k=-.故选:D.6.(2022•湖北黄石中考真题)如图,反比例函数kyx=的图象经过矩形ABCD对角线的交点E和点A,点B、C在x轴上,OCE△的面积为6,则k=______________.【答案】8.【解析】设C (m ,0),由题意知E 为AC 中点,因为△OCE 面积为6,所以E 点纵坐标为12m,所以E 12,12km m æöç÷èø,A 24,6km m m æö-ç÷èø,又A 在反比例函数图像上所以246km m k mæö-×=ç÷èø解得k =8【方法二】解:如图作EF ⊥BC ,则12EF AB =,设E 点坐标为(a ,b ),则A 点的纵坐标为2b ,则可设A 点坐标为(c ,2b ),∵点A ,E 在反比例函数k y x=上,∴ab =k =2bc ,解得:a =2c ,故BF =FC =2c -c =c ,∴OC =3c ,故113622OEC S OC EF c b =´´=´´=V ,解得:bc =4,∴k =2bc =8,故答案为:8.7.(2022•贵州六盘水中考真题)如图,正比例函数与反比例函数的图象交于,两点.y x =4y x=A B(1)求,两点的坐标;(2)将直线向下平移个单位长度,与反比例函数在第一象限的图象交于点,与轴交于点,与轴交于点,若,求的值.【答案】(1);(2)【解析】(1)解:联立与,解得,;(2)【方法一】解:如图,过点作轴于点,A B y x =a C x D y E 13CD DE =a ()()2,2,2,2A B --3a =y x =4y x=121222,22x x y y ==-ììíí==-îî()()2,2,2,2A B \--C CF y ^F,,,直线向下平移个单位长度得到,根据图象可知,令,得,令,得,,,,,与反比例函数在第一象限的图象交于点,,将代入,得,解得或(舍去).【方法二】CF OD \∥Q 13CD DE =13OF CD OE DE \==Q y x =a y x a =-0a >0x =y a =-0y =x a =()0,E a \-(),0D a 10,3F a æö\ç÷èø13c y a \=Q y x a =-4y x=C 41213c x aa \==121,3C a a æöç÷èøy x a =-1123a a a=-3a =3a =-如图,连接OC ,过C 作CE ⊥x 轴,因为CD :DE =1:3,CE ∥OE则△CDE ∽△EDO ,相似比为1:3,面积比为1:9,易知△ODE 面积为212a ,△OCE 的面积为12k =2,所以△OCD 的面积为2-2118a ,又△OCD 与△ODE 的面积比为1:3,所以2-2118a =21132a ´,解得:a =3或a =-3(舍)8.(2022•安徽中考真题)如图,平行四边形OABC 的顶点O 是坐标原点,A 在x 轴的正半轴上,B ,C 在第一象限,反比例函数1y x =的图象经过点C ,()0k y k x=¹的图象经过点B .若OC AC =,则k =________.【答案】3.【解析】【方法一】设C 1,m m æöç÷èø,因为OC =AC所以A ()2,0m ,又OABC 为平行四边形所以B 13,m m æöç÷èø因为B 点在k y x =上,所以k =133m m ×=【方法二】解:过点C 作CD ⊥OA 于D ,过点B 作BE ⊥x 轴于E ,∴CD ∥BE ,∵四边形ABCO 为平行四边形,∴CB OA ∥ ,即CB DE ∥,OC =AB ,∴四边形CDEB 为平行四边形,∵CD ⊥OA ,∴四边形CDEB 为矩形,∴CD =BE ,∴在Rt △COD 和Rt △BAE 中,OC AB CD EB =ìí=î,∴Rt △COD ≌Rt △BAE (HL ),∴S △OCD =S △ABE ,∵OC =AC ,CD ⊥OA ,∴OD =AD ,∵反比例函数1yx=的图象经过点C,∴S△OCD=S△CAD=12,∴S平行四边形OCBA=4S△OCD=2,∴S△OBA=11 2OCBAS=平行四边形,∴S△OBE=S△OBA+S△ABE=13122+=,∴3232k=´=.故答案为3.。
专题:反比例函数中k的几何意义

专题:反比例函数中k 的几何意义知识要点:反比例函数中k 的几何意义1、反比例函数与矩形面积:若Q(x ,y)为反比例函数y = kx (k≠0)图像上的任意一点如图2所示,过Q 作QA ⊥x 轴于A(或作QB ⊥y 轴于B),连结QO ,则所得矩形的面积为S =|k |.说明:以上结论与点在反比例函数图像上的位置无关. 2、反比例函数与三角形面积:若Q(x ,y)为反比例函数y = k x (k≠0)图像上的任意一点如图2所示,过Q 作QA ⊥x 轴于A(或作QB ⊥y 轴于B),连结QO ,则所得三角形的面积为:S △QOA =|k |2(或S △QOB =|k |2).说明:以上结论与点在反比例函数图像上的位置无关.【跟踪训练】1. (2019∙凉山)如图,正比例函数y=kx 与反比例函数y= 4x 的图象相交于A 、C 两点,过点A 作x 轴的垂线交x 轴于点B ,连接BC ,则△ABC 的面积等于( ) A. 8 B. 6 C. 4 D. 22. (2019∙黑龙江)如图,在平面直角坐标系中,点O 为坐标原点,平行四边形OABC 的顶点A 在反比例函数y=1x上,顶点B 在反比例函数y= 5x 上,点C 在x 轴的正半轴上,则平行四边形OABC 的面积是( ) A. 32B. 52C. 4D. 63. (2019∙山西)如图,在平面直角坐标中,点O 为坐标原点,菱形ABCD 的顶点B 在x 轴的正半轴上,点A 坐标为(−4,0),点D 的坐标为(−1,4),反比例函数y= kx (x>0)的图象恰好经过点C ,则k 的值为___.4. (2019∙巴中)如图,反比例函数y= kx (x>0)经过A. B 两点,过点A 作AC⊥y 轴于点C,过点B 作BD⊥y 轴于点D,过点B 作BE⊥x 轴于点E,连结AD,已知AC=1、BE=1、S 矩形BDOE =4.则S △ACD =___.于点E,BD⊥x轴于点F,AC=2,BD=4,EF=3,则k2−k1=____________.B. 1C. 2D. 3A. 13且与矩形的对角线OB交于点D,连接EF.若OD:OB=2:3,则△BEF的面积为___.。
2024九年级数学下册第26章用反比例函数比例系数k的几何意义解与面积相关的应用课件新版新人教版

【解】∵直线 AB 交 y 轴于点 C,∴点 C(0,2), ∴S 四边形 COMN=S△OMN+S△OCN=32+12×2×t. ∵S 四边形 COMN>3,∴32+12×2×t>3,∴t>32.
【点方法】 当反比例函数图象中的几何图形的面积无法直接
求出时,可将其转化为与比例系数k相关的矩形或直 角三角形的面积,通过面积的和或差进行计算.
在 Rt△ ACE 中,CE= AC2-AE2=3, ∴OE=8,∴A(8,4),∴k=4×8=32, ∴反比例函数的解析式为 y=3x2. 将 A 和 C 的坐标代入一次函数解析式中, 得85aa++bb==40,,解得ab= =-43,230. ∴一次函数的解析式为 y=43x-230.
(2)请直接写出不等式 ax+b>kx的解集. 【解】不等式 ax+b>kx的解集为 x>8 或-3<x<0.
(2)若y轴上有一点C(0,n),△ABC的面积为4,求点C的 坐标. 【解】解方程组yy==2x2,x,得xy11==21,,xy22==--21., ∴点 B 的坐标为(-1,-2).
如图,过点 A,B 分别作 y 轴
的垂线,垂足分别为 E,F,
∵A(1,2),B(-1,-2),C(0,n), ∴AE=BF=1,OC=|n|. ∵S△ ABC=S△ AOC+S△ BOC=4, ∴12OC·AE+12OC·BF=4, 即|n|×1+|n|×1=8,∴|n|=4,∴n=±4, ∴点 C 的坐标为(0,4)或(0,-4).
【点方法】 一次函数与反比例函数常常放在一起考查,所以
要牢牢掌握它们各自的性质与图象特征,综合考虑, 解题时要关注两种函数图象的交点.
5 [2023·乐山]如图,一次函数 ym,4),与 x 轴交于点 B,与 y 轴交于点 C(0,3).
《用反比例函数比例系数k的几何意义解与面积相关的应用》PPT课件

(3)若 M(x1,y1),N(x2,y2)是反比例函数 y=mx 图 象上的两点,当 x1<x2<0 时,比较 y1 与 y2 的大小关系.
解:∵M(x1,y1),N(x2,y2)是反比例函数 y= -2x图象上的两点,且 x1<x2<0,∴y1<y2.
6.如图是由四条曲线围成的广告标志,建立平面直角坐 标系,双曲线对应的函数表达式分别为 y=-6x,y=6x. 现用四根钢条固定这四条曲线,这种钢条加工成矩形 产品按面积计算,每单位面积 25 元,请你帮助工人 师傅计算一下,所需钢条一共花多少钱?
(3)在x轴正半轴上是否存在点M,使得△MAB 为等腰三角形?若存在,请直接写出M点的 坐标;若不存在,说明理由.
解:M(-1+ 23,0)或(3+ 31,0).
3.【2019·东营】如图,在平面直角坐标系中,直线 y=mx 与双曲线 y=nx相交于 A(-2,a),B 两点, BC⊥x 轴,垂足为 C,△ AOC 的面积是 2. (1)求 m,n 的值;
(2)求两函数图象的交点A,C的坐标;
解:由yy= =- -3xx+,2,解得xy11==3-,1,xy22==-3,1. ∴点 A,C 的坐标分别为(-1,3),(3,-1).
(3)若点P是y轴上一动点,且S△APC=5,求点P的坐标.
解:设点 P 的坐标为(0,m),直线 y=-x+2 与 y 轴 的交点为 M,则 M 的坐标为(0,2). ∵S△ APC=S△ AMP+S△ CMP=12×PM×(|-1|+|3|)=5, ∴PM=52,即|m-2|=52.∴m=92或 m=-12. ∴点 P 的坐标为0,92或0,-12.
反比例函数中的面积问题(共26张PPT)

课后精练
解:(1)如图,过点 D 作 DH⊥x 轴于点 H, ∵直线 AB 的解析式为 y=-2x+4,∴B 点坐标为(0,4), A 点坐标为(2,0). ∵∠OAB+∠DAH=90°,∠ADH+∠DAH=90°, ∴∠BAO=∠ADH. 又∵∠BOA=∠AHD,∴△AOB∽△DHA. ∴ADOH=ABOH=AADB=12.∴D2H=A4H=12,解得 DH=4,AH=8. ∴D(10,4),则 k=10×4=40. 故答案为:40.
③若 M 点的横坐标为 1,△OAM 为等边三角形,则 k=2+ 3;
7.如图,函数 y=kx(k 为常数,k>0)的图象与过原点的 O 的直线 相交于 A,B 两点,点 M 是第一象限内双曲线上的动点(点 M 在点 A 的左侧),直线 AM 分别交 x 轴,y 轴于 C,D 两点,连接 BM 分别 交 x 轴,y 轴于点 E,F.现有以下四个结论:
课后精练
∵D(10,4),∴D′(10,-4). 设直线 CD′的解析式为 y=ax+d, 则180a+a+dd==8- ,4,解得da==-566. , 故直线 CD′的解析式为 y=-6x+56. 当 y=0 时,x=238,故 P 点坐标为238,0. 延长 CD 交 x 轴于 Q,此时|QC-QD|的值最大, ∵CD∥AB,D(10,4),∴直线 CD 的解析式为 y=-2x+24. ∴Q(12,0).∴PQ=12-238=83. 故 P 点坐标为238,0,Q 点坐标为(12,0),线段 PQ 的长为83.
专题2 反比例函数中的面积问题
考点解读
反比例函数中的面积类问题是最能体现数形结合思想 方法的一类问题,几何中的函数问题使图形性质代数 化,函数中的几何问题使代数知识图形化,利用“数”
反比例函数中的面积问题

解得 k=2 评注:第①小题中由图形所在象限可确定k>0,应用结论可直接求k值。 第②小题首先应用三角形面积的计算方法分析得出四个三角形面积相 等,列出含k的方程求k值。
例2(2008贵州省黔南州)如图,矩形ABOD的顶点A是函数 与函数 在第二象限的交点, 轴于B, 轴于D,且矩形ABOD的பைடு நூலகம்积为3. (1)求两函数的解析式. (2)求两函数的交点A、C的坐标.
图象上,∴
解得x=1从而所求面积为π 评注:对于较复杂的图形面积计算问题,先应观察图形的特征,若具有 对称特征,则应用对称关系可以简化解题过程。
四、 讨论与面积有关的综合问题 例8.(2008山东省)(1)探究新知:
如图1,已知△ABC与△ABD的面积相等, 试判断AB与CD的位置关系,并说明理由. (2)结论应用:
与x轴交于点C,其中点A的坐标为(-2,4),点B的横坐标为-4. (1)试确定反比例函数的关系式; (2)求△AOC的面积.
.解:(1)∵点A(-2,4)在反比例函数图象上 ∴k=-8 ∴反比例函数解析式为y=
(2)∵B点的横坐标为-4, ∴纵坐标为y=2 ∴B(-4,2) ∵点A(-2,4)、 点B(-4,2)在直线y=kx+b上 ∴ 4=-2k+b 且2=-4k+b 解得 k=1 b=6 ∴直线AB为y=x+6 与x轴的交点坐标C(-6,0)
(3)若点P是y轴上一动点,且 , 求点P的坐标.
解:(1)由图象知k<0,由结论及已知条件得 -k=3 ∴
∴反比例函数的解析式为 ,一次函数的解析式为 (2)由 ,解得 ,
∴点A、C的坐标分别为(
,3),(3, ) (3)设点P的坐标为(0,m) 直线 与y轴的交点坐标为M(0,2) ∵
专题:反比例函数中的面积问题

微专题 反比例函数中的面积问题
模型一 一点一垂线
反比例函数图象上一点与坐标轴垂线、另一坐标轴上一点(含原点)围成的三 角形面积= |k|.
1
S△ABC= 2 |k|
S△ABC=12 |k|
1
S△AOC= 2 |k|
1. 如图,点A在反比例函数y=- 4 的图象上,AM⊥y轴于点M,点P是x轴上的一
方法一:S△EOF=S△EOD-S△FOD. 方法二:作EM⊥x轴于点M,交OF于点B,FA⊥x轴于点A,则S△OEB=S四边形 BMAF(划归到模型一),则S△EOF=S直角梯形EMAF.
类型一 两交点在反比例函数同一支上
Байду номын сангаас
方法一:当
BE CE
或
BFFA=m时,则S四边形OFBE=m|k|.
方法二:作EM⊥x轴于点M,
A. 1
B. m-1
C. 2
D. m
第3题图
模型四 两点两垂线
反比例函数与正比例函数的交点及由交点向坐标轴所作两条垂线围成的图形 面积=2|k|.
SABC 2 | k |
易得四边形ANBM是平行四边形, ∴S四边形ANBM=AM·NM=AM·2OM=2|k|
模型四 两点两垂线 反比例函数与正比例函数的交点及由交点向坐标轴所作两条垂线围成的图形
= =
1
2
1
OM·AM+12 OM·BC |k|+1 |k|=|k|
22
S△ABM=S△ADM+S△MDB
=
1 2
MD·|yB-yA|
S△ABM=S△BMO+S△AMO
=
1 2
MO·|xB-xA|
3. 如图,直线y=mx与双曲线y=k (k≠0)交于点A,B,过点A作
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
专题四反比例函数中“K”与面积一:问题背景
反比例函数y=k
x
中,比例系数k有一个很重要的几何意义,那就是:过反
比例函数y=k
x
图象上任一点P作x轴、y轴的垂线PM、PN,垂足为M、N(如
图1所示),则矩形PMON的面积S=PM·PN=|y|·|x|=|xy|=|k|。
所以,对双曲线上任意一点作x轴、y轴的垂线,它们与x轴、y轴所围成的矩形面积为常数|k|,由此基本图形带来的衍生图形也很多,他们与K都有固定的结论。
在解有关反比例函数的问题时,若能灵活运用这些基本图形,会给解题带来很多方便。
二:基本图形
S四边形PEOF =|K|
S△ABO=|K|
S△ABM=|K|
S△ABC=2|K|
S四边形ABCD=2|K| S△AOC=S四边形ACEF
基础题型
1、如图,直线y=mx与双曲线y=k
x
交于点A,B、过点A作AM⊥x轴,垂足为
点M,连接BM.若△ABM的面积为1,则k的值是________
2、如图A,B是函数y=的图象上关于O原点对称的任意两点,AC∥Y 轴,BC∥X轴,△ABC的面积记为S,则S=_________
3、如图,点A、B是双曲线y=上的点,分别经过A、B两点向X轴、Y
轴作垂线段,若S
阴影=1,则S
1
+S
2
=________
4、如图,点A是反比例函数y=k
x
图象上的一点,过点A作AB⊥x轴,垂足为
点B,点C为y轴上的一点,连接AC,BC.若△ABC的面积为3,则k的值是。
5、如图,点A在函数y=的图象上,点B在函数y=k
x
(x﹥0)的图象上,连接
AB,AB垂直x轴于点M,且AM︰MB=1︰2,则k=。
6、如图,点A在双曲线y=上,点B上,且AB∥x轴,
C、D在x轴上,若四边形ABCD为矩形,则S ABCD=。
7、双曲线y1、y2在第一象限的图象如图,y1=,过y1上的任意一点A,作x轴的平行线交y2于B,交y轴于C,若S△AOB=1,则y2的解析式是
_____。
8、(陕西2011中考)如图所示,过y轴正半轴上的任意一点P,作x轴的平行
线,分别与反比例函数y=和y=的图象交于点A和点B,若点C 是x轴上任意一点,连接AC、BC,则S△ABC=____。
9、如图,等边三角形OAB的顶点A在反比例函数y=的图象上,点B在y 轴上,若将△OAB沿x轴正方向平移,当点B落在反比例函数的图象上时,点A的坐标为_____。
10、如图所示,在平面直角坐标系中,点A和点C分别在y轴和x轴正半轴
上,以OA、OC为边作矩形OABC,双曲线y= (x>0)交AB于点E,AE:EB=1:3,则矩形OABC的面积是_____。
11、如图,已知矩形OABC的面积为,它的对角线OB与双曲线y=k
x
相交于点
D,且OB:OD=5:3,则k=_____。
12、如图,点A、B在反比例函数y=k
x
(k>0,x>0)的图象上,过点A、B作
x轴的垂线,垂足分别为M、N,延长线段AB交x轴于点C,若OM=MN=NC,且△AOC的面积为6,则k的值为_____ 。
13、(陕西2017中考)如图,在平面直角坐标系中,过点M(-3,2)分别作x
轴,y轴的垂线与反比例函数y=4
x
的图象交于A,B两点,则四边形MAOB的面
积为________.
14、如图,在Rt△OAB中,∠OBA=90°,点B在x轴上,点A在第二象限,已
知双曲线y=k
x
(k<0)经过Rt△OAB斜边OA的中点D,且与直角边AB相交于
点C.若点A的坐标为(-6,4),△AOC的面积为________.
15、如图,点A是反比例函数y=的图象上任意一点,AB∥x轴交反比例函数
y=的图象于点B,以AB为边作平行四边形ABCD,其中C、D在x轴上,则四边形ABCD的面积为_____ 。
16、反比例函数y=与y=的图像在同一坐标戏中如图所示,P
为y=上任意一点,过P作PQ平行于y轴,交y=于点Q,M为y轴上一点,则S△PMQ是_____ 。
17、如图,矩形ABCD的对角线BD经过坐标原点,矩形的边分别平行于坐标
轴,点C在反比例函数y=k
x
(k≠0)的图象上。
若点A的坐标为(-2,-2),则k
的值为_____ 。
提高型
1、如图,反比例函数y=在第二象限的图象上有两点A、B,它们的
横坐标分别为-1,-3,直线AB与x轴交于点C,则△AOC的面积为
_____ 。
2、如图,反比例函数y=k
x
(x>0)的图象经过平行四边形ABCO的顶点A和对角
线的交点E,点A的横坐标为3,对角线AC所在的直线交y轴于(0,6)点,则函
数y=k
x
的表达式为_____ 。
3、如图,A、B是双曲线y=k
x(K>0)
上的点,A、B两点的横坐标分别是a、2a,
线段AB的延长线交x轴于点C,若s△AOC=9,则k=_____ 。
.
4、如图,点A在反比例函数y=图象上,点B在反比例函数y=的图象上,且∠AOB=90°,则tan∠OAB的值为_____ 。
5、如图,已知双曲线y=k
x
(K>0)经过直角三角形OAB斜边OB的中点D,与
直角边AB相交于点C。
若△OBC的面积为3,则k=_____ 。
6、如图,点A在双曲线y=上,过A作AC⊥x轴,垂足为C,OA的垂直平分线交OC于点B,当OA=4时,则△ABC周长为_____。
7、直线y=-与反比例函数y=k
x(X<0)
的图象交于点A,与x轴相交于
点B,过点B作x轴垂线交双曲线于点C,若AB=AC,则k的值为_____ 。
8、如图,一次函数y1=﹣x﹣1的图象与x轴交于点A,与y轴交于点B,与反
比例函数y=k
x
图象的一个交点为M(﹣2,m).则点B到直线OM的距离为_
____。
9、如图,已知梯形OABC 的底边D 在x 轴上,CB ∥OA ,BA ⊥OA ,过点C 的双曲线y =k x 交OB 于D,且OD :DB=1:2.若s △OBC=3,则k 的值为_____ 。
10、如图,在平面直角坐标系中,经过点A 的双曲线
y =k x
(x >0)同时经过点B ,且点A 在点B 的左侧,点A 的横坐标为,∠AOB=∠OBA=45°,则k 的值为.
11、如图A ,B 两点分别在反比例函数y=(x <0)和y =k x
(k >0,x >0)的图象上,连接OA 、OB ,若OA ⊥OB ,OB=2OA ,则k 的值为_____ 。
12、如图,点E,F在函数y=的图象上,直线EF分别与x轴、y轴交于点
A、B,且BE:BF=1:3,则△EOF的面积是_____ 。
13、如图,已知第一象限内的图象是反比例函数y=图象的一个分支,
第二象限内的图象是反比例函数y=图象的一个分支,在x轴的上方有一条平行于x轴的直线m与它们分别交于点A、B,过点A、B作x轴的垂线,垂足分别为C、D。
若四边形ABCD的周长为8,且AB<AC,则点A的坐标为_____ 。
