组距式变量分布数列 ppt课件
合集下载
数列ppt课件

判断一个数列是否为混合数列;
详细描述 利用混合数列的性质进行计算; 求混合数列的前n项和。
05
数列的发展历史与未来展望
数列的发展历史
中世纪数列
随着欧洲中世纪的数学发展,数 列研究逐渐丰富,如斐机技术的发展,数列的 应用领域不断扩大,如组合数学 、概率论和统计学等。
递推公式的求解方法
可以通过迭代法、特征根法、归纳法等方法求解递推公式。
03
数列的应用
数列在数学分析中的应用
数学分析基础
数列是数学分析中的基本概念, 是研究连续函数的基础。通过数 列,可以理解函数的极限、连续 性和可微性等基本性质。
级数理论
数列在级数理论中有着重要的应 用。通过数列的收敛性,可以研 究无穷级数的和,以及其在数学 分析中的各种应用。
在此添加您的文本16字
判断一个数列是否为等差数列。
等比数列习题与解析
总结词:等比数列是数列中的重要类 型,其习题主要考察等比数列的定义
、通项公式和性质等知识点。
详细描述
求等比数列的通项公式;
求等比数列的前n项和; 利用等比数列的性质进行计算;
判断一个数列是否为等比数列。
混合数列习题与解析
总结词:混合数列是由等差数列和等比数列混合而成的 数列,其习题主要考察混合数列的定义、通项公式和性 质等知识点。 求混合数列的通项公式;
数列的习题与解析
等差数列习题与解析
在此添加您的文本17字
总结词:等差数列是数列中的基础类型,其习题主要考察 等差数列的定义、通项公式和性质等知识点。
在此添加您的文本16字
详细描述
在此添加您的文本16字
求等差数列的通项公式;
在此添加您的文本16字
求等差数列的项数;
详细描述 利用混合数列的性质进行计算; 求混合数列的前n项和。
05
数列的发展历史与未来展望
数列的发展历史
中世纪数列
随着欧洲中世纪的数学发展,数 列研究逐渐丰富,如斐机技术的发展,数列的 应用领域不断扩大,如组合数学 、概率论和统计学等。
递推公式的求解方法
可以通过迭代法、特征根法、归纳法等方法求解递推公式。
03
数列的应用
数列在数学分析中的应用
数学分析基础
数列是数学分析中的基本概念, 是研究连续函数的基础。通过数 列,可以理解函数的极限、连续 性和可微性等基本性质。
级数理论
数列在级数理论中有着重要的应 用。通过数列的收敛性,可以研 究无穷级数的和,以及其在数学 分析中的各种应用。
在此添加您的文本16字
判断一个数列是否为等差数列。
等比数列习题与解析
总结词:等比数列是数列中的重要类 型,其习题主要考察等比数列的定义
、通项公式和性质等知识点。
详细描述
求等比数列的通项公式;
求等比数列的前n项和; 利用等比数列的性质进行计算;
判断一个数列是否为等比数列。
混合数列习题与解析
总结词:混合数列是由等差数列和等比数列混合而成的 数列,其习题主要考察混合数列的定义、通项公式和性 质等知识点。 求混合数列的通项公式;
数列的习题与解析
等差数列习题与解析
在此添加您的文本17字
总结词:等差数列是数列中的基础类型,其习题主要考察 等差数列的定义、通项公式和性质等知识点。
在此添加您的文本16字
详细描述
在此添加您的文本16字
求等差数列的通项公式;
在此添加您的文本16字
求等差数列的项数;
组距式变量分布数列

际需要来确定
确定组数:组数应 根据数据分布特征 和实际需要来确定, 组数过多会导致数 据分布过于分散, 组数过少则会导致 数据分布过于集中
确定组限:组限 的确定应遵循不 重复、不遗漏的 原则,同时也要 考虑数据的实际
分布情况
确定组中值:组 中值是组距式变 量分布数列中的 重要概念,应根 据数据的实际分
用于确定未来事件发生的 概率
用于评估未来事件的影响 和结果
用于制定针对未来事件的 策略和措施
能够反映变量分 布的集中趋势
能够反映变量分 布的离散程度
能够反映变量分 布的偏态和峰度
能够根据需要灵 活地分组,适应 性强
计算复杂:组距式变量分布数列的 计算过程相对复杂,需要更多的时 间和精力。
无法准确反映数据分布情况:由于组 距的存在,组距式变量分布数列无法 准确反映数据分布情况,可能会产生 误导。
连续变量数列: 适用于连续变 量,按其取值 范围分组形成
的数列
组距相等:各 组的组距相等, 组数越多,组
距越小
变量取值范围: 变量取值范围 较小,各组频
数相差不大
适用于大量数 据:适用于大 量数据的整理
和分析
确定组距:根据变 量分布特征和数据 个数,确定合适的 组距
确定组数:根据数 据个数和组距,确 定合适的组数
添加标题
累积频率:指将各组的频率逐一相加求和,得到总频率。
添加标题
累积频数与累积频率的关系:累积频数等于各组频数的累加和,而累积频率等于各组频率的 累加和。
添加标题
累积频数与累积频率的应用:在组距式变量分布数列中,累积频数和累积频率可以用于描述 数据的分布情况,帮助我们更好地了解数据的特征和规律。
频数分布图:以频数分布表为基础,将频数分布情况用直方图或折线图表示,用以描述变量分布 情况。
确定组数:组数应 根据数据分布特征 和实际需要来确定, 组数过多会导致数 据分布过于分散, 组数过少则会导致 数据分布过于集中
确定组限:组限 的确定应遵循不 重复、不遗漏的 原则,同时也要 考虑数据的实际
分布情况
确定组中值:组 中值是组距式变 量分布数列中的 重要概念,应根 据数据的实际分
用于确定未来事件发生的 概率
用于评估未来事件的影响 和结果
用于制定针对未来事件的 策略和措施
能够反映变量分 布的集中趋势
能够反映变量分 布的离散程度
能够反映变量分 布的偏态和峰度
能够根据需要灵 活地分组,适应 性强
计算复杂:组距式变量分布数列的 计算过程相对复杂,需要更多的时 间和精力。
无法准确反映数据分布情况:由于组 距的存在,组距式变量分布数列无法 准确反映数据分布情况,可能会产生 误导。
连续变量数列: 适用于连续变 量,按其取值 范围分组形成
的数列
组距相等:各 组的组距相等, 组数越多,组
距越小
变量取值范围: 变量取值范围 较小,各组频
数相差不大
适用于大量数 据:适用于大 量数据的整理
和分析
确定组距:根据变 量分布特征和数据 个数,确定合适的 组距
确定组数:根据数 据个数和组距,确 定合适的组数
添加标题
累积频率:指将各组的频率逐一相加求和,得到总频率。
添加标题
累积频数与累积频率的关系:累积频数等于各组频数的累加和,而累积频率等于各组频率的 累加和。
添加标题
累积频数与累积频率的应用:在组距式变量分布数列中,累积频数和累积频率可以用于描述 数据的分布情况,帮助我们更好地了解数据的特征和规律。
频数分布图:以频数分布表为基础,将频数分布情况用直方图或折线图表示,用以描述变量分布 情况。
分配数列-统计表-统计图ppt课件

因此有:
首组 组中值
首组上限
首组假定下限
2
首组 上限
相邻组组距 2
末组 组中值
末组下限
末组假定上限 2
末组 下限
相邻组组距 2
组中值=U-d/2 =50-25=25
某地区100个百货商店 月销售额与流通费用情况
销售额(万 元)
商店数 (个)
每百元商品销售 额中支付的流通
费(元)
50以下
10
14.2
异距数列适用于
3.标志值按一定比例发展变化的场合
例: 大城市百货商店营业额差别很大的,比如营 业额从5万到5千万元,可采取公比为10的不等距 分组,即:5-50万元,50-500万元,500-5000万 元,如果采用等距分组,即便组距为100万元, 也得分50组,显然是不合适的。
计算组数(组数不宜过多,也不宜太少)
(三)分配数列的分类
变量数列
离散型变量数列 连续型变量数列
变量数列
单项数列 组距数列
等距数列 异距数列
二、分配数列的编制
(一) 品质数列
编制品质数列,只要根据统计研究目的,正 确选择分组标志,确定分组标准,则事物性质的 差异可以明确地表现出采,也就容易划分总体中 各组的性质界限。因此,在通常情况下,品质数 列能够较准确地反映总体各单位的分布状态和特 征。
7.4 12.6 29.0 2.0 12.4 7.0 14.8 17.5 15.0 18.2 18.7 15.5 12.8 26.0 17.3 8.3 14.7 12.0 3.5 6.8 25.0 19.3 6.4 4.0 11.9 8.5 13.2 14.5 17.1 15.6 13.4 4.5 9.5 20.0 15.7 6.0 11.4 23.0 14.2 16.7 21.0 16.0 13.6 10.0 13.9 5.0 5.8 10.5 16.3 22.0
模块三统计整理精品PPT课件

项目一 统计资料的整理
单元二 统计分组
三、分配数列的编制
(二)变量数列的编制
表3-5 某班学生年龄分组表
按年龄分组(岁)
16 17 18 19 20
合计
学生数f(人)
2 9 13 10 2
36
比重f/∑f(%)
5.56 25.00 36.10 27.78 5.56
100.0
项目一 统计资料的整理
项目一 统计资料的整理
单元一 统计数据整理的步骤
二、统计整理的内容与步骤
(一)统计整理的内容 根据研究任务的要求,选择应整理的指标 ,并根据分析的需要确定具体的分组;
对统计资料进行汇总、计算;
通过统计表描述汇总的结果。
项目一 统计资料的整理
单元一 统计数据整理的步骤
二、统计整理的内容与步骤
(二)统计整理的步骤
打开“数据分析” 对话框
打开“直方图” 对话框。
输入数据
图3-2 “直方图”对话框
项目一 统计资料的整理
单元三 Excel在统计数据整理中的运用
二、定性分析数据
(一)利用频数函数
在数据整理过程中,不仅需要整理 以变量数列形式表现的资料,有时 也需要整理以文字形式表现的品质 数列资料,如性别、职业、文化程 度等品质数列资料。
单元二 统计分组
三、分配数列的编制
(二)变量数列的编制
组距式数列的 编制
数据排序
确定组限 计算频数和 频率
确定组距数 列的类型
确定组数和 组距
计算累计频数 和累计频率
项目一 统计资料的整理
单元三 Excel在统计数据整理中的运用
一、定量分析数据
(一)使用频数函数编制频数分布表
第四章 统计整理 《应用统计学——以Excel为分析工具》PPT课件

• (1) 递增排序:设一组数据为x1,x2,… ,xn,递增排序后可表示为: x(1)<x(2)<…<x(n)。
• (2)递减排序:可表示为: x(1)>x(2)>…>x(n)。
• 无论是定性数据还是定量数据,其排序均 可借助EXCEL完成。下面通过实例说明 EXCEL2007中进行数据排序的操作。
• 编制好的统计台账和加工整理后的统计资料,必须 妥善保管,不得损坏和遗失。
• 以上五个方面是相互衔接的,其中,统计分组是统 计整理的基础,统计汇总是统计整理的中心内容, 统计表和统计图是统计整理结果的表现形式。
第二节 统计调查资料的预处理
• 统 计 调 查 资 料 的 预 处 理 (Statistical data pretreatment) 是 数 据 分 组 整 理 的 先 前 步 骤 ,内容包括调查数据的审核与插补、筛选 (第三章已经介绍)、排序、分类汇总等 过程
一、统计分组的含义
• 统计分组是根据统计研究的目的和任务要 求,按照统计分组标志将总体划分成性质 不同的若干个部分或组别,使组和组之间 具有差异性,而同一组内具有同质性。
二、统计分组的作用
• 1、区分事物的性质 • 如企业按照经济性质分组,分为国有经济、集体
经济、私营经济、个体经济、外商投资经济、港 澳台经济。 • 2、研究事物内部结构 • 如将国民生产总值按照三次产业划分,计算出各 个产业所占比重,以便研究内部结构是否合理。 • 3、研究现象之间的关系 • 在统计分作的基础上,研究现象和现象之间的相 互依存关系。如施肥量和亩产量之间的关系;商 业企业规模和商品流通费用率之间的关系等。
三、统计调查资料的分类汇总
• 在对数据进行预处理时,有时需要对某些 字段按条件进行汇总,称为数据的分类汇 总。如果只是针对一个字段进行分类汇总 ,称为单字段分类汇总;如果同时对两个 及两个以上字段进行分类汇总称为多字段 分类汇总。
• (2)递减排序:可表示为: x(1)>x(2)>…>x(n)。
• 无论是定性数据还是定量数据,其排序均 可借助EXCEL完成。下面通过实例说明 EXCEL2007中进行数据排序的操作。
• 编制好的统计台账和加工整理后的统计资料,必须 妥善保管,不得损坏和遗失。
• 以上五个方面是相互衔接的,其中,统计分组是统 计整理的基础,统计汇总是统计整理的中心内容, 统计表和统计图是统计整理结果的表现形式。
第二节 统计调查资料的预处理
• 统 计 调 查 资 料 的 预 处 理 (Statistical data pretreatment) 是 数 据 分 组 整 理 的 先 前 步 骤 ,内容包括调查数据的审核与插补、筛选 (第三章已经介绍)、排序、分类汇总等 过程
一、统计分组的含义
• 统计分组是根据统计研究的目的和任务要 求,按照统计分组标志将总体划分成性质 不同的若干个部分或组别,使组和组之间 具有差异性,而同一组内具有同质性。
二、统计分组的作用
• 1、区分事物的性质 • 如企业按照经济性质分组,分为国有经济、集体
经济、私营经济、个体经济、外商投资经济、港 澳台经济。 • 2、研究事物内部结构 • 如将国民生产总值按照三次产业划分,计算出各 个产业所占比重,以便研究内部结构是否合理。 • 3、研究现象之间的关系 • 在统计分作的基础上,研究现象和现象之间的相 互依存关系。如施肥量和亩产量之间的关系;商 业企业规模和商品流通费用率之间的关系等。
三、统计调查资料的分类汇总
• 在对数据进行预处理时,有时需要对某些 字段按条件进行汇总,称为数据的分类汇 总。如果只是针对一个字段进行分类汇总 ,称为单字段分类汇总;如果同时对两个 及两个以上字段进行分类汇总称为多字段 分类汇总。
统计学之统计整理培训教材经典课件(PPT86页)

单项数列 组距数列
等距数列 异距数列
二、分配数列的编制
(一) 品质数列
编制品质数列,只要根据统计研究目的,正 确选择分组标志,确定分组标准,则事物性质的 差异可以明确地表现出采,也就容易划分总体中 各组的性质界限。因此,在通常情况下,品质数 列能够较准确地反映总体各单位的分布状态和特 征。
2020/12/16
2020/12/16
(三)分配数列的分类
按照标志的性质不同 1.品质分配数列 指按品质标志对总体分组形成的数列,简 称为品质数列。 2.变量分配数列 指按数量标志对总体分组形成的数列,简 称为变量数分配数列的分类
变量数列
离散型变量数列 连续型变量数列
变量数列
2020/12/16
2.等量的标志值具有不同意义的场合
例:进行人口疾病研究的年龄分组,应采用异 距分组,即:1岁以下按月分组,1-10岁按照年 龄分组,11-20按照5年分组,21岁以上按照10年 分组等。
2020/12/16
异距数列适用于
3.标志值按一定比例发展变化的场合
例: 大城市百货商店营业额差别很大的,比如营 业额从5万到5千万元,可采取公比为10的不等距 分组,即:5-50万元,50-500万元,500-5000万 元,如果采用等距分组,即便组距为100万元, 也得分50组,显然是不合适的。
月工资分组(元) 2000 以下 2000-2500 2500 以上 合计
组别(变量)
工人数(人) 占总数比重(%)
210
39.6
187
35.3
133
25.1
530
100.0
频数(次数) 频率(比率)
2020/12/16
思考: 分配数列与分组的区别? 分配数列是在分组的基础上加
第三章 变量分布特征的描述 《统计学》PPT课件

2.四分位差:四分位差作为变异程度的一种度量,能够克服 异常值的影响。它是第三个四分位数与第一个四分位数的差 值。也就是说,四分位差是中间50%的数据的全距。
Qd QU QL
四分位差弥补了全距容易受极端值影响的缺陷。剔除数据中最小25%和最 大25%的数据,反映了中间50%数据的离散趋势。数值越小,说明中间的 数据越集中;数值越大,说明中间的数据越分散。
x me mo
3.根据经验,在轻微偏态时,不论是左偏还是右偏,众数与算术平均
数的距离约等于中位数与算术平均数距离的3倍,即 mo x 3me -x
右偏分布
M0 Me x
对称分布
左偏分布
x
x Me M0
Me
M0
第二节 离中趋势的描述
所谓离中趋势,就是变量分布中各变量值背离中心值的倾向。 如果说集中趋势体现变量分布的同质性,那么离中趋势就是变 量分布变异性的体现。对离中趋势的描述就是要反映变量分布 中各变量值远离中心值的程度,以反映变量分布的特征。
H 20 3
3
15.83
20 20 20 1 1 1
18 16 14 18 16 14
2.加权调和平均数:当各组的标志总量不相等时,所计算的 调和平均数要以各组的标志总量为权数,其结果即为加权调 和平均数。
H m1 m2 m1 m2 x1 x2
k
mk
mk
mi
i 1
k mi
x x1 x2 xn 95% 92% 90% 85% 80% 88.40%
n
5
G n x1 x2 x3 xn 5 95%92%90%85%80% 88.24%
2.加权几何平均数:当计算几何平均数的各变量值出现的次 数不等,即数据经过了统计分组时,则应采用加权几何平均 数。
管理统计学第四章组距数列众数
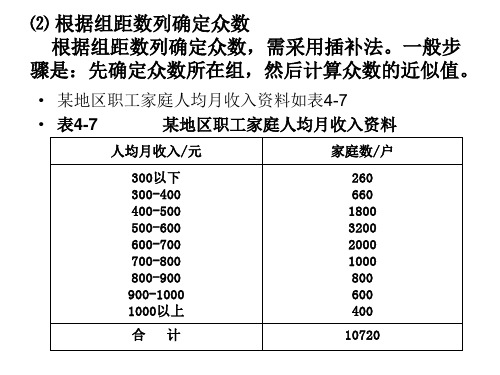
⑵ 根据组距数列确定众数 根据组距数列确定众数,需采用插补法。一般步 骤是:先确定众数所在组,然后计算众数的近似值。
• 某地区职工家庭人均月收入资料如表4-7 • 表4-7 某地区职工家庭人均月收入资料
人均月收入/元 家庭数/户
300以下 300-400 400-500 500-600 600-700 700-800 800-900 900-1000 1000以上
答案:
首先根据表格资料可知众数所在组为350~400组,则 有: L0 =350, U0 =400,d=50, △ 1 =70-20=50, △2 =70-37=33 利用下限公式得众数: M0=L0+△1/(△ 1 + △2)*d =350+50/(50+33)*50 =380.12(元) 利用上限公式得众数: M0=U0-△ 2 /(△ 1 + △2)*d =400-33/(50+33)*50 =380.12(元)
?某地区职工家庭人均月收入资料如表47?表47某地区职工家庭人均月收入资料人均月收入元家庭数户300以下30040040050050060060070070080080090090010001000以上2606601800320020001000800600400合计10720人均月收入元家庭数户300以下30040040050050060060070070080080090090010001000以上2606601800320020001000800600400合计10720从表47中可知家庭户数最多的是3200户它所对应的人均月收入户它所对应的人均月收入500600元为众数所在组
• 3)众数的特点及应用众数注意的问题 • ●由于众数是根据变量值出现次数的多少来确定的, 不需要通过全部变量值来计算,因此称其为位置平 均数,它不受极端变量值的影响。 • ●在组距数列中,各组分布的次数受组距大小的影 响,所以,根据组距数列确定众数时,要保证各组 组距相等。 • ●在一个次数分布中有多个众数时,称为多重众数, 此时说明总体内存在不同性质的事物。 • ●当数列没有明显的集中趋势而趋于均匀分布时, 不存在众数。
• 某地区职工家庭人均月收入资料如表4-7 • 表4-7 某地区职工家庭人均月收入资料
人均月收入/元 家庭数/户
300以下 300-400 400-500 500-600 600-700 700-800 800-900 900-1000 1000以上
答案:
首先根据表格资料可知众数所在组为350~400组,则 有: L0 =350, U0 =400,d=50, △ 1 =70-20=50, △2 =70-37=33 利用下限公式得众数: M0=L0+△1/(△ 1 + △2)*d =350+50/(50+33)*50 =380.12(元) 利用上限公式得众数: M0=U0-△ 2 /(△ 1 + △2)*d =400-33/(50+33)*50 =380.12(元)
?某地区职工家庭人均月收入资料如表47?表47某地区职工家庭人均月收入资料人均月收入元家庭数户300以下30040040050050060060070070080080090090010001000以上2606601800320020001000800600400合计10720人均月收入元家庭数户300以下30040040050050060060070070080080090090010001000以上2606601800320020001000800600400合计10720从表47中可知家庭户数最多的是3200户它所对应的人均月收入户它所对应的人均月收入500600元为众数所在组
• 3)众数的特点及应用众数注意的问题 • ●由于众数是根据变量值出现次数的多少来确定的, 不需要通过全部变量值来计算,因此称其为位置平 均数,它不受极端变量值的影响。 • ●在组距数列中,各组分布的次数受组距大小的影 响,所以,根据组距数列确定众数时,要保证各组 组距相等。 • ●在一个次数分布中有多个众数时,称为多重众数, 此时说明总体内存在不同性质的事物。 • ●当数列没有明显的集中趋势而趋于均匀分布时, 不存在众数。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(4)写出组限并据以归类汇总计算各组次数。 归类汇总是指依据各个总体单位的具体标志值,将其归入某一 具体组中。 归类汇总时,要遵循“不重复,不遗漏”的基本原则。 相邻两组之间的组限以相同数值标记,称为重限分组。 重限分组时,要遵循“上限不在内”的原则。如表2-13所示。
组距式变量分布数列
(5)编制整理表 将数据用表格形式表现出来。 左端是各组的变量值,右端是各组变量值出现的频数(频率)。 可以通过画“正”字来记录每组变量值出现的频数。表2-13所示。 归类汇总后,便可计算频数如表2-14所示。
按等距变量编制数列,其结果如表2-15。 表2-15 某班学生某科考试成绩
考试成绩(分)不含上限
30-40 40-50 50-60 60-70 70-80 80-90 90-100 合计
考试人数(人)
1 0 1 8 16 10 3 39
组距式变量分布数列
2.开口组组距变量分布数列 注意:变量值是否会因上限不在内而被漏掉了。 表2-15中,100分者被漏掉了。 成绩在60分以下只有2人,特意为这2人开设三个组没有必要。 并且此2人皆属于不及格者, 为了避免出现空白组或个别极端值被遗漏可以采用开口组标记。 组距变量数列中缺上限或缺下限的组叫开口组。 第一组和最后一组可以标记为:“XX以下”、“XX以上”。 开口组的组距通常以相邻组组距作为其组距。 重新编制该班学生考试成绩的,其结果如表2-16所示。
(1)将原始资料按变量指大小的顺序重新排列。 36 56 60 60 64 64 64 68 68 68 70 70 75 75 75 75 78 78 78 78 78 78 79 79 79 79 84 84 85 85 88 88 89 89 89 89 95 95 98 100
组距式变量分布数列
组距式变量分布数列
(3)确认组限、组距和组数。 组限是指每个组的两端变量值。 每个组的最大值(或称终点值)为上限。 每个组的最小值(或称起点值)为下限。 组距是指每个组中的最大值与最小值之差。 组距=上限-下限 组数是指某个变量数列应划分为多少个组。
组数=
全距 组距
组距=
全距 组数
组距式变量分布数列
适用于离散型变量和连续型变量,变量值多,变动范围 较大的情况。
组距式变量分布数列
二、组距式变量数列的编制
①将原始数据按顺序排列起来,并确定变量性质 ②计算全距 ③确定组限、组距和组数 ④写出组限并据以归类汇总计算各组次数 ⑤编制整理表
组距式变量分布数列
三、组距式变量分布数列的类型:
类
1、等距变量分布数列
组距式变量分布数列
3、异距式变量分布数列
异距数列:各组组距不相等的数列。 任何事物都有质和量两个方面。没有质,也就没有量; 没有量,也就没有质。 统计所研究的量,都有质的规定性,离开事物质的规定 性,统计就不能研究它的量。 同时,量变会引起质变。 因此,在兼顾质与量两个方面时,可采用异距式变量分 布数列。
组距式变量分布数列
(2)计算全距。确认全距是是为了适当进行分组。 全距是指在全部变量值中最大变量值与最小变量值的差距。 全距=最大变量值-最小变量值 上例中,该班成绩全距=99-52=47 在计算组数与组距时所使用的变量值 最小值略低于现实资料的最小值,自50分开始, 最大值略高于现实资料的最大值,取至100分。 则全距为 100-50=50。
2、对一些企业按计划完成程度不同分为三组;第一组为80%~100%
,第二组为100%~120%,第三组为120%以上,则(AB )
A.若将上述各组组别及次数依次排列,就是变量分布数列
B.该数列的变量属于连续变量,所以相邻组的组限必须重叠
C.此类数列只能是等距数列,不可能采取异距数列
D.各组的上限分别为80%、100%、120%,某企业计划完成100%
A.7
B.8
C.9
D.10
多项选择题
1、将某班学生的统计考试成绩分为60分一下、60~70分、70~80分、
80~90分、90~100分共五个组。正确的说法是( BCD )
A.某学生的成绩如果是80分,他应分为70~80分这一组。
B.第一组的组中值是55
C.相邻组组限是重叠的
D.第三组组中值是75
《统计基础》 财会部
许丽君
课 前 变量分布数列 回 单项式变量分布数列 顾
组距式变量分布数列
【教学目标】
组距式变量分布数列概念、类型、编制
【教学重点、难点】
组距式变量分布数列的编制
组距式变量分布数列
一、组距式变量分布数列的概念
组距式变量分布数列
概
每一组别都是由数域(区间)表示,则
念
称为组距式变量分布数列。
组距式变量分布数列
(1)将原始数据按顺序排列起来,并确定变量性质。 该例的变量为连续变量。确认变量性质,是为了正确
进行数列的编制和确认组限的表示方法。 根据例2-7,对数据按成绩有低到高排列可得到: 52 54 60 62 66 68 70 71 73 75 76 77 77 78 78 78 79 80 80 80 81 82 82 83 84 85 85 85 86 88 88 89 89 89 89 90 93 95 97 99
应归第一组
3、组中值的计算公式为( ABD )。
A.组中值=(上限+下限)÷2 B.组中值=上限+(上限-下限)÷2
C.组中值=上限÷2+下限 D.组中值=下限+(上限-下限)÷2
习题册P24: 17题编制组距为15的组距式变量分布数列
感谢您的光临!
4.组距式变量分布数列的图形描述
常用的用于描述组距式变量分布数列的图形有直 方图、折线图、圆滑曲线图。
组距式变量分布数列
(2)编制开口组组距变量数列。
两个开口组,第一组与最末组组距分别是?
每个组上限与下限的中点值叫组中值,它是各组变量值的代 表性水平。
组距式变量分布数列
组中值的一般计算方法如下: 闭口组(上下限齐全)的组中值,可按下列公式计算:
缺上限或缺下限的开口组的组中值,可按下列公式计算:
? 第一组组中值是 ? 第二组组中值是 ? 最末组组中值是
(1)直方图
(2)折线图
(3)圆滑曲线图
例:某林地上有云杉1000株,分组整理得到分布数列, 如图所示。
组距式变量分布数列
【例2-8】对某班40名学生某次考试成绩按试卷登记得到如下资料 64 70 89 64 56 95 98 79 88 88 78 89 60 78 68 79 79 95 68 70 78 89 100 36 75 84 78 64 78 85 85 79 70 84 68 75 89 75 78 75
例题中全距为 100-50=50一定,而组数与组距是可变的。 一般组距应尽可能取5或10的整倍数,而组数则必须是整数。 根据例2-7确定组数为:
若组距为5,组数=全距/组距=50/5=10(组) 若组距为10,组数=全距/组距=50/10=5(组) 上例适合以10为组距,分为5组。
组距式变量分布数列
2、开口组组距变量分布数列
型
3、异距变量分布数列
组距式变量分布数列
1、等距式变量分布数列 等距数列:各组组距相等的数列。 适用于变量值变动比较均匀、集中的情况。
例2-7:对某班40名学生某科某次考试成绩按试卷登记得到 如下资料:
54 60 62 97 8 86 93 70 81 78 89 71 89 80 85 75 78 90 66 78 73 82 82 99 77 88 84 75 88 76 80
组距式变量分布数列
组距式变量分布数列
? 第一组组中值是 ? 第二组组中值是 ? 最末组组中值是
组距式变量分布数列
组距式变量分布数列的概念 组距式变量分布数列的编制 组距式变量分布数列的类型
单项选择题
1、某村农民人均收入最高为426元,最低为270元,据此分为 六个组,形成闭口式等距数列,则组距应为( B )
A .71
B.26
C.156
D.348
2、编制组距式变量分布数列(从小到大)顺序排列时,划分组 限时相邻组的上下限重叠时,则( C ) A.与上限相等的标志值计入小一组 B.与下限相等的标志值计入大一组 C.与上限相等的标志值计入大一组 D.与下限相等的标志值计入小一组
3、一个容量为80的样本最小值是50,最大值是143,其组距为 10,则可以分成( D )组。
组距式变量分布数列
(5)编制整理表 将数据用表格形式表现出来。 左端是各组的变量值,右端是各组变量值出现的频数(频率)。 可以通过画“正”字来记录每组变量值出现的频数。表2-13所示。 归类汇总后,便可计算频数如表2-14所示。
按等距变量编制数列,其结果如表2-15。 表2-15 某班学生某科考试成绩
考试成绩(分)不含上限
30-40 40-50 50-60 60-70 70-80 80-90 90-100 合计
考试人数(人)
1 0 1 8 16 10 3 39
组距式变量分布数列
2.开口组组距变量分布数列 注意:变量值是否会因上限不在内而被漏掉了。 表2-15中,100分者被漏掉了。 成绩在60分以下只有2人,特意为这2人开设三个组没有必要。 并且此2人皆属于不及格者, 为了避免出现空白组或个别极端值被遗漏可以采用开口组标记。 组距变量数列中缺上限或缺下限的组叫开口组。 第一组和最后一组可以标记为:“XX以下”、“XX以上”。 开口组的组距通常以相邻组组距作为其组距。 重新编制该班学生考试成绩的,其结果如表2-16所示。
(1)将原始资料按变量指大小的顺序重新排列。 36 56 60 60 64 64 64 68 68 68 70 70 75 75 75 75 78 78 78 78 78 78 79 79 79 79 84 84 85 85 88 88 89 89 89 89 95 95 98 100
组距式变量分布数列
组距式变量分布数列
(3)确认组限、组距和组数。 组限是指每个组的两端变量值。 每个组的最大值(或称终点值)为上限。 每个组的最小值(或称起点值)为下限。 组距是指每个组中的最大值与最小值之差。 组距=上限-下限 组数是指某个变量数列应划分为多少个组。
组数=
全距 组距
组距=
全距 组数
组距式变量分布数列
适用于离散型变量和连续型变量,变量值多,变动范围 较大的情况。
组距式变量分布数列
二、组距式变量数列的编制
①将原始数据按顺序排列起来,并确定变量性质 ②计算全距 ③确定组限、组距和组数 ④写出组限并据以归类汇总计算各组次数 ⑤编制整理表
组距式变量分布数列
三、组距式变量分布数列的类型:
类
1、等距变量分布数列
组距式变量分布数列
3、异距式变量分布数列
异距数列:各组组距不相等的数列。 任何事物都有质和量两个方面。没有质,也就没有量; 没有量,也就没有质。 统计所研究的量,都有质的规定性,离开事物质的规定 性,统计就不能研究它的量。 同时,量变会引起质变。 因此,在兼顾质与量两个方面时,可采用异距式变量分 布数列。
组距式变量分布数列
(2)计算全距。确认全距是是为了适当进行分组。 全距是指在全部变量值中最大变量值与最小变量值的差距。 全距=最大变量值-最小变量值 上例中,该班成绩全距=99-52=47 在计算组数与组距时所使用的变量值 最小值略低于现实资料的最小值,自50分开始, 最大值略高于现实资料的最大值,取至100分。 则全距为 100-50=50。
2、对一些企业按计划完成程度不同分为三组;第一组为80%~100%
,第二组为100%~120%,第三组为120%以上,则(AB )
A.若将上述各组组别及次数依次排列,就是变量分布数列
B.该数列的变量属于连续变量,所以相邻组的组限必须重叠
C.此类数列只能是等距数列,不可能采取异距数列
D.各组的上限分别为80%、100%、120%,某企业计划完成100%
A.7
B.8
C.9
D.10
多项选择题
1、将某班学生的统计考试成绩分为60分一下、60~70分、70~80分、
80~90分、90~100分共五个组。正确的说法是( BCD )
A.某学生的成绩如果是80分,他应分为70~80分这一组。
B.第一组的组中值是55
C.相邻组组限是重叠的
D.第三组组中值是75
《统计基础》 财会部
许丽君
课 前 变量分布数列 回 单项式变量分布数列 顾
组距式变量分布数列
【教学目标】
组距式变量分布数列概念、类型、编制
【教学重点、难点】
组距式变量分布数列的编制
组距式变量分布数列
一、组距式变量分布数列的概念
组距式变量分布数列
概
每一组别都是由数域(区间)表示,则
念
称为组距式变量分布数列。
组距式变量分布数列
(1)将原始数据按顺序排列起来,并确定变量性质。 该例的变量为连续变量。确认变量性质,是为了正确
进行数列的编制和确认组限的表示方法。 根据例2-7,对数据按成绩有低到高排列可得到: 52 54 60 62 66 68 70 71 73 75 76 77 77 78 78 78 79 80 80 80 81 82 82 83 84 85 85 85 86 88 88 89 89 89 89 90 93 95 97 99
应归第一组
3、组中值的计算公式为( ABD )。
A.组中值=(上限+下限)÷2 B.组中值=上限+(上限-下限)÷2
C.组中值=上限÷2+下限 D.组中值=下限+(上限-下限)÷2
习题册P24: 17题编制组距为15的组距式变量分布数列
感谢您的光临!
4.组距式变量分布数列的图形描述
常用的用于描述组距式变量分布数列的图形有直 方图、折线图、圆滑曲线图。
组距式变量分布数列
(2)编制开口组组距变量数列。
两个开口组,第一组与最末组组距分别是?
每个组上限与下限的中点值叫组中值,它是各组变量值的代 表性水平。
组距式变量分布数列
组中值的一般计算方法如下: 闭口组(上下限齐全)的组中值,可按下列公式计算:
缺上限或缺下限的开口组的组中值,可按下列公式计算:
? 第一组组中值是 ? 第二组组中值是 ? 最末组组中值是
(1)直方图
(2)折线图
(3)圆滑曲线图
例:某林地上有云杉1000株,分组整理得到分布数列, 如图所示。
组距式变量分布数列
【例2-8】对某班40名学生某次考试成绩按试卷登记得到如下资料 64 70 89 64 56 95 98 79 88 88 78 89 60 78 68 79 79 95 68 70 78 89 100 36 75 84 78 64 78 85 85 79 70 84 68 75 89 75 78 75
例题中全距为 100-50=50一定,而组数与组距是可变的。 一般组距应尽可能取5或10的整倍数,而组数则必须是整数。 根据例2-7确定组数为:
若组距为5,组数=全距/组距=50/5=10(组) 若组距为10,组数=全距/组距=50/10=5(组) 上例适合以10为组距,分为5组。
组距式变量分布数列
2、开口组组距变量分布数列
型
3、异距变量分布数列
组距式变量分布数列
1、等距式变量分布数列 等距数列:各组组距相等的数列。 适用于变量值变动比较均匀、集中的情况。
例2-7:对某班40名学生某科某次考试成绩按试卷登记得到 如下资料:
54 60 62 97 8 86 93 70 81 78 89 71 89 80 85 75 78 90 66 78 73 82 82 99 77 88 84 75 88 76 80
组距式变量分布数列
组距式变量分布数列
? 第一组组中值是 ? 第二组组中值是 ? 最末组组中值是
组距式变量分布数列
组距式变量分布数列的概念 组距式变量分布数列的编制 组距式变量分布数列的类型
单项选择题
1、某村农民人均收入最高为426元,最低为270元,据此分为 六个组,形成闭口式等距数列,则组距应为( B )
A .71
B.26
C.156
D.348
2、编制组距式变量分布数列(从小到大)顺序排列时,划分组 限时相邻组的上下限重叠时,则( C ) A.与上限相等的标志值计入小一组 B.与下限相等的标志值计入大一组 C.与上限相等的标志值计入大一组 D.与下限相等的标志值计入小一组
3、一个容量为80的样本最小值是50,最大值是143,其组距为 10,则可以分成( D )组。
