单位根过程
单位根过程联合检验的Bootstrap研究
Ｂｏ ０ ｔ ｓ ｔ ｒ ａ ｐ ｐ ｉ ｎ ｇ Ｒｅ ｓ ｅ ａ ｒ ｃ ｈ ｏ ｎ Ｊ ｏ ｉ ｎ ｔ Ｔｅ ｓ ｔ ｆ ｏ ｒ Ｕｎ ｉ ｔ Ｒｏ ｏ ｔ Ｐ ｒ ｏ ｃ ｅ ｓ ｓ ｅ ｓ
ｅ ￣ｏ ｎ ｅ ｏ ｕ ｓ ｊ ｕ ｄ ｇ ｍｅ ｎ ｔ ｆ ｏ ｒ ｔ ｈ ｒ ｅ ｅ ｊ ｏ ｉ ｎ ｔ ｔ ｅ ｓ ｔ ｓ ａ ｒ ｅ ２ ． ２ ２ ％ ，３ ． ７ ０ ％ ，０ ， ０ ０ ％ ｆ ｏ ｒ Ｂ ｏ ｏ ｔ ｓ ｔ ｒ ａ ｐ ｍｅ ｔ ｈ ｏ ｄ ａ ｎ ｄ ｈ ｉ ｇ ｈ ｕ ｐ ｔ ｏ ２ ２ ． ２ ２ ％，
上， Ｂ ｏ ｏ ｔ ｓ ｔ ｒ ａ ｐ方 法 下 三 个检 验 量 的误 判 率 分 别 为 ２ ． ２ ２ ％、 ３ ． ７ ０ ％和０ ． ０ ０ ％， 而 临界值 的误判率 分别 高达 ２ ２ ． ２ ２ ％、 １ １ ． １ 】 ％和 １ ５ ． ５ ６ ％； 在精 确程 度 上 ， Ｂ ｏ ｏ ｔ ｓ ｔ ｒ ａ ｐ 方 法 的精 度 分 别 是 临 界 值 方 法 的 １ １ ． ２ ５倍 、 ２ ６倍 和 ６ ． ５倍 。模 拟 表 明
Ｂｏ ｏ ｔ ｓ ｔ ｒ ａ ｐ ｍｅ ｔ ｈ ｏ ｄ ｃ ｏ ｎ ｓ ｔ ｒ ｕ ｃ ｔ ｅ ｄ ｉ ｎ ｔ ｈｉ ｓ ｐ ａ ｐｅ ｒ ｃ ａ ｎ ｎ ｏ ｔ ｏ ｎ ｌ ｙ ｒ ｅ ｐ ｌ ａ ｃ ｅ ｔ ｈｅ ｃ ｒ ｉ ｔ ｉ ｃ ａ ｌ ｖ ａ ｌ ｕ ｅ ｔ ｅ ｃ ｈｎ ｏ ｌ ｏ ｇ ｙ ｈｕ ｔ ａ ｌ ｓ ｏ ｈ ａ ｓ ｔ ｈｅ ｏ ｂ ｖ ｉ ｏ ｕ ｓ
单位根过程——精选推荐
单位根过程1、单位根的定义随机过程{t y ，t = 1，2，....}，若1t t t y y u ρ-=+，其中，ρ= 1，{t u }为一平稳过程，且E （t u ）= 0，cov (t u ，t s u -) =t μ<∞，这里s = 0，1，2，...，称为单位根过程（unit root process ）。
（当然，如果||1ρ<，t y 本身就是平稳过程）特别地，若1t t t y y ε-=+，其中，{t ε}为独立同分布（即白噪声或完全随机），且E （t ε）= 0，D(t ε)=2σ<∞，则{t y }为一随机漫步（游走）（random walk process)。
可以看出，随机游动过程是单位根过程的一个特例。
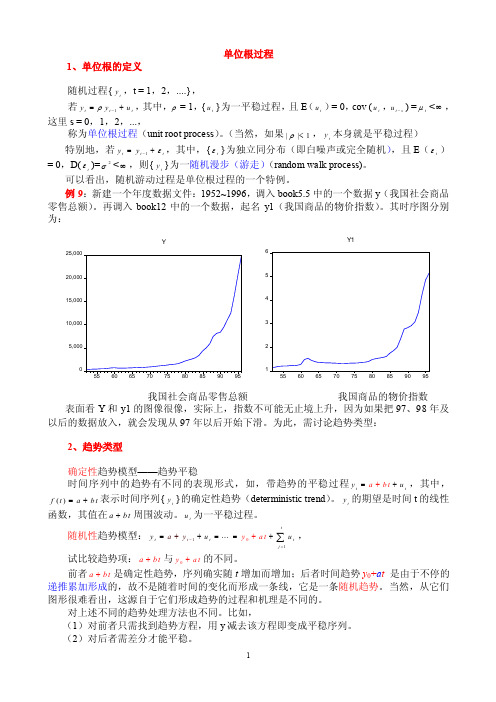
例9：新建一个年度数据文件：1952~1996，调入book5.5中的一个数据y （我国社会商品零售总额）。
再调入book12中的一个数据，起名y1（我国商品的物价指数）。
其时序图分别表面看Y 和y1的图像很像，实际上，指数不可能无止境上升，因为如果把97、98年及以后的数据放入，就会发现从97年以后开始下滑。
为此，需讨论趋势类型：2、趋势类型确定性趋势模型——趋势平稳时间序列中的趋势有不同的表现形式，如，带趋势的平稳过程t t a b y u t +=+，其中，()f t a b t =+表示时间序列{t y }的确定性趋势（deterministic trend ）。
t y 的期望是时间t 的线性函数，其值在a bt +周围波动。
t u 为一平稳过程。
随机性趋势模型：110t t t t j t y a y a u y t u -==+==+++∑ ， 试比较趋势项：a bt +与0y a t +的不同。
前者a bt +是确定性趋势，序列确实随t 增加而增加；后者时间趋势y 0+a t 是由于不停的递推累加形成的，故不是随着时间的变化而形成一条线，它是一条随机趋势。
单位根检验的原理
单位根检验的原理
单位根检验是时间序列分析中常用的方法之一，用于判断一个时间序列是否具有单位根。
单位根是指一个时间序列中的波动在长期内不会消失，即存在一个固定的平均回归值。
单位根检验的原理是基于单位根过程（unit root process）的概念，如果一个时间序列是单位根过程，说明它是一个非平稳过程，对应的模型是一个随机漫步模型，也就是说未来的值与现有值之间没有固定的关系。
常用的单位根检验方法包括ADF检验（Augmented Dickey-Fuller test）和KPSS检验（Kwiatkowski-Phillips-Schmidt-Shin test）。
ADF检验基于一个经济学模型，通过检验回归系数是
否为零来判断是否存在单位根。
KPSS检验则是通过检验序列
平方和的变化是否平稳来判断是否存在单位根。
在进行单位根检验时，我们通常会设定一个阈值，比如显著性水平为0.05，如果计算得到的检验统计量小于临界值，那么就可以拒绝存在单位根的假设，即认为时间序列是平稳的；反之，如果大于临界值，则无法拒绝存在单位根的假设，即认为时间序列是非平稳的。
进行单位根检验的目的是为了判断时间序列的性质，因为平稳序列与非平稳序列在建模和预测上有着不同的要求和方法。
平稳序列的统计性质更容易掌握，而非平稳序列可能存在漂移、趋势等问题，需要特殊的处理和修正。
单位根检验为我们提供了判断时间序列平稳性的有效手段。
单位根检验的基本步骤
单位根检验的基本步骤一、单位根检验是啥呢？单位根检验就像是给一组数据做个小检查，看看这组数据是不是平稳的。
这在经济学、统计学里可老重要啦。
你想啊，如果数据不平稳，就像盖房子的地基不稳，那后面基于这些数据做的分析啥的，可能就会出问题。
二、单位根检验的基本步骤1. 选择合适的检验方法常见的有ADF检验（Augmented Dickey - Fuller Test）。
这就好比你要去一个地方，有好几条路可以走，ADF检验就是其中一条比较常用的路。
还有PP检验（Phillips - Perron Test）等其他方法。
选择的时候要根据数据的特点来，要是数据有趋势，那得选能对付这种有趋势数据的检验方法；要是数据有季节性，那也得考虑这个因素。
2. 确定检验的模型形式有三种模型形式呢。
第一种是不带常数项和趋势项的模型，这种适合那种数据看起来就比较简单，没有什么明显的常数特征或者趋势特征的情况。
就像是一个很单纯的数列，没有什么额外的“装饰”。
第二种是带常数项，不带趋势项的模型。
这就好比数列有个基本的“起点”，有个常数在那儿撑着，但没有上升或者下降的趋势。
第三种是带常数项和趋势项的模型。
如果数据看起来像是有个固定的起点，然后还朝着某个方向有趋势地变化，就像股票价格有时候会有上涨或者下跌的趋势，还有个基本的价格底线，那这种模型就比较合适。
3. 设定检验的显著性水平这个显著性水平啊，就像是一个门槛。
一般我们常用的有0.05或者0.01。
这是什么意思呢？就是说如果我们得到的检验统计量比这个门槛对应的临界值更极端，那我们就可以拒绝原假设。
比如说，显著性水平是0.05，就好像是在说，这件事情只有5%的可能性是巧合，要是超过这个巧合的范围，那我们就认为有问题啦。
4. 计算检验统计量根据我们选择的检验方法和模型形式，把数据代入相应的公式里，就像做数学题一样，算出那个检验统计量。
这个过程可不能马虎，要是数据代错了，那结果肯定就不对啦。
计量名词解释
同期内生：内生解释变量与随机干扰项同期相关，两阶段最小二乘法：2SLS, Two Stage Least Squares：两阶段最小二乘法是一种既适用于恰好识别的结构方程，以适用于过度识别的结构方程的单方程估计方法。
方差膨胀因子：是指解释变量之间存在多重共线性时的方差与不存在多重共线性时的方差之比，VIF=1⁄1 –r^2。
容忍度的倒数，VIF越大，显示共线性越严重。
经验判断方法表明:当0<VIF<10，不存在多重共线性;当10≤VIF<100，存在较强的多重共线性;当VIF≥100，存在严重多重共线性完全共线性：如果存在不全为零，即某一解释变量可以用其他解释变量的线性组合表示，则称为解释变量间存在完全共线性。
异方差稳健标准误法：极大似然估计：也称为最大概似估计或最大似然估计，是求估计的另一种方法，找到参数θ的一个估计值，使得当前样本出现的可能性最大。
平稳性：是指时间序列的统计规律不会随着时间的推移而发生变化。
加权最小二乘法：是对原模型进行加权，使之成为一个新的不存在异方差性的模型，然后采用普通最小二乘法估计其参数的方法。
序列相关性：多元线性回归模型的基本假设之一是模型的随机干扰项相互独立或不相关。
如果模型的随机干扰项违背了相互独立的基本假设，称为存在序列相关性。
多重共线性：在经典回归模型中总是假设解释变量之间是相互独立的。
如果某两个或多个解释变量之间出现了相关性，则称为多重共线性。
解释变量的内生性：解释变量与随机误差项之间往往存在某种程度的相关性此时就称模型存在内生性问题，与随机误差项相关的解释变量称为内生解释变量。
虚拟变量：根据定性因素的属性类别，构造的只取“0”或“1”的人工变量，通常称为虚拟变量。
人工构造的作为属性因素代表的变量。
高斯－马尔可夫定理：在给定经典假定下，普通最小二乘（OLS）估计量具有线性性、无偏性和有效性等性质，即OLS 估计量是最佳线性无偏估计量。
异方差性：对于不同的解释向量，被解释变量的随机误差项的方差不再是常数，而互不相同，则认为出现了异方差性。
计量经济 第二章单位根过程及其检验
14第二章 单位根过程及其检验所谓数据生成过程(Data Generating Process,DGP)是指变量的数据源于具有何种特征的随机过程。
我们以下首先介绍稳定过程，由此引入非稳定过程，特别的单位根过程。
§2.1稳定过程§2.2.1 随机过程的稳定性1．稳定的定义定义1：对随机过程}),({T t t x X ∈=,对T 的任意子集(t 1,…,t n )，以及任意的h ，h T h t i ,∈+为实数，i =1,…,n ，若联合分布函数)(⋅F 满足F (x (t 1),x (t 2), …,x (t n ))=F (x (t 1+h ),…x (t n +h ))则称随机过程X 严格稳定。
严格稳定隐含了这个过程的所有矩为常数。
定义2：对定义1中所定义的随机过程X ，若满足① E (x (t i ))=E (x (t i +h ))=μ＜+∞② E [x (t i )2]=E [x i (t i +h )]2＝μ2＜+∞③ E [x (t i )x (t j )]=E [x (t i +h )x (t j +h )]=μi j ＜+∞则称随机过程x 为弱稳定，或者说二阶稳定，或协方差稳定。
从上述条件可以看出，二阶矩即方差和协方差不随时间而改变，且协方差只与间隔的时间长度有关而与时间本身无关，故称为二阶稳定，或协方差稳定。
如不加特别说明，今后的稳定均指弱稳定。
用这一定义虽然可以验证白噪音过程是弱稳定过程。
即对}1,{≥t x t ，其0)(,)(,022===+h t t t t x x E x E Ex σ,称这一过程为白噪音过程，它显然满足①②③，因而为弱稳定过程，进一步，若x t 为正态分布，则这一过程还为严格稳定，因为此时高阶矩仅为1和2阶矩（即0和2σ）的函数，故高阶矩存在且不随时间而改变。
从以上定义可以看出，一个稳定过程的数据图形特征为：数据围绕长期均值E (x t )=μ波动，偏离均值之后，有复归均值的调整；方差有限且不随时间改变；其自相关函数随时间衰减。
研究生计量经济学讲义(1)
协方差平稳（定义）
随机过程 { yt } 是协方差平稳的，那么，该过程的均值、方差以及协方差是不 随机时间变化的。 若随机过程 { yt } 不满足上述条件，则称该随机过程是非平稳的。也就是说， 非平稳过程的均值、方差以及协方差是随时间变化的。非平稳性行为可能是带有 趋势的、周期性的、随机游走，也可能是三者的结合物。
最简单的平稳过程：白噪声过程 A sequence {ε t } is a whitc-noise proccss if each value in the sequence has a mean
2
计量经济学－时间序列讲义
统计系
郭万山
of zero,a constant variance,and is serially uncorrelated.
趋势平稳和差分平稳 （Trend and Difference Stationary） 差分平稳 不包含漂移项的随机游走 y t = y t-1 + ε t ，以及包含漂移项的随机游走模型
y t 间序列，两者均可以通过差分变换转换为平稳
时间过程：
y t - y t-1 = ε t y t - y t-1 = α + ε t
① 纯随机游走过程（pure random walk） 所谓随机游走是指变量 yt yt 1 t ，其中， t 为白噪声过程， t ~ iid (0, 2 ) ； 随机游走也称为一阶单整过程（process integrated of one order），单位根过程 （process with a unit root） 或带有随机趋势过程 （process with a stochastic trend） 。 随机游走过程是非均值回归过程，它可以以正的或反的方向偏离均值。随机游 走的另一个特征是方差随时间变化，当时间趋于无穷大时，方差也趋于无穷大。 因此，随机游走并不能被预测（a random walk cannot be predicted）。 ② 带漂移项的随机游走过程(random walk with a drift )
单位根检验
影响
31
针对第四个问题,Perron提出
1. xt c t xt1 t H0 : 0
如果拒绝零假设,那么检验过程停止,该过 程是平稳过程 .不能拒绝,说明存在单位根,过 程非平稳,那么回归模型中的时间趋势项是不 是多余的参数呢?如果是,会导致检验的势降 低,进入步骤2.
包含一个确定性趋势和一个随机趋势
单位根过程
满足下面表达式的过程成为单位根过程
(1 B)xt t 1 t1 (B)t
其中
(1) 0,
j0
2 j
,程对时间序列的增量进行刻画，增 量平稳，但水平变量不平稳。
2. xt c t xt1 t H0 : 0
使用统计量 3 ,检验零假设. F统计量 (r为约束条件, k为无约束模型中的待估计参数)
j
[RSS(restricted) RSS(un restricted)] / RSS(restricted) / (T k)
单位根检验
非平稳过程
多数经济变量的时间序列都有随着时间增 加而增长的趋势, 不具有均值回复的特点.
两种刻画: 带趋势的平稳随机过程(前面已讲) 单位根过程
随机趋势过程
有一类随机过程, 如果再 t 时刻扰动项发生 变化, 那么它的影响会一直存在下去,不会随 着时间 t 增大会立刻衰减到0. 这样过程成为 随机趋势过程。 随机游动(走) 带常数项的随机游动 单位根过程
(B)ts (B)ts1 (B)t xt
所以
xt s
t
s
1
第九章单位根与协整
9.7
其中， －1。则原假设与备择假设变为
H0：＝0 vs H1： <0
对方程 9.7 使用OLS可得估计量ˆ及相应的t统计量
此t统计量称为ADF统计量（简记为ADF）。ADF统 计量的分布有没有解析解，其临界值也要通过蒙特 卡罗模拟得到。与DF检验一样，ADF检验也是左边 单侧检验，其拒绝域只在分布的最左边。
简记为DF统计量。 可以证明，DF统计量的渐近分布为布朗运动的函
数，并不服从渐近正态分布。由于其分布没有解
析解，故临界值须通过蒙特卡罗模拟来获得。
显然，DF统计量越小（绝对值很大的负数），则 越倾向于拒绝原假设。因此，DF检验是左边单侧 检验，即其拒绝域只在分布的最左边。比如，5％ 的临界值为－2.886，如果DF<－2.886，则拒绝原 假设；反之，则接受原假设 2、Augmented Dickey-Fuller单位根检验（ADF检验）
中心极限定理不再适用。虽然p
lim
n
ˆ1＝（1 仍为一
致估计），但在有限样本下可能存在较大偏差。
使用蒙特卡罗法可以得到ˆ1的大样本分布
2 传统的t检验失效：由于ˆ1不是渐近正态分布
t统计量也不服从渐近标准正态分布，传统的区间
估计与假设检验是无效的。更一般地，建立于平
稳性假设基础之上的大样本理论不再适用。
然而实际结果并非如此，因为扰动项
t＝yt－－
x
也是非平稳的（为什么？）
t
（因为 t＝yt－）
这一结论最初由Granger通过蒙特卡罗模拟而发现。
t 之非平稳部分会进入到OLS模型中去，从而 造成ˆ 0。
如何避免伪回归？方法之一，先对变量作一阶差 分，然后再回归。（差分后平稳了）
单位根过程
单位根过程
“单位根过程”是数学中的一个重要概念，是许多数学领域都应用的基础概念和方法。
单位根过程的核心思想是一个复数的一次方差可以写作其一次方的乘积，如z的一次方等
于z*z，z为复数。
这意味着复数中的一次方有一个单位根，即z，它是其本身；以及它的负根，即-z，它是自我相反的数。
负根和正根构成了一个完美的对立体系，这是计算复数
动力学中的基础。
在代数中，单位根过程用于求解等式，特别是多项式方程：通过给定一个等式，然后找出之间的关系，求出代数等式的根，最终得到方程的解。
例如，解x^2-1=0，用单位根过程，根据1和-1的平方的乘积等于-1，可以得出其解为x=1, -1。
此外，单位根过程还可以用于复数函数：例如，如果求函数表达式f(z)的极值点，即求函
数的最大值和最小值，可以通过此单位根过程解析函数，有助于求解函数极值点的位置。
总之，单位根过程是数学中一个重要的概念，它用于多个数学领域：代数，复数函数等，是计算复数动力学中的重要基础。
它可以帮助我们解决复杂的代数问题，比如多项式方程的求解。
同时，它还可以帮助我们求解极值点问题，帮助我们更好地理解数学中的复杂问题。
单位根检验PPT课件
❖ R-squared
0.379331
Mean dependent var
0.001161
❖ Adjusted R-squared 0.350463
S.D. dependent var
0.217449
❖ S.E. of regression 0.175250
是在相互独立的序列进行的实际回归中，经R2常 伴随着 高的 ，并且 系数显著。这种现象就
称为为伪回归（虚假回归）现象。
3
虚假回归（伪回归） ：定义
❖ 虚假回归：两个没有任何逻辑联系的序列进行回 归 ， 含 有很 高 的 R2， 因 为 两个 序 列 都与 时俱 进 （具有时间趋势，随时间推移而发生变化）。例 子，考研人数与手机数量。
❖ 可以通过数学推导证明； ❖ 已知随机步游是非平稳的，当 | |1 时，
AR(1)过程 {yt}为一随机步游过程。
14
单位根检验：定义
❖ 看图识平稳 ：
15
单位根检验：定义
❖ 看图识平稳 ：
16
单位根检验：定义
❖ 看图识平稳 ：
17
单位根检验：定义
❖ I(d)过程：有时原始序列是非平稳过程，但对 原始序列经过d次差分后可变为平稳过程，则 原序列记为I(d)过程；
31
单位根检验：DF和ADF检验
❖ DF和ADF检验在Eviews中的实现： ❖ 选择Quick/Series Statistics/Unit Root test，
输入序列名即可。 ❖ Lagged differences 为0即为DF检验 ❖ Lagged differences 不为0即为ADF检验
ADF检验为保证方程中的为白噪声，设随机过
近单位根过程脉冲响应函数的置信区间
归 （ Ａ 模 型描 述， 后利用样 本数据 估计 Ｖ Ｒ Ｖ Ｒ） 然 Ａ
模 型 的参数 ， 后根 据 这 些 参 数 值 计 算 脉 冲 响应 函 最 数 。但很 多 情形 下 ， 希 望 知 道 一 元 时 间 序列 模 型 也
归 系 数 估 计 的偏 误 ， 后 利 用 标 准 自举 方 法 构 造 脉 冲 响 应 函数 的置 信 区 间 。 蒙特 卡 罗 模 拟 结 果 表 明 在 小 样 本 时新 然
方 法 的表 现要 明 显 优 于 已有 的方 法 。新 方 法 的 实 际 覆 盖 率 能 够 一 致 地 达 到 或 超 过 名 义 置 信 水 平 。 关键 词 ： 冲 响应 ； 信 区间 ； 脉 置 自举 ； 位 根 单
中图分类号 ：２２ ０ １ 文献标识码 ： Ａ 文 章 编 号 ：０ ２— ５ ５ ２ １ ） １— ０ ９— ７ １０ ４ ６ （ ０ ２ Ｏ ０ｓ ｆ ｒ Ｕｎｉ ａ ｉ ｔ ｍ ｐ ｓ ｓ ｎ ｅ ｎ ｅ ｅ Ｉ ｅ ｖ ｌ ｏ ｉ ｖ ｒａ ｅ Ｉ ｕｌｅ Ｒｅ ｐｏ ｓ ｓ ｗｉｈ ａ Ｎｅ ｒ Ｕｎ ｔ Ｒｏ ｔ ｔ ａ ｉ ｏ
果 要 好 于解析 方法 。但 是 当真实 数据 过程是 非平 稳 或接 近非 平稳 时 ， 果仍 然不 好 ， 出现实 际覆 盖率 效 会 低 于名义 置 信 水 平 的情 况 。这 是 因 为 在 这 种 情 况
下 ， 型参 数估 计 量 的 有 偏 问 题会 更 严 重 。但 是 在 模
ｕｓ ｓ ｓａ ａ ｄ ｂｏ ｔｔａ ｍｅ ｈ ｄ ｔ ｃ ｎ ｔ ｃ ｃ ｎ ｄ ｎｃ ｉｔ ｒａ ｓ ｅ ｔｎｄ ｒ ｏ ｓｒｐ ｔ ｏ ｏ ｏ ｓｒ ｔ ｏ ｆ ｅ ｅ ｎ ｅｖ ｌ ．Ｍ ｏ ｔ Ｃａ ｌ ｉ ａ ｉｎ ｐｒ ｖ ｓ ｈａ ｈ ｗ ｍｅ ｈ ｄ ｓ ｕ ｉ ｎｅ ｒｏ ｓｍｕｌｔｏ ｏ ｅ ｔ ｔｔ ｅ ｎｅ ｔ ｏ ｉ
计量经济学讲义第八讲(共十讲)
第八讲 平稳时间序列与单位根过程一、随机时间序列模型概述在严格意义上，随机过程{}t X 的平稳性是指这个过程的联合和条件概率分布随着时间t 的改变而保持不变。
在实践中，我们更关注弱意义上的平稳或者所谓的协方差平稳：2();();(,)t t t t j j E X Var X Cov X X μδδ+===显然20δδ=。
在本讲义中，平稳皆指协方差平稳。
当上述条件中的任意一个被违背时，则称{}t X 是非平稳的。
（一）平稳随机过程的例子 1、白噪声过程{}t ε：20()0;();(,)0,t t t t j j E Var Cov εεδεε+≠===2、AR(1)过程：011,11t t t y a a y a ε<-=++，{}t ε是白噪声过程为了验证上述过程满足平稳性条件，我们首先通过迭代得到：1111010t t i it ii i t t y a a a y a ε---===++∑∑。
接下来注意到，111)0(t i i t t E y a a a y -==+∑，进一步假设数据生成过程发生了很久，即t 趋于无穷大，则01)1(t a E y aμ-==；其次也有110()()t it i i t Var y Var a ε--==∑，当t 趋于无穷大时，21221()11()i t Var a a Var y εδ-=-=；最后，当t 趋于无穷大时，有：1211111111222 (1241)11121......(...)[()()][()()]s s t t s t s t t s t s t s t t s s s s s a a a a a E y y E a a a a μμδδεεεεεεε+-----------++--+++++++++++=== 关于AR(p)过程的平稳性，见附录。
3、MA(P)过程：11...pt t t p t y a a εεε--=+++，{}t ε是白噪声过程显然，任意有限阶MA 过程都是平稳的。
高等时间序列
第一章 单位根过程1.平稳过程随机过程{X ,t 1,2,}t =⋅⋅⋅，其中t X 为一随机变量，若：（1）在每一时刻t ,1,2,t =⋅⋅⋅,且(X )t E ξ=（常数）（2）(t 1,2,)t X =⋅⋅⋅的协方差(X ,X )t j COV ，只与随机变量,t j X X 在过程中的间隔t j -有关，与它们的具体位置无关，即(X ,X )E{(X )(X )}t t s t t s s COV ξξξ--=--=（常数）例1.1 l 利用MATLAB 求100,500,1000的平稳过程.a=randn(100,1);y(1)=a(1);for i=(2:100);y(i)=0.5*y(i-1)+a(i);end plot(y)ρ=0.92.单位根过程随机过程{y ,t 1,2,}t =⋅⋅⋅是一单位根过程，若1;t 1,2,t t t y y u ρ-=+=⋅⋅⋅，其中1ρ=，{u }t 为一稳定过程，且(u )0,COV(u ,u )t t t s s E ξ-==，0,1,2,s =⋅⋅⋅当1ρ=时，模型1t t t y y u -=+称为“醉步模型，是一非平稳过程。
3.维纳过程标准维纳过程{W(t),t [0,1]}∈是定义在闭区间[0,1]上的连续变化的单变量的随机过程，满足：(a)(0)0W =(b)对闭区间[0,1]上任何一组有限分割1201k t t t ≤<<⋅⋅⋅<=，相应的(t )(j 1,2,k)j W =⋅⋅⋅的变化量21321[W(t )W(t )],[W(t )W(t )],[W(t )W(t )]k k ---⋅⋅⋅-为相互独立的随机变量(c)对任何01s t ≤<≤，有(t)(s)N(0,t s)W W --标准维纳过程(t)W 在任何一给定时刻t 为一随机变量（即(t)W 是时间t 的函数），对任何12,[0,1]t t ∈和12t t <，将1(t )W 和2(t )W 之间的距离定义为12(t ,t )d =4.中心极限定理，连续映照定理（1）,1,2,i X i =⋅⋅⋅(0,1)N（2）[0,1]D →1R 上的连续映照函数为()g ⋅。
单位根过程和单位根检验
第二章单位根过程和单位根检验第一节单位根过程从本章开始我们进入时间序列的非平稳分析和建模研究。
前面的章 节的内容主要考虑的是平稳时间序列的建模和预测问题，但对于非平 稳的时间序列，只有先进行差分处理，将其转换为平稳的时间序列模 型。
这样会损失部分信息。
本章从理论上介绍非平稳时间序列的性质, 讨论非平稳时间序列数据建模的伪回归问题。
非平稳序列的分析建立在维纳过程（布朗运动）和泛函中心极限定 理之上。
若干定义 定义1:（1） 白噪声过程（white noise ，如图1 ）。
属于平稳过程。
2Y t =也t〜iid （0,（T ）图3是日元兑美元差分序列（收益序列），近似于白噪声序列。
（2） 随机游走过程（random walk ,如图2）。
属于非平稳过程2Y t =Y t-i ；t, i 〜iid （0,（T ）随机游走过程是非平稳的，这是因为:y t =y o + U i + U 2 + W u tE(y t ) = E(y 0 + U 1+ U 2+丨1( u 」= y o2 2 —D(y t ) = D(y o + U i + U 2 + IH+U t ) = E(u i + U 2 + 1卄+U t ) = t ^一 ：定义2 :单位根过程随机过程｛y t,t = 1,2,|||｝是一单位根过程，若y t =y t_i + u t = 1,2|||U t 为一平稳过程，且 E(U t )= 0,cov(U t ,U t-s )= Ms S= 0,1,2|||CT 2=1 )随机游走的差分过程是平稳过程（白噪声过程）。
心yt =§定义3 :维纳过程维纳过程(Wie ner Process) 也称为布朗运动过程(Brow nianMoti on Process) 。
设W(t)是定义在闭区间［0，1］上一连续变化的随机过程，若该过程满足：(a) W(0)=0 ;(b) 对闭区间［0 , 1］上任意一组分割0 < t1 < t2^ < t k = 1 , W(t)的变化量：W t2 -W t1 , W t3 -W t2 ，川，W t k -W t k-1为相互独立的随机变量；(c) 对任意0 < s<t < 1 ,有W(t) -W(s) ~ N(0,t - s)则称W(t)为标准维纳过程(或标准布朗运动过程)。
单位根
单位根一、单位根过程的模拟 用阶梯函数模拟随机行走图2.1.2 阶梯函数模拟随机行走它表明了随着T 的增加随机行走过程与阶梯函数的近似情况。
为了进一步看清阶梯函数的特性，将其展开()⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧=<≤<≤=∑=1,21,10,011r T u Tr T Tu T r r R Tt t T当∞→T 时，阶梯函数快速的趋近于随机行走过程，即∞→T ，()r R T在[]1,0上渐增地变得稠密而且在某些正则性条件下弱收敛于标准维那过程，这个概念泛函中心极限定理要涉及到。
将它写成一个重要的结果()()r W r R T ⇒，“⇒”是弱收敛的意思。
这是著名的Donsker 定理的结论。
为了研究弱相关性和异方差性的误差分布，1984年它的结果已经被Herrndorf 进行了推广。
其中有一个重要的结论用于单位根过程的近似理论．()()()()r W f r R f T ⇒定理 (泛函中心极限定理(functional central limit theorem) 设随机变量序列{},,2,1, =t u t 是独立同分布的，且满足(),0=t u E ()()∞<==22σt t u E u Var ；r 为闭区间[]1,0上的任一正实数，给定样本T u u u ,.,21 ，取前[]Tr 部分样本作统计量()[]∑==Tr t tT uTr R 11，则当∞→T ,()[]∑==Tr t tT u Tr R 11 弱收敛于()()r B r W ≡σ既 ()()[]()r B r W u Tr R Tr t tT ≡⇒=∑=11σ ()r B 为布郎运动过程。
泛函中心极限定理是以后研究维那过程的理论基础，至此为维那过程和非平稳经济过程的进一步研究构造了数学理论框架。
二、利用EViews 进行单位根检验由t t t u y y +=-1生成的序列 由t t t u y y ++=-1μ生成的序列由t t t u y t y +++=-1νμ生成的序列 由t t u t y ++=νμ生成的序列由各种单位根过程生成的时序图经济时间序列常常呈现明显的时间趋势，在宏观经济时间序列中表现的更突出一些。
n次单位根求法
n次单位根求法
n次单位根的求法如下：
定义n次单位根公式是指当复数z的n次方等于1时，z的取
值情况。
即，当z^n=1时，z的取值为n个解，这些解被称为n次
单位根。
要推导n次单位根公式，首先需要了解欧拉公式，即e^ix = cos(x) + isin(x)，其中e为自然对数的底，i为虚数单位，x为实数。
根据欧拉公式，可以得到z^n = (e^ix)^n = e^inx = cos(nx) + isin(nx)。
由于z^n=1，所以有cos(nx) + isin(nx) = 1。
根据三角函数的周期性，可以得到cos(nx) = cos(2πk)，sin(nx) = sin(2πk)，其中k为整数。
将cos(nx)和sin(nx)展开，可以得到cos(nx) = cos^k(2πk) - C(n，k)cos^k-2(2πk)sin^2(2πk)
+ ... + (-1)^kC(n，k)sin^k(2πk)，sin(nx) = C(n，1)cos^k-
1(2πk)sin(2πk) - C(n，3)cos^k-3(2πk)sin^3(2πk) + ... + (-1)^kC(n，k)sin^k(2πk)，其中C(n，k)为组合数。
令cos(nx) = cos(2πk)，sin(nx) = sin(2πk)，可以得到n次单位根的解为z = cos(2πk/n) + isin(2πk/n)，其中k为0到n-1的整数。
以上就是n次单位根的求法，希望可以帮助到您。
单位根检验
为了借用DF检验的方法，将模型变为如下式： 模型I： Yt Yt -1 i Yt -i t
i 1 p
模型Ⅱ：Yt Yt -1 i Yt -i t
i 1
p
模型Ⅲ：Yt t Yt -1 i Yt -i t
当 t 时，序列的方差趋于无穷大，说明随机游动过 程是非平稳的。
单位根过程
如果一个序列是随机游动过程，则称这个序列 是一个“单位根过程”。 为什么称为“单位根过程”？
将一阶自回归模型表示成如下形Fra bibliotek：Yt - Yt -1 εt 或 (1- L)Yt εt
其中， L 是滞后算子，即 LYt Yt -1
结论:
随机游动过程是非平稳的。 因此，检验序列的非平稳性就变为检验特征 方程是否有单位根，这就是单位根检验方法 的由来 。
从单位根过程的定义可以看出，含一个单位根 的过程，其一阶差分：
Yt Yt - Yt -1 ut
是一平稳过程，像这种经过一次差分后变为平
稳的序列称为一阶单整序列(Integrated Process)， Yt。 I（1） 记为
ˆ - t ˆ ˆ
Dickey、Fuller研究发现，DF检验的临界值同序列的 数据生成过程以及回归模型的类型有关，因此他们 针对如下三种方程编制了临界值表，后来Mackinnon 把临界值表加以扩充，形成了目前使用广泛的临界 值表，在EViews软件中使用的是Mackinnon临界值 表。
当 1 ，则序列的生成过程变为如下随机游动过程 (Random Walk Process)： 其中{ t } 独立同分布且均值为零、方差恒定为 。随机 游动过程的方差为：
2
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
单位根过程
1、为什么进行单位根检验
单位根检验是检验序列中是否存在单位根，因为存在单位根就是非平稳时间序列了。
单位根就是指单位根过程，可以证明，序列中存在单位根过程就不平稳，会使回归分析中存在伪回归。
但是进行单位根检验的序列需服从I（d）过程。
当然从变量的自相关图和偏相关图也可以判断序列是否平稳，但准确度不高。
而单位根检验平稳性是比较准确的，主要方法是DF检验以及ADF检验。
2、什么是单位根检验
单位根检验是针对宏观经济数据序列、货币金融数据序列中是否具有某种统计特性而提出的一种平稳性检验的特殊方法，单位根检验的方法有很多种，包括ADF检验、PP检验、NP检验等。
单位根检验时间序列的单位跟研究是时间序列分析的一个热点问题。
时间序列矩特性的时变行为实际上反映了时间序列的非平稳性质。
对非平稳时间序列的处理方法一般是将其转变为平稳序列，这样就可以应用有关平稳时间序列的方法来进行相应得研究。
对时间序列单位根的检验就是对时间序列平稳性的检验，非平稳时间序列如果存在单位根，则一般可以通过差分的方法来消除单位根，得到平稳序列。
对于存在单位根的时间序列，一般都显示出明显的记忆性和波动的持续性，因此单位根检验是本书中有关协整关系存在性检验和序列波动持续性讨论的基础。
3、单位根过程
定义2-1 随机序列{x_t }，t=1,2,…是一单位根过程，若x_t=ρx_t-1+ε，t=1,2…（1）其中ρ=1，{ε}为一平稳序列，且 E[ε]=0, V(ε)=σ<∞, Cov(ε,ε)=μ<∞这里τ=1,2…。
特别地，若{ε}是独立同分布的，且E[ε]=0，V(ε)=σ<∞，则式（1）就变成一个随机游走序列，因此随机游走序列是一种最简单的单位根过程。
将式（1）改写为下列形式：（ 1-ρL）x_t=ε，t=1,2,…其中L 为滞后算子，1-ρL为滞后算子多项式，其特征方程为1-ρz=0,有根z= 。
当ρ=1时，时间序列存在一个单位根，此时{ }是一个单位根过程。
当ρ<1时，{x_t}为平稳序列。
而当ρ〉1时，{x_t}为一类具有所谓爆炸根的非平稳过程，它经过差分后仍然为非平稳过程，因此不为单整过程。
一般情况下，单整过程可以称作单位根过程。
在经济、金融时间序列中，常会遇到ρ非常接近1的情况，成为近似单位根现象。
近似单位根是介于平稳序列I（0）和单正序列I（1）之间。
一般情况下，单整过程可以称作单位根过程。
4、单位根检验的基础
单位根检验是建立ARMA模型、ARIMA模型、变量间的协整分析、因果关系检验等的基础。
自Nelson和Plosser利用ADF检验研究了美国名义GNP等14
个历史经济和金融时间序列的平稳性以后，单位根检验业已成为分析经济和金融时间序列变化规律和预测的重要组成部分。
因此，单位根检验作为一种特殊的假设检验，其可靠性的研究以及如何寻求可靠性较高的检验方法或统计量多年来一直是时间序列分析中的重要课题。