从计算机的核心思想探讨一种进制转换的方法
关于二进制、十进制、八进制、十六进制数据转换计算方法详细总结
在我们接触编程知识时,总会接触有关进制转换的知识,最常见的就是10进制与二进制或十六进制之间的转换,很多时候我们总会遗忘,虽然现在也出现了很多可以直接使用的网络在线的进制转换工具,但考试中,我们就要靠自己通过公式进行运算了。
今天就跟大家分享一下有关进制转换的理论知识,大家可以通过对比从里面发现共同点,这样便于我们理解记忆。
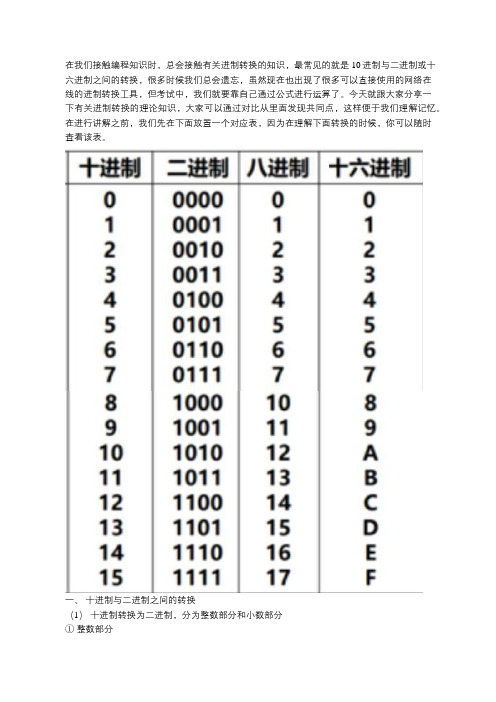
在进行讲解之前,我们先在下面放置一个对应表,因为在理解下面转换的时候,你可以随时查看该表。
一、十进制与二进制之间的转换(1)十进制转换为二进制,分为整数部分和小数部分①整数部分方法:除2取余法,即每次将整数部分除以2,余数为该位权上的数,而商继续除以2,余数又为上一个位权上的数,这个步骤一直持续下去,直到商为0为止,最后读数时候,从最后一个余数读起,一直到最前面的一个余数。
下面举例:例:将十进制的168转换为二进制得出结果将十进制的168转换为二进制,(10101000)2分析:第一步,将168除以2商84余数为0。
第二步,将商84除以2,商42余数为0。
第三步,将商42除以2,商21余数为0。
第四步,将商21除以2,商10余数为1。
第五步,将商10除以2,商5余数为0。
第六步,将商5除以2,商2余数为1。
第七步,将商2除以2,商1余数为0。
第八步,将商1除以2,商0余数为1。
第九步,读数,因为最后一位是经过多次除以2才得到的,因此它是最高位,读数字从最后的余数向前读,即10101000②小数部分方法:乘2取整法,即将小数部分乘以2,然后取整数部分,剩下的小数部分继续乘以2,然后取整数部分,剩下的小数部分又乘以2,一直取到小数部分为零为止。
如果永远不能为零,就同十进制数的四舍五入一样,按照要求保留多少位小数时,就根据后面一位是0还是1,取舍,如果是零,舍掉,如果是1,向入一位。
换句话说就是0舍1入。
读数要从前面的整数读到后面的整数,下面举例:例1:将0.125换算为二进制得出结果:将0.125换算为二进制(0.001)2分析:第一步,将0.125乘以2,得0.25则整数部分为0小数部分为0.25;第二步将小数部分0.25乘以2得0.5则整数部分为0小数部分为0.5;第三步将小数部分0.5乘以2得1.0则整数部分为1小数部分为0.0;第四步读数从第一位读起读到最后一位即为0.001。
进制转换方法范文

进制转换方法范文进制转换是计算机科学中非常重要的一项基本运算。
在计算机中,常见的进制有二进制、八进制、十进制和十六进制,不同进制之间的转换对于理解和处理计算机中的数据很关键。
本文将介绍进制转换的基本方法和原理。
一、二进制转换为十进制二进制是计算机中最基础的进制,只有0和1两个数字。
要将二进制转换为十进制,可以使用连乘法则。
首先将二进制的每一位数字从右到左按权重依次乘以2的幂次,再将乘积相加,即可得到十进制数。
例如,二进制数1101转换为十进制:(1×2^3)+(1×2^2)+(0×2^1)+(1×2^0)=8+4+0+1=13二、十进制转换为二进制要将十进制转换为二进制,可以使用除2取余法。
将十进制数除以2,并将余数记录下来,然后再将商继续除以2,直到商为0为止,最后将记录的余数倒序排列,即为二进制数。
例如,十进制数13转换为二进制:13÷2=商6余16÷2=商3余03÷2=商1余11÷2=商0余1倒序排列余数,得到二进制数1101三、二进制转换为八进制将二进制数按照三位一组进行分组,不足三位的高位可以用0补齐。
然后将每组三位的二进制数转换为对应的八进制数,最后将八进制数按照从左到右的顺序排列,即得到八进制数。
011010110326最终得到八进制数326四、八进制转换为二进制将八进制数的每一位转换为对应的三位二进制数,然后将这些三位二进制数按照从左到右的顺序排列,即得到二进制数。
例如,八进制数326转换为二进制:326011010110五、二进制转换为十六进制将二进制数按照四位一组进行分组,不足四位的高位可以用0补齐。
然后将每组四位的二进制数转换为对应的十六进制数,最后将十六进制数按照从左到右的顺序排列,即得到十六进制数。
11010110D6最终得到十六进制数D6六、十六进制转换为二进制将十六进制数的每一位转换为对应的四位二进制数,然后将这些四位二进制数按照从左到右的顺序排列,即得到二进制数。
任意进制间的转换方法

任意进制间的转换方法
在计算机科学中,我们经常需要在不同进制之间进行转换,例如将十进制数转换为二进制数,或将八进制数转换为十六进制数。
以下是任意进制间的转换方法:
1. 将原数按照目标进制进行除法运算,直到商为0为止。
每次将余数记录下来,最终从下往上排列即可得到转换后的数。
2. 将原数转换为十进制数,再将十进制数转换为目标进制数。
这种方法需要掌握不同进制数的权重,例如十六进制数的权重为16的n次方。
3. 对于二进制转换为八进制或十六进制的情况,可以将二进制数按照每3位一组进行分组,然后将每组转换为对应的八进制或十六进制数即可。
4. 对于十六进制转换为二进制的情况,可以先将每个十六进制数转换为4位二进制数,然后将它们按照顺序连接起来即可。
5. 对于八进制转换为二进制的情况,可以先将每个八进制数转换为3位二进制数,然后将它们按照顺序连接起来即可。
无论采用哪种方法,都需要对不同进制之间的转换规则有一定的了解。
只有掌握了这些规则,才能快速准确地进行进制转换。
- 1 -。
进制之间的转换方法

进制之间的转换方法进制是计算机科学中非常重要的概念,它涉及到了数字的表示和计算。
在计算机中,常见的进制有二进制、八进制、十进制和十六进制。
不同进制之间的转换是我们在计算机编程和数据处理中经常需要用到的操作。
下面,我们将介绍几种常见的进制之间的转换方法。
首先,我们来看二进制和十进制之间的转换。
二进制是计算机中最基本的进制,它由0和1组成。
而十进制是我们平常生活中最常用的进制,由0到9的数字组成。
二进制到十进制的转换方法是将二进制数按权展开,然后相加得到十进制数。
例如,二进制数1011可以转换为十进制数的方法是,12^3 + 02^2 + 12^1 + 12^0 = 8 + 0 +2 + 1 = 11。
接下来,我们来看十进制到二进制的转换方法。
十进制到二进制的转换方法是通过不断除以2得到余数,然后将余数倒序排列得到二进制数。
例如,将十进制数13转换为二进制数的方法是,13÷2=6余1,6÷2=3余0,3÷2=1余1,1÷2=0余1,所以13的二进制表示为1101。
除了二进制和十进制之间的转换,我们还需要了解八进制和十六进制的转换方法。
八进制是由0到7的数字组成,而十六进制是由0到9和A到F的数字和字母组成。
八进制和十六进制到二进制的转换方法和十进制到二进制的转换方法类似,只是需要按照不同的进制规则进行计算。
总结一下,进制之间的转换方法是计算机科学中的基础知识,掌握了这些方法可以帮助我们更好地理解计算机的运行原理和进行数据处理。
通过本文介绍的方法,我们可以轻松地进行二进制、八进制、十进制和十六进制之间的转换,为我们的计算机编程和数据处理工作提供了便利。
希望本文的介绍对大家有所帮助,谢谢阅读!。
二进制和十六进制算法

二进制和十六进制算法二进制和十六进制是计算机科学中常用的进制表示方法,可以用来表示数字、字符和图像等数据。
这两种进制在计算机领域有着广泛的应用,掌握它们的算法对理解计算机系统和编程非常重要。
下面将详细介绍二进制和十六进制的算法和应用。
一、二进制算法1.二进制表示法二进制是一种由0和1组成的进制系统,它是一种基于二的进制系统。
二进制数的每一位称为一个比特(bit),由于二进制每一位只有两个可能的取值0或1,所以在计算机中更容易处理和存储。
2.二进制到十进制的转换算法二进制转换为十进制是将二进制数按位展开,根据权值相加得到十进制数。
具体转换公式为:二进制数B的第n位×2的n次方相加,其中n为该位数的位置,从右向左依次为0、1、2、3等。
举例说明:1011(二进制)=1×2^3+0×2^2+1×2^1+1×2^0=8+0+2+1=11(十进制)3.十进制到二进制的转换算法十进制转换为二进制是将十进制数不断除以2,直到商为0为止,然后把每次的余数倒序排列即可。
举例说明:11(十进制)=1×2^3+0×2^2+1×2^1+1×2^0=1011(二进制)4.二进制运算算法二进制运算包括加法、减法、乘法和除法等基本运算。
其运算规则与十进制运算类似,只不过操作数和结果都是用二进制表示的。
举例说明:1011(二进制)+1100(二进制)___________如果两个二进制数位数不同,则需要在较短的数前面补零,然后才能进行运算。
5.二进制逻辑运算算法二进制逻辑运算主要包括与、或、非和异或等运算。
这些运算是基于逻辑的,常用于电路设计和位操作。
例如:0010(二进制)AND1011(二进制)_______________0010(二进制)1.十六进制表示法十六进制是一种由0-9和A-F(A、B、C、D、E、F分别对应10-15)组成的进制系统,它是一种基于十六的进制系统。
二进制化为十进制的算法

二进制化为十进制的算法1.引言1.1 概述概述部分:二进制和十进制是计算机科学中最基本的数制系统,二进制由0和1组成,而十进制由0至9的十个数字组成。
在计算机科学中,经常需要将二进制数转换为十进制数进行计算和表示。
因此,本文将探讨二进制转十进制的算法原理和应用意义。
在计算机领域,二进制数具有重要的意义。
因为计算机中的所有数据和指令都需要以二进制形式来表示和处理。
然而,对于人类来说,习惯于十进制数的计算和表达方式,因此需要学习和理解二进制转十进制的算法,以便更好地理解计算机中的数据表示和运算过程。
本文将首先介绍二进制和十进制的基本概念,包括它们的定义、表示方式以及在计算机中的应用。
然后,将详细讨论二进制转十进制的算法原理,解释转换过程中的关键步骤和计算方法。
通过掌握这些算法原理,读者将能够准确地将任意二进制数转换为对应的十进制数。
此外,本文还将总结二进制转十进制的算法,强调其重要性和实用性。
对于计算机科学领域的学习者和从业者来说,掌握二进制转十进制的算法是必不可少的基础知识。
它不仅有助于理解计算机中数据的存储和运算方式,还能够应用于数据转换、编码和解码等各种计算机应用领域。
最后,本文将探讨二进制转十进制算法的应用和意义。
无论是在计算机科学领域还是现实生活中,都有许多场景需要将二进制数据转换为十进制,例如网络通信、数据传输和数据分析等。
因此,深入理解二进制转十进制的算法对于开发高效的计算机系统和算法具有重要意义。
通过本文的学习和理解,读者将能够掌握二进制转十进制的算法原理和应用技巧,提高对计算机系统和编程的理解和应用能力,为进一步学习和研究计算机科学打下坚实的基础。
此外,对于对计算机感兴趣的非专业读者来说,本文也能够解析了解计算机中数据表示和处理的基本原理,增进对计算机科学的认识和兴趣。
1.2文章结构1.2 文章结构本文将分为引言、正文和结论三个部分来讨论二进制化为十进制的算法。
具体结构安排如下:引言部分将概述本篇长文的主题和目的,简要介绍二进制和十进制的基本概念,并说明本文的文章结构。
二进制数、八进制数、十进制数、十六进制数相互转换方法
二进制数、八进制数、十进制数、十六进制数相互转换方法有一个公式:二进制数、八进制数、十六进制数的各位数字分别乖以各自的基数的(N-1)次方,其和相加之和便是相应的十进制数。
个位,N=1;十位,N=2...举例:110B=1*2的2次方+1*2的1次方+0*2的0次方=0+4+2+0=6D110Q=1*8的2次方+1*8的1次方+0*8的0次方=64+8+0=72D110H=1*16的2次方+1*16的1次方+0*16的0次方=256+16+0=272D2、十进制数转二进制数、八进制数、十六进制数方法是相同的,即整数部分用除基取余的算法,小数部分用乘基取整的方法,然后将整数与小数部分拼接成一个数作为转换的最后结果。
3、二进制数转换成其它数据类型3-1二进制转八进制:从小数点位置开始,整数部分向左,小数部分向右,每三位二进制为一组用一位八进制的数字来表示,不足三位的用0补足,就是一个相应八进制数的表示。
010110.001100B=26.14Q八进制转二进制反之则可。
3-2二进制转十进制:见13-3二进制转十六进制:从小数点位置开始,整数部分向左,小数部分向右,每四位二进制为一组用一位十六进制的数字来表示,不足四位的用0补足,就是一个相应十六进制数的表示。
00100110.00010100B=26.14H十进制转各进制要将十进制转为各进制的方式,只需除以各进制的权值,取得其余数,第一次的余数当个位数,第二次余数当十位数,其余依此类推,直到被除数小于权值,最后的被除数当最高位数。
一、十进制转二进制如:55转为二进制2|5527――1 个位13――1 第二位6――1 第三位3――0 第四位1――1 第五位最后被除数1为第七位,即得110111二、十进制转八进制如:5621转为八进制8|5621702 ―― 5 第一位(个位)87 ―― 6 第二位10 ―― 7 第三位1 ――2 第四位最后得八进制数:127658三、十进制数十六进制如:76521转为十六进制16|765214726 ――5 第一位(个位)295 ――6 第二位18 ――6 第三位1 ――2 第四位最后得1276516二进制与十六进制的关系2进制 0000 0001 0010 0011 0100 0101 0110 0111 16进制 0 1 2 3 4 5 6 72进制 1000 1001 1010 1011 1100 1101 1110 111116进制 8 9 a(10) b(11) c(12) d(13) e(14) f(15)可以用四位数的二进制数来代表一个16进制,如3A16 转为二进制为:3为0011,A 为1010,合并起来为00111010。
二进制八进制十进制十六进制之间的转换方法
二进制八进制十进制十六进制之间的转换方法二进制、八进制、十进制和十六进制是计算机中常用的数制表示方法。
在进行转换时,可以利用其数制规则和特点来进行相互转换。
以下将详细介绍二进制、八进制、十进制和十六进制之间的转换方法。
1.二进制转八进制:二进制数是由0和1组成的数,八进制数是由0-7组成的数。
每3位二进制数可以转换为1位的八进制数,所以将二进制数从右到左以3位一组进行分组,并用八进制数表示每组即可。
2.二进制转十进制:二进制数转换为十进制数的方法是将二进制数分别乘以2的n次方,并将结果相加,其中n从0开始递增,对应于从右到左的二进制位数。
3.二进制转十六进制:二进制数转换为十六进制数的方法是将二进制数分组为4位一组,然后将每组转换为十六进制数。
4.八进制转二进制:八进制数转换为二进制数的方法是将八进制数的每位转换为对应的3位二进制数。
例如:将八进制数326转换为二进制数,可以将其每位转换为对应的3位二进制数,得到结果:011010110。
5.八进制转十进制:八进制数转换为十进制数的方法是将八进制数分别乘以8的n次方,并将结果相加,其中n从0开始递增,对应于从右到左的八进制位数。
例如:将八进制数326转换为十进制数,可以分别计算3*8^2+2*8^1+6*8^0,得到结果:2066.八进制转十六进制:将八进制数转换为十六进制数,首先将八进制数转换为二进制数,然后将二进制数转换为十六进制数。
例如:将八进制数326转换为十六进制数,可以先将其转换为二进制数011010110,然后将二进制数转换为十六进制数,得到结果:D67.十进制转二进制:将十进制数转换为二进制数的方法是将十进制数不断除以2,然后将余数逆序排列,最后将得到的余数连接在一起。
8.十进制转八进制:将十进制数转换为八进制数的方法是将十进制数不断除以8,然后将余数逆序排列,最后将得到的余数连接在一起。
例如:将十进制数214转换为八进制数,可以依次计算214/8=26余6,26/8=3余2,3/8=0余3、最后将得到的余数逆序排列,得到结果:3269.十进制转十六进制:将十进制数转换为十六进制数的方法是将十进制数不断除以16,然后将余数逆序排列,对于10~15的余数,分别用A~F表示,最后将得到的余数连接在一起。
4种整数进制的转换方法
4种整数进制的转换方法1.引言1.1 概述整数进制转换是数学中常见的概念,它涉及将一个整数从一种进制表示转换为另一种进制表示的过程。
常见的整数进制有二进制、八进制、十进制和十六进制。
每种进制都有自己的特点和应用场景。
在本文中,我们将探讨四种整数进制的转换方法,分别是二进制、八进制、十六进制和其他进制的转换方法。
我们将学习如何将一个整数转换为其他进制的表示,并了解每种进制表示的特点和用途。
在现代计算机科学中,二进制是最基础且最常用的整数进制。
计算机通过电子开关的开和关来表示二进制数的0和1。
了解二进制转换方法和二进制数的表示对于理解计算机的原理和运作方式至关重要。
八进制和十六进制是二进制的衍生进制。
八进制中使用了0-7这八个数字,而十六进制则使用了0-9这十个数字和A-F这六个字母。
八进制和十六进制拥有更高的进位制,可以用更短的长度表示一个大的二进制数,因此在计算机领域中经常使用。
除了二进制、八进制和十六进制之外,还有其他进制的表示方法。
这些进制常用于特定领域的计算,如四进制用于表示棋盘上的位置,十二进制用于时间的计量等。
了解不同进制的转换方法可以帮助我们更好地理解这些特殊领域的计算过程。
通过学习和掌握四种整数进制的转换方法,我们可以扩展我们的数字概念和计算能力,更深入地理解数学和计算机科学的原理。
本文将系统地介绍各种进制的转换方法,并探讨它们在不同领域的应用场景。
无论您是学生、工程师还是数学爱好者,本文都将为您提供有价值的知识和信息。
让我们开始学习四种整数进制的转换方法吧!1.2文章结构文章结构部分的内容的主要目的是介绍本文的组织结构,让读者能够清楚地了解整篇文章的内容布局。
在本篇文章中,主要分为引言、正文和结论三个部分。
引言部分首先进行了概述,对整数进制转换方法的主题进行了简要介绍,引起读者的兴趣。
接着,明确了本文的结构,即引言、正文和结论,为接下来的内容做了铺垫。
正文部分是文章的核心内容,主要介绍了四种整数进制的转换方法,分别是二进制、八进制、十六进制以及其他进制的转换方法。
十进制转二进制快速算法
十进制转二进制快速算法1.引言概述部分的内容:1.1 概述在计算机科学中,将十进制数转换为二进制数是非常常见的操作。
在实际应用中,我们经常需要将十进制数转换为二进制数,以实现更高效地存储和处理数据。
传统的十进制转二进制算法需要逐位地进行除二取余的运算,这在处理大数时效率较低。
为了解决这个问题,快速算法被引入到十进制转二进制的过程中。
快速算法通过一系列的位运算和移位操作,大大提高了转换的效率。
它能够以更快的速度将给定的十进制数转换为相应的二进制数,从而在计算机科学和计算机工程领域有着广泛的应用。
本文将介绍十进制转二进制快速算法的基本原理和实现方式。
首先,我们将简要介绍十进制转二进制的基本原理,然后对传统的十进制转二进制算法进行总结和分析。
接着,我们将引入快速算法的概念,并详细讨论其实现方式。
最后,我们将得出结论,并给出关于快速算法的一些建议和展望。
通过阅读本文,读者将能够了解十进制转二进制的基本概念和原理,掌握传统算法的步骤和流程,更重要的是理解快速算法的思想和实现方式。
这将有助于读者在实际应用中更高效地进行十进制转二进制的操作,提升数据处理和存储的效率。
在接下来的章节中,我们将深入探讨这些内容,希望读者能够通过本文对十进制转二进制快速算法有一个全面的了解。
1.2文章结构1.2 文章结构本文将分为三个主要部分来介绍十进制转二进制快速算法。
以下是各个部分的简要概述:2.1 十进制转二进制的基本原理本节将介绍十进制转二进制的基本原理,包括十进制和二进制的表示方式以及它们之间的转换关系。
我们将探讨十进制数的每一位在二进制中的对应表示,以及如何通过短除法来进行转换。
2.2 传统的十进制转二进制算法在这一节中,我们将介绍传统的十进制转二进制算法。
这是一种逐个位计算的方法,习惯上也称为长除法。
我们将详细介绍该算法的步骤和计算过程,并通过几个示例来说明如何将十进制数转换为二进制数。
3. 结论在这一节中,我们将引入快速算法的概念,并介绍它在十进制转二进制中的应用。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
【文章标题】从计算机的核心思想探讨一种进制转换的方法
【文章作者】曾健生
【作者邮箱】zengjiansheng1@
【作者QQ】190678908
【作者博客】/newjueqi
/
【编程环境】JDK 1.6.0_01
【作者声明】欢迎转载文章,但转载请保留文章的完整性以及注明文章的出处。
******************************************************************************* 在本人写的博客文章《一种进制转换的特殊方法》(http://)本人从“计算机上所有数据都是二进制数据”这个角度探讨了一种进制转换的方法,但由于这个思想比较难理解,而且举的例子也有一定的难度,所以写了本文作为补充,举了一个简单的八进制转换为16进制的算法(因为本人认为这个例子比较容易理解想要阐述的思想)。
如果《一种进制转换的特殊方法》(http://)一文看得不太明白,可先阅读本文。
大家知道,计算机是基于二进制的,所有数据都是以0和1的方式存放的,我们在屏幕上看到的丰富多彩的数据(包括各种声音,图像等)在计算机上都是一大串0和1,同样的道理,我们在屏幕上看到的以各种进制表示的数据在硬盘和内存中都是以二进制的形式存放的。
换句话来说,无论我们怎样转换进制,但最后存储在电脑上的都是二进制数,编程实现的进制转换只是改变数据的显示形式,但对在硬盘或内存中的存储的实际数据没有丝毫改变,因为数据在硬盘中永远只有0和1。
虽然以上的一段话讲的都是一些很闲浅的知识点,只要有一点计算机基础的同学都知道,但只有深刻理解上面一段话,才能弄明白本文所阐述的算法思想。
下面开始阐述这个进制转换的思想:
因为所有数据在计算机中都是以二进制的形式存放的,所以用编程实现的进制转换本质是把二进制数据用不同的进制形式显示出来,切记,进制转换只是改变数据的显示形式,在计算机中存放的依然是原来的二进制数据。
下面举一个例子,譬如有以下的语句:
int num=045;
这个语句的作用是把八进制值045赋予给变量num,虽然我们输入的八进制值045,但在计算机中存储的数据实际上是100101,为什么是100101呢?因为在计算中所有的数据都是以二进制的方式存储的,无论我们输入的值是十进制,八进制或者16进制,在计算机中存储的都是二进制数据。
既然各种进制的数据在计算机中都是以二进制的形式存储的,那么在转换进制时就能得到一个等效的进制转换思想:在计算机中所有的M进制转N进制,都等效为二进制转N进制。
为什么这样?因为所有的M进制在计算机上都是以二进制的形式存储。
所以用上一篇博文《一种进制转换的特殊方法》(http://)中的程序1(把8进制转16进制)实现进制转换,如果想修改为十进制转16进制,只需要把输入的数据改为十进制的形式,算法根本不需要修改,究其原因是算法的原理是把输入数据转换为二进制数据看待的。
用位操作实现进制转换的算法能同时适用于多种进制的原因是位操作能舍弃各种进制的外相(譬如十进制,八进制或者16进制的表现形式),直指数据在计算机中的本质:二进制,所以针对二进制数据的操作就能适用于多种进制。
下面详细分析一段程序代码例子,这段代码的作用是把八进制数据067转换为10进制数据显示出来,这个算法就是把八进制数据转换为二进制数据处理
//程序2:EightHexToTen.java
/**
*程序用途:通过移位实现八进制转换为10进制
*作者:曾健生
*日期:2009-4-6
*个人博客: /newjueqi
*/
class EightHexToTen
{
public static void main(String args[])
{
int num=067; //输入八进制数据067
int temp=0; //存储临时的数据
int multiple=1; //累积的倍数
int sum=0; //存储最终的结果
while( num>0 )
{
temp=num&1; //语句①,把二进制位取出来
sum=sum+multiple*temp; //语句②,把这位所表示的十进制数累加
multiple=multiple<<1; //语句③,累加的数*2
num=num>>1; //语句④,把下一位移到第一位的位置上}
System.out.println(sum);
}
}
输出结果为55
算法的过程如下:
(1)当执行完语句int num=067 后,num的值为067,在计算机中实际存储的数据是110111
(由于num是int型数据占据32位,实际110111前还有一大串0,但是为了阅读的方便,把110111前的0省略掉)
(2)要把八进制数据转换为二进制数据处理,就必须用到位运算,而二进制转换为十进制的
方法是把二进制中的每一位的数字乘以2的N次方(N为二进制数据的第M位减1)累积相加。
那现在的问题是怎么把二进制中需要的位提出来?在逻辑与(&)运算中,任何数和1进行与(&)运算都是它的本身,任何数和0进行与(&)运算都变为0,现在程序开始执行要把二进制数据110111的第一位提出来,换个角度就是把第一位置1,其它位置0,所以需要把二进制数据110111和000001进行逻辑与(&),也就是语句①(temp=num&1),执行完这句后temp存储的值就是110111中的第一位1。
(3)语句②(sum=sum+multiple*temp)是根据二进制转换为十进制的方法,把二进制中的
每一位的数字乘以2的N次方(N为二进制数据的第M位减1)累积相加。
先把第一位的值1乘以这个位对应的2的0次方的值(即multiple的初始值1),把结果存储在一个累积变量。
(4)由于下一次执行语句②时multiple的值必须变为2的1次方,所以把multiple的值*2,
也就是语句③(multiple=multiple<<1)
(5)现在已经处理完二进制数据110111的第一位,那么下次进入while循环后就必须处理
110111的第二位,这时又有一个新的问题:由于需要把110111的第二位提出来,就需要用二进制数10和110111进行与运算(&),那么第三次,第四次呢?如果这样就意味着每提110111中的一位出来,都需要构造一个新的数和110111进行与运算(&),这是多么麻烦的一件事情!!!所以我们需要移位运算的帮助,在进入下一次while循环前把num的值右移一位,就不需要每次都构造新的数字和110111进行与运算(&),用了语句④(num=num>>1)后每次进入新的循环就只需执行语句①(temp=num&1)就能把需要的位数提出来。
(6)不断地重复(2)(3)(4)(5)的过程,直到num的值等于0,那就表示所有位都已经
处理完毕,结束循环,输出结果。
如果现在不想用八进制转10进制,想玩玩别的进制转换,想把16进制转10进制,那也很简单,只需要把语句int num=067中的值改为16进制数。
我们可以试验一下把16进制数0xA4转换为10进制,把语句int num=067改为int num=0xA4,编译,运行程序,得到结果如下图:
不需要修改算法就能把原来的八进制转10进制变为16进制转10进制的根本原因是由于我们的进制转换算法是针对计算机中数据的核心:二进制数据,所进行的,不需要理会数据的外相(十进制,八进制或者16进制)。
最后总结一下:
在计算机中所有的数据都是以二进制的形式存储的(无论是十进制,八进制或者16进制),所以在进制转换的过程中,如果我们不理会进制的外相(即十进制,八进制或者16进制等表现形式)而直指数据在计算及中的核心:二进制,就能方便的实现进制的转换。
附:在上篇博客文章《一种进制转换的特殊方法》(http://)末给了个问题:用移位的方法实现10进制转8进制,在这里贴一份参考代码
/**
*程序名称:TenToOct.java
*程序用途:移位的方法实现10进制转8进制
*作者:曾健生
*日期:2009-4-6
*个人博客: /newjueqi
*状态:调试通过
*/
class TenToOct
{
public static void main(String args[])
{
int num=98; //输入的十进制数据
int temp=0; //临时变量
StringBuffer sb=new StringBuffer();
while( num>0 )
{
temp=num&7; //提出需要的位
sb.append(temp);
num=num>>3; //由于是转化为8进制,所以需要移3位}
sb.reverse();
System.out.println(sb);
}
}。
