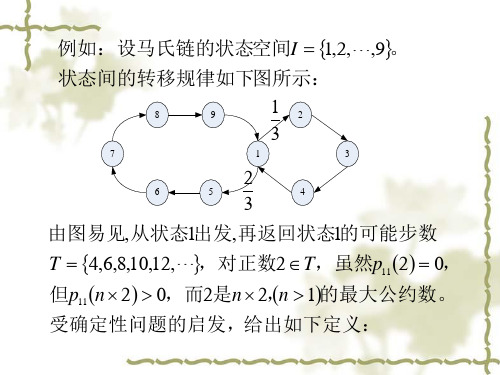
第4章_随机过程的非线性变换

非线性变换的直接分析法
例 2 ：假定全波线性检波器的输入为零均值平稳正态随
机过程，其方差为 ，求输出的一维概率密度和均值。
2
x y | x | x
x0 x0
y 0
fY ( y, t ) | J1 | f X ( x1 , t ) | J 2 | f X ( x2 , t ) fY ( y) | J1 | f X ( x1 ) | J 2 | f X ( x2 )
非线性系统分析的级数展开法
前提条件： y
g ( x) 可以在 x 0 处用台劳级数展开
1 d k h( x ) ak k ! dx k
y g ( x) a0 a1 x a2 x 2 ....
均值：
E[Y (t )] E[a0 a1 X (t ) an X n (t ) ]
若非线性函数不绝对可积，则转移函数用拉氏变换。
F (s) g ( x)e sx dx


s j
1 j sx y g ( x) F ( s ) e ds 2 j j
非线性系统分析的变换法
特征函数的定义 一维随机变量的特征函数为
X () E[e

D
F ( s1 ) F (s2 ) X ( s1 , s2 , )ds1ds2
D
普赖斯（Price）运用特征函数法，在输入随机过 程是高斯分布的特定条件下，将输入端的相关函数 和输出端的相关函数联系起来，称为普赖斯定理。
非线性系统分析的变换法
2. Price定理
假定输入为零均值平稳正态随机过程，输出过程为
相关函数： Y (t1 ) a0 a1 X (t1 ) an X n (t1 )
Y (t2 ) a0 a1 X (t2 ) an X (t2 )
n
2 RY [t1 , t2 ] E[Y (t1 )Y (t2 )] E[a0 a0a1 X (t1 ) X (t2 )]
非线性系统分析的级数展开法
例：非线性器件具有抛物线性质，即
g ( x) b1 x b2 x
2
输入随机信号是彼此不相关的正弦信号与噪声之和，
X (t ) S (t ) N (t )
正弦信号 S (t ) a cos(0t ) ，幅度a与角频率 0 是恒定 的，初相是随机的，在【－，】上均匀分布，噪声N(t) 是正态平稳过程，相关函数为 RN ( ) 2e 。求输出信 号Y(t)的均值、相关函数。

X ( 1 , 2 , ) g( x1 )e


dx1 g( x2 )e j2 x2 dx2d 1d 2


X ( 1 , 2 , )F ( 1 )F ( 2 )d 1d 2
如果用拉普拉斯变换表示，则为
1 RY () 2 (2j )

D
F ( s1 ) F (s2 ) X ( s1 , s2 , )ds1ds2
D
非线性系统分析的变换法
2. Price定理
1 RY () 2 4



X (1 , 2 , ) F (1 ) F (2 )d 1d 2
1 RY () (2j )2
X 1 ： X (t ) 在 t 时刻对应的随机变量 X 2 ： X (t ) 在
t
时刻对应的随机变量
非线性系统分析的变换法
例4：假定全波线性检波器的输入为零均值平稳正态随机过 程，其自相关函数已知，求输出过程的自相关函数。
x z | x | x
x0 x0
d X t dX t
Y(t)=g[X(t)]，则输出Y(t)的自相关函数满足如下关系：
d ( k ) RY () (k ) (k ) g ( x ) g ( x2 ) f X ( x1 , x2 , )dx1dx2 1 (k ) dRX () (k ) (k ) E g ( X ) g ( X 2 ) 1
x0 x0
0
x
随机过程的非线性变换
非线性变化的分析方法
非线性变换的直接分析法 非线性系统分析的变换法 非线性系统分析的级数展开法
非线性变换的直接分析法 -参考1.6节 随机变量函数概率密度的确定方法
X(t) Y=h(x)
Y(t)
已知：输入的统计特性（一维和二维概率密度、均值、 自相关函数）、系统的非线性变换函数 求解：输出的统计特征（概率密度、均值、 自相关函数）。 方法：直接根据定义求解。 特点：简单、直观。
无惰性时不变非线性系统
无惰性系统：输出 Y(t) 在 t1 时刻的特性完全由 X(t)
在 t1 时刻的特性决定，而不取决于 X(t) 在其他时刻
的特性，这样的系统称为无惰性系统。
时不变系统： Y (t ) h[ X (t )]
随机过程的非线性变换
典型的无惰性时不变非线性系统
1 1
X 0 X 0
d X t d X t dRZ () E h( X 1 )h( X 2 ) E dRX () dX t dX t
1P{X t X t 0} 1P{X t X t 0}
对线性系统，只需知道系统的特性函数和输入随机过程的数
字特征；对非线性系统，还需已知输入过程的一、二维分布律，
甚至高维分布律或高阶矩。
对一般非线性系统（动态非线性系统或称为有惰性非线性系
统）的特性描述，甚至测量都非常困难。
随机过程的非线性变换
非线性系统
X(t) Y=h(x) h(x)为非线性函数 Y(t)
(x1 , x 2 ) J (y1 , y 2 ) x1 x2 y2 y2 x1 x2 y1 y1
非线性变换的直接分析法
2. 均值和自相关函数
X(t)

Y(t) X(t) 的一维概率密度 Y=g(x)
E Y (t ) E{g[ X (t )]}

g ( x) f X ( x, t )dx

非线性变换的直接分析法
例1：若X(t)为零均值高斯平稳过程，相关函数、功率谱 密度已知，非线性系统传输特性为
yx
2
(1) 求输出过程Y(t)的一维概率密度；
(2) 求Y(t)的均值、方差、相关函数及功率谱密度；
fY ( y) | J1 | f X ( x1 ) | J 2 | f X ( x2 )
非线性变换的直接分析法
1. 求y(t)的概率密度 ：一维概率密度
X(t)
Y=g(x) Y(t)
y g ( x) 单调
f Y ( y, t ) | J | f X ( x, t )
y g ( x) 不单调
fY ( y, t ) | J1 | f X ( x1 , t ) | J 2 | f X ( x2 , t )
非线性系统分析的变换法
d ( k ) RY () (k ) (k ) g ( x1 ) g ( x2 ) f X ( x1 , x2 , )dx1dx2 (k ) dRX () (k ) (k ) E g ( X ) g ( X 2 ) 1
Price定理：将输入统计特性、非线性系统传输特性、输 出统计特性联系起来。 局限： •要求输入为零均值平稳正态随机过程； •要求非线性系统传输特性经过微分后能得到冲激函数， 才能使积分得到简化。
(1)平方律检波 y
y bx2 b 0
0
x
随机过程的非线性变换
典型的无惰性时不变非线性系统
(2)全波线性检波 y
x y | x | x
x0 x0
0
x
随机过程的非线性变换
典型的无惰性时不变非线性系统
(3)半波线性检波 y
x y ( x | x |) / 2 0
E Y (t ) E{g[ X (t )]}

g ( x) f X ( x)dx
第四章结束
非线性系统分析的变换法
1. 变换法的基本公式
若非线性函数关系满足




| g ( x) | dx
F ( ) g ( x)e j x dx 非线性系统的转移函数 1 j x y g ( x) F ( )e d 2

非线性系统分析的变换法
输出的自相关函数：
RY () E{Y (t )Y (t )} E{g[ X (t )]g[ X (t )]}



g ( x1 ) g ( x2 ) f X ( x1 , x2 , )dx1dx2
由概率密度与特征函数关系：
1 j1x1 j2 x2 f X ( x1 , x2 , ) 2 X (1 , 2 , )e d 1d 2 4
E Y (t1 )Y (t2 ) E{g[ X (t1 )]g[ X (t2 )]}



g ( x1 ) g ( x2 ) f X ( x1 , x2 , t1 , t2 )dx1dx2
X(t)的二维概率密度
若输入 X (t ) 二阶严平稳，则Y(t)的均值为常数，相关函数只与 有 关 则输出 Y (t )是广义平稳的。
第4章：随机过程的非线性变换
在电子系统中，除了大量的线性系统外，还有许多 非线性系统，如检波器、变频器、限幅器、鉴频器等。 非线性系统不满足迭加原理（也就是不能用中心极限定 理），因此不能采用第 3章介绍的线性系统的分析方法。 本章针对无惰性的时不变非线性系统。
随机过程的非线性变换
X(t) Y=g(x) Y(t) 已知：输入的统计特性和系统的非线性特性 求解：输出的统计特征。 难点：