高等传热学相变导热解(移动边界)
高等传热学知识点总结2024

引言概述:在高等传热学中,掌握各种传热方式以及其基本原理是非常重要的。
本文将分析五个大点,其中包括传热方式的分类、传热边界条件、传热传导、传热对流以及传热辐射。
每个大点都将进一步分解为五到九个小点,详细阐述相关知识。
通过本文的学习和理解,读者将能够深入了解高等传热学的知识点。
正文内容:一、传热方式的分类1.传热方式的基本分类2.对流传热与传导传热的区别3.辐射传热的特点及其应用4.相变传热的机理及其实例5.传热方式在工程中的应用案例二、传热边界条件1.传热边界条件的定义及分类2.壁面传热通量的计算方法3.壁面传热系数的影响因素4.壁面传热条件的实验测定方法5.边界条件的选择与优化三、传热传导1.传热传导的基本原理2.导热系数的计算方法3.等效导热系数的定义及其应用4.传热传导方程的推导和求解方法5.传热传导的数值模拟方法及其应用四、传热对流1.对流传热的基本原理2.传热换热系数的计算方法3.流体流动与传热的耦合关系4.对流传热的实验测定方法5.传热对流的同非稳态传热问题五、传热辐射1.辐射传热的基本原理2.黑体辐射的特性和计算方法3.辐射传热过程的数学模型4.辐射系数的影响因素及其计算方法5.传热辐射的应用案例和工程实例总结:通过对高等传热学知识点的总结,我们深入了解了传热方式的分类、传热边界条件、传热传导、传热对流以及传热辐射等重要知识点。
掌握这些知识,可以帮助我们更好地理解传热现象的基本原理及其在工程实践中的应用。
同时,对于热传导与辐射换热和传热对流以及其边界条件的掌握,有助于我们解决工程中的传热问题,优化设计和提高热能利用效率。
在今后的学习和实践中,我们应不断巩固和拓展这些知识,以更好地应对传热学的挑战,并为实际工程问题提供合理的解决方案。
高等传热学 ppt课件

高等传热学
高等传热学
高等传热学
解 释
高等传热学
高等传热学
高等传热学
高等传热学
高等传热学
用同样的方 法可以求得圆 筒、球等在有 内热源情况下 的温度表达式, 在此不再赘述。
高等传热学
高等传热学
高等传热学
高等传热学
高等传热学 以过余温度表达式为:
高等传热学
高等传热学
高等传热学
高等传热学
高等传热学
结论
高等传热学
高等传热学
第5章 外掠物体层流对流传热
高等传热学
(1) (2)
高等传热学
高等传热学
高等传热学
高等传热学
高等传热学
高等传热学
高等传热学
类
高等传热学
高等传热学
高等传热学
高等传热学
高等传热学
高等传热学
高等传热学
高等传热学
高等传热学
高等传热学 a0=a2=0
高等传热学
高等传热学
高等传热学
高等传热学
高等传热学
高等传热学
高等传热学
高等传热学
高等传热学
心
6.1.1
高等传热学
6.1.1
高等传热学
6.1.1
高等传热学
6.1.2
高等传热学
1)基本特征
常物性,则有
高等传热学 6.1.2 圆管,则有
6.1.2
高等传热学
高等传热学
1.2.2运动方程
高等传热学
1.2.2运动方程
高等传热学
1.2.2运动方程
高等传热学
1.2.2运动方程
高等传热学
1.2.3传热方程
高等热值交换技术 边界层的流动和换热

平均
1 L tw t f tw t f L 0 温差
1 Lq q L x x dx L 0 h dx L 0 Nu dx x x
qL 平均努塞尔数: Nu tw t f Nu 0.680Re1/ 2 Pr1/ 3 偏差2.4% 1/ 2 1/3 Nu 0.664Re Pr
第三章 层流边界层的流动和换热
3-1 外掠平板层流边界层流动的相似解 h=f(u,tw,tf,λ,ρ,c,η,α,l,ψ)
流体平行外掠平板强迫对流换热的解,可以表示成特征数关联 式的形式,即
Nu=f(Re,Pr)
特征数关联式中变量个数大为减少,更突出地反映相关物理量 之间的依赖关系,及其对对流换热的综合影响。
1. 布拉修斯无量纲参数得到外掠平壁的层流边界层流 动的相似解; 2. 戈尔德斯坦研究在什么条件下,可实现相似变量的 变换而求得相似解; 3. 赛比西和布雷德肖 应用龙格-库塔法求得同样问题 的解; 4. 豪沃思用数值积分得到的结果如下表:
由上述计算得到的外掠 平壁层流边界层 流动的速度分布:
(1) 流动边界层厚度
这一结果与理论分析结果一致。附加项Prf/Prw 用以考虑物性变化和热流方向的影响。
43
作业:
1. 试证明:Prw<<1 的流体外掠平壁层流边界层流动换热的局 部努谢尔特数为:
Nu
1
Re x Pr
2
1
1
2
2. 试证明:Prw>>1 的流体外掠平壁层流边界层流动换热, 若假定速度分布与温度分布均为直线,使用积分方程求解证 明:
对有限控制容积建立动量热量平衡方程 对边界层微分方程进行积分
积分方程 25
高等传热学-傅立叶导热定律及导热方程

热传导过程的能量平衡及其表现形式
energy balance for heat conduction and its mathematical form
导热方程式是以数学形式体现的在热传导过程中、特定考 虑区域内的能量守恒规律,即简化的热力学 thermodynamics 第一定律。 它揭示了温度场在时——空领域内的内在联系。
(unit volume) 发热量(heat generation rate)为Q(x,τ)
的内热源(inner heat source)开始发热,按照经典的傅
立叶导热定律,其定解(unique solution)问题可以用以
下表达:
t
=a
2t x 2
f
(x, )
t(x, ) 0 0
导热微分方程在正交坐标系(orthogonal curvilinear coordinates)中表述
梯度 (gradient) 一般表达式在附录(Appendix) 3 中式(9)
1 H1
q1
e1
1 H2
q2
e2
1 H3
q3
e3
按温度变量(variable)有:
t n dA
A
V qv dV
这就是导热积分方程(integral equation),它针对物体内 任意区域。
高等传热学
ห้องสมุดไป่ตู้
导热微分方程及其推导
曾经的推导方式是怎样? 在具体坐标系下,对微元体(different
element) 应用能量平衡原理
基于导热积分方程,利用散度定理 (divergence theorem) 推导
高等传热学_第一章_导热理论和导热微分方程

q gradt
1-1 导热基本定律
一般来说,材料的导热系数是温度的函数。大多数纯金属的导热
系数随温度的升高而减小,而气体与介电材料的导热系数随温度 的升高而增加。在极低温条件下(0-60 K),金属的导热系数随 温度有剧烈的变化,且可以达到很高的值。例如,纯铜在10 K时 的导热系数可达1.9×104W/(m· K)。对于液体和气体,特别是在接 近临界状态的条件下,导热系数还与压力有关。接近真空的稀薄 气体中的传热已不属于经典的导热过程。 在求解导热问题时常常假定导热系数是常量,即不随温度变化。 根据傅里叶定律,此时热流与温度梯度成线性关系,问题的求解 可以得到很大简化。在需要考虑导热系数随温度变化而温度变化 范围又不太大时,工程上常用线性关系来近似导热系数与温度的 关系,即
动力工程及工程热物理学科研究生
高等传热学(32课时)
高等传热学内容
第一章 第二章 第三章 第四章 第五章 第六章 第七章 第八章 第九章 第十章 第十一章 第十二章 第十三章 导热理论和导热微分方程 稳态导热 非稳态导热 凝固和熔化时的导热 导热问题的数值解 对流换热基本方程 层流边界层的流动与换热 槽道内层流流动与换热 湍流流动与换热 自然对流 热辐射基础 辐射换热计算 复合换热
1-1 导热基本定律
1-1-2 等温面与温度梯度
物体内温度相同的点的集合所构成的面叫做等温面。对应不同温
度值的等温面构成等温面族。等温面与任一截面的交线形成等温 线。由于等温线具有形象直观的优点,二维温度场常用等温线来 表示温度分布。 由于在同一时刻物体的一个点上只能有一个温度值,所以不同的 等温面不可能相交。它们或者在域内形成封闭曲线,或者终止于 物体的边界。 如图1-l所示,在物体内某一点P处,沿空间某一方向l的温度的变 化率
高等热质交换技术 边界层的分析
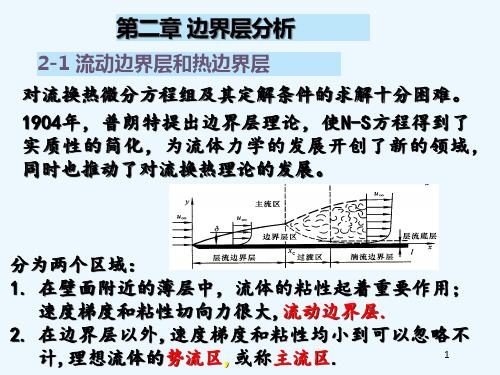
1.速度边界层(流动边界层) 速度发生明显变化 的 流体薄层。
流动边界层厚度 :
u 0.99u
流场的划分: 主流区:y< 理想流体
紊流核 心
u 边界层区: y 速度梯度存在与粘性力的作用区。
边界层的流态: 层流边界层、过渡区、紊流边界层
2
临界距离xc : 边界层从层流开始向紊流过渡的距 离。其大小取决于流体的物性、固体壁面的粗糙度等 几何因素以及来流的稳定度,由实验确定的临界雷诺 数Rc给定。
对流项 导热项
对流项进行比较分析
1.假定Δ/Δ ≥ 1,在这种情形下,导热项的系数就应 该等于 1 1 t P r Re 2 t
由于
1 Re
t
1 Re P r
Pr t
这种情形下成立的条件只能是Pr ≥ 1,意味着这样的流 体,流动边界层厚度大于或等于温度边界层厚度.
温度的无量纲参数采用: T Tw T Tw
变化范围0-1
热边界层厚度δ t度不一定等于流动边界层厚度δ, δ=LΔt , Δt是某个百分数。
无量纲参数:
x X L
y Y L
1 2 2 2 U V 2 2 2 X t Y c p Lu t X Y
导热项是偏微分方程中最高阶项,必须考虑,但 2 2 2 远小于 可以忽略不计。 2 2 X Y
无量纲能量方程
1 1 2 U V 2 X t Y Pr Re 2 Y t
有量纲边界层能量 方程
T T 2T u v x y cp p y 2
u v 0 x y
边界层对流 换热微分方 程组:
高等传热学相变导热解(移动边界)
⾼等传热学相变导热解(移动边界)⾼等传热学导热理论——相变导热(移动边界问题)讨论第五讲:相变导热(移动边界问题):移动边界的导热问题有许多种,本讲只讲固液相变时的导热模型。
5.1 相变换热特点与分类:特点:(1) 相变处存在⼀个界⾯把不同相的物质分成两个区间(实际不是⼀个⾯,⽽是⼀个区)。
(2) 相变⾯随时间移动,移动规律时问题的⼀部分。
(3) 移动⾯可作为边界,决定了相变问题是⾮线性问题。
分类:(1) 半⽆限⼤体单区域问题(Stefan Question ) (2) 半⽆限⼤体双区域问题(Neumman Question ) (3) 有限双区域问题5.2 相变导热的数学描述和解:假定:固液两相内部只有导热,没有对流(适⽤于深空中相变)。
物性为常量。
不考虑密度变化引起的体积变化。
控制⽅程:对固相: 221s s s t t a x τ??=?? 对液相:221l ll t t a x τ??=??初值条件:0:s l t t t τ∞=== 边界条件:0:::s l w l s l s x t ort t x t ort orx t ort t ∞===∞≠∞=?=在相变界⾯,热量守恒,温度连续,Q l 为相变潜热:()():s l sl l l s l p t t d x Q and t t t x x d δτδτλλρτ==+== 5.2.1 半⽆限⼤体单区域问题(Stefan Question )的简化解:以融解过程为例:忽略液相显热,2210l ll t t a xτ??==??,⽅程解为⼀直线,由边界条件得:()/l w p w t t t t x δ=+-对固相,忽略温差:w p t t t ∞==,即固相温度恒等于相变温度等于初始温度。
由相变处得换热条件求δ的变化规律:()()():0()l l ll l p w l l t d d x Q t t Q x dx d λδτδτδτλρρδτδ?==+=-+?==式中:()/l l p w l Ste c t t Q =-叫Stefan ’s Number ,物理意义是相变时液相显热和液固潜热⽐。
相变传热
+hiT=fi
r,t
Si
5
解析解
——分离变量法
平板
T
x,t
t
2T x,t
x2
T 0 x
k T hT 0 x
T F x
0 x L,t 0 x 0, t 0 x L, t 0 t 0, 0 x L
T x,t X xt
1 dt 1 d2X x t dt X x dx2
引起数学处理较为困难的其他因素:
在相变前、进行中和后,其物理性质依赖于温度,而温度分布是 三维的和瞬时的变化。
有时,溶解和凝结时发生的复杂又令人困惑的现象,使得传统的分 析方法无法解决。
2
热传导方程
静止的均匀物体内含有热源的各向同性物体的热传导方程
cp
T r,t
t
(kT
r,t
)
q& r,t
/
1/2 2
)
erfc
x
T3(x, t) Ti
41t
Tm2 Ti
erfc(2
1/2 2
/31/2
)
32
相界面的位置
s1(t) 21 1t s2 (t) 22 2t
利用相界面的能量守恒条件
Ste1
1
exp(12
)
erf ()
11
exp(121 /2 )
erf (2 ) erf (1 1 /2 )
(5 c)
h k2T
rV
(6)
t
=
s l
k=
k
s
k l
h hs h hl
把原来在两个活动区域及固液界面成立的方程组转换为在一个固定 区域内成立的方程,无需跟踪界面。便于数值计算。
高等传热复习重点
高等传热学(对流-相变部分)复习题一、解释概念(数学表达式、物理含义)粘性耗散效应及耗散函数Φ; 随动导数τD Db ;热边界层;热充分发展流; 雷诺热流t j q ; 雷诺应力,t i j τ;湍流强度J ;湍动能K ;湍流耗散项ε;湍流热扩散系数a t ;湍流动量扩散系数t ν;滞止温度、滞止焓;高速流边界层绝热壁面温度;蒸汽干度、截面含汽率;沸腾起始点、临界点。
各向异性介质导热系数,i j λ;非傅里叶效应。
二、论述问题与数学描述1. 阐述雷诺输运定理,并写出其数学公式;2. 一般形式的Navier-Stokes 方程的适用条件?3. 边界层的几何特征及其动量和热量传递的特征?4. 常物性、不可压缩牛顿流体绕流等温平壁的层流边界层对流换热数学描述。
5. 阐述层流边界层对流换热的特点,并指出其微分方程的数学和物理性质与一般微分方程相比发生了哪些变化?6. 简述定热流、定壁温下管内层流热起始段、充分发展流的流动与换热特点。
7. 论述层流边界层相似解法的基本思想、存在相似解的条件及相似变量一般形式。
8. 试论湍流的基本结构及产生原因,并列举几个导致湍流的因素;9. 简述湍流边界层的结构特点,并写出冯·卡门的三层结构模型和通用速度分布。
10. 论述K ε-模型的基本思想,并简要导出用K ε、表达的νt 计算关系。
11. 试说明自然对流产生的条件及Boussinesq 假设。
12. 试说明过热液体中汽化成核机制与加热壁面汽化成核机制的异同。
13. 试说明均温过热液体中气泡成长的过程机制与特点。
14. 试说明核态池沸腾过程中热量传递的主要途径。
15. 解释流动沸腾中的环状流与反环状流的流型成因与传热特点。
16. 试说明如何表示各向异性介质的导热系数.三、推导分析1. 圆管内层流热充分发展段的局部换热系数t tan cons x =α,且当t tan cons q w =时有0x)r ,x (T 22=∂∂; 2. 简述普朗特混合长模型的基本思想,并推导出湍流热扩散系数的表达式dyu d L 2t a =。
高等传热学热传导理论PPT课件
Copyright by HIT
哈尔滨工业大学航空航天热物理研究所
考虑到导热速度有限这一概念,得到导热的基本定律与傅立叶 定律不同。某时某点的瞬时热流密度表达式
21:00
Copyright by HIT
哈尔滨工业大学航空航天热物理研究所
21:00
Copyright by HIT
哈尔滨工业大学航空航天热物理研究所
21:00
Copyright by HIT
哈尔滨工业大学航空航天热物理研究所
时间条件的一般表达式
三类边界条件的一般表达式
21:00
Copyright by HIT
哈尔滨工业大学航空航天热物理研究所
二、各向异性介质中的导热
各个方向上导热系数都相同的均匀物质,称为各向同性介 质。此外,还有许多天然和人造材料,它们在各个方向上的结 构不同、因而不同方向上的导热系数也不相同,这样的物质称 为各向异性介质,例如晶体、木材、石墨、天然沉积岩、强化 结构纤维等都是典型的各向异性材料。晶体的导热系数随晶格 的不同排列方向而变化;木材沿纤维方向、垂直于木纹方向以 及环绕木纹方向上的导热系数各不相同。有的材料虽然本身是 各向同性的,但从实际应用的角度看,却往往表现出各向异性 的特征,例如由硅钢片叠合而成的变压器铁芯、电机的定子等, 沿叠层方向的导热系数值小于垂直于叠层方向的导热系数值。 傅里叶定律只适用于各向同性材料。
21:00
Copyright by HIT
哈尔滨工业大学航空航天热物理研究所
傅里叶定律例题1,任意方向的热流密度
21:00
Copyright by HIT
哈尔滨工业大学航空航天热物理研究所
傅里叶定律例题2,沿边界面总换热
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
高等传热学导热理论——相变导热(移动边界问题)讨论
第五讲:相变导热(移动边界问题):
移动边界的导热问题有许多种,本讲只讲固液相变时的导热模型。
5.1 相变换热特点与分类: 特点:
(1) 相变处存在一个界面把不同相的物质分成两个区间(实际不是一个面,
而是一个区)。
(2) 相变面随时间移动,移动规律时问题的一部分。
(3) 移动面可作为边界,决定了相变问题是非线性问题。
分类:
(1) 半无限大体单区域问题(Stefan Question ) (2) 半无限大体双区域问题(Neumman Question ) (3) 有限双区域问题
5.2 相变导热的数学描述和解:
假定:固液两相内部只有导热,没有对流(适用于深空中相变)。
物性为常量。
不考虑密度变化引起的体积变化。
控制方程:
对固相: 221s s s t t a x τ∂∂=∂∂ 对液相:221l l
l t t a x τ∂∂=∂∂
初值条件:0:s l t t t τ∞=== 边界条件:
0:::s l w l s l s x t ort t x t ort or
x t ort t ∞
===∞≠∞
=∆=
在相变界面,热量守恒,温度连续,Q l 为相变潜热:
()
():s l s
l l l s l p t t d x Q and t t t x x d δτδτλλρτ
∂∂==+==∂∂ 5.2.1 半无限大体单区域问题(Stefan Question )的简化解:
以融解过程为例:
忽略液相显热,2210l l
l t t a x
τ∂∂==∂∂,方程解为一直线,由边界条件得:
()/l w p w t t t t x δ=+-
对固相,忽略温差:w p t t t ∞==,即固相温度恒等于相变温度等于初始温度。
由相变处得换热条件求δ的变化规律:
()()():0()l l l
l l p w l l t d d x Q t t Q x dx d λδτδτδτλρρδτδ∂==+=-+∂==
式中:()/l l p w l Ste c t t Q =-叫Stefan ’s Number ,物理意义是相变时液相显热和液固潜热比。
液体厚度与时间的开平方成正比。
所以:
进入物体的融解热流密度为:0
)l l
x w p t q t t x
λ=∂=-=
-∂,
热流密度与时间的开平方成反比。
5.2.2 半无限大体单区域问题(Stefan Question )的精确解:
同样以融解过程为例:
对液相,221l l
l t t a x
τ∂∂=∂∂,设方程解为(满足初始条件)
:
(l t A Berf x =+
由边界温度条件得:l w p w t t t t -=- 对固相,忽略温差:w p t t t ∞==,即固相温度恒等于相变温度等于初始温度。
由相变处得换热条件求δ
的变化规律,设δΩ=度也与时间的开平方成正比。
上式是关于凝固常数的方程,叫相变问题的特征方程。
进入物体的融解热流密度为:0
()l l
x t t t q x
λλ=-∂=-=
∂,热流密度同样
与时间的开平方成反比。
5.2.3 半无限大体双区域问题(Neumman Question )的精确解:
同样以融解过程为例:
对液相,221l l
l t t a x
τ∂∂=∂∂,设方程解为(满足初始条件)
:
2()():)0exp()()())/l l l l
p w l w p l l l l t d x Q x d t t erf t t Q a Ste δτδτλρτλ∂=+∂=
-=ΩΩΩ=-=
(l w t t Aerf x =+
由边界温度条件得:
l w p w t t t t -=-
,t t A -= 对固相,22
1s s
s t t a x τ∂∂=
∂∂,设方程解为(满足初始条件):
(l t t Berfc x ∞=+
由边界温度条件得:
s p t t t t ∞∞-=-
,t t B -= 由相变处得换热条件求δ
的变化规律,设δΩ=
度也与时间的开平方成正比,δΩ=
得相变问题的特征方程:
(
)2
l x t A x e
δ
=Ω∂=
∂(
)2
s x t B
x
e
δ
β=Ω∂=-
∂
(
)()
22))
()/()/exp()()
exp()()
p w p l w p l l l s p l l l t t t t t t a Q t t a Q erf erfc λρλβρ∞∞-=----
=ΩΩΩΩΩΩ
22/exp()()exp()()
l s s l
Ste Ste erf erfc βρρ-=ΩΩΩΩΩΩ
进入物体的融解热流密度为:0
()l l
x t t t q x
λλ=-∂=-=
∂,热流密度还是
与时间的开平方成反比。
5.2.4 非线性问题求解方法总结:
对非线性问题,直接求解难度大,一般是进行适当简化,在简化基础上构造
()
():l s
l l l s t t d x Q x d x
δτδτλρλτ∂∂=+=∂∂
一个满足大多数唯一性条件的,保留部分待解常数的解函数。
将这个解函数代入余下的唯一性条件,求出待解常数,即为近似解或精确解。
5.3 关于湖水结冰问题的讨论:
几何条件假定:湖面很大,也很深,看成半无限大体。
换热条件假定:结冰前湖水均温,为t ∞,湖水主体温度一直保持t ∞。
大气环境温度为t a ,湖面与大气间的表面传热系数为常量h 1,冰层下表面与湖水间的表面传热系数也为常量h 2。
物性假定:因为在0℃附近,冰的比热c s 《Q l ,忽略冰层热容作用。
由此可得在冰层中的温度分布为直线。
设坐标原点在湖面,冰层厚度为δ,我们根据能量守恒和平壁导热规律得:
21()1//p a p s l
s
t t d h t t Q h d δ
ρδλτ
∞-=-++ (1) 冰层温度分布:()/s w p w t t t t x δ=+- 求解δ,令
()()()()()
112
2
21
1///////s p p a s s s p a l
s s s s s h m t t t t R h h Ste Fo
Ste c t t Q Fo h c a h δδλττρλτλ∞==--===-==
代入(1)式:
()()2211()111(1)
1p s s l p a p a h t t d d Q mR d h t t h t t d d mR d λδδρδττδδτδ
∞-=+=++---+=+
00,,00s t t ττδδ∞=→===→=
(
)
2
11
11(1)
0.5
/(1d d mR du δδ
δτ
δτ++=-+=-⎰
{ln[1/(1)]}/(,)mR mR mR f mR τδδδ=----=
讨论:当()max ,1/mR mR τδ→∞→-。
mR 一定时,冰层的最大厚度也就确定。
此时湖水对冰层的自然对流热流量等于湖面对大气散发的热流量,湖水凝结停止。
当0p t t mR ∞=→=,湖水比热无穷大,(
)2
2111τδδ=+-→=此种情况冰层没有极大值,可一直增厚。
即11)/s h δλ=。
当1mR =,冰层得到的热流量等于散出的热流量,
ln 0,c c τδδτδ=--→==-,此种情况由于厚度不能为负值,故不会结冰,尽
管t a 小于冰点。
当,p w a t t t t ∞==,湖水比热无穷大(或湖水与冰间的换热系数无穷大),湖面与大气换热系数无穷大,有:p w
p w s
s l s s l
t t t t d Q d d d Q δ
λρλτδδδ
τρ--=→=
δ== 此即Stefan 近似解。
此处的分析方法又叫做准稳态近似法。
