圆波导中三种常用模式PPT课件
合集下载
电磁场课件第三章圆截面金属波导
H z ) r
H r
1 kc2
j
(
E z
r
H z ) r
H
1 kc2
j (
E z r
H z )
r
TM波解
Ez
rR
0, Jm (kcr)
0, Jm (Pmn )
0, kc
Pmn R
Ez
E0J m
圆波导TE11场结构分布图
方圆波导变换器
2 轴对称TM01模
• TM01模是圆波导的第一个高次模； • 其场分布有轴对称性故不存在极化简并模，
常作为雷达天线与馈线的旋转关节中的工 作模式； • 因其磁场只有Hφ分量, 故波导内壁电流只 有纵向分量,它可以有效地和轴向流动的电 子流交换能量, 由此将其应用于微波电子 管中的谐振腔及直线电子加速器中的工作 模式。
Pmn R
r
cos m sin m
e
j z
Hr
m0 n1
j mR2
Pm2n r
Emn
Jm
Pmn R
r
sin m cos m
e
jt
z
H
m0 n1
j R
Nm(x)图,m=0,1,2,3
Bessel函数的递推公式
Bm
x
Bm1
x
m x
Bm
x
m x
Bm
x
Bm1
x
圆形波导的理论分析和特性 28页PPT文档
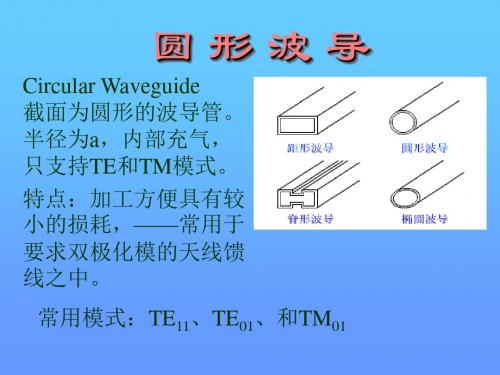
E z r
3.2 1a
r x 1
r f y
圆形波导分析 3 -- 纵横关系
w
E H
r f
H
r
j
k
2 c
r
r
0
Ef
0
w
0 0
0 0
w
0
0
w
r
r
对任意r，f均成立，左右两端均必须为常数: (设为kf2)，则有：
圆形波导分析 6 – TE modes（续一）
d2F(f) df2
kf2F(f)
0
3.27/8
r2
d2R(r) dr2
r
dR(r) dr
(kc2
kf2)R(r)
0
3.2-7通解可取：
F f = B1cos kff+B2sinkff 3.29
圆形波导分析 6 – TE modes(续三).
于是得到基本解为:
f f f H z(r ,,z )= H m n J m (u m a n'r)c s o in s m m e jz
3 .2 1 5 a
其中：Hmn=A1B为波型指数,每一个mn均对应 一个基本函数,其线性组合也必为本征方程的 解。通解为:
由于f的方向必须是周期性变化的，故kf必须 为整数m 。上面的结可写为：
圆形波导分析 6 – TE modes（续二）
f c o sm 3 .2 -1 0 f f f f F ()= B 1 c o sm + B 2 s in m= B s in mm = 0 ,1 ,...
四、圆波导中几种常用模式的场结构及其应用 微波技术基础 课件 PPT
o 磁场有Hr和Hz分量，在管壁上， H ＝0,只有Hz分量，因此圆波导壁上只有沿圆周方向的表面电流，
没有纵向电流；
o 在传输功率不变时，TE01波型的衰减常数随着频率增高而降低， （对于TE0n波型，都有这一特性），当工作频率很高时，衰减可以非常小，
适用于毫米波长距离传输以及高Q值的微波谐振腔。
o (但需要抑制其他模式：可在圆波导壁上开许多环形的窄缝）
四、圆波导中几种常用模式的场结构及其应用——（1）主模TE11
➢ 微波通信收发共用天线中的极化分离器．
四、圆波导中几种常用模式的场结构及其应用
2）圆对称TM01模
• 圆波导的第一个高次模
• 场分量表达式为： （v01＝2.405，C ＝2.61R）
Er
j
R
2.405
E0
J1
2.405 R
r
3）损耗最小的TE01模
• 场分量表达式为： （01＝3.832，C ＝1.64R）
J
' 0
(
Kcr)
J1
(Kcr)
E
j
wH 0 R
3.832
J
' 0
3.832 R
r
e
jz
j
wH 0 R
3.832
J1
3.832 R
r
e
jz
Hr
j H0R
3.832
J
' 0
3.832 R
r
e
jz
j
H 0 R
四、圆波导中几种常用模式的场结构及其应用——（3）TE01
叠片波导 螺旋波导
3.832
J1
3.832 R
பைடு நூலகம்
没有纵向电流；
o 在传输功率不变时，TE01波型的衰减常数随着频率增高而降低， （对于TE0n波型，都有这一特性），当工作频率很高时，衰减可以非常小，
适用于毫米波长距离传输以及高Q值的微波谐振腔。
o (但需要抑制其他模式：可在圆波导壁上开许多环形的窄缝）
四、圆波导中几种常用模式的场结构及其应用——（1）主模TE11
➢ 微波通信收发共用天线中的极化分离器．
四、圆波导中几种常用模式的场结构及其应用
2）圆对称TM01模
• 圆波导的第一个高次模
• 场分量表达式为： （v01＝2.405，C ＝2.61R）
Er
j
R
2.405
E0
J1
2.405 R
r
3）损耗最小的TE01模
• 场分量表达式为： （01＝3.832，C ＝1.64R）
J
' 0
(
Kcr)
J1
(Kcr)
E
j
wH 0 R
3.832
J
' 0
3.832 R
r
e
jz
j
wH 0 R
3.832
J1
3.832 R
r
e
jz
Hr
j H0R
3.832
J
' 0
3.832 R
r
e
jz
j
H 0 R
四、圆波导中几种常用模式的场结构及其应用——（3）TE01
叠片波导 螺旋波导
3.832
J1
3.832 R
பைடு நூலகம்
3.4圆波导
P S max F= = a L
(3-1)
很明显，数字研究早就指出：在相同周长的条件下， 很明显，数字研究早就指出：在相同周长的条件下， 圆面积最大
一、圆波导的一些特点
可见，要探索小衰减，大功率传输线，想到圆波 可见，要探索小衰减，大功率传输线， 导是自然的。 导是自然的。
一、圆波导的一些特点
4. 矩形波导中存在的一个矛盾 当我们深入研究波导衰减， 当我们深入研究波导衰减，发现频率升高时衰减 在矩形波导中上升很快。仔细分析表明， 在矩形波导中上升很快。仔细分析表明，衰减由两部 分组成：一部分称纵向电流衰减， 分组成：一部分称纵向电流衰减，另一部分是横向电 流衰减。 流衰减。 当频率升高时，横向电尺寸加大， 当频率升高时，横向电尺寸加大，使横向电流衰 减反而减少。这样所构成的矛盾因素使衰减有了极值， 减反而减少。这样所构成的矛盾因素使衰减有了极值， 同时形成频率升高时衰减增加。 同时形成频率升高时衰减增加。 而以后在圆波导中将会发现，有的波型( 而以后在圆波导中将会发现，有的波型(圆波导 波型)无纵向电流，因此， 中H01波型)无纵向电流，因此，若采用这种波型会使 高频时衰减减小。 高频时衰减减小。
(3-13)
∂Ez jωµ ∂Hz = +γ r ∂ϕ ∂r
二、圆波导一般解
jωε −γ 1 ∂Hz r ∂ϕ = jωε ∂Ez + γ ∂Hz ∂Ez ∂r r ∂ϕ ∂r
Dϕ =
得到第一组解
∂Ez γ ∂Hz 1 + Hϕ = − 2 jωε ∂r r ∂ϕ kc E = − 1 jωµ ∂Hz +γ ∂Ez r 2 kc r ∂ϕ ∂r
可以把上面两个Maxwell旋度方程分解成两组 旋度方程分解成两组 可以把上面两个
(3-1)
很明显，数字研究早就指出：在相同周长的条件下， 很明显，数字研究早就指出：在相同周长的条件下， 圆面积最大
一、圆波导的一些特点
可见，要探索小衰减，大功率传输线，想到圆波 可见，要探索小衰减，大功率传输线， 导是自然的。 导是自然的。
一、圆波导的一些特点
4. 矩形波导中存在的一个矛盾 当我们深入研究波导衰减， 当我们深入研究波导衰减，发现频率升高时衰减 在矩形波导中上升很快。仔细分析表明， 在矩形波导中上升很快。仔细分析表明，衰减由两部 分组成：一部分称纵向电流衰减， 分组成：一部分称纵向电流衰减，另一部分是横向电 流衰减。 流衰减。 当频率升高时，横向电尺寸加大， 当频率升高时，横向电尺寸加大，使横向电流衰 减反而减少。这样所构成的矛盾因素使衰减有了极值， 减反而减少。这样所构成的矛盾因素使衰减有了极值， 同时形成频率升高时衰减增加。 同时形成频率升高时衰减增加。 而以后在圆波导中将会发现，有的波型( 而以后在圆波导中将会发现，有的波型(圆波导 波型)无纵向电流，因此， 中H01波型)无纵向电流，因此，若采用这种波型会使 高频时衰减减小。 高频时衰减减小。
(3-13)
∂Ez jωµ ∂Hz = +γ r ∂ϕ ∂r
二、圆波导一般解
jωε −γ 1 ∂Hz r ∂ϕ = jωε ∂Ez + γ ∂Hz ∂Ez ∂r r ∂ϕ ∂r
Dϕ =
得到第一组解
∂Ez γ ∂Hz 1 + Hϕ = − 2 jωε ∂r r ∂ϕ kc E = − 1 jωµ ∂Hz +γ ∂Ez r 2 kc r ∂ϕ ∂r
可以把上面两个Maxwell旋度方程分解成两组 旋度方程分解成两组 可以把上面两个
电磁场与微波技术教学课件-2.3 圆形波导
1.TE波场分量表示式
HzH 0Jm(Kcr)c siom m n sejz
(2-131)
横向场与纵向场的关系
Ht
Kc2
t
Hz
或
E t ZTzE ˆH t
者
ZTE
j
Ht
Kjc2tHz
E t K 1c2jzˆtHz
§2.3 圆形波导
四个横向场分量为
E rj K c 2 m r H 0Jm (K cr)c sio m m n s ejz
这是一个以Kc为参变量，以r为自变量的贝塞尔方程,解为
R r A 1 J m K c r A 2 N m K c r
第一类m阶Bessel函数 图2-21
第二类m阶Bessel函数 /Neuman函数 图2-22
§2.3 圆形波导
由图2-22知，当r趋于0时，圆波导中心处场强为
无穷大，但在实际中是不可能的，故A2应等于零。
R为波导半径，由边界条件，当r=R时，Eφ=0
则必须
Jm ' (KcR)0
(2-134)
设μmn为m阶Bessel函数的导数的第n个根
部分TE
则
K c R m( m n 0 , 1 , 2 ; n 1 , 2 , 3 , )波型的
圆形波导中TE波的截止波数
Kc
mn
R
μmn及λc 值如书
中表2-
t 2 H ( r ,) K c 2 H ( r ,) 0
(2-110) (2-131)
一般意义上，柱坐标下，电场和磁场为
E ( r ,) r ˆ E r ( r ,) ˆ E ( r ,) z ˆ E z ( r ,)
H ( r ,) r ˆ H r ( r ,) ˆ H ( r ,) z ˆ H z ( r ,)
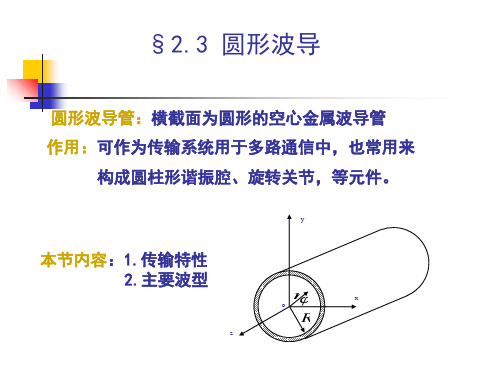
HzH 0Jm(Kcr)c siom m n sejz
(2-131)
横向场与纵向场的关系
Ht
Kc2
t
Hz
或
E t ZTzE ˆH t
者
ZTE
j
Ht
Kjc2tHz
E t K 1c2jzˆtHz
§2.3 圆形波导
四个横向场分量为
E rj K c 2 m r H 0Jm (K cr)c sio m m n s ejz
这是一个以Kc为参变量，以r为自变量的贝塞尔方程,解为
R r A 1 J m K c r A 2 N m K c r
第一类m阶Bessel函数 图2-21
第二类m阶Bessel函数 /Neuman函数 图2-22
§2.3 圆形波导
由图2-22知，当r趋于0时，圆波导中心处场强为
无穷大，但在实际中是不可能的，故A2应等于零。
R为波导半径，由边界条件，当r=R时，Eφ=0
则必须
Jm ' (KcR)0
(2-134)
设μmn为m阶Bessel函数的导数的第n个根
部分TE
则
K c R m( m n 0 , 1 , 2 ; n 1 , 2 , 3 , )波型的
圆形波导中TE波的截止波数
Kc
mn
R
μmn及λc 值如书
中表2-
t 2 H ( r ,) K c 2 H ( r ,) 0
(2-110) (2-131)
一般意义上，柱坐标下，电场和磁场为
E ( r ,) r ˆ E r ( r ,) ˆ E ( r ,) z ˆ E z ( r ,)
H ( r ,) r ˆ H r ( r ,) ˆ H ( r ,) z ˆ H z ( r ,)
圆形波导
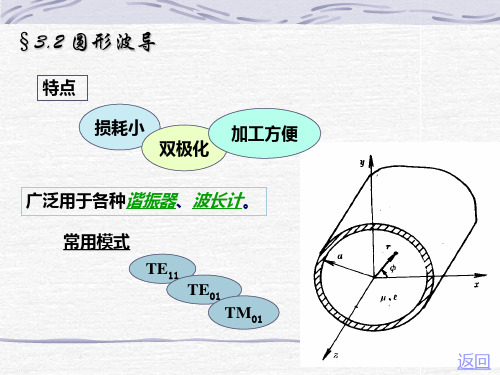
场沿圆周方向按正弦或余弦函数形式变化，波 型指数m表示场沿圆周分布的整波数。
TEmn导模的各参数：
波阻抗：
Z TE
Er H
E Hr
k
传播常数： mn
k2
k2 cmn
k
2
um n
2
a
截止波长： 截止频率：
cmn
2a
u m n
f cmn
k cmn
2
um n
2a
▪TE11模
u11 1.841对应本征值为最小值
bh k
传播常数： mn
k2
k2 cmn
k2
umn
2
a
截止波长：
cmn
2a
u mn
截止频率：
f cmn
k cmn
2
umn
2a
TM01模
u01 2.405 最小值 c 2.62a
圆波导中的 传输特性：
圆波导中传输条件 l c > l , f > fc
圆波导的主模是TE11模，cTE11 3.41a ； TM01模为次主模 cTE11 2.62a
必须为整数m
cos m () B1 cos m B2 sin m B sin m ,
m 0,1,2,...
由于圆波导结构具有轴对称性，场的极化方向具有不
确定性，使导波场在φ方向存在 cos m和sin m两
种可能的分布。它们独立存在，相互正交（两个线性 无关的独立成份），截止波长相同，构成同一波导的 极化简并模。
R(贝塞尔方程)的解为
R(r) A1J m (kc r) A2Ym (kc r) 式中 J m (k为crm) 阶贝塞尔函数，
第2.3节圆波导
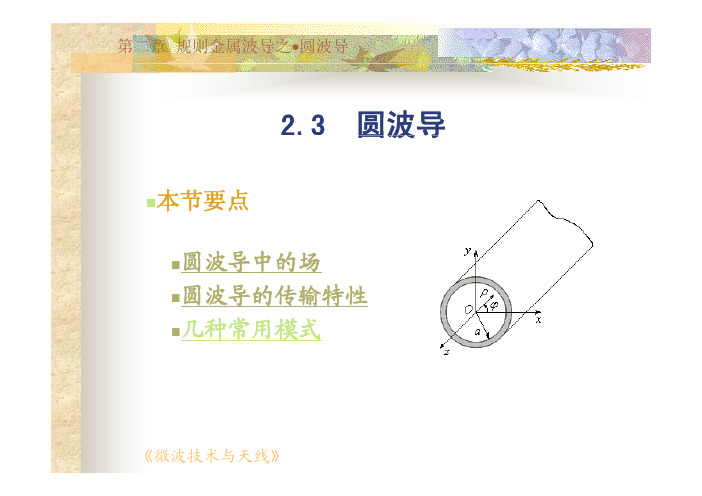
圆波导本节要点圆波导的传输特性几种常用模式衰减应用损耗小双极化¾波长计采用分离变量法及边界条件求得纵向磁场的通解为zj mn m mn z m J H z H βϕρμϕρ−∞∞⎟⎞⎜⎛⎟⎞⎜⎛=e i cos ),,(采用分离变量法及边界条件，求得纵向磁场的通解为ϕ==⎟⎠⎜⎝⎠⎝∑∑sin 01阶贝塞尔函数J m (x )为m 阶贝塞尔函数； μmn 为m 阶贝塞尔函数的一阶导数的第个根独立存在, 相互正交, 截止波长相同,n 个根， k cTEmn = μmn /a 。
截止波长相同, 极化简并模()xJ()xJ1()xJ2()xJ3m ν∞∞⎟⎛cos与TE 波相同的分析，可求得TM 波纵向电场通解为：zj mn m mn m n z m a J E z E βϕϕρϕρ−==⎟⎟⎠⎞⎜⎜⎝⎛⎠⎞⎜⎝=∑∑e sin ),,(01(个根其中)个根，的第阶贝塞尔函数是其中，n x J m m mn νak mn /mn TM c ν=且结论：圆波导中存在着无穷多种TE 和TM 模，不同的m 和22TM 22TEmn mn,⎟⎠⎞⎜⎝⎛−=⎟⎠⎞⎜⎝⎛−=a k a k mn mn νβμβ它们的相移常数分别为mnμ=TE mnν（1）截止波长k mn cTE ak =mn cTM mnmnaaνπλμπλ22mnmncTMcTE==aaa6398.16127.24126.3010111cTE cTM cTE ===λλλk k mnmnc νμπλ===mn mn cTM cTE 2aak cTE ()E H 0n 模和TM 1n 模简并)()(10x J x J −=′1nn0TMc TE c λλ=(a)E-H简并圆波导具有轴对称性对m≠0的任意非圆对称模式横向电磁场可以有任外的所有模式均对m≠0的任意非圆对称模式, 横向电磁场可以有任意的极化方向而截止波数相同存在极化简并水平极化波垂直极化波模的传输功率分别为222TE mn 和TM mn 模的传输功率分别为：)()1(2πc 2m 222mn TE TE a k J a k m H Z k a P c m mn−⎟⎟⎠⎞⎜⎜⎝⎛=βδ2222E a mn′⎞⎛=βπm 其中)(2TM a k J Z k P c m TMc m mn⎟⎟⎠⎜⎜⎝δ⎧=≠=102m m δ其中，场结构分布图方圆波导变换器Tips：TE11模存在极化简并，因此利用波导尺寸不能实现单模传输，可利用☆通常不采用圆波导来传输微波能量和信号磁场只有Hϕ分量波导内壁电流：线与馈线的旋转关节中的工作模式。
圆波导中三种常用模式教学文稿
圆，r 0 处，H 0 ，管壁电流只有分量 J z 。
此课件下载可自行编辑修改，仅供参考！ 感谢您的支持，我们努力做得更好！谢谢
（1）电磁场沿 方向不变化，场分布具有轴对称，不存在
极化简并；
（2）电场只有 E 分量，电力线在横截面内是一些同心圆，
在波导中心和波导壁附近为零；
（3）在管壁附近只有H z 分量，所以管壁电流只有分量 J ； （4） TE 01 模的导体损耗功率随频率的升高而单调下降，适合
远距离传输。
(3)圆波导中的 TM01 模
场量表达式为
E zE 0J0(kcr)ejkzz
式中
kc
2.405 a
Er jkzkE c0J1(kcr)ejkzz
HjkcE0J1(kcr)ejkzz
EHrHz0
TM01
电场线 磁场线
圆波导中 TM01 模的场结构分布图
（1）电磁场沿 方向不变化，场分布具有轴对称，不
存在极化简并；
（2）磁场只有 H 分量，磁力线在横截面内是一些同心
圆波导中三种常用模式
图7-10 圆波导中 TE11 模的场结构分布图
圆波导模 TE11 的场结构与矩形波导模 TE10 的场结构
相似，因此圆波导模 TE11 很容易通过矩形波导模 TE10
过渡得到。
由于 TE11 模具有极化简并，即使这样也不能保证圆波
导的单模传播，所以在实用中不用圆波导传输信号。
（2）圆波导中的 TE 01 模
场量表达式为： HzH0J0(3.8 a3r)2ejkzz
HrjkzkH c0J1(3.8a3r)2ejkzz
EjkcH0J1(3.8 a3r)2 ejkzz
Er EzH0
此课件下载可自行编辑修改，仅供参考！ 感谢您的支持，我们努力做得更好！谢谢
（1）电磁场沿 方向不变化，场分布具有轴对称，不存在
极化简并；
（2）电场只有 E 分量，电力线在横截面内是一些同心圆，
在波导中心和波导壁附近为零；
（3）在管壁附近只有H z 分量，所以管壁电流只有分量 J ； （4） TE 01 模的导体损耗功率随频率的升高而单调下降，适合
远距离传输。
(3)圆波导中的 TM01 模
场量表达式为
E zE 0J0(kcr)ejkzz
式中
kc
2.405 a
Er jkzkE c0J1(kcr)ejkzz
HjkcE0J1(kcr)ejkzz
EHrHz0
TM01
电场线 磁场线
圆波导中 TM01 模的场结构分布图
（1）电磁场沿 方向不变化，场分布具有轴对称，不
存在极化简并；
（2）磁场只有 H 分量，磁力线在横截面内是一些同心
圆波导中三种常用模式
图7-10 圆波导中 TE11 模的场结构分布图
圆波导模 TE11 的场结构与矩形波导模 TE10 的场结构
相似，因此圆波导模 TE11 很容易通过矩形波导模 TE10
过渡得到。
由于 TE11 模具有极化简并，即使这样也不能保证圆波
导的单模传播，所以在实用中不用圆波导传输信号。
（2）圆波导中的 TE 01 模
场量表达式为： HzH0J0(3.8 a3r)2ejkzz
HrjkzkH c0J1(3.8a3r)2ejkzz
EjkcH0J1(3.8 a3r)2 ejkzz
Er EzH0
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
圆波导中三 种常用模式
2020/3/23
1
（1）圆波导中的主模 TE模11
场量表达式为
Hz
H
0
J
1
(1.841 a
r
cos )sin
e
jk
z
z
Hr
jkzH0 kc
J
1
(1.841 a
r
)scions
ห้องสมุดไป่ตู้
e
jk
z
z
H
j kzH0
k
2 c
r
J1
(1.841 a
s in r) cos
e
jkz
z
kc
1.841 a
Jz
2020/3/23
7
J1
(
3.832 a
r )e jk z z
Er Ez H 0
式中，
kc
3.832 a
2020/3/23
4
TE01
电场线 磁场线
圆波导中 TE模01的场结构分布图
（1）电磁场沿 方向不变化，场分布具有轴对称，不存在
极化简并；
（2）电场只有 E分 量，电力线在横截面内是一些同心圆，
H
j E0
kc
J1 (kc r)e jkz z
E H r H z 0
式中
kc
2.405 a
2020/3/23
6
TM01
电场线 磁场线
圆波导中 TM 01 模的场结构分布图
（1）电磁场沿 方向不变化，场分布具有轴对称，不存
在极化简并；
（2）磁场只有 H分 量，磁力线在横截面内是一些同心圆，
处，r 0，管壁电H流 只 0有分量 。
过渡得到T。E10
由于 T模E具11有极化简并，即使这样也不能保证圆波导的
单模传播，所以在实用中不用圆波导传输信号。
2020/3/23
3
（2）圆波导中的 TE模01
场量表达式为：
Hz
3.832 H0J0( a
r)e jkz z
Hr
j kz H0 kc
J1
(
3.832 a
r)e jkzz
E
jH0
kc
在波导中心和波导壁附近为零；
（3）在管壁附近只有H分z 量，所以管壁电流只有分量 J； （4） TE模01的导体损耗功率随频率的升高而单调下降，适合
远距离传输。
2020/3/23
5
(3)圆波导中的 TM模01
场量表达式为
E z E0 J 0 (kc r)e jkz z
Er
j kz E0 kc
J1 (kc r)e jkz z
Er
jH0
k c2 r
J1
(1.841 a
s in r) cos
e
jk
z
z
E
jH0
kc
J
1
(1.841 a
r
cos )sin
e
jk
z
z
2020/3/23
2
圆波导模 此圆波导模
图7-10 圆波导中 T模E1的1 场结构分布图
T的E场11结构与矩形波导模 的场T结E1构0 相似，因
很容易通TE过11矩形波导模
2020/3/23
1
（1）圆波导中的主模 TE模11
场量表达式为
Hz
H
0
J
1
(1.841 a
r
cos )sin
e
jk
z
z
Hr
jkzH0 kc
J
1
(1.841 a
r
)scions
ห้องสมุดไป่ตู้
e
jk
z
z
H
j kzH0
k
2 c
r
J1
(1.841 a
s in r) cos
e
jkz
z
kc
1.841 a
Jz
2020/3/23
7
J1
(
3.832 a
r )e jk z z
Er Ez H 0
式中，
kc
3.832 a
2020/3/23
4
TE01
电场线 磁场线
圆波导中 TE模01的场结构分布图
（1）电磁场沿 方向不变化，场分布具有轴对称，不存在
极化简并；
（2）电场只有 E分 量，电力线在横截面内是一些同心圆，
H
j E0
kc
J1 (kc r)e jkz z
E H r H z 0
式中
kc
2.405 a
2020/3/23
6
TM01
电场线 磁场线
圆波导中 TM 01 模的场结构分布图
（1）电磁场沿 方向不变化，场分布具有轴对称，不存
在极化简并；
（2）磁场只有 H分 量，磁力线在横截面内是一些同心圆，
处，r 0，管壁电H流 只 0有分量 。
过渡得到T。E10
由于 T模E具11有极化简并，即使这样也不能保证圆波导的
单模传播，所以在实用中不用圆波导传输信号。
2020/3/23
3
（2）圆波导中的 TE模01
场量表达式为：
Hz
3.832 H0J0( a
r)e jkz z
Hr
j kz H0 kc
J1
(
3.832 a
r)e jkzz
E
jH0
kc
在波导中心和波导壁附近为零；
（3）在管壁附近只有H分z 量，所以管壁电流只有分量 J； （4） TE模01的导体损耗功率随频率的升高而单调下降，适合
远距离传输。
2020/3/23
5
(3)圆波导中的 TM模01
场量表达式为
E z E0 J 0 (kc r)e jkz z
Er
j kz E0 kc
J1 (kc r)e jkz z
Er
jH0
k c2 r
J1
(1.841 a
s in r) cos
e
jk
z
z
E
jH0
kc
J
1
(1.841 a
r
cos )sin
e
jk
z
z
2020/3/23
2
圆波导模 此圆波导模
图7-10 圆波导中 T模E1的1 场结构分布图
T的E场11结构与矩形波导模 的场T结E1构0 相似，因
很容易通TE过11矩形波导模