机械原理课程设计说明书--平面六杆机构
平面六杆机构课程设计

平面六杆机构课程设计一、课程目标知识目标:1. 让学生掌握平面六杆机构的基本构成和特点,理解其运动规律和动力学特性。
2. 使学生了解平面六杆机构在实际工程中的应用,并能结合具体案例进行分析。
3. 帮助学生理解平面六杆机构与其他类型机构之间的区别与联系。
技能目标:1. 培养学生运用平面六杆机构进行简单机构设计的能力,能够根据实际需求进行参数优化。
2. 提高学生运用计算机软件(如CAD等)进行平面六杆机构运动仿真和分析的能力。
3. 培养学生运用数学工具对平面六杆机构进行运动学和动力学计算的能力。
情感态度价值观目标:1. 培养学生对机械设计学科的兴趣和热情,激发其创新意识和探索精神。
2. 培养学生具备良好的团队合作精神和沟通能力,使其在项目实践中能够相互协作、共同进步。
3. 引导学生关注我国机械工程技术的发展,培养其爱国情怀和社会责任感。
本课程针对高年级学生,结合学科特点和教学要求,将目标分解为具体的学习成果,以使学生能够在实际操作中掌握平面六杆机构的相关知识,提高综合运用能力。
在教学过程中,注重理论联系实际,充分调动学生的主观能动性,培养其创新意识和实践能力。
通过本课程的学习,使学生能够为今后的机械设计工作打下坚实基础。
二、教学内容1. 平面六杆机构基本概念:介绍平面六杆机构的定义、分类及其应用场景,对应教材第二章第一节。
- 六杆机构的构成与特点- 六杆机构的运动副类型及功能2. 平面六杆机构运动分析:- 分析平面六杆机构的运动规律,对应教材第二章第二节;- 掌握平面六杆机构的自由度和速度、加速度的计算方法。
3. 平面六杆机构动力学分析:- 动力学基本方程及其应用,对应教材第二章第三节;- 力、力矩和功率的计算方法。
4. 平面六杆机构设计方法:- 介绍平面六杆机构设计的基本原则和步骤,对应教材第二章第四节;- 结合实际案例,进行参数设计和优化。
5. 计算机辅助设计与分析:- 利用CAD软件进行平面六杆机构建模和运动仿真,对应教材第二章第五节;- 学会对仿真结果进行分析和优化。
机械原理课程设计_课程设计教案

动图解法绘制机构给定位置的速度和加速度多边形;
3)选取位移比例尺μl、速度比例尺μv、加速度比例尺 μa和转角比例尺μφ(时间比例尺μt),绘制滑块5的位移 线图s-φ(t)、速度线图V-φ(t)和加速度线图a-φ(t);
4)整理设计计算说明书:内容包括:原始数据和设 计要求。将机构一个运动循环中的下列各个运动参数填 入表中,并以机构的某一位置为例,说明采用相对运动 图解法求机构的速度和加速度的过程。
《机械原理课程设计》
目的:
在于进一步巩固和加深所学到的理论知识,培养 独立解决实际问题和机械系统运动方案创新设计的能 力,使学生对机构的运动学和动力学分析和设计有一 个较为完整的概念,并进一步提高其计算、制图和使 用技术资料的能力。
要求:
用1号图纸一张和2号图纸一张绘制设计图。图纸 绘制过程中必须严格按照机械制图国家标准的要求进 行绘制,最后整理出设计计算说明书一份。全部的课 程设计应在一周内完成。
q
k
mm mm mm mm mm mm mm mm
n r/min
6、设计计算步骤 1)选取机构比例尺μl、按照数据表中给定的有关参数
绘制机构运动简图。将曲柄圆周分成6等份,作为曲柄的 6个位置,其作法为:取曲柄OA与连杆AB共线时所对应 的位置作为起始位置,曲柄按照顺时针方向依次标出A1、 A2、A3、A4、A5、A6 6个位置。再根据曲柄位置画出机构 的六个位置简图;
1、方法:矢量方程图解法(相对运动图解法)。
矢量方程图解法?
同一构件上两点之间的速度关系 3 C
B
VC=VB+VCB
2
A
大小: ? 方向: √
√? √ ⊥CB 1
机械原理课程设计之压床机构

机械原理课程设计说明书设计题目:学院:班级:设计者:学号:指导老师:目录一、机构简介与设计数据.机构简介图示为压床机构简图,其中六杆机构为主体机构;图中电动机经联轴器带动三对齿轮将转速降低,然后带动曲柄1转动,再经六杆机构使滑块5克服工作阻力rF而运动;为了减少主轴的速度波动,在曲柄轴 A 上装有大齿轮6z并起飞轮的作用;在曲柄轴的另一端装有油泵凸轮,驱动油泵向连杆机构的供油;a压床机构及传动系统机构的动态静力分析已知:各构件的重量G及其对质心轴的转动惯量Js曲柄1和连杆4的重力和转动惯量略去不计,阻力线图图9—7以及连杆机构设计和运动分析中所得的结果;要求:确定机构一个位置的各运动副中的反作用力及加于曲柄上的平衡力矩;作图部分亦画在运动分析的图样上;凸轮机构构设计已知:从动件冲程H,许用压力角α.推程角δ;,远休止角δ,回程角δ',从动件的运动规律见表9-5,凸轮与曲柄共轴;要求:按α确定凸轮机构的基本尺寸.求出理论廓线外凸曲线的最小曲率半径ρ;选取滚子半径r,绘制凸轮实际廓线;以上内容作在2号图纸上.设计数据设计内容连杆机构的设计及运动分析符号单位mm 度mm r/min数据I 50 140 220 60 1201501/2 1/4 100 1/2 1/2 II 60 170 260 60 1201801/2 1/4 90 1/2 1/2III 70 200 310 60 120 210 1/2 1/4 90 1/2 1/2 连杆机构的动态静力分析及飞轮转动惯量的确定δG2 G3 G5N1/30 660 440 300 40001/30 1060 720 550 70001/30 1600 1040 840 11000凸轮机构设计a ΦΦΦˊS0mm 016 120 40 80 20 7518 130 38 75 20 9018 135 42 65 20 75二、压床机构的设计.传动方案设计2.1.1.基于摆杆的传动方案优点:结构紧凑,在C点处,力的方向与速度方向相同,所以传动角γ=︒,传动效果最好;满足急回90运动要求;缺点:有死点,造成运动的不确定,需要加飞轮,用惯性通过;2.1.2.六杆机构A2.1.3.六杆机构B综合分析:以上三个方案,各有千秋,为了保证传动的准确性,并且以满足要求为目的,我们选择方案三;.确定传动机构各杆的长度已知:mmhmmhmmh2203,1402,501=== ,' 360ϕ=︒,''3120ϕ=︒,1180,,2CEH mmCD==优点:能满足要求,以小的力获得很好的效果;缺点:结构过于分散:优点:结构紧凑,满足急回运动要求;缺点:机械本身不可避免的问题存在;如右图所示,为处于两个极限位置时的状态;根据已知条件可得:︒=⇒==8.122205021tan θθh h在三角形ACD 和'AC D 中用余弦公式有:由上分析计算可得各杆长度分别为:三.传动机构运动分析项目 数值单位.速度分析已知:m in /1001r n =s rad n w /467.1060100260211=⨯==ππ,逆时针; 大小 ? 0.577 ? ? √方向 CD ⊥ AB ⊥ BC ⊥ 铅垂 √EF ⊥选取比例尺mmsm u v /0105.0=,作速度多边形如图所示;由图分析得:pc u v v c ⋅==×=0.07484m/s bc u v v CB ⋅==×=0.486m/s pe u v v E ⋅==×=0.11224m/s pf u v v F ⋅==×=0.0828m/s ef u v v FE ⋅==×=0.05744m/s 22ps u v v s ⋅==×69.32mm =0.27728m/s33ps u v v s ⋅==×14.03mm =0.05612m/s∴2ω=BCCBl v ==s 顺时针ω3=CD C l v ==s 逆时针 ω4=EFFE l v ==s 顺时针速度分析图:项目 数值单位.加速度分析=⋅=AB B l w a 21×=5.405m/s 2BC n BC l w a ⋅=22=×=1.059m/s 2 CD n CD l w a ⋅=23=×=0.056m/s 2EFn EF l w a ⋅=24=×=0.088m/s 2c a = a n CD + a t CD = a B + a t CB + a n CB大小: √ √ √方向: C →D ⊥CD B →A ⊥BC C →B 选取比例尺μa=m/s 2/mm,作加速度多边形图''c p u a a c ⋅==×=4.5412m/s 2''e p u a a E ⋅==×=6.8116m/s2''c b u a a tCB ⋅==×=2.452 m/s 2''c n u a a tCD ⋅==×=4.5408 m/s 2 a F= a E+ an FE+ a tFE 大小: √ √方向: √ ↑ F →E ⊥FE''f p u a a F ⋅==×=5.1768 m/s 2'2'2s p u a a s ⋅==×=4.8388m/s 2'3'3s p u a a s ⋅==×= 3.406m/s 2''f p u a a F ⋅==×= 5.1768m/s 2CB t CBl a =2α==10.986 m/s 2 逆时针t CDl a =3α==45.408 m/s 2 顺时针. 机构动态静力分析 g a G a m F s s s g 22222⋅=⋅==660×=与2s a 方向相同 g aG a m F s s g 33333⋅=⋅==440×=与3s a 方向相反gaG a m F F F g ⋅=⋅=555=300×=与F a 方向相反10max r r FF ==4000/10=400N222α⋅=s I J M =×= 顺时针 333α⋅=s I J M =×= 逆时针222g I g F M h ===9.439mm 333g I g F M h ===25.242mm 2.计算各运动副的反作用力 1分析构件5对构件5进行力的分析,选取比例尺,/10mm N u F =作其受力图 构件5力平衡: 0456555=+++R R G F g 则4545l u R F ⋅-==-10×= 4543R R -==2分析构件2、3 单独对构件2分析:杆2对C 点求力矩,可得:0222212=⋅-⋅-⋅Fg g G BC tl F l G l R 单独对构件3分析: 杆3对C 点求矩得:解得: N R t103.26563= 对杆组2、3进行分析:R43+Fg3+G3+R t 63+ Fg2+G2+R t 12+R n 12+R n63=0 大小:√ √ √ √ √ √ √ 方向:√ √ √ √ √ √ √ √ √ 选取比例尺μF=10N/mm,作其受力图则 R n 12=10×=1568N ; R n63=10×=..基于soildworks 环境下受力模拟分析:装配体环境下的各零件受力分析Soild works 为用户提供了初步的应力分析工具————simulation,利用它可以帮助用户判断目前设计的零件是否能够承受实际工作环境下的载荷,它是COMOSWorks 产品的一部分;Simulation 利用设计分析向导为用户提供了一个易用、分析的设计分析方法;向导要求用户提供用于零件分析的信息,如材料、约束和载荷,这些信息代表了零件的实际应用情况;Simulation 使用了当今最快的有限元分析方法——快速有限元算法FFE,它完全集成在windows 环境中并与soild works 软件无缝集成,被广泛应用于玩具、钟表、相机、机械制造、五金制品等设计之中;连杆受力情况Soild works中的simulation模块为我们提供了很好的零件应力分析途径,通过对构件的设置约束点与负载,我们很容易得到每个零件在所给载荷后的应力分布情况;由于不知道该零件的具体材料,所以我选用了soild works中的合金钢材料,并且在轴棒两端加载了两个负载,经过soild works simulation运算后得到上图的应力分布图,通过不同色彩所对应的应力,我们可以清楚的看到各个应力的分布情况,虽然负载与理论计算的数据有偏差,不过对于我们了解零件的应力分布已经是足够了;四、凸轮机构设计有45.00=r H,即有mm H r 778.3745.01745.00===; 取mm r 380=,取mm r r 4=; 在推程过程中:由200222cos δδπδπ⎪⎪⎭⎫⎝⎛=hw a 得当δ0 =550时,且00<δ<,则有a>=0,即该过程为加速推程段, 当δ0 =550时,且δ>=, 则有a<=0,即该过程为减速推程段所以运动方程2cos 10⎥⎦⎤⎢⎣⎡⎪⎪⎭⎫ ⎝⎛-=δπδh s在回程阶段,由2'0222)cos('δδπδπ⋅-=hw a 得:当δ0′=850时,且00<δ<,则有a<=0,即该过程为减速回程段, 当δ0′=850时,且δ>=, 则有a>=0,即该过程为加速回程段所以运动方程 2]cos 1['h s ⋅⎪⎪⎭⎫ ⎝⎛+=δπδ凸轮廓线如下:五、齿轮设计.全部原始数据 .设计方法及原理考虑到负传动的重合度虽然略有增加,但是齿厚变薄,强度降低,磨损增大:正传动的重合度虽然略有降低,但是可以减小齿轮机构的尺寸,减轻齿轮的磨损程度,提高两轮的承载能力,并可以配凑中心距,所以优先考虑正传动;.设计及计算过程1、变位因数选择 ⑴求标准中心距a :;5.1222)(21mm z z m a =+=⑵选取mm a 5.127'=,由此可得啮合角;25'5.12720cos 5.122'cos 'cos :'=⇒⨯==ααααa a ⑶求变位因数21x x +之和:1044.1tan 2)'()(2121≈-⋅+=+αααinv inv z z x x ,然后在齿数组合为38,1121==z z 的齿轮封闭线上作直线1044.121=+x x ,此直线所有的点均满足变位因数之和和中心距122.5mm 的要求,所以5304.0,574.021==x x ,满足两齿根相等的要求; 2、计算几何尺寸由021>+x x 可知,该传动为正传动,其几何尺寸计算如下:a.中心距变动系数:155.1225.127)'(=-=-=m a a yb.齿顶高变动系数:1044.011044.121=-=-+=∂y x xc.齿顶高:d.齿根高:e.齿全高:f.分度圆直径:g.齿顶圆直径:h.齿根圆直径: i.基圆直径: j.节圆直径: k.顶圆压力角: l.重合度:3.131.114.32)25tan 062.29(tan 38)25tan 136.42(tan 112)'tan (tan )'tan (tan 2211>=⨯-⨯+-⨯=⋅-⋅+-⋅= πααααεa a a z z 满足重合度要求;m.分度圆齿厚:参考文献1.孙恒,陈作模,葛文杰.机械原理M.7版.北京:高等教育出版社,2001.2.崔洪斌,陈曹维.AutoCAD实践教程.北京:高等教育出版社,2011.3.邓力,高飞.soild works 2007机械建模与工程实例分析,清华大学出版社.2008.4.soildworks公司,生信实维公司.soildworks高级零件和曲面建模.机械工业出版社.2005.5.上官林建,魏峥.soildworks三维建模及实例教程,北京大学出版社.2009.。
机械原理课程设计大作业平面六杆机构
evy=0:360;
ev=0:360;
fori=1:1:361
evx(i)=-l6*w6(i)*sind(thed6(i))-l5*w5(i)*sind(thed5(i));
evy(i)=l6*w6(i)*cosd(thed6(i))+l5*w5(i)*cosd(thed5(i));
%angularvelocity.m%
%-------------------------角速度-------------------------%
w2=0:360;
w3=0:360;
w5=0:360;
w6=0:360;
fori=1:1:361
V1=[-105.6*sind(thed2(i)) 67.5*sind(thed3(i)) 0 0;
ev(i)=(evx(i)^2+evy(i)^2)^0.5;
end
figure(4);
x=0:360;
y1=[evx;evy;ev];
plot(x,y1);
xlabel('\theta1');
ylabel('Evx,Evy,Ev');
gridminor;
legend('Evx','Evy','Ev');
L4
L5
L6
α
xG
yG
1-A
26.5
105.6
65.0
67.5
87.5
34.4
25.0
600
153.5
41.7
题目要求:
两人一组计算出原动件从0到360时(计算点数361)所要求的各运动变量的
西工大机械原理研讨课-平面六杆机构 PPT

一、基本概念及设计 (3) 含有三个移动副的六杆机构,其中一个为输出的移动副
当构件 6 为原动件,3 为输出移动副滑块时与之相对应的机构-7 SⅢ3P4P5P 六杆机构
二、平面六杆机构的应用
二、平面六杆机构的应用 牛头刨床
一、基本概念及设计
平面六杆机构的分类
1. 按自由度的数目进行分类,存在三个自由度的平面六杆机构。 我们都知道自由度是:机构的各构件之间应具有确定的相对运确,显然,
不能产生相对运动或作无规则运动的一堆构件难以用来传递运动,为了使组 合起来的构件能产生相对运动并具有运动确定性,有必要探讨机构自由度各 机构具有确定运动的条件。F:自由度;N:活动构件(含有机架);pl:低副; ph:高副;公式为:F=3(N-1)-(2pl+ph);
三、研讨总结
三、研讨总结
• 平面六杆机构不仅在众多工业生产中得到普遍应用,而且在其他
领域方面如人造卫是,航空航天中太阳能的展开机构.还有人体假肢 机构中采用的就是平面六杆机构。金属加工机床、起重运输机械, 采矿机械、农业机械、交通运输机械和仪表等都应用到了平面六 杆机构。
• 现总结其优缺点如下:
由于平面机构中一般不含有高副,所以平面六杆机构的自由度F=3(N-1) -2Pl。当自由度为3时可得出构架和低副的几种构型(N,PL )(6,6)(8, 9)(10,12)
2. 根据闭环个数进行分类。在我们一般生产生活中,我们一般是用自由度
数来区分的平面六杆机构,但是用这种方法不利于我们生活中的应用。
图 2-1 带有一个输出移动副的 WⅡ型六杆机构
图 2-2 带有一个输出移动副的 SⅢ型六杆机构
一、基本概念及设计 (2) 含有两个移动副的平面六杆机构,其中一个为输出移动副
机械原理课程设计六杆机构运动与动力分析

机械原理课程设计六杆机构运动与动⼒分析⽬录第⼀部分:六杆机构运动与动⼒分析⼀.机构分析分析类题⽬ 3 1分析题⽬ 32.分析内容 3 ⼆.分析过程 4 1机构的结构分析 42.平⾯连杆机构运动分析和动态静⼒分析 53机构的运动分析8 4机构的动态静⼒分析18 三.参考⽂献21第⼆部分:齿轮传动设计⼀、设计题⽬22⼆、全部原始数据22三、设计⽅法及原理221传动的类型及选择22 2变位因数的选择22四、设计及计算过程241.选取两轮齿数242传动⽐要求24 3变位因数选择244.计算⼏何尺⼨25 五.齿轮参数列表26 六.计算结果分析说明28 七.参考⽂献28第三部分:体会⼼得29⼀.机构分析类题⽬3(⽅案三)1.分析题⽬对如图1所⽰六杆机构进⾏运动与动⼒分析。
各构件长度、构件3、4绕质⼼的转动惯量如表1所⽰,构件1的转动惯量忽略不计。
构件1、3、4、5的质量G1、G3、G4、G5,作⽤在构件5上的阻⼒P⼯作、P空程,不均匀系数δ的已知数值如表2所⽰。
构件3、4的质⼼位置在杆长中点处。
2.分析内容(1)对机构进⾏结构分析;(2)绘制滑块F的运动线图(即位移、速度和加速度线图);(3)绘制构件3⾓速度和⾓加速度线图(即⾓位移、⾓速度和⾓加速度线图);(4)各运动副中的反⼒;(5)加在原动件1上的平衡⼒矩;(6)确定安装在轴A上的飞轮转动惯量。
图1 六杆机构⼆.分析过程:通过CAD制图软件制作的六杆机构运动简图:图2 六杆机构CAD所做的图是严格按照题所给数据进⾏绘制的。
并机构运动简图中活动构件的序号从1开始标注,机架的构件序号为0。
每个运动副处标注⼀个字母,该字母既表⽰运动副,也表⽰运动副所在位置的点,在同⼀点处有多个运动副,如复合铰链处或某点处既有转动副⼜有移动副时,仍只⽤⼀个字母标注。
见附图2所⽰。
1.机构的结构分析如附图1所⽰,建⽴直⾓坐标系。
机构中活动构件为1、2、3、4、5,即活动构件数n=5。
机械原理课程教案—平面连杆机构及其分析与设计

机械原理课程教案一平面连杆机构及其分析与设计一、教学目标及基本要求1掌握平面连杆机构的基本类型,掌握其演化方法。
2,掌握平面连杆机构的运动特性,包括具有整转副和存在曲柄的条件、急回运动、机构的行程、极限位置、运动的连续性等;3.掌握平面连杆机构运动分析的方法,学会将复杂的平面连杆机构的运动分析问题转换为可用计算机解决的问题。
4.掌握连杆机构的传力特性,包括压力角和传动角、死点位置、机械增益等;正确理解自锁的概念,掌握确定自锁条件的方法。
5,了解平面连杆机构设计的基本问题,掌握根据具体设计条件及实际需要,选择合适的机构型式;学会按2~3个刚体位置设计刚体导引机构、按2~3个连架杆对应位置设计函数生成机构及按K值设计四杆机构;对机构分析与设计的现代解析法有清楚的了解。
二、教学内容及学时分配第一节概述(2学时)第二节平面连杆机构的基本特性及运动分析(4.5学时)第三节平面连杆机构的运动学尺寸设计(3.5学时)三、教学内容的重点和难点重点:1.平面四杆机构的基本型式及其演化方法。
2.平面连杆机构的运动特性,包括存在整转副的条件、从动件的急回运动及运动的连续性;平面连杆机构的传力特性,包括压力角、传动角、死点位置、机械增益。
3.平面连杆机构运动分析的瞬心法、相对运动图解法和杆组法。
4.按给定2~3个位置设计刚体导引机构,按给定的2~3个对应位置设计函数生成机构,按K值设计四杆机构。
难点:1.平面连杆机构运动分析的相对运动图解法求机构的加速度。
2.按给定连架杆的2~3个对应位置设计函数生成机构。
四、教学内容的深化与拓宽平面连杆机构的优化设计。
五、教学方式与手段及教学过程中应注意的问题充分利用多媒体教学手段,围绕教学基本要求进行教学。
在教学中应注意要求学生对基本概念的掌握,如整转副、摆转副、连杆、连架杆、曲柄、摇杆、滑块、低副运动的可逆性、压力角、传动角、极位夹角、行程速度变化系数、死点、自锁、速度影像、加速度影像、装配模式等;基本理论和方法的应用,如影像法在机构的速度分析和加速度分析中的应用、连杆机构设计的刚化一反转法等。
六杆机构—机械原理课程设计

一、题目:计算平面连杆机构的运动学分析 (2)二、平面连杆机构的运动分析方程 (2)三、程序流程图 (5)四、计算源程序 (6)五、计算结果数据 (12)六、运动线图及分析 (238)七、体会及建议 (337)八、参考书 (337)一、题目:计算平面连杆机构的运动学分析1,图a 所示的为一平面六杆机构。
假设已知各构件的尺寸如表1所示,原动件1以等角速度ω1=1rad/s 沿着逆时针方向回转,试求各从动杆件的角位移、角速度和角加速度以及E 点的位移、速度和加速度的变化情况。
a)表1 平面六杆机构的尺寸参数(单位:mm)二、平面连杆机构的运动分析方程1)位置分析建立封闭矢量多边形l 1+l 2= l 4+l 3 (即AB+BC=AD+DC )l 1+l 2+ l 2’= AG+l 5+l 6 (即AB+BC+CE =AG+GF+FE ) (式1)将机构的封闭矢量方程式(1)写成在两坐标上的投影式:1*cos 12*cos 243*cos 31*sin 12*sin 23*sin 31*cos 12*cos 22'*cos(2)5*cos 56*cos 61*sin 12*sin 22'*sin(2)5*sin 56*sin 6l l l l l l l l l l xg l l l l l yg l l q q q q q q q q q q q q q q q q ü+=+ïïïï+=ïýï++-a =++ïïï++-a =++ïþ化简整理成方程左边仅含未知量项的形式,即得:2*cos 23*cos 341*cos 1(1)2*sin 23*sin 31*sin 1(2)2*cos 22'*cos(2)5*cos 56*cos 61*cos 1(3)2*sin 22'*sin(2)5*sin 56*sin 61*sin 1(4)l l l l l l l l l l l xg l l l l l yg l q q q q q q q q q q q q q q q q ü-=--=-+-a --=-+-a --=-………………………………………………………………………ïïïïïýïïïïïþ(式2)在求解(式2)中各变量时,用牛顿迭代法会比较直观,但由于牛顿迭代法不便于限制l 5,l 6的位置,在有两种位置均满足上式时,无法限定它得出题中要求的解。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
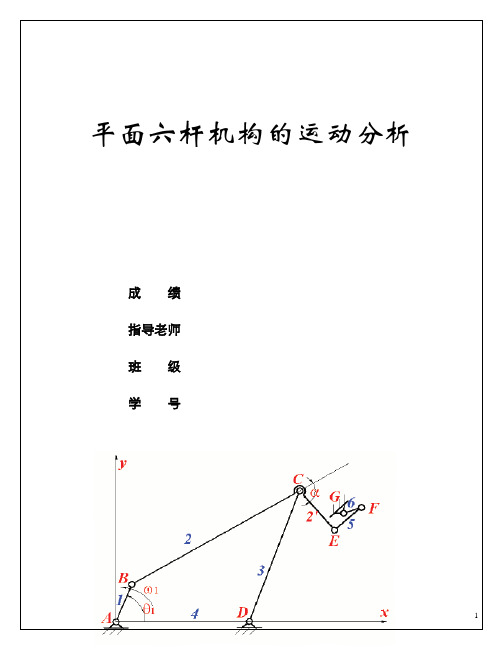
机械原理课程设计说明书设计题目:平面六杆机构学院:机械工程学院姓名:林立班级:机英101同组人员:刘建业张浩指导老师:王淑芬题目三:平面六杆机构.一. 机构简介1.此平面六杆机构主要由一个四杆机构,和一个曲柄滑块机构构成,其中四杆机构是由1杆,2杆,3杆和机架构成的曲柄摇杆机构,1杆为主动件,转速为90rpm ,匀速转动。
其中滑块机构由3杆,4杆,滑块5和机架构成,以四杆机构的摇杆为主动件2.设计要求:各项原始数据如图所示,要求对机构的指定位置进行运动分析和动态静力分析,计算出从动件的位移,速度(角速度),加速度(角加速度)和主动件的平衡力偶M ,进行机构运动分析,建立数学模型。
之后进行动态静力分析,建立数学模型,必须注意,工作行程和返回行程阻力的大小,方向,主动件处于何位置时有力突变,需要计算两次。
二. 机构运动分析:1.首先分析1杆,2杆,3杆和机架组成的四杆机构,可列复数矢量方程 (1-1) 应用欧拉公式 将实部和虚部分 离得332211cos cos cos θθθl b l l +=+ 332211sin sin sin θθθl a l l +=+把以上两式消元整理得0cos sin 33=++CB A θθ36213621θθθθi i i i l e l l l e e e +=+θθθsin cos i i +=e其中)sin cos (22cos 22sin 21112223212231313131θθθθa b l b a l l l C bl l l B al l l A ++----=-=-=解之可得)/(])([)2/tan(2/12223C B C B A A --+±=θ (1)速度分析将式(1-1)对时间t 求导,可得333222111cos cos cos θθθw l w l w l =+ 333222111sin sin sin θθθw l w l w l =+联解以上两式可求得两个未知角速度,3杆和2杆的角速 度3w 和2w)]-sin()/[l -sin(l )]sin(/[)sin(3223111223321113θθθθθθθθw w l l w w -=--=(2)加速度分析将式(1-1)对时间t 两次求导。
可得323333322222221211323333322222221211sin cos sin cos sin cos sin cos sin cos θθαθθαθθθαθθαθw l l w l l w l w l l w l l w l -=--+=+++联解以上两式可求得两个未知的角加速度,3杆和2杆的角 加速度3α和2α)sin()cos()cos()sin()cos()cos(3233233222231121223323323222211213θθθθθθαθθθθθθα-+----=---+-=l l w l w l w l l w l w l w2.分析由3杆,4杆,滑块5和机架构成的对心曲柄滑块机构 可列复数矢量方程,其中7l 为滑块的位移74343l e l e l i i =+θθ (2-2) 将实部和虚部分离得744334433cos cos 0sin sin l l l l l =+=+θθθθ(1)速度分析将式(2-2)对时间t 求导,可得滑块的速度V444333sin sin θθw l w l V+-=四杆的角速度4w 443334cos cos θθl w l w -=(2)加速度分析将式(2-2)对时间t 两次求导,可得滑块的加速度C4444443233333cos sin cos sin θθαθθαw l l w l l c ----= 四杆的角加速度4α 443333334444cos cos sin sin 22θθαθθαl l w l w l -+=三.动态静力分析1.首先分析滑块5,其受重力G ,支持力,支座反力F45,阻力Pr=2000KN ,惯性力555a m F I = 由滑块的力 平衡方程可得到r 5545P +=a m F x 。
2.分析杆4,使用静待换则Kg m c 6.95.0/2.0244=⨯=, C 点有支座反力24F 和34F ,惯性力44442αl m F c tI =, 44442l w m F c N I =,E 处有支座反力54F ,对E 点取矩可列平衡方程 0cos )(sin )(4444434244434242=-+-+αθθl m l F F l F F c y y x x 力平衡方程x c c x x F l m l w m F F 45444444443424sin cos 2=--+θαθ 由此可得444444444534242434sin cos 2θαθl m l w m F F F F c c x x x x ++=+=4444342444434242434cos sin )(2θθαl l F F l m F F F x x c y y y -+-=+= 3.分析杆3,C 点处有支座反力43F 和23F ,因杆3质量忽 略,故无惯性力,对D 点取矩可列平衡方程0cos )(sin )(333423333423=-+-θθl F F l F F y y x x4.分析杆2,C 处有支座反力32F 和42F ,惯性力2222αl m F c Ct I = 22222l w m F c CN I = 对B 点取矩。
可列平衡方程 0cos )(sin )(2222224232224232=---+--αθθl m l F F l F F c y y x x 5.根据以上所列方程可解得233232322332243432322434332222324sin cos sin cos sin cos sin sin sin 2θθθθθθθθθαl l l l l l F l l F l l m F y x c y ----=333324343323243324342324sin cos cos sin θθθθl l F l F l F F y y x x +-= 6.继续分析杆2,B 处有支座反力12F ,惯性力11222l w m F B BN I =,可列力的平衡方程 111222222222232412cos cos sin 22θθθαl w m l w m l m F F b c c x x --+=111222222222232412sin sin cos 22θθθαl w m l w m l m F F b c c y y --+=7.分析杆1,由于杆1质量忽略,故无惯性力,在B 处有支座 反力12F ,和加在杆上的力偶矩M ,对A 点取矩,可列力 的平衡方程得11121112cos sin θθl F l F M y x +-=四.用matlab 进行计算并得出滑块的位移、速度、加速度以及作用在主动件的平衡力偶的图像1.滑块位移图像2.滑块速度图像3.滑块加速度曲线4.平衡力偶图像五.机构运动简图1.起始位置2.任意位置六.设计结果分析与设计心得1.结果分析:经过使用复数矢量法建立数学模型,并通过Matlab的计算与绘图可知,滑块的位移图像为余弦函数,当曲柄的转动角度为(0.377+2Kπ)rad时,有最大值0.6638m,当曲柄的角度为[0.377+(2K+1)π]rad时,有最小位移为0.4502m。
滑块的速度图像为余弦函数,滑块的最大速度为0.8868m/s,最小速度为0m/s.滑块的加速度图像近似于余弦函数,最大加速度为7.7421m/s*s,最小加速度为-20.2257m/s*s.加在曲柄上的平衡力矩图像也同样为余弦函数,最大力矩为227.6055KN*m.最小力矩为-342.7158.2.设计心得:这次第一次做课程设计,我们小组遇到了挺大的挑战。
我们从一开始自学matlab到重新学课本上并没有掌握很好的知识。
我们花了很多精力和时间。
许多看似简单的问题,但当我们真正下手去解决时发现,我们之前想的太简单了。
我们不得不从最基本的重新来做。
我们在这次设计中学会了脚踏实地,也学会了互相合作。
这些对我们日后的生活,学习,工作都有很多的益处。
我们也学会了不轻视任何一个简单的问题。
七.matlab设计源程序clc;clearw1=3*pi;a=0.36;b=0.32;l1=0.10;l2=0.43;l3=0.22;l4=0.52;m2=6;m4=25;m5=45;m4c=9.6;m2c=2.8;m2b=2.8;Js2=0.02;Js4=0.28;pr=2100;t=0.3770:2*pi/50:4*pi+0.3770;for i=1:length(t);x1=t(i);A=-2*l1*l3*sin(x1)+2*l3*a;B=-2*l1*l3*cos(x1)+2*l3*b;C=-l2^2+l1^2+l3^2+a^2+b^2-2*l1*(b*cos(x1)+a*sin(x1));y=(A-sqrt(A^2+B^2-C^2))/(B-C);x3=2*atan(y);x2=asin((l3*sin(x3)-l1*sin(x1)/l2));x4=asin((l3*sin(x3))/l4);w2=(-w1*l1*sin(x1-x3))/(l2*sin(x2-x3));w3=(w1*l1*sin(x1-x2))/(l3*sin(x3-x2));w4=-(l3*w3*cos(x3))/(l4*cos(x4));c2=-(w1^2*l1*cos(x1-x3)-w2^2*l2*cos(x2-x3)+w3^2*l3)/(l3*sin(x2-x3 ));c3=(w1^2*l1*cos(x1-x2)+w2^2*l2-w3^2*l3*cos(x3-x2))/(l3*sin(x3-x2) );c4=(l4*w4^2*sin(x4)+l3*w3^2*sin(x3)-c3*l3*cos(x3))/(l4*cos(x4)); v=-l3*w3*sin(x3)-l4*w4*sin(x4);s=l3*cos(x3)+l4*(sqrt(1-(l3/l4*sin(x3))^2));c=-c3*l3*sin(x3)-l3*w3^2*cos(x3)-c4*l4*sin(x4)-l4*w4^2*cos(x4); F45x=m5*c+pr*1000;F2434x=F45x+m4c*w4^2*l4*cos(x4)+m4c*l4*c4*sin(x4);F2434y=(m4c*l4^2*c4-F2434x*l4*sin(x4))/(-l4*cos(x4));F2324y=(-m2c*l2^2*c2*l3*sin(x3)-F2434x*l2*l3*sin(x2)*sin(x3)-F243 4y*l2*l3*cos(x3)*sin(x2))/(l2*l3*cos(x2)*sin(x3)-l2*l3*cos(x3)*si n(x2));F2324x=(F2434x*l3*sin(x3)-F2324y*l3*cos(x3)+F2434y*l3*cos(x3))/(l 3*sin(x3));F21x=-F2324x-m2c*l2*c2*sin(x2)+m2c*w2^2*l2*cos(x2)-m2b*w1^2*l1;F21y=-F2324y-m2c*l2*c2*cos(x2)+m2c*w2^2*l2*sin(x2)+m2b*w1^2*l1*si n(x1);M=(F21x*l1*sin(x1)-F21y*l1*cos(x1))/1000;p(i)=s;q(i)=v;o(i)=c;u(i)=M;end% plot(t,p)% xlabel('曲柄转动的角度(rad)')% ylabel('滑块的位移(m)')% title('滑块位移图像')% plot(t,q)% xlabel('曲柄转动的角度(rad)')% ylabel('滑块的速度(m/s)')% title('滑块速度图像')% plot(t,o)% xlabel('曲柄转动的角度(rad)')% ylabel('滑块的加速度(m/s*s)')% title('滑块加速度图像')% plot(t,u)% xlabel('曲柄转动的角度(rad)')% ylabel('平衡力矩(KN*m)')% title('平衡力矩图像')八.主要参考资料【1】机械原理,孙恒,陈作模,葛文杰主编。
