CPFSK与Viterbi译码的实现和分析
基于FPGA的删除卷积码Viterbi软判决译码器的研究

基于FPGA的删除卷积码Viterbi软判决译码器的研究熊磊;姚冬苹;谈振辉;牟丹【期刊名称】《北京交通大学学报》【年(卷),期】2004(028)005【摘要】采用FPGA实现删除卷积码Viterbi软判决译码,与传统方式相比,提高了译码器的工作速度和可靠性,降低了功耗.在译码器的设计中,提出了"ACS全复用结构"和采用路径的相对量度取代绝对量度的方法,并得出了相对量度的上边界,从而有效地降低译码器的复杂度,使得利用单片FPGA芯片实现删除卷积码Viterbi软判决译码成为现实.对各种软判决的距离度量的计算方法进行了分析比较,得出了采用"1范数"和相关值取代欧氏距离最为合适.仿真结果表明,所设计的译码器具有良好的性能,与理论边界值只有0.2~0.4 dB的差距.【总页数】4页(P36-39)【作者】熊磊;姚冬苹;谈振辉;牟丹【作者单位】北京交通大学,电子信息工程学院,北京,100044;北京交通大学,电子信息工程学院,北京,100044;北京交通大学,电子信息工程学院,北京,100044;北京交通大学,电子信息工程学院,北京,100044【正文语种】中文【中图分类】TN911.22【相关文献】1.具有信道估计功能的Viterbi软判决译码器的FPGA实现 [J], 王培;倪天龙;王群生2.基于FPGA的卷积码Viterbi译码器性能研究 [J], 陈新永;杨瑞娟;肖玉芬;曾浩3.(2,1,7)卷积码Viterbi译码器FPGA实现方案 [J], 韩可;邓中亮;施乐宁4.基于FPGA的卷积码Viterbi编码/译码器的设计与实现 [J], 张成;杨健5.基于FPGA的卷积码Viterbi译码器实现方法 [J], 李明阳;柏鹏;屈鹏;张毓桐因版权原因,仅展示原文概要,查看原文内容请购买。
viterbi译码算法详解

viterbi译码算法详解Viterbi译码算法是一种常用的序列解码算法,广泛应用于语音识别、自然语言处理、通信等领域。
本文将详细介绍Viterbi译码算法的原理和步骤,以及它的应用。
Viterbi译码算法是一种动态规划算法,用于在给定观测序列的情况下,求解最可能的隐藏状态序列。
在这个过程中,算法会基于概率模型和观测数据,通过计算每个可能的状态路径的概率,选择概率最大的路径作为输出。
Viterbi译码算法的基本原理是利用动态规划的思想,将问题分解为一系列子问题,并利用子问题的最优解来求解整体问题的最优解。
在Viterbi译码算法中,我们假设隐藏状态的转移概率和观测数据的发射概率已知,然后通过计算每个时刻的最优路径来递推地求解整个序列的最优路径。
具体而言,Viterbi译码算法包括以下步骤:1. 初始化:对于初始时刻t=0,计算每个隐藏状态的初始概率,即P(x0=s)。
2. 递推计算:对于时刻t>0,计算每个隐藏状态的最大概率路径。
假设在时刻t-1,每个隐藏状态的最大概率路径已知,则在时刻t,可以通过以下公式计算:P(xt=s) = max(P(xt-1=i) * P(xi=s) * P(ot=s|xi=s))其中,P(xt=s)表示在时刻t,隐藏状态为s的最大概率路径;P(xt-1=i)表示在时刻t-1,隐藏状态为i的最大概率路径;P(xi=s)表示从隐藏状态i转移到隐藏状态s的转移概率;P(ot=s|xi=s)表示在隐藏状态s的情况下,观测到观测值为s的发射概率。
3. 回溯路径:在最后一个时刻T,选择概率最大的隐藏状态作为最终的输出,并通过回溯的方式找到整个序列的最优路径。
通过上述步骤,Viterbi译码算法可以求解出给定观测序列下的最可能的隐藏状态序列。
这个算法的时间复杂度为O(N^2T),其中N 是隐藏状态的个数,T是观测序列的长度。
Viterbi译码算法在实际应用中有着广泛的应用。
FEC前向纠错,卷积编码之维特比译码

FEC前向纠错,卷积编码之维特⽐译码因为要学习做WCDMA的流程解析,需要先提取卷积数据,⾸先就要做FEC卷积译码。
于是⽹上翻了好⼤⼀圈,特地学习了下viterbi译码算法,费很⼤⼒⽓才凑齐能够正确跑起来的代码,特记录⼀下。
说点题外话:viterbi是个⼈,全名Andrew J. Viterbi,⼀枚数学家,美国⾼通公司的创始⼈之⼀(没错,就是现在⼿机上那个⾼通芯⽚的⾼通),现代⽆线数字通讯⼯程的奠基⼈。
此外,viterbi算法不但可⽤来做卷积译码,另外⼀个⼴泛的应⽤是做股票证券量化预测计算(隐马模型预测)。
没错,就是⾼频量化交易炒股的算法基础。
美国量化对冲基⾦的传奇,⼤奖章基⾦背后的⽼板James Simons,⾸创将隐马模型预测⽤于炒股,也是⼀枚数学家。
两枚玩数学算法的巨富,谁说学数学算法没⽤的?FEC前向纠错译码⽤的viterbi算法代码摘抄⾃libfec,⾥⾯的实现很全⾯,还有mmx,sse加速版。
测试是做WCDMA,所以解交织和译码⽤的3GPP WCDMA的卷积编码参数(⼀帧编码长度262bits,卷积编码多项式是 r=1/2 k=9),我就只摘取了需要的viterbi29部分,有需要全部实现的同学可以⾃⾏去下载libfec。
下⾯是写来⽤于测试验证算法正确性的线程代码。
从IQ⽂件中⼀次读取2个float数,读取262+8(⼀帧viterbi译码长度)个数据后进⾏译码,若译码成功程序停在对应的测试断点上。
UINT CALLBACK ProcessIQDataThread(void *p_param){Convolution2Viterbi_t *p_sys = (Convolution2Viterbi_t *)p_param;vector<double> *p_data = NULL;int framebits = 262;struct v29 *vp;vector<float> uninter1;vector<float> uninter2;vector<float> radioFrame;vector<float> frameL;vector<float> frameR;vector<uint8_t> viterbi_in;uint8_t viterbi_out[33];uninter2.resize((framebits + 8));uninter1.resize((framebits + 8) * 2);viterbi_in.resize((framebits + 8) * 2);if ((vp = (struct v29 *)create_viterbi29_port(framebits)) == NULL) {return -1;}while (!p_sys->exit_thread){if (!p_data){WaitForSingleObject(p_sys->iq_data_event, 200);p_sys->iq_data_list.Lock();p_data = p_sys->iq_data_list.GetUse();p_sys->iq_data_list.UnLock();}if (!p_data)continue;// 读取2个浮点数for (int i = 0; i < p_data->size() / 2; i++){frameL.push_back(p_data->at(0));frameR.push_back(p_data->at(1));}// ⼀帧译码长度if (frameL.size() >= (framebits + 8)){// 解交织inter2deInterleavingNP(30, inter2Perm, frameL, uninter2);radioFrame.insert(radioFrame.end(), uninter2.begin(), uninter2.end());deInterleavingNP(30, inter2Perm, frameR, uninter2);radioFrame.insert(radioFrame.end(), uninter2.begin(), uninter2.end());if (radioFrame.size() >= (framebits + 8) * 2){// 解交织inter1deInterleavingNP(inter1Columns[1], inter1Perm[1], radioFrame, uninter1);radioFrame.clear();// 使⽤Viterbi算法做FEC译码for (int i = 0; i < (framebits + 8) * 2; i++){viterbi_in.push_back( ((int)uninter1[i] >> 24) );}init_viterbi29_port(vp, 0);update_viterbi29_blk_port(vp, viterbi_in.data(), framebits + 8);chainback_viterbi29_port(vp, viterbi_out, framebits, 0);#ifdef _DEBUG// 数据验证for (int i = 0; i < 33 - 4; i++) {if (viterbi_out[i] == 0x98 && viterbi_out[i + 1] == 0x54 && viterbi_out[i + 2] == 0xA0 && viterbi_out[i + 3] == 0x00) int bbb = 0;if (viterbi_out[i] == 0x05 && viterbi_out[i + 1] == 0x33 && viterbi_out[i + 2] == 0x00 && viterbi_out[i + 3] == 0x0c) int bbb = 0;if (viterbi_out[i] == 0x00 && viterbi_out[i + 1] == 0x03 && viterbi_out[i + 2] == 0xf4 && viterbi_out[i + 3] == 0x40) int bbb = 0;if (viterbi_out[i] == 0xc5 && viterbi_out[i + 1] == 0x80 && viterbi_out[i + 2] == 0x05 && viterbi_out[i + 3] == 0x5a) int bbb = 0;if (viterbi_out[i] == 0xe4 && viterbi_out[i + 1] == 0x00 && viterbi_out[i + 2] == 0x33 && viterbi_out[i + 3] == 0xe6) int bbb = 0;if (viterbi_out[i] == 0x72 && viterbi_out[i + 1] == 0x08 && viterbi_out[i + 2] == 0x38)int bbb = 0;if (viterbi_out[i] == 0xe2 && viterbi_out[i + 1] == 0x00 && viterbi_out[i + 2] == 0x38)int bbb = 0;}#endif}frameL.clear();frameR.clear();}p_sys->iq_data_list.Lock();p_sys->iq_data_list.PushEmpty(p_data);p_data = p_sys->iq_data_list.GetUse();p_sys->iq_data_list.UnLock();}return 0;}解交织 Interleaving.h#pragma once#include <vector>#include <assert.h>const int inter1Columns[4] = {1, // TTI = 10ms2, // TTI = 20ms4, // TTI = 40ms8 // TTI = 80ms};// 25.212 4.2.5.2 table 4: Inter-Column permutation pattern for 1st interleaving:const char inter1Perm[4][8] = {{0}, // TTI = 10ms{0, 1}, // TTI = 20ms{0, 2, 1, 3}, // TTI = 40ms{0, 4, 2, 6, 1, 5, 3, 7} // TTI = 80ms};// 25.212 4.2.11 table 7: Inter-Column permutation pattern for 2nd interleaving:const char inter2Perm[30] = { 0,20,10,5,15,25,3,13,23,8,18,28,1,11,21,6,16,26,4,14,24,19,9,29,12,2,7,22,27,17 };/* FIRST steps two pointers through a mapping, one pointer into the interleaved* data and the other through the uninterleaved data. The fifth argument, COPY,* determines whether the copy is from interleaved to uninterleaved, or back.* FIRST assumes no padding is necessary.* The reason for the define is to minimize the cost of parameterization and* function calls, as this is meant for L1 code, while also minimizing the* duplication of code.*/#define FIRST(UNINTERLEAVED,UNINTERLEAVEDP,INTERLEAVED,INTERLEAVEDP,COPY) \assert(UNINTERLEAVED.size() == INTERLEAVED.size()); \unsigned int rows = UNINTERLEAVED.size() / columns; \assert(rows * columns == UNINTERLEAVED.size()); \const char *colp = permutation; \float *INTERLEAVEDP = &INTERLEAVED[0]; \for (unsigned i = 0; i < columns; i++) { \float *UNINTERLEAVEDP = &UNINTERLEAVED[*colp++]; \for (unsigned int j = 0; j < rows; j++) { \COPY; \UNINTERLEAVEDP += columns; \} \}/** interleaving with No Padding */void interleavingNP(const unsigned int columns, const char *permutation, vector<float> &in, vector<float> &out) {FIRST(in, inp, out, outp, *outp++ = *inp)}/** de-interleaving with No Padding */void deInterleavingNP(const unsigned int columns, const char *permutation, vector<float> &in, vector<float> &out) {FIRST(out, outp, in, inp, *outp = *inp++)}/* SECOND steps two pointers through a mapping, one pointer into the interleaved* data and the other through the uninterleaved data. The fifth argument, COPY,* determines whether the copy is from interleaved to uninterleaved, or back.* SECOND pads if necessary.* The reason for the define is to minimize the cost of parameterization and* function calls, as this is meant for L1 code, while also minimizing the* duplication of code.*/#define SECOND(UNINTERLEAVED,UNINTERLEAVEDP,INTERLEAVED,INTERLEAVEDP,COPY) \assert(UNINTERLEAVED.size() == INTERLEAVED.size()); \int R2 = (UNINTERLEAVED.size() + columns - 1) / columns; \int padding = columns * R2 - UNINTERLEAVED.size(); \int rows = R2; \int firstPaddedColumn = columns - padding; \const char *colp = permutation; \float *UNINTERLEAVEDP = &UNINTERLEAVED[0]; \for (int i = 0; i < columns; i++) { \int trows = rows - (*colp >= firstPaddedColumn); \float *INTERLEAVEDP = &INTERLEAVED[*colp++]; \for (int j = 0; j < trows; j++) { \COPY; \INTERLEAVEDP += columns; \} \}/** interleaving With Padding */void interleavingWP(const int columns, const char *permutation, vector<float> &in, vector<float> &out){SECOND(in, inp, out, outp, *outp = *inp++)}/** de-interleaving With Padding */void deInterleavingWP(const int columns, const char *permutation, vector<float> &in, vector<float> &out){SECOND(out, outp, in, inp, *outp++ = *inp)}/*Determining the constants.From the standard we know:* All frame sizes for the BCH.* transport block is 246 bits* there are two radio frames, 270 bits each* TTI is 20 ms* SF is 256* parity word Li is 16 bits* For all downlink TrCH except BCH, the radio frame size is 2*38400/SF = 76800/SF.* For SF=256 that's 300.* For SF=4 that's 19200.* The maximum code block size for convulutional coding is 540 bits (25.212 4.2.2.2).* That corresponds to a radio frame size of 1080 bits, or a spreading factor of 71,meaning that the smallest spreading factor that can be used is 128.* 76800/128 = 600 coded bits -> roughly 300 data bits.* That corresponds to an input rate of roughly 30 kb/s at.* The maximum code block size for turbo coding is 5114 bits (25.212 4.2.2.2).* That corresponds to a radio frame size of 15342 bits, or a spreading factor of 5,meaning that the smallest spreading factor that can be used is 8.* 76800/8 = 9600 coded bits -> roughly 3200 data bits.* That corresponds to an input rate of roughly 320 kb/s.OK - SO HOW DO YOU GET HIGHER RATES?? HOW CAN YOU USE SF=4??A: Use the full 5114-but code block and then expand it with rate-matching.You still can't get the full ~640 kb/s implied by SF=4, but you get to ~500 kb/s.(pat) A: They considered this problem. See 25.212 4.2.2.2 Code block segmentation.In Layer1, after transport block concatenation, you then simply chop the result upinto the largest pieces that can go through the encoder, then put them back together after. From "higher layers" we are given:* SF: 4, 8, 16, 32, 64, 128, 256.* P: 24, 16, 8, 0 bits* TTI: 10, 20, 40 ms.To simplify things, we set:* TTI 10 ms always on DCH and FACH, 20 ms on PCH and BCH* BCH and PCH are always rate-1/2 convolutional code* DCH and FACH are always rate-1/3 turbo code* no rate-matching, no puncturing* parity word is always 16 bits* So the only parameter than changes is spreading factor.* We will only support 15-slot (non-compressed) slot formats.From our simplifications we also know:* For non-BCH/PCH TrCH there is one radio frame,76800/SF channel (coded) bits, per transport block.* DCH and FACH always use rate-1/3 turbo code,which has 12 terminating bits in the output.* For DCH and FACH, the transport block size is((76800/SF - 12)/3) - P = (25600/SF) - 4 - P data bits,where P is the parity word size.* Fix P=16 for simplicity and transport block size is (25600/SF) - 20.* for SF=256, that's 80 bits.* for SF=16, that's 1580 bits.* for SF=8, that's 3180 bits.* For PCH there is one radio frame,76800/SF channel (coded) bits, per transport block.* SF=64, for that's 1200 channel bits.* It's a rate-1/2 conv code, so that's 1200/2 - 8 - P data bits.* P=16 so that's 1200/2 - 24 = 576 transport bits. Really?*/#if 0const int inter1Columns[] = { 1, 2, 4, 8 };const char inter1Perm[4][8] = {{0},{0, 1},{0, 2, 1, 3},{0, 4, 2, 6, 1, 5, 3, 7}};const char inter2Perm[] = {0, 20, 10, 5, 15, 25, 3, 13, 23, 8, 18, 28, 1, 11, 21,6, 16, 26, 4, 14, 24, 19, 9, 29, 12, 2, 7, 22, 27, 17};vector<char> randomBitVector(int n){vector<char> t(n);for (int i = 0; i < n; i++) t[i] = random() % 2;return t;}void testInterleavings(){int lth1 = 48;int C2 = 30;for (int i = 0; i < 4; i++) {vector<char> v1 = randomBitVector(lth1);vector<char> v2(lth1);vector<char> v3(lth1);v1.interleavingNP(inter1Columns[i], inter1Perm[i], v2);v2.deInterleavingNP(inter1Columns[i], inter1Perm[i], v3);cout << "first " << i << " " << (veq(v1, v3) ? "ok" : "fail") << endl;}for (int lth2 = 90; lth2 < 120; lth2++) {vector<char> v1 = randomBitVector(lth2);vector<char> v2(lth2);vector<char> v3(lth2);v1.interleavingWP(C2, inter2Perm, v2);v2.deInterleavingWP(C2, inter2Perm, v3);cout << "second " << lth2 << " " << (veq(v1, v3) ? "ok" : "fail") << endl;}for (int lth = 48; lth <= 4800; lth *= 10) {TurboInterleaver er(lth);cout << "Turbo Interleaver permutation(" << lth << ") " << (permutationCheck(er.permutation()) ? "ok" : "fail") << endl; vector<char> er1 = randomBitVector(lth);vector<char> er2(lth);er.interleave(er1, er2);vector<char> er3(lth);er.unInterleave(er2, er3);cout << "Turbo Interleaver(" << lth << ") " << (veq(er1.sliced(), er3) ? "ok" : "fail") << endl;}}#endifviterbi译码partab实现 partab.c/* Utility routines for FEC support* Copyright 2004, Phil Karn, KA9Q*/#include <stdio.h>#include "fec.h"unsigned char Partab[256] = {0};int P_init = 0;/* Create 256-entry odd-parity lookup table* Needed only on non-ia32 machines*/void partab_init(void) {int i, cnt, ti;/* Initialize parity lookup table */for (i = 0; i < 256; i++) {cnt = 0;ti = i;while (ti) {if (ti & 1)cnt++;ti >>= 1;}Partab[i] = cnt & 1;}P_init = 1;}/* Lookup table giving count of 1 bits for integers 0-255 */int Bitcnt[] = {0, 1, 1, 2, 1, 2, 2, 3,1, 2, 2, 3, 2, 3, 3, 4,1, 2, 2, 3, 2, 3, 3, 4,2, 3, 3, 4, 3, 4, 4, 5,1, 2, 2, 3, 2, 3, 3, 4,2, 3, 3, 4, 3, 4, 4, 5,2, 3, 3, 4, 3, 4, 4, 5,3, 4, 4, 5, 4, 5, 5, 6,1, 2, 2, 3, 2, 3, 3, 4,2, 3, 3, 4, 3, 4, 4, 5,2, 3, 3, 4, 3, 4, 4, 5,3, 4, 4, 5, 4, 5, 5, 6,2, 3, 3, 4, 3, 4, 4, 5,3, 4, 4, 5, 4, 5, 5, 6,3, 4, 4, 5, 4, 5, 5, 6,4, 5, 5, 6, 5, 6, 6, 7,1, 2, 2, 3, 2, 3, 3, 4,2, 3, 3, 4, 3, 4, 4, 5,2, 3, 3, 4, 3, 4, 4, 5,3, 4, 4, 5, 4, 5, 5, 6,2, 3, 3, 4, 3, 4, 4, 5,3, 4, 4, 5, 4, 5, 5, 6,3, 4, 4, 5, 4, 5, 5, 6,4, 5, 5, 6, 5, 6, 6, 7,2, 3, 3, 4, 3, 4, 4, 5,3, 4, 4, 5, 4, 5, 5, 6,3, 4, 4, 5, 4, 5, 5, 6,4, 5, 5, 6, 5, 6, 6, 7,3, 4, 4, 5, 4, 5, 5, 6,4, 5, 5, 6, 5, 6, 6, 7,4, 5, 5, 6, 5, 6, 6, 7,5, 6, 6, 7, 6, 7, 7, 8,};fec.h/* User include file for libfec* Copyright 2004, Phil Karn, KA9Q* May be used under the terms of the GNU Lesser General Public License (LGPL)*/#ifndef _FEC_H_#define _FEC_H_#ifdef __cplusplusextern "C" {#endif/* r=1/2 k=9 convolutional encoder polynomials */#define V29POLYA 0x1af#define V29POLYB 0x11dvoid *create_viterbi29_port(int len);void set_viterbi29_polynomial_port(int polys[2]);int init_viterbi29_port(void *p, int starting_state);int chainback_viterbi29_port(void *p, unsigned char *data, unsigned int nbits, unsigned int endstate); void delete_viterbi29_port(void *p);int update_viterbi29_blk_port(void *p, unsigned char *syms, int nbits);void partab_init();static inline int parityb(unsigned char x) {extern unsigned char Partab[256];extern int P_init;if (!P_init) {partab_init();}return Partab[x];}static inline int parity(int x) {/* Fold down to one byte */x ^= (x >> 16);x ^= (x >> 8);return parityb(x);}#ifdef __cplusplus}#endif#endif /* _FEC_H_ */viterbi29_port.c/* K=9 r=1/2 Viterbi decoder in portable C* Copyright Feb 2004, Phil Karn, KA9Q* May be used under the terms of the GNU Lesser General Public License (LGPL)*/#include <stdio.h>#include <stdlib.h>#include <memory.h>#include "fec.h"typedef union { unsigned int w[256]; } metric_t;typedef union { unsigned long w[8]; } decision_t;static union { unsigned char c[128]; } Branchtab29[2];static int Init = 0;/* State info for instance of Viterbi decoder */struct v29 {metric_t metrics1; /* path metric buffer 1 */metric_t metrics2; /* path metric buffer 2 */decision_t* dp; /* Pointer to current decision */metric_t* old_metrics, * new_metrics; /* Pointers to path metrics, swapped on every bit */decision_t* decisions; /* Beginning of decisions for block */};/* Initialize Viterbi decoder for start of new frame */int init_viterbi29_port(void* p, int starting_state) {struct v29* vp = p;int i;if (p == NULL)return -1;for (i = 0; i < 256; i++)vp->metrics1.w[i] = 63;vp->old_metrics = &vp->metrics1;vp->new_metrics = &vp->metrics2;vp->dp = vp->decisions;vp->old_metrics->w[starting_state & 255] = 0; /* Bias known start state */return 0;}void set_viterbi29_polynomial_port(int polys[2]) {int state;for (state = 0; state < 128; state++) {Branchtab29[0].c[state] = (polys[0] < 0) ^ parity((2 * state) & abs(polys[0])) ? 255 : 0; Branchtab29[1].c[state] = (polys[1] < 0) ^ parity((2 * state) & abs(polys[1])) ? 255 : 0; }Init++;}/* Create a new instance of a Viterbi decoder */void* create_viterbi29_port(int len) {struct v29* vp;if (!Init) {int polys[2] = { V29POLYA,V29POLYB };set_viterbi29_polynomial_port(polys);}if ((vp = (struct v29*)malloc(sizeof(struct v29))) == NULL)return NULL;if ((vp->decisions = (decision_t*)malloc((len + 8) * sizeof(decision_t))) == NULL) {free(vp);return NULL;}init_viterbi29_port(vp, 0);return vp;}/* Viterbi chainback */int chainback_viterbi29_port(void* p,unsigned char* data, /* Decoded output data */unsigned int nbits, /* Number of data bits */unsigned int endstate) /* Terminal encoder state */{struct v29* vp = p;decision_t* d;if (p == NULL)return -1;d = vp->decisions;/* Make room beyond the end of the encoder register so we can* accumulate a full byte of decoded data*/endstate %= 256;/* The store into data[] only needs to be done every 8 bits.* But this avoids a conditional branch, and the writes will* combine in the cache anyway*/d += 8; /* Look past tail */while (nbits-- != 0) {int k;k = (d[nbits].w[(endstate) / 32] >> (endstate % 32)) & 1;data[nbits >> 3] = endstate = (endstate >> 1) | (k << 7);}return 0;}/* Delete instance of a Viterbi decoder */void delete_viterbi29_port(void* p) {struct v29* vp = p;if (vp != NULL) {free(vp->decisions);free(vp);}}/* C-language butterfly */#define BFLY(i) {\unsigned int metric,m0,m1,decision;\metric = (Branchtab29[0].c[i] ^ sym0) + (Branchtab29[1].c[i] ^ sym1);\ m0 = vp->old_metrics->w[i] + metric;\m1 = vp->old_metrics->w[i+128] + (510 - metric);\decision = (signed int)(m0-m1) > 0;\vp->new_metrics->w[2*i] = decision ? m1 : m0;\d->w[i/16] |= decision << ((2*i)&31);\m0 -= (metric+metric-510);\m1 += (metric+metric-510);\decision = (signed int)(m0-m1) > 0;\vp->new_metrics->w[2*i+1] = decision ? m1 : m0;\d->w[i/16] |= decision << ((2*i+1)&31);\}/* Update decoder with a block of demodulated symbols* Note that nbits is the number of decoded data bits, not the number* of symbols!*/int update_viterbi29_blk_port(void* p, unsigned char* syms, int nbits) { struct v29* vp = p;decision_t* d;if (p == NULL)return -1;d = (decision_t*)vp->dp;while (nbits--) {void* tmp;unsigned char sym0, sym1;int i;for (i = 0; i < 8; i++)d->w[i] = 0;sym0 = *syms++;sym1 = *syms++;for (i = 0; i < 128; i++)BFLY(i);d++;tmp = vp->old_metrics;vp->old_metrics = vp->new_metrics;vp->new_metrics = tmp;}vp->dp = d;return 0;}。
关于基于Xilinx FPGA 的高速Viterbi回溯译码器的性能分析和应用介绍
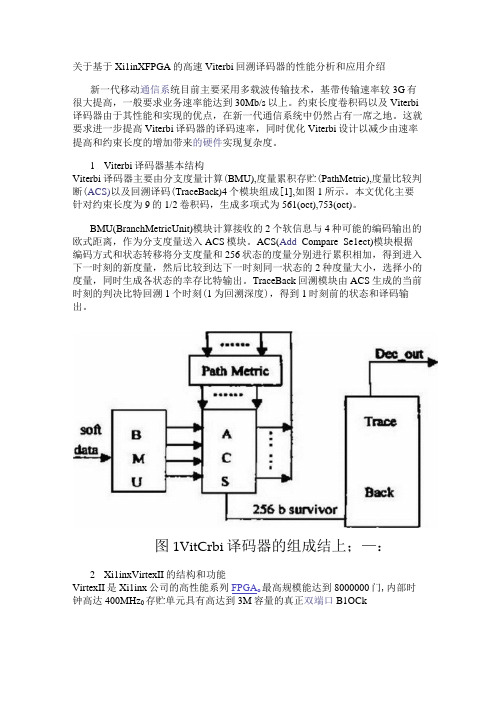
关于基于Xi1inXFPGA的高速Viterbi回溯译码器的性能分析和应用介绍新一代移动通信系统目前主要采用多载波传输技术,基带传输速率较3G有很大提高,一般要求业务速率能达到30Mb/s以上。
约束长度卷积码以及Viterbi 译码器由于其性能和实现的优点,在新一代通信系统中仍然占有一席之地。
这就要求进一步提高Viterbi译码器的译码速率,同时优化Viterbi设计以减少由速率提高和约束长度的增加带来的硬件实现复杂度。
1Viterbi译码器基本结构Viterbi译码器主要由分支度量计算(BMU),度量累积存贮(PathMetric),度量比较判断(ACS)以及回溯译码(TraceBack)4个模块组成[1],如图1所示。
本文优化主要针对约束长度为9的1/2卷积码,生成多项式为561(oct),753(oct)。
BMU(BranchMetricUnit)模块计算接收的2个软信息与4种可能的编码输出的欧式距离,作为分支度量送入ACS模块。
ACS(Add_Compare_Se1ect)模块根据编码方式和状态转移将分支度量和256状态的度量分别进行累积相加,得到进入下一时刻的新度量,然后比较到达下一时刻同一状态的2种度量大小,选择小的度量,同时生成各状态的幸存比特输出。
TraceBack回溯模块由ACS生成的当前时刻的判决比特回溯1个时刻(1为回溯深度),得到1时刻前的状态和译码输出。
图1VitCrbi译码器的组成结上;—:2Xi1inxVirtexII的结构和功能VirtexII是Xi1inx公司的高性能系列FPGA o最高规模能达到8000000门,内部时钟高达400MHz0存贮单元具有高达到3M容量的真正双端口B1OCkRamo 运算单元中包括最多168b 的专用乘法器。
VirtexII 中的可配置单元为C1B(Configurab1e1og ic B1occks)。
C1B 中的资源可以灵活配置成多种结构。
viterbi译码算法详解

viterbi译码算法详解Viterbi译码算法详解Viterbi译码算法是一种在序列估计问题中广泛应用的动态规划算法。
它被用于恢复在一个已知的输出序列中最有可能的输入序列。
该算法最初由Andrew Viterbi在1967年提出,并被广泛应用于各种领域,如语音识别、自然语言处理、无线通信等。
Viterbi译码算法的基本思想是在一个已知的输出序列中寻找最有可能的输入序列。
它通过计算每个可能的输入序列的概率,并选择概率最大的输入序列作为最终的估计结果。
该算法的关键是定义一个状态转移模型和一个观测模型。
状态转移模型描述了输入序列的转移规律,即从一个输入状态转移到另一个输入状态的概率。
观测模型描述了输入序列和输出序列之间的关系,即给定一个输入状态,产生一个输出状态的概率。
在Viterbi译码算法中,首先需要进行初始化。
假设有n个可能的输入状态和m个可能的输出状态,我们需要初始化两个矩阵:状态概率矩阵和路径矩阵。
状态概率矩阵记录了每个时刻每个状态的最大概率,路径矩阵记录了每个时刻每个状态的最大概率对应的前一个状态。
接下来,我们通过递归的方式计算状态概率和路径矩阵。
对于每个时刻t和每个可能的输入状态i,我们计算当前状态的最大概率和对应的前一个状态。
具体的计算方式是通过上一个时刻的状态概率、状态转移概率和观测概率来计算当前时刻的状态概率,并选择其中最大的概率作为当前状态的最大概率。
我们通过回溯的方式找到最有可能的输入序列。
从最后一个时刻开始,选择具有最大概率的状态作为最终的估计结果,并通过路径矩阵一直回溯到第一个时刻,得到整个输入序列的最有可能的估计结果。
Viterbi译码算法的优势在于它能够处理大规模的状态空间和观测空间。
由于使用动态规划的思想,该算法的时间复杂度为O(nmT),其中n和m分别为可能的输入状态和输出状态的数量,T为输出序列的长度。
因此,在实际应用中,Viterbi译码算法能够高效地处理各种序列估计问题。
通过Viterbi译码算法实现译码器优化实现方案

通过Viterbi译码算法实现译码器优化实现方案
1 引言
由于卷积码优良的性能,被广泛应用于深空通信、卫星通信和2G、3G移动通信中。
卷积码有三种译码方法:门限译码、概率译码和Viterbi算法,其中Viterbi算法是一种基于网格图的最大似然译码算法,是卷积码的最佳译码方式,具有效率高、速度快等优点。
从工程应用角度看,对Viterbi译码器的性能*价指标主要有译码速度、处理时延和资源占用等。
本文通过对Viterbi译码算法及卷积码编码网格图特点的分析,提出一种在FPGA设计中,采用全并行结构、判决信息比特与路径信息向量同步存储以及路径度量最小量化的译码器优化实现方案。
测试和试验结果表明,该方案与传统的译码算法相比,具有更高的速度、更低的时延和更简单的结构。
2 卷积编码网格图特点
图1所示为卷积编码网格图结构,图中每一状态有两条输入支路和两条输出支路。
2.1 输入支路的特点
任意一个状态节点Si都有两条输入支路,且这两条输入支路对应的源节点分别为:
此外,i为偶数时,两条输入支路的输入信息都为‘1’;i为奇数时,两条输入支路的输入信息都为‘0’。
2.2 输出支路的特点
任意一个状态节点Si都有两条输出支路,且两条输出支路对应的目的节点分别为:
此外,目的节点是Sj1的输出支路对应的输入信息都为‘0’;目的节点是Sj2的输出支路对应的输入信息都为‘1’。
3 Viterbi译码器的优化算法
3.1 判决信息比特与路径信息向量同步存储算法。
FPGA_ASIC-卷积码的Viterbi高速译码方案

投稿栏目:嵌入式与SOC——PLD CPLD FPGA应用卷积码的Viterbi高速译码方案A High-speed viterbi-decoding Scheme for Convolutional Code(1.南京师范大学分析测试中心,2.南京师范大学物理科学与技术学院)刘国锦1王济生2时斌1朱晓舒1(1. Analysis and Testing Center of Nanjing Normal University, 2. School of Physics and Technology of Nanjing Normal University) LIU Guo-jin1 WANG Ji-sheng2摘要:本文探讨了无线通信中广泛涉及的差错控制问题,介绍了卷积码的编译码原理。
提出了一种卷积码编码,及其高速Viterbi译码的实现方案,对译码的各个组成部分作了分析,并在FPGA中实现了该译码方案。
仿真结果表明,在纠正能力范围内,能够正确纠错并译码,且具有高速译码的优点,达到了预期的效果,该设计方案可以非常容易地应用到很多差错控制的通信系统中。
Abstract: This paper discusses the issue of error-control involved widely in wireless communications, and introduces the coding and endcoding principle of Convolutional Code. A scheme of encoding of Convolutional Code and its high-speed viterbi decoding is proposed, and the components of decoding are analysed, then the scheme is implemented in FPGA. The simulation result indicates that it can correct the error bits exactly within the range of capability error-correcting, and it has the advantage of high-speed decoding. Prospective effect is realized.This design scheme can be applied easily in many communication systems with error-control.关键词:差错控制;卷积码;Viterbi译码;寄存器交换Key words: error-control; Convolutional Code; viterbi decoding; register-exchange中图分类号:TN492 文献标识码:A0 引言在无线通信过程中,由于信道中噪声干扰的存在,会不可避免地造成发送端的码元经过有噪信道到达接收端后,接受的码元中发生了差错,从而影响了无线数据通信的可靠性。
高速VITERBI译码器的优化和实现

摘要:大约束度卷积码作为信道纠错编码在通信中得到了广泛的应用,而其相应的Viterbi 译码器硬件复杂度大,限制了译码速度。
分析了Viterbi译码器的结构,优化了各模块,合理地组织了存储器结构,简化了接口电路。
用FPGA实现Viterbi译码器,提高了译码器速度。
关键词:卷积码Viterbi译码ACS路径度量存储FPGA实现Viterbi算法是一种基于最大后验概率的卷积译码算法,应用广泛。
CDMA的IS-95标准和WCDMA3GPP标准将卷积码作为高速实时数据传输的信道纠错编码,使Viterbi译码器成为移动通信系统的重要组成部分。
为保证纠错性能,卷积码结束度一般选择比较大的,在3GPP中规定约束度K=9。
出于实时性的考虑,移动通信系统中对译码时延的要求比较高,需要高速译码器的支持。
可是Viterbi译码算法的复杂度、所需存储器容量与结束长度成指数增长关系,成为限制译码器速度的瓶颈。
Viterbi译码器每解码一位信息位就需对2k-1个寄存器的状态进行路径度量,并对相应的存储单元进行读写。
这种情况下,可以采用状态路径存储单元分块的方法,以提高其译码性能,缺点是ACS单元与存储器之间的接口电路十分复杂,不易实现。
本文分析和优化了Viterbi译码器的结构,提出了一种FPGA实现方案,简化了接口电路,提高了速度。
用这种结构实现的单片集成译码器译码速率达350kbps、时钟频率30MHz。
以下先分析译碱器总体结构,然后对各模块设计和实现做详细说明。
1算法简述及译码器结构本文采用3GPP标准规定的K=9,码率r=1/2的(753,561)卷积码,卷积编码器送出的码序列C,经过信道传输后送入译码器的序列为R。
译码器根据接受序列R,按最大似然准则力图找出正确的原始码序列。
Viterbi译码过程可用状态图表示,图1表示2个状态的状态转移图。
Sj,t和Sj+N/2,t 表示t时刻的两个状态。
在t+1时刻,这两个状态值根据路径为0或者1,转移到状态S2j+1和S2j+1,t+1。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
C、本文安排
本文安排如下,第 II 部分给出 2CPFSK、 h=0.25 的 4CPFSK 等效基带的产 生和功率谱密度分析;第 III 部分讨论 h=0.25 的 4CPFSK 的 Viterbi 译码实现和 误码率分析。
4 4 44
m
决定相位 ������������ 。同样的,对于所以对于从
State_odd 到 State_even 的 16 条 路 径 , 有 16 个 标 准 状 态 , 为
Standard_odd_to_even(:, m, n) 对于每一个周期的接收符号,判断它是奇数还是偶数编号符号后,将确定它
化为:(π , − 3π , − π)程序运行结果示意图如下:
444
图 3 Viterbi 译码过程举例
随机产生 10000 个点,仿真得到 Viterbi 译码的误码率曲线为:
BER of 4CPFSK h=0.25 using Viterbi Decoding
0
10
-1
10
BER
-2
10
10-3
4
相同。 下面研究相位连续性对信号功率谱的影响。下面是 h=0.5,2CPFSK; h=0.25,
4CPFSK; h=0.25,4CPFSK 的功率谱密度(这些功率谱各自对自己归一化,频率 对符号周期归一化):
0
h=0.5 2CPFSK
h=0.25 2CPFSK
-10
h=0.25 4CPFSK
X: 1.001
,
π 4
,
−
π 4
,
π 4)
相位网格图由这两组状态交替组成。对于编号为奇数的符号,状态由
State_even变 为 State_odd; 对 于 编 号 为 偶 数 的 符 号 , 状 态 由 State_odd变 为
State_even。每一个状态将有四条入路径和四条出路径。
对于每一条路径,都对应一个标准符号。所以对于从State_even 到 State_odd
所对应的状态转换图。和 16 个标准符号之一作对比,求出各自的均方误差。对 于每一个当前状态节点,一共有 4 条如路径,这四条路径的“距离”定义为均方 误差和各条路径出发状态“权重”的和,选择 4 个“距离”中最小的作为本当前 状态的“权重”,并且记录路径来源。这就做完了一级“加比选”。直到最终 4
0
-0.2
-0.4
-0.6
-0.8
-1
-1
-0.5
0
0.5
1
In-Phase
h=0.25 2CPFSK Stellerplot 1
0.8
0.6
0.4
0.2
0
-0.2
-0.4
-0.6
-0.8
-1
-1
-0.5
0
0.5
1
In-Phase
h=0.25 4CPFSK Stellerplot 1
0.8
0.6
0.4
2、试产生 4 进制的 CPFSK,h=0.25,观察其功率谱,并编写维特比检测器, 统计其误码曲线
B、CPFSK 和 Viterbi 译码简介
CPFSK(Continuous-Phase Frequency Shift Keying),即连续相位频移键控, 射频信号相位连续的调制方式。其包络恒定,具有较小功率谱占用率。MSK 是 FSK 信号的相位始终保持连续变化的一种特殊方式。可以看成是调制指数为 0.5 的一种 CPFSK 信号。
= (−3, −1,1,3)
ℎ
=
������ ������
,为有理调制系数
������ −1
������������ = ������ℎ ∑ ������������ ,为累计相位
������ =0
将������0置为 0,可以直接产生调制信号。采用如下电平映射
符号比特
电平值
符号比特 电平值
10
+3
+
������������������)
由当前状态 n 和之前的状态 m 的差值决定������������,也就是频率(注意一旦差值 超过������,则要减去 2������;小于-������,则要加上 2������,来保证本符号相位的变化在集合
(3π , π , − π , π)中);由之前的状态
0.2
0
-0.2
-0.4
-0.6
-0.8
-1
-1
-0.5
0
0.5
1
In-Phase
图 1 CPFSK 星座图(h=0.5,2CPFSK;h=0.25,2CPFSK;h=0.25,4CPFSK)
可以看到,采用了 CPFSK 之后,相位连续变化,星座图上的信号点密集地 在圆上“跑”,不在分立的少数几个点之间跳变。这就是相位连续的表现。同时看
的 16 条路径,有 16 个标准状态,为Standard_even_to_odd(:, m, n), n 代表当前 状态编号,m 代表上一状态编号。由下面式子:
������(������)
=
exp (������������ℎ
������������(������
− ������������
������������������)
-4
10
-12
-10
-8
-6
-4
-2
0
2
4
Eb/n0
图 4 Viterbi 译码误码率曲线
可见,由于 CPFSK 的相位记忆特性,Viterbi 译码后的误码率较低。
5/5
1/5
CPFSK 与 Viterbi 译码的实现和分析
清华大学电子工程系 杨雨潇
2012/6/7
II 2CPFSK 与 4 CPFSK 的等效基带产生和功率谱密度分析
对于 CPFSK,主要特点是本个符号的初始相位是之前所有符号相位变化的累
积和,以此来保证相位连续。其等效基带数学表达式如下:
������(������)
2/5
CPFSK 与 Viterbi 译码的实现和分析
清华大学电子工程系 杨雨潇
2012/6/7
到,在同一进度调制的情况下,h 小,相位越连续。 同时可以看到,对于 h=0.25 的 2、4 进制 CPFSK,它们的星座图一样,这
是由于,对于 h=0.25 的 CPFSK,它们的相位变化都是(± π)的整数倍,所以轨迹
0
-1
00
+1
1
+1
01
-1
11
-3
表 1 二进制与四进制电平映射
随机产生 N=1000 个 0、1 值作为比特流,利用上面的式子可以得到调制信
号。画出三个星座图:
Quadrature Quadrature Quadrature
h=0.5 CPFSK Stellerplot 1
0.8
0.6
0.4
0.2
CPFSK 与 Viterbi 译码的实现和分析
清华大学电子工程系 杨雨潇
2012/6/7
CPFSK 与 Viterbi 译码的实现和分析
清华大学电子工程系 无 99 班 杨雨潇 2009011209 联系方式:yyx09@
I、介绍
A. 题目介绍
1、以等效基带的方式仿真一个过采样率为 10 的 2CPFSK,g(t)为非归零方 波,h 分别为 0.5(即 MSK)和 0.25,观察其功率谱
=
exp (������������ℎ ������������ (������−������������������ )
������������
+
������������������)
其中:
�������� + 1)������
������������为本个符号对应的电平值,对于 2 进制,������������ = (−1,1);对于 4 进制,������������
-20
Y: -22.75
X: 1.001 Y: -30.79
-30
X: 1.001
-40
Y: -33.68
PSD
-50
-60
-3
-2
-1
0
1
2
3
Normalized Frequency(Normalized to bit rate)
图 2 CPFSK 功率谱密度
首先整体上由于是复数基带,三个功率谱的正负频率略有不对称。 接下来,对比 2CPFSK 的 h=0.5 和 0.25 的图,发现 h=0.25 的旁瓣电平更低, 第一旁瓣为-30dB,比 h=0.5 的第一旁瓣-23dB 低约 7dB。所以,CPFSK 中,相 位越连续,带外功率谱越低,带外功率谱下降越快。这也是使用连续相位调制的 初衷之一。 对比 h=0.25 的 2CPFSK 和 4CPFSK 的图,发现对比特率归一化后,4CPFSK 的功率谱带外衰减更快,第一旁瓣为-33dB,约比 2CPFSK 的第一旁瓣-30dB 低约 3dB。这说明多进制 CPFSK 调制的带宽更窄,频谱效率越高。4 进制的频谱利用 率为 2 进制的 2 倍,功率谱下降恰好约为 3dB,这两者之间有无必然联系需要进 一步研究。
3/5
CPFSK 与 Viterbi 译码的实现和分析
清华大学电子工程系 杨雨潇
2012/6/7
