Matlab范例_飞行航程计算
matlab飞机轨迹代码

matlab飞机轨迹代码
编写飞机轨迹的 MATLAB 代码涉及许多复杂的数学和物理概念,这需要考虑飞机的速度、加速度、风阻等因素。
以下是一个简单的
示例,展示了如何使用 MATLAB 绘制一个简单的飞机轨迹。
matlab.
% 飞机轨迹示例代码。
% 飞机的初始位置。
x0 = 0;
y0 = 0;
% 飞机的速度和方向。
v = 100; % 假设飞机速度为100单位/时间。
theta = pi/4; % 假设飞机方向为45度(以弧度表示)。
% 飞机飞行的时间。
t = 0:0.1:10; % 假设飞行时间为10个时间单位,每0.1个时间单位取一个点。
% 飞机的轨迹方程。
x = x0 + v cos(theta) t; % 飞机的x坐标随时间变化。
y = y0 + v sin(theta) t; % 飞机的y坐标随时间变化。
% 绘制飞机轨迹。
plot(x, y, 'b-'); % 绘制飞机轨迹,线条颜色为蓝色。
xlabel('X 坐标'); % x轴标签。
ylabel('Y 坐标'); % y轴标签。
title('飞机轨迹'); % 图表标题。
这段代码创建了一个简单的飞机轨迹模拟,假设飞机以固定速度和方向飞行。
实际上,真实的飞机轨迹涉及更多复杂的因素,比如飞机的加速度、风速和风向等。
如果你需要更复杂的飞机轨迹模拟,你可能需要使用更复杂的数学模型和物理模拟来实现。
数学实验飞行航程计算实验报告
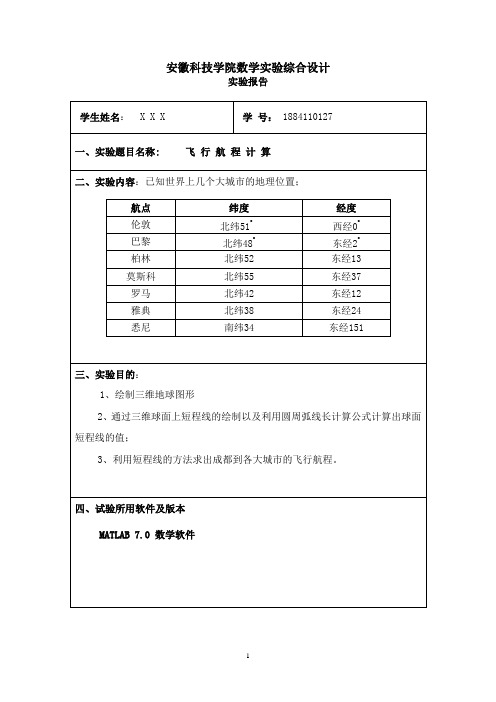
通过对本实验的整体操作,运行。使得我们学会了如何运用数学软件来解决现实生活中所存在的实际问题,同时对于实验的细节,我们也熟悉的掌握了数学软件的操作方式,对于图形的绘制,函数的运用,程序的汇编,以及简单问题的处理方法。不过对于软件的性能及其他用途运用还比较生疏,以后多加操作练习,更好地掌握MATLAB这款数学软件。
2、在图形上通过经纬度确定各大城市的具体位置。
3、球面短程线是过球面上两点P1和P2以及坐标原点O的平面与球面的交线,由于P1、P2在截平面上,故利用圆周上弧线长的计算公式可以计算出球面短程线的近似值。
六、模型假设与变量符号说明:
模型假设:将地球视为半径为R=6400(km)的球体。假设飞机在一万米高空平稳飞行,则应该以6410代替上面的数据。设球面上两点分别为:
七、模型建立与求解(算法,程序):
1、绘制三维球形
由于θ-φ平面矩形区域上的点与球面上的点可建立1-1对应。故将矩形域作剖分
θ=θi(i =1,…,m),φ=φj(j =1,…,n)
所形成的网线将对应于球面上的经线和纬线。所以形成R2R3的映射,由网格点(θi,φj)对应于球面上点(xij,yij,zij),映射关系如下
P1(x1,y1,z1),P2(x2,y2,z2)
则球面上过P1和P2两点的短程线长度计算公式为
L = R×α
变量符号说明:其中,α是从球心指向P1,P2两点的两向量的夹角(弧度),即
cosα= (x1,y1,z1)·(x2,y2,z2) / ( ||(x1,y1,z1)|| ||(x2,y2,z2)|| )
6、成都到雅典的飞行航程:D17 = 7.2456e+003
7、成都到悉尼的飞行航程:D18 = 4.4430e+003
matlab实验二飞行航程计算

其中, 是OP1与OP2之间夹角(单位:弧度)
4/10
经纬度转换为地心直角坐标公式
θ是P点处球面法线和赤道面的夹角(– 90o ~ +90o).向北 取正为北纬,向南取负为南纬. φ是P点与地球自转轴所 在平面与起始子午面的夹角(– 180o ~ +180o).由起始子
午线起算,向东取正为东经,向西取负为西经。
经度
ER 的球面上 P1(x1,y1,z1)和P2(x2,y2,z2),
x1 x 2 y1 y2 z1 z 2 cos 2 R x1 x2 y1 y2 z1 z 2 arccos( ) 2 R
球面短程线长度计算公式 L =
R×
新航线飞越北极,途经俄罗斯、加拿大两国.加拿大 航空管理部门官员称: 新航线至少节约了四小时飞行 时间。
2/10
假设:飞机飞行高度为10km,飞行速度为每小时980 公里;地球半径为6400km 新航线(飞越北极) 航程: 10914.77(km) 飞行时间:11.14(h) 航点 纬度 北京 N40o 纽约 N41o
6/10
航点 纬度
北京 N40o
上海 N31o
东京 N36o
旧金山 N37o
纽约 N41o
经度
E116o
E122 o
E140 o W123 o W76o
太平洋航线航程 直飞航线航程 航程差
7/10
思考问题
1. 根据“北京时间2002年9月27日14点,航班从北京 起飞,纽约时间9月27日15点30分,降落在纽约” 这段消息,分析两地经差和时差,计算飞行时间。 2. 如果飞机时速为980公里/小时,则两条飞行航线的 飞行时间差异是多大(设旧航线上中转站不停) 3.数学实验所用的计算方法是近似方法,其误差跟哪 些参数有关?如何提高精度? 4.在互联网上利用“谷歌地球”(google earth),了解 电子地图,寻找“北京、纽约”的经纬度等数据。
航位推算源程序matlab

航位推算源程序matlab//2016年5月25//千岛湖//write by大灰狼#include<stdio.h>#include<stdlib.h>#include<math.h>#include<string.h>#include<time.h>#define N24//数据的列数,时间分为两列#define fearth(1/298.257)//定值:椭圆度#define Re6378137.0000//定值:椭圆半长轴#define navdt0.5//推算周期0.5秒#define Ang_Hud(3.14159265358979/180.0)//角度、弧度转换#define Hud_Ang(1/Ang_Hud)void main(){static char s[240000][50];//一次可读取120000行数据,进行120000推算static double D[30000000];long int num=0,i=0,j,t,K=0;double auv_pos_auto[]={118.9807861,29.5480167};//AUV的初始位置double Headi;//AUV当前航向角,单位度double for_speed;//AUV当前前向速度,单位米/秒double ror_speed;//AUV当前右向速度,单位米/秒double s1,c,vts_f,vts_r,vtc_r,vtc_f,L,RM,RN;FILE*fp,*fp1,*fp2;fp=fopen("lake.txt","r");fp1=fopen("GPS.txt","w");//创建文件fp2=fopen("result.txt","w");printf("---------------------提取的数据--------------------\n");while(1)//读入文本字符串{fscanf(fp,"%s",&s[num]);if(feof(fp))break;//printf("%s\n",s);//fprintf(fp1,"%s\n",s[num]);//输入检测num++;};fclose(fp);printf("----------------------------------------------------\n");printf("一共有%ld个数据,一共进行%ld次推算运算。
matlab飞行管理问题的模型求解及验证

文章标题:深度探讨MATLAB飞行管理问题的模型求解及验证摘要:MATLAB在飞行管理问题中的应用已经成为航空领域研究人员的重要工具。
本文将深入探讨MATLAB在飞行管理问题中的模型求解及验证,从简单到复杂,由浅入深地展示MATLAB在飞行管理问题中的应用。
一、MATLAB在飞行管理问题中的模型求解1. 简介在飞行管理问题中,MATLAB可以用于建立模型进行求解,例如飞机的动力学模型、导航模型和控制模型等。
2. 动力学模型求解通过MATLAB建立飞机的动力学模型,可以对飞机的运动进行精确描述,包括高度、速度和加速度等参数。
3. 导航模型求解利用MATLAB建立飞机的导航模型,可以对飞机的航线规划、转弯半径和航向角等进行精确计算。
4. 控制模型求解利用MATLAB建立飞机的控制模型,可以对飞机的稳定性和操纵性进行分析和优化。
二、MATLAB在飞行管理问题中的模型验证1. 验证原理在建立模型后,需要进行验证以确保模型的准确性和可靠性,MATLAB提供了丰富的工具和方法来进行模型验证。
2. 飞机动力学模型验证通过MATLAB进行飞机动力学模型的验证,可以对飞机的实际运动状态和模型预测进行比对,验证模型的准确性。
3. 飞机导航模型验证利用MATLAB进行飞机导航模型的验证,可以对飞机实际航线和模型计算结果进行比对,验证模型的可靠性。
4. 飞机控制模型验证通过MATLAB进行飞机控制模型的验证,可以对飞机的操纵响应和模型预测进行比对,验证模型的稳定性和操纵性。
三、总结和回顾1. 模型求解和验证的重要性在飞行管理问题中,模型求解和验证是确保飞机安全和高效运行的重要环节,MATLAB提供了强大的工具来进行模型求解和验证。
2. MATLAB在飞行管理问题中的应用前景随着航空技术的不断发展,MATLAB在飞行管理问题中的应用前景十分广阔,将继续发挥重要作用。
个人观点:MATLAB作为飞行管理问题的求解和验证工具,具有极大的优势和潜力。
Matlab技术在飞行器导航中的应用案例分享

Matlab技术在飞行器导航中的应用案例分享随着航空事业的迅猛发展,飞行器的导航系统越来越重要。
无人机、航天器和民航飞机等飞行器的导航精度要求越来越高,对导航算法的需求也变得更为复杂。
在这方面,Matlab技术发挥了重要的作用。
本文将通过几个实际案例,分享Matlab技术在飞行器导航中的应用。
案例一:无人机航迹规划无人机的航迹规划是一项关键任务,它确定了无人机的轨迹和航线。
Matlab具备强大的数学计算和图形绘制功能,可以帮助无人机航迹规划专家进行快速且精确的计算。
通过Matlab,专家可以编写航迹规划算法,并将其可视化展示。
这使得无人机航迹规划人员可以更好地理解无人机的轨迹,并做出优化点评。
案例二:卫星导航系统设计卫星导航系统是现代飞行器导航的核心,例如全球定位系统(GPS)。
在卫星导航系统设计中,Matlab被广泛用于信号处理、接收机设计和导航算法验证。
用Matlab编写的仿真程序可以模拟各种导航场景,并评估系统性能。
此外,Matlab还支持与硬件设备的接口,可以实现实时的导航算法验证。
案例三:传感器融合与状态估计在飞行器导航中,传感器融合和状态估计是至关重要的。
在传感器融合过程中,来自不同传感器的数据被整合,以获得更准确的飞行器状态信息。
而状态估计则是根据传感器融合结果推测飞行器的位置和姿态。
Matlab拥有丰富的滤波器设计和优化工具,可以帮助工程师实现高效且稳定的传感器融合与状态估计算法。
案例四:飞行器导航性能评估对飞行器导航性能的评估是及时优化和改进导航系统的有效手段。
Matlab提供了多种性能评估工具,如误差分析、性能指标计算和数据可视化等。
通过这些工具,工程师可以分析导航系统的弱点,并针对性地进行改进。
同时,Matlab还支持批量处理数据,使得对于大量导航数据的性能评估更为高效。
总结Matlab技术在飞行器导航中发挥了重要的作用。
它不仅帮助实现了高精度的航迹规划和卫星导航系统设计,还支持传感器融合与状态估计的优化以及导航性能的评估。
matlab2021asimulink飞机纵向飞行示例讲解

matlab2021asimulink飞机纵向飞行示例讲解摘要:1.MATLAB 和Simulink 简介2.飞机纵向飞行示例概述3.飞机纵向飞行模型的构建4.模型的仿真和结果分析5.总结与展望正文:一、MATLAB 和Simulink 简介MATLAB 是一款广泛应用于科学计算、数据分析和可视化的软件,其强大的矩阵计算能力为各种工程问题提供了解决方案。
而Simulink 是MATLAB 的一个子模块,主要用于动态系统的建模、仿真和分析。
通过Simulink,用户可以轻松地创建和模拟复杂的实时系统。
二、飞机纵向飞行示例概述飞机纵向飞行示例是MATLAB 和Simulink 在航空领域的一个典型应用,主要用于讲解飞机在垂直方向上的运动控制。
该示例以一个简单的飞机模型为基础,通过构建和仿真不同的控制律,分析飞机的纵向飞行性能。
三、飞机纵向飞行模型的构建1.构建飞机的物理模型:根据飞机的结构特点和工作原理,构建一个包含质量、弹性和阻尼器的飞机模型。
2.添加控制律:为了实现飞机的纵向飞行,需要编写相应的控制律,例如常见的PID 控制。
3.构建仿真环境:通过Simulink 搭建飞机模型和控制律的仿真环境,为后续的仿真和分析提供基础。
四、模型的仿真和结果分析1.仿真设置:设置仿真参数,如时间步长、求解器等,为仿真运行做好准备。
2.仿真运行:运行仿真环境,观察飞机在纵向上的运动状态,分析飞机的稳定性和控制性能。
3.结果分析:根据仿真结果,分析不同控制律对飞机纵向飞行性能的影响,提出改进措施。
五、总结与展望通过飞机纵向飞行示例的讲解,我们可以看到MATLAB 和Simulink 在航空领域的广泛应用。
通过仿真和分析,可以提高飞机的设计水平和飞行性能。
matlab飞行管理问题的模型求解及验证

matlab飞行管理问题的模型求解及验证【原创实用版】目录1.引言2.飞行管理问题的概述3.MATLAB 在飞行管理问题中的应用4.模型求解5.模型验证6.结论正文1.引言飞行管理问题在航空领域中具有重要意义。
如何有效地对飞行过程进行管理,关系到飞行的安全、舒适与经济性。
随着计算机技术的发展,使用 MATLAB 等数学软件工具求解飞行管理问题成为了研究热点。
本文将探讨 MATLAB 在飞行管理问题中的应用,并通过实例对模型求解及验证进行说明。
2.飞行管理问题的概述飞行管理问题涉及多个方面,如飞行轨迹优化、燃油消耗最小化、飞行安全性评估等。
在解决这些问题时,需要考虑多种因素,如气象条件、飞机性能、空域限制等。
因此,飞行管理问题具有较高的复杂性和综合性。
3.MATLAB 在飞行管理问题中的应用MATLAB 是一种强大的数学软件,可以用于构建、求解和验证飞行管理问题的模型。
MATLAB 提供了丰富的函数库和工具箱,如优化工具箱、曲线拟合工具箱等,为飞行管理问题的求解提供了便利。
4.模型求解以飞行轨迹优化问题为例,首先需要建立飞行模型,包括气象模型、飞机性能模型、空域模型等。
然后,利用 MATLAB 中的优化工具箱求解模型,得到最优飞行轨迹。
5.模型验证为了验证模型的有效性,需要对模型进行验证。
可以采用多种验证方法,如对比实测数据、与其他模型比较等。
以燃油消耗最小化问题为例,可以通过对比实测数据验证模型的准确性。
6.结论MATLAB 在飞行管理问题的模型求解及验证中发挥了重要作用。
通过构建飞行模型并利用 MATLAB 求解,可以有效地解决飞行管理问题。
同时,通过对模型进行验证,可以确保模型的准确性和可靠性。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
思考问题
1. 根据“北京时间2002年9月27日14点航班从北京起 飞,纽约时间9月27日15点30分在纽约降落”这段 消息,分析两地经差和时差,计算首次飞行时间。 2. 如果飞机时速为980公里/小时,则两条飞行航线的 飞行时间差异是多大(设旧航线上中转站不停) 3.数学实验所用的计算方法是近似方法,其误差跟哪 些参数有关?如何提高度数据。确定一条最佳环游航 线。
球面短程线长度计算公式 L =
R×
4/10
经纬度转换为地心直角坐标公式
x = R cosθ cosφ y = R cosθ sinφ z = R sinθ
航点 纬度 北京 N40o 上海 N31o 东京 N36o 旧金山 N37o 纽约 N41o
经度
E116o
E122 o
E140 o W123 o W76o
8/10
function skyway(p1,p2) city=[p1;p2]; theta=city(:,1)*pi/180;fai=city(:,2)*pi/180; x=cos(theta).*cos(fai); y=cos(theta).*sin(fai); z=sin(theta); t=linspace(0,1,20); xt=(1-t)*x(1)+t*x(2); yt=(1-t)*y(1)+t*y(2); zt=(1-t)*z(1)+t*z(2); r=sqrt(xt.*xt+yt.*yt+zt.*zt); xt=xt./r;yt=yt./r;zt=zt./r; plot3(x,y,z,'ro',xt,yt,zt,'b','linewidth',2)
新航线飞越北极,途经俄罗斯、加拿大两国.加拿大 航空管理部门官员称: 新航线至少节约了四小时飞行 时间。
2/10
假设:飞机飞行高度为10km,飞行速度为每小时980 公里;地球半径为6400km 新航线(飞越北极) 航程: 10914.77(km) 飞行时间:11.14(h) 航点 纬度 北京 N40o 纽约 N41o
9/10
《实验报告》用于表达数据和信息,基本要求: 数据和文字无涂改; 表达信息形式简洁清楚; 设计数据表格,反映实验结果 实验结果与分析——
获取了哪些数据,反映哪方面信息?
实验结论—— 实验数据的应用价值?现有数据是否足以支持实验 结论? 实验涉及的技术、原理(或数学模型)?
10/10
ห้องสมุดไป่ตู้
7/10
5.下面程序(mlab22)模拟北京到纽约两城市之间飞 行航线,试对程序中的语句作功能性注释 city=[40,116;31,122;36,140;37,-123;41,-76]; figure(1),sphere(24),colormap([1 1 1]) axis off,hold on p1=city(1,:);p2=city(5,:); skyway(p1,p2) figure(2),sphere(24),colormap([1,1,1]) axis off,hold on for k=1:4 p1=city(k,:);p2=city(k+1,:); skyway(p1,p2) end
5/10
北京纽约直飞航程计算(mlab21) city=[40,116;41,-76]; %city=[40,116;31,122;36,140;37,-123;41,-76]; R=6400+10; theta=city(:,1)*pi/180; 两地飞行距离:10993.77 fai=city(:,2)*pi/180; x=R*cos(theta).*cos(fai); y=R*cos(theta).*sin(fai); z=R*sin(theta); op=[x,y,z]; 电子地图数据: 11008km format bank Dmatrix=R*acos(op*op'/R^2)
飞行航程计算实验
问题背景与球面短程线
经纬度转换和实验任务
练习题和思考题 飞行航线演示程序
1/10
航程计算的问题背景
北京时间2002年9月27日14点, 国航CA981航班从首都国际 机场起飞 · · · · · · · · · · 当地时间9月27日15点30分,降落在纽约肯尼迪机场; “北京 纽约” 新航线正式开通。 在此之前,“北京 纽约” 航线为 北京 上海 东京 旧金山 纽约
经度
E116o
W76o
3/10
球面短程线计算公式
设地球半径 R =6400(km)
利用两城市的经纬度可算出球面上两点坐标
P1(x1,y1,z1)和P2(x2,y2,z2),
x1 x2 y1 y2 z1 z2 cos 2 R x1 x2 y1 y2 z1 z2 arccos( ) (单位:弧度) 2 R
