变分原理基础_讲义
弹性力学变分原理PPT课件

fiuikdv
tiuikds
s
ij
k ij
dv
V
S
V
并取
s ij
ij
fi (ui ui )dv ti (ui ui )ds
外荷载做功的增量: W
弹性体 应 变能增 量: V
对于弹性静力学问题,根据热力学第一定律:
W V
第21页/共83页
微元体在某一应变状态获得的应变能增量为
V fiuidv tiuids
V
V
其中,ui为弹性体变形过程中的位移增量。
利用高斯公式得:
fiδ uidv σij n jδ uids
弹性体应变能是状态函数,故上式积分与 路径无关。
对于线性问题,可假设在变形过程中应力、 应变分量等比例增长。
* ij
:
0
tij
(0
t
1)
* ij
:
0
t
ij
(0
t
1)
v
1
σ
* ij
δε
* ij
1
tσij εijt
0
0
1 2
σij εij
第27页/共83页
2. 余应变能、余应变能密度
对于单向拉伸问题
a
a
结论:变分运算和积分运算可以交换次序
第11页/共83页
四、泛函的驻值与极值
1、函数的驻值和极值
如果函数y(x)在x=x0的邻近任一点上的值都 不大于或都不小于y(x0),即
y(x)-y(x0)≤0或≥0
则称函数y(x)在x=x0处达到极大值或极小
值。极值的必要条件为
dy dx
0
第12页/共83页
变分法.doc讲解

§1 变分法简介作为数学的一个分支,变分法的诞生,是现实世界许多现象不断探索的结果,人们可以追寻到这样一个轨迹:约翰·伯努利(Johann Bernoulli ,1667-1748)1696年向全欧洲数学家挑战,提出一个难题:“设在垂直平面内有任意两点,一个质点受地心引力的作用,自较高点下滑至较低点,不计摩擦,问沿着什么曲线下滑,时间最短?”这就是著名的“最速降线”问题(The Brachistochrone Problem )。
它的难处在于和普通的极大极小值求法不同,它是要求出一个未知函数(曲线),来满足所给的条件。
这问题的新颖和别出心裁引起了很大兴趣,罗比塔(Guillaume Francois Antonie de l'Hospital 1661-1704)、雅可比·伯努利(Jacob Bernoulli 1654-1705)、莱布尼茨(Gottfried Wilhelm Leibniz,1646-1716)和牛顿(Isaac Newton1642—1727)都得到了解答。
约翰的解法比较漂亮,而雅可布的解法虽然麻烦与费劲,却更为一般化。
后来欧拉(Euler Lonhard ,1707~1783)和拉格朗日(Lagrange, Joseph Louis ,1736-1813)发明了这一类问题的普遍解法,从而确立了数学的一个新分支——变分学。
有趣的是,在1690年约翰·伯努利的哥哥雅可比·伯努利曾提出著名的悬链线问题 (The Hanging Chain Problem)向数学界征求答案,即,固定项链的两端,在重力场中让它自然垂下,问项链的曲线方程是什么。
在大自然中,除了悬垂的项链外,我們还可以观察到吊桥上方的悬垂钢索,挂着水珠的蜘蛛网,以及两根电线杆之间所架设的电线,这些都是悬链线(catenary )。
伽利略(Galileo, 1564~1643)比贝努利更早注意到悬链线,他猜测悬链线是抛物线,从外表看的确象,但实际上不是。
变分学讲义

变分学讲义
变分学是数学中的一个分支,主要研究函数的变化,通过对函数的微小的变化进行研究,得出函数最值及其性质的一门学科。
而“变分学讲义”就是介绍变分学基本概念及相关算法的一本教材。
下面对该讲义进行分步骤的阐述。
第一步:基本概念的介绍。
讲义首先介绍了变分学中的一些基本概念,例如自由度、泛函、变分、拉格朗日方程等等,这些概念是我们学习变分学的必备基础。
第二步:泛函及其变分。
教材接下来介绍了不同类型的泛函及其变分。
例如,长度泛函、曲线与面积泛函、最小曲面问题等等。
这些内容都是通过不同类型的泛函进行讲解的,让读者深入理解变分学的应用。
第三步:极值原理。
极值原理是变分学中最基础的理论之一,涉及到许多在力学、化学、物理等领域中使用的极值问题。
该讲义对此进行了详细的讲解,包括Euler-Lagrange方程及其应用、Legendre变换、Hamilton-Jacobi方程等等。
第四步:偏微分方程及变分原理。
除此之外,该讲义也介绍了偏微分方程及其与变分原理之间的联系。
利用变分原理可以求出偏微分方程的解,而偏微分方程也可以用来描述泛函的极值问题。
第五步:算法及应用。
最后,该讲义也介绍了许多变分学中的算法及其应用。
例如最小化算法、修正正交法等等。
这些算法可应用于不同领域,例如计算机图形学、机器学习、物理学等等。
综上所述,“变分学讲义”是一本介绍变分学基本概念及其相关算法的教材。
该讲义通过分步骤的方式,深入浅出地阐述了变分学的核心概念,可以帮助读者全面掌握变分学的理论基础及其应用。
通俗简易讲解变分问题ppt课件

• 世界上有两个学术中心,引起各国学者的 注意,一个是美国麻省理工学院的赖斯纳、 日本著名学者鹫津久一郎、卞学鐄等人, 另一个就是钱伟长等一批中国的科学家。
• 以往的变分原理工作,大都是凑出来的,即首先写 出泛函,再取驻值验证。所以每一个新原理的出现 都是一项重要成果。钱伟长试图找到系统的做法, 他首先从最小位能原理和最小余能原理出发,把约 束条件利用拉格朗日乘子引入泛函,从而先放松条 件,得到相应广义化的变分原理。在变分中可以把 待定的拉氏乘子确定下来,这是对建立广义变分原 理的泛函提出合乎逻辑的数学方法,无疑是一个重 要成果。
• 一直到1977年,国外的文献上才有这一方面的 论述。O.C·钦科维奇(Zienkiewicz)在《有限元 法》一书中明确地把Courant和Hilbert的经典著 作中有关变分约束条件,待定拉格朗日乘子法 加以讲解,应用到弹性力学变分原理中。比起 钱伟长1964年的工作已晚了13年。
补充几个概念
1
y'2 dx
l
,泛函
a 0
Fl
(x,
y,
y' )dx
ydx
0
•构造一个新函数 F y 1 y'2
λ —拉格朗日乘子。
根据降阶欧拉公式 :
F
y
'
F' y
'
C
y 1 y '2 y ' 2y '
C
2 1 y '2
y (1 y'2 ) y'2 C
1 y'2
数值的总个数)的待定问题,具有按分布 形式的节点及其一定的节点参数子区域 e称 为单元。
变分原理——精选推荐

§9 变分原理9.1 弹性变形体的功能原理学习要点:本节讨论弹性体的功能原理。
能量原理为弹性力学开拓了新的求解思路,使得基本方程由数学上求解困难的偏微分方程边值问题转化为代数方程组。
而功能关系是能量原理的基础。
首先建立静力可能的应力和几何可能的位移概念;静力可能的应力和几何可能的位移可以是同一弹性体中的两种不同的受力状态和变形状....................态,二者彼此独立而且无任何关系。
................建立弹性体的功能关系。
功能关系可以描述为:对于弹性体,外力在任意一组几何可能的位移上所做的功,等于任意一组静力可能的应力在与上述几何可能的位移对应的应变分量上所做的功。
9.1.1 静力可能的应力:假设弹性变形体的体积为V,包围此体积的表面积为S。
表面积为S 可以分为两部分所组成:一部分是表面积的位移给定,称为Su;另外一部分是表面积的面力给定,称为Sσ。
显然S=S u+Sσ假设有一组应力分量σij在弹性体内部满足平衡微分方程在面力已知的边界Sσ,满足面力边界条件这一组应力分量称为静力可能的应力。
静力可能的应力未必是真实的应力,................因为真实的应力还....................必须满足应力表达的变形协调方程...............,但是真实的应力分量必然是静力可能的应力。
.........为了区别于真实的应力分量,我们用表示静力可能的应力分量。
9.1.2 几何可能的位移:假设有一组位移分量u i和与其对应的应变分量εij,它们在弹性体内部满足几何方程在位移已知的边界S u上,满足位移边界条件这一组位移称为几何可能的位移。
几何可能的位移未必是真实的位移,因为真实的位移还必须在弹性体内部满足位移表示的平衡微分方程..........;在面力已知的边界..................。
但是,真实的位移必然是...S.σ.上,必须满足以位移表示的面力边界条件几何可能的。
附录2-变分原理
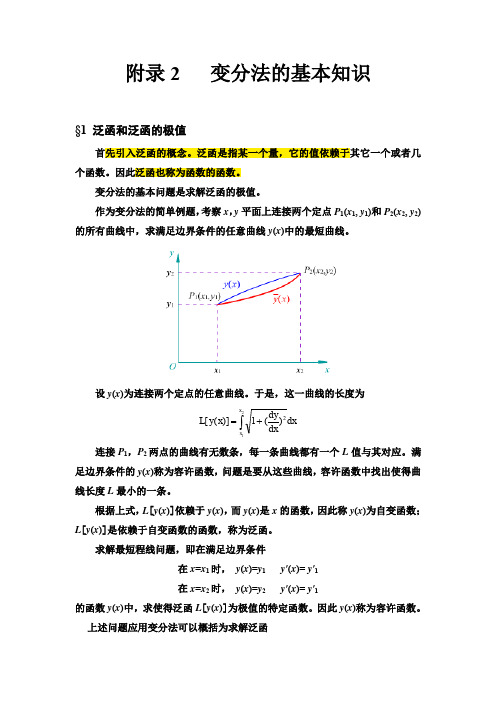
π/2
满足边界条件 y(0) 0 , y(π / 2) 1,试求泛函在什么曲线上取极值。 解:此泛函的欧拉方程为
2y
d (2 y) 0 dx
y y 0
通解:
y C1 cos x C2 sin x
根据边界条件,可得: C1 = 0, C2 = 1 所以
y sin x
δ( F1 F2 ) F2δF1 F1δF2
δ( F1 1 ) 2 ( F2δF1 F1δF2 ) F2 F2
δ( F ) n nF n1δF
§ 5 变分法的基本引理
引理 1:设函数 f ( x) 在区间[a, b]上连续,任意函数 g ( x) 在区间[a, b]上具有 n 阶连续导数,且对于某个正数 m(m = 0, 1, … , n),当满足条件
y´ = y( x) -y´ (x) = ´ (x)
应该注意y 与函数 y(x)的微分 dy 之间的差别,dy 是自变量 x 的改变量 dx 引起的 y(x)的无穷小增量。而变分y 是 y(x)的任意一个微小的改变量。 设泛函增量
J [ y ] F ( x, y , y ' )dx F ( x, y, y ' )dx
的函数 y(x)中,求使得泛函 L[y(x)]为极值的特定函数。因此 y(x)称为容许函数。 上述问题应用变分法可以概括为求解泛函
J [ y ] F ( x, y, y ' )dx
x1
x2
在边界条件 y(x1)=y1, y(x2)=y2 的极小值问题。
§ 2 泛函极值的必要条件-欧拉方程
假设函数 y(x)是使得泛函 J[y]为最小的特定函数(真实的)。变分法有兴 趣研究的是邻近于 y(x)的任意容许函数 y ( x) 引起泛函 J[ y ( x) ]的改变。设
弹性力学变分原理培训课件

弹性力学的基本方程
描述物体的物理性质与外 力的关系。
描述物体在变形过程中形 状的变化。
描述物体在力系作用下的 平衡状态。
平衡方程
几何方程
物理方程
02
变分原理概述
变分法的概念
最小作用量原理
在给定的约束条件下,物理系统的真实运动是使得作用量取极值的路径。
极值条件
在最小作用量原理中,物理系统的真实运动应满足欧拉方程和边界条件。
泛函与变分问题
泛函
泛函是一个函数,其值是另一个函数 在某个特定点上的值。
变分问题
变分问题是指求泛函的极值问题,即 在给定约束条件下,求泛函的极值。
欧拉方程与极值条件
欧拉方程
欧拉方程是变分问题的基本方程,它 描述了物理系统的运动规律。
极值条件
在求解欧拉方程时,需要满足极值条 件,即物理系统的运动应使得泛函取 极值。
实例解析
以有限元软件ANSYS为例,介绍如何使用有限元方法对弹 性问题进行建模、分析和求解。通过具体的实例操作,展 示如何将实际问题转化为有限元模型,并进行求解得到结 构的位移和应力分布。
THANKS
感谢观看
弹性力学变分原理培训课 件
• 弹性力学基础 • 变分原理概述 • 弹性力学中的变分原理 • 变分原理的应用 • 弹性力学变分原理的实例解析
01
弹性力学基础
弹性力学简介
弹性力学
一门研究弹性物体在外力作用下变形和内力的 学科。
弹性力学的重要性
为工程结构的设计、分析和优化提供理论基础。
弹性力学的发展历程
04
变分原理的应用
弹性力学问题的变分形式
弹性力学中的应力、应变和位移等物理量可以通过变分原理转换为对应的泛函极值 问题。
变分法基本原理

变分法基本原理【1】变分法(Variational method)是一种数学方法,用于解决泛函的极值问题。
泛函是把函数映射到实数的映射,而泛函的极值问题是要找到使得泛函取得极值的函数。
变分法广泛应用于物理学、工程学、应用数学等领域中的最优化问题。
【2】变分法的基本原理可以概括为以下几个步骤:步骤一:定义泛函首先,要明确定义所研究的泛函。
泛函可以是一个函数的积分、一个函数的级数或者其他数学表达式。
要根据具体问题的特点来选择合适的泛函。
步骤二:提出变分函数接下来,通过引入一个假设的函数(称为变分函数)作为泛函的自变量,使泛函成为这个变分函数的函数。
变分函数通常具有一定的约束条件,如满足特定边界条件或其他限制条件。
步骤三:计算变分利用变分函数的小扰动,即在该函数上加上一个小的修正项,计算泛函的变分。
变分是泛函在变分函数上的一阶近似变化率。
步骤四:应用欧拉-拉格朗日方程将变分代入到泛函中,得到泛函的表达式。
然后,通过应用欧拉-拉格朗日方程,将泛函转化为一个微分方程。
这个微分方程是通过对变分函数求导,然后令导数为零得到的。
步骤五:求解微分方程解决微分方程,得到最优解的表达式。
这个最优解是使得泛函取得极值的函数。
【3】变分法的基本原理是通过引入一个变分函数,将泛函的极值问题转化为求解一个微分方程的问题。
这种方法的优势在于可以将复杂的极值问题转化为求解微分方程的问题,简化了求解的过程。
【4】变分法在物理学中的应用非常广泛。
例如,它可以用于求解经典力学中的最小作用量原理,即通过将作用量泛函取极值来得到物体的运动方程。
此外,变分法还可以应用于量子力学中的路径积分方法、场论中的泛函积分等问题的求解。
【5】总之,变分法是一种数学方法,用于求解泛函的极值问题。
它的基本原理是通过引入一个变分函数,将泛函的极值问题转化为求解一个微分方程的问题。
变分法广泛应用于物理学、工程学、应用数学等领域,并具有很好的应用前景。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
变分原理基础罗建辉2009年夏季1 能量原理能量原理是以能量形式表述的力学定律。
概括地说,在所有满足一定的约束条件的可能状态中,真实状态应使其能量取极值或驻值。
本课程讨论结构力学、弹性力学、薄板的能量原理,只讨论线性平衡问题。
2 弹性系统真实平衡状态的能量特征举例从能量角度看,弹性系统的真实平衡状态具有如下的能量特征:即与其他可能状态相比,真实状态的能量为极值或驻值。
对这一能量特征举几个简例。
例0—1. 弹簧系统真实平衡状态的能量特征图0—1 所示为一弹簧下端挂一重物。
弹簧的刚度系数为k ,重物的重力为P 。
用∆表示位移,当弹簧系统处于平衡状态时,求得位移∆的真解为kP =∆=∆0)(真解 (1)真解的能量特征是弹簧系统的势能p ∏为极小。
现检验如下:∆-∆=∏P k p221 (2)式(2)右边第一项是弹簧的应变能,第二项是重力P 的势能。
系统势能p ∏是位移∆的二次式。
由式(2)得221()22pP Pk kk∏=∆--(3)现考察真解的能量特征。
显然,真解(1)使势能p ∏取极小值。
换一个角度,求p ∏的一阶及二阶导数,得Pk d d p-∆=∆∏ (4)22>=∆∏k d d p(5)将真解(1)代入式(4),得0=∆∏d d p,故知势能p∏为驻值。
根据式(5),又知势能p∏变分原理广义变分原理单变量形式多变量形式为极小值。
例0—2 超静定梁真实平衡状态的能量特征图0—2a 所示为一超静定梁,取图0—2b 所示静定梁为其基本结构。
根据平衡条件,基本结构的弯矩可表示为PMX M M +=11 (6)其中p M 是在荷载作用下基本结构的弯矩,1M 是在单位多余力11=X 作用下基本结构的弯矩,1X 是任意值。
式(6)同时也是超静定梁满足平衡条件的可能弯矩,由于1X 是任意参数,因此超静定梁的可能弯矩尚未唯一确定。
为了确定1X 的真解,还必须应用变形协调条件)(1111=∆+p X 真解δ (7)式中⎰=∆dxEI M M pp 11 (8)⎰=dxEIM 2111δ试验证真解的能量特征是梁的余能c ∏为极小值,余能c ∏的表示式为dxMX M EIdx EIMpc ⎰⎰+==∏2112)(212 (9)余能c ∏是1X 的二次函数,由式(9)得11111122211221212211112221111111111(2)21[2]21[2]21[()]2p c p p p p p p p p M X M M X M dxEIM dx M M dx M dx X X EIEI EIM dx X X EIM dx X EIδδδδ∏=++=++=+∆+=+∆-∆+⎰⎰⎰⎰⎰⎰(10)由式(10)可知变形协调条件(7)使余能c ∏取极小值。
换一个角度,求c ∏的一阶及二阶导数,得ppc X dx M MX M EIdXd 11111111)(1∆+=+=∏⎰δ(11)11212>=∏δdXd c(12)由于真解满足式(7),代入式(11),得01=∏dXd c ,故知余能c ∏为驻值。
根据式(12),又知余能c ∏为极小值。
3 基本能量原理两个基本原理:最小势能原理和最小余能原理。
对应于结构力学中的位移法和力法两种基本解法对应于弹性力学中的位移法和力法两种基本解法最小势能原理――在弹性平衡问题中,与一切满足位移边界条件(包括几何方程和位移边界条件)的可能位移相比,真实位移使势能为极小值。
最小余能原理――在几何连续问题中,与一切满足平衡条件(包括平衡微分程和外力边界条件)的可能应力(或可能内力)相比,真实应力(或真实内力)使余能为极小值。
基本能量原理提出得最早,起初是从物理概念上自然提出的,也称为自然能量原理。
其中的最小势能原理以位移为基本变量,最小余能原理以应力为基本变量。
总之,基本能量原理是取单类变量(位移或应力)作为基本变量的能量原理。
4广义变分原理结构力学和弹性力学中的混合解法其基本变量是混合型的,例如混合选取位移}{σ作为基本变量,又{u和应力}如混合选取位移}{σ作为基本变量。
总之,在混合解法中所选{ε、应力}{u、应变}取的基本变量不是单类变量,而是多类变量。
广义变分原理与之对应,在能量原理中也有混合变分原理,也称多类变量变分原理,也称广义变分原理,由基本能量原理推广而得到的能量原理。
广义变分原理中最常用的有两个,即Hellinger-Reissner变分原理(H-R原理)和胡海昌一鹫津变分原理(H-W原理)。
其中H-R原理以位移}{u和应力}{σ作为基本变量,H-W原理以位移}{σ作为基本变量。
{ε、应力}{u、应变}由基本能量原理推广而得到的能量原理。
5能量原理的外部和内部的对应关系学习能量原理时,要注意左右沟通、前后呼应,清晰地了解其中的经纬脉络和来龙去脉。
现指出以下几种对应关系,包括与其他学科之间的关系以及内部内容之间的关系。
1. 能量原理与泛函变分原理的对应关系本书讨论弹性结构静力分析的能量原理。
与它相关的学科还有结构动力分析的哈密尔顿原理,塑性力学的变分原理,流体力学某些问题的变分原理,最优控制问题的变分原理。
这些属于不同学科的原理各具特色,但在数学上都归属于泛函变分原理。
这里是个别与一般、具体与抽象的关系。
学习能量原理时要与泛函变分原理相联系,借鉴其通用的概念和方法,扩大视野。
(外部)2. 能量变分形式与微分方程形式的等价关系讨论弹性结构静力分析问题有两种表达形式。
通常作法是用微分方程和边界条件来表述,属于微分方程形式。
另一作法是用能量极值或驻值问题来表述,属于能量变分形式。
在一定条件下,能量变分形式与微分方程形式是等价的。
要了解两种形式的等价性及其适用条件。
对两种形式要进行沟通,由此及彼,能进能出。
还要比较其异同,了解其优点和缺点。
(内部)3. 能量解法与传统解法的对偶关系在传统解法中,我们学过位移法、力法和混合法。
在能量解法中,分别由势能原理、余能原理和广义变分原理导出的解法实际上与位移法、力法、混合法是等价的。
它们之间形成一种对偶关系。
运用对偶关系来学习能量原理,将收到事半功倍、学一知二的效果。
(内部)4.能量变分原理与近似解法(里兹法、有限元法)的源流关系有限元已经发展为广泛采用的工程分析工具,而能量原理是其理论基础。
有限元的发展离不开能量原理的指导,也丰富了原理的内容。
它们之间是源与流的关系。
欣赏源时要远望着流,欣赏流时要上溯到源。
5.各类能量原理之间的变换关系能量原理有多种类型,本书主要介绍其中四类,即最小势能、余能原理,H -R和H-W原理。
它们都归结为各自的能量驻值条件,可用统一形式来表述。
既要了解四类能量原理的各自特点,又要了解它们之间的相互关系,特别是由此及彼的变换关系。
把四类能量原理编成一个网,四通八达。
这样掌握的知识才能灵活驾取,运用自如。
参考文献[1] 胡海昌,弹性力学的变分原理及其应用,科学出版社,1981。
[2] 钱伟长,变分法及有限元(上册),科学出版社,1980。
[3] Washizu K., Variational Methods in Elasticity and Plasticity, Pergamon Press,1968, 1975, 1982 (1,2,3版)[4] 龙驭球,包世华. 结构力学教程(Ⅱ).北京: 高等教育出版社,2001[5] 卓永寿.弹塑性力学中的广义变分原理:2002年,第2版[6] 熊祝华,刘子廷.弹性力学变分原理:1988年[7] 罗建辉.弹性力学求解体系研究.湖南大学博士学位论文:2003年[8] 龙驭球,变分原理•有限元•壳体分析,辽宁科技出版社,1987。
[9] 彭旭麟,罗汝梅,变分法及其应用,华中工学院出版社,1983。
第一章 变分原理的基本概念-------能量原理与泛函变分原理的对应关系、泛函、变分的概念从数学角度看,能量原理属于泛函变分原理。
前者是典型的力学范例,后者是一般的数学形式。
为了说明数学概念的物理背景,我们结合梁的最小势能原理这个简例,引出泛函、变分和变分方法等概念。
1 一个简例――梁的最小势能原理例1—1梁的最小势能原理图1—1所示为一等截面简支梁,其抗弯刚度EI 为常数,梁上有分布荷载)(x q 作用。
按位移法求解。
以挠度函数)(x v 作为基本变量,求)(x v 的真解。
首先介绍通常作法。
由基本变量)(x v 可导出曲率κ和弯矩M 表示式2222d v dxd v M E Idxκ=-=- (13)利用平衡微分方程,可得到关于v 的控制微分方程:44=-q dxv d EI(14)边界条件分为两类,位移边界条件为0,0,0x v x l v ==== (15)力的边界条件为22220,0,0d v x M EIdxd v x l M EIdx==-===-=(16)根据微分方程(13)以及边界条件(14)和(15)即可求出)(x v 。
其次介绍能量法。
这里按最小势能原理来叙述。
图3按照位移法思路,仍以挠度)(x v 作为基本变量。
令)(x v 事先满足位移边界条件(14)。
隐含了位移的连续性。
这种位移称为可能位移。
写出弹性系统的势能p ∏的表达式,p ∏由梁的应变能U 和荷载的势能p U 两部分组成:dx dx vd EI dx k EI U ll222222⎪⎪⎭⎫⎝⎛==⎰⎰(17a)qvdxUlp⎰-=0(17b)dxqv dxv d EI UU lpp⎥⎥⎦⎤⎢⎢⎣⎡-⎪⎪⎭⎫⎝⎛=+=∏⎰22202(17c)在各种可能位移中,真实位移使势能为极小值=∏p 极值 真实位移即由势能极值条件求出。
2 由能量引出泛函的概念力学中的能量驻值原理,在数学中概括为泛函变分原理。
首先介绍泛函的概念,并与函数的概念加以比较。
式(17)中的三个能量U ,P U 和p ∏有一个共同特点,它们的值都依赖于所选取的函数)(x v 。
每给定一个函数)(x v ,就可确定它们的一个对应值,这是一种函数与变量之间的对应关系,自变量是函数,因变量是变量。
这种对应关系叫做泛函关系,而称p U U ,和p ∏为泛函,即以函数集)}({x v 为定义域的三个泛函,分别记为)]([)],([x v U x v U p 和)]([x v p ∏。
一般来说,设)}({x v 是已给的函数集。
如果对其中任一函数)(x v ,∏恒有某个确定的值与之对应,则称∏是依赖于)}({x v 的一个泛函,记为)]([x v ∏。
换句话说,泛函∏是依赖于函数)(x v 的函数,简言之,是函数的函数。
其中的函数)(x v 称为自变函数。
在上例中,挠度v 扮演了两个角色:在同一个挠度曲线上,v 是坐标x 的函数,v 因x 而变。
对于能量∏来说,)(x v 是∏的自变函数,∏因)(x v 而变。
