矩形波导的传输特性
矩形波导的特点

矩形波导的特点矩形波导是一种常见的电磁波传输器件。
它是由一对平行的金属板组成,中间夹着一段介质。
矩形波导可以传输高频电磁波,因为金属板可以防止电磁波向外辐射,而介质起到传输电磁波的作用。
矩形波导还有一些其他的特点,这篇文章将详细介绍矩形波导的特点。
1. 频率范围宽矩形波导的频率范围非常宽,一般从几千兆赫到几百兆赫都可以使用。
这意味着矩形波导可以用于传输多种高频电磁波。
在实际应用中,矩形波导被广泛用于微波通信、雷达、遥感、卫星通信、物联网等领域。
2. 低损耗矩形波导的传输损耗非常小,可以在长距离传输高频信号时保持很好的信号质量。
这是因为矩形波导中的介质可以降低电磁波的传输损耗,使其在传输时能够更好地保持信号的强度和功率。
3. 占用空间小相比于其他高频传输器件,矩形波导占用的空间非常小。
这是因为矩形波导是一种平面结构,可以将其与其他电路元件集成到一个小型电路板中。
这种特点使得矩形波导在微波通信、雷达、卫星通信等领域应用非常广泛。
4. 带宽宽矩形波导的带宽非常宽,可以传输多种不同频率的电磁波。
这是因为矩形波导的工作原理与传统的同轴电缆不同,矩形波导不需要套管,因此不会受到频率限制。
这种特点使得矩形波导在高速数据传输和宽带通信领域应用非常广泛。
5. 结构简单矩形波导的结构非常简单,由一对平行的金属板和中间的介质组成。
这种结构简单性使得矩形波导的制造成本非常低,且容易维护和升级。
这也是矩形波导被广泛应用的原因之一。
总之,矩形波导具有频率范围宽、低损耗、占用空间小、带宽宽、结构简单等特点。
这些特点使得矩形波导在微波通信、雷达、卫星通信、物联网等领域应用非常广泛。
矩形波导的传播特性

4
第九章 导行电磁波
矩形波导纵向电场 Ez ( x, y, z) Ez 0 ( x, y)e jkz z
kc2 =k 2 -kz2
k
z分量振幅满足标 2 E ( x, y ) 2 E ( x, y ) 2 z0 z0 k c E z 0 ( x, y ) 0 2 2 量亥姆赫兹方程 x y 设 Ez 0 ( x, y) X ( x)Y ( y) 将这个表达式代入上面方程并进行化简可以得到
其它模式开始出现,呈现多模式。
继续前面的讨论 a 2b
TE10
主模区
截 止 区
2a
a
c
1. 若波导的工作波长满足关系式 a 2a ,即可实现电磁波的 单模传输。单模传输的惟一模式就是 TE10 波。
2. TE10 波是矩形波导中的常用模式,称为主模。
2019/1/2
2 c 2 kc
电磁场理论
第九章 导行电磁波
以TM波为例来讨论: m n E z ( x, y , z ) E0 sin( x )sin( y )e jk z z a b
kz k 1 (
fc 2 ) f
kz 为实数, e jkz z 表示沿正z方向传播的波, (1)当 f fc 时, 波矢 kz为z方向的传播常数。 频率大于波导的截止频率的波能够在导波系统中传播。 kz 为虚数,e jkz z =ekz ( fc / f ) 1 ,表明这种波 (2)当 f f c 时, 是沿着z方向不断衰减的凋落场,不能正常传播。 频率低于波导的截止频率的波不能够在导波系统中传播。
c02 a 2, TE02
a 8cm b 4cm
矩形波导的特点

矩形波导的特点
矩形波导(Rectangular waveguide)是一种常用的传输微波能量的波导结构。
它具有以下特点:
1. 大功率承载能力:矩形波导的内部电场分布比较均匀,因此在相同的输入功率下,其最大输出功率较其他波导结构要高。
2. 低传输损耗:矩形波导的传输损耗比传输线要小,因为传输线上的电磁波要通过导线进行传输,而矩形波导中的电磁波只需要在金属面之间传播即可,传输效率更高。
3. 宽频带:矩形波导的宽度和高度可按一定的比例调节,以适应不同频率下的传输要求。
一般较宽的矩形波导具有更宽的工作频带。
4. 可靠性高:矩形波导结构简单,容易制造,结构稳定,因此具有较高的可靠性。
参考文献:
[1] 陈国强, 许海德. 波导与天线学[M]. 北京: 国防工业出版社, 1996.
[2] 孙利朝. 电磁场与微波技术[M]. 西安: 西安电子科技大学出版社, 2001.
[3] 李文琦, 刘国祥. 微波技术基础[M]. 北京: 电子工业出版社, 2005.。
矩形波导的特点

矩形波导的特点
矩形波导是一种常见的波导结构,其特点是可以在一定范围内传输多种类型的电磁波,具有相对较低的传输损耗和较高的抗干扰能力。
它广泛应用于微波电子学、通信、雷达、天线等领域中,是一种重要的无线电频率传输和控制装置。
矩形波导的特点主要包括以下几个方面:
第一,低传输损耗。
矩形波导的传输损耗相对较低,能够传输带宽较宽的高频信号和微波信号,可以达到几百GHz的工作
频率。
第二,高度可靠。
由于矩形波导采用金属材料制成,具有较高的机械强度和耐腐蚀性,因此在恶劣的环境条件下仍然能够稳定工作。
第三,抗干扰能力强。
在高频信号传输中,容易受到外界干扰,而矩形波导的结构本身就具有较高的屏蔽能力,因此对于外部噪声和干扰的抵抗能力比较强。
第四,结构简单。
矩形波导的结构比较简单,易于制造和安装,且成本相对较低。
第五,易于控制传输特性。
矩形波导的传输特性可以通过调整其尺寸和形状来实现控制,因此具有较高的灵活性和可调性。
综上所述,矩形波导作为电磁波传输的一种重要形式,具有多
种优越特性。
它被广泛应用于无线电通信、雷达、航天、天线等领域中,发挥着日益重要的作用。
微波技术基础中矩形波导传输特性教学方法研究

68海外文摘OVERSEAS DIGEST 海外文摘2021年第10期总第851期No.10,2021Total of 8511 介绍微波技术基础是电子信息类专业的专业基础课,主要讲授电磁波在各种传输线中的传播特性等知识。
矩形波导是一种很重要、很常用的微波传输线,因此在这门课程里,详细讲述了矩形波导中电磁波的传播方程、电磁波的传播条件以及传播特性参量等知识。
其中的传播特性参量主要有电磁波的频率、工作波长、截止波长、波导波长、相速、群速、特性阻抗以及模式等。
与在自由空间中传播时相比,电磁波在矩形波导中传播时,很多传输特性参量将产生变化,例如波长、相速以及群速等,其中的波长的变化最大,也最基础。
能够形象理解工作波长接近截止波长时电磁波在波导中的传播特性,对理解电磁波在矩形波导中的传输特性有很重要的意义。
传统的微波技术在这一部分的教学中,一般采用原理介绍以及公式推导的方式进行,导致学生对电磁波进入矩形波导后的性能变化没有直观的理解,影响其对此处知识的掌握。
传统的教学方式可以给出电磁波在波导中正常传播时,波导内的电场分布情况,但是没有给出工作在截止波长附近电磁波在波导内的电场分布情况,使学生不能对截止波长有比较形象的理解。
本文利用HFSS 软件辅助,针对工作在矩形波导截止波长附近的电磁波在波导内的传播特性进行建模,给出不同频率情况下电磁波在波导内的电场分布情况,从而使学生对截止模式以及传输模式有比较直观的理解,可以改善学生对矩形波导传输特性的理解程度[1-2]。
2 利用HFSS 软件辅助矩形波导传输特性教学微波技术基础中,电磁波在矩形波导中传播特点的理论基础比较清晰。
以标准的BJ-10波导为例,其宽边和窄边的尺寸为22.86mm×10.16mm。
因此其截止波长为宽边长度的2倍,也即45.72mm,换算成频率为6.56GHz,也即只有频率大于6.6GHz 的电磁波才能在波导中传播;低于此频率,波导处于截止状态,全反射。
第3章矩形波导

《微波技术》
Harbin Harbin Engineering Engineering University University
3-5 矩形波导
一、矩形波导中传输波型及其场分量 (一)TM波
d2 X ( x ) 2 + k X ( x) = 0 x 2 dx d 2Y ( y ) 2 k + yY ( y ) = 0 2 dy ⎫ ⎪ ⎪ ⎬ ⎪ ⎪ ⎭
Note:
k +k =k
2 x 2 y
2 c
通解为
X ( x ) = C1 cos k x x + C2 sin k x x Y ( y ) = C3 cos k y y + C4 sin k y y
Ez = − j Hz = 0 U sin x ⎟ sin ⎜ y ⎟ e β 0 ⎜ a ⎝ ⎠ ⎝b ⎠ ⎪ ⎪ ⎪ ⎪ ⎭
⎛ mπ ⎞ ⎛ mπ ⎞ ⎛ nπ ⎞ j(ω t − β z ) Ex = −U 0 ⎜ x ⎟ sin ⎜ y⎟e ⎟ cos ⎜ ⎝ a ⎠ ⎝ a ⎠ ⎝ b ⎠ ⎛ nπ ⎞ ⎛ mπ ⎞ ⎛ nπ ⎞ j(ω t − β z ) E y = −U 0 ⎜ ⎟ sin ⎜ x ⎟ cos ⎜ y⎟e ⎝ b ⎠ ⎝ a ⎠ ⎝ b ⎠
截止波数为
⎛ mπ ⎞ ⎛ nπ ⎞ kc = ⎜ ⎟ +⎜ ⎟ ⎝ a ⎠ ⎝ b ⎠
《微波技术》
2 2
Harbin Harbin Engineering Engineering University University
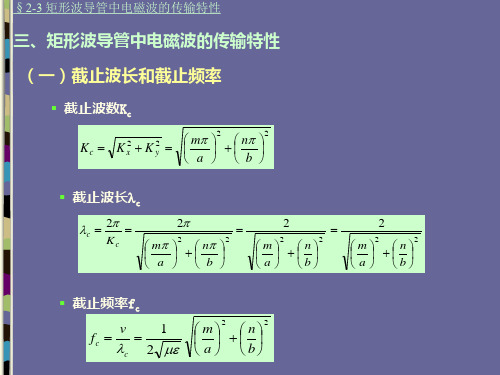
三、矩形波导管中电磁波的传输特性 微波技术基础 课件 PPT
2
1
m
2
n
2
a b
§2-3 矩形波导管中电磁波的传输特性——三、矩形波导管中电磁波的传输特性
❖ 简并现象:不同波型具有相同截止波长(或截止频率)的现象
简并波型的kc、fc、vg、vp以及g都是相同的 kc
o 一般情况下: ▪ TE0n和TEm0是非简并模(TM最低次模为TM11)
2 m 2 n 2 a b
矩形波导管管壁电流立体分布图
❖ 左右两侧壁的电流 ❖ 只有Jy分量 ❖ 大小相等,方向相同。
❖ 上下宽壁内的电流 ❖由Jz和Jx合成, ❖ 同一位置上下宽壁内的管壁电流大小 相等,方向相反。
§2-3 矩形波导管中电磁波的传输特性——四、矩形波导管的管壁电流
了解管壁电流的分布情况,对解决某些实际问题有帮助
ax
s
in
2
a
x dxdy
Em2 axb
2ZTE10
a sin 2
0
a
x dx ab
2ZTE10
Em2 ax
§2-3 矩形波导管中电磁波的传输特性——三、矩形波导管中电磁波的传输特性
▪ 功率容量Pbr:波导能够传输(承受)的最大允许功率(极限功率)
Emax Ey xa / 2 Ebr
a 0.7
b 0.4 ~ 0.5a
▪ 使用的波导已标准化:可根据需要选用
§2-3 矩形波导管中电磁波的传输特性——
四、矩形波导管的管壁电流
▪ 导行波在金属波导内壁表面上将感应出高频电流,称为管壁电流。
▪ 管壁电流如何分布?
假定内表面是理想导体, ▪ Js表示内表面上的表面电流密度矢量 ▪ H表示内表面处切线方向的磁场强度 ▪ an表示内表面法线方向的单位矢量
9-3矩形波导中的TE10波

a x b
y
y
Hz
a
Ey
Hx
x
电场线
磁场线
y
g
Hx
z
TE10 波电场强度振幅和磁 场强度振幅的空间分布(电 场和磁场合在一起)
传播方向垂直于电场方向
y Hz
Ey
电场方向垂直于磁场方向
2019/6/15
电磁场理论
8
第九章 导行电磁波
几种高次模的场分布
TE10
TE11
TE20
TE21
第九章 导行电磁波
电磁场理论
第9章 导行电磁波 9-3 矩形波导中的TE10波
2019/6/15
电磁场与电磁波
1
第九章 导行电磁波 复习9-2矩形波导的传播特性(1)
矩形波导截止频率:能够传输的最低频率 y
fc
=
2
kc
2
1
(m)2 (n)2 ab
b ,
x
a
z
频率大于截止频率的电磁波才能在矩形波导中传输。
ez
jkz (
a )H0
sin( a
x)
exH0
cos(
a
x)
2019/6/15
z x
电磁场理论
x
a
内壁电流
11
第九章 导行电磁波
TE10波的主要传播特性参数
截止频率
fc
=
c 2
(1)2 (0)2 c a b 2a
截止波长 c 2
(1)2 (0)2 =2a ab
纵向波矢 kz k 1 ( fc f )2 k 1 ( c )2 波导波波长 g 1 ( fc f )2 1 ( c )2
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Ex
kc2
m
a
E0
cos(
m
a
x)sin( n
b
y)e z
Ey
kc2
n
b
E0
sin(
m
a
x) cos( n
b
y)e z
Hx
j
kc2
n
b
E0
sin(
m
a
x) cos( n
b
y)e z
Hy
j
kc2
m
a
E0
cos(
m
a
x)sin( n
b
y)e z
其中:m,n取不同的值就对应着不同的模式。
3、矩形波导的传输特性
Et
1 kc2
(
jaˆz
t Hz )
j
kc2
(
H z y
aˆx
H z x
aˆy )
可得:
Ex
j
kc2
(
H z y
)
Ey
j
kc2
( Hz x
)
在 x=0 和 x=a 两个窄边上: Ey 0
Ey
j
kc2
( Hz x
)
Hz 0 x
Hz x
kx (Acos kx x
Bsin kx x)(C sin ky y
1 X
d2X dx2
1 Y
d2Y dy2
kc2
上式在0x a, 0y b 范围内任意位置都成立,只有等式左边两项均为常
数,即可得下列常微分方程:
1 X
d2X dx 2
kx2
1 Y
d2Y dy2
k
2 y
其中:k
2 x
k
2 y
kc2
解:
1 X
d2X dx 2
kx2
解:
1 Y
d2Y dy2
k
2 y
X (x) Asin kx x B cos kx x Y (x) C sin ky y D cos ky y
得到: B 0, D 0
kx
m
a
,
m 1, 2,...
ky
n
b
,
n 1, 2,...
综合起来 Ez 的解为:
Ez
E0sin
m
a
x
sin
n
b
y
e
z
其中: m,n均不能为零
电磁场的横向分量 由下式可以得到:
Et
1 kc2
(t Ez )
Ht
1 kc2
(
j aˆz
t Ez )
横向场分量:
综合起来 Hz 的解为:
Hz
H0cos
m
a
x
cos
n
b
y
e
z
其中:m,n不能同时为零,H0由波导的激励条件确定。
电磁场的横向由下式可以得到:
Et
j
kc2
(aˆz
t
Hz
)
Ht
1 kc2
(t Hz )
电磁场的横向分量:
Ex
j
kc2
n
b
H0
cos(
m
a
x)sin( n
b
y)e z
Ey
j
kc2
m
所以 Hz 的通解为:
Hz (Asin kx x B cos kx x)(C sin ky y D cos ky y)
其中:系数A、B、C 和 D ,及 kx 、ky由边界条件来确定。
边界条件:在 波导壁上,电场强度的切线分量为零。
已知:
Et
1 kc2
(t
Ez
jaˆz t Hz )
因 Ez 0 :
a
H0
sin(
m
a
x) cos( n
b
y)e z
Hx
kc2
m
a
H0
sin(
m
a
x) cos( n
b
y)e z
Hy
kc2
n
b
H0
cos(
m
a
x)sin( n
b
y)e z
其中:m,n取不同的值就对应着不同的模式。
b. TM波
在纵向(z向)只有电场分量,没有磁场分量,即: Hz 0
Ez满足的方程为:
2Ez x 2
截止频率:
fc
kc
2
2
1
(m)2 (n)2 ab
可见:不同的m和n对应的截止波长和截止频率也不同。
BJ32波导和BJ100波导不同波型的截止波长
波型 公式
TE10 TE20
2a a
TE01
2b
TE11 TM11
2 (1)2 (1)2 ab
BJ-32 c a 72.14mm 142.28 b 34.04mm
第7章 规则波导和空腔谐振腔
第一讲:规则波导中电磁波的一般特性 第二讲:矩形波导的传输特性 第三讲:矩形波导主模的传输特性 第四讲:圆形波导的传输特性 第五讲:空腔谐振器
1. 矩形波导的概念
矩形波导:指横截面为矩形的导体管道。
假设:波导管沿 z 方向均匀无限长, 管壁为理想导体,管内填充均 匀理想介质。
2Ez y2
kc2Ez
0
Ez 0
利用分离变量法可以得到 Ez 的通解为:
Ez ( Asin kx x Bcos kx x)(C sin ky y D cos ky y)
在波导的四个边上, Ez 满足切向电场为零的边界条件。
即: x 0 x a
y0 yb
Ez ( Asin kx x Bcos kx x)(C sin ky y D cos ky y) 0
72.4
BJ-100
45.72
a 22.86mm b 10.16mm
22.86
68.08 10.32
61.57 18.57
TE30 2a 3
TE21 TM21
2 (2)2 (1)2 ab
48.09
49.51
15.24
15.19
可以看出:不同尺寸的矩形波导中的不同模式具有不同的截止波长。
下图给出BJ100型波导(22.8610.16mm2)的截止波长。
TE20 TE01 TM11 TE30 TE21 TM21
TE10
单模
工作区域
截 止
区
0
1
2
3
4
5
c (cm)
可见:所有模式中TE10模的截止波长最长,截止频率最低,该模式称 为矩形波导中的主波型或主模,主模以外的其它模式均称为高次模。
工程上,通常要求波导中只传输一种模式,即单模传输,这个模 式通常为主模。
为了保证单模(主模)传输,工作波长应该满足:
c
TE10
c c
TE20
TE01
两者中的大的一个
即:
2a
a 2b
两者中的大的一个
工程上,波导尺寸已经标准化,可以参考工程手册。
Dcosky y)
0
可得: A 0
kxa m
kx
m
a
,
m 0,1, 2,...
在 y=0 和 y=b 两个宽边上
Ex
j
kc2
(
H z y
)
Hz 0 y
Ex 0
Hz y
ky( Asin kx x
B cos kx x)(C cos ky y
Dsin ky y)
0
可得: C 0
ky
n
b
,
n 0,1, 2,...
横截面的尺寸为 a b
注意:矩形波导中不能传输TEM波。
2. 传输波型及场分量的表达式
a. TE波
在纵向(z向)只有磁场分量,没有电
场分量,即:Ez 0H Nhomakorabea 0Hz 满足的方程为:
2Hz x2
2Hz y2
kc2 Hz
0
采用分离变量法求解,设: Hz X (x)Y ( y)
将Hz代入方程得:
(1)传播常数
不论是TE还是TM波,传播常数均为: kc2 k2
由
kc2
k
2 x
+k
2 y
得到: kc
k
2 x
+k
2 y
( m )2 ( n )2
a
b
传播常数:
kc2 k 2
[(m )2 (n )2 ] 2
a
b
(2)截止波长和截止频率
截止波长:
c
2
kc
2 (m)2 (n)2
ab
