95剪力分配法
结构力剪力分配法
二、基本假设(应用条件)
1. 横梁刚度无穷大 2. 工程上对 i梁 3 时也可应用
i柱
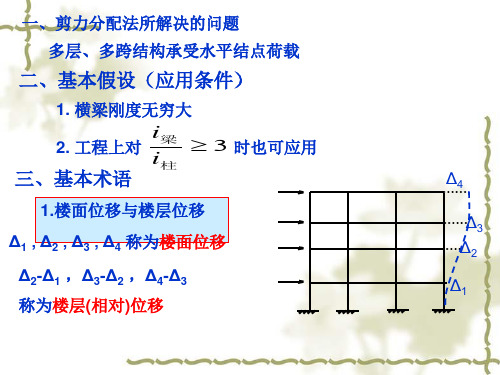
三、基本术语
1.楼面位移与楼层位移 Δ1 , Δ2 , Δ3 , Δ4 称为楼面位移
Δ2-Δ1 ,Δ3-Δ2 ,Δ4-Δ3 称为楼层(相对)位移
Δ4
Δ3 Δ2 Δ1
③分配剪力与5杆的轴力
V1
V2
1 48 3
16kN
V3
V4
1 48 12
4kN
N5
1 6
48
8kN
④分配弯矩
16
-16
4
-4
ቤተ መጻሕፍቲ ባይዱ
-8
32
32
32
16
16
-8
16
16 kNm
32
32
32
16
16
-8
48 48
16
16
16
-8
例题4 用剪力分配法计算如图所示的弯矩图,EI=常数,
10 kN/m
M AB
4i A
2i B
6EI L2
M BA
2i A
4i B
6EI L2
DAB
VAB
12EI L3
6EI L2
A
6EI L2
B
要解决以下问题:
1、杆件有转角时的侧移刚度是多少? 2、反弯点----弯矩为零的点在那?
由于横梁刚度无穷大,每根柱 视为两端固定杆 1、每根柱的侧移刚度12EI/L3 2、每根柱弯矩为零的点在正中----反弯点在中间。
V V
V
VH M 0
2
M
剪力分配法进行排架内力计算的步骤

剪力分配法进行排架内力计算的步骤剪力分配法进行排架内力计算,可真是一门有趣的学问!嘿,首先想象一下,建筑就像一位优雅的舞者,跳动在风中。
每个部分都在默默配合,谁都不想出错,这可真是考验团队合作的时刻。
那我们就来聊聊剪力分配法的步骤,轻松一点,让这个话题不再严肃。
想象一下,我们要在一个大型的舞台上布置演员,每个演员都要承担起自己的角色。
这时候,架构师就得考虑到每根梁和柱的负荷。
就像一个家庭聚会,大家都想尽量多吃一点,但要确保最后的披萨能分到每个人的手里。
剪力分配法的核心就是在这一点上:如何将剪力合理分配给每一个部分,确保它们都能稳稳当当地“站着”。
然后,咱们得了解这些力的来源。
想象一下,一场大雨来临,屋顶上雨水聚集,压力就增加了。
为了搞清楚这些力量的来源,我们需要进行静力平衡的分析。
就像是校对账本,所有的收入和支出都得清清楚楚,不能有漏网之鱼。
咱们得确定各个节点的剪力。
就像是推销员,在推销自己的产品时,得知道哪个客户需要什么。
每根梁的剪力,就像是每个客户的需求,必须精确。
我们通过计算,能得出每根梁上需要承担的剪力。
这个过程可得仔细,不能掉以轻心。
然后,我们就来分配这些剪力了。
哎,别小看这个步骤,它就像是给队伍分配任务,谁负责哪一块。
一般来说,我们会用比例分配的方式来计算,也就是说,看每根梁的支撑能力,然后按比例分配这些剪力。
别忘了,最终得保证所有的剪力总和是零,才能保证整个结构的稳定性。
咱们来聊聊内力计算。
这个就像是在算每个人的表现,得好好评估一下每个部分的承载能力。
通过计算内力,我们能更清晰地了解哪根梁有可能会“打瞌睡”,从而提前采取措施,避免发生意外。
咱们可不想看到“剧组”里的某个演员突然摔倒,得尽早预防呀!然后呢,还得考虑到各种可能的外部因素,比如风的吹袭、地震的颤动。
这些就像是意外的观众,突然跑来捣乱,得随时准备应对。
结构在设计的时候,得考虑到这些,才能确保在突发情况下依旧稳如老狗。
最终,我们得总结一下这些计算结果,确保所有的内力都是合理的。
9.4 无剪力分配法

BA
i
i 3
2i
1 7
,
BC
i
3 2i 3 2i
6 7
§9.4 无剪力分配法
固定结点时:柱AB的剪力是静定的 。 放松结点时:柱B端的分配弯矩乘以-1传到A端, AB
杆的弯矩为常数而剪力为0。
在力矩的分配传递过程中,柱中原 有的剪力保持不变而不增加新的剪力 —无剪力分配法。
EI
§9.4 无剪力分配法
§9.4 无剪力分配法
在结构力学的计算方法中,力矩分配法与无剪力分配法作为两种传统的方法, 在工程实际中得到了广泛的应用。从基本理论上讲,二者都是以位移法为理 论基础,以渐进法为解题方法。传统上二者的区别只是应用条件不同,分别 对应用于无侧移刚架和特殊的有侧移刚架。更准确的说,力矩分配法适用于 无结点线位移的刚架,无剪力分配法适用于凡有结点线位移的杆件都是剪力 静定的刚架。实际上力矩分配法与无剪力分配法本是一种方法,即力矩分配 法实际上包括了无剪力分配法。
弯矩图如图b。
求F点的竖向位移时,静定的基本体系如图c。
ΔFy
1 EI
Fl [ 1523l 10000 2
1 3
2l 3
1811l 2
2 3
2l 3
1155l 2
5 6
2l 3
511l 4 2l 770l 2 2l 896l 1 2l
Fl3
] 0.0476 ()
2 63 2 63 2 63
§9.4 无剪力分配法
图a 所示刚架,各横梁均为无侧移杆,各竖柱均为剪力静定杆。只 加刚臂阻止各结点的转动,不阻止其线位移,如图b。
9.5 剪力分配法
Z1,FS34
3i34 h2
Z1,FS56
3i56 h2
Z1
§9.5 剪力分配法
令
D1
3i12 h2
,D2
3i34 h2
,D3
3i56 h2
侧移刚度:即杆件发生单位侧移时,所产生的杆端剪力。
将剪力代入平衡条件,可求出线位移 从而可得各柱顶剪力为
Z1
F D1 D2
D3
F Di
剪力分配法:利用剪力分配系数求柱顶剪力的方法。
§9.5 剪力分配法
图a所示结构,荷载作用在柱上。将结构分解为只有结点 线位移和只有荷载q的单独作用,如图b、c所示。
图b中各柱的内力可查表得到,从而求出附加链杆上的反力F1。 图c可用剪力分配法进行计算。 原结构内力=图b结构的内力+图c结构的内力
§9.5 剪力分配法
弯矩图如图b
实际结构: 横梁刚度并非无穷大,各柱的 反弯点高度在不同处。当I梁/I柱 >5时计算结果足够精确。
当I梁/I柱逐渐减小时: 底层柱的反弯点位置逐渐升高; 顶部层柱的反弯点位置逐渐降低; 中间各层柱的反弯点位置在中点附 近。
剪力分配法的假设: 横梁刚度无穷大,各刚结点均无转角,各柱的反弯点在其高度 一半处。
由剪力可确定各竖柱的弯矩。
§9.5 剪力分配法
例9-6 试用剪力分配法求图a所示刚架竖柱的弯矩图。竖柱E 为常数。
解:为计算方便,设12EI/h3=1。 则上层各竖柱的侧移刚度为 D1=D2=D3=1
下层各竖柱(左到右)的侧移刚度为
D4
1,D5
12E 2I h3
2,D6
12E 2I (3h / 2)3
均布荷载剪力计算公式

均布荷载剪力计算公式
(实用版)
目录
1.均布荷载的概念及其计算方法的重要性
2.均布荷载的计算公式及其应用
3.均布荷载计算公式的局限性和未来的发展方向
正文
一、均布荷载的概念及其计算方法的重要性
均布荷载是指在建筑结构或工程部件上分布的荷载,其特点是大小和分布相对均匀。
均布荷载计算方法是工程设计和结构分析中非常重要的一环,因为它可以帮助我们更好地理解结构的受力情况,从而为设计出更加安全、稳定和经济的结构提供依据。
二、均布荷载的计算公式及其应用
均布荷载的计算公式通常根据结构的类型、尺寸和边界条件等因素来确定。
由于结构的特性和边界条件的不同,不可能有统一的计算公式,但有三个基本原则:1)荷载位于结构的中心;2)荷载在结构上的分布均匀;3)荷载的大小和方向不随时间变化。
在实际应用中,均布荷载的计算公式通常通过简化结构的模型,假设一些理想的条件,然后根据物理学原理推导得到。
例如,对于一个简单的均匀梁,其均布荷载的计算公式为:
Q = F / L
其中,Q 表示均布荷载,F 表示集中荷载,L 表示梁的长度。
三、均布荷载计算公式的局限性和未来的发展方向
尽管均布荷载计算公式在实际应用中具有很高的价值,但它也存在一
些局限性。
首先,均布荷载计算公式是基于理想条件下的简化模型,不能完全反映实际情况下结构的受力情况;其次,均布荷载计算公式的应用范围有限,对于复杂的结构和非均匀分布的荷载,计算结果可能会有较大的误差。
利用剪力分配法求解等高排架的探讨

出不动铰支座的 水平 反力 Ri ; 第二 步: 撤消 附加 的 不动 铰支 座,
n
! 并在此排架 柱 顶加 上 - R i , 然后 按 照剪 力分 配 系数 进行 分 i= 1
配; 第三步: 将以上两步中求出的内力叠加。
按照以上的三步可 以求出在任意荷载 作用下各柱柱顶剪 力。
在使用以上方法 的过 程中 发现 任意 荷 载( 包 括柱 顶 水平 集中 力 F) 作用时的计算过程包括 只有柱 顶水平 集中力 的计算过 程。但 在计算任意荷载时( 如果这些荷载中包 括柱顶水平 集中力 F ) , 对 于水平集中力 F 何时参与分 配或者 也作为任 意荷载 考虑则 容易 引起计算的混淆。比如是否先将柱顶水平集中力 F 分配 , 再将剩 余的作用力按照第 二步 进行 计算, 然后 叠加, 或 将除柱 顶水 平集
1
Vi =
!n
ui F = 1
i= 1 u i
iF 。
其中, V i 为第 i 根柱子的柱顶剪力; ui 为第 i 根柱子在单位
水平力作用下柱顶的水平位移; i 为第 i 根柱子的剪力分配系数。
2) 任意 荷载( 包括柱顶水平集 中力) 作用时, 计算分为 三个步
骤: 第一步: 先在排架柱 顶附加不动铰支座以 阻止水平位移, 并求
2 剪力墙的等效刚度计算
等效悬臂杆件 在倒 三角 形水平 荷载、均布 水平 荷载、顶 部集
中水平荷载作用 下只 考虑 弯 曲变 形时, 顶点 水平 位 移分 别按 式
( 1) ~ 式( 3) 计算。
u1= 11q maxH 4 / 120EcI c
( 1)
u2= q maxH 4 / 8EcI c
( 2)
1) 将柱顶水平集 中力 F 作为单 独作用 时, 先分配, 得到 各柱 顶剪力 Vi 1; 2) 计算没有柱 顶水平集中力 F 时其他任 意荷载作用 下的柱顶剪力 V i2 ; 3) 叠加上述剪力得到 V i = Vi 1+ V i2。
第六章位移法

第六章位移法学习目的和要求位移法是超静定结构计算的基本方法之一,许多工程中使用的实用计算方法都是由位移法演变出来的,是本课程的重点内容之一。
本章的基本要求:1.熟练掌握位移法基本未知量和基本结构的确定、位移法典型方程的建立及其物力意义、位移法方程中的系数和自由项的物理意义及其计算、最终弯矩图的绘制。
2.熟记一些常用的形常数和载常数。
3.熟练掌握由弯矩图绘制剪力图和轴力图的方法。
4.掌握利用对称性简化计算。
5.重点掌握荷载荷载作用下的计算,了解其它因素下的计算。
6.位移法方程有两种建立方法,写典型方程法和写平衡方程法。
要求熟练掌握一种,另一种了解即可。
学习内容位移法的基本概念。
跨超静定梁的形常数、载常数和转角位移方程。
位移法基本未知量和位移法基本结构的确定。
用位移法计算刚架和排架。
利用对称性简化位移法计算。
直接用结点、截面平衡方程建立位移法方程。
§6.1位移法基本概念1、位移法的特点:欲求超静定结构先取一个基本体系,然后让基本体系在受力方面和变形方面与原结构完全一样。
超静定结构计算的两大基本方法是力法和位移法。
力法的特点:基本未知量——多余未知力;基本体系——静定结构;基本方程——位移条件(变形协调条件)。
位移法的特点:基本未知量——独立结点位移;(例子86)基本体系——一组单跨超静定梁;(例子87)基本方程——平衡条件。
(例子88)因此,位移法分析中应解决的问题是:①确定单跨梁在各种因素作用下的杆端力。
②确定结构独立的结点位移。
③建立求解结点位移的位移法方程。
下面先看第一个问题:确定单跨梁在各种因素作用下的杆端力。
2、杆端力和杆端位移的正负规定:杆端转角θA 、θB,弦转角β=Δ/l都以顺时针为正。
杆端弯矩对杆端以顺时针为正,对结点或支座以逆时针为正。
剪力使分离体有顺时针转动趋势时为正,否则为负。
(与材料力学相同)3、等截面直杆的形常数:由单位杆端位移引起的单跨超静定梁的杆端力。
如右图两端固定梁,由右端单位转角作用下产生的杆端力,可用力法求解,并令:得到杆端弯矩(即形常数)为:各种情形的形常数都可有力法求出如下表:4、等截面直杆的载常数:仅由跨中荷载引起单跨超静定梁的杆端力称为载常熟,也叫固端力。
剪力图与弯矩图的画法

例题 计算 下图中的梁 C、 E 两横截面上的 剪力和弯矩。
解: 在AC段中 q=0 ,且 QA=RA
q
A
B
CE
D
0.2
1.6
1
2
q
在AC段中 Qc = 80KN,剪力图
A
B
CE
D
为矩形,MA =0
0.2
1.6
1
2
80KN (b)
+
80KN
q
在CE段中,剪力图为三角形
A
B
CE
D
QC=80KN,MC=16KN.m
最大剪力发生在DB段中的 任一横截面上
RA 1 P 2
A C
P 3 RB
B D
200
115
1265
23.6
+
1.7 27
弯矩图 每段梁的弯矩图均为斜直线。且 梁上无集中力偶。故只需计算A、 C、D、B各点处横截面上的弯矩。
RA 1 P 2
A C
200
1265
P 3 RB
B D
115
4.72 3.11
q 1KN m
A
c
D
RB
P2 2KN BE
4m
4m
7KN
3KN
+
1KN
F X =5m
4m
3m
2KN
+
-
3KN
RA
P1 2KN
m 10KN .m
q 1KN m
A
cF
D
RB
P2 2KN BE
4m
4m
4m
3m
6
-
6
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
弯矩图如图b
实际结构: 横梁刚度并非无穷大,各柱的 反弯点高度在不同处。当I梁/I柱 >5时计算结果足够精确。
当I梁/I柱逐渐减小时: 底层柱的反弯点位置逐渐升高; 顶部层柱的反弯点位置逐渐降低; 中间各层柱的反弯点位置在中点附 近。
剪力分配法的假设: 横梁刚度无穷大,各刚结点均无转角,各柱的反弯点在其高度 一半处。
各柱顶的剪力分别为
FS14
1F
F 3
,FS25
FS36
F 3
FS47 4 3F 0.835F,FS58 1.67F,FS69 0.495F
各柱端的弯矩分别为
M14
M 41
FS14h 2
Fh 6
M 25
M 52
M 36
M 63
Fh 6
M
ห้องสมุดไป่ตู้
47
M 74
FS47 h 2
0.418Fh
M 58
M 85
§9.5 剪力分配法
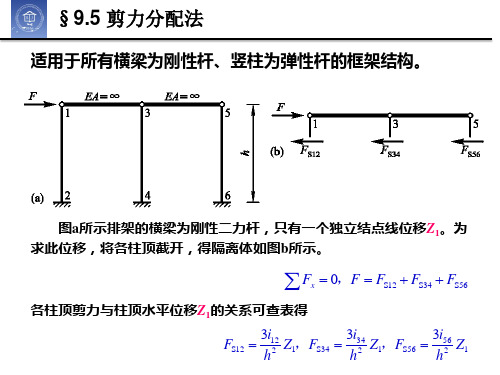
适用于所有横梁为刚性杆、竖柱为弹性杆的框架结构。
图a所示排架的横梁为刚性二力杆,只有一个独立结点线位移Z1。为 求此位移,将各柱顶截开,得隔离体如图b所示。
Fx 0,F FS12 FS34 FS56
各柱顶剪力与柱顶水平位移Z1的关系可查表得
FS12
3i12 h2
Z1,FS34
10kN/m EI 6m
10kN/m
A
1
2
EI
6m
(a)
BC
10kN/m EI 6m
6m
3m
(b)
A
-30 -4.95 -34.95
0.33 0.67
B
30 0
-9.9 -20.1
C
0 20.1
21.9 -20.1 20.1
(c)
q=12kN/m
A i1 3
10m
B i2 3
10m
160kN m
D2 Di
F
2F,FS56
D3 Di
F
3F
式中 1
D1 Di
, 2
D2 Di
, 3
D3 Di
剪力分配系数
各柱固定端的弯矩为 M 21 FS12h,M 43 FS43h,M65 FS65h
剪力分配法:利用剪力分配系数求柱顶剪力的方法。
§9.5 剪力分配法
图a所示结构,荷载作用在柱上。将结构分解为只有结点 线位移和只有荷载q的单独作用,如图b、c所示。
3i34 h2
Z1,FS56
3i56 h2
Z1
§9.5 剪力分配法
令
D1
3i12 h2
,D2
3i34 h2
,D3
3i56 h2
侧移刚度:即杆件发生单位侧移时,所产生的杆端剪力。
将剪力代入平衡条件,可求出线位移 从而可得各柱顶剪力为
Z1
F D1 D2
D3
F Di
FS12
D1 Di
F
1F,FS34
下层各竖柱(左到右)的侧移刚度为
D4
1,D5
12E 2I h3
2,D6
12E 2I (3h / 2)3
16 27
上、下层各柱顶的剪力分配系数为
1
2
3
1 111
1 3
16
4
1
1 2
16
0.2784, 5
1
2 2
16
0.5567, 6
1
27 2
16
0.1649
27
27
27
§9.5 剪力分配法
FS58h 2
0.835Fh
3h M 69 M 96 FS69 2 2 0.371Fh
各竖柱弯矩求出后, 确定刚性横梁的弯矩。
结点连接一根刚性横梁: 由结点的力矩平衡条件确定横 梁在该结点的杆端弯矩。
结点连接两根刚性横梁: 近似认为两根横梁的转动刚度 相同,从而分配到相同的杆端 弯矩。
§9.5 剪力分配法
D
C i3 4
10m
分配系数
0.5 0.5
0.5 0.5
固端弯矩 放松结点C 放松结点B 放松结点C 放松结点B
杆端弯矩
-100
-15
-1 -116
100 0 -40
-30 -30 4
-2 -2 68 -68
00 -80 -80 -15
88 -1 -88 -72
图b中各柱的内力可查表得到,从而求出附加链杆上的反力F1。 图c可用剪力分配法进行计算。 原结构内力=图b结构的内力+图c结构的内力
§9.5 剪力分配法
图示结构只有一个独立结点线位移,
可采用剪力分配法进行计算。各住的侧移
刚度为
D1
12EI1 h13
,D2
12EI2 h23
,D3
12EI3 h33
由剪力分配系数求得各柱顶剪力;
各柱的杆端弯矩=柱顶剪力×h/2。
图示结构由水平投影平衡条件可知, 任一层的总剪力等于该层以上所有水平荷 载的代数和,并按剪力分配系数分配到该 层的各个柱顶。
由剪力可确定各竖柱的弯矩。
§9.5 剪力分配法
例9-6 试用剪力分配法求图a所示刚架竖柱的弯矩图。竖柱E 为常数。
解:为计算方便,设12EI/h3=1。 则上层各竖柱的侧移刚度为 D1=D2=D3=1
