9.5 剪力分配法
结构力剪力分配法
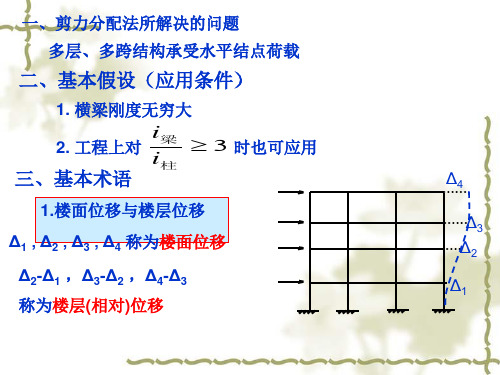
二、基本假设(应用条件)
1. 横梁刚度无穷大 2. 工程上对 i梁 3 时也可应用
i柱
三、基本术语
1.楼面位移与楼层位移 Δ1 , Δ2 , Δ3 , Δ4 称为楼面位移
Δ2-Δ1 ,Δ3-Δ2 ,Δ4-Δ3 称为楼层(相对)位移
Δ4
Δ3 Δ2 Δ1
③分配剪力与5杆的轴力
V1
V2
1 48 3
16kN
V3
V4
1 48 12
4kN
N5
1 6
48
8kN
④分配弯矩
16
-16
4
-4
ቤተ መጻሕፍቲ ባይዱ
-8
32
32
32
16
16
-8
16
16 kNm
32
32
32
16
16
-8
48 48
16
16
16
-8
例题4 用剪力分配法计算如图所示的弯矩图,EI=常数,
10 kN/m
M AB
4i A
2i B
6EI L2
M BA
2i A
4i B
6EI L2
DAB
VAB
12EI L3
6EI L2
A
6EI L2
B
要解决以下问题:
1、杆件有转角时的侧移刚度是多少? 2、反弯点----弯矩为零的点在那?
由于横梁刚度无穷大,每根柱 视为两端固定杆 1、每根柱的侧移刚度12EI/L3 2、每根柱弯矩为零的点在正中----反弯点在中间。
V V
V
VH M 0
2
M
剪力分配法进行排架内力计算的步骤

剪力分配法进行排架内力计算的步骤剪力分配法进行排架内力计算,可真是一门有趣的学问!嘿,首先想象一下,建筑就像一位优雅的舞者,跳动在风中。
每个部分都在默默配合,谁都不想出错,这可真是考验团队合作的时刻。
那我们就来聊聊剪力分配法的步骤,轻松一点,让这个话题不再严肃。
想象一下,我们要在一个大型的舞台上布置演员,每个演员都要承担起自己的角色。
这时候,架构师就得考虑到每根梁和柱的负荷。
就像一个家庭聚会,大家都想尽量多吃一点,但要确保最后的披萨能分到每个人的手里。
剪力分配法的核心就是在这一点上:如何将剪力合理分配给每一个部分,确保它们都能稳稳当当地“站着”。
然后,咱们得了解这些力的来源。
想象一下,一场大雨来临,屋顶上雨水聚集,压力就增加了。
为了搞清楚这些力量的来源,我们需要进行静力平衡的分析。
就像是校对账本,所有的收入和支出都得清清楚楚,不能有漏网之鱼。
咱们得确定各个节点的剪力。
就像是推销员,在推销自己的产品时,得知道哪个客户需要什么。
每根梁的剪力,就像是每个客户的需求,必须精确。
我们通过计算,能得出每根梁上需要承担的剪力。
这个过程可得仔细,不能掉以轻心。
然后,我们就来分配这些剪力了。
哎,别小看这个步骤,它就像是给队伍分配任务,谁负责哪一块。
一般来说,我们会用比例分配的方式来计算,也就是说,看每根梁的支撑能力,然后按比例分配这些剪力。
别忘了,最终得保证所有的剪力总和是零,才能保证整个结构的稳定性。
咱们来聊聊内力计算。
这个就像是在算每个人的表现,得好好评估一下每个部分的承载能力。
通过计算内力,我们能更清晰地了解哪根梁有可能会“打瞌睡”,从而提前采取措施,避免发生意外。
咱们可不想看到“剧组”里的某个演员突然摔倒,得尽早预防呀!然后呢,还得考虑到各种可能的外部因素,比如风的吹袭、地震的颤动。
这些就像是意外的观众,突然跑来捣乱,得随时准备应对。
结构在设计的时候,得考虑到这些,才能确保在突发情况下依旧稳如老狗。
最终,我们得总结一下这些计算结果,确保所有的内力都是合理的。
9.5 剪力分配法
Z1,FS34
3i34 h2
Z1,FS56
3i56 h2
Z1
§9.5 剪力分配法
令
D1
3i12 h2
,D2
3i34 h2
,D3
3i56 h2
侧移刚度:即杆件发生单位侧移时,所产生的杆端剪力。
将剪力代入平衡条件,可求出线位移 从而可得各柱顶剪力为
Z1
F D1 D2
D3
F Di
剪力分配法:利用剪力分配系数求柱顶剪力的方法。
§9.5 剪力分配法
图a所示结构,荷载作用在柱上。将结构分解为只有结点 线位移和只有荷载q的单独作用,如图b、c所示。
图b中各柱的内力可查表得到,从而求出附加链杆上的反力F1。 图c可用剪力分配法进行计算。 原结构内力=图b结构的内力+图c结构的内力
§9.5 剪力分配法
弯矩图如图b
实际结构: 横梁刚度并非无穷大,各柱的 反弯点高度在不同处。当I梁/I柱 >5时计算结果足够精确。
当I梁/I柱逐渐减小时: 底层柱的反弯点位置逐渐升高; 顶部层柱的反弯点位置逐渐降低; 中间各层柱的反弯点位置在中点附 近。
剪力分配法的假设: 横梁刚度无穷大,各刚结点均无转角,各柱的反弯点在其高度 一半处。
由剪力可确定各竖柱的弯矩。
§9.5 剪力分配法
例9-6 试用剪力分配法求图a所示刚架竖柱的弯矩图。竖柱E 为常数。
解:为计算方便,设12EI/h3=1。 则上层各竖柱的侧移刚度为 D1=D2=D3=1
下层各竖柱(左到右)的侧移刚度为
D4
1,D5
12E 2I h3
2,D6
12E 2I (3h / 2)3
底部剪力法计算过程

底部剪力法计算过程底部剪力法是一种常用的结构力学计算方法,用于计算梁结构的内力分布。
在工程设计和施工中,底部剪力法被广泛应用于各种梁的设计和分析。
本文将详细介绍底部剪力法的计算过程,以帮助读者更好地理解和应用这一方法。
底部剪力法的计算过程可以分为以下几个步骤:1. 确定梁的支座情况:首先需要确定梁的支座情况,包括支座的位置和类型。
常见的支座类型有固定支座、滑动支座和铰支座。
支座的类型和位置将决定梁的受力状态。
2. 划分梁的截面:将梁按照需要计算的精度进行截面划分,通常将梁等分为若干个截面。
截面的划分要考虑梁的受力情况和计算精度的要求。
3. 计算剪力:根据支座情况和受力分析,逐个计算各个截面的剪力。
计算剪力时,可以采用平衡法、弹性力学理论或有限元分析等方法。
4. 绘制剪力图:根据计算得到的各个截面的剪力值,绘制剪力图。
剪力图通常以横轴表示梁的长度,纵轴表示剪力的大小,可以直观地反映梁在不同位置的受力情况。
5. 计算内力:根据剪力图,可以计算梁在不同截面的内力,包括弯矩和轴力。
内力的计算可以通过积分方法或图解法进行,具体方法可以根据实际情况选择。
6. 绘制内力图:根据计算得到的各个截面的内力值,绘制内力图。
内力图通常以横轴表示梁的长度,纵轴表示内力的大小和类型,可以直观地反映梁在不同位置的受力情况。
7. 分析结果:根据剪力图和内力图,可以分析梁的受力状态和承载能力。
如果发现梁的受力超过了设计要求或承载能力,需要进行适当的调整和加固。
底部剪力法是一种简便有效的结构力学计算方法,适用于各种梁的设计和分析。
通过合理地划分梁的截面,计算剪力和内力,可以全面了解梁的受力情况和承载能力。
在工程实践中,底部剪力法的应用可以提高设计和施工的效率,确保结构的安全可靠。
总结起来,底部剪力法的计算过程包括确定梁的支座情况、划分梁的截面、计算剪力、绘制剪力图、计算内力、绘制内力图和分析结果。
通过合理地运用这一方法,可以为梁的设计和分析提供科学准确的依据,保证结构的安全可靠。
底部剪力法计算过程

底部剪力法计算过程底部剪力法是结构力学中常用的一种计算方法,用于计算梁或框架结构底部的剪力分布。
底部剪力法的基本原理是将梁或框架结构看作一个整体,通过平衡力的原理来计算底部的剪力分布。
下面将详细介绍底部剪力法的计算过程。
我们需要确定结构的荷载情况和边界条件。
荷载情况包括集中荷载、均布荷载、弯矩等,边界条件包括支座情况和悬臂长度。
在计算中,我们需要将这些荷载和边界条件转化为力的大小和作用点。
接下来,我们需要画出结构的受力图。
受力图是结构受力情况的图形表示,它可以帮助我们清楚地了解结构的力学状态。
在画受力图时,我们需要标出结构的支座和荷载的作用点,并根据荷载的大小和方向画出相应的力。
然后,我们需要选择一个截面,以该截面为界将结构分成两部分。
在底部剪力法中,我们通常选择底部截面作为分界面。
分界面的选择应该尽可能靠近荷载的作用点,这样可以减少计算的复杂性。
接下来,我们将结构分成两个部分,分别计算每个部分的受力情况。
首先,我们可以通过受力图来确定每个部分的受力大小和方向。
然后,我们可以根据平衡力的原理来计算每个部分的底部剪力分布。
在计算底部剪力分布时,我们可以使用力的平衡条件。
即每个部分受到的底部剪力的合力为零。
根据这个条件,我们可以列出方程,并求解出每个部分的底部剪力。
我们可以将每个部分的底部剪力分布绘制在受力图上。
这样,我们就可以清楚地了解结构底部的剪力分布情况。
底部剪力法的计算过程比较复杂,需要一定的力学基础和计算能力。
在实际工程中,我们通常使用计算软件来进行底部剪力的计算,这样可以减少计算的复杂性和错误的可能性。
总结起来,底部剪力法是一种常用的结构计算方法,用于计算梁或框架结构底部的剪力分布。
它通过平衡力的原理来计算底部的剪力分布,可以帮助我们清楚地了解结构的力学状态。
在实际应用中,我们通常使用计算软件来进行底部剪力的计算,以提高计算的准确性和效率。
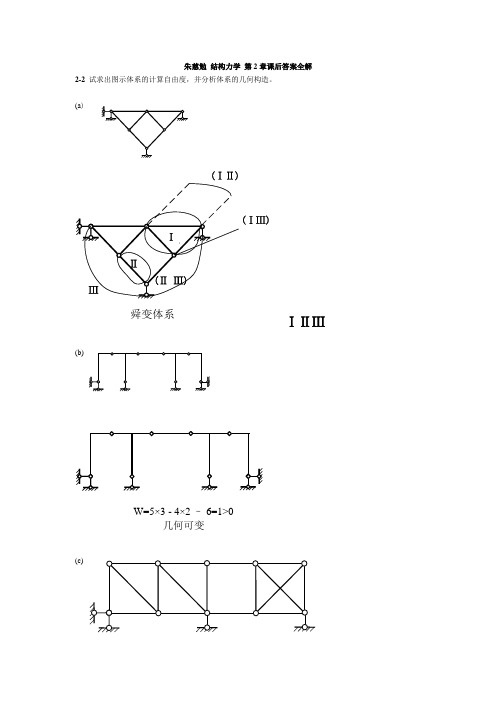
结构力学1-9章答案
1 8
2 36
1 4
3 ( 1 3 2 1 6 2 (3) 1 (6))
6EI 2
2
+ 2 6 1 2 5 ()
6EI
2EI
(c)
2kN/m 6m
2kN 2kN
B 2EI C
EI
EI
1
A
D
3m 3m 3m
1 6
2
2
3
3
42
18
36
30
6
MP
M
xc
6
3 2EI
(2
18
2
0
C
F RC [( 1 ) a] a (方向与图示一致)
h
h
(b)
c1 c2 c3
A A′
2a
BC
D
B′ C′
D′
Δ C
a
2a
1
0.5
1.5
0
FR 图
yc
t h
M ds
t
5 4
5
+t 5 5 t (1) 12 t ( 1 4 3 2 4 3)
4
2
h2
54.5t()
5-10 试求图示结构在支座位移作用下的位移:(a) ΔC ;(b) ΔyC , ΔC 。 (a)
C D
D′
E E′
C′ΔC
h
b
A
l 2
B
B′
l 2
a
1
1
1
h
h
0
A
B
C
D
E
FG
H
2m 2m 2m 2m 2m 2m 2m 3m
A
M 7.5
利用剪力分配法求解等高排架的探讨

出不动铰支座的 水平 反力 Ri ; 第二 步: 撤消 附加 的 不动 铰支 座,
n
! 并在此排架 柱 顶加 上 - R i , 然后 按 照剪 力分 配 系数 进行 分 i= 1
配; 第三步: 将以上两步中求出的内力叠加。
按照以上的三步可 以求出在任意荷载 作用下各柱柱顶剪 力。
在使用以上方法 的过 程中 发现 任意 荷 载( 包 括柱 顶 水平 集中 力 F) 作用时的计算过程包括 只有柱 顶水平 集中力 的计算过 程。但 在计算任意荷载时( 如果这些荷载中包 括柱顶水平 集中力 F ) , 对 于水平集中力 F 何时参与分 配或者 也作为任 意荷载 考虑则 容易 引起计算的混淆。比如是否先将柱顶水平集中力 F 分配 , 再将剩 余的作用力按照第 二步 进行 计算, 然后 叠加, 或 将除柱 顶水 平集
1
Vi =
!n
ui F = 1
i= 1 u i
iF 。
其中, V i 为第 i 根柱子的柱顶剪力; ui 为第 i 根柱子在单位
水平力作用下柱顶的水平位移; i 为第 i 根柱子的剪力分配系数。
2) 任意 荷载( 包括柱顶水平集 中力) 作用时, 计算分为 三个步
骤: 第一步: 先在排架柱 顶附加不动铰支座以 阻止水平位移, 并求
2 剪力墙的等效刚度计算
等效悬臂杆件 在倒 三角 形水平 荷载、均布 水平 荷载、顶 部集
中水平荷载作用 下只 考虑 弯 曲变 形时, 顶点 水平 位 移分 别按 式
( 1) ~ 式( 3) 计算。
u1= 11q maxH 4 / 120EcI c
( 1)
u2= q maxH 4 / 8EcI c
( 2)
1) 将柱顶水平集 中力 F 作为单 独作用 时, 先分配, 得到 各柱 顶剪力 Vi 1; 2) 计算没有柱 顶水平集中力 F 时其他任 意荷载作用 下的柱顶剪力 V i2 ; 3) 叠加上述剪力得到 V i = Vi 1+ V i2。
剪力以及弯矩剪力图以及弯矩图

剪力图和弯矩图在工程管理中的应用
结构设计:用于计 算结构受力确定结 构尺寸和材料
施工管理:用于 指导施工确保施 工质量和安全
维护管理:用于 评估结构状态制 定维护计划
优化设计:用于 优化结构设计降 低成本和能耗
剪力图和弯矩图的注意 事项
绘制剪力图和弯矩图时应注意的事项
确保数据准确无误 注意单位换算确保单位一致 绘制过程中注意比例尺和坐标轴的设置 绘制完成后检查图例、标题、标注等是否清晰明确
添加副标题
剪力和弯矩剪力图以及弯矩 图
汇报人:
目录
CONTENTS
01 添加目录标题
02 剪力和弯矩的基本 概念
03 剪力图和弯矩图的 绘制
04 剪力图和弯矩图的 解读
05 剪力图和弯矩图的 应用
06 剪力图和弯矩图的 注意事项
添加章节标题
剪力和弯矩的基本概念
剪力和弯矩的定义
剪力:作用在物体表面上的力使物体发生剪切变形 弯矩:作用在物体表面上的力使物体发生弯曲变形 剪力图:表示剪力在物体表面上的分布情况 弯矩图:表示弯矩在物体表面上的分布情况
剪力和弯矩的计算方法
剪力:作用在物体上的力使物体发生剪切变形 弯矩:作用在物体上的力使物体发生弯曲变形 剪力计算方法:根据力的平衡原理利用剪力公式进行计算 弯矩计算方法:根据力的平衡原理利用弯矩公式进行计算
剪力和弯矩的单位和符号
剪力:单位为牛顿(N) 符号为F
弯矩:单位为牛顿·米 (N·m)符号为M
证结构安全
剪力图和弯矩图在施工中的应用
确定结构受力情况: 通过剪力图和弯矩图 可以了解结构的受力 情况为施工提供依据。
优化施工方案:根据 剪力图和弯矩图可以 优化施工方案提高施 工效率和质量。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
§9.5 剪力分配法
图a所示结构,荷载作用在柱上。将结构分解为只有结点 线位移和只有荷载q的单独作用,如图b、c所示。
图b中各柱的内力可查表得到,从而求出附加链杆上的反力F1。 图c可用剪力分配法进行计算。 原结构内力=图b结构的内力+图c结构的内力
§9.5 剪力分配法
图示结构只有一个独立结点线位移,
可采用剪力分配法进行计算。各住的侧移
刚度为
D1
12EI1 h13
,D2
12EI2 h23
,D3
12EI3 h33
由剪力分配系数求得各柱顶剪力;
各柱的杆端弯矩=柱顶剪力×h/2。
图示结构由水平投影平衡条件可知, 任一层的总剪力等于该层以上所有水平荷 载的代数和,并按剪力分配系数分配到该 层的各个柱顶。
FS12
D1 Di
F
1F,FS34
D2 Di
F
2F,FS56
D3 Di
F
3F
式中 1
D1 Di
, 2
D2 Di
, 3
D3 Di
剪力分配系数
各柱固定端的弯矩为 M 21 FS12h,M 43 FS43h,M65 FS65h
10kN/m EI 6m
10kN/m
A
1
2
EI
6m
(a)
BC
10kN/m EI 6m
6m
3m
(b)
A
-30 -4.95 -34.95
0.33 0.67
B
30 0
-9.9 -20.1
C
0 20.1
21.9 -20.1 20.1
(c)
q=12kN/m
A i1 3
10m
B i2 3
10m
160kN m
F 3
FS47 4 3F 0.835F,FS58 1.67F,FS69 0.495F
各柱端的弯矩分别为
M14
M 41
FS14h 2
Fh 6
M 25
M 52
M 36
M 63
Fh 6
M
47
M 74
FS47 h 2
0.418Fh
M 58
M 85
FS58h 2
D
C i3 4
10m
分配系数
0.5 0.5
0.5 0.5
固端弯矩 放松结点C 放松结点B 放松结点C 放松结点B
杆端弯矩
-100
-15
-1 -116
100 0 -40
-30 -30 4
-2 -2 68 -68
00 -80 -80 -15
88 -1 -88 -72
§9.5 剪力分配法
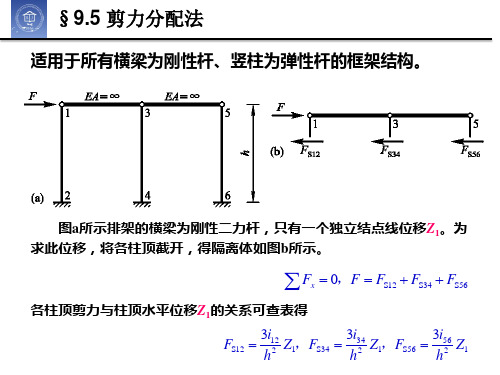
适用于所有横梁为刚性杆、竖柱为弹性杆的框架结构。
图a所示排架的横梁为刚性二力杆,只有一个独立结点线位移Z1。为 求此位移,将各柱顶截开,得隔离体如图b所示。
Fx 0,F FS12 FS34 FS56
各柱顶剪力与柱顶水平位移Z1的关系可查表得
FS12
3i12 h2
弯矩图如图b
实际结构: 横梁刚度并非无穷大,各柱的 反弯点高度在不同处。当I梁/I柱 >5时计算结果足够精确。
当I梁/I柱逐渐减小时: 底层柱的反弯点位置逐渐升高; 顶部层柱的反弯点位置逐渐降低; 中间各层柱的反弯点位置在中点附 近。
剪力分配法的假设: 横梁刚度无穷大,各刚结点均无转角,各柱的反弯点在其高度 一半处。
0.835Fh
3h M 69 M 96 FS69 2 2 0.371Fh
各竖柱弯矩求出后, 确定刚性横梁的弯矩。
结点连接一根刚性横梁: 由结点的力矩平衡条件确定横 梁在该结点的杆端弯矩。
结点连接两根刚性横梁: 近似认为两根横梁的转动刚度 相同,从而分配到相同的杆端 弯矩。
§9.5 剪力分配法
由剪力可确定各竖柱的弯矩。
§9.5 剪力分配法
例9-6 试用剪力分配法求图a所示刚架竖柱的弯矩图。竖柱E 为常数。
解:为计算方便,设12EI/h3=1。 则上层各竖柱的侧移刚度为 D1=D2=D3=1
下层各竖柱(左到右)的侧移刚度为
D4
1,D5
12E 2I h3
2,D6
12E 2I (3h / 2)3
16 27Fra bibliotek上、下层各柱顶的剪力分配系数为
1
2
3
1 111
1 3
16
4
1
1 2
16
0.2784, 5
1
2 2
16
0.5567, 6
1
27 2
16
0.1649
27
27
27
§9.5 剪力分配法
各柱顶的剪力分别为
FS14
1F
F 3
,FS25
FS36
Z1,FS34
3i34 h2
Z1,FS56
3i56 h2
Z1
§9.5 剪力分配法
令
D1
3i12 h2
,D2
3i34 h2
,D3
3i56 h2
侧移刚度:即杆件发生单位侧移时,所产生的杆端剪力。
将剪力代入平衡条件,可求出线位移 从而可得各柱顶剪力为
Z1
F D1 D2
D3
F Di
