基于EEMD-ARIMA模型的气温预测研究
基于Elman神经网络的气温时间序列预测
系统,给定初值 0,即可得到混沌时间序列
(
)。前 300 个数据用来训练网络,
后 40 个数据与预测值作比较。
仿真预测结果如图 2,图 3 所示。由图可
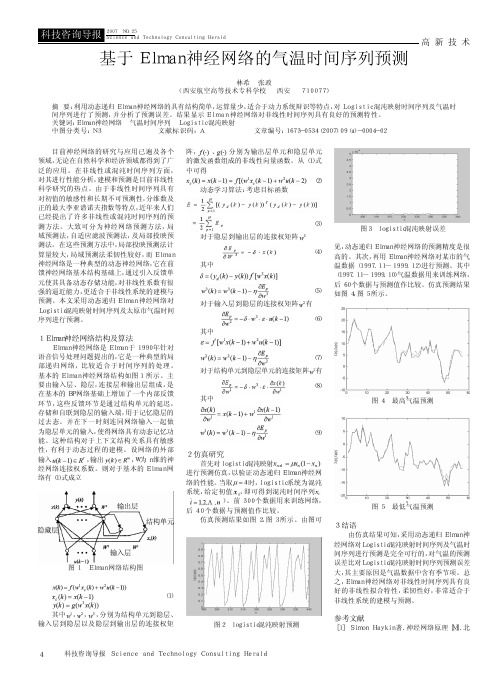
图 1 Elman 网络结构图
(1) 其中 , , ,分别为结构单元到隐层、 输入层到隐层以及隐层到输出层的连接权矩
图2 logistic混沌映射预测
图3 logistic混沌映射误差 见,动态递归 Elman 神经网络的预测精度是很 高的。其次,再用 Elman 神经网络对某市的气 温数据(1997.11~1999.12)进行预测。其中 (1997.11~1999.10)气温数据用来训练网络, 后 60 个数据与预测值作比较。仿真预测结果 如图 4,图 5 所示。
许令周 (中国石油大学物理科学与技术学院 山东东营 257062)
摘 要:采用两种方法对条状偶极层的电场进行了计算,重点讨论了采用旋度源理论计算的方法及其意义。
关键词:偶极层 旋度源
中图分类号: O 4
文献标识码: A
文章编号:1673-0534(2007)09(a)-0005-01
条状偶极层是指可以看成宽度为 ,长 度无限长的偶极层, 从剖面上看是一条线, 如 图 1 , 设其单位面积上的电动势为 , 分布均 匀。
络有(1)式成立
阵, 、 分别为输出层单元和隐层单元 的激发函数组成的非线性向量函数。从(1)式 中可得
(2) 动态学习算法:考虑目标函数
(3)
对于隐层到输出层的连接权矩阵
其中
(4)
(5) 对于输入层到隐层的连接权矩阵 有
环节, 这些反馈环节是通过结构单元的延迟,
存储和自联到隐层的输入端,用于记忆隐层的
过去态。并在下一时刻连同网络输入一起做
ARIMA模型---时间序列分析---温度预测
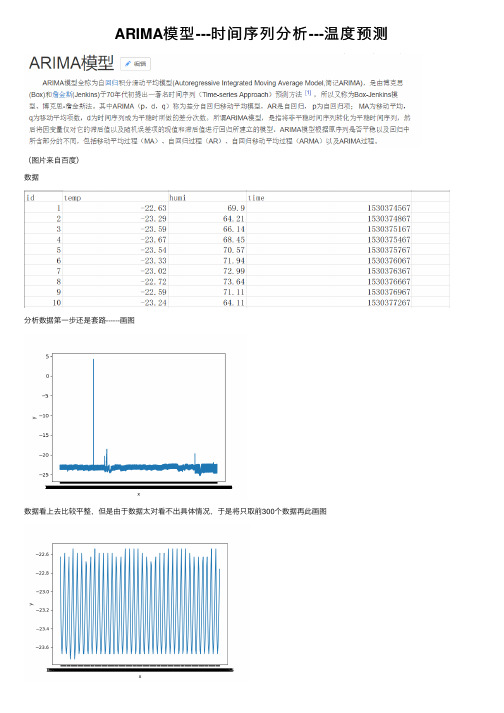
ARIMA模型---时间序列分析---温度预测(图⽚来⾃百度)数据分析数据第⼀步还是套路------画图数据看上去⽐较平整,但是由于数据太对看不出具体情况,于是将只取前300个数据再此画图这数据看上去很不错,感觉有隐藏周期的意思代码#coding:utf-8import csvimport matplotlib.pyplot as pltdef read_csv_data(aim_list_1, aim_list_2, file_name):i = 0csv_file = csv.reader(open(file_name,'r'))for data in csv_file:if (i == 0):i += 1continueaim_list_1.append(float(data[1]))aim_list_2.append(data[3])returndef plot_picture(x, y):plt.xlabel('x')plt.ylabel('y')plt.plot(x, y)plt.show()returnif__name__ == '__main__':temp = []tim = []file_name = 'C:/Users/lichaoxing/Desktop/testdata.csv'read_csv_data(temp, tim, file_name)plot_picture(tim[:300], temp[:300])使⽤ARIMA模型(ARMA)第⼀步观察数据是否是平稳序列,通过上图可以看出是平稳的如果不平稳,则需要进⾏预处理,⽅法有对数变换差分对于平稳的时间序列可以直接使⽤ARMA(p, q)模型进⾏拟合ARMA (p, q) : AR(p) + MA(q)此时参数p和q的确定可以通过观察ACF和PACF图来确定通过观察PACF图可以看出,阶数为9也就是p=9,这⾥ACF图看出⾃相关呈现震荡下降收敛,但是怎么决定出q,我没太明⽩,这⾥姑且拍脑袋才⼀个吧就q=3但是这⾥我遇到了⼀个问题,没有搞懂,就是平稳的序列,如果我进⾏⼀阶差分后应该仍然是平稳的序列,但是这个时候我⼜画了⼀个ACF 与PACF图,竟然是下图这样,lag的范围是-0.04到0.04(不懂)lag的范围是-0.04到0.04的问题原因(修改于再次使⽤此模型)原因:当时,我使⽤的是⼀阶差分,也就是让数据的后⼀个值减去前⼀个值得到新的值,这样就会导致第⼀个值变为缺失值(下⾯的数据是再此使⽤此模型时的数据,与原博客数据⽆关)就是因为此处的值为缺失值,导致绘制ACF与PACF时数据有问题⽽⽆法成功显⽰解决办法,在绘制上述图形前,将第⼀个数据去除:dta= dta.diff(1)dta = dta.truncate(before= ym[1])#删除第⼀个缺失值其实还有就是使⽤ADF检验,得到的结果如图,这个p值很⼩===》平稳画图代码def acf_pacf(temp, tim):x = timy = tempdta = pd.Series(y, index = pd.to_datetime(x))fig = plt.figure(figsize=(9,6))ax1 = fig.add_subplot(211)fig = sm.graphics.tsa.plot_acf(dta,lags=50,ax=ax1)ax2 = fig.add_subplot(212)fig = sm.graphics.tsa.plot_pacf(dta,lags=50,ax=ax2)show()ADF检验代码def test_stationarity(timeseries):dftest = adfuller(timeseries, autolag='AIC')return dftest[1]这⾥先使⽤ARMA(9,3)来实验测试⼀下效果,取前300个数据中的前250个作为train,后⾯的作为test 效果可以说这个模型是真的强⼤,预测的还是⼗分准确的代码def test_300(temp, tim):x = tim[0:300]y = temp[0:300]dta = pd.Series(y[0:249], index = pd.to_datetime(x[0:249]))fig = plt.figure(figsize=(9,6))ax1 = fig.add_subplot(211)fig = sm.graphics.tsa.plot_acf(dta,lags=30,ax=ax1)ax2 = fig.add_subplot(212)fig = sm.graphics.tsa.plot_pacf(dta,lags=30,ax=ax2)arma_mod = sm.tsa.ARMA(dta, (9, 3)).fit(disp = 0)predict_sunspots = arma_mod.predict(x[200], x[299], dynamic=True)fig, ax = plt.subplots(figsize=(9, 6))ax = dta.ix[x[0]:].plot(ax=ax)predict_sunspots.plot(ax=ax)show()其实,可以通过代码来⾃动的选择p和q的值,依据BIC准则,⽬标就是bic越⼩越好代码def proper_model(timeseries, maxLag):init_bic = 100000000init_properModel = Nonefor p in np.arange(maxLag):for q in np.arange(maxLag):model = ARMA(timeseries, order=(p, q))try:results_ARMA = model.fit(disp = 0, method='css')except:continuebic = results_ARMA.bicif bic < init_bic:init_properModel = results_ARMAinit_bic = bicreturn init_properModel遇到的问题,预测时predict函数没怎么使⽤明⽩当写于某些预测区间的时候,会报 “start”或“end”的相关错误,还有⼀个函数forcast,这个函数使⽤就是forcast(N):预测后⾯N个值返回的是预测值(array型)标准误差(array型)置信区间(array型)还有:对于构造时间序列,时间可以是时间格式:如 “2018-01-01” 或者就是个时间戳,在⽤时间戳的时候,其实在序列⾥它会⾃动识别时间戳,并加上起始时间1970-01-01 00:00:01形式附录(代码)预测⼀序列中某⼀点的值#coding:utf-8import csvimport timeimport pandas as pdimport numpy as npfrom statsmodels.tsa.arima_model import ARMAimport argparseimport warningswarnings.filterwarnings('ignore')def timestamp_datatime(value):value = time.localtime(value)dt = time.strftime('%Y-%m-%d %H:%M',value)return dtdef time_timestamp(my_date):my_date_array = time.strptime(my_date,'%Y-%m-%d %H:%M')my_date_stamp = time.mktime(my_date_array)return my_date_stampdef read_csv_data(aim_list_1, aim_list_2, file_name):i = 0csv_file = csv.reader(open(file_name,'r'))for data in csv_file:if (i == 0):i += 1continueaim_list_1.append(float(data[1])) #1:温度 2:湿度dt = int(data[3])aim_list_2.append(dt)returndef proper_model(timeseries, maxLag):init_bic = 100000000init_properModel = Nonefor p in np.arange(maxLag):for q in np.arange(maxLag):model = ARMA(timeseries, order=(p, q)) #bugtry:results_ARMA = model.fit(disp = 0, method='css')except:continuebic = results_ARMA.bicif bic < init_bic:init_properModel = results_ARMAinit_bic = bicreturn init_properModeldef test_300(temp, tim, time_in):x = []y = []end_index = len(tim)for i in range(0, len(tim)):if (time_in - (tim[i]) < 300):end_index = ibreakif (end_index < 100):x = tim[0: end_index]y = temp[0: end_index]else:x = tim[end_index - 100: end_index]y = temp[end_index - 100: end_index]tidx = pd.DatetimeIndex(x, freq='infer')dta = pd.Series(y, index = tidx)print(dta)arma_mod = proper_model(dta, 9)predict_sunspots = arma_mod.forecast(1)return predict_sunspots[0]def predict_temperature(file_name, time_in):temp = []tim = []read_csv_data(temp, tim, file_name)result_temp = test_300(temp, tim, time_in)return result_tempif__name__ == '__main__':parser = argparse.ArgumentParser()parser.add_argument('-f', action='store', dest='file_name')parser.add_argument('-t', action='store', type = int, dest='time_')args = parser.parse_args()file_name = args.file_nametime_in = args.time_result_temp = predict_temperature(file_name, time_in)print ('the temperature is %f ' % result_temp)在上⾯的代码中,预测某⼀点的值我采⽤序列中此点的前100个点作为训练集如果给出待预测的多个点,由于每次都要计算模型的p和q以及拟合模型,时间会很慢,于是考虑将给定的待预测时间点序列切割成⼩段,使每⼀段中最⼤与最⼩的时间间隔在某⼀范围内在使⽤forcast(n)函数⼀次预测多点,然后在预测值中找到与待预测的时间值相近的值,速度⼤⼤提升,思路如图代码#coding:utf-8import csv#import timeimport pandas as pdimport numpy as npfrom statsmodels.tsa.arima_model import ARMAimport warningswarnings.filterwarnings('ignore')def proper_model(timeseries, maxLag):init_bic = 1000000000init_p = 1init_q = 1for p in np.arange(maxLag):for q in np.arange(maxLag):model = ARMA(timeseries, order=(p, q))try:results_ARMA = model.fit(disp = 0, method='css')except:continuebic = results_ARMA.bicif bic < init_bic:init_p = pinit_q = qinit_bic = bicreturn init_p, init_qdef read_csv_data(file_name, clss = 1):i = 0aim_list_1 = [] #temperature(1) or humidity(2)aim_list_2 = [] #timecsv_file = csv.reader(open(file_name,'r'))for data in csv_file:if (i == 0):i += 1continueaim_list_1.append(float(data[clss]))dt = int(data[3])aim_list_2.append(dt)tidx = pd.DatetimeIndex(aim_list_2, freq = None)dta = pd.Series(aim_list_1, index = tidx)init_p, init_q = proper_model(dta[:aim_list_2[100]], 9)return init_p, init_q, aim_list_2, dtadef for_kernel(p, q, tim, dta, tmp_time_list, result_dict):interval = 20end_index = len(tim) - 1for i in range(0, len(tim)):if (tmp_time_list[0]["time"] - tim[i] < tim[1] - tim[0]):end_index = ibreakif (end_index < 100):dta = dta.truncate(after = tim[end_index])else:dta = dta.truncate(before= tim[end_index - 101], after = tim[end_index])arma_mod = ARMA(dta, order=(p, q)).fit(disp = 0, method='css')#为未来interval天进⾏预测,返回预测结果,标准误差,和置信区间predict_sunspots = arma_mod.forecast(interval)####################################for tim_i in tmp_time_list:for tim_ in tim:if tim_i["time"] - tim_ >= 0 and tim_i["time"] - tim_ < tim[1] - tim[0]:result_dict[tim_i["time"]] = predict_sunspots[0][tim.index(tim_) - end_index] returndef kernel(p, q, tim, dta, time_in_list):interval = 20time_first = time_in_list[0]det_time = tim[1] - tim[0]result_dict = {}tmp_time_list = []for time_ in time_in_list:if time_first["time"] + det_time * interval > time_["time"]:tmp_time_list.append(time_)continuetime_first = time_for_kernel(p, q, tim, dta, tmp_time_list, result_dict)tmp_time_list = []tmp_time_list.append(time_first)for_kernel(p, q, tim, dta, tmp_time_list, result_dict)return result_dictdef predict_temperature(file_name, time_in_list, clss = 1):p, q, tim, dta = read_csv_data(file_name, clss)result_temp_dict = kernel(p, q, tim, dta, time_in_list)return result_temp_dictdef predict_humidity(file_name, time_in_list, clss = 2):p, q, tim, dta = read_csv_data(file_name, clss)result_humi_dict = kernel(p, q, tim, dta, time_in_list)return result_humi_dictif__name__ == '__main__':file_name = "testdata.csv"time_in = [{"time":1530419271,"temp":"","humi":""},{"time":1530600187,"temp":"","humi":""},{"time":1530825809,"temp":"","humi":""}] #time_in = [{"time":1530600187,"temp":"","humi":""},]result_temp = predict_temperature(file_name, time_in)print(result_temp)由于后续⼜改动了需求,需要预测温度以及湿度,完成了项⽬在github。
时间序列预测模型在天气预报中的应用研究

时间序列预测模型在天气预报中的应用研究第一章:引言天气预报是一项重要的公共服务,对人类社会的生产、生活、安全等方面都有着至关重要的影响。
随着现代化技术的快速发展和大量数据的产生,时间序列预测模型在天气预报中得到了广泛的应用。
本文将介绍时间序列预测模型在天气预报中的应用研究,以及相关的技术和方法。
第二章:时间序列分析时间序列分析是一种能够自动发现数据中的规律性和趋势性的方法。
在天气预报中,时间序列分析可以分析一定时期内的气象数据,来预测未来的气象情况。
常见的时间序列预测模型包括ARIMA模型、分解模型等。
2.1 ARIMA模型ARIMA模型是一种基于时间序列的统计模型。
它可以对时间序列进行建模,并对未来的值进行预测。
ARIMA模型一般包括3个部分:自回归模型(AR)、差分模型(I)、移动平均模型(MA)。
ARIMA模型适用于同一时间段内的数据具有相关关系的领域,如气象、经济等领域。
2.2 分解模型分解模型是将时间序列分解成趋势、季节和随机三部分来进行预测的一种方法。
在天气预报中,分解模型可以将数据分解成相应的趋势、季节和随机成分,分别进行预测。
通过分析不同成分预测结果的加权影响,得到最终天气预报结果。
第三章:时间序列预测在天气预报中的应用实例3.1 城市气象预报在城市气象预报中,时间序列预测模型可以对气温、湿度、风力、降水量、大气压力等进行预测。
以气温预测为例,可以利用ARIMA模型对气温进行建模,并对未来数天的气温进行预测。
在实际应用中,气象预报员可以以ARIMA模型的预测结果为依据,提供更为准确的气象预报信息。
3.2 农业气象预报在农业气象预报中,时间序列预测模型可以对作物的生长、成熟、产量等进行预测。
以预测玉米的产量为例,可以将历年的气象数据分解成趋势、季节和随机成分,然后利用分解模型预测未来几年的玉米产量。
在实际应用中,农业预报员可以根据预测结果对农作物进行更为精准的管理和决策。
第四章:时间序列预测在天气预报中的优缺点4.1 优点时间序列预测模型可以利用历史气象数据对未来气象变化进行预测,预测结果更加准确。
基于EEMD-ARIMA的年降水预测拟合模型研究

第37卷第11期 计算机应用与软件Vol 37No.112020年11月 ComputerApplicationsandSoftwareNov.2020基于EEMD ARIMA的年降水预测拟合模型研究李智强 邹红霞 齐 斌 郭江昆(航天工程大学航天信息学院 北京101400)收稿日期:2019-06-19。
国家高技术研究发展计划项目(2015AAxxx2078)。
李智强,硕士,主研领域:数据挖掘。
邹红霞,副教授。
齐斌,硕士。
郭江昆,硕士。
摘 要 针对传统ARIMA模型对非线性的降水时间序列拟合效果差、预测精度低的缺点,建立基于集合经验模态分解的差分自回归移动平均预报模型(EEMD ARIMA)。
用EEMD方法将序列分解简化,采用不同的ARIMA模型进行建模,并重构各拟合分量。
建立EMD、EEMD、ARIMA和EMD ARIMA4个模型进行对比实验,结果表明,EEMD ARIMA模型的拟合效果最好,其预测准确率可达到82.46%,该模型在年降水预测应用中能够更准确地描述年降水量的变化规律,具有实际意义。
关键词 EMD算法 ARIMA模型 EEMD ARIMA 降水预测中图分类号 TP3 文献标志码 A DOI:10.3969/j.issn.1000 386x.2020.11.008AFITTINGMODELOFANNUALPRECIPITATIONPREDICTIONBASEDONEEMD ARIMALiZhiqiang ZouHongxia QiBin GuoJiangkun(AcademyofAerospaceInformation,SpaceEngineeringUniversity,Beijing101400,China)Abstract AimingattheshortcomingsoftraditionalARIMAmodelonthepoorfittingofnonlinearprecipitationtimeseriesandlowpredictionaccuracy,weestablishadifferentialautoregressivemovingaveragepredictionmodelbasedoncollectiveempiricalmodedecomposition(EEMD ARIMA).TheEEMDmethodwasusedtosimplifythesequencedecomposition,andthendifferentARIMAmodelswereusedtomodelandreconstructthefittingcomponents.FourmodelsofEMD,EEMD,ARIMAandEMD ARIMAwereestablishedforcomparativeexperiments.TheexperimentalresultsshowthattheEEMD ARIMAmodelhasthebestfittingeffect,andtheaccuracyofpredictionreaches82.46%.Inannualprecipitationprediction,thismodelcanmoreaccuratelydescribethechangelawofannualprecipitation,whichhaspracticalsignificance.Keywords EMDalgorithm ARIMAmodel EEMD ARIMA Precipitationprediction0 引 言年降水量变化一直都是气象科学界对气候变化研究的热点问题。
基于ARIMA模型对定西天气数据的分析与预测

基于ARIMA模型对定西天气数据的分析与预测
赵子鹏;魏新奇;唐龙;高丙翻;康亮河
【期刊名称】《现代信息科技》
【年(卷),期】2024(8)9
【摘要】由于天气对农业生产、水资源管理和自然灾害预防等具有重要影响,文章采用ARIMA模型来实现对天气的有效预测。
通过利用ACF和PACF图粗略确定ARIMA模型的参数,最终确定最优模型:ARIMA(1,1,1)为日最低气温模型,其残差序列自相关函数与偏自相关函数基本落在95%置信区间内;同时Ljung-Box Q统计结果表明残差不存在相关关系(P>0.05),即残差为白噪声,满足随机性假设;最终计算误差(日最低气温)RMSE、MAPE、MAE分别为2.63、1.22%、2.06,预测结果良好,为定西天气的预测提供了可行的方案。
【总页数】4页(P140-143)
【作者】赵子鹏;魏新奇;唐龙;高丙翻;康亮河
【作者单位】甘肃农业大学
【正文语种】中文
【中图分类】TP391.1
【相关文献】
1.基于ARIMA模型的军事训练数据分析和预测
2.基于ARIMA模型对全国农业受灾面积的数据分析与预测
3.基于ARIMA模型的地铁客流量数据分析与预测
4.基于ARIMA模型的上海虹桥枢纽客流数据分析预测
因版权原因,仅展示原文概要,查看原文内容请购买。
天气预测模型研究和优化

天气预测模型研究和优化一、背景介绍在现代社会中,天气预测已成为我们生活中不可或缺的一部分。
预测准确的天气模型可以为人们的生产和生活提供有力的保障,有助于减少灾害的发生,并降低对能源等资源的过度消耗。
因此,为了更好地预测未来的天气,研究和优化天气预测模型已成为科学家们的一项重要工作。
二、常见天气预测模型1. 基于统计学的模型这种模型通过收集历史气象数据来预测未来的天气。
常见的统计模型有ARIMA、SARIMA等。
2. 数值天气预报模型数值天气预报模型是天气预报的主要手段之一。
它基于大气气体运动、物理量守恒原理和边界条件,使用计算机数值模拟方法,对未来天气的演变进行模拟。
3. 人工神经网络模型人工神经网络模型是一种能够模拟人脑神经网络的数学模型。
它是一种机器学习算法,可以自适应地根据给定的输入来提高预测的准确性。
三、天气预测模型的优化1. 数据分析与处理在构建天气预测模型之前,需要对原始数据进行预处理和分析。
这包括去除异常值,对缺失值进行填补,并对数据进行标准化。
2. 特征选择特征选择是指从原始数据中筛选出预测中有用的特征。
特征选择能够提高模型的准确性和效率,同时降低系统复杂度。
3. 模型参数选择在确定模型参数时,需要根据不同模型的特点和预测任务的需求进行选择。
在确定模型参数时,可以使用参数调优算法,如网格搜索或随机搜索。
4. 集成学习集成学习通过组合多个模型来提高预测准确性。
常见的集成学习方法包括随机森林和XGBoost等。
四、案例分析以中国气象局的未来3天天气预测为例,可以将数值天气预报模型和人工神经网络模型相结合。
一方面,数值天气预报模型可以提供良好的初始条件,另一方面,人工神经网络模型可以通过学习历史气象数据来提高预测准确度。
五、结论及展望天气预测模型的研究和优化是一项艰巨的任务。
通过数据分析、特征选择、模型参数选择和集成学习等方法,可以提高预测准确性和效率。
未来,随着数据科学和机器学习的快速发展,天气预测模型的研究将迎来更加精彩的发展。
基于人工智能的天气预测模型研究

基于人工智能的天气预测模型研究随着人工智能技术的不断发展,越来越多的领域开始应用智能算法来解决问题。
其中,天气预测是人工智能领域应用最广泛的一个领域之一。
人们需要准确的天气预报来安排生活和工作,所以提高天气预报的准确率一直是科学家们的研究方向之一。
在传统的天气预报中,多种气象因素被综合分析,以推断出某一时刻的天气状况。
传统的数据源主要来自气象观测站,但单个观测站的面积较小,数据的时效性和准确性也无法得到保证。
因此,在基于人工智能的天气预报模型研究中,数据的质量和数量显得尤为重要。
人工智能算法在天气预报中的应用首先,我们需要清楚地知道,深度学习(Deep Learning)是人工智能领域的一种方法。
深度学习通过构建复杂的神经网络层次结构,来模拟人类的感知、理解和决策等功能,从而拥有诸多优势。
在天气预报中,深度学习算法也得到了广泛应用。
传统的天气预报算法需要人为设定各种物理规则和参数,但深度学习算法可以通过训练数据,找到其中的隐藏规律,快速地学习和预测气象因素的变化。
近年来,基于卷积神经网络(Convolutional Neural Networks,CNN)的天气预测模型备受关注。
CNN是一种常见的深度学习结构,这种结构处理比较适合处理图像数据,它通过卷积层和池化层的交替,逐渐减小筛选的范围从而提高了模型的准确度。
通过卷积神经网络算法,天气预测模型可以利用海量的气象数据不断学习适应和优化,最终实现预测准确度的提升。
在实际应用过程中,天气预测模型可以根据历史气象数据,预测接下来几天、甚至几周的天气情况。
另一方面,基于循环神经网络(Recurrent Neural Networks,RNN)的天气预测模型也受到了越来越多的关注。
循环神经网络的主要特点是可以处理序列数据,这种结构通过隐状态处理学习,将先前的状态信息与当前状态信息关联起来,从而更好地预测未来几天的天气情况。
在实际应用中,循环神经网络天气预测模型可以将历史的气象数据作为输入,通过不断调整隐状态,生成预测结果,对天气的预测准确率也得到了提高。
基于ARIMA模型和CNN-LSTM组合模型的全球气温预测分析

DOI :10.15913/ki.kjycx.2024.02.005基于ARIMA模型和CNN-LSTM组合模型的全球气温预测分析*严 迅,铁承城,鄢 薇,何杰艳,管春春,吕井明(贵州理工学院,贵州 贵阳 550000)摘 要:全球气温预测研究对于国家环境健康状况评价、环境问题分析和预防污染物浓度管理具有重大价值。
为有效提升温度预报准确率,首次引入了ARIMA (自回归移动平均模型)模型进行温度预测,而后又给出了一个基于卷积层神经网络(Convolutional Neural Networks ,CNN )和长短期记忆神经网络(Long Short-Term Memory ,LSTM )相结合的温度预报模型。
利用CNN 卷积层和池化层为特征提取模块,从而获得了数据特征;将重构信息注入LSTM 网络中挖掘气温的时序特征。
结果表明,与单独使用LSTM 、CNN 进行预测及使用ARIMA 模型预测相比,CNN-LSTM 模型预测结果具有更高的准确率。
关键词:CNN-LSTM 模型;ARIMA 时间序列模型;全球气温预测;环境问题中图分类号:X144 文献标志码:A 文章编号:2095-6835(2024)02-0019-04——————————————————————————*[基金项目]贵州省重点支持领域项目“基于神经网络模型优化的城市空气污染物浓度预测”(编号:S202214440125)近年来,多地气温突破历史纪录,创造了新纪录。
1850—2022年全球气温上升了0.78 ℃。
自然因素中,森林火灾是全球变暖的关键原因之一。
森林在森林碳循环中起着重要作用,并对全球气候变化产生影响。
森林可燃物燃烧是大气中温室气体的主要来源之一,其中CO 2排放量占碳排放总量的90%。
1997—2016年全球每年平均火灾碳排放量为2.2 PgC 。
由于森林大火所产生的温室气体含量增加,将改变整个局地甚至全世界的气候系统,促进世界变暖,并在大气碳积累过程和世界变暖期间产生正向反馈作用。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
306
统计学与应用
贾雨杰 等
Θ ( B) =1−θ1B − −θq Bq ,为平稳可逆 ARMA(p, q)模型的移动平滑系数多项式。ARIMA(p, d, q)模型可
简记为: ∇d xt
Θ(B) = Φ ( B) εt
,式中{εt }
为零均值白噪声序列。
3.2. EEMD-ARIMA 模型
气温是一个非平稳序列,所以在预测之前要先对序列进行平稳化处理。因此,本文建立基于 EEMD 分解的 EEMD-ARIMA 预测模型。模型的建模流程如图 1 所示。
把分解多次的本征模态函数(IMF)和趋势项取均值,该值为最终的 IMF 分量和 rs 余项。利用 EEMD 分解 原始信号的具体步骤如下:
1) 添加白噪声的次数(即试验总次数) ne 和幅值系数 ε 。
2) 将白噪声加入原始信号 x (t ) 中, w(t ) 是第 i 次加入的白噪声序列,可得到信号 X ′(t ) :
Φ
E
( B)∇d xt = Θ( B) (ε=t ) 0,Var (ε=t )
ε
t
σ
2 t
,
E
(ε
t
ε= s )
0, s ≠ t
(8)
E
(
xsε
t
)
=
0, ∀s < t
式中, ∇d
=
(1
−
B
)d
;
Φ
(
B
)
=
1
−
φ1B
−
−
φp
B
p
,为平稳可逆
ARMA(p,
q)模型的自回归系数多项式;
DOI: 10.12677/sa.2020.92033
Keywords
Empirical Mode Decomposition (EMD), Ensemble Empirical Mode Decomposition (EEMD), ARIMA Model, Average Annual Temperature, Forecast
基于EEMD-ARIMA模型的气温预测研究
1998 年,N.E. Huang 提出了一种新的信号分析方法——经验模态分解(EMD) [7]。该方法在处理非平 稳非线性的数据上具有很大的优势,一经提出后,就在不同的工程领域得到了迅速有效的应用,例如在 海洋、大气、天体观测资料与地震记录分析、机械故障诊断[8]、密频动力系统的阻尼识别以及大型土木 工程结构的模态参数识别等方面。但是,如果数据出现模态混叠现象,该方法的性能会出现大幅度下降 的情况,因此 N.E. Huang 为了改进 EMD 的不足,提出了 EEMD 方法[9],用以解决 EMD 中的模态混叠 问题,该方法在气候、工程等领域有较多的应用。
气温数据具有非平稳非线性、时间相关性的特征。为了提高气温预测的准确性,本文提出 EEMD 和 ARIMA 模型相结合的方法对气温数据进行预测。EEMD 能对非平稳数据进行平稳化处理,并且能有效解 决数据中存在的模态混叠问题,使其达到时间序列数据分析的要求,ARIMA 时间序列分析又充分考虑到了 气温数据的时间相关性,将两种方法结合起来对气温数据进行处理及预测,将会有效提高预测的准确性。
0.2~0.3。 X ′(t ) 经步骤(3)至步骤(7)处理后即可得到不同尺度的 IMF 和余项。
( ) ∑T X k′′−21 (t ) − X k′′2 (t ) 2
SD = tቤተ መጻሕፍቲ ባይዱ0
T
(4)
∑ X k′′−21 (t )
t=0
8) 利用白噪声频谱的均值为零,将 ne 次分解得到的各 IMF 进行均值处理,得到 EEMD 分解后最终
贾雨杰 等
Copyright © 2020 by author(s) and Hans Publishers Inc. This work is licensed under the Creative Commons Attribution International License (CC BY 4.0). /licenses/by/4.0/
4) b1 (t ) 为上下包络线的平均值。将信号 X ′(t ) 与 b1 (t ) 相减,得到新序列:
X= 1′′(t ) X ′(t ) − b1 (t )
(2)
5) 判断 X1′′(t ) 是否满足 IMF 分量的条件,如果满足,则 X1′′(t ) 是筛选出的第一个 IMF 分量为 IMF1 ; 如果不满足, X1′′(t ) 将作为新的原始序列重新回到步骤(3)和步骤(4)继续进行筛选,直到满足 IMF 分量的
Figure 1. Flow chart of EEMD-ARIMA prediction model 图 1. EEMD-ARIMA 预测模型流程图
EEMD-ARIMA 预测模型的具体步骤如下:
1) 首先,将原始信号 X (t ) 输入 EEMD 中进行分解, X (t ) 会被分解成若干个 IMF 和余项 rs。
X ′(t=) x (t ) + ε ∗ w(t )
(1)
DOI: 10.12677/sa.2020.92033
305
统计学与应用
贾雨杰 等
3) 找出要分解的时间序列 X ′(t ) 所有的局部最大值点和最小值点,利用三次样条函数的方法拟合
X ′(t ) 所有的最大值点和最小值点,构成上包络线和下包络线。
条件。
6) 把 IMF1 从信号 X ′(t ) 中减去得到 x1 ,如式(3)所示。把 x1 作为要分解的新信号,重复步骤(3)至步骤
(6) n 次,直到 xn 或者 IMFn 小于给定的数值或 xn 为单调函数,即可结束分解。
=x1 X ′(t ) − IMF1
(3)
7) 用 SD (限值标准差)判断筛选是否终止。当 SD 小于阈值α 时,筛选结束。α 的一般取值范围是
贾雨杰,陈鹏蕾,朱 莉 宁波工程学院,浙江 宁波
收稿日期:2020年4月9日;录用日期:2020年4月22日;发布日期:2020年4月29日
摘要
采用集合经验模态分解(EEMD)与差分整合移动平均自回归(ARIMA)模型相结合的方法对年均气温数据 进行建模预测。首先对年均气温做加噪处理后进行经验模态分解(EMD),使其分量平稳化,然后再对各 分量采用ARIMA模型预测,最后将各预测结果叠加得到年均气温的预测值。通过比较发现,EEMD-ARIMA 模型比EMD-ARIMA模型及ARIMA模型的预测结果具有更高的精确度。
2) 其次,因为通过 EEMD 分解得到的若干个 IMF 和 rs 之间相互独立,所以,对每一个 IMF 和 rs 进行 ARIMA 建模,并求出相应的预测值。
3) 最后,将所求得的每个分量的预测值相加,其和为最终的气温预测数据。
4. 模型应用
本节利用 EEMD-ARIMA 模型对沈阳市年平均气温数据建模分析。采用 1951 至 2013 年的年平均气 温数据作为训练样本,并用 2014 年至 2018 年的年均气温作为测试集。将 EEMD-ARIMA 的结果与 EMD-ARIMA 和 ARIMA 的结果对比分析。
3.1. ARIMA 模型
ARIMA(p, d, q)是最常用的时间序列模型[10] [11],其中 AR 是自回归过程,参数 p 是其自回归项项 数;MA 是移动平均过程,参数 q 是其移动平均项数;参数 d 是使研究对象的时间序列达到平稳状态的 差分次数。ARIMA(p, d, q)模型结构为:
Statistics and Application 统计学与应用, 2020, 9(2), 304-311 Published Online April 2020 in Hans. /journal/sa https:///10.12677/sa.2020.92033
Prediction of Temperature Based on EEMD-ARIMA Model
Yujie Jia, Penglei Chen, Li Zhu Ningbo University of Technology, Ningbo Zhejiang
Received: Apr. 9th, 2020; accepted: Apr. 22nd, 2020; published: Apr. 29th, 2020
Open Access
1. 引言
气温是描述某一地区气候特征的一个主要因素,通过对气温进行预测,可以在极端天气来临前起到 预警作用,并及时采取预防措施。传统的预测方法主要有多元线性回归法[1]、自回归移动平均法[2]和灰 色预测法[3]等,这些方法的预测结果比较趋于平均值,不仅难以应付海量的数据和天气的动态变化,而 且用于预测的气象数据多为时间序列,传统预测方法没有将数据的时间相关性考虑在内,导致出现预测 准确率低的问题,因此正逐渐被淘汰[4]。目前,应用较广泛的是以支持向量机、人工神经网络等为代表 的人工智能算法。如小波分析和非线性自回归(NVR)神经网络结合技术[5]、多元时间序列局部支持向量 回归方法[6],这些研究都能考虑到气象要素的时序多元性,却没实现精细化的气温预测,只能对相对稳 定的平均气温进行预测,限于研究的手段限制,最终得到的精度有限。
4.1. EMD 与 EEMD 去噪效果分析
用 EMD 和 EEMD 分别对沈阳 1951 至 2013 年的年平均气温数据进行处理。对原始信号进行 EMD 处理后得到 4 个 IMF 分量和 1 个残余分量,如图 2 所示。在图 2 中,分量 IMF1 代表着信号高频成分, 含有的噪声成分最多;分量 IMF2 和分量 IMF3 尺度区分不明显,存在模态混叠现象。
的 IMF 分量 cn (t ) 和趋势项 r (t ) :
∑ cs
(t) =
1 ne
ne
IMFis (t )
