蚂蚁怎么走最近(2)
蚂蚁怎么走最近

蚂蚁怎样走最近素材内容:八年级上册第一章《勾股定理》第3课第1课时《蚂蚁怎样走近》P22~P23知识与技能:探索、发现事物中隐含的勾股定理及其逆及理,并用它们解决生活实际问题.教育功能:学会观察图形,勇于探索图形间的关系,培养学生的空间观念. 前后联系:前----七年级上册第一章《丰富的图形世界》的《展开与折叠》,八年级上册第一章《勾股定理》计算与证明;后----八年级上册第四章《四边形性质的探索》 。
素材分析: 在教学活动中,首先通过设计具体有趣的问题情境,引起学生的学习数学的兴趣,经历一般规律的探索过程。
在将实际问题抽象成几何图形过程中提高分析问题、解决问题的能力及渗透数学建模的思想,体验数学学习的实用性.教学设计:一、创设情境,激发学习情趣.(学生观察、猜想)如图:在一个圆柱,它的高等于12厘米,底面半径等于12厘米,在圆柱下底面的A 点有一只蚂蚁,它想吃到上底面与A 点相对的食物在B 点处的食物,沿圆柱侧面从A 处爬向B 处,你们想一想,蚂蚁怎么走最近?(π取3)二、小组合作,探究规律学生分为4人活动小组,合作探究蚂蚁爬行的最短路线,充分讨论后,汇总各小组的方案,在全班范围内讨论每种方案的路线计算方法,通过具体计算,总结出最短路线。
学生汇总了四种方案:(1) (2) (3) (4)学生很容易算出:情形(1)中A →B 的路线长为(设直径为d):AC +d , 情形(2)中A →B 的路线长为:AC +2d π C C’ C ’ C ’所以情形(1)的路线比情形(4)要短.学生在情形(3)和(4)的比较中出现困难,但还是有学生提出用剪刀沿母线AA ’剪开圆柱得到矩形,前三种情形A →B 是折线,而情形(4)是线段,故根据两点之间线段最短可判断(4)最短.如图:(1)中A →B 的路线长为:AC ’+d ;(2)中A →B 的路线长为:AC +CB >AB ;(3)中A →B 的路线长为:AM +MB >AB ;(4)中A →B 的路线长为:AB .三、总结规律,归纳算法 让学生发现:沿圆柱体母线剪开后展开得到矩形,研究“蚂蚁怎么走最近”就是研究两点连线最短问题,引导学生体会利用数学解决实际问题的方法:建立数学模型,构图,计算.得出结论:利用展开图中两点之间,线段最短解决问题.在这个环节中,可让学生沿母线剪开圆柱体,具体观察.接下来后提问:怎样计算AB ?在Rt △ACB 中,利用勾股定理可得222AC CB AB +=,已知圆柱体高为12cm ,底面半径为3cm ,π取3,则22212(33),15AB AB =+⨯∴=.M B C A。
蚂蚁怎样走最近习题

随堂练习1、放学以后,小红和小颖从学校分手,分别沿东南方向和西南方向回家,若小红和小颖行走的速度都是40米/分,小红用15分钟到家,小颖20分钟到家,小红和小颖家的直线距离为()A.600米 B. 800米 C. 1000米 D. 不能确定2、如图,在水塔O的东北方向32m处有一抽水站A,在水塔的东南方向24m处有一建筑工地B,在AB间建一条直水管,则水管的长为()A. 45mB.40mC. 50mD.56m.3、已知在Rt△ABC中,∠C=90°,①若a=14,b=48,则c=________;②若a=8,c=17,则b=_______.4、在△ABC中,∠C=900,,BC=60cm,CA=80cm,一只蜗牛从C点出发,以20cm/s的速度沿CA-AB-BC 的路径再回到C点,需要分的时间.5、在水塔O的东北方向32m处有一抽水站A,在水塔的东南方向24m处有一建筑工地B,在AB间建一条直水管,则水管的长为()A. 45mB.40mC. 50mD.56m.6、如图,四边形是正方形,垂直于,且=3,=4,阴影部分的面积是______.7、在直角三角形中,斜边=2,则=______.8、有一圆柱体高为10cm,底面圆的半径为4cm,AA1、BB1为相对的两条母线。
在AA1上有一个蜘蛛Q,QA=3cm;在BB1上有一只苍蝇P,PB1=2cm。
蜘蛛沿圆柱体侧面爬到P点吃苍蝇,最短的路径是_________ cm。
(结果用带π和根号的式子表示)9、如图是一个长方体长4、宽3、高12,则图中阴影部分的三角形的周长为__________10、如图,已知正方体的棱长为2cm(1)求一只蚂蚁从A 点到F 点的距离。
(2)如果蚂蚁从A 点到G 点,求蚂蚁爬行的距离。
(3)如果蚂蚁从A 点到CG 边中点M ,求蚂蚁爬行的距离。
变式:将正方体改为长方体,长为AB=4cm ,宽BC=2cm ,高GC=3cm , 试求上述蚂蚁行走的对应路线的长。
1.3蚂蚁怎样走最近习题
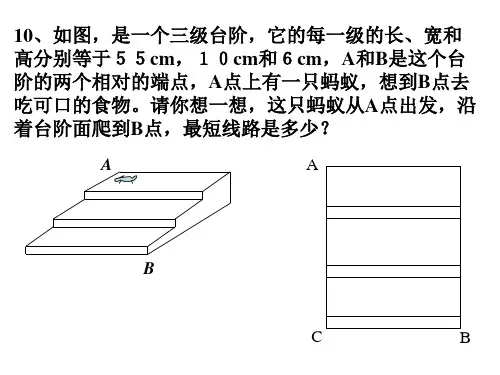
10、如图,是一个三级台阶,它的每一级的长、宽和 、如图,是一个三级台阶,它的每一级的长、 高分别等于55 55cm,10cm和 高分别等于55 ,10 和6cm,A和B是这个台 , 和 是这个台 阶的两个相对的端点, 点上有一只蚂蚁 想到B点去 点上有一只蚂蚁, 阶的两个相对的端点,A点上有一只蚂蚁,想到 点去 吃可口的食物。请你想一想,这只蚂蚁从A点出发 点出发, 吃可口的食物。请你想一想,这只蚂蚁从 点出发,沿 着台阶面爬到B点 最短线路是多少? 着台阶面爬到 点,最短线路是多少?
A A
B
C
B
11、如图,把长方形纸片ABCD折叠,使顶 点A与顶点C重合在一起,EF为折痕。若 AB=9,BC=3,试求以折痕EF为边长的正方 形面积。
E D C
A
G
F
B
12、假期中,王强和同学到某海岛上去玩 探宝游戏,按照探宝图,他们登陆后先往 东走8千米,又往北走2千米,遇到障碍后 又往西走3千米,在折向北走到6千米处往 东一拐,仅走1千米就找到宝藏,问登陆点 A 到宝藏埋藏点B的距离是多少千米?
H G F B
D A C
H
B1
F
B3
G
B2
A
C
D
在一棵树的10米高处 有两只猴子 在一棵树的 米高处B有两只猴子, 米高处 有两只猴子, 其中一只猴子爬下树走到离树20米的 其中一只猴子爬下树走到离树 米的 池塘A,另一只猴子爬到树顶D后直接 池塘 ,另一只猴子爬到树顶 后直接 跃向池塘的A处 跃向池塘的 处,如果两只猴子所经过 距离相等,试问这棵树有多高? 距离相等,试问这棵树有多高? D B. C A
1 6 3 2 A 8 B
探索与提高:
如图所示,现在已测得长方体木块的长 3厘米,宽4厘米,高24厘米。一只蜘蛛潜 伏在木块的一个顶点A处,一只苍蝇在这 个长方体上和蜘蛛相对的顶点B处。
蚂蚁怎样走最近训练题

蚂蚁怎样走最近训练题蚂蚁可真是个聪明的家伙,走路不光是为了找食物,还是为了找到最短的路。
这种本能真是让人忍不住赞叹,它们就像天生的“寻路小能手”,只要一有目标,立刻就能找到通往目的地的捷径。
你可能会好奇,蚂蚁到底是怎么做到的呢?难道它们不迷路吗?答案很简单,蚂蚁的“智慧”就藏在它们的习性里。
说实话,蚂蚁的找路能力简直可以用“如鱼得水”来形容。
你看啊,一只蚂蚁走得慢吞吞的,好像完全没什么紧张感,走得自得其乐。
但是它每次出发,都不是瞎走,它是有“路线图”的!从它家出发,直接走到食物源,这路上的每一步,都不是空走的。
它靠的,就是自己留在地上的“信息素”。
没错,蚂蚁的“智慧”就是靠这些化学物质来进行导航的。
蚂蚁一走过,脚下就会留下气味,这个气味就像是一种信号,告诉其他蚂蚁:“嘿,我找到路了!走这条路快!”而且最妙的是,蚂蚁之间的沟通根本不是嘴巴聊的,它们完全靠这种“气味语言”来互通信息。
你想啊,蚂蚁走了一段,发现路好像不太对劲,走了一段又掉头,这些信息都会通过留下的气味,快速地传递给它们的同伴。
于是,蚂蚁就会一边走,一边感应到别的蚂蚁走过的气味,慢慢地找到了最优的路径。
你能想象吗?这一整套操作,看似简单,实际却高效得不得了。
不过啊,要说到最神奇的,还是蚂蚁在面对选择的时候,它们完全不是盲目地跟随别人走。
它们会根据地上不同的气味强度来判断,哪条路更短,哪条路更有效率。
就像是你去吃饭时,看到大街上的人排队,看到哪个餐厅排的人多,你就觉得那个地方的饭肯定好吃,顺着人流走。
蚂蚁也是这么做的,它们会跟着气味最浓的那条路走,越走越快,越走越准,最后竟然找到了最佳的路线。
我们人类也能从蚂蚁的行为中学到点东西。
就拿我们自己找工作来说吧,如果找工作的方法不对,可能就会绕弯子,白白浪费时间。
就像蚂蚁一样,找到捷径才是王道,千万别总是觉得漫无目的地走一走就能找到对的东西。
你想想,蚂蚁都能靠气味找到最近的路,我们怎么能不动脑筋呢?说到这里,我不得不提个小细节:蚂蚁并不是一开始就能找到最短的路。
1.3勾股定理的应用 蚂蚁怎样走最近说课稿 北师大版 八年级数学上册 第一章 勾股定理

1.3 勾股定理的应用引言勾股定理是数学中的一个重要定理,它是我们学习数学的基础。
在八年级数学上册的第一章中,我们学习了勾股定理以及它的应用。
在本文档中,我们将重点讨论勾股定理的应用之一:蚂蚁怎样走最近。
蚂蚁怎样走最近在我们的日常生活中,我们经常会遇到类似的问题:蚂蚁在平面上的两个点之间移动,它应该选择怎样的路径才能够走得最近呢?这个问题可以通过勾股定理来解决。
假设蚂蚁需要从点A到达点B,我们可以将平面上的点A和点B连接起来,形成一条直线。
根据勾股定理,直角三角形的斜边的长度等于两个直角边长度的平方和的平方根。
因此,我们可以通过计算直线AB的长度,再结合其他已知条件,来确定蚂蚁应该走的最短路径。
解决问题的步骤在解决蚂蚁怎样走最近的问题时,我们可以按照以下步骤进行:1.确定两点的坐标:首先,我们需要确定点A和点B的坐标。
假设点A的坐标为(x1, y1),点B的坐标为(x2, y2)。
2.计算直线AB的长度:根据勾股定理,直线AB的长度可以通过以下公式计算:AB = √((x2-x1)^2 + (y2-y1)^2)。
3.根据其他条件确定最短路径:除了直线AB的长度,我们还需要根据其他条件来确定最短路径,例如是否存在障碍物等。
示例接下来,我们通过一个示例来演示蚂蚁怎样走最近的问题。
假设蚂蚁需要从点A(1, 2)到达点B(4, 6),我们需要确定蚂蚁应该走的最短路径。
首先,我们可以计算直线AB的长度:AB = √((4-1)^2 + (6-2)^2) = √(3^2 + 4^2) = √(9 + 16) = √25 = 5因此,直线AB的长度为5。
接下来,我们需要根据其他条件确定最短路径。
假设在点C(2, 4)处存在一个障碍物,蚂蚁不能穿过障碍物。
根据直线AB的长度为5,我们可以尝试绘制一条与直线AB等长的线段CD,并且使得线段CD与直线AB垂直相交。
请注意,我们可以使用勾股定理来计算线段CD的长度。
假设线段CD的长度为d,则有:d^2 + 4^2 = 5^2解方程,我们可以得到:d^2 + 16 = 25d^2 = 9d = 3因此,线段CD的长度为3。
第3节 蚂蚁怎么走最近

思考2:将圆柱侧面剪开展成一个长方形,从A点到B点的 最短路线是什么?你画对了吗?
答案:因为两点之间的连线中线段最短所以最短走法A→B.
拓展提升
已知油罐的底面周长是18米,高是12米,那么蚂蚁从A点出 发爬到B点,它需要的最短路程是多少呢?(π取3) 答案:当我们把圆柱的侧面展成长方形时,因为油罐的底 面周长是18米,即 2 r 18 ,因为π取3 所以 r 3 , 在Rt△AA′B中,已知AA′=12米,
要求: ⑴口头展示,声音洪亮、清楚;书面展示要分层次、 书写要认真、 规范。 ⑵非展示同学巩固基础知识、整理落实学案,做好拓展,不浪费 一分钟,小组长做好安排和检查。
展示内容
(一)基础知识探究: 探究点1 探究点2
点评小组
5、6组 3、4组 1、2组 7、8组
(二)知识综合应用究: 探究点1
探究点2
• 第三节 蚂蚁怎样走最近
导入新课
有一个圆柱形桶,在桶下底面的A点有 一只蚂蚁,它想吃到上底面与A点相对 的B处的食物,你知道蚂蚁爬行的最短 路线吗? B
A
学习目标
• 1.掌握勾股定理及其逆定理,能运用勾股定理 及直角三角形的判别条件解决简单的实际问题, 提高逻辑推理能力。 • 2.通过动手实践、合作探究,学会解决最短路 径问题的方法。 • 3.激情投入,体验成功学习的快乐。
要求: (1)人人参与,热烈讨论,大声表达自己的思想。 (2)组长控制好讨论节奏,先一对一分层讨论,再小组 内集中讨论。 (3)没解决的问题组长记录好,准备质疑。
展示内容
(一)基础知识探究: 探究点1 探究点2 (二)知识综合应用究: 探究点1 探究点2
展示小组
1、2组 7、8组
3、4组 5、6组
(北师大版)1.3蚂蚁怎样走最近课件
要对名称和术语的含义加以描述,作出明
确的规定,也就是给出它们的定义.
例如:
1、“具有中华人民共和国国籍的人,叫做中华人民共和国公民”
是“中华人民共和国公民”的定义;
2、“两点之间线段的长度,叫做两点之间的距距离”是“两点之
间的距离"的定义
3、“在一个方程中,只含有一个未知数,并且未知的指数是1,这
可;但要判断一个命题是真命题,该怎么办呢?
能用以前学习的观察、实验、验证特例的方法吗?
这我们在以前的学习过程中已经探讨过,这种方法不可
靠.那么,是否可以根据已经知道的真命题证实呢?试想一
下,这样的真命题又该如何证实它是正确的呢?
•如何证实一个命题是真命题呢?
其实,在数学发展史上,数学家们也遇到类似
据.这样公认为正确的命题叫做公理.
例如:“两点之间线段最短”,“三边分别相等的两个三角形全等”,“过直线外一点,有
且只有一条直线与已知直线平行”……
(2)什么是定理?它和公理有什么区别和联系?
定理:用推理的方法判断为正确的命题叫做定理.
定理和公理都可以作为判断其他命题真假的依据.
本套教科书选用九条基本事实作为证明的出发点和依据,我们已经认识了其中的八条:
注意:1、只要作出判断,无论正确与否,都是命题
2、没有作出判断,就不是命题
条件
结论
如果……那么……
例如:熊猫没有翅膀。
改写为:如果这个动物是熊猫,那么它就没有翅膀。
正确的命题
称为真命题,
不正确的命题
称为假命题。
说明假命题的方法:
举反例
使之具有命题的条件,而不具有命题的结论
要判断一个命题是假命题,只需要举出一个反例即
3.蚂蚁怎样走最近
(2) 如图所示,将圆柱侧面剪开展成一个长方形,
从A点到B点最短路线是什么?你画对了吗? B B
A
A
(3) 蚂蚁从A点出发,想吃到B点上的食物, 它需要爬行的最短路程是多少?
例1 李叔叔想要检测雕塑底座正面AD 边和BC边是否分别垂直于底边AB, 但他随身只带了卷尺.
.
(1)你能替他想办法完成 任务吗?
3 蚂蚁怎样走最近?
——勾股定理及其逆定理的
运用
问题:
• 如图所示,有一个圆柱, 它的高为12厘米,它的 半径为3厘米,在圆柱底 的A点有一只蚂蚁,它 想吃到上面与A对应的 B点 的食物,需要爬行 的最短路程是多少?
3
12
B
A
蚂蚁
(1)自己做 一个圆柱,尝试从A点到B点沿圆柱 侧面画出几条路线,你 觉得哪条路最近?
(2) 李叔叔量得AD边长30厘 米,AB
D
C
长是40厘米,BD长是50厘米.AD A 边垂直AB边吗?
(3) 小明随身只有一个长度为20厘米的
B
刻度尺,他能有办法检验AD边是否 垂直 AB边吗?BC与AC边呢?
三.导练:
例2.
甲.乙两位探险者到沙漠进 行探险.某日早晨8:00甲先出发, 他以6千米/时的速度向东行走.1 小时后乙出发,他以5千米/时的 速度向北行走.上午10:00,甲, 乙两人相距多远?
例3.• 已知某开发区有一块四边形的空地
ABCD ,如图所示.先计划在该空地 上种上草皮,经测量,∠A=900, AB=3cm,BC=12cm,CD=13cm, DA=4cm.若每平方米草皮需要200元, 问需要多少投入?
D C
A
BБайду номын сангаас
1.3勾股定理的应用-《蚂蚁怎样走最近》教案
一、教学内容
《蚂蚁怎样走最近》为七年级数学1.3勾股定理的应用部分。教学内容主要包括以下三个方面:
1.勾股定理的理解:回顾勾股定理的概念及证明方法,使学生深刻理解直角三角形两条直角边与斜边之间的关系。
2.勾股定理在实际问题中的应用:以蚂蚁走最近路线为例,让学生学会将实际问题转化为数学模型,运用勾股定理求解。
(二)新课讲授(用时10分钟)
1.理论介绍:首先,我们要了解勾股定理的基本概念。勾股定理描述的是直角三角形两条直角边与斜边之间的数量关系。它是数学中非常重要的定理,广泛应用于建筑、工程等领域。
2.案例分析:接下来,我们来看一个具体的案例——《蚂蚁怎样走最近》。这个案例展示了勾股定理在实际中的应用,以及它如何帮助我们解决最短路径问题。
在今后的教学中,我会继续改进教学方法,例如:
1.加强与生活的联系,让学生在学习中感受到数学的实用价值;
2.创设更多的问题情境,培养学生的批判性思维和问题解决能力;
3.注重学生的个体差异,因材施教,提高他们的自信心和自主学习能力;
4.加强课堂互动,鼓励学生提问,营造良好的学习氛围。
-如何在复杂情境中识别直角三角形,并确定哪两边是直角边,哪一边是斜边。
-解决问题的灵活性:难点在于培养学生的灵活思维,能够根据问题情境选择合适的解决方法,具体包括:
-面对不同的实际问题,能够灵活选择和应用勾股定理;
-在解决问题的过程中,能够考虑到多种可能性,并选择最优解。
四、教学流程
(一)导入新课(用时5分钟)
-勾股定理的定义及其表达式的记忆与理解;
-直角三角形三条边的关系,特别是斜边与两条直角边的关系;
-通过具体实例,如《蚂蚁怎样走最近》,让学生掌握如何将实际问题转化为直角三角形模型,并应用勾股定理求解。
3_蚂蚁怎样走最近_课件1
《九章算术》
“今有池方一丈,葭生其中央,出水一尺。引 葭赴岸,适与岸齐。问水深、葭长各几何?”
注:方:正方形 葭:芦苇.
1
丈:长度单位。1丈=10尺
5
《九章算术》
“今有池方一丈,葭生其中央,出水一尺。引 葭赴岸,适与岸齐。问水深、葭长各几何?” 解:设水池的深度为x尺, 则芦苇的长度为x+1尺 由勾股定理得 5 1 x2 +52=(x+1)2 x x2 +25= x2+2x+1 x+1 24= 2x x=12 答:水池的深度为12尺,芦苇的长度为13尺
B
3
①
A′ ③
B
12
B’ ② A A
(3)若圆柱的高为12,底面半径为3时,3条 路线分别多长? (π取3)
B
r
①
A′
③
B
h
B’ ② A
路线①
A
路线② 21 路线③ 15 最短 ③ ①③
h=12,r=3 h=3.75,r=3 h=2.625,r=3
18 9.75
12.75 9.75
8.625 11.625 9.375 ①
感谢您对文章的阅读跟下载,希望本 篇文章能帮助到您,建议您下载后自 己先查看一遍,把用不上的部分页面 删掉哦,当然包括最后一页,最后祝 您生活愉快!
其实,世上最温暖的语言,“ 不是我爱你,而是在一起。” 所以懂得才是最美的相遇!只有彼此以诚相待,彼
义务教育课程标准实验教科书
蚂蚁 怎样走最近?
1、你知道勾股定理的内容吗?
2、一个三角形的三条边分别为
温 故 而 知 新
a、b、c(c>a,b),如何判断
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
A
◆在长30cm、宽50 cm、高40 cm的木 箱中,如果在箱内的A处有一只昆虫, 它要在箱壁上爬行到B处,至少要爬多 远? B 30
D
.B
第一种情况 40
.A
C
30 50
B
40
A
D
30
D
图① 8040 8000
2 2
50
C
C
40
50
.B
B
50
. A
C
30
D
2
C
勾股定理的实际运用
蚂蚁怎样走最近
1、如图,是一个三级台阶,它的每一级的长、宽和高 分别等于55cm,10cm和6cm,A和B是这个台 阶的两个相对的端点,A点上有一只蚂蚁,想到B点去 吃可口的食物。请你想一想,这只蚂蚁从A点出发,沿 着台阶面爬到B点,最短线路是多少?
A A
B
解:台阶的展开图如图:连结AB 在Rt△ABC中根据勾股定理 AB2=BC2+AC2 =552+482=5329 ∴AB=73cm
你学会了吗?
讲解
想一想
思考:若该只蚂蚁从点A出发,沿着圆柱的表面爬
行到点C,那它爬行的最短路程还是约为10.77cm吗?
问题的延伸:
如图,在棱长为10厘米的
B
正方体的一个顶点A处有 一只蚂蚁,现要向顶点B 处爬行,已知蚂蚁爬行的 速度是1厘米\秒,且速度 保持不变,问蚂蚁能否在 20秒内从A爬到B?
A
问题的延伸:
40
第二种情况
3090 9000A 30
2
D
图②
C
40
30
.B
第三种情况
B
D
30
. A
C 50
C
40
2
D 5070 7400
2
50
A
图③
H
B
F
1
B
3
G
B
2
A
C
D
通过今天的学习, 用你自己的话说说你的收获和体会?
本节课主要是应用勾股定理和它的逆定理来解 决实际问题,在应用定理时,应注意:1、没 有图的要按题意画好图并标上字母;2、不要 用错定理。
C
B
例题
例1:如图,一圆柱体的底面周长为20cm,高AB为 4cm,BC是上底面的直径.一只蚂蚁从点A出发,沿着 圆柱的侧面爬行到点C,试求出爬行的最短路程(精确 到0.01cm)
想一想
讲解
分析:蚂蚁实际上是在圆柱的半个侧面内爬行, 如果将这半个侧面展开(如图),得到矩ABCD, 根据“两点之间,线段最短”,所求的最短路程 就是侧面展开图矩形对角线AC之长.
