信号与系统第一次作业
福师《信号与系统》在线作业一满分答案

福师《信号与系统》在线作业一试卷总分:100 测试时间:--一、单选题(共25 道试题,共50 分。
)1. 周期矩形脉冲的谱线间隔与( )。
A. 脉冲幅度有关B. 脉冲宽度有关C. 脉冲周期有关D. 周期和脉冲宽度有关满分:2 分2. 单位序列响应h(n)=2u(n)的系统是( )系统。
A. 因果及稳定B. 非因果及稳定C. 因果及非稳定D. 非因果及非稳定满分:2 分3. 一个含有3个电容、2个电感和3个电阻的系统,以下叙述正确的是( )。
A. 一定是2阶系统B. 一定是5阶系统C. 至多是2阶系统D. 至多是5阶系统满分:2 分4. f(t)的频宽是200Hz,那么f(-2t-6)的奈奎斯特频率为( )。
A. 400HzB. 200HzC. 800HzD. 100Hz满分:2 分5. 激励为x(n)时,响应y(n)=x(n)sin(2πn/7+π/6)的系统是( )系统。
A. 线性且时不变B. 非线性且时不变C. 线性且时变D. 非线性且时变满分:2 分6. 在变换域中解差分方程时,首先要对差分方程两端进行( )。
A. 傅立叶变换B. 拉普拉斯变换C. Z变换D. 以上答案都不正确满分:2 分7. 一个含有5个电容、1个电感和2个电阻的系统,以下叙述正确的是( )。
A. 一定是3阶系统B. 一定是6阶系统C. 至多是3阶系统D. 至多是6阶系统满分:2 分8. 信号f(t)=Acos(2000πt)+Bsin(200πt)的归一化功率等于( )。
A. A+BB. (A+B)/2C. A*A+B*BD. (A*A+B*B)/2满分:2 分9. 信号f(t)=Sa(100t)+Sa(50t)的最低抽样率等于( )。
A. 100/πB. π/100C. 100D. 1/100满分:2 分10. 某系统的系统函数为H(z)=z/[(z-4)*(z-1)],若该系统是稳定系统,则其收敛区为( )。
A. |z|<1B. |z|>4C. 1<|z|<4D. 以上答案都不对满分:2 分11. 信号f(t)=Sa(100t)+Sa(50t)的奈奎斯特间隔等于( )。
2014年9月份考试信号与系统第一次作业

2014年9月份考试信号与系统第一次作业一、单项选择题(本大题共100分,共 40 小题,每小题 2.5 分)1. 已知 f(t),为求f(t0-at) 应按下列哪种运算求得正确结果?(式中t,a都为正值)()。
A.B. f(at) 右移t0 C. f(at) 左移t/a D. f(-at) 右移t/a2. 系统函数H(s)与激励信号X(s)之间是()。
A. 反比关系 B. 无关系C. 线性关系D. 不确定3. 下列论断正确的为()。
A. 两个周期信号之和必为周期信号; B. 非周期信号一定是能量信号; C. 能量信号一定是非周期信号; D. 两个功率信号之和仍为功率信号。
4. 序列f(n)=cos(πn2)[ξ(n−2)−ξ(n−5)]的正确图形是()A.B.C.D.5. 已知某系统的系统函数为H(s),唯一决定该系统单位冲激响应h(t)函数形式的是( ) A. H(s)的零点 B. H(s)的极点 C. 系统的输入信号 D. 系统的输入信号与H(s)的极点6. 信号f 1(t ),f 2(t )波形如图所示,设f (t )=f 1(t )∗f 2(t ),则f (0)为( )A. 1B. 2C. 3D. 47. 某信号的频谱密度函数为则f(t) =( )。
A.B.C.D.8. 积分 (t −2)δt t0−ⅆt 等于( )A.B.C.D.9. 积分 e −2t t−∞δ(τ)ⅆτ等于( ) A.B.C.D.10. 信号f 1(t ),f 2(t )波形如图所示,设f (t )=f 1(t )∗f 2(t ),则f (0)为( )A. 0B. 1C. 2D. 311. 信号f 1(t ) 和 f 2(t )分别如图(a )和图(b)所示,已知 [f 1(t )]=F 1(jω),则f2(t)的傅里叶变换为()A.B.C.D.12. f(5-2t)是如下运算的结果————————() A. f(-2t)右移5B. f(-2t)左移5C. f(-2t)右移5/2D. f(-2t)左移5/213. 图(b)中与图(a)所示系统等价的系统是()A.B.C.D.14. 若系统的起始状态为0,在x(t)的激励下,所得的响应为———() A. 强迫响应 B. 稳态响应 C. 暂态响应 D. 零状态响应15. 已知信号f(t)的傅里叶变换<mml:math xmlns:mml="/1998/Math/MathML" xmlns:m="/officeDocument/2006/math"><mml:mrow ><mml:mi>F</mml:mi><mml:mo>(</mml:mo><mml:mi>j</mml:mi><mml:mi>&omega ;</mml:mi><mml:mo>)</mml:mo><mml:mo>=</mml:mo><mml:mi>δ</mml:mi ><mml:mo>(</mml:mo><mml:mi>ω</mml:mi><mml:mo>−</mml:mo><m ml:msub><mml:mrow><mml:mi>ω</mml:mi></mml:mrow><mml:mrow><mml:m n>0</mml:mn></mml:mrow></mml:msub><mml:mo>)</mml:mo></mml:mrow></mml: math>,则f(t)为()A.<mml:math xmlns:mml=" /1998/Math/MathML" xmlns:m=" /officeDocument/2006/math"><mml:mact ionactiontype="link"><mml:mrow><mml:mfrac><mml:mrow><mml:mn>1</mml:mn></ mml:mrow><mml:mrow><mml:mn>2</mml:mn><mml:mi>π</mml:mi></mml:mrow></ mml:mfrac><mml:msup><mml:mrow><mml:mi>e</mml:mi></mml:mrow><mml:mrow> <mml:mi>j</mml:mi><mml:msub><mml:mrow><mml:mi>w</mml:mi></mml:mrow><m ml:mrow><mml:mn>0</mml:mn></mml:mrow></mml:msub><mml:mi>t</mml:mi></m ml:mrow></mml:msup></mml:mrow></mml:math>B.<mml:math xmlns:mml=" /1998/Math/MathML" xmlns:m=" /officeDocument/2006/math"><mml:mact ionactiontype="link"><mml:mrow><mml:mfrac><mml:mrow><mml:mn>1</mml:mn></ mml:mrow><mml:mrow><mml:mn>2</mml:mn><mml:mi>π</mml:mi></mml:mrow></ mml:mfrac><mml:msup><mml:mrow><mml:mi>e</mml:mi></mml:mrow><mml:mrow> <mml:mo>−</mml:mo><mml:mi>j</mml:mi><mml:msub><mml:mrow><mml:mi>w</mml:mi></mm l:mrow><mml:mrow><mml:mn>0</mml:mn></mml:mrow></mml:msub><mml:mi>t</m ml:mi></mml:mrow></mml:msup></mml:mrow></mml:math>C.<mml:math xmlns:mml=" /1998/Math/MathML" xmlns:m=" /officeDocument/2006/math"><mml:mact ionactiontype="link"><mml:mrow><mml:mfrac><mml:mrow><mml:mn>1</mml:mn></ mml:mrow><mml:mrow><mml:mn>2</mml:mn><mml:mi>π</mml:mi></mml:mrow></ mml:mfrac><mml:msup><mml:mrow><mml:mi>e</mml:mi></mml:mrow><mml:mrow> <mml:mi>j</mml:mi><mml:msub><mml:mrow><mml:mi>w</mml:mi></mml:mrow><m ml:mrow><mml:mn>0</mml:mn></mml:mrow></mml:msub><mml:mi>t</mml:mi></m ml:mrow></mml:msup><mml:mi>ξ</mml:mi><mml:mrow><mml:mo>(</mml:mo><mml:mi>t</mml:mi><mml:mo>)</mml :mo></mml:mrow></mml:mrow></mml:math>D.<mml:math xmlns:mml=" /1998/Math/MathML" xmlns:m=" /officeDocument/2006/math"><mml:mact ionactiontype="link"><mml:mrow><mml:mfrac><mml:mrow><mml:mn>1</mml:mn></ mml:mrow><mml:mrow><mml:mn>2</mml:mn><mml:mi>π</mml:mi></mml:mrow></ mml:mfrac><mml:msup><mml:mrow><mml:mi>e</mml:mi></mml:mrow><mml:mrow> <mml:mo>−</mml:mo><mml:mi>j</mml:mi><mml:msub><mml:mrow><mml:mi>w</mml:mi></mm l:mrow><mml:mrow><mml:mn>0</mml:mn></mml:mrow></mml:msub><mml:mi>t</m ml:mi></mml:mrow></mml:msup><mml:mi>ξ</mml:mi><mml:mrow><mml:mo>(</mml:mo><mml:mi>t</mml:mi><mml:mo>)</mml :mo></mml:mrow></mml:mrow></mml:math>16. 离散信号f(n)是指()A. n的取值是连续的,而f(n)的取值是任意的信号B. n的取值是离散的,而f(n)的取值是任意的信号C. n的取值是连续的,而f(n)的取值是连续的信号D. n的取值是连续的,而f(n)的取值是离散的信号17. 连续信号f(t)与δ(t−t0)的卷积,即f(t)∗δ(t−t0)=()) C.A. f(t)B. f(t-tδ(t)D.δ(t−t0)18. 信号f(t)=2e−2tξ(t)的拉氏变换及收敛域为()A.B.C.D.19. 若序列f(n)的图形如图(a)所示,那么f(-n+1)的图形为图(b)中的()A.B.C.D.20. 的拉氏反变换为()A.B.C.D.21. 若周期信号 f(t)是时间 t的奇函数,则其三角形傅里叶级数展开式中只含( )。
信号与系统第一次作业

《信号与系统》第一次作业姓名:学号:1. 判定以下系统是不是为线性系统,其中()y t 、[]y k 为系统的完全响应,(0)x 为系统初始状态,()f t 、[]f k 为系统输入鼓励。
(1)()(0)lg ()=y t x f t 解:在判定具有初始状态的系统是不是线性时,应从三个方面来判定。
一是可分解性,即系统的输出响应可分解为零输入响应与零状态响应之和。
二是零输入线性,系统的零输入响应必需对所有的初始状态呈现线性特性。
三是零状态线性,系统的零状态响应必需对所有的输入信号呈现线性特性。
只有这三个条件都符合,该系统才为线性系统。
()(0)lg ()=y t x f t 不具有可分解性,因此系统是非线性系统。
(2)[](0)[][1]=+-y k x f k f k解:y[k]具有可分解性,零输入响应x(0)是线性的,但零状态响应f[k]f[k-1]是非线性的,因此系统是非线性系统。
2. 判定以下系统是不是为线性非时变系统,什么缘故?其中()f t 、[]f k 为输入信号,()y t 、[]y k 为零状态响应。
(1)()()()=y t g t f t解:在判定系统的时不变特性时,不涉及系统的初始状态,只考虑系统的零状态响应。
系统零状态响应,g(t)f(t)知足均匀性和叠加性,因此系统是线性系统。
因为T{f(t-t0)}=g(t).f(t-to)而 y(t-t0)=g(t-t0).f(t-t0) ≠T{f(t-t0)},故该系统为时变系统。
因此该系统为线性时变系统(2)220[][],(0,1,2,)+===∑k i y k kf i k 解:220[][],(0,1,2,)+===∑k i y k k f i k 为线性时变系统。
3. 已知信号()f t 的波形如题1-3图所示,绘出以下信号的波形。
1t1f(t)-2-1-1题1-3图(1)(36)-+f t解:f(t) ——(波形数轴对称):f(-t)——【波形t轴方向,t值缩小至1/3,f(t)值不变】:f(-3t)——【波形往右横移6】:(36)-+f t最终画出波形图如下:(2)(1)3tf-+解:f(t) ——(波形数轴对称):f(-t)——【波形t轴方向,t值扩大3倍,f(t)值不变】:f(-⅓t)——【波形往右横移1】:(1)3tf-+最终画出波形图如下:4. 已知()(4)2(1)(1)2(1)tf t t t t t e u tδδδ-'=+-+++++,绘出()f t波形。
信号与系统 陈后金 第二版 课后习题答案(完整版)

(1) f (t) = 3sin 2t + 6 sinπ t
(2) f (t) = (a sin t) 2
(8)
f
(k)
=
cos⎜⎛ ⎝
πk 4
⎟⎞ ⎠
+
sin⎜⎛ ⎝
πk 8
⎟⎞ ⎠
−
2
cos⎜⎛ ⎝
πk 2
⎟⎞ ⎠
解:(1)因为 sin 2t 的周期为π ,而 sin πt 的周期为 2 。
显然,使方程
−∞
0
2-10 已知信号 f (t) 的波形如题 2-10 图所示,绘出下列信号的波形。
f (t)
2
1
−1 0
t 2
题 2-10 图
(3) f (5 − 3t) (7) f ′(t) 解:(3)将 f (t) 表示成如下的数学表达式
(5) f (t)u(1 − t)
由此得
⎧2
f
(t)
=
⎪ ⎨ ⎪ ⎩
f (t)u(1− t) 2
1
0.5
t
−1 0
1
(7)方法 1:几何法。由于 f (t) 的波形在 t = −1处有一个幅度为 2 的正跳变,所以 f ′(t) 在 此处会形成一个强度为 2 的冲激信号。同理,在 t = 0 处 f ′(t) 会形成一个强度为 1 的冲激信 号(方向向下,因为是负跳变),而在 0 < t < 2 的区间内有 f ′(t) = −0.5 (由 f (t) 的表达式可
第 1 页 共 27 页
《信号与系统》(陈后金等编)作业参考解答
(2)显然,该系统为非线性系统。 由于
T{f (t − t0 )}= Kf (t − t0 ) + f 2 (t − t0 ) = y(t − t0 )
信号与系统 于敏慧(第二版)第二周作业答案

y0(t)
1
t
0
2
4
(6) x(t) = dx0 (t) , h(t) = dh0 (t) 。
dt
dt
x(t) * h(t) = dx0 (t) * dh0 (t) = d 2 y0 (t)
dt dt
dt 2
x(t) ∗ h(t) = 0.5δ(t) − 0.5δ(t − 2)
2.10 求 y[n] = x1[n]* x2[n]* x3[n] 。 其 中 x1[n] = (0.5)n u[n] , x2[n] = u[n + 3] 和
(2)利用(1)的结果,求系统的逆系统的单位样值(脉冲)响应。
(3)利用(2)的结果,结合卷积性质,求一信号 x[n],使之满足
x[n]* h[n] = 2n (u[n] − u[n − 4])
解:(1) h[n] − Ah[n −1] = δ [n],其中 h[n] = (1 )n u[n] , 2
(通项: an = a1q n−1 )
n
∑ 此题: a1 = 1, q = 2 ; x[n]* h[n] = 2nu[n]*u[n] = ( 2k )u[n] = (2n+1 −1)u[n] k =0
2.6 计算图 2-45(b)与(c)所示信号 x(n)与 h(n)的卷积和,注意:N=4。 解:(b)利用脉冲信号δ(n)的卷积性质以及卷积的延时性质计算:
k =−∞
+ 3] =
u[n + 3] 0.5k
k =0
;
= 2(1 − 0.5n+4 )u[n + 3]
(2) x1[n]* x2[n]* x3[n] = 2(1 − 0.5n+4 )u[n + 3]* (δ [n] − δ [n −1]) ; = 2(1 − 0.5n+4 )u[n + 3] − 2(1 − 0.5n+3 )u[n + 2]
东南大学信号与系统MATLAB实践第一次作业

<信号与系统MATLAB实践> 练习一实验一二. 熟悉简单的矩阵输入1.实验代码>>A=[1,2,3;4,5,6;7,8,9]实验结果A =1 2 34 5 67 8 93.实验代码>>B=[9,8,7;6,5,4;3,2,1]C=[4,5,6;7,8,9;1,2,3]实验结果:B =9 8 76 5 43 2 1C =4 5 67 8 91 2 3 4.>> AA =1 2 34 5 67 8 9>> BB =9 8 76 5 43 2 1C =4 5 67 8 91 2 3三. 根本序列运算1.>>A=[1,2,3],B=[4,5,6]A =1 2 3B =4 5 6 >> C=A+BC =5 7 9 >> D=A-BD =-3 -3 -3 >> E=A.*BE =4 10 18 >> F=A./BF =>> G=A.^B1 32 729 >> stem(A)>>stem(B)>> stem(D)>> stem(F)再举例:>> a=[-1,-2,-3] a =-1 -2 -3 >> b=[-4,-5,-6]b =-4 -5 -6 >> c=a+bc =-5 -7 -9 >> d=a-bd =3 3 3 >> e=a.*be =4 10 18 >> f=a./bf =>> g=a.^bg =>> stem(a)>> stem(c)>> stem(e)>> stem(g)2. >>t=0:0.001:10f=5*exp(-t)+3*exp(-2*t);plot(t,f)ylabel('f(t)');xlabel('t');title('(1)');>> t=0:0.001:3;f=(sin(3*t))./(3*t);plot(t,f)ylabel('f(t)');xlabel('t');title('(2)');>> k=0:1:4;f=exp(k); 1 1.52 2.53 3.54 4.550102030405060四. 利用MATLAB求解线性方程组2.>>A=[1,1,1;1,-2,1;1,2,3]b=[2;-1;-1]x=inv(A)*bA =1 1 11 -2 11 2 3b =2-1-1x =4.>> A=[2,3,-1;3,-2,1;1,2,1]b=[18;8;24]x=inv(A)*bA =2 3 -13 -2 11 2 1b =18824x =468实验二二.1.>> k=0:50x=sin(k);stem(x)xlabel('k');ylabel('sinX');title('sin(k)ε(k)');2.>> k=-25:1:25x=sin(k)+sin(pi*k); stem(k,x)xlabel('k');ylabel('f(k)');title('sink+sinπk');3.>> k=3:50x=k.*sin(k);stem(k,x)xlabel('k');ylabel('f(k)');title('ksinkε(k-3)');4.%函数function y=f1(k)if k<0y=(-1)^k;else y=(-1)^k+(0.5)^k; end%运行代码for k=-10:1:10;y4(k+11)=f1(k);endk=-10:1:10;stem(k,y4);xlabel('k');ylabel('f(k)');title('4');七.2.>> f1=[1 1 1 1];f2=[3 2 1];conv(f1,f2)ans =3 5 6 6 3 1 3.函数定义:function [r]= pulse( k )if k<0r=0;elser=1;endend运行代码for k=1:10f1(k)=pulse(k);f2(k)=(0.5^k)*pulse(k);endconv(f1,f2)结果ans =Columns 1 through 10 Columns 11 through 20 Columns 21 through 30 Columns 31 through 394for i=1:10f1(i)=pulse(i);f2(i)=((-0.5)^i)*pulse(i); endconv(f1,f2)结果ans =Columns 1 through 10 Columns 11 through 20 Columns 21 through 30 Columns 31 through 39实验三2.clear;x=[1,2,3,4,5,6,6,5,4,3,2,1];N=0:11;w=-pi:0.01:pi;m=length(x);n=length(w);for i=1:nF(i)=0;for k=1:mF(i)=F(i)+x(k)*exp(-1j*w(i)*k);endendF=F/10;subplot(2,1,1);plot(w,abs(F),'b-');xlabel('w');ylabel('F');title('幅度频谱');grid subplot(2,1,2);plot(w,angle(F),'b-');xlabel('w');X=fftshift(fft(x))/10;subplot(2,1,1);hold on;plot(N*2*pi/12-pi,abs(X),'r.');legend('DIFT算法','DFT算法');subplot(2,1,2);hold on;plot(N*2*pi/12-pi,angle(X),'r.');xlabel('w');ylabel('相位');title('相位频谱');grid三.1.function y=fun1(x)if((-pi<x) && (x<0))y=pi+x;elseif ((0<x) && (x<pi))y=pi-x;elsey=0endclear allclcfor i=1:1000g(i)=fun1(2/1000*i-1);w(i)=(i-1)*0.2*pi;endfor i=1001:10000g(i)=0;w(i)=(i-1)*0.2*pi;endG=fft(g)/1000;subplot(1,2,1);plot(w(1:50),abs(G(1:50)));xlabel('w');ylabel('G');title('DFT幅度频谱'); subplot(1,2,2);plot(w(1:50),angle(G(1:50)))xlabel('w');ylabel('Fi');title('DFT相位频谱');0102030400.511.522.53wGDFT 幅度频谱010203040-3.5-3-2.5-2-1.5-1-0.5wF iDFT 相位频谱2.function y=fun2(x) if x<1 && x>-1 y=cos(pi*x/2); elsey=0; endfor i=1:1000g(i)=fun2(2/1000*i-1); w(i)=(i-1)*0.2*pi; endfor i=1001:10000 g(i)=0;w(i)=(i-1)*0.2*pi; endG=fft(g)/1000; subplot(1,2,1);plot(w(1:50),abs(G(1:50)));xlabel('w');ylabel('G');title('幅度频谱');subplot(1,2,2);plot(w(1:50),angle(G(1:50)))xlabel('w');ylabel('Fi');title('相位频谱');0102030400.10.20.30.40.50.60.7wGDFT 幅度频谱010203040-4-3-2-1123wF iDFT 相位频谱3.function y=fun3(x) if x<0 && x>-1 y=1;elseif x>0 && x<1 y=-1; elsey=0 endfor i=1:1000g(i)=fun3(2/1000*i-1); w(i)=(i-1)*0.2*pi; endfor i=1001:10000 g(i)=0;w(i)=(i-1)*0.2*pi;G=fft(g)/1000; subplot(1,2,1);plot(w(1:50),abs(G(1:50)));xlabel('w');ylabel('G');title('DFT 幅度频谱'); subplot(1,2,2);plot(w(1:50),angle(G(1:50)))xlabel('w');ylabel('Fi');title('DFT 相位频谱');0102030400.10.20.30.40.50.60.70.8wGDFT 幅度频谱010203040-4-3-2-1123wF iDFT 相位频谱练习二实验六一.用MA TLAB 语言描述如下系统,并求出极零点、 1.>> Ns=[1]; Ds=[1,1];sys1=tf(Ns,Ds) 实验结果: sys1 =-----s + 1>> [z,p,k]=tf2zp([1],[1,1])z =Empty matrix: 0-by-1p =-1k =12.>>Ns=[10]Ds=[1,-5,0]sys2=tf(Ns,Ds)实验结果:Ns =10Ds =1 -5 0sys2 =10---------s^2 - 5 s>>[z,p,k]=tf2zp([10],[1,-5,0]) z =Empty matrix: 0-by-1p =5k =10二.系统的系统函数如下,用MATLAB描述如下系统。
信号与系统第一次作业题及答案.doc
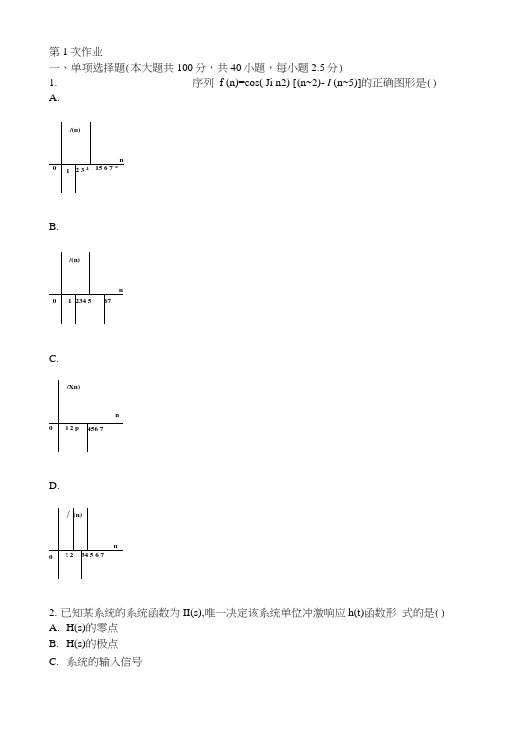
第1次作业一、单项选择题(本大题共100分,共40小题,每小题2.5分)1.序列f (n)=cos( Ji n2) [ (n~2)- I (n~5)]的正确图形是()A.B.C.D.2.已知某系统的系统函数为II(s),唯一决定该系统单位冲激响应h(t)函数形式的是()A.H(s)的零点B.H(s)的极点C.系统的输入信号D.系统的输入信号与H(s)的极点3.2人⑷1 ■—1 0 1 f信号fl(t),f2(t)波形如图所示,设f (t)=fl(t)*f2(t),则班0)为()A. 1B. 2C. 3D. 44.积分 / 0-1(1-2) 5 uBt 等于()A.-25(0B.—2 E(f)C.E(f — 2)D.28(Z - 2)5.积分f -°°tc-2t S ( T ) T等于()A.5(t)B.s(t)6(t) + £(t)6.信号fl(t),f2(t)波形如图所示,设f (t)二fl(t)*f2(t),则班0)为()7.信号fl(t)和f2(t)分别如图(a)和图(b)所示,已知[fl (t)]二Fl (j 3),则f2(t)的傅里叶变换为()A.B.Fi3)严C.F](-j3)"t D.F](j3)R8. f (5-2t)是如下运算的结果-------------------- ()A. f (-2t)右移5 B.f (-2t)左移5 C. f (-2t)右移5/2 D. f (-2t)左移5/29.图(b)中与图(a)所示系统等价的系统是()°_也⑷]- 低5}怙3(nj—B.C.D.°~T片⑹+対«亍和硏10.若系统的起始状态为0,在X (t)的激励下,所得的响应为------------ ()A.强迫响应B.稳态响应C.暂态响应D.零状态响应11.已知信号f(t)的傅里叶变换F (jo)=8 (G)-G)0),则f(t)为()A.12 兀ejwOtB.12 n e-jwOtC.12 n ejwOt g (t)D.12 n e-jwOt C (t)12.离散信号f(n)是指()A.n的取值是连续的,而f(n)的取值是任意的信号B.n的取值是离散的,而f(n)的取值是任意的信号C.n的取值是连续的,而f(n)的取值是连续的信号D.n的取值是连续的,而f(n)的取值是离散的信号13.连续信号f(t)与5 (t-tO)的卷积,即f(t)*6 (t-tO)=()A.f(t)B.f(t-t0)C.[M_0358B313EDB3D0D4D6B97EE407844428]D.[M_AF1077E401C920A05C155CBlBB3B2274]14.信号f(t)=2e-2tg (t)的拉氏变换及收敛域为()A.丄;止何>2a— 2B.丄,班⑻<-2s+ 2C.护心2D.1s+215.若序列f(n)的图形如图(a)所示,那么f(-n+1)的图形为图(b)中的Il •< 1 -t •> |e::)B.心:|1f /Q •» -1 T 0 1 t 3c.• /(•*•!>11 *•1 •> •: • 1 ■ ■ ■0 13 3D.4…1 卜m :11・▼ ■ ■ ▼ ■ M •> <2 •; 0.2316. 警尸/+6饨⑸>一2的拉氏反变换为()A.[戶+2尹向)B.[戶-2尹]屮)C.80) + 已亠£0)D.17.若周期信号f(t)是吋间t的奇函数,则其三角形傅里叶级数展开式中只含()。
信号与系统第一章作业

10 级《信号与系统》 第一章作业 物理与电子工程学院 电子系 专业班级班 学号 姓名 题号一 二 三 四 五 六 七 八 九 十 总分 评卷人 分数20 20 10 50 100 评分 承江红一、单项选择题(每小题2分,共20分)1、已知 f(t),为求 f(32t),应按下列哪种运算求得正确结果?答案:_____A. f(2t)左移 3个单位B. f(2t)右移 3 个单位C. f(2t)左移 3/2个单位D. f(2t)右移 3/2 个单位2、下列说法正确的是:__________________A.线性时不变系统一定具备叠加性与均匀性;B.线性时不变系统一定是无记忆系统;C.线性时不变系统一定是稳定系统;D.线性时不变系统一定是可逆系统;3、下列函数式中哪一个是连续时间信号的表示?答案:_____________A.e at sin w tB.cos(n p )C.(0.5) nD. Sin(n w 0)4、下列各式为描述连续时间系统的微分方程,已知系统的激励为 e(t),响应为 r(t)。
其中______ 方程描述的系统是线性时不变系统。
A. ) ( ) 4 5 sin( ( t e t t r + = )B. ) ( ) ( 3 ) ( 2 t e t r dtt dr t = + C. ) 2 ( ) ( t e t r = D. ) ( ) ( 3 ( 2 ) ( 3 ) ( 2 2 2 2 t e dtt e d t r dt t dr dt t r d + = + + ) 5、下列各式为描述离散时间系统的差分方程,已知系统的激励为 y(n),响应为 x(n)。
其中______ 方程描述的系统是线性、时不变、无记忆的系统。
A. )( 3 ) ( n x n y = B. ) 3 cos( ) ( 2 ) ( n n x n y = C. ) ( ( 2 n x n y = ) D. )( ) 1 ( 4 ) ( n x n y n y = - + 6、信号x(n), n=0,1,2,3,…是能量有限的意思是 ( )a) x (n )有限;b) |x (n )|有界;c) ( ) 2 0 n x n ¥= <¥ å ; d) ( ) 0 1 Nn x n N = <¥ å 。
