管理运筹学线性规划在工商管理中的应用
运筹学应用例题
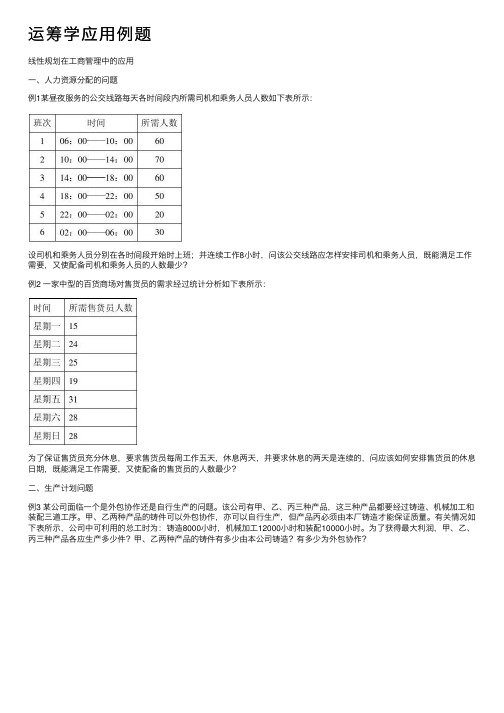
运筹学应⽤例题线性规划在⼯商管理中的应⽤⼀、⼈⼒资源分配的问题例1某昼夜服务的公交线路每天各时间段内所需司机和乘务⼈员⼈数如下表所⽰:设司机和乘务⼈员分别在各时间段开始时上班;并连续⼯作8⼩时,问该公交线路应怎样安排司机和乘务⼈员,既能满⾜⼯作需要,⼜使配备司机和乘务⼈员的⼈数最少?例2 ⼀家中型的百货商场对售货员的需求经过统计分析如下表所⽰:为了保证售货员充分休息,要求售货员每周⼯作五天,休息两天,并要求休息的两天是连续的,问应该如何安排售货员的休息⽇期,既能满⾜⼯作需要,⼜使配备的售货员的⼈数最少?⼆、⽣产计划问题例3 某公司⾯临⼀个是外包协作还是⾃⾏⽣产的问题。
该公司有甲、⼄、丙三种产品,这三种产品都要经过铸造、机械加⼯和装配三道⼯序。
甲、⼄两种产品的铸件可以外包协作,亦可以⾃⾏⽣产,但产品丙必须由本⼚铸造才能保证质量。
有关情况如下表所⽰,公司中可利⽤的总⼯时为:铸造8000⼩时,机械加⼯12000⼩时和装配10000⼩时。
为了获得最⼤利润,甲、⼄、丙三种产品各应⽣产多少件?甲、⼄两种产品的铸件有多少由本公司铸造?有多少为外包协作?三、套裁下料问题例4 某⼯⼚要做100套钢架,每套钢架需要长度分别为2.9⽶、2.1⽶、和1.5⽶的圆钢各⼀根。
已知原料每根长7.4⽶,问应如何下料,可使所⽤原料最省?四、配料问题例5某⼯⼚要⽤三种原料1、2、3混合调配出三种不同规格的产品甲、⼄、丙,产品的规格要求、产品的单价、每天能供应的原材料数量及原材料单价如下表所⽰:问该⼚应如何安排⽣产,才能使利润最⼤?五、投资问题例6 某部门现有资⾦200万元,今后五年内考虑给以下的项⽬投资:项⽬A :从第⼀年到第五年每年年初都可以投资,当年末能收回本利110%;项⽬B :从第⼀年到第四年每年年初都可以投资,次年末能收回本利125%,但规定每年最⼤投资额不能超过30万元;项⽬C :第三年初需要投资,到第五年末能收回本利140%,但规定每年最⼤投资额不能超过80万元;项⽬D :第⼆年初需要投资,到第五年末能收回本利155%,但规定每年最⼤投资额不能超过100万元。
线性规划在工商管理中的应用

A
B C
3.1
2.1 1.2
1
2 4
现在问题归结于:采用上述五种截法各截多少根圆钢,才能配成100套轴件,且使 总下料所用圆钢根数最少?
•
设x1,x2,x3,x4,x5分别为上面 5 种方案下料的原材料根数。这样我们建 立如下的数学模型。 – 目标函数: Minz= x1 + x2 + x3 + x4 + x5 – 约束条件: s.t. x1 + x2 + ≥ 100 x1 +2x3 + x4 ≥ 200 2x2 + x3+ 2x4+ 4x5 ≥ 400 x1, x2, x3, x4, x5 ≥ 0
3
套裁下料问题
• • •
制造某种机床,需要A,B,C三种轴件,其规格与数量见表三,各类轴件都用 5,。5米长的同一种圆钢下料。若生产机床100太,至少要用多少根圆钢? 首先考虑一根长5.5米的圆钢A,B C3种轴的毛坯有哪些具体的下料方式? 表三: 表四: 轴件 规格 每台机床所 需轴件数 五 0 0 4 4.8 0.7 四 0 1 2 4.5 1 三 0 2 1 5.4 0.1 二 1 0 2 5.5 0 一 1 1 0 5.2 0.3 3.1 2.1 1.2 合计 剩余
零部件
基座 BM-1电子管 TE-1电子管 BM-1面板 TE-1面板
部件制 自制成本 造工时 1 3 2.5 1 1.5 0.50 3.75 3.30 0.60 0.75
购买成本
0.60 4.00 3.90 0.65 0.78
需求量
5000 3000 2000 3000 2000
• 解:设: x1, x2, x3, x4, x5,分别为上述5中零部件的自制数量。相应设, y1,y2,y3, y4, y5分别为各部件的外购量。设y0为加工时书,怎问题的目标函数为:
线性规划在工商管理中的应用

线性规划的定义
01
线性规划是一种优化方法,用于解决线性约束条件下的优化问题
02
线性规划的目标是找到一组决策变量,使得目标函数达到最优值
03
线性规划的约束条件包括线性不等式约束和线性等式约束
04
线性规划的决策变量可以是连续的,也可以是离散的,但目标函数必须是线性的
线性规划的适用范围
01 线性规划适用于解决线性 目标函数和线性约束条件 的优化问题
线性规划在库存管理中的应用:通过优化库存 管理,降低库存成本,提高库存周转率
线性规划在供应链管理中的应用:通过优化供 应链管理,降低供应链成本,提高供应链效率
线性规划在销售预测中的应用:通过优化销售 预测,提高销售预测准确性,降低销售风险
运输与配送优化
D
线性规划在运输与配送优化中的实际应用案例
C 线性规划在运输与配送优化中的求解方法
粒子群优化算法: 模拟鸟群飞行,实 现全局优化
模拟退火算法:模 拟金属退火过程, 实现全局优化
启发式优化算法: 根据问题特点,实 现局部优化
跨学科的融合与创新
01
线性规划与其他 学科的融合:如 经济学、统计学、
计算机科学等
02
创新方法:如遗 传算法、模拟退 火算法、神经网
络等
03
应用领域:如供 应链管理、人力 资源管理、财务
某投资公司风险评估案例
背景:某投资公 司需要对其投资 项目进行风险评 估,以确定投资 策略
目标:通过线性 规划方法,评估 投资项目的风险 和收益
模型构建:建立 线性规划模型, 包括投资项目、 风险因素、收益 因素等变量
求解:通过求解 线性规划模型, 得到最优投资策 略
结果:根据求解 结果,确定投资 项目的风险和收 益,为投资决策 提供依据
《管理运筹学》第三版习题答案(韩伯棠教授)

0.057(其他
c 不变时, c 在 2 到正无穷的范围内变化,其最优解不变
2 1
e 约束条件 1 的右边值在 300000 到正无穷的范围内变化,对偶价格仍为 0.1 约束条件 2 的右边值在 0 到 1200000 的范围内变化,对偶价格仍为-0.06 600000 300000 f + = 100% 故对偶价格不变 900000 900000 4、解: a x1 = 8 5 x2 = 1 5 x3 = 0 x4 = 1 最优目标函数 18.5
s = 0, s = 0, s = 13
1 2 3
6 、解: b 1 ≤ c1 ≤ 3 c 2 ≤ c2 ≤ 6 d x1 = 6 x2 = 4
e x 1 ∈ [ 4 , 8 ] x 2 = 16 − 2 x 1 f 变化。原斜率从 − 7、解: 模型:
1
2 3
变为− 1
max z = 500x + 400x 2x 1 ≤ 300 3x 2 ≤ 540 2x + 2x ≤ 440
设按 14 种方案下料的原材料的根数分别为 x1,x2,x3,x4,x5,x6,x7,x8,x9, x10, x11,x12,x13,x14,则可列出下面的数学模型: min f = x1+x2+x3+x4+x5+x6+x7+x8+x9+x10+x11+x12+x13+x14 s.t. 2x1+x2+x3+x4 ≥ 80 x2+3x5+2x6+2x7+x8+x9+x10 ≥ 350 x3+x6+2x8+x9+3x11+x12+x13 ≥ 420 x4+x7+x9+2x10+x12+2x13+3x14 ≥ 10 x1,x2,x3,x4,x5,x6,x7,x8,x9,x10,x11,x12,x13,x14≥ 0 用 管理运筹学软件我们可以求得此问题的解为: x1=40,x2=0,x3=0,x4=0,x5=116.667,x6=0,x7=0,x8=0, x9 =0,x10=0,x11=140,x12=0,x13=0,x14=3.333 最优值为 300。 2、解:从上午 11 时到下午 10 时分成 11 个班次,设 xi表示第 i 班次安排的临时 工的人数,则可列出下面的数学模型: min f = 16 ( x1+x2+x3+x4+x5+x6+x7+x8+x9+x10+x11 ) s.t. x1+1 ≥ 9 x1+x2+1 ≥ 9 x1+x2+x3+2 ≥ 9 x1+x2+x3+x4+2 ≥ 3
管理运筹学

管理运筹学第一章绪论P2 1.问题解决的过程的七个步骤:1)认清问题2)找出一些可供选择的方案3)确定目标或评估方案的标准4)评估各个方案5)选择一个最优方案6)执行此方案7)进行后评估:问题是否得到圆满解决P2 2.运筹学的分支:1)线性规划2)整数线性规划3)图与网络模型4)存储论5)排队论6)对策论7)排序与统筹论8)决策分析9)动态规划10)预测P3 3.运筹学在工商管理中的应用:1)生产计划2)库存管理3)运输问题4)人事管理5)市场营销6)财务和会计第二章线性规划的图解法1.线性规划问题的建模过程:(1)理解要解决的问题(2)定义决策变量(3)写出目标函数(4)表示约束条件2.一个“≤”约束条件中没有使用的资源或能力称之为松弛量,相应的变量称为松弛变量;对于“≥”约束条件,可以增加一些代表最低约束的超过量,称之为剩余变量。
把所有的约束条件都写出等式,称为线性规划模型的标准化,所得结果称为线性规划的标准形式。
3.灵敏度分析包括目标函数中的系数的灵敏度分析和约束条件中的常数项的灵敏度分析。
4.在约束条件常数项中增加一个单位而使最优目标函数值得到改进的数量称之为这个约束条件的对偶价格。
当约束条件中的松弛变量(或剩余变量)不为零时,这个约束条件的对偶价格就为零。
※第三章线性规划问题的计算机求解1.理解图3-3的数据的含义。
※2.相差值提供的数值表示相应的决策变量的目标系数需要改进的数量,使得该决策变量有可能取正数值,当决策变量已取正数值时相差值为零。
3.所谓的上限与下限是指目标的决策变量的系数在此范围内变化时,其线性规划的最优解不变。
※4.百分之一百法则:对于所有变化的目标函数决策变量系数,当其所有允许增加百分比和允许减少百分比之和不超过百分之一百时,最优解不变。
第四章线性规划在工商管理中的应用1.人力资源分配问题p39例1和例2.2.生产计划的问题p41例3和例4.3.套裁下料问题p46例5.4.投资问题p51例8.第七章运输问题1.p128运输问题的线性规划模型。
管理运筹学--线性规划在工商管理中的应用 ppt课件

§1人力资源分配的问题
解:设 xi ( i = 1,2,…,7)表示星期一至日开始上班的 人数,这样我们建立如下的数学模型P40E21.lpp)。 目标函数: Min F = x1 + x2 + x3 + x4 + x5 + x6 + x7 约束条件: x4 + x5 + x6 + x7 + x1 ≥ 15 x5 + x6 + x7 + x1 + x2 ≥ 24 x6 + x7 + x1 + x2 + x3 ≥ 25 s.t. x7 + x1 + x2 + x3 + x4 ≥ 19 x1 + x2 + x3 + x4 + x5 ≥ 31 x2 + x3 + x4 + x5 + x6 ≥ 28 x3 + x4 + x5 + x6 + x7 ≥ 28 x1,x2,x3,x4 ,x5,x6,x7 ≥ 0 6 ppt课件
设备 A1 A2 B1 B2 B3 原料(元/件) 售价(元/件) Ⅰ 5 7 6 4 7 0.25 1.25 产品单件工时 Ⅱ Ⅲ 10 9 12 8 11 0.35 2.00 0.50 2.80
线性规划在工商管理中的应用

线性规划在工商管理中的应用摘要线性规划是运筹学的一个重要分支,它被广泛应用于工业、农业、商业等领域,来解决实际中的问题。
本文通过介绍线性规划及其在工商管理中应用的实例,来说明它在工商管理中的重要作用。
关键词运筹学;线性规划;方法;应用1.线性规划在工商管理中运用的广泛性工商管理[1]是研究工商企业经济管理基本理论和一般方法的学科,它通过运用现代管理的方法和手段来进行有效的企业管理和经营决策,保证企业的生存和发展。
在当今社会,随着市场竞争的日益加剧,如何统筹安排,合理利用有限的人力、物力、财力等资源,使总的经济效益最好,已经成为企业经营管理过程中实现利益最优必须解决的问题。
例如:人力资源分配:用最少的劳动力来满足工作的需要?产品生产计划:合理利用人力、物力、财力等,使获利最大?套裁下料:如何在保证生产的条件下,下料最少?配料问题:在原料供应量的限制下如何获取最大利润?投资问题:从投资项目中选取方案,使投资回报最大?运输问题:如何制定调运方案,使总运费最小?这样的问题常常可以化成或近似地化成“线性规划”(Linear Programming, 简记为LP)问题。
线性规划所研究的是:在一定条件下,合理安排人力物力等资源,使经济效果达到最好。
一般地,求线性目标函数在线性约束条件下的最大值或最小值的问题,统称为线性规划问题[2]。
利用线性规划我们可以解决很多问题,例如上述人力资源分配、计划安排、套裁下料等诸多方面的问题,在本文的后面我们将用线性规划方法对企业在生产中的具体问题进行探讨。
2.线性规划的模型线性规划[2]是运筹学的一个重要分支。
自1947年丹捷格(G. B. Dantzig)提出了一般线性规划问题求解的方法——单纯形法之后,线性规划在理论上趋向成熟,在实用中日益广泛与深入。
特别是在电子计算机能处理成千上万个约束条件和决策的线性规划问题之后,线性规划的适用领域更为广泛了,它已是现代科学管理的重要手段之一了。
线性规划在工商管理中的应用

线性规划在工商管理中的应用
一、引言
线性规划是一种数学优化方法,可以帮助在给定约束条件下找到最优解,其在工商管理中有着广泛的应用。
本文将探讨线性规划在工商管理中的具体应用情况。
二、供应链管理中的线性规划应用
供应链管理是工商管理中一个重要的领域,线性规划可以帮助优化供应链中的货物流动和库存管理。
通过优化运输路线和库存水平,企业可以降低成本,提高效率。
三、生产计划中的线性规划应用
线性规划可以帮助企业制定最优生产计划,平衡生产能力和市场需求之间的关系。
通过合理安排生产资源和生产顺序,企业可以实现生产成本最小化和生产效率最大化。
四、营销策略中的线性规划应用
在制定营销策略时,线性规划可以帮助企业确定最优的销售推广方式和渠道选择,以最大化收益。
通过考虑市场需求和销售成本等因素,企业可以制定更具有效果的营销策略。
五、人力资源管理中的线性规划应用
线性规划在人力资源管理中也有着重要的应用,例如员工排班和资源分配等方面。
通过线性规划方法,企业可以合理安排员工工作时间和工作任务,以提高员工效率和满足企业需求。
六、财务管理中的线性规划应用
在财务管理中,线性规划可以帮助企业进行财务规划和资金管理。
通过优化投资组合和资金分配,企业可以实现财务风险的最小化和资金利用效率的最大化。
结论
综上所述,线性规划在工商管理中有着广泛的应用,可以帮助企业优化决策和提高经营效率。
在实际运营中,企业可以结合线性规划方法,制定更科学合理的管理策略,从而实现经济效益的最大化。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
30
设司机和乘务人员分别在各时间段一开始时上班,并 连续工作八小时,问该公交线路怎样安排司机和乘务人员, 既能满足工作需要,又配备最少司机和乘务人员?
管理运筹学
1
§1 人力资源分配的问题
解:设 xi 表示第i班次时开始上班的司机和乘务人员数,
这样我们建立如下的数学模型。
目标函数: Min x1 + x2 + x3 + x4 + x5 + x6 约束条件:s.t. x1 + x6 ≥ 60
可得到 xi (i = 1,2,3,4,5) 的利润分别为 15、10、7、13、9
元。
管理运筹学
6
§2 生产计划的问题
通过以上分析,可建立如下的数学模型:
目标函数: Max 15x1 + 10x2 + 7x3 + 13x4 + 9x5 约束条件: 5x1 + 10x2 + 7x3 ≤ 8000
6x1 + 4x2 + 8x3 + 6x4 + 4x5 ≤ 12000 3x1 + 2x2 + 2x3 + 3x4 + 2x5 ≤ 10000
x1,x2,x3,x4,x5,x6,x7 ≥ 0
管理运筹学
4
§2 生产计划的问题
例3.某公司面临一个是外包协作还是自行生产的问题。 该公司生产甲、乙、丙三种产品,都需要经过铸造、机加 工和装配三个车间。甲、乙两种产品的铸件可以外包协作, 亦可以自行生产,但产品丙必须本厂铸造才能保证质量。 数据如表。问:公司为了获得最大利润,甲、乙、丙三种 产品各生产多少件?甲、乙两种产品的铸造中,由本公司 铸造和由外包协作各应多少件?
7x112 + 9x212 + 12x312 ≤ 10000 ( 设备 A2 )
6x121 + 8x221
≤ 4000
( 设备 B1 )
4x122
+ 11x322 ≤ 7000
( 设备 B2 )
7x123
≤ 4000
( 设备 B3 )
x111+ x112- x121- x122- x123 = 0 (Ⅰ产品在A、B工序加工的数量相等)
时间 星期日 星期一 星期二 星期三 星期四 星期五 星期六
所需售货员人数 28 15 24 25 19 31 28
管理运筹学
3
§1 人力资源分配的问题
解:设 xi ( i = 1,2,…,7)表示星期一至日开始休息
的人数,这样我们建立如下的数学模型。
目标函数: Min x1 + x2 + x3 + x4 + x5 + x6 + x7 约束条件:s.t. x1 + x2 + x3 + x4 + x5 ≥ 28
工,但对B工序,只能在B1设备上加工;Ⅲ只能在A2与B2设 备上加工。数据如表。问:为使该厂获得最大利润,应如
何制定产品加工方案?
设备
A1 A2 B1 B2 B3 原料(元/件) 售价(元/件)
产品单件工时
Ⅰ
Ⅱ
Ⅲ
5
10
7
9
12
6
8
4
11
7
0.25 0.35 0.50
1.25 2.00 2.80
设备的 有效台时
6000 10000 4000 7000 4000
满负荷时的 设备费用
300 321 250 783 200
管理运筹学
8
§2 生产计划的问题
解:设 xijk 表示第 i 种产品,在第 j 种工序上的第 k 种设备上加工的
数量。建立如下的数学模型:
s.t. 5x111 + 10x211
≤ 6000
( 设备 A1 )
x2 + x3 + x4 + x5 + x6 ≥ 15 x3 + x4 + x5 + x6 + x7 ≥ 24 x4 + x5 + x6 + x7 + x1 ≥ 25 x5 + x6 + x7 + x1 + x2 ≥ 19 x6 + x7 + x1 + x2 + x3 ≥ 31 x7 + x1 + x2 + x3 + x4 ≥ 28
x211+ x212- x221
= 0 (Ⅱ产品在A、B工序加工的数量相等)
x312
- x322
= 0 (Ⅲ产品在A、B工序加工的数量相等)
xijk ≥ 0 , i = 1,2,3; j = 1,2; k = 1,2,3
管理运筹学
9
x1,x2,x3,x4,x5 ≥ 0
管理运筹学
7
§2 生产计划的问题
例4.永久机械厂生产Ⅰ、Ⅱ、Ⅲ三种产品,均要经过A、B两
道工序加工。设有两种规格的设备A1、A2能完成 A 工序; 有三种规格的设备B1、B2、B3能完成 B 工序。Ⅰ可在A、B 的任何规格的设备上加工;Ⅱ 可在任意规格的A设备上加
§1 人力资源分配的问题
例1.某昼夜服务的公交线路每天各时间段内所需司机 和乘务人员数如下:
班次
时间
所需人数
1
6:00 —— 10:00
60
2 10:00 —— 14:00
70
3 14:00 —— 18:00
60
4 18:00 —— 22:00
50
5
22:00 —— 2:00
20
6
2:00 —— 6:00
x1 + x2 ≥ 70 x2 + x3 ≥ 60 x3 + x4 ≥ 50 x4 + x5 ≥ 20 x5 + x6 ≥ 30 x1,x2,x3,x4,x5,x6 ≥ 0
管理运筹学
2
§1 人力资源分配的问题
例2.一家中型的百货商场,它对售货员的需求经过统 计分析如下表所示。为了保证售货人员充分休息,售货人 员每周工作5天,休息两天,并要求休息的两天是连续的。 问应该如何安排售货人员的作息,既满足工作需要,又使 配备的售货人员的人数最少?
种产品的件数。
求 xi 的利润:利润 = 售价 - 各成本之和
产品甲全部自制的利润
=23-(3+2+3)=15
产品甲铸造外协,其余自制的利润 =23-(5+2+3)=13
产品乙全部自制的利润
=18-(5+1+2)=10
产品乙铸造外协,其余自制的利润 =18-(6+1+2)=9
产品丙的利润
=16-(4+3+2)=7
甲
乙
丙
资源限制
铸造工时(小时/件)
5
10
7
8000
机加工工时(小时/件)
6
4
8
12000
装配工时(小时/件)
3
2
2
10000
自产铸件成本(元/件)
3
5
4
外协铸件成本(元/件)
5
6
--
机加工成本(元/件)
2
1
3
装配成本(元/件价(元/件)
23
18
16
管理运筹学
5
§2 生产计划的问题
解:设 x1,x2,x3 分别为三道工序都由本公司加工的甲、乙、丙三种 产品的件数,x4,x5 分别为由外协铸造再由本公司加工和装配的甲、乙两
