硬化指数测试研究方法
合集下载
金属薄板带应变硬化指数和厚向异性指数测定方法
（） ３ 诊断功能：该功能是帮助操作者判断故 障的类型与部位， 找到排除故障的途径及方法，确 保整个光谱分析系统是否正常运行。 （） ４ 数据库管理及计算功能： 数据库可以存 储数百个标准样品的成千上万个标准含量，以及近 百条校准曲线， 数百个钢种的技术标准， 数千个试 样分析结果。另外如Ｄ 等，还存有数百条分析 Ｖ６ －
Ｘ一ｎ ；Ｉ ； ｅ 鱿 Ｉ； 一ｎ ａ
在数据对的选取上， 力值最小的数据点应大于 材料的屈服点； 力值最大的数据点应尽可能接近材
料的最大强度值。 曲线拟合法测得的 ｎ 值因采用试验数据多点
当； 时，材料宽度方向比厚度方向容易产生变 ＞１ 形，即意味材料不易变薄或变厚。在拉深变形中加 大植 ， 板料宽度方向较厚度方向易于变形， 毛坯 的变形区切向收缩而不易起皱失稳；毛坯的传力区 其厚度方向不易减薄而导致破裂失稳， 有利于提高
向异性指数ｒ 的测定方法简介如下。 ｌ 直
Ｉ 应变硬化指数月 值的测定 应变硬化指数 ｎ 值的物理意义，是指材料均 匀变形的能力。ｎ值大则意味着材料加工硬化严 重，材料的变形易于从变形区向未变形区、从大变 形区向小变形区传递， 宏观表现为材料应变分布的 均匀性好，不易进人分散失稳。ｎ 值对伸长类变形
的数理统计、 月报表、日 报表及各种分类作表等， 还有为现场提供加料计算、产量统计、 原材料消耗 统计 、成本和利润统计等。极大的满足了用户需
要。
当然，随着信息化时代的到来， 光谱分析数据 的网络化已在很多企业应用， 给企业带来了很大效 益。只有认真的总结光谱的应用知识， 才可以使光 谱技术得到更进一步的发展。
一
了 使试验数据尽可能接近失稳点 。Ｂ Ｂ Ｚ 和 相差较小； 另一 为了 方面 使取得的 数据不致太 靠近， 和 ３ 典 Ｂ 相
动态的动脉硬化指数的应用及意义
鉴别诊断
动态动脉硬化指数可以辅助鉴别心 血管疾病与其他疾病，提高诊断的 准确性。
指导心血管疾病的治疗方案
个体化治疗
根据动态动脉硬化指数的检测结 果，可以为患者制定个体化的治 疗方案，针对不同的血管情况和 疾病阶段，选择合适的药物和治
疗措施。
监测治疗效果
动态动脉硬化指数可以实时监测 治疗效果，及时调整治疗方案， 提高治疗效果和患者的生活质量
02
评估治疗效果
ABI可以评估药物治疗和康复治疗的效果，有助于医生制定更加精准的
治疗方案。
03
指导生活方式
ABI可以指导患者调整生活方式，如控制饮食、适当运动等，的方面
标准化测量方法
目前ABI的测量方法尚未完全统一，需要进一步研究和标准化，以 提高测量的准确性和可重复性。
评估年轻人的风险
目前的研究主要集中在中老年人群体，对于年轻人尤其是高危人群 的研究仍不够充分，需要加强这方面的研究。
结合其他指标
ABI可以作为心血管疾病的预测指标之一，但还需要结合其他指标 如血脂、血糖等综合评估，以提高预测的准确性。
THANKS
感谢观看
AI还可以用于评估治疗效果和监测疾病的进展。例如，通 过治疗降低AI值可以降低心血管疾病的风险。
02
动态动脉硬化指数的应用
诊断心血管疾病
辅助诊断
动态动脉硬化指数可以辅助诊断心血管 疾病，特别是对于早期无症状的患者。
VS
区分类型
动态动脉硬化指数可以帮助医生区分动脉 硬化的类型，如动脉粥样硬化、动脉中膜 硬化等。
动态的动脉硬化指数的应用 及意义
2023-11-10
• 动脉硬化指数简介 • 动态动脉硬化指数的应用 • 动态动脉硬化指数的意义 • 动态动脉硬化指数的未来展望 • 总结
动态动脉硬化指数可以辅助鉴别心 血管疾病与其他疾病，提高诊断的 准确性。
指导心血管疾病的治疗方案
个体化治疗
根据动态动脉硬化指数的检测结 果，可以为患者制定个体化的治 疗方案，针对不同的血管情况和 疾病阶段，选择合适的药物和治
疗措施。
监测治疗效果
动态动脉硬化指数可以实时监测 治疗效果，及时调整治疗方案， 提高治疗效果和患者的生活质量
02
评估治疗效果
ABI可以评估药物治疗和康复治疗的效果，有助于医生制定更加精准的
治疗方案。
03
指导生活方式
ABI可以指导患者调整生活方式，如控制饮食、适当运动等，的方面
标准化测量方法
目前ABI的测量方法尚未完全统一，需要进一步研究和标准化，以 提高测量的准确性和可重复性。
评估年轻人的风险
目前的研究主要集中在中老年人群体，对于年轻人尤其是高危人群 的研究仍不够充分，需要加强这方面的研究。
结合其他指标
ABI可以作为心血管疾病的预测指标之一，但还需要结合其他指标 如血脂、血糖等综合评估，以提高预测的准确性。
THANKS
感谢观看
AI还可以用于评估治疗效果和监测疾病的进展。例如，通 过治疗降低AI值可以降低心血管疾病的风险。
02
动态动脉硬化指数的应用
诊断心血管疾病
辅助诊断
动态动脉硬化指数可以辅助诊断心血管 疾病，特别是对于早期无症状的患者。
VS
区分类型
动态动脉硬化指数可以帮助医生区分动脉 硬化的类型，如动脉粥样硬化、动脉中膜 硬化等。
动态的动脉硬化指数的应用 及意义
2023-11-10
• 动脉硬化指数简介 • 动态动脉硬化指数的应用 • 动态动脉硬化指数的意义 • 动态动脉硬化指数的未来展望 • 总结
动脉硬化指数参考表
风险评估
AI可用于评估个体心血管疾病的风险，以指导预防和治疗策略。 AI可以作为心血管疾病风险评估的补充指标，以弥补传统危险因素评估的不足。
AI可用于识别高危个体，以便早期采取干预措施，降低心血管疾病的发生率。
预防与治疗建议
基于AI的风险评估结果，应采 取积极的预防措施，如改善生 活方式、控制危险因素等。
低风险（AIx＜10%） 中风险（10%≤AIx＜20%） 高风险（AIx≥20%）
测量与评估参考表
测量方法
采用脉搏波传导速度（PWV）和血压测量结合的方法，计算出AIx值。
评估指标
根据AIx值，结合年龄、性别、血压、血脂等指标进行综合评估。
THANKS
感谢观看
通过测量和计算动脉硬化指数，可以早期发现血管病变，及时采取措施预防和治 疗心血管疾病。
计算方法
动脉硬化指数的计算公式为：AI = (收缩压 - 舒张压) / (收缩 压 + 舒张压) × 100%。
在实际操作中，需要测量受试者的收缩压和舒张压，并按照 上述公式计算得出AI值。
正常范围
根据目前普遍接受的标准，动脉硬化指数的正常范围为010%。
CT和MRI扫描法
通过CT或MRI扫描，观察血管壁的形态和结构，判断动脉硬化的 程度。
评估标准
01
02
03
正常范围
动脉硬化指数低于10， 提示动脉硬化风险较低。
偏高
动脉硬化指数在10-14之 间，提示动脉硬化风险偏 高。
高风险
动脉硬化指数高于14， 提示动脉硬化风险较高， 需要进一步检查和干预。
注意事项
对于不同人群，如孕妇、老年人或患有特定疾 病的人群，动脉硬化指数的参考值和解释可能 有所不同，需要进一步的研究来确定。
金属材料形变硬化指数的测定
Ri （MPa） Ai (％) i （MPa） i （％）
1
331.24
0.0838
359.00
0.0804
2
383.17
0.1177
428.27
0.1113
3
419.05
0.1561
484.46
0.1451
4
442.37
0.1994
530.58
0.1818
5
454.77
0.2431
565.32
0.2176
由 σ kε2
得 lgσ =lgκ +nlgε
硬化指数（n）为该线性方程的斜率拟合曲线如下图 3-2 所示：
计算结果
N
K（MPa） V(n)
Q
6
20.95
0.219
0.995
线性方程的斜率拟合曲线 3-2：
拟合曲线图 3-2
时效铝合金的形变硬化指数
d=8.94mm
So
d 2 4
62.90 m m2
实验名称
金属材料形变硬化指数（n）的测定 金属材料形变硬化指数（n）的测定
实验目的
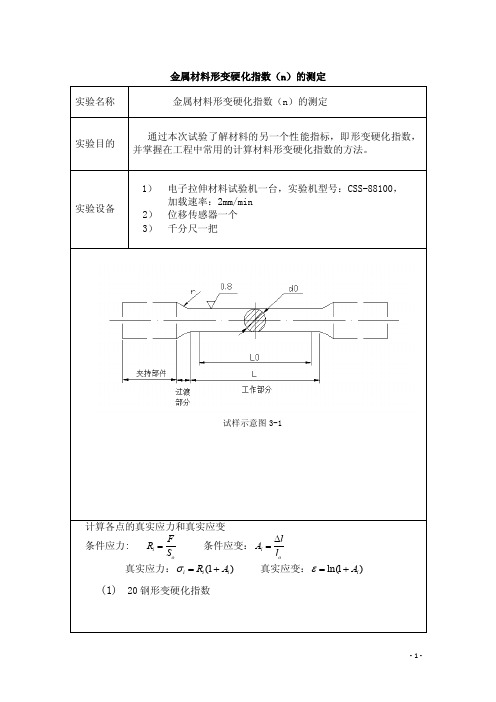
通过本次试验了解材料的另一个性能指标，即形变硬化指数， 并掌握在工程中常用的计算材料形变硬化指数的方法。
实验设备
1） 电子拉伸材料试验机一台，实验机型号：CSS-88100， 加载速率：2mm/min
2） 位移传感器一个 3） 千分尺一把
ΣΣ ΣΣ 标准偏差
S (n)
N
N Yi
i 1 N
N Xi
i 1
2 2
-
N
( Yi )2
i 1 N
( Xi )2
i 1
动态的动脉硬化指数的应用及意义
02
动态的动脉硬化指数的测量方 法
测量原理
基于脉搏波传导速度（PWV）的测量
动态的动脉硬化指数是通过测量脉搏波传导速度来评估动脉硬化程度的一种方法。脉搏波是心脏收缩 时产生的压力波，它随着血液流动，通过血管壁传播到全身。动脉硬化会导致血管壁变硬，使得脉搏 波传播速度加快，因此通过测量脉搏波的传播速度可以评估动脉硬化的程度。
评估动脉壁的硬度
除了PWV，动态的动脉硬化指数还可以通过测量其他参数来综合评估动脉壁的硬度，如血压、血脂水 平、血糖水平等。这些参数可以提供更全面的信息，帮助医生更准确地评估患者的动脉硬化程度。
测量方法与步骤
• 测量设备：动态的动脉硬化指数的测量设备包括血压计、 心电图机、超声设备等。
测量方法与步骤
引言
动脉硬化的定义与危害
01
动脉硬化是一种心血管疾病，主 要涉及动脉血管壁的硬化和增厚 ，导致血管弹性降低，影响心脏 和大脑的血液供应。
02
动脉硬化的危害包括心脏病、中 风、肾功能不全等多种并发症， 严重影响患者的生命质量和预期 寿命。
动态的动脉硬化指数的提
动态的动脉硬化指数是一种新型的检 测指标，旨在评估动脉硬化的程度和 预测心血管事件的风险。
对公共卫生政策的启示
加强健康教育
通过加强健康教育，提高公众对动脉硬化的 认识和重视程度，促进预防和控制工作的开 展。
制定针对性的防控策略
根据不同地区、不同人群的实际情况，制定针对性 的防控策略，提高防控效果。
加强科研和技术支持
加强科研和技术支持，不断探索新的预防和 控制方法，为公共卫生政策的制定提供科学 依据。
THANKS
谢谢您的观看
在疾病控制中的应用
01
AZ31镁合金板单向拉伸应变硬化指数的试验测定
力与真实应变的函数 关 系，反 映 了 材 料 的 应 变 强 化 能 力，表征材料在塑性 变 形 时 的 硬 化 强 度。 金 属 的ｎ 值 越大，其硬 化 效 应 越 明 显，抗 局 部 颈 缩 失 稳 的 能 力 越 强 ，这 样 ，变 形 就 可 以 不 断 地 扩 展 ，使 变 形 更 均 匀 ，成 形 极限越高。在大多数情况下，ｎ 值越大，板 料 的 局 部 应 变 能 力 越 强 ，失 稳 极 限 应 变 越 大 ，应 变 分 布 越 趋 向 均 匀 化，板料的总体成 形 能 力 越 高。 当 制 件 以 拉 伸 变 形 为 主要成形方式时，材料 的ｎ 值 小，变 形 不 均 匀，变 形 部 位来不及迅速硬化而 导 致 裂 纹；而ｎ 值 大 说 明 材 料 的 拉 伸 失 稳 点 来 的 较 晚 ，不 易 出 现 局 部 的 集 中 变 形 ，可 获 得较大的极限变形程度。当制件以压延变形为主要成 形方式时，材料的ｎ 值 大，应 变 均 匀 化 的 能 力 就 强，危 险断面承载能力就高。对深冲或薄板类零件都要求材 料的ｎ 值达到规定值 之 上，以 便 材 料 在 加 工 过 程 中 应 变能够均 匀 化，从 而 不 会 因 为 局 部 变 形 集 中 而 报 废。 对于理想弹性 体，ｎ＝１；对 于 理 想 塑 性 体，ｎ＝０；对 于 大 多 数 金 属 材 料 而 言 ，ｎ＝０．１～０．５。
真实应变）的数学关系接近幂函数关系 ： ［５］
ｓ＝Ｃｅｎ ．
（８）
其中：Ｃ 为应变强化系数。对式（８）等号两边取自然对
数 ，得 ：
Ｙ＝ｎＸ＋ｌｎＣ ．
（９）
其中
Ｙ＝ｌｎｓ＝ｌｎ［σ（１＋ε）］．
（１０）
Ｘ＝ｌｎｅ＝ｌｎ［ｌｎ（１＋ε）］．
（１１）
真实应变）的数学关系接近幂函数关系 ： ［５］
ｓ＝Ｃｅｎ ．
（８）
其中：Ｃ 为应变强化系数。对式（８）等号两边取自然对
数 ，得 ：
Ｙ＝ｎＸ＋ｌｎＣ ．
（９）
其中
Ｙ＝ｌｎｓ＝ｌｎ［σ（１＋ε）］．
（１０）
Ｘ＝ｌｎｅ＝ｌｎ［ｌｎ（１＋ε）］．
（１１）
硬化指数测试分析方法
基于GB/T 5028-2008的硬化指数n检测分析方法原理简介均匀变形阶段（变形硬化）右上图为典型的塑性材料常温塑形拉伸应力-应变曲线，这种曲线为工程应力-应变曲线。
但是，在图中的均匀变形阶段，工程应力-应变曲线并非试样中的真实应力，真实应力-应变如右下图。
在均匀塑形变形部分，真实应力-真实塑形应变遵循公式：等号两边取对数：既为：在均匀塑形变形部分，真实应力-真实塑形应变遵循公式：等号两边取对数：既为：线性函数形式，其中：问题转化要想获得的函数，需要几组（x, y ），通过线性回归，获得A 、B 的取值。
既：需要获取几组（σtrue , εtrue ）数据，真实应力-应变可以通过常温拉伸试验获得。
常温拉伸测试获得的通常是工程应力-应变曲线及相关数据包。
而真实应力、应变可由下列公式得出：因为σE≪1，式可用作：线性回归使用“最小二乘法”获得线性回归函数，可由Excel 实现。
右侧线性回归举例中：y = 1.0429x -0.06670123456701234567线性回归X 值123456Y 值1 1.9 3.2 4.2 4.9 6.3注意事项为保证计算出的硬化指数准确性，还需要注意几点：①拉伸试验机状态级别满足GB/T 16825.1一级要求；②拉伸试验过程要满足GB/T 288要求；③均匀塑形表型区间和散点的选取；④多次测量校验；⑤人工计算方式和自动测量方式相互校验。
以上便可得到材料的：硬化指数n常函数C。
【15】拉伸变形应变硬化指数的实验测量及其精细分析
=
icivi
i =1 n
.
civi
(24)
i =0
把 (24) 式及初始标距长度 l0 和瞬时标距长度 l 代入 (11) 式 ,再把 l 和 v 转化为ε,便得
nε(ε) = φ2 (ε) .
(25)
nv :在任意一条恒 v 的 p2l 曲线上 ,因ε= v/ l ,所以用计算机模拟 p2ε可求得相应的多项式
i =1 n
.
biεi
(20)
i =0
把 (20) 式及对应的初始长度 l0 和瞬时长度 l 代入 (12) 式 , 利用 l = v/ε和ε= lg ( l/ l0) , 在
某恒 v 条件下 ,均可将 l 和ε转化为ε的函数 ,于是便得
nv (ε) = <1 (ε) .
(21)
np :作一条恒 p1 与一组恒ε(ε1 ,ε2 , …) 的 p2l 曲线相交 , 得 l1 , l2 , …, 将 l0 和 l1 , l2 …代入
只要在拉伸实验中记录了材料均匀变形的一组恒ε(ε1 ,ε2 , …) 的 p2l 曲线 , 便可同时测得 nε, nv 和 np.
传统方法 (这是目前普遍采用的测量方法) : nε:在任意一条恒ε的 p2l 曲线上 ,可直接测得 ( p1 , p2) , ( l1 , l2) , 因 v1 =ε1 l1 , v2 =ε1 l2 , 所 以在恒ε的 p2l 曲线上又可直接测得 v1 和 v2. 把 ( p1 , p2) , ( v1 , v2) 试样标距初始长度 l0 和瞬 时长度 l1 及ε1 = ln ( l1/ l0) 代入 (14) 式 ,便可求得在恒ε条件下对应于ε1 的 nε. nv :在两条相邻恒 ε的 p2l 曲线上 , 利用 v = lε的关系 , 在恒速度 v 的条件下 , 可测得 ( p1 ,ε1) , ( p2 ,ε2) 和ε1 = ln ( l1/ l0) ,同理代入 (15) 式 ,便可求得在恒 v 条件下对应于ε1 的 nv . np :在一条恒ε的 p2l 曲线上 ,对应于恒 p1 ,便可与 p2l 曲线相交于确定的 l1 ,把 l0 和 l1 代 入 (13) 式 ,便得恒 p 条件下对应于ε1 的 np. 计算机模拟方法 :在以上的测量中 ,除 np 外 ,一则 nε和 nv 的测量中都用了差分公式 ,这就必 然存在理论误差 ,再则都是手工测量 ,这也必然产生因人而异的随机误差. 若用计算机模拟法测 量 ,均可基本消除这些误差. 因为如果模拟 lg p ,lgv 和 lgε的误差为Δp ,Δv 和Δε,而对 p , v 和ε 引起的误差分别为 10Δp ,10Δv和 10Δε,所以模拟 p , v 和ε,要比模拟 lg p ,lg v 和 lgε更为精确. nε:在任一条恒ε的 p2l 曲线上 ,利用 v =εl ,可得 p2v 模拟多项式
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
基于GB/T 5028-2008的硬化指数n检测分析方法
原理简介
均匀变形阶段（变形硬化）
右上图为典型的塑性材料常温塑形拉伸应力-应变曲线，这种曲线为工程应力-应变曲线。
但是，在图中的均匀变形阶段，工程应力-应变曲线并非试样中的真实应力，真实应力-应变如右下图。
在均匀塑形变形部分，真实应力-真实塑形应变遵循公式：
等号两边取对数：
既为：
在均匀塑形变形部分，真实应力-真实塑形应变遵循公式：
等号两边取对数：
既为：
线性函数形式，其中：
问题转化
要想获得的函数，需要几组（x, y ），通过线性
回归，获得A 、B 的取值。
既：需要获取几组（σtrue , εtrue ）数据，真实应力-应变可以通过常温拉伸试验获得。
常温拉伸测试获得的通常是工程应力-应变曲线及相关数据包。
而真实应力、应变可由下列公式得出：
因为σE
≪1，式可用作：
线性回归
使用“最小二乘法”获得线性回归函数
，可由Excel 实现。
右侧线性回归举例中：
y = 1.0429x -0.0667
01
2345670
1
2
3
4
5
6
7
线性回归
X 值123456Y 值1 1.9 3.2 4.2 4.9 6.3
注意事项
为保证计算出的硬化指数准确性，还需要注意几点：
①拉伸试验机状态级别满足GB/T 16825.1一级要求；
②拉伸试验过程要满足GB/T 288要求；
③均匀塑形表型区间和散点的选取；
④多次测量校验；
⑤人工计算方式和自动测量方式相互校验。
以上便可得到材料的：
硬化指数n
常函数C。